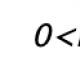Persamaan kuadratik... Diskriminasi. Penyelesaian, contoh.
Perhatian!
Ada tambahan
bahan dalam Bahagian Khas 555.
Bagi mereka yang sangat "tidak sangat ..."
Dan bagi mereka yang "sangat ...")
Jenis persamaan kuadratik
Apakah Persamaan Kuadratik? Bagaimana rupanya? Dari segi persamaan kuadratik kata kunci adalah "segi empat sama". Ia bermaksud bahawa dalam persamaan semestinya mesti ada x kuasa dua. Selain dia, persamaannya mungkin (atau mungkin tidak!) Hanya x (pada kekuatan pertama) dan hanya nombor (ahli percuma). Dan tidak boleh ada x hingga darjah lebih besar daripada dua.
Secara matematik, persamaan kuadratik adalah persamaan bentuk:
Di sini a, b dan c- beberapa nombor. b dan c- sama sekali, tapi a- apa-apa selain sifar. Sebagai contoh:

Di sini a =1; b = 3; c = -4

Di sini a =2; b = -0,5; c = 2,2

Di sini a =-3; b = 6; c = -18
Baiklah, anda mendapat idea ...
Dalam persamaan kuadratik ini, di sebelah kiri, terdapat set penuh ahli. X kuasa dua dengan pekali a, x ke daya pertama dengan pekali b dan istilah percuma dengan.
Persamaan kuadratik tersebut disebut penuh.
Bagaimana jika b= 0, apa yang kita dapat? Kami ada X akan hilang pada darjah satu. Ini berlaku dari pendaraban dengan sifar.) Ternyata, sebagai contoh:
5x 2 -25 = 0,
2x 2 -6x = 0,
-x 2 + 4x = 0
Dan lain-lain. Dan jika kedua-dua pekali tersebut, b dan c sama dengan sifar, masih lebih sederhana:
2x 2 = 0,
-0.3x 2 = 0
Persamaan seperti itu, di mana ada sesuatu yang hilang, disebut persamaan kuadratik yang tidak lengkap. Yang agak logik.) Harap maklum bahawa kuasa dua x terdapat dalam semua persamaan.
By the way, mengapa a tidak boleh sifar? Dan anda menggantikan a sifar.) X di petak akan hilang dari kami! Persamaan menjadi linear. Dan ia diputuskan dengan cara yang sama sekali berbeza ...
Ini semua jenis utama persamaan kuadratik. Lengkap dan tidak lengkap.
Menyelesaikan persamaan kuadratik.
Menyelesaikan persamaan kuadratik yang lengkap.
Persamaan kuadratik mudah diselesaikan. Mengikut formula dan peraturan yang jelas dan sederhana. Pada peringkat pertama, perlu membawa persamaan yang diberikan ke bentuk standard, iaitu untuk melihat:
Sekiranya persamaan sudah diberikan kepada anda dalam bentuk ini, anda tidak perlu melakukan peringkat pertama.) Perkara utama adalah menentukan semua pekali dengan betul, a, b dan c. Rumus untuk mencari punca persamaan kuadratik seperti ini:

Ungkapan di bawah tanda akar dipanggil diskriminasi... Tetapi mengenai dia - di bawah. Seperti yang anda lihat, untuk mencari x, kami menggunakan hanya a, b dan c.
Mereka. pekali dari persamaan kuadratik. Ganti nilai dengan berhati-hati a, b dan c ke dalam formula ini dan hitung. Pengganti dengan tanda-tanda anda!
Contohnya, dalam persamaan:

a =1; b = 3; c= -4. Oleh itu, kami menulis:
Contohnya hampir dapat diselesaikan:


Inilah jawapannya.
Semuanya sangat sederhana. Menurut anda, apa yang mustahil untuk disalah anggap? Baiklah, bagaimana ...
Kesalahan yang paling biasa adalah kekeliruan dengan tanda makna. a, b dan c... Sebaliknya, bukan dengan tanda-tanda mereka (di mana harus bingung?), Tetapi dengan penggantian nilai negatif dalam formula untuk mengira punca. Di sini, notasi terperinci formula dengan penjimatan nombor tertentu. Sekiranya terdapat masalah pengiraan, berbuat demikian!
Katakan anda perlu menyelesaikan contoh ini:

Di sini a = -6;
b = -5;
c = -1
Katakan anda tahu bahawa anda jarang mendapat jawapan pada kali pertama.
Jangan malas. Anda akan memerlukan 30 saat untuk menulis baris tambahan dan jumlah kesalahan akan menurun dengan mendadak... Oleh itu, kami menulis secara terperinci, dengan tanda kurung dan tanda:


Nampaknya sukar untuk melukis dengan teliti. Tapi nampaknya begitu. Cuba ia. Baik, atau pilih. Mana yang lebih baik, pantas, atau betul? Selain itu, saya akan membuat anda bahagia. Selepas beberapa ketika, tidak perlu melukis semuanya dengan teliti. Ia akan berjaya dengan sendirinya. Terutama jika anda menggunakan teknik amali, yang dijelaskan di bawah. Contoh jahat ini dengan banyak kekurangan dapat diselesaikan dengan mudah dan tanpa kesalahan!
Tetapi, selalunya, persamaan kuadratik kelihatan sedikit berbeza. Contohnya, seperti ini:

Adakah anda mendapat tahu?) Ya! ia persamaan kuadratik yang tidak lengkap.
Menyelesaikan persamaan kuadratik yang tidak lengkap.
Mereka juga dapat diselesaikan dengan menggunakan formula umum. Anda hanya perlu mengetahui dengan tepat apa yang sama dengannya a, b dan c.
Adakah anda sudah mengetahuinya? Pada contoh pertama a = 1; b = -4; a c? Dia sama sekali tidak ada! Ya, betul, betul. Dalam matematik, ini bermaksud c = 0
! Itu sahaja. Ganti sifar dalam formula dan bukannya c, dan kita akan berjaya. Begitu juga dengan contoh kedua. Tidak ada yang kita ada di sini dengan, a b !
Tetapi persamaan kuadratik yang tidak lengkap dapat diselesaikan dengan lebih mudah. Tanpa formula. Pertimbangkan persamaan tidak lengkap pertama. Apa yang boleh anda lakukan di sebelah kiri? Anda boleh meletakkan tanda x dari kurungan! Mari kita keluarkan.

Dan apa itu? Dan hakikat bahawa produk itu sama dengan sifar jika, dan hanya jika, apabila salah satu faktornya sama dengan sifar! Tidak percaya? Oleh itu, fikirkan dua nombor bukan sifar yang, apabila didarabkan, akan memberikan sifar!
Tidak berfungsi? Itu dia ...
Oleh itu, kita boleh menulis dengan yakin: x 1 = 0, x 2 = 4.
Semuanya. Ini akan menjadi punca persamaan kita. Kedua-duanya sesuai. Semasa menggantikan salah satu dari mereka ke dalam persamaan asal, kita mendapat identiti yang betul 0 = 0. Seperti yang anda lihat, penyelesaiannya jauh lebih mudah daripada menggunakan formula umum. Saya akan perhatikan, by the way, X mana yang pertama, dan mana yang kedua - sama sekali tidak peduli. Adalah mudah untuk menuliskannya mengikut urutan, x 1- apa yang kurang, dan x 2- apa yang lebih.
Persamaan kedua juga dapat diselesaikan secara sederhana. Gerakkan 9 ke sebelah kanan. Kita mendapatkan:
Masih ada untuk mengekstrak akar dari 9, dan itu sahaja. Ia akan berubah:

Juga dua akar .
x 1 = -3, x 2 = 3.
Ini adalah bagaimana semua persamaan kuadratik yang tidak lengkap diselesaikan. Sama ada dengan tanda kurung x, atau pemindahan sederhana nombor di sebelah kanan, diikuti dengan pengekstrakan akar.
Sangat sukar untuk mengelirukan teknik ini. Hanya kerana dalam kes pertama, anda harus mengekstrak akar dari x, yang entah bagaimana tidak dapat difahami, dan dalam kes kedua tidak ada apa-apa yang perlu dikeluarkan dari tanda kurung ...
Diskriminasi. Formula diskriminasi.
Kata sihir diskriminasi
! Seorang pelajar sekolah menengah yang jarang ditemui tidak pernah mendengar perkataan ini! Ungkapan "memutuskan melalui diskriminasi" adalah meyakinkan dan meyakinkan. Kerana tidak perlu menunggu muslihat kotor dari orang yang diskriminasi! Ia mudah digunakan dan bebas masalah.) Saya ingat formula penyelesaian yang paling umum ada persamaan kuadratik:

Ungkapan di bawah tanda akar disebut diskriminan. Biasanya diskriminasi dilambangkan dengan huruf D... Formula diskriminasi:
D = b 2 - 4ac
Dan apa yang luar biasa mengenai ungkapan ini? Mengapa ia layak mendapat nama khas? Apa maksud diskriminasi? Lagipun -b, atau 2a dalam formula ini mereka tidak menyebut secara khusus ... Huruf dan huruf.
Inilah perkara. Semasa menyelesaikan persamaan kuadratik menggunakan formula ini, adalah mungkin hanya tiga kes.
1. Diskriminasi itu positif. Ini bermaksud anda boleh mengekstrak akarnya. Akar yang baik diekstrak, atau buruk - soalan lain. Yang penting adalah apa yang diekstrak pada asasnya. Maka persamaan kuadratik anda mempunyai dua punca. Dua penyelesaian berbeza.
2. Diskriminasi adalah sifar. Maka anda mempunyai satu penyelesaian. Oleh kerana penambahan-pengurangan sifar dalam pengangka tidak mengubah apa-apa. Tegasnya, ini bukan satu akar, tetapi dua serupa... Tetapi, dalam versi yang dipermudah, adalah kebiasaan untuk dibincangkan satu penyelesaian.
3. Diskriminasi adalah negatif. Dari nombor negatif punca kuasa dua tidak diekstrak. Baiklah. Ini bermaksud bahawa tidak ada jalan penyelesaian.
Secara jujur, dengan penyelesaian mudah persamaan kuadratik, pengertian tentang diskriminasi tidak begitu diperlukan. Kami menggantikan nilai pekali ke dalam formula, tetapi kami mengira. Di sana, semuanya berubah dengan sendirinya, dan dua akar, dan satu, dan bukan satu. Namun, ketika menyelesaikan tugas yang lebih kompleks, tanpa pengetahuan makna dan formula diskriminasi tidak cukup. Terutama - dalam persamaan dengan parameter. Persamaan seperti itu adalah aerobatik pada Peperiksaan Negeri dan Ujian Negeri Bersatu!)
Jadi, cara menyelesaikan persamaan kuadratik melalui diskriminasi yang anda ingat. Atau telah belajar, yang juga tidak buruk.) Anda tahu cara mengenal pasti dengan betul a, b dan c... Kamu tahu bagaimana dengan penuh perhatian gantikannya dalam formula akar dan dengan penuh perhatian baca hasilnya. Anda mendapat idea bahawa kata kunci di sini adalah dengan penuh perhatian?
Buat masa ini, perhatikan amalan terbaik yang dapat mengurangkan kesilapan secara drastik. Yang sangat disebabkan oleh perhatian. ... Yang kemudian itu menyakitkan dan menghina ...
Penerimaan pertama
... Jangan malas membawanya ke bentuk standard sebelum menyelesaikan persamaan kuadratik. Apakah maksud ini?
Katakan, setelah beberapa transformasi, anda mendapat persamaan berikut:

Jangan tergesa-gesa untuk menulis formula akar! Anda pasti akan mencampurkan kemungkinan. a, b dan c. Bina contoh dengan betul. Pertama, X adalah kuasa dua, kemudian tanpa petak, kemudian anggota bebas. Seperti ini:

Dan sekali lagi, jangan tergesa-gesa! Kekurangan di hadapan x di dataran boleh membuat anda benar-benar sedih. Sangat mudah untuk melupakannya ... Menghilangkan tolak. Bagaimana? Ya, seperti yang diajarkan dalam topik sebelumnya! Anda harus mengalikan keseluruhan persamaan dengan -1. Kita mendapatkan:

Tetapi sekarang anda boleh menuliskan formula akarnya dengan selamat, menghitung diskriminasi dan melengkapkan contohnya. Buat sendiri. Anda harus mempunyai akar 2 dan -1.
Penerimaan yang kedua.
Periksa akarnya! Oleh teorema Vieta. Jangan risau, saya akan menerangkan semuanya! Memeriksa perkara terakhir persamaan. Mereka. yang kami tuliskan formula untuk akarnya. Sekiranya (seperti dalam contoh ini) pekali a = 1, memeriksa akarnya mudah. Ia cukup untuk menggandakannya. Anda harus mendapatkan ahli percuma, iaitu dalam kes kami, -2. Perhatikan, bukan 2, tetapi -2! Ahli percuma dengan tanda saya
... Sekiranya ia tidak berfungsi, maka ia sudah habis. Cari pepijat.
Sekiranya berjaya, anda perlu melipat akarnya. Pemeriksaan terakhir dan terakhir. Anda harus mendapat pekali b dengan sebaliknya
biasa. Dalam kes kami, -1 + 2 = +1. Dan pekali b yang sebelum x ialah -1. Jadi, semuanya betul!
Sangat disayangkan bahawa ini sangat mudah hanya untuk contoh di mana x kuasa dua adalah murni, dengan pekali a = 1. Tetapi sekurang-kurangnya dalam persamaan seperti itu, periksa! Semuanya kurang kesilapan akan.
Penerimaan ketiga
... Sekiranya anda mempunyai pekali pecahan dalam persamaan anda, hilangkan pecahan! Darabkan persamaan dengan penyebut biasa seperti yang dijelaskan dalam pelajaran "Bagaimana Menyelesaikan Persamaan? Transformasi yang Sama." Semasa bekerja dengan pecahan, untuk beberapa sebab, kesalahan cenderung muncul di ...
Ngomong-ngomong, saya berjanji akan mempermudah contoh jahat dengan banyak kekurangan. Tolong! Ini dia.

Agar tidak keliru dalam minus, kita mengalikan persamaan dengan -1. Kita mendapatkan:

Itu sahaja! Dengan senang hati membuat keputusan!
Jadi, untuk meringkaskan topik.
Nasihat praktikal:
1. Sebelum menyelesaikan, kami membawa persamaan kuadratik ke bentuk piawai, membinanya betul.
2. Sekiranya terdapat pekali negatif di hadapan x di petak, kita menghapuskannya dengan mengalikan keseluruhan persamaan dengan -1.
3. Sekiranya pekali pecahan, kita menghilangkan pecahan dengan mengalikan keseluruhan persamaan dengan faktor yang sesuai.
4. Jika x kuadrat adalah murni, pekali padanya sama dengan satu, penyelesaiannya dapat disahkan dengan mudah oleh teorema Vieta. Lakukannya!
Sekarang anda boleh membuat keputusan.)
Selesaikan persamaan:
8x 2 - 6x + 1 = 0
x 2 + 3x + 8 = 0
x 2 - 4x + 4 = 0
(x + 1) 2 + x + 1 = (x + 1) (x + 2)



Jawapan (dalam kekacauan):
x 1 = 0
x 2 = 5
x 1.2 =2
x 1 = 2
x 2 = -0.5
x - sebarang nombor
x 1 = -3
x 2 = 3
tiada jalan penyelesaian
x 1 = 0.25
x 2 = 0.5
Adakah semuanya sesuai? Baik! Persamaan kuadratik bukanlah sakit kepala anda. Tiga yang pertama bekerja, tetapi yang lain tidak? Maka masalahnya bukan dengan persamaan kuadratik. Masalahnya adalah dalam transformasi persamaan yang sama. Berjalan di pautan, ini berguna.
Tidak cukup bersenam? Atau tidak berfungsi sama sekali? Kemudian Bahagian 555 akan menolong anda. Di sana semua contoh ini disusun secara berasingan. Ditunjukkan yang utama kesilapan dalam penyelesaiannya. Sudah tentu, ia juga membincangkan penggunaan transformasi yang sama dalam penyelesaian pelbagai persamaan. Membantu banyak!
Sekiranya anda menyukai laman web ini ...
Ngomong-ngomong, saya ada beberapa laman web yang lebih menarik untuk anda.)
Anda boleh berlatih menyelesaikan contoh dan mengetahui tahap anda. Ujian pengesahan segera. Belajar - dengan minat!)
anda boleh berkenalan dengan fungsi dan derivatif.
|
5x (x - 4) = 0
5 x = 0 atau x - 4 = 0
x = ± √ 25/4
Tentu saja, setelah mengetahui bagaimana menyelesaikan persamaan darjah pertama, anda ingin bekerja dengan orang lain, khususnya, dengan persamaan darjah kedua, yang sebaliknya disebut kuadratik.
Persamaan kuadratik adalah persamaan jenis ax ² + bx + c = 0, di mana pemboleh ubahnya adalah x, nombor akan menjadi - a, b, c, di mana a tidak sama dengan sifar.
Sekiranya dalam persamaan kuadrat satu atau pekali lain (c atau b) sama dengan sifar, maka persamaan ini akan merujuk kepada persamaan kuadratik yang tidak lengkap.
Bagaimana menyelesaikan persamaan kuadratik yang tidak lengkap sekiranya pelajar hanya dapat menyelesaikan persamaan darjah satu setakat ini? Pertimbangkan persamaan kuadratik yang tidak lengkap pelbagai jenis dan kaedah mudah untuk menyelesaikannya.
a) Jika pekali c sama dengan 0, dan pekali b tidak sama dengan sifar, maka ax ² + bx + 0 = 0 diturunkan menjadi persamaan bentuk ax ² + bx = 0.
Untuk menyelesaikan persamaan seperti itu, anda perlu mengetahui formula untuk menyelesaikan persamaan kuadratik yang tidak lengkap, iaitu sebelah kiri faktorkannya dan kemudian gunakan syarat persamaan produk menjadi sifar.
Contohnya, 5x ² - 20x = 0. Faktorkan sisi kiri persamaan, sambil melakukan perkara biasa operasi matematik: mengeluarkan faktor sepunya dari tanda kurung
5x (x - 4) = 0
Kami menggunakan syarat bahawa produk sama dengan sifar.
5 x = 0 atau x - 4 = 0
Jawapannya ialah: akar pertama adalah 0; punca kedua ialah 4.
b) Jika b = 0, dan istilah bebas tidak sama dengan sifar, maka persamaan ax ² + 0x + c = 0 diturunkan menjadi persamaan bentuk ax ² + c = 0. Persamaan diselesaikan dengan dua cara : a) dengan memperluas polinomial persamaan di sebelah kiri menjadi faktor; b) menggunakan sifat aritmetik punca kuasa dua... Persamaan seperti itu diselesaikan dengan salah satu kaedah, misalnya:
x = ± √ 25/4
x = ± 5/2. Jawapannya: akar pertama ialah 5/2; akar kedua ialah - 5/2.
c) Jika b sama dengan 0 dan c sama dengan 0, maka ax ² + 0 + 0 = 0 akan menjadi persamaan bentuk ax ² = 0. Dalam persamaan tersebut, x akan sama dengan 0.
Seperti yang anda lihat, persamaan kuadratik yang tidak lengkap tidak boleh mempunyai lebih daripada dua punca.
Persamaan kuadratik sering muncul ketika menyelesaikan pelbagai masalah dalam fizik dan matematik. Dalam artikel ini kita akan melihat bagaimana menyelesaikan kesamaan ini secara universal "melalui diskriminasi". Contoh penggunaan pengetahuan yang diperoleh juga diberikan dalam artikel.
Apa persamaan yang kita bicarakan?
Rajah di bawah menunjukkan formula di mana x adalah pemboleh ubah yang tidak diketahui dan simbol Latin a, b, c mewakili beberapa nombor yang diketahui.
Setiap simbol ini dipanggil pekali. Seperti yang anda lihat, nombor "a" berada di hadapan pemboleh ubah kuasa dua x. Ini adalah kekuatan maksimum ungkapan yang dipersembahkan, itulah sebabnya ia disebut persamaan kuadratik. Nama lain sering digunakan: persamaan pesanan kedua. Nilai itu sendiri adalah pekali kuadrat (berdiri untuk pemboleh ubah kuasa dua), b adalah pekali linear (di sebelah pemboleh ubah dinaikkan ke daya pertama), dan akhirnya, angka c adalah istilah bebas.
Perhatikan bahawa bentuk persamaan yang ditunjukkan dalam rajah di atas adalah ungkapan segiempat sama biasa. Di samping itu, terdapat persamaan urutan kedua lain di mana pekali b, c boleh menjadi sifar.
Apabila masalah diajukan untuk menyelesaikan persamaan yang dipertimbangkan, ini bermaksud bahawa nilai pemboleh ubah x perlu dijumpai yang akan memuaskannya. Di sini, perkara pertama yang perlu diingat adalah perkara berikut: kerana tahap maksimum x adalah 2, ungkapan jenis ini tidak boleh mempunyai lebih daripada 2 penyelesaian. Ini bermaksud bahawa jika, ketika menyelesaikan persamaan, didapati 2 nilai x yang memuaskannya, maka anda dapat memastikan bahawa tidak ada nombor ketiga, menggantikan yang bukan x, persamaan juga akan berlaku. Penyelesaian untuk persamaan dalam matematik disebut akar.
Kaedah untuk menyelesaikan persamaan urutan kedua
Menyelesaikan persamaan jenis ini memerlukan pengetahuan tentang beberapa teori mengenainya. Kursus algebra sekolah menguji 4 kaedah yang berbeza penyelesaian. Mari senaraikannya:
- menggunakan pemfaktoran;
- menggunakan formula untuk petak penuh;
- dengan menggunakan graf fungsi kuadratik yang sesuai;
- menggunakan persamaan diskriminasi.
Kelebihan kaedah pertama terletak pada kesederhanaannya, namun ia tidak dapat diterapkan pada semua persamaan. Kaedah kedua adalah universal, tetapi agak membebankan. Kaedah ketiga terkenal kerana kejelasannya, tetapi tidak selalu mudah dan boleh digunakan. Dan, akhirnya, menggunakan persamaan diskriminasi adalah cara universal dan cukup mudah untuk mencari akar sama sekali persamaan orde kedua. Oleh itu, dalam artikel itu kita hanya akan mempertimbangkannya.
Formula untuk mendapatkan punca persamaan
Mari beralih ke Pandangan umum persamaan kuadratik. Mari tuliskan: a * x² + b * x + c = 0. Sebelum menggunakan kaedah menyelesaikannya "melalui diskriminasi", persamaan harus selalu dikurangkan kepada bentuk bertulis. Iaitu, ia mesti terdiri daripada tiga istilah (atau kurang jika b atau c adalah 0).
Contohnya, jika terdapat ungkapan: x²-9 * x + 8 = -5 * x + 7 * x², maka anda mesti memindahkan semua istilahnya ke satu sisi persamaan dan menambahkan istilah yang mengandungi pemboleh ubah x di kuasa yang sama.
Dalam kes ini, operasi ini akan membawa kepada ungkapan berikut: -6 * x²-4 * x + 8 = 0, yang bersamaan dengan persamaan 6 * x² + 4 * x-8 = 0 (di sini kita mengalikan kiri dan sisi kanan persamaan dengan -1) ...

Dalam contoh di atas, a = 6, b = 4, c = -8. Perhatikan bahawa semua syarat persamaan yang dipertimbangkan selalu dijumlahkan di antara mereka, jadi jika tanda "-" muncul, ini bermaksud bahawa pekali yang sesuai adalah negatif, seperti juga angka c dalam kes ini.

Setelah meneliti titik ini, kita sekarang beralih ke rumus itu sendiri, yang memungkinkan untuk memperoleh akar dari persamaan kuadratik. Ia mempunyai bentuk yang ditunjukkan dalam foto di bawah.

Seperti yang anda lihat dari ungkapan ini, ia membolehkan anda memperoleh dua punca (anda harus memperhatikan tanda "±"). Untuk melakukan ini, cukup untuk menggantikan pekali b, c, dan a ke dalamnya.
Konsep diskriminasi
Pada perenggan sebelumnya, diberikan formula yang membolehkan anda menyelesaikan persamaan pesanan kedua dengan cepat. Di dalamnya, ungkapan radikal disebut diskriminan, yaitu, D = b²-4 * a * c.
Mengapa bahagian formula ini diasingkan, malah ada nama sendiri? Faktanya ialah diskriminan menghubungkan ketiga-tiga pekali persamaan itu menjadi satu ungkapan. Fakta terakhir bermaksud bahawa ia sepenuhnya membawa maklumat mengenai akarnya, yang dapat dinyatakan dalam senarai berikut:
- D> 0: persamaan mempunyai 2 penyelesaian yang berbeza, kedua-duanya adalah nombor nyata.
- D = 0: Persamaan hanya mempunyai satu punca dan nombor nyata.
Tugas menentukan diskriminasi

Mari kita berikan contoh mudah bagaimana mencari diskriminasi. Biarkan persamaan berikut diberikan: 2 * x² - 4 + 5 * x-9 * x² = 3 * x-5 * x² + 7.
Kami membawanya ke bentuk standard, kami mendapat: (2 * x²-9 * x² + 5 * x²) + (5 * x-3 * x) + (- 4-7) = 0, dari mana kami mencapai persamaan : -2 * x² + 2 * x-11 = 0. Di sini a = -2, b = 2, c = -11.
Sekarang anda boleh menggunakan formula bernama untuk diskriminan: D = 2² - 4 * (- 2) * (- 11) = -84. Nombor yang dihasilkan adalah jawapan kepada tugas. Oleh kerana dalam contoh itu diskriminasi kurang daripada sifar, maka kita dapat mengatakan bahawa persamaan kuadratik ini tidak mempunyai akar sebenarnya. Hanya nombor kompleks yang akan menjadi penyelesaiannya.
Contoh ketidaksamaan melalui diskriminasi
Mari selesaikan masalah jenis yang sedikit berbeza: memandangkan persamaan -3 * x²-6 * x + c = 0. Anda perlu mencari nilai c yang mana D> 0.
Dalam kes ini, hanya 2 dari 3 pekali yang diketahui, jadi tidak mungkin untuk menghitung nilai tepat dari diskriminan, tetapi diketahui bahawa positif. Kami menggunakan fakta terakhir ketika membuat kesamaan: D = (-6) ²-4 * (- 3) * c> 0 => 36 + 12 * c> 0. Penyelesaian ketaksamaan yang diperoleh membawa kepada hasil: c> -3.
Mari periksa nombor yang diterima. Untuk melakukan ini, hitung D untuk 2 kes: c = -2 dan c = -4. Nombor -2 memenuhi hasil yang diperoleh (-2> -3), diskriminan yang sesuai akan mempunyai nilai: D = 12> 0. Pada gilirannya, nombor -4 tidak memenuhi ketaksamaan (-4 Oleh itu, sebarang nombor c yang lebih besar daripada -3 akan memenuhi syarat.
Contoh menyelesaikan persamaan
Mari kita kemukakan masalah, yang bukan hanya dalam mencari diskriminasi, tetapi juga dalam menyelesaikan persamaan. Anda perlu mencari punca persamaan -2 * x² + 7-9 * x = 0.
Dalam contoh ini, diskriminasi adalah nilai seterusnya: D = 81-4 * (- 2) * 7 = 137. Kemudian punca persamaan ditakrifkan seperti berikut: x = (9 ± √137) / (- 4). Ini adalah nilai akar yang tepat, jika anda mengira anggaran punca, maka anda mendapat nombor: x = -5.176 dan x = 0.676.
Masalah geometri
Mari kita selesaikan masalah yang memerlukan bukan sahaja kemampuan untuk mengira diskriminasi, tetapi juga penggunaan kemahiran berfikir abstrak dan pengetahuan tentang cara membuat persamaan kuadratik.
Bob mempunyai selimut 5 x 4 meter. Kanak-kanak itu mahu menjahit jalur berterusan kain cantik... Betapa tebalnya jalur ini jika Bob diketahui mempunyai 10 m² kain.

Biarkan jalur mempunyai ketebalan x m, maka luas kain sepanjang sisi panjang selimut akan berukuran (5 + 2 * x) * x, dan kerana terdapat 2 sisi panjang, kami mempunyai: 2 * x * (5 + 2 * x). Di sisi pendek, luas kain yang dijahit akan menjadi 4 * x, kerana ada 2 sisi ini, kita mendapat nilai 8 * x. Perhatikan bahawa 2 * x telah ditambahkan ke sisi panjang kerana panjang selimut telah meningkat dengan bilangan itu. Luas keseluruhan kain yang dijahit ke selimut adalah 10 m². Oleh itu, kita mendapat persamaan: 2 * x * (5 + 2 * x) + 8 * x = 10 => 4 * x² + 18 * x-10 = 0.
Untuk contoh ini, diskriminan adalah: D = 18²-4 * 4 * (- 10) = 484. Akarnya ialah 22. Dengan menggunakan formula, kita dapati akar yang diperlukan: x = (-18 ± 22) / (2 * 4) = (- 5; 0.5). Jelas, dari dua punca, hanya nombor 0.5 yang sesuai dengan pernyataan masalah.
Oleh itu, jalur kain yang dijahit oleh Bob ke selimutnya selebar 50 cm.
Persamaan kuadratik yang tidak lengkap berbeza dengan persamaan klasik (lengkap) kerana faktor atau pintasannya sama dengan sifar. Graf fungsi seperti itu adalah parabola. Bergantung pada penampilan umum mereka, mereka dibahagikan kepada 3 kumpulan. Prinsip penyelesaian untuk semua jenis persamaan adalah sama.
Tidak ada yang sukar dalam menentukan jenis polinomial yang tidak lengkap. Sebaiknya pertimbangkan perbezaan utama dengan contoh ilustrasi:
- Sekiranya b = 0, maka persamaannya adalah ax 2 + c = 0.
- Sekiranya c = 0, maka ungkapan kapak 2 + bx = 0 harus dipecahkan.
- Sekiranya b = 0 dan c = 0, maka polinomial menjadi persamaan jenis kapak 2 = 0.
Kes terakhir adalah kemungkinan teori dan tidak pernah berlaku dalam tugas ujian pengetahuan, kerana satu-satunya nilai pemboleh ubah yang sah dalam ungkapan adalah sifar. Pada masa akan datang, kaedah dan contoh penyelesaian persamaan kuadratik 1) dan 2) jenis yang tidak lengkap akan dipertimbangkan.
Algoritma umum untuk mencari pemboleh ubah dan contoh dengan penyelesaian
Terlepas dari jenis persamaan, algoritma penyelesaian merangkumi langkah-langkah berikut:
- Bawa ungkapan ke bentuk yang sesuai untuk mencari akar.
- Lakukan pengiraan.
- Catat jawapan anda.
Kaedah termudah untuk menyelesaikan persamaan yang tidak lengkap adalah dengan memfaktorkan bahagian kiri dan meninggalkan sifar di sebelah kanan. Oleh itu, formula untuk persamaan kuadratik yang tidak lengkap untuk mencari punca dikurangkan untuk mengira nilai x bagi setiap faktor.
Anda hanya boleh belajar menyelesaikannya dalam praktik, jadi pertimbangkan contoh khusus mencari punca persamaan yang tidak lengkap:
Seperti yang anda lihat, dalam kes ini b = 0. Faktorkan sebelah kiri dan dapatkan ungkapan:
4 (x - 0,5) ⋅ (x + 0,5) = 0.
Jelas, produk itu sifar apabila sekurang-kurangnya salah satu faktornya adalah sifar. Nilai pemboleh ubah x1 = 0.5 dan (atau) x2 = -0.5 memenuhi syarat ini.
Untuk menangani tugas penguraian dengan mudah dan cepat trinomial segi empat sama mengikut faktor, anda harus ingat formula berikut:
Sekiranya tidak ada istilah bebas dalam ungkapan, tugasnya akan sangat dipermudahkan. Cukup sekadar mencari dan mengeluarkan penyebut yang sama. Untuk kejelasan, pertimbangkan contoh bagaimana menyelesaikan persamaan kuadratik yang tidak lengkap dari bentuk ax2 + bx = 0.
Mari keluarkan pemboleh ubah x dari tanda kurung dan dapatkan ungkapan berikut:
x ⋅ (x + 3) = 0.
Dengan berpandukan logik, kami sampai pada kesimpulan bahawa x1 = 0, dan x2 = -3.
Penyelesaian tradisional dan persamaan kuadratik yang tidak lengkap
Apa yang akan berlaku sekiranya anda menggunakan formula diskriminan dan cuba mencari punca polinomial, dengan pekali sama dengan sifar? Mari kita ambil contoh dari koleksi tugas khas untuk peperiksaan matematik pada tahun 2017, menyelesaikannya menggunakan formula standard dan kaedah pemfaktoran.
7x 2 - 3x = 0.
Mari kita hitung nilai diskriminan: D = (-3) 2 - 4 ⋅ (-7) ⋅ 0 = 9. Ternyata polinomial mempunyai dua punca:
Sekarang, mari selesaikan persamaan dengan memfaktorkan dan membandingkan hasilnya.
X ⋅ (7x + 3) = 0,
2) 7x + 3 = 0,
7x = -3,
x = -.
Seperti yang anda lihat, kedua-dua kaedah memberikan hasil yang sama, tetapi menyelesaikan persamaan dengan kaedah kedua ternyata jauh lebih mudah dan cepat.
Teorema Vieta
Tetapi apa yang perlu dilakukan dengan teorema Vieta yang dikasihi? Bolehkah kaedah ini diterapkan dengan trinomial yang tidak lengkap? Mari cuba memahami aspek lakonan bukan menyelesaikan persamaan Ke penampilan klasik ax2 + bx + c = 0.
Sebenarnya, adalah mungkin untuk menerapkan teorema Vieta dalam kes ini. Hanya perlu membawa ungkapan itu ke bentuk umum, menggantikan anggota yang hilang dengan sifar.
Sebagai contoh, untuk b = 0 dan a = 1, untuk menghilangkan kemungkinan kekeliruan, tugas harus ditulis dalam bentuk: ax2 + 0 + c = 0. Kemudian nisbah jumlah dan produk akar dan faktor polinomial dapat dinyatakan seperti berikut:

Pengiraan teori membantu mengenal intipati masalah, dan selalu memerlukan latihan kemahiran ketika menyelesaikannya tugas tertentu... Mari kembali ke buku rujukan tugas khas untuk peperiksaan dan cari contoh yang sesuai:
Marilah kita menulis ungkapan dalam bentuk yang sesuai untuk penerapan teorema Vieta:
x 2 + 0 - 16 = 0.
Langkah seterusnya adalah membuat sistem syarat:

Jelas, akar polinomial persegi akan menjadi x 1 = 4 dan x 2 = -4.
Sekarang, mari berlatih membawa persamaan ke bentuk umum. Ambil contoh berikut: 1/4 × x 2 - 1 = 0
Untuk menerapkan teorema Vieta pada ungkapan, perlu menghilangkan pecahan. Gandakan sisi kiri dan kanan dengan 4, dan lihat hasilnya: x2–4 = 0. Persamaan yang dihasilkan siap diselesaikan dengan teorema Vieta, tetapi jauh lebih mudah dan cepat untuk mendapatkan jawapannya hanya dengan memindahkan c = 4 di sebelah kanan persamaan: x2 = 4.
Menyimpulkan, harus dikatakan bahawa cara yang paling baik penyelesaian persamaan yang tidak lengkap adalah pemfaktoran, adalah yang paling mudah dan kaedah cepat... Sekiranya anda menghadapi kesukaran dalam proses mencari akar, anda boleh menghubungi kaedah tradisional mencari akar melalui diskriminasi.
Rumus untuk punca persamaan kuadratik. Kes-kes akar sebenar, berganda dan kompleks dipertimbangkan. Memfaktorkan trinomial segiempat sama. Tafsiran geometri. Contoh menentukan punca dan pemfaktoran.
Rumusan asas
Pertimbangkan persamaan kuadratik:
(1)
.
Akar Kuadratik(1) ditentukan oleh formula:
;
.
Rumusan ini boleh digabungkan seperti ini:
.
Apabila akar persamaan kuadratik diketahui, maka polinomial darjah kedua dapat ditunjukkan sebagai produk faktor (faktor):
.
Selanjutnya, kami menganggap bahawa adalah nombor nyata.
Pertimbangkan diskriminasi kuadratik:
.
Sekiranya diskriminan positif, maka persamaan kuadratik (1) mempunyai dua punca sebenar yang berbeza:
;
.
Maka faktorisasi trinomial segi empat sama adalah:
.
Sekiranya diskriminan adalah sifar, maka persamaan kuadratik (1) mempunyai dua punca (sama) sebenarnya:
.
Pemfaktoran:
.
Sekiranya diskriminan itu negatif, maka persamaan kuadratik (1) mempunyai dua punca konjugat kompleks:
;
.
Berikut adalah unit khayalan,;
dan - bahagian akar sebenar dan khayalan:
;
.
Kemudian
.
Tafsiran grafik
Sekiranya anda membina graf fungsi
,
yang merupakan parabola, maka titik persilangan graf dengan paksi akan menjadi punca persamaan
.
Bila, graf melintasi paksi absis (paksi) pada dua titik.
Bila, grafik menyentuh paksi absis pada satu titik.
Bila, graf tidak melintasi paksi absis.
Berikut adalah contoh grafik sedemikian.
Persamaan Kuadratik Berguna
(f.1) ;
(f.2) ;
(f.3) .
Derivasi formula untuk punca persamaan kuadratik
Kami melakukan transformasi dan menerapkan formula (f.1) dan (f.3):
,
di mana
;
.
Oleh itu, kami mendapat formula untuk polinomial darjah kedua dalam bentuk:
.
Oleh itu dilihat bahawa persamaan
dilakukan di
dan.
Artinya, mereka adalah akar dari persamaan kuadratik
.
Contoh menentukan punca persamaan kuadratik
Contoh 1
(1.1)
.
Penyelesaian
.
Membandingkan dengan persamaan kami (1.1), kami dapati nilai pekali:
.
Kami dapati diskriminasi:
.
Oleh kerana diskriminasi positif, persamaan mempunyai dua punca sebenar:
;
;
.
Dari ini kita mendapat pemfaktoran trinomial segi empat sama:
.
Graf fungsi y = 2 x 2 + 7 x + 3 melintasi paksi absis pada dua titik.
Mari plot fungsinya
.
Grafik fungsi ini adalah parabola. Ia melintasi paksi absis (paksi) pada dua titik:
dan.
Titik-titik ini adalah punca persamaan asal (1.1).
Jawapan
;
;
.
Contoh 2
Cari punca persamaan kuadratik:
(2.1)
.
Penyelesaian
Mari tulis persamaan kuadratik dalam bentuk umum:
.
Membandingkan dengan persamaan asal (2.1), kita dapati nilai pekali:
.
Kami dapati diskriminasi:
.
Oleh kerana diskriminan adalah sifar, persamaan mempunyai dua punca (sama):
;
.
Maka faktorisasi trinomial adalah:
.

Graf fungsi y = x 2 - 4 x + 4 menyentuh paksi absis pada satu titik.
Mari plot fungsinya
.
Grafik fungsi ini adalah parabola. Ia menyentuh paksi absis (paksi) pada satu titik:
.
Titik ini adalah punca persamaan asal (2.1). Oleh kerana akar ini memasuki pemfaktoran dua kali:
,
maka akar seperti itu biasanya disebut berganda. Mereka percaya bahawa terdapat dua akar yang sama:
.
Jawapan
;
.
Contoh 3
Cari punca persamaan kuadratik:
(3.1)
.
Penyelesaian
Mari tulis persamaan kuadratik dalam bentuk umum:
(1)
.
Kami menulis semula persamaan asal (3.1):
.
Membandingkan dengan (1), kita dapati nilai pekali:
.
Kami dapati diskriminasi:
.
Diskriminasi adalah negatif,. Oleh itu, tidak ada akar yang sah.
Akar kompleks boleh didapati:
;
;
.
Kemudian
.

Graf fungsi tidak melintasi paksi absis. Tidak ada akar yang sah.
Mari plot fungsinya
.
Grafik fungsi ini adalah parabola. Ia tidak melintasi paksi absis (paksi). Oleh itu, tidak ada akar yang sah.
Jawapan
Tidak ada akar yang sah. Akar kompleks:
;
;
.