Bahagian tapak
Pilihan editor:
- Apakah perbezaannya?
- Mandela Nelson - biografi
- Biografi orang terkenal di China
- 1 koordinat pesawat
- Pesawat koordinat kosong
- Apakah sudut luaran parallelogram?
- Bagaimana untuk mencari bilangan peraturan peratus
- Persamaan tangen kepada graf fungsi
- Valery yakovlevich bruce berfungsi
- Persamaan parabola kubik
Pengiklanan
| Ketidakseimbangan trigonometri adalah kaedah penyelesaian. Penyelesaian ketidaksamaan trigonometri paling mudah |
|
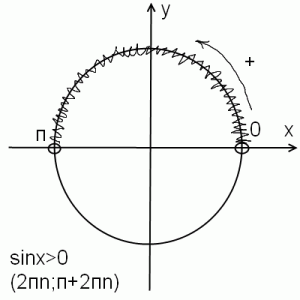
Ketidakseimbangan trigonometri yang paling mudah dari bentuk sin x\u003e a adalah asas untuk menyelesaikan ketidaksamaan trigonometri yang lebih kompleks. Pertimbangkan penyelesaian ketidaksamaan trigonometri paling mudah dari bentuk sin x\u003e a pada lingkaran unit. 1) pada 0 Menggunakan persatuan cosine-kolobok (kedua-duanya bermula dengan ko, kedua-duanya adalah "kemas"), kita ingat bahawa cosine adalah x, masing-masing, sinus adalah y. Dari sini kita merancang y \u003d a - garisan selari dengan lembu paksi. Sekiranya ketidaksamaan adalah ketat, titik persilangan bulatan unit dan garis lurus y \u003d a dibubarkan, jika ketidaksamaan itu tidak ketat, kita melukis pada titik-titik (betapa mudahnya diingat apabila titik punca keluar, apabila diisi, lihat). Kesukaran yang paling besar dalam menyelesaikan kesenjangan trigonometri yang paling mudah ialah penemuan yang betul mengenai titik persilangan bulatan unit dan garisan y \u003d a. Mata pertama adalah mudah dicari - ini adalah arcsin a. Kita menentukan laluan yang mana dari titik pertama kita pergi ke tempat kedua. Pada baris y \u003d a sinx \u003d a, di atas, di atas garis, sin x\u003e a, dan di bawah, di bawah garis, sin x 2) a \u003d 0, iaitu, sin x\u003e 0 Dalam kes ini, titik pertama jurang ialah 0, yang kedua ialah n. Kami menambah 2pn ke kedua-dua hujung jurang, dengan mengambil kira tempoh sine.
3) untuk a \u003d -1, iaitu, sinx\u003e -1 Dalam kes ini, titik pertama adalah n / 2, dan untuk mendapatkan yang kedua, kita pergi ke seluruh bulatan lawan jam. Kita sampai ke titik -n / 2 + 2n \u003d 3n / 2. Untuk mengambil kira semua jangka masa yang menjadi penyelesaian kepada ketidaksamaan ini, kami menambah 2n ke kedua-dua hujungnya.
4) sinx\u003e -a, pada 0 Titik pertama adalah, seperti biasa, arcsin (-a) \u003d - arcsina. Untuk sampai ke titik kedua, kita pergi ke laluan atas, iaitu, ke arah meningkatkan sudut. Kali ini kita pergi ke n. Berapa banyak kita pergi ke? Pada arcsin x. Jadi titik kedua adalah n + arcsin x. Kenapa tidak ada tolak? Kerana tolak dalam -arcsin entri menunjukkan pergerakan arah jam, dan kami melawannya. Dan sebagai kesimpulan, kami menambah 2pn untuk setiap akhir selang.
5) sinx\u003e a jika a\u003e 1. Lingkaran unit terletak sepenuhnya di bawah garisan y \u003d a. Tidak ada titik tunggal di atas garisan. Jadi tidak ada penyelesaian. 6) sinx\u003e -a, di mana\u003e 1. Dalam kes ini, seluruh pusingan unit terletak sepenuhnya di atas garisan y \u003d a. Oleh itu, mana-mana titik memenuhi syarat sinx\u003e a. Jadi x adalah sebarang nombor.
Dan di sini x adalah mana-mana nombor, kerana titik -n / 2 + 2nn dimasukkan dalam penyelesaian, berbeza dengan ketaksamaan ketat sinx\u003e -1. Tiada apa-apa untuk menolaknya. Satu-satunya titik pada bulatan yang memenuhi syarat ini adalah n / 2. Memandangkan tempoh sinus, penyelesaian untuk ketidaksamaan ini adalah set mata x \u003d n / 2 + 2n. Contohnya, selesaikan ketidaksamaan sinx\u003e -1/2:
Ketaksamaan adalah hubungan bentuk a\u003e b, di mana a dan b adalah ungkapan yang mengandungi sekurang-kurangnya satu pembolehubah. Ketaksamaan boleh ketat - \u003c,\u003e dan tidak ketat - ≥, ≤. Ketidaksamaan trigonometri adalah ungkapan bentuk: F (x)\u003e a, F (x) \u003ca, F (x) ≤ a, F (x) ≥ a, di mana F (x) diwakili oleh satu atau lebih fungsi trigonometri. Satu contoh ketidaksamaan trigonometri paling mudah adalah: sin x \u003c1/2. Penyelesaian masalah tersebut dibuat secara grafik, untuk kedua-dua kaedah ini telah dibangunkan. Kaedah 1 - Menyelesaikan ketidaksamaan dengan merancang fungsiUntuk mencari jurang yang memenuhi syarat ketidaksamaan sin x \u003c1/2, anda mesti melakukan langkah-langkah berikut:
Apabila tanda-tanda ketat hadir dalam ungkapan, titik persilangan bukan penyelesaian. Oleh kerana tempoh positif sinusoid positif adalah 2π, kita menulis jawapannya seperti berikut:
Sekiranya tanda-tanda ungkapan tidak ketat, maka jeda keputusan mesti disertakan dalam kurungan persegi -. Jawapan kepada masalah ini juga boleh ditulis sebagai ketidaksamaan lain: Kaedah 2 - Menyelesaikan ketidaksamaan trigonometri menggunakan bulatan unitMasalah yang sama mudah diselesaikan dengan bantuan bulatan trigonometri. Algoritma carian jawapannya sangat mudah:
Marilah kita analisis langkah-langkah penyelesaian menggunakan contoh ketidaksamaan sin x\u003e 1/2. Titik α dan β ditandakan pada bulatan - nilai
Titik arus yang terletak di atas α dan β adalah selang larutan suatu ketidaksamaan yang diberi.
Jika anda perlu menyelesaikan contoh untuk cos, maka arc jawapan akan terletak bersimetri ke paksi OX, bukan OY. Anda boleh mempertimbangkan perbezaan antara selang penyelesaian untuk dosa dan kos dalam gambarajah di bawah.
Penyelesaian graf untuk ketidakseimbangan tangen dan cotangent akan berbeza daripada kedua-dua sinus dan kosinus. Ini disebabkan sifat-sifat fungsi.
Tangga lengkung dan arc tangen adalah tangen kepada bulatan trigonometri, dan tempoh positif minimum bagi kedua-dua fungsi adalah π. Untuk menggunakan kaedah kedua dengan cepat dan betul, anda harus ingat pada mana paksi nilai-nilai dosa, cos, tg dan ctg diplotkan. Tangent tangen berjalan sejajar dengan paksi OY. Jika kita menangguhkan nilai arctan a pada lingkaran unit, maka titik yang diperlukan kedua akan terletak pada suku diagonal. Sudut Mereka memecah mata untuk fungsi, kerana grafik cenderung kepada mereka, tetapi tidak pernah mencapai mereka.
Dalam kes cotangent, tangen berjalan selari dengan paksi OX, dan fungsi tersebut terganggu pada titik π dan 2π.
Ketidaksamaan trigonometri kompleksSekiranya hujah fungsi ketidaksamaan diwakili bukan hanya oleh pemboleh ubah, tetapi oleh keseluruhan ungkapan yang tidak diketahui, maka kita bercakap mengenai ketidaksamaan yang kompleks. Kursus dan urutan penyelesaiannya agak berbeza daripada kaedah yang dinyatakan di atas. Katakan anda perlu mencari penyelesaian kepada ketidaksamaan berikut:
Penyelesaian graf melibatkan pembinaan sinusoid konvensional y \u003d sin x dari nilai-nilai yang dipilih sewenang-wenang x. Kami mengira jadual dengan koordinat untuk titik kawalan grafik:
Hasilnya mestilah lengkung yang indah. Untuk memudahkan mencari penyelesaian, gantikan hujah fungsi kompleks
Kebanyakan pelajar tidak menyukai ketidaksamaan trigonometri. Tetapi sia-sia. Sebagai satu watak yang biasa dikatakan
Jadi bagaimana untuk "memasak" dan bagaimana untuk menerapkan ketidaksamaan dengan sinus, kita akan memahami dalam artikel ini. Kami akan menyelesaikan dengan cara yang paling mudah - menggunakan bulatan unit. Jadi, pertama sekali, kita memerlukan algoritma berikut. Algoritma untuk menyelesaikan ketidaksamaan dengan sinus:
Batasan algoritmaPenting: dalgoritma tidak berfungsi untuk ketidaksamaan bentuk $ \\ sin (x)\u003e 1; \\ \\ sin (x) \\ geq 1, \\ \\ sin (x)< -1, \ \sin{x} \leq -1$. В строгом случае эти неравенства не имеют решений, а в нестрогом – решение сводится к решению уравнения $\sin{x} = 1$ или $\sin{x} = -1$. Kes-kes khas dalam menyelesaikan ketidaksamaan dengan sinusIa juga penting untuk ambil perhatian kes-kes berikut, yang lebih mudah untuk menyelesaikan secara logik tanpa menggunakan algoritma di atas. Kes khas 1. Selesaikan ketidaksamaan: $ \\ sin (x) \\ leq 1. $ Oleh kerana julat fungsi trigonometri $ y \u003d \\ sin (x) $ tidak lebih daripada $ 1 $ modulo, sebelah kiri ketidaksamaan untuk mana-mana sahaja$ x $ dari domain definisi (dan domain definisi sinus adalah semua nombor nyata) tidak melebihi $ 1 $. Dan sebagainya, sebagai tindak balas, kami menulis: $ x \\ in R $. Akibatnya: $ \\ sin (x) \\ geq -1. $ Kes khas 2. Selesaikan ketidaksamaan: $ \\ sin (x)< 1.$ Memohon hujah-hujah yang serupa dengan kes tertentu 1, kita dapati bahawa sebelah kiri ketidaksamaan adalah kurang daripada $ 1 $ untuk semua $ x \\ dalam R $, kecuali untuk mata yang merupakan penyelesaian kepada persamaan $ \\ sin (x) \u003d 1 $. Menyelesaikan persamaan ini, kami akan mempunyai: $ x \u003d (-1) ^ (n) \\ arcsin (1) + \\ pi n \u003d (-1) ^ (n) \\ frac (\\ pi) (2) + \\ pi n. $ Oleh itu, sebagai tindak balas, kita menulis: $ x \\ in R \\ backslash \\ left \\ (- 1) ^ (n) \\ frac (\\ pi) (2) + \\ pi n \\ right \\) $. Akibatnya: ketidaksamaan diselesaikan sama $ \\ sin (x)\u003e -1. $ Contoh penyelesaian ketidaksamaan menggunakan algoritma.Contoh 1:Selesaikan ketidaksamaan: $ \\ sin (x) \\ geq \\ frac (1) (2). $
Oleh itu, keputusan akan mengambil bentuk: $ x \\ in \\ left [\\ frac (\\ pi) (6) + 2 \\ pi n; \\ frac (5 \\ pi) (6) + 2 \\ pi n \\ kanan], \\ n \\ in Z. $ Contoh 2:Selesaikan ketidaksamaan: $ \\ sin (x)< -\frac{1}{2}$ Kami menandakan koordinat $ - \\ frac (1) (2) $ pada paksi sinus dan lukis garis lurus selari dengan paksi kosinus dan melalui titik ini. Perhatikan titik persilangan. Mereka tidak akan diisi, kerana ketidaksamaan itu ketat. Tanda ketidaksamaan $<$, а, значит, закрашиваем область ниже прямой, т.е. меньший полукруг. Неравенство превращаем в равенство и решаем его: $ \\ sin (x) \u003d - \\ frac (1) (2) $ $ x \u003d (- 1) ^ (n) \\ arcsin (\\ left (- \\ frac (1) (2) \\ right)) + \\ pi n \u003d (- 1) ^ (n + 1) \\ frac (\\ pi ) (6) + \\ pi n $. Menetapkan lagi $ n \u003d 0 $, kita dapati titik persimpangan pertama: $ x_ (1) \u003d - \\ frac (\\ pi) (6) $. Kawasan kami masuk ke arah negatif dari titik pertama, jadi kami menetapkan $ n $ sama dengan $ -1: $ x_ (2) \u003d (- 1) ^ (- 1 + 1) \\ frac (\\ pi) (6) + \\ pi \\ cdot (-1) \u003d - \\ pi + \\ frac (\\ pi) (6) \u003d - \\ frac (5 \\ pi) (6) $.
$ x \\ in \\ left (- \\ frac (5 \\ pi) (6) + 2 \\ pi n; - \\ frac (\\ pi) (6) + 2 \\ pi n \\ Contoh 3:Selesaikan ketidaksamaan: $ 1 - 2 \\ sin (\\ left (\\ frac (x) (4) + \\ frac (\\ pi) (6) \\ right)) \\ leq 0. $ Contoh ini tidak dapat diselesaikan segera dengan bantuan algoritma. Pertama anda perlu menukarnya. Kami melakukan persis seperti yang kita lakukan dengan persamaan, tetapi jangan lupa tentang tanda itu. Membahagikan atau mengalikan dengan nombor negatif membalikkannya! Oleh itu, kami memindahkan semua yang tidak mengandungi fungsi trigonometri ke sebelah kanan. Kami mendapat: $ - 2 \\ sin (\\ left (\\ frac (x) (4) + \\ frac (\\ pi) (6) \\ kanan)) \\ leq -1. $ Bahagikan sisi kiri dan kanan dengan $ -2 $ (jangan lupa tentang tanda!). Kami akan mempunyai: $ \\ sin (\\ left (\\ frac (x) (4) + \\ frac (\\ pi) (6) \\ right)) \\ geq \\ frac (1) Sekali lagi kita mempunyai ketidaksamaan yang tidak dapat kita selesaikan menggunakan algoritma. Tetapi di sini sudah cukup untuk melakukan penggantian berubah: $ t \u003d \\ frac (x) (4) + \\ frac (\\ pi) (6). $ Kami mendapat ketidaksamaan trigonometri, yang boleh diselesaikan menggunakan algoritma: $ \\ sin (t) \\ geq \\ frac (1) (2). $ Ketidaksamaan ini diselesaikan dalam Contoh 1, jadi kami meminjam jawapannya dari sana: $ t \\ in \\ left [\\ frac (\\ pi) (6) + 2 \\ pi n; \\ frac (5 \\ pi) (6) + 2 \\ pi n \\ kanan]. $ Walau bagaimanapun, keputusan itu belum lagi berakhir. Kita perlu kembali ke pemboleh ubah asal. $ (\\ frac (x) (4) + \\ frac (\\ pi) (6)) \\ in \\ left [\\ frac (\\ pi) (6) + 2 \\ pi n; \\ frac (5 \\ pi) (6) + 2 \\ pi n \\ kanan]. $ Bayangkan jurang dalam bentuk sistem: $ \\ left \\ (\\ begin (array) (c) \\ frac (x) (4) + \\ frac (\\ pi) (6) \\ geq \\ frac (\\ pi) (6) + 2 \\ pi n, \\ frac (x) (4) + \\ frac (\\ pi) (6) \\ leq \\ frac (5 \\ pi) (6) + 2 \\ pi n. Di sebelah kiri sistem adalah ungkapan ($ \\ frac (x) (4) + \\ frac (\\ pi) (6) $), yang tergolong dalam jurang. Untuk ketidaksamaan pertama, sempadan kiri jurang bersesuaian, dan untuk yang kedua, hak. Selain itu, kurungan memainkan peranan yang penting: jika pendakap adalah persegi, maka ketidaksamaan akan menjadi tidak ketat, dan jika ia bulat, maka ketat. tugas kami adalah untuk mendapatkan $ x $ di sebelah kiri dalam kedua-dua ketidaksamaan. Pindah $ \\ frac (\\ pi) (6) $ dari kiri ke kanan, kami dapat: $ \\ left \\ (\\ begin (array) (c) \\ frac (x) (4) \\ geq \\ frac (\\ pi) (6) + 2 \\ pi n - \\ frac (\\ pi) (6), \\ \\ frac (x) (4) \\ leq \\ frac (5 \\ pi) (6) + 2 \\ pi n - \\ frac (\\ pi) (6). \\ end (array) Memudahkan, kami akan mempunyai: (\\) \\ frac (x) (4) \\ geq 2 \\ pi n, \\\\ \\ frac (x) (4) \\ leq \\ frac (2 \\ pi) + 2 \\ pi n. \\ End (array) \\ right. $ Mengalikan bahagian kiri dan kanan dengan $ 4 $, kami dapat: $ \\ left \\ (\\ begin (array) (c) x \\ geq 8 \\ pi n, \\\\ x \\ leq \\ frac (8 \\ pi) (3) + 8 \\ pi n. \\ end (array) \\ right. $ Meletakkan sistem dalam jurang, kami mendapat jawapannya: $ x \\ in \\ left [8 \\ pi n; \\ frac (8 \\ pi) (3) + 8 \\ pi n \\ kanan], \\ n \\ in Z. $ 1. Jika hujahnya adalah kompleks (berbeza dengan x), kemudian gantikannya dengan t. 2. Kami membina satu pesawat koordinat tOy fungsi graf y \u003d kos dan y \u003d a. 3. Cari seperti itu dua titik persimpangan bersebelahan grafikantara yang terletak lebih tinggi daripada garis lurus y \u003d a. Kami mendapati abscissas perkara ini. 4. Kami menulis ketidaksamaan berganda untuk hujah tmemandangkan tempoh kosinus ( t akan menjadi antara abscissas yang dijumpai). 5. Lakukan penggantian terbalik (kembali kepada hujah asal) dan nyatakan nilai x daripada ketidaksamaan berganda, kita menulis jawapan dalam bentuk selang berangka. Contoh 1
Seterusnya, menurut algoritma, kita menentukan nilai-nilai hujah tersebut tdi mana sinusoid terletak di atas langsung. Kami menuliskan nilai-nilai ini dalam bentuk ketidaksamaan berganda, dengan mengambil kira berkala fungsi kosinus, dan kemudian kembali kepada hujah asal x.
Contoh 2 Pilih julat nilai-nilai tdi mana sinusoid berada di atas garis lurus.
Tulis semula nilai sebagai ketidaksamaan berganda t memuaskan keadaan. Jangan lupa bahawa tempoh fungsi terkecil y \u003d kos sama dengan 2π. Kembali ke pembolehubah x, secara beransur-ansur menyederhanakan semua bahagian ketidaksamaan berganda. Jawapannya ditulis dalam bentuk selang berangka tertutup, kerana ketidaksamaan itu tidak ketat. Contoh 3
Kami akan berminat dengan pelbagai nilai tdi mana titik sinusoid akan terletak di atas garisan.
Nilai t kita menulis dalam bentuk ketidaksamaan berganda, kita menulis semula nilai yang sama untuk 2x dan nyatakan x. Kami menulis jawapan dalam bentuk selang berangka. Dan lagi formula itu kos\u003e a. Jika kos\u003e a, (-1≤tetapi≤1), kemudian - arccos a + 2πn< t < arccos a + 2πn, nєZ. Gunakan formula untuk menyelesaikan ketidaksamaan trigonometri, dan anda akan menjimatkan masa ujian ujian. Dan sekarang formula itu
yang perlu anda gunakan pada peperiksaan Ujian UNT atau Sentralisasi apabila menyelesaikan ketidaksamaan trigonometri bentuk kos Jika kos , (-1≤tetapi≤1), kemudian arccos a + 2πn< t < 2π — arccos a + 2πn, nєZ. Gunakan formula ini untuk menyelesaikan ketidaksamaan yang dibincangkan dalam artikel ini, dan anda akan mendapat jawapan dengan lebih cepat dan tanpa sebarang graf!
Kami menyelesaikan ketidaksamaan kedua:
Dalam menyelesaikan ketidaksamaan kedua, kita terpaksa mengubah sebelah kiri ketidaksamaan ini menggunakan rumus sinus hujah ganda untuk mendapatkan ketidaksamaan bentuk: sintetaa. Seterusnya, kami mengikuti algoritma. Kami menyelesaikan ketidaksamaan ketiga:
Para graduan dan pemohon yang terhormat! Perlu diingat bahawa kaedah seperti menyelesaikan masalah ketidaksamaan trigonometri sebagai kaedah grafik di atas dan, mungkin, anda tahu, cara menyelesaikan dengan bantuan satu lingkaran trigonometri (lingkaran trigonometri) hanya berlaku pada peringkat pertama kajian bahagian trigonometri "Penyelesaian persamaan trigonometri dan ketaksamaan". Saya fikir anda akan ingat bahawa anda pada mulanya menyelesaikan persamaan trigonometri paling mudah menggunakan graf atau bulatan. Walau bagaimanapun, kini tidak berlaku kepada anda untuk menyelesaikan persamaan trigonometri dengan cara ini. Bagaimana anda menyelesaikannya? Betul, mengikut formula. Oleh itu, ketidaksamaan trigonometri perlu diselesaikan dengan formula, terutamanya dalam ujian, apabila setiap minit. Jadi, selesaikan tiga ketidaksamaan dalam pelajaran ini dengan menggunakan formula yang sesuai. Jika sint\u003e adi mana -1 ≤ a≤1 kemudian arcsin a + 2πn< t < π — arcsin a + 2πn, nєZ. Ketahui formula! Dan akhirnya: adakah anda tahu bahawa matematik adalah definisi, peraturan, dan FORMULAS? Sudah tentu anda tahu! Dan yang paling ingin tahu, setelah mempelajari artikel ini dan menonton video itu, berkata: "Berapa lama dan sukar! Tetapi ada formula yang membolehkan kita menyelesaikan ketidaksamaan ini tanpa sebarang graf dan bulatan? "Ya, tentu saja, ada! UNTUK MENYELESAIKAN KEPIMPINAN SPESIES: sint (-1≤tetapi≤1) formula berikut adalah benar: - π - arcsin a + 2πn< t < arcsin a + 2πn, nєZ. Sapukan kepada contoh di atas dan anda akan mendapat jawapan lebih cepat! Kesimpulan: BELAJAR FORMULAS, RAKAN! Halaman 1 dari 1 1 Dalam pelajaran praktikal, kami akan mengulangi jenis tugas asas dari topik "Trigonometri", kami akan menganalisis lebih lanjut masalah peningkatan kerumitan dan mempertimbangkan contoh-contoh untuk menyelesaikan pelbagai ketaksamaan trigonometri dan sistem mereka. Pelajaran ini akan membantu anda mempersiapkan salah satu jenis tugas B5, B7, C1 dan C3. Mari kita mulakan dengan mengulangi jenis utama tugas yang kita sampaikan dalam topik "Trigonometri" dan menyelesaikan beberapa masalah yang tidak standard. Nombor petugas 1. Tukar sudut kepada radian dan darjah: a); b) a) Kami menggunakan formula untuk menukar darjah kepada radian
Gantikan nilai yang dinyatakan ke dalamnya. b) Kami menggunakan formula untuk menukarkan radian kepada darjah
Mari kita buat penggantian Jawapannya. a); b) Nombor petugas 2. Kira: a); b) a) Oleh kerana sudut jauh melebihi jadual, kita mengurangkannya dengan mengurangkan tempoh sinus. Kerana sudut ditunjukkan dalam radian, maka kita akan mempertimbangkan tempoh sebagai. b) Dalam kes ini, keadaannya sama. Oleh kerana sudut ditunjukkan dalam darjah, kita juga akan mempertimbangkan tempoh tangen sebagai. Sudut yang dihasilkan, walaupun kurang daripada tempoh, tetapi lebih besar, yang bermaksud bahawa ia tidak lagi merujuk kepada utama, tetapi kepada bahagian lanjutan meja. Untuk tidak melatih ingatan kita sekali lagi dengan mengingati jadual nilai-nilai fungsi trigo yang dilanjutkan, kita tolak tempoh tangen semula: Kami menggunakan fungsi tangen ganjil. Jawapannya. a) 1; b) Nombor petugas 3. Kira Kami mengurangkan keseluruhan ungkapan kepada tangen, membahagi pengangka dan penyebut pecahan oleh. Pada masa yang sama, kita tidak boleh takut bahawa, kerana dalam kes ini, nilai tangen tidak akan wujud. Nombor petugas 4. Mudahkan ekspresi. Ungkapan ini ditukar menggunakan formula cast. Hanya saja mereka direkodkan secara luar biasa dengan menggunakan darjah. Ungkapan pertama biasanya merupakan nombor. Memudahkan semua fungsi trigo pula: Kerana , maka fungsi itu berubah kepada fungsi bersama, iaitu. pada cotangent, dan sudut jatuh ke suku kedua, di mana tangen awal mempunyai tanda negatif.
Atas alasan yang sama seperti ungkapan sebelumnya, fungsi berubah menjadi fungsi bersama, iaitu. pada cotangent, dan sudut jatuh pada suku pertama, di mana tangen awal mempunyai tanda positif. Gantikan semuanya dalam ungkapan yang mudah: Nombor petugas 5. Mudahkan ekspresi. Kami menulis tangen sudut berganda mengikut formula yang sepadan dan memudahkan ungkapan: Identiti terakhir adalah salah satu formula penggantian universal untuk kosinus. Nombor petugas 6. Untuk mengira. Perkara utama bukanlah untuk membuat ralat standard dan tidak memberi jawapan yang sama. Anda tidak boleh menggunakan harta utama arctangent sementara ada pengganda dalam bentuk padanan di dekatnya. Untuk menghilangkannya, kami akan menulis ungkapan mengikut formula tangen sudut berganda, dan pada masa yang sama kami melayannya sebagai hujah biasa.
Sekarang kita boleh menggunakan harta utama arc tangent, ingat bahawa tidak ada batasan ke atas hasil berangka. Nombor petugas 7. Selesaikan persamaan. Apabila menyelesaikan persamaan pecahan, yang bersamaan dengan sifar, selalu ditunjukkan bahawa pengangka adalah sifar, dan penyebutnya tidak, kerana tidak boleh dibahagikan dengan sifar.
Persamaan pertama adalah kes khas persamaan yang paling mudah, yang diselesaikan menggunakan bulatan trigonometri. Ingat kaedah penyelesaian ini sendiri. Ketaksamaan kedua diselesaikan sebagai persamaan paling mudah dengan formula umum akar tangen, tetapi hanya dengan notasi tanda tidak sama rata.
Seperti yang anda dapat lihat, satu keluarga akar mengecualikan yang sama persis dengan keluarga penampilan akar yang tidak memenuhi persamaan. I.e. tiada akar. Jawapannya. Tiada akar. Nombor petugas 8. Selesaikan persamaan. Hanya ambil perhatian bahawa kita boleh mengambil faktor yang sama dan melakukan ini: Persamaan itu dikurangkan kepada salah satu bentuk piawai apabila produk beberapa faktor sama dengan sifar. Kita sudah tahu bahawa dalam kes ini, salah seorang daripada mereka sama dengan sifar atau yang lain, atau ketiga. Kami menulis ini sebagai satu set persamaan:
Dua persamaan pertama adalah kes-kes tertentu yang paling mudah, kita telah menemui persamaan sedemikian banyak kali, jadi kita segera menunjukkan penyelesaiannya. Persamaan ketiga dikurangkan kepada satu fungsi menggunakan formula sinus dua sudut.
Kami secara berasingan menyelesaikan persamaan terakhir:
Persamaan ini tidak mempunyai akar, kerana nilai sinus tidak boleh dilangkau Oleh itu, penyelesaiannya adalah hanya dua keluarga pertama akar, mereka boleh digabungkan menjadi satu, yang mudah ditunjukkan pada bulatan trigonometri:
Ini adalah keluarga semua bahagian, iaitu Kami meneruskan penyelesaian kepada ketidaksamaan trigonometri. Pertama, kita akan menganalisis pendekatan untuk menyelesaikan contoh tanpa menggunakan formula penyelesaian umum, tetapi dengan bantuan bulatan trigonometri. Nombor petugas 9. Selesaikan ketidaksamaan. Marilah kita melukis garis tambahan pada lingkaran trigonometri yang bersamaan dengan nilai sinus yang sama dengan, dan tunjukkan selang sudut yang memuaskan ketidaksamaan.
Sangat penting untuk memahami bagaimana untuk menunjukkan jarak selang yang diperolehi, iaitu apakah permulaannya dan apa yang akhir. Permulaan jurang akan menjadi sudut yang bersamaan dengan titik di mana kita akan masuk pada permulaan jurang jika kita bergerak lawan jam. Dalam kes kita, ini adalah titik yang di sebelah kiri, kerana bergerak lawan arah dan lulus titik yang betul, kita, sebaliknya, keluar dari sudut sudut yang perlu. Oleh itu, titik yang betul akan sesuai dengan hujung jurang. Kini adalah perlu untuk memahami nilai-nilai sudut awal dan akhir jurang penyelesaian kepada ketidaksamaan. Kesilapan biasa adalah untuk menunjukkan dengan segera bahawa titik yang betul sepadan dengan sudut, kiri dan memberi jawapan. Ini salah! Sila ambil perhatian bahawa kami hanya menunjukkan jurang yang sepadan dengan bahagian atas bulatan, walaupun kami berminat dengan yang lebih rendah, dengan kata lain, kami bercampur dengan permulaan dan penghujung selang keputusan yang kami perlukan. Agar selang permulaan bermula dari sudut titik yang betul, dan berakhir dengan sudut titik kiri, maka sudut pertama yang ditunjukkan adalah kurang daripada yang kedua. Untuk melakukan ini, kita perlu mengukur sudut titik yang betul dalam arah rujukan negatif, iaitu. mengikut arah jam dan ia akan sama. Kemudian, bermula dari arah itu dengan arah yang positif mengikut arah jam, kita akan sampai ke titik yang betul selepas titik kiri dan mendapatkan nilai sudut untuk itu. Sekarang permulaan selang sudut adalah kurang daripada akhir, dan kita boleh merakam selang penyelesaian tanpa mengambil kira tempoh: Memandangkan selang tersebut akan diulangi bilangan kali yang terhingga selepas mana-mana nombor lilitan lilitan, kami memperoleh penyelesaian umum dengan mengambil kira tempoh sine: Kami meletakkan tanda kurung kerana fakta bahawa ketidaksamaan itu ketat, dan kami menusuk mata pada bulatan yang sesuai dengan hujung jurang. Bandingkan jawapan yang diperoleh dengan formula untuk penyelesaian umum yang kami sampaikan dalam kuliah. Jawapannya. Kaedah yang ditunjukkan adalah baik untuk memahami di mana rumus untuk penyelesaian umum dari trigonequalities yang paling mudah berasal. Di samping itu, ia berguna bagi mereka yang terlalu malas untuk mempelajari semua formula besar ini. Walau bagaimanapun, kaedah itu sendiri juga sukar, memilih cara pendekatan penyelesaiannya paling mudah untuk anda. Untuk menyelesaikan ketidaksamaan trigonometri, seseorang juga boleh menggunakan graf fungsi di mana garisan tambahan dibina sama dengan kaedah yang ditunjukkan menggunakan bulatan unit. Sekiranya anda berminat, cuba tentukan pendekatan ini untuk penyelesaiannya sendiri. Dalam apa yang berikut, kami akan menggunakan formula umum untuk menyelesaikan ketidaksamaan trigonometri yang paling mudah. Nombor petugas 10. Selesaikan ketidaksamaan. Kami menggunakan formula penyelesaian umum dengan mengambil kira bahawa ketidaksamaan tidak ketat: Kami masuk dalam kes kami: Jawapannya. Nombor petugas 11. Selesaikan ketidaksamaan. Kami menggunakan formula penyelesaian am untuk ketidaksamaan ketat yang sama: Jawapannya. Nombor petugas 12. Menyelesaikan ketidaksamaan: a); b) Dalam ketidaksamaan yang ditunjukkan, seseorang tidak perlu tergesa-gesa untuk menggunakan formula penyelesaian am atau bulatan trigonometri, ia cukup untuk mengingati semula nilai sinus dan kosinus. a) Oleh kerana b) kerana Begitu juga, sinus apa-apa hujah sentiasa memuaskan ketidaksamaan yang dinyatakan dalam keadaan. Oleh itu, ketidaksamaan itu dipenuhi oleh semua nilai yang sah hujah. Jawapannya. a) tiada keputusan; b) Tugas 13. Selesaikan ketidaksamaan |
| Baca: |
|---|
Baru
- Apa yang memecahkan baron "kaku"?
- Ahli pergerakan Putih
- Jalan Suvorov dan pasukan ke tanah air mereka
- Fungsi F (x) dipanggil antiderivatif untuk fungsi f (x) jika F` (x) \u003d f (x) atau dF (x) \u003d f (x) dx
- Program pengurangan frasa darjah
- Istilah yang serupa, pengurangan mereka, contohnya
- Pengembara Rusia lazarev
- Menyelesaikan persamaan kuadrat tidak lengkap
- Penyelesaian persamaan kuadratik, formula akar, contohnya
- Pesawat menyelaras (Gred 6) - Pasar raya pengetahuan



















 Jadi, penyelesaian kepada ketidaksamaan ini adalah jurang:
Jadi, penyelesaian kepada ketidaksamaan ini adalah jurang:







 Memandangkan periodik fungsi sinus, kita menulis ketidaksamaan berganda untuk nilai-nilai hujah tmemuaskan ketidaksamaan terakhir. Kembali ke pemboleh ubah asal. Kami mengubah ketidaksamaan ganda yang terhasil dan menyatakan pembolehubah xJawapannya ditulis dalam bentuk jurang.
Memandangkan periodik fungsi sinus, kita menulis ketidaksamaan berganda untuk nilai-nilai hujah tmemuaskan ketidaksamaan terakhir. Kembali ke pemboleh ubah asal. Kami mengubah ketidaksamaan ganda yang terhasil dan menyatakan pembolehubah xJawapannya ditulis dalam bentuk jurang.