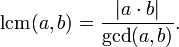Tetapi banyak nombor semulajadi juga dibahagikan sepenuhnya ke nombor semula jadi yang lain.

Contohnya:

Nombor 12 dibahagikan dengan 1, 2, 3, 4, 6, 12;

Nombor 36 dibahagikan dengan 1, 2, 3, 4, 6, 12, 18, 36.

Nombor-nombor yang mana nombor dibahagi sepenuhnya (untuk 12 ialah 1, 2, 3, 4, 6, dan 12) dipanggil pembahagi nombor. Pembahagi nombor semulajadi a  adalah nombor semulajadi yang membahagikan nombor yang diberikan a  tanpa kesan. Nombor semulajadi yang mempunyai lebih daripada dua pembahagi dipanggil komposit .

Perhatikan bahawa nombor 12 dan 36 mempunyai pembahagi biasa. Nombor-nombor ini ialah: 1, 2, 3, 4, 6, 12. Yang terbesar dari pembahagi nombor-nombor ini ialah 12. Pembahagi biasa dua nombor yang diberikan a  dan b  adalah nombor di mana kedua nombor diberi dibahagikan tanpa baki adan b.

Berbilang biasa  nombor berganda dipanggil nombor yang dibahagikan dengan setiap nombor ini. Contohnya, angka-angka 9, 18 dan 45 mempunyai gandaan biasa sebanyak 180. Tetapi 90 dan 360 juga merupakan gandaan biasa mereka. Daripada kesemua j jumlah gandaan, selalu ada yang terkecil, dalam kes ini 90. Nombor ini dipanggil yang terkeciljumlah berganda (NOC).

NOC sentiasa nombor semulajadi, yang mesti lebih besar daripada yang paling banyak nombor yang mana ia ditentukan.

Paling jarang berbilang (NLC). Hartanah

Commutativity:

Persamaan:

Khususnya, jika dan nombor coprime, maka:

Gandakan sekurang-kurangnya dua bulat mdan   n  adalah pembahagi semua gandaan umum yang lain mdan   n. Selain itu, banyak gandaan biasa m, n  bertepatan dengan set gandaan untuk NOC ( m, n).

Asymptotics untuk dapat dinyatakan dalam bentuk beberapa fungsi teoretis nombor.

Jadi   Fungsi Chebyshev  . Dan juga:

Ini adalah dari definisi dan sifat-sifat fungsi Landau g (n).

Apa yang berikut dari undang-undang pengedaran prima.

Menemukan pelbagai biasa terkecil (LCL).

NOC ( a, b) boleh dikira dalam beberapa cara:

1. Jika pembahagi umum terbesar diketahui, anda boleh menggunakan hubungannya dengan NOC:

2. Biarkan penaksiran kanonik kedua-dua nombor diketahui:

di mana p 1, ..., p k  - pelbagai nombor utama, dan d 1, ..., d k  dan e 1, ..., e k  - integer bukan negatif (mereka boleh nol jika perdana sepadan tidak berada dalam pengembangan).

Kemudian NOC ( a,b) dikira dengan formula:

Dengan kata lain, pengembangan LCL mengandungi semua faktor utama yang muncul dalam sekurang-kurangnya salah satu penguraian nombor a, b, dan yang terbesar dari kedua-dua pendorong faktor ini diambil.

Contoh:

Pengiraan nombor umum terkecil beberapa nombor boleh dikurangkan kepada beberapa perhitungan NOC berturut-turut dua nombor:

Peraturan ini.  Untuk mencari NOC sejumlah nombor, anda perlu:

- menguraikan nombor menjadi faktor utama;

- memindahkan penguraian terbesar ke dalam faktor-faktor produk yang dikehendaki (hasil daripada faktor nombor terbesar diberikan), dan kemudian tambahkan faktor-faktor dari penguraian nombor-nombor lain yang tidak berlaku pada nombor pertama atau kurang dalam;

- produk utama faktor utama akan menjadi NOC nombor yang diberikan.

Mana-mana dua atau lebih nombor semula jadi mempunyai NOC mereka sendiri. Sekiranya nombor tidak berganda antara satu sama lain atau tidak mempunyai faktor yang sama dalam pengembangan, maka LCL mereka sama dengan produk nombor-nombor ini.

Faktor mudah 28 (2, 2, 7) ditambah dengan faktor 3 (angka 21), produk yang dihasilkan (84) akan menjadi nombor terkecil yang dibahagi 21 dan 28.

Faktor mudah bilangan terbesar 30 ditambah dengan faktor 5 dari bilangan 25, produk yang dihasilkan 150 lebih besar daripada bilangan terbesar 30 dan dibahagi dengan semua nombor yang diberikan tanpa baki. Ini adalah produk terkecil yang mungkin (150, 250, 300 ...), yang mana semua nombor diberi adalah gandaan.

Nombor 2,3,11,37 adalah perdana, jadi LCL mereka sama dengan produk nombor yang diberikan.

Peraturan ini. Untuk mengira NOC prima, anda perlu mengalikan semua nombor ini di kalangan mereka.

Pilihan lain:

Untuk mencari nombor biasa terkecil (LCL) beberapa nombor yang anda perlukan:

1) mewakili setiap nombor sebagai produk faktor utama, contohnya:

504 \u003d 2 · 2 · 2 · 3 · 3 · 7,

2) menulis kuasa semua faktor utama:

504 \u003d 2 · 2 · 2 · 3 · 3 · 7 \u003d 2 3 · 3 2 · 7 1,

3) tulis semua pembahagi (faktor) yang mudah bagi setiap nombor ini;

4) memilih tahap yang paling besar dari setiap mereka, yang terdapat dalam semua pengembangan bilangan ini;

5) untuk darab darjah ini.

Contoh  . Cari nombor NOC: 168, 180, dan 3024.

Penyelesaian  . 168 \u003d 2 · 2 · 2 · 3 · 7 \u003d 2 3 · 3 1 · 7 1,

180 \u003d 2 · 2 · 3 · 3 · 5 \u003d 2 2 · 3 2 · 5 1,

3024 \u003d 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 \u003d 2 4 · 3 3 · 7 1.

Kami menulis derajat terbesar dari semua pembahagi mudah dan membiak mereka:

NOC \u003d 2 4 · 3 3 · 5 1 · 7 1 \u003d 15120.

Nombor kedua:   b \u003d

Pemisah bit  Tiada ruang pembatas "'

Keputusan:

Pembahagi umum terbesar GCD ( a,b)=6

Paling tidak banyak NOC biasa ( a,b)=468

Integer positif terbesar di mana nombor a dan b boleh dibahagi tanpa selebihnya dipanggil faktor umum yang paling besar  (GCD) nombor-nombor ini. Ia ditetapkan GCD (a, b), (a, b), gcd (a, b) atau hcf (a, b).

Paling jarang  (NOC) dua bulat a dan b adalah integer positif terkecil yang boleh dibahagikan dengan a dan b tanpa baki. Ia ditetapkan NOC (a, b), atau lcm (a, b).

Integer a dan b dipanggil saling mudahjika mereka tidak mempunyai faktor yang sama selain +1 dan -1.

Faktor yang paling besar

Letakkan dua nombor positif diberikan a  1 dan a  2 1). Ia dikehendaki untuk mencari pembahagi umum nombor-nombor ini, iaitu. mencari nombor sedemikian λ yang membahagikan nombor a  1 dan a  2 pada masa yang sama. Kami menerangkan algoritma.

1) Dalam artikel ini, nombor perkataan akan difahami sebagai integer.

Biarkan a 1 ≥ a  2 dan biarkan

di mana m 1 , a  3 beberapa bulat a 3 <a  2 (baki bahagian a  1 pada a  2 sepatutnya kurang a 2).

Anggapkan itu λ   membahagi a  1 dan a  2 kemudian λ   membahagi m 1 a  2 dan λ   membahagi a 1 −m 1 a 2 =a  3 (Pernyataan 2 dari artikel "Pembezaan nombor. Tanda tanda yang tidak dapat dilihat"). Ia mengikuti setiap pembahagi biasa a  1 dan a  2 adalah pembahagi biasa a  2 dan a  3. Berbincang juga benar jika λ   faktor biasa a  2 dan a  3 kemudian m 1 a  2 dan a 1 =m 1 a 2 +a  3 juga dibahagikan kepada λ . Oleh itu pembahagi biasa a  2 dan a  3 terdapat pembahagi yang biasa juga a  1 dan a  2. Sejak itu a 3 <a 2 ≤a  1, maka kita boleh mengatakan bahawa penyelesaian kepada masalah mencari pembagi nombor yang biasa a  1 dan a  2 dikurangkan kepada masalah yang lebih mudah untuk mencari pembahagi nombor yang biasa a  2 dan a 3 .

Jika a  3 ≠ 0, maka boleh dibahagikan a  2 pada a  3. Kemudian

,

di mana m  1 dan a  4 beberapa bulat, ( a  4 baki bahagian a  2 pada a 3 (a 4 <a  3)). Dengan sebab yang sama, kami menyimpulkan bahawa pembahagi nombor biasa a  3 dan a  4 pertandingan pembahagi nombor biasa a  2 dan a  3, dan juga dengan pembahagi yang biasa a  1 dan a  2. Sejak itu a 1 , a 2 , a 3 , a  4, ... nombor-nombor yang sentiasa berkurang, dan kerana terdapat bilangan bilangan bulat antara a  2 dan 0, kemudian pada beberapa langkah n, baki bahagian a  n pada a  n + 1 akan menjadi sifar ( a  n + 2 \u003d 0).

.

Setiap pembahagi biasa λ   nombor a  1 dan a  2 juga pembahagi nombor a  2 dan a 3 , a  3 dan a 4 , .... a  n dan a  n + 1. Yang bercakap juga benar, pembahagi nombor biasa a  n dan a  n + 1 juga adalah pembahagi nombor a  n - 1 dan a  n, ...., a  2 dan a 3 , a  1 dan a  2. Tetapi pembahagi nombor yang biasa a  n dan a  n + 1 ialah nombor a  n + 1, kerana a  n dan a n + 1 boleh dibahagikan dengan a  n + 1 (ingat bahawa a  n + 2 \u003d 0). Oleh itu a  n + 1 juga merupakan pembahagi nombor a  1 dan a 2 .

Perhatikan bahawa nombor itu a  n + 1 adalah yang terbesar divisyen nombor a  n dan a  n + 1, sejak pembahagi terbesar a  n + 1 adalah dirinya sendiri a  n + 1. Jika a  n + 1 boleh direpresentasikan sebagai produk bilangan bulat, maka nombor-nombor ini juga merupakan pembagi nombor biasa a  1 dan a  2. Nombor a  n + 1 dipanggil   faktor umum yang paling besar  nombor a  1 dan a 2 .

Nombor a  1 dan a  2 boleh menjadi nombor positif dan negatif. Jika salah satu nombor adalah sifar, maka pembahagi lazim nombor-nombor ini akan sama dengan nilai mutlak nombor lain. Pembahagi biasa nombor sifar tidak ditakrifkan.

Algoritma di atas dipanggil algoritma Euclideanuntuk mencari pembahagi lazim terbesar dua bulat.

Satu contoh mencari pembahagi umum yang paling besar dalam dua nombor

Cari faktor umum yang paling besar dari kedua nombor 630 dan 434.

• Langkah 1. Bahagikan nombor 630 hingga 434. Selebihnya ialah 196.
• Langkah 2. Bahagikan nombor 434 hingga 196. Selebihnya ialah 42.
• Langkah 3. Bahagikan nombor 196 hingga 42. Selebihnya ialah 28.
• Langkah 4. Bahagikan nombor 42 hingga 28. Selebihnya ialah 14.
• Langkah 5. Bahagikan nombor 28 hingga 14. Selebihnya ialah 0.

Dalam langkah 5, baki bahagian adalah 0. Oleh itu, pembahagi umum nombor 630 dan 434 adalah 14. Perhatikan bahawa nombor 2 dan 7 juga adalah pembahagi nombor 630 dan 434.

  Nombor nombor secara bersamaan

Definisi 1.   Biarkan pembahagi nombor yang paling umum a  1 dan a  2 adalah sama dengan satu. Kemudian nombor ini dipanggil nombor nombor salingtidak mempunyai pembahagi biasa.

Teorem itu 1.   Jika a  1 dan a  2 adalah nombor coprime, dan λ   beberapa nombor, maka mana-mana pembahagi nombor biasa λa  1 dan a  2 juga merupakan pembahagi nombor biasa λ   dan a 2 .

Bukti. Pertimbangkan algoritma Euclidean untuk mencari penunjuk umum nombor terbesar a  1 dan a  2 (lihat di atas).

.

Dari syarat-syarat teorem ia adalah berikut bahawa pembahagi nombor yang paling besar a  1 dan a  2, dan oleh itu a  n dan a  n + 1 ialah 1. i.e. a  n + 1 \u003d 1.

Maju semua kesamaan ini dengan λ kemudian

.

Biarkan faktor biasa a 1 λ   dan a  2 makan δ . Kemudian δ   adalah faktor dalam a 1 λ , m 1 a 2 λ   dan dalam a 1 λ -m 1 a 2 λ =a 3 λ   (lihat "Pembezaan nombor", Proposisi 2). Seterusnya δ   adalah faktor dalam a 2 λ   dan m 2 a 3 λ , dan oleh itu, adalah faktor dalam a 2 λ -m 2 a 3 λ =a 4 λ .

Penalaran jadi kami yakin itu δ   adalah faktor dalam a  n - 1 λ   dan m  n - 1 a  n λ , dan oleh itu dalam a  n - 1 λ −m  n - 1 a  n λ =a  n + 1 λ . Sejak itu a  n + 1 \u003d 1, kemudian δ   adalah faktor dalam λ . Oleh itu nombor itu δ   adalah pembahagi nombor biasa λ   dan a 2 .

Kami menganggap kes-kes tertentu Teorem 1.

Akibatnya 1.   Biarkan a  dan c  prima adalah relatif b. Kemudian produk mereka ac  adalah relatif utama kepada b.

Benar. Daripada Teorem 1 ac  dan b  mempunyai pembahagi biasa yang sama seperti c  dan b. Tetapi nombor c  dan b  saling mudah, iaitu mempunyai satu faktor yang sama 1. Kemudian ac  dan b juga mempunyai satu faktor yang sama 1. Oleh itu ac  dan b  saling mudah.

Akibatnya 2.   Biarkan a  dan b  nombor coprime dan biarkan b  membahagi ak. Kemudian b  membahagikan dan k.

Benar. Dari kenyataan kenyataan ak  dan b  mempunyai pembahagi biasa b. Oleh sebab Teorem 1, b  mestilah pembahagi biasa b  dan k. Oleh itu b  membahagi k.

Corollary 1 boleh diperkatakan.

Akibatnya 3.   1. Biarkan nombor-nombor a 1 , a 2 , a 3 , ..., a  m perdana berkenaan dengan nombor tersebut b. Kemudian a 1 a 2 , a 1 a  2 a 3 , ..., a 1 a 2 a  3 ··· a  m, hasil nombor-nombor ini adalah prima berkenaan dengan nombor tersebut b.

2. Marilah kita mempunyai dua baris nombor

supaya setiap nombor dalam baris pertama adalah perdana berkenaan dengan setiap nombor dalam baris kedua. Kemudian produk itu

Ia dikehendaki untuk mencari nombor sedemikian yang boleh dibahagikan oleh setiap nombor ini.

Sekiranya nombor dibahagikan dengan a  1, maka ia mempunyai bentuk sa  1 di mana s  beberapa nombor. Jika q  adalah pembahagi nombor yang paling umum a  1 dan a  2 kemudian

di mana s  1 ialah integer. Kemudian

adalah pelbagai biasa terkecil a  1 dan a 2 .

a  1 dan a  2 adalah coprime, maka bilangan nombor yang paling tidak biasa a  1 dan a 2:

Anda perlu mencari nombor terkecil dari bilangan ini.

Daripada yang tersebut di atas, ia mengikuti mana-mana nombor berganda a 1 , a 2 , a  3 mestilah nombor berganda ε   dan a  3, dan sebaliknya. Biarkan nombor berganda yang paling biasa ε   dan a  3 makan ε   1. Seterusnya, pelbagai nombor a 1 , a 2 , a 3 , a  4 mestilah nombor berganda ε   1 dan a  4. Biarkan nombor berganda yang paling biasa ε   1 dan a  4 makan ε   2. Oleh itu, kami mendapati bahawa semua nombor berganda a 1 , a 2 , a 3 ,...,a  m bertepatan dengan gandaan beberapa nombor tertentu ε   n, yang dipanggil nombor umum terkecil daripada nombor yang diberikan.

Dalam kes tertentu apabila nombor tersebut a 1 , a 2 , a 3 ,...,a  m adalah coprime, maka bilangan nombor paling kurang biasa a 1 , a  2 seperti yang ditunjukkan di atas mempunyai bentuk (3). Selanjutnya, sejak a  3 utama dengan nombor a 1 , a  2 kemudian a  3 utama berkenaan dengan nombor tersebut a  1 a  2 (Corollary 1). Jadi bilangan nombor yang paling kurang biasa a 1 ,a 2 ,a  3 adalah nombor a  1 a  2 a  3. Berunding dengan cara yang sama, kami tiba di pernyataan berikut.

Kelulusan 1.   Gandakan biasa yang sama sekali berbeza a 1 , a 2 , a 3 ,...,a  m adalah sama dengan produk mereka a  1 a  2 a  3 ··· a  m.

Kelulusan 2.   Mana-mana nombor yang dibahagikan oleh setiap nombor utama a 1 , a 2 , a 3 ,...,a  m juga dibahagikan dengan produk mereka a  1 a  2 a  3 ··· a  m.

Definisi  Integer positif terbesar, yang boleh dibahagikan tanpa baki nombor a dan b, dipanggil faktor umum yang paling besar (GCD)  nombor ini.

Cari pembahagi umum nombor 24 dan 35.
  Pembahagi 24 ialah nombor 1, 2, 3, 4, 6, 8, 12, 24, dan pembahagi 35 ialah nombor 1, 5, 7, 35.
  Kita lihat bahawa nombor 24 dan 35 hanya mempunyai satu faktor biasa - nombor 1. Nombor tersebut dipanggil saling mudah.

Definisi  Nombor semula jadi dipanggil saling mudahjika faktor biasa terbesar mereka (GCD) adalah 1.

Faktor umum yang paling besar (GCD)  boleh didapati tanpa menulis semua pembahagi nombor yang diberikan.

Faktor nombor 48 dan 36, kami dapat:
48 = 2 * 2 * 2 * 2 * 3, 36 = 2 * 2 * 3 * 3.
  Dari faktor-faktor yang termasuk dalam pengembangan nombor-nombor pertama ini, menyebarkan mereka yang tidak termasuk dalam pengembangan bilangan kedua (iaitu dua dada).
  Faktor-faktor 2 * 2 * 3 kekal.Produk mereka adalah 12. Nombor ini adalah faktor umum yang paling besar iaitu 48 dan 36. Mereka juga mendapati faktor umum yang paling besar dari tiga atau lebih nombor.

Untuk mencari faktor umum yang paling besar

  2) dari faktor-faktor yang termasuk dalam pengembangan salah satu nombor ini, menyeberang yang tidak termasuk dalam pengembangan bilangan lain;
  3) mencari produk faktor yang selebihnya.

Sekiranya semua nombor diberi dibahagikan dengan salah satu daripadanya, maka nombor ini adalah faktor umum yang paling besar  nombor yang diberikan.
  Sebagai contoh, pembahagi umum nombor 15, 45, 75 dan 180 akan menjadi nombor 15, kerana semua nombor lain dibahagikan kepada: 45, 75, dan 180.

Paling jarang yang biasa (NLC)

Definisi Paling jarang yang biasa (NLC)  integer positif a dan b adalah integer positif terkecil yang berganda dari kedua a dan b. Nombor biasa terkecil (LCL) nombor 75 dan 60 boleh didapati tanpa menulis gandaan berturut-turut nombor-nombor ini. Untuk melakukan ini, kita mengurai 75 dan 60 ke dalam faktor mudah: 75 \u003d 3 * 5 * 5, dan 60 \u003d 2 * 2 * 3 * 5.
  Kami menuliskan faktor-faktor yang termasuk dalam pengembangan pertama nombor-nombor ini, dan menambah faktor yang hilang 2 dan 2 dari pengembangan nombor kedua kepada mereka (iaitu, menggabungkan faktor-faktor).
  Kami mendapat lima faktor 2 * 2 * 3 * 5 * 5, produknya ialah 300. Nombor ini adalah gandaan biasa terkecil 75 dan 60.

Mereka juga mencari gandaan yang paling tidak biasa untuk tiga atau lebih nombor.

Untuk mencari gandaan yang kurang biasa  beberapa nombor semulajadi, perlu:
  1) menguraikannya menjadi faktor utama;
  2) menuliskan faktor-faktor yang termasuk dalam pengembangan salah satu nombor;
  3) menambah kepada mereka faktor-faktor yang hilang dari penguraian nombor baki;
  4) mencari produk faktor-faktor yang terhasil.

Ambil perhatian bahawa jika salah satu daripada nombor ini dibahagikan dengan semua nombor lain, maka nombor ini adalah nombor biasa terkecil dari nombor-nombor ini.
  Sebagai contoh, gandaan biasa terkecil daripada 12, 15, 20, dan 60 akan menjadi 60, kerana ia dibahagikan dengan semua nombor yang diberikan.

Pythagoras (abad ke-6 SM) dan para pelajarnya mengkaji persoalan nombor yang boleh dilihat. Nombor yang sama dengan jumlah semua pembahaginya (tanpa bilangan itu sendiri), mereka memanggil nombor yang sempurna. Sebagai contoh, nombor 6 (6 \u003d 1 + 2 + 3), 28 (28 \u003d 1 + 2 + 4 + 7 + 14) adalah sempurna. Nombor sempurna seterusnya ialah 496, 8128, 33 550 336. Pythagorean hanya tahu tiga nombor pertama yang sempurna. Keempat - 8128 - dikenali pada abad ke-1. n e. Yang kelima - 33,550,336 - telah dijumpai pada abad XV. Menjelang tahun 1983, 27 nombor sempurna sudah diketahui. Tetapi sehingga kini, saintis tidak tahu sama ada terdapat nombor sempurna yang ganjil, sama ada terdapat nombor sempurna yang paling besar.
  Kepentingan para ahli matematik purba dalam prima adalah disebabkan oleh fakta bahawa mana-mana nombor adalah sama ada perdana atau boleh diwakili sebagai produk prima, iaitu, prima adalah seperti bata dari mana bilangan semula jadi yang ada dibina.
  Anda mungkin perasan bahawa bilangan prima dalam satu siri nombor semula jadi tidak seimbang - di beberapa bahagian siri terdapat lebih banyak, di lain-lain - kurang. Tetapi selanjutnya kita bergerak di sepanjang garis nombor, bilangan prima kurang biasa. Persoalan timbul: adakah terdapat nombor prima (terbesar) yang terakhir? Ahli matematik Yunani purba Euclid (abad ke-3 SM) dalam bukunya "Beginnings", yang selama dua ribu tahun adalah buku teks utama matematik, membuktikan bahawa terdapat banyak bilangan yang tidak terhingga, iaitu, terdapat perdana yang lebih besar di belakang setiap perdana nombor.
  Untuk mencari nombor perdana, satu lagi ahli matematik Yunani pada masa yang sama, Eratosthenes, mencipta kaedah sedemikian. Dia menulis semua nombor dari 1 ke nombor tertentu, dan kemudian dia menyeberang sebuah unit yang bukan perdana atau nombor kompaun, maka ia melintasi satu angka yang akan datang setelah 2 (angka yang dapat dilihat oleh 2, iaitu 4, 6 , 8, dan sebagainya). Nombor baki yang pertama selepas 2 ialah 3. Kemudian, semua dua nombor selepas 3 dipadam selepas dua (nombor yang gandaan 3, iaitu 6, 9, 12, dan lain-lain). pada akhirnya, hanya angka perdana yang masih tidak diselubungi.

Murid diberi banyak tugas dalam matematik. Di antara mereka, masalah dengan rumusan sedemikian adalah sangat biasa: terdapat dua makna. Bagaimana untuk mencari gandaan biasa terkecil untuk nombor yang diberikan? Adalah perlu untuk melaksanakan tugasan tersebut, kerana kemahiran yang diperolehi digunakan untuk bekerja dengan pecahan dengan penyebut yang berbeza. Dalam artikel ini kita akan menganalisis bagaimana untuk mencari NOC dan konsep asas.

Sebelum anda menemui jawapan kepada persoalan bagaimana untuk mencari NOC, anda perlu membuat keputusan mengenai istilah berbilang. Selalunya, kata-kata konsep ini adalah seperti berikut: pelbagai nilai tertentu A dipanggil nombor semulajadi yang akan dibahagikan oleh A. Tanpa selebihnya, 8, 12, 16, 20, dan sebagainya, hingga batas yang diperlukan, akan menjadi 4 gandaan.

Lebih-lebih lagi, bilangan pembahagi untuk nilai tertentu boleh dibataskan, dan banyak gandaan tak terhingga. Juga ada nilai yang sama untuk nilai semula jadi. Ini adalah penunjuk yang dibahagikan kepada mereka tanpa jejak. Setelah berurusan dengan konsep nilai terkecil untuk petunjuk tertentu, kami akan meneruskan cara untuk mencarinya.

Cari NOC

Gandaan terkecil dari dua atau lebih penunjuk adalah bilangan semulajadi terkecil yang dibahagikan sepenuhnya oleh semua nombor yang ditunjukkan.

Terdapat beberapa cara untuk mencari nilai sedemikian., pertimbangkan kaedah berikut:

1. Sekiranya bilangannya kecil, tuliskan pada baris yang semuanya dibahagikan kepadanya. Sentiasa melakukan ini sehingga anda mendapati yang biasa di kalangan mereka. Dalam rekod mereka dilambangkan dengan huruf K. Sebagai contoh, untuk 4 dan 3, gandaan terkecil ialah 12.
2. Sekiranya ia besar atau jika anda ingin mencari pelbagai untuk 3 atau lebih nilai, maka anda harus menggunakan teknik lain yang melibatkan nombor penguraian menjadi faktor utama. Pertama, letakkan terbesar yang ditentukan, kemudian semua yang lain. Setiap daripada mereka mempunyai bilangan faktor sendiri. Contohnya, kita mengurai 20 (2 * 2 * 5) dan 50 (5 * 5 * 2). Bagi yang lebih kecil daripada mereka, menekankan faktor-faktor dan menambah yang terbesar. Hasilnya adalah 100, yang akan menjadi bilangan biasa terkecil untuk nombor di atas.
3. Apabila mencari 3 nombor (16, 24 dan 36), prinsip-prinsip adalah sama dengan yang lain dua. Marilah kita mengembangkan masing-masing: 16 \u003d 2 * 2 * 2 * 2, 24 \u003d 2 * 2 * 2 * 3, 36 \u003d 2 * 2 * 3 * 3. Hanya dua deretan dari penguraian nombor 16 tidak termasuk dalam penguraian yang terbesar. Kami menambahnya dan kami memperoleh 144, yang merupakan hasil terkecil bagi nilai-nilai berangka yang ditunjukkan sebelumnya.

Sekarang kita tahu apakah metodologi umum untuk mencari nilai terkecil untuk dua, tiga atau lebih nilai.   Walau bagaimanapun, terdapat kaedah peribadi.membantu mencari NOC jika yang sebelumnya tidak membantu.

Bagaimana untuk mencari GCD dan NOC.

Cara peribadi untuk mencari

Bagi mana-mana bahagian matematik, terdapat kes-kes khas mencari NOC yang membantu dalam situasi tertentu:

• jika salah satu daripada nombor dibahagikan kepada yang lain tanpa bakinya, maka bilangan paling rendah dari nombor ini sama dengannya (LCL 60 dan 15 ialah 15);
• nombor nombor saling tidak mempunyai pembahagi utama biasa. Nilai terkecil mereka adalah sama dengan produk nombor-nombor ini. Oleh itu, untuk nombor 7 dan 8, ini akan menjadi 56;
• peraturan yang sama juga berfungsi untuk kes-kes lain, termasuk kes-kes khas, yang boleh dibaca dalam kesusasteraan khusus. Ini juga termasuk kes-kes penguraian nombor komposit, yang menjadi topik artikel individu dan juga disertasi calon.

Kes-kes khas kurang biasa daripada contoh standard. Tetapi terima kasih kepada mereka, anda boleh belajar untuk bekerja dengan pecahan pelbagai peringkat kerumitan. Ini amat sesuai untuk pecahan.di mana terdapat penyebut yang berbeza.

Beberapa contoh

Mari kita lihat beberapa contoh, terima kasih kepada yang kita dapat memahami prinsip mencari paling kurang:

1. Kami mendapati NOC (35; 40). Kami mengurai terlebih dahulu 35 \u003d 5 * 7, maka 40 \u003d 5 * 8. Tambah 8 digit terkecil dan dapatkan NOC 280.
2. NOC (45; 54). Kami menguraikan setiap daripada mereka: 45 \u003d 3 * 3 * 5 dan 54 \u003d 3 * 3 * 6. Tambahkan nombor 6 hingga 45. Kami mendapat NOC sama dengan 270.
3. Nah, contoh terakhir. Terdapat 5 dan 4. Tidak ada gandaan mudah untuk mereka, jadi gandaan yang kurang umum dalam kes ini akan menjadi produk mereka, bersamaan dengan 20.

Terima kasih kepada contoh, anda boleh memahami bagaimana NOC terletak, apa nuansa dan apa makna manipulasi itu.

Cari NOC adalah lebih mudah daripada yang mungkin kelihatan pada mulanya. Untuk ini, kedua-dua penguraian mudah dan pendaraban nilai-nilai mudah antara satu sama lain digunakan. Keupayaan untuk bekerja dengan bahagian matematik ini membantu dalam kajian lanjut tentang topik matematik, terutamanya pecahan pelbagai tahap kerumitan.

Jangan lupa untuk menyelesaikan contoh-contoh secara berkala menggunakan pelbagai kaedah, ini membangunkan alat logik dan membolehkan anda mengingati banyak istilah. Ketahui kaedah mencari penunjuk sedemikian dan anda boleh bekerja dengan baik dengan bahagian matematik yang lain. Bersenang-senang belajar matematik!

Video

Video ini akan membantu anda memahami dan mengingati cara untuk mencari gandaan biasa yang paling kecil.

Kami meneruskan perbincangan mengenai beberapa perkara yang paling tidak biasa yang kami mulakan di bahagian "NOC - pelbagai, definisi, contoh biasa yang terkecil". Dalam topik ini, kita akan melihat cara untuk mencari NOC untuk tiga atau lebih nombor, kita akan meneliti persoalan bagaimana untuk mencari NOC nombor negatif.

Yandex.RTB R-A-339285-1

Pengiraan jumlah biasa terkecil (NLC) melalui GCD

Kami telah menubuhkan sambungan beberapa yang paling biasa dengan pembahagi biasa yang terbesar. Sekarang kita akan belajar menentukan NOC melalui GCD. Pertama, mari kita fikirkan bagaimana untuk melakukannya untuk nombor positif.

Definisi 1

Ganjil biasa terkecil boleh didapati dengan menggunakan faktor umum terbesar dengan formula NOC (a, b) \u003d a · b: GCD (a, b).

Contoh 1

Anda perlu mencari nombor NOC 126 dan 70.

Penyelesaian

Kami mengambil \u003d 126, b \u003d 70. Kami menggantikan nilai-nilai dalam formula untuk mengira gandaan yang paling tidak biasa melalui pembahagi umum yang terbesar LCL (a, b) \u003d a · b: GCD (a, b).

Cari GCD nombor 70 dan 126. Untuk ini kita memerlukan algoritma Euclidean: 126 \u003d 70 · 1 + 56, 70 \u003d 56 · 1 + 14, 56 \u003d 14 · 4, oleh itu, GCD (126 , 70) = 14 .

Kami mengira NOC: NOC (126, 70) \u003d 12670: GCD (126, 70) \u003d 12670: 14 \u003d 630.

Jawapannya ialah:  NOC (126, 70) \u003d 630.

Contoh 2

Cari ketukan nombor 68 dan 34.

Penyelesaian

NOD dalam kes ini, ia tidak sukar untuk meneutralkan, kerana 68 dibahagikan dengan 34. Kami mengira gandaan biasa terkecil dengan formula: NOC (68, 34) \u003d 68 · 34: GCD (68, 34) \u003d 68 · 34: 34 \u003d 68.

Jawapannya ialah:  NOC (68, 34) \u003d 68.

Dalam contoh ini, kita menggunakan peraturan untuk mencari bilangan yang paling tidak biasa untuk integer positif a dan b: jika nombor pertama dibahagikan oleh yang kedua, maka LCM nombor-nombor ini akan sama dengan nombor pertama.

Menemukan NOC oleh nombor pemfaktoran menjadi faktor utama

Sekarang mari kita lihat jalan untuk mencari NOC, yang berdasarkan penguraian nombor ke dalam faktor utama.

Definisi 2

Untuk mencari pelbagai yang paling biasa, kita perlu melakukan beberapa langkah mudah:

• kami mengarang produk semua faktor nombor utama yang mana kita perlu mencari NOC;
• tidak termasuk produk yang diperolehi mereka semua faktor utama;
• produk yang diperoleh selepas menghapuskan faktor utama yang sama akan sama dengan NOC nombor-nombor ini.

Kaedah mencari gandaan biasa terkecil adalah berdasarkan persamaan NOC (a, b) \u003d a · b: GCD (a, b). Jika anda melihat formula, ia menjadi jelas: produk nombor a dan b adalah sama dengan produk semua faktor yang terlibat dalam pengembangan dua nombor ini. Selain itu, GCD dua nombor bersamaan dengan produk semua faktor utama yang secara serentak hadir dalam faktorisasi kedua-dua nombor ini.

Contoh 3

Kami mempunyai dua nombor 75 dan 210. Kita boleh faktor mereka seperti berikut:   75 \u003d 3 · 5 · 5  dan   210 \u003d 2 · 3 · 5 · 7. Jika kita menyusun produk semua faktor dua nombor sumber, kita dapat:   2 · 3 · 3 · 5 · 5 · 5 · 7.

Sekiranya kita mengecualikan faktor-faktor yang sama untuk kedua-dua nombor, 3 dan 5, kita mendapat produk daripada bentuk berikut:   2 · 3 · 5 · 5 · 7 \u003d 1050. Kerja ini akan menjadi NOC kami untuk nombor 75 dan 210.

Contoh 4

Cari nombor NOC 441   dan 700 pemfaktoran kedua-dua nombor menjadi faktor utama.

Penyelesaian

Cari semua faktor utama nombor yang diberikan dalam keadaan:

441 147 49 7 1 3 3 7 7

700 350 175 35 7 1 2 2 5 5 7

Kami mendapat dua rantai nombor: 441 \u003d 3 · 3 · 7 · 7 dan 700 \u003d 2 · 2 · 5 · 5 · 7.

Produk semua faktor yang mengambil bahagian dalam penguraian nombor-nombor ini akan kelihatan seperti:   2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 · 7. Cari faktor yang sama. Inilah nombor 7. Kami mengecualikannya daripada kerja am:   2 · 2 · 3 · 3 · 5 · 5 · 7 · 7. Ternyata NOC   (441, 700) \u003d 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 \u003d 44 100.

Jawapannya ialah:  NOC (441, 700) \u003d 44 100.

Marilah kita memberi satu lagi kaedah untuk mencari LCL dengan menguraikan nombor menjadi faktor utama.

Definisi 3

Sebelum ini, kami mengecualikan faktor biasa bagi kedua-dua nombor dari jumlah faktor. Sekarang kita akan melakukan sebaliknya:

• faktor kedua-dua nombor menjadi faktor utama:
• tambah kepada produk faktor utama nombor pertama faktor yang hilang dari nombor kedua;
• kita mendapat produk, yang akan menjadi NOC yang dikehendaki dua nombor.

Contoh 5

Marilah kita kembali ke nombor 75 dan 210, yang mana kita telah mencari NOC dalam salah satu contoh terdahulu. Kami menguraikannya sebagai faktor utama:   75 \u003d 3 · 5 · 5  dan   210 \u003d 2 · 3 · 5 · 7. Kepada produk faktor 3, 5 dan 5   nombor 75 menambah faktor yang hilang 2   dan 7   nombor 210. Kami mendapat:   2 · 3 · 5 · 5 · 7.Inilah NOC nombor 75 dan 210.

Contoh 6

Ia perlu mengira nombor NOC 84 dan 648.

Penyelesaian

Kami menguraikan nombor dari keadaan menjadi faktor utama:   84 \u003d 2 · 2 · 3 · 7  dan   648 \u003d 2 · 2 · 2 · 3 · 3 · 3 · 3. Tambah kepada produk faktor 2, 2, 3 dan 7   84 faktor hilang 2, 3, 3 dan
3   nombor 648. Kami mendapat produk   2 · 2 · 2 · 3 · 3 · 3 · 3 · 7 \u003d 4536.  Ini adalah gandaan biasa terkecil daripada 84 dan 648.

Jawapannya ialah:  NOC (84, 648) \u003d 4,536.

Mencari NOC tiga atau lebih nombor

Tidak kira berapa banyak nombor yang kita hadapi, algoritma tindakan kita akan selalu sama: kita akan mencari NOC dua angka secara berturut-turut. Terdapat teorem untuk kes ini.

Teorem 1

Katakan kita mempunyai bilangan bulat   a 1, a 2, ..., a k. NOC   m k  nombor ini dijumpai dalam pengiraan berturut-turut m 2 \u003d NOC (a 1, a 2), m 3 \u003d NOC (m 2, a 3), ..., m k \u003d NOC (m k - 1, a k).

Sekarang kita akan mempertimbangkan bagaimana teorem boleh digunakan untuk menyelesaikan masalah tertentu.

Contoh 7

Adalah perlu untuk mengira gandaan biasa terkecil dari empat nombor 140, 9, 54 dan 250 .

Penyelesaian

Kami memperkenalkan notasi: 1 \u003d 140, 2 \u003d 9, 3 \u003d 54, 4 \u003d 250.

Untuk memulakan, kita mengira m 2 \u003d NOC (a 1, a 2) \u003d NOC (140, 9). Kami menggunakan algoritma Euclidean untuk mengira GCD nombor 140 dan 9: 140 \u003d 9 · 15 + 5, 9 \u003d 5 · 1 + 4, 5 \u003d 4 · 1 + 1, 4 \u003d 1 · 4. Kami mendapat: GCD (140, 9) \u003d 1, NOC (140, 9) \u003d 140 · 9: GCD (140, 9) \u003d 140 · 9: 1 \u003d 1,260. Oleh itu, m 2 \u003d 1,260.

Sekarang, dengan algoritma yang sama, kita mengira m 3 \u003d NOC (m 2, a 3) \u003d NOC (1,260, 54). Semasa pengiraan, kita memperoleh m 3 \u003d 3,780.

Ia tetap untuk kita mengira m 4 \u003d NOC (m 3, a 4) \u003d NOC (3 780, 250). Kami mengikuti algoritma yang sama. Kami mendapat m 4 \u003d 94 500.

NOC dari empat nombor dari keadaan contoh ialah 94500.

Jawapannya ialah:  NOC (140, 9, 54, 250) \u003d 94 500.

Seperti yang anda dapat lihat, pengiraan adalah mudah, tetapi memakan masa. Untuk menjimatkan masa, anda boleh pergi dengan cara lain.

Definisi 4

Kami menawarkan algoritma tindakan berikut:

• kita menguraikan semua nombor menjadi faktor utama;
• tambah faktor yang hilang dari hasil nombor kedua kepada produk faktor nombor pertama;
• kepada produk yang diperoleh pada peringkat sebelumnya, tambahkan faktor yang hilang dari nombor ketiga, dan sebagainya;
• produk yang dihasilkan akan menjadi nombor biasa terkecil daripada semua nombor dari keadaan.

Contoh 8

Ia perlu mencari NOC daripada lima nombor 84, 6, 48, 7, 143.

Penyelesaian

Kami menguraikan semua lima nombor menjadi faktor utama: 84 \u003d 2 · 2 · 3 · 7, 6 \u003d 2 · 3, 48 \u003d 2 · 2 · 2 · 2 · 3, 7, 143 \u003d 11 · 13. Nombor Perdana, iaitu nombor 7, tidak dikecualikan menjadi faktor utama. Nombor sedemikian bertepatan dengan faktorisasi mereka.

Sekarang ambil produk faktor utama 2, 2, 3 dan 7 daripada 84 dan tambahkan faktor yang hilang dari nombor kedua kepada mereka. Kami mengurai nombor 6 menjadi 2 dan 3. Faktor-faktor ini sudah ada dalam produk nombor pertama. Oleh itu, kita menghilangkannya.

Kami terus menambah faktor yang hilang. Kami melewati angka 48, dari hasil faktor utama yang kita ambil 2 dan 2. Kemudian tambahkan faktor utama 7 yang keempat dan faktor 11 dan 13 yang kelima. Kami dapat: 2 · 2 · 2 · 2 · 3 · 7 · 11 · 13 \u003d 48 048. Ini adalah nombor umum terkecil daripada lima nombor sumber.

Jawapannya ialah:  NOC (84, 6, 48, 7, 143) \u003d 48 048.

Menemukan beberapa angka negatif terkecil

Untuk mencari bilangan biasa nombor terkecil daripada nombor negatif, nombor ini mesti diganti dengan nombor dengan tanda yang bertentangan, dan kemudian melakukan pengiraan dengan menggunakan algoritma di atas.

Contoh 9

NOC (54, - 34) \u003d NOC (54, 34), dan NOC (- 622, - 46, - 54, - 888) \u003d NOC (622, 46, 54, 888).

Tindakan sedemikian adalah dibenarkan kerana hakikat bahawa jika kita menerimanya   a  dan   - a  - nombor bertentangan,
  maka banyak nombor berganda a  padan pelbagai plural   - a.

Contoh 10

Ia perlu mengira NOC nombor negatif − 145   dan − 45 .

Penyelesaian

Kami akan menggantikan nombor − 145   dan − 45   pada nombor bertentangan 145 dan 45 . Sekarang, menurut algoritma, kita mengira NOC (145, 45) \u003d 145 · 45: GCD (145, 45) \u003d 145 · 45: 5 \u003d 1 305, setelah menentukan GCD menggunakan algoritma Euclidean.

Kami mendapat bahawa NOC nombor adalah 145 dan − 45   sama dengan 1 305 .

Jawapannya ialah:  NOC (- 145, - 45) \u003d 1 305.

Jika anda melihat ralat di dalam teks, sila pilih dan tekan Ctrl + Enter