Bahagian tapak
Pilihan editor:
- Apakah perbezaannya?
- Mandela Nelson - biografi
- Biografi orang terkenal di China
- 1 koordinat pesawat
- Pesawat koordinat kosong
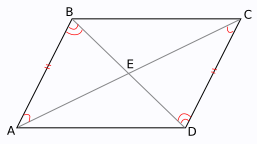
- Apakah sudut luaran parallelogram?
- Bagaimana untuk mencari bilangan peraturan peratus
- Persamaan tangen kepada graf fungsi
- Valery yakovlevich bruce berfungsi
- Persamaan parabola kubik
Pengiklanan
| Bagaimana untuk mencari fungsi antiderivatif pada satu ketika. Fungsi F (x) dipanggil antiderivatif untuk fungsi f (x) jika F` (x) \u003d f (x) atau dF (x) \u003d f (x) dx |
|
Tujuan:
Analisis matematik adalah koleksi sekumpulan matematik yang ditumpukan kepada kajian fungsi dan generalisasi mereka dengan kaedah pembezaan dan integral kalkuli. Jika setakat ini kita telah mengkaji satu bahagian analisis matematik yang disebut kalkulus kebezaan, intinya adalah untuk mengkaji fungsi dalam "kecil". I.e. penyiasatan fungsi dalam kawasan kejiranan yang kecil di setiap titik definisi. Salah satu operasi pembezaan ialah mencari derivatif (pembezaan) dan memohon kepada kajian fungsi. Sama pentingnya ialah masalah songsang. Jika tingkah laku fungsi di sekitar setiap titik takrifnya diketahui, maka bagaimana untuk memulihkan fungsi secara keseluruhannya, iaitu. dalam keseluruhan bidang takrifannya. Tugas ini adalah subjek kajian kalkulus integral yang dipanggil. Integrasi ialah kebalikan dari pembezaan. Atau pemulihan fungsi f (x) daripada derivatif yang diberikan f` (x). Perkataan Latin "integro" bermaksud pemulihan. Contoh No. 1. Katakan (x) `\u003d 3x 2. Penyelesaian: Berdasarkan peraturan pembezaan, mudah untuk meneka bahawa f (x) \u003d x 3, kerana (x 3), \u003d 3x 2 Sejak terbitan masing-masing adalah 3x2. (Derivatif pemalar adalah 0). Semua fungsi ini berbeza antara satu sama lain dengan jangka masa yang tetap. Oleh itu, penyelesaian umum masalah boleh ditulis dalam bentuk f (x) \u003d x 3 + C, di mana C adalah bilangan sebenar yang tetap. Mana-mana fungsi yang dijumpai f (x) dipanggil PENTING untuk fungsi F` (x) \u003d 3x 2 Definisi
Fungsi F (x) dipanggil antiderivatif untuk fungsi f (x) pada selang yang diberikan J, jika untuk semua x dari selang ini F` (x) \u003d f (x). Jadi fungsi F (x) \u003d x 3 adalah antiderivatif untuk f (x) \u003d 3x 2 pada (- ∞; ∞). Seperti yang telah kita perhatikan, fungsi ini mempunyai bilangan antiderivatif yang tidak terhingga (lihat contoh No. 1). Contoh No. 2.
Fungsi F (x) \u003d x adalah antiderivatif untuk semua f (x) \u003d 1 / x pada selang (0; +), kerana untuk semua x dari selang waktu ini, persamaan dipegang. Contoh No. 3.
Fungsi F (x) \u003d tg3x adalah antiderivatif untuk f (x) \u003d 3 / cos3x dalam selang (-n / 2;
n / a 2), Contoh No. 4.
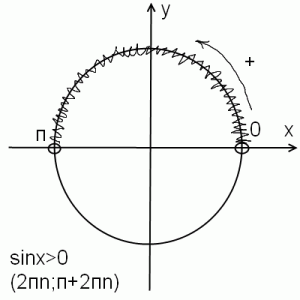
Fungsi F (x) \u003d 3sin4x + 1 / x-2 adalah antiderivatif untuk f (x) \u003d 12cos4x-1 / x 2 pada selang (0; ∞) Kuliah 2. Tema: antiderivatif. Harta utama fungsi primitif. Dalam mengkaji antiderivatif, kami akan bergantung kepada kenyataan berikut. Tanda kekukuhan fungsi: Jika derivatif Ψ (x) fungsi pada selang J adalah 0, maka fungsi Ψ \u200b\u200b(x) adalah malar pada selang ini. Kenyataan ini boleh ditunjukkan secara geometri. Telah diketahui bahawa Ψ` (x) \u003d tanα, γ ialah sudut kecenderungan tangen kepada graf fungsi Ψ \u200b\u200b(x) pada titik dengan abscissa x 0. Jika Ψ` (υ) \u003d 0 pada mana-mana titik jeda J, maka tgα \u003d 0 δ untuk sebarang tangen kepada graf fungsi Ψ \u200b\u200b(x). Ini bermakna bahawa tangen kepada graf fungsi pada mana-mana titik selari dengan paksi abscissa. Oleh itu, pada selang yang dinyatakan, graf fungsi Ψ \u200b\u200b(x) bertepatan dengan segmen garis lurus y \u003d C. Jadi, fungsi f (x) \u003d c adalah malar pada selang J jika f` (x) \u003d 0 pada selang ini. Sesungguhnya, untuk suatu arbitrase x 1 dan x 2 dari selang J, oleh teorem pada nilai purata fungsi, kita boleh menulis: Teorem: (Harta utama fungsi primitif) Jika F (x) adalah salah satu antidivatif untuk fungsi f (x) pada selang J, maka set semua antidivatif fungsi ini mempunyai bentuk: F (x) + C, di mana C adalah nombor sebenar. Bukti: Let F` (x) \u003d f (x), maka (F (x) + C) `\u003d F` (x) + C` \u003d f (x) Satu contoh: Cari set antiderivatif fungsi f (x) \u003d cos x. Lukiskan graf tiga yang pertama. Penyelesaian: Sin x adalah salah satu antidivatif untuk fungsi f (x) \u003d cos x F 1 (x) \u003d Sin x-1 Ilustrasi geometri: Graf sebarang antiderivatif F (x) + C boleh didapati dari graf antiderivatif F (x) menggunakan pemindahan selari r (0; c). Satu contoh: Untuk fungsi f (x) \u003d 2x, cari antiderivatif yang grafiknya melalui T.M (1; 4) Penyelesaian: F (x) \u003d x 2 + C adalah set semua antidivatif, F (1) \u003d 4 - oleh keadaan masalah. Antiderivatif. Orang primitif mudah difahami dengan contoh. Ambil fungsi y \u003d x 3. Seperti yang kita ketahui dari bahagian sebelumnya, berasal dari x 3 adalah 3 x 2: (x 3)" = 3x 2 . Oleh itu, dari fungsi tersebut y \u003d x 3 kita mendapat fungsi baru: pada = 3x 2 . Itulah: fungsi y \u003d x 3 adalah primitif untuk fungsi pada = 3x 2 . Definisi antiderivatif: Dalam contoh kami ( x 3)" = 3x Oleh itu y \u003d x 3 - antidivatif untuk pada = 3x 2 . Integrasi Seperti yang anda ketahui, proses mencari derivatif berkenaan dengan fungsi tertentu dipanggil pembezaan. Dan operasi terbalik disebut integrasi. Contoh Penjelasan: pada = 3x 2 + dosa x. Penyelesaian: Kami tahu bahawa antiderivatif untuk 3 x 2 adalah x 3 . Antidivatif untuk dosa x adalah -cos x. Tambah dua antidivatif dan dapatkan antiderivatif untuk fungsi tertentu: y \u003d x 3 + (-cos x), y \u003d x 3 - kos x. Jawapannya ialah: Contoh Penjelasan: Cari antiderivatif untuk fungsi tersebut pada \u003d 2 dosa x. Penyelesaian: Kita perhatikan bahawa k \u003d 2. Antidivatif untuk dosa x adalah -cos x. Oleh itu, untuk fungsi itu pada \u003d 2 dosa x antidivatif adalah fungsi pada \u003d -2 cos x. Contoh Penjelasan: Cari antiderivatif untuk fungsi tersebut y \u003d dosa 2 x. Penyelesaian: Perhatikan itu k \u003d 2. Antidivatif untuk dosa x adalah -cos x. Kami menggunakan formula kami apabila mencari antiderivatif untuk fungsi tersebut y \u003d cos 2 x: 1 cos 2 x cos 2 x
Contoh Penjelasan. Ambil fungsi dari contoh terdahulu: y \u003d dosa 2 x. Untuk fungsi ini, semua antiderivatif mempunyai bentuk: cos 2 x Penjelasan. Ambil baris pertama. Ia berbunyi seperti ini: jika fungsi y \u003d f ( x) adalah 0, maka antiderivatif untuk itu adalah 1. Mengapa? Kerana derivatif unit adalah sifar: 1 "\u003d 0. Garis yang tinggal dibaca dalam susunan yang sama. Bagaimana untuk menulis data dari jadual? Ambil garisan kedapan: (-cos x) "\u003d dosa x Kami menulis bahagian kedua dengan tanda terbitan, maka tanda dan derivatif yang sama. Kita membaca: antidivatif untuk fungsi dosa x adalah fungsi -cos x. Atau: -cos berfungsi x adalah primitif untuk fungsi dosa x. Pertimbangkan pergerakan titik di sepanjang garis lurus. Biarkan masa t dari permulaan pergerakan, titik melaluinya s (t). Kemudian kelajuan serta-merta v (t) sama dengan terbitan fungsi s (t) iaitu v (t) \u003d s "(t). Dalam amalan, masalah terbalik dihadapi: untuk halaju titik tertentu v (t) cari jalannya s (t), iaitu mencari fungsi sedemikian s (t) yang derivatifnya v (t). Fungsi s (t) seperti itu s "(t) \u003d v (t)dipanggil fungsi primitif v (t). Sebagai contoh, jika v (t) \u003d padadi mana tetapiAdakah nombor diberikan, maka fungsi itu Fungsi F (x) dipanggil fungsi antiderivatif f (x)pada selang tertentu, jika untuk semua xdari jurang ini F "(x) \u003d f (x). Sebagai contoh, fungsi itu F (x) \u003d sin xadalah fungsi primitif f (x) \u003d cos x,sejak itu (sin x) "\u003d cos x; fungsi F (x) \u003d x 4/4adalah fungsi primitif f (x) \u003d x 3sejak itu (x 4/4) "\u003d x 3. Pertimbangkan masalah ini. Cabaran. Buktikan bahawa fungsi x 3/3, x 3/3 + 1, x 3/3 - 4 adalah antidivatif fungsi yang sama f (x) \u003d x 2. Penyelesaian. 1) Nyatakan F 1 (x) \u003d x 3/3, maka F "1 (x) \u003d 3 ∙ (x 2/3) \u003d x 2 \u003d f (x). 2) F 2 (x) \u003d x 3/3 + 1, F "2 (x) \u003d (x 3/3 + 1)" \u003d (x 3/3) "+ (1) x). 3) F 3 (x) \u003d x 3/3 - 4, F "3 (x) \u003d (x 3/3 - 4)" \u003d x 2 \u003d f (x). Secara umum, sebarang fungsi x 3/3 + C, di mana C adalah malar, adalah primitif fungsi x 2. Ini adalah dari kenyataan bahawa derivatif pemalar sama dengan sifar. Contoh ini menunjukkan bahawa untuk fungsi tertentu, antidivatifnya ditakrifkan dengan jelas. Let F 1 (x) dan F 2 (x) menjadi dua antidivatif fungsi yang sama f (x). Kemudian F 1 "(x) \u003d f (x) dan F" 2 (x) \u003d f (x). Derivatif bagi perbezaan mereka g (x) \u003d F 1 (x) - F 2 (x) adalah sama dengan sifar, kerana g "(x) \u003d F" 1 (x) (x) \u003d 0. Jika g "(x) \u003d 0 pada selang tertentu, maka tangen kepada graf fungsi y \u003d g (x) pada setiap titik selang ini selari dengan paksi Ox. Oleh itu, graf fungsi y \u003d g (x) adalah garis lurus selari dengan paksi Ox, (x) \u003d F 1 (x) - F 2 (x) ia mengikuti bahawa F 1 (x) \u003d F 2 (x) + C. Oleh itu, jika fungsi F (x) adalah antiderivatif fungsi f (x) pada beberapa selang, maka semua antiderivatif f (x) ditulis dalam bentuk F (x) + C, di mana C adalah pemalar sewenang-wenangnya. Pertimbangkan graf semua antidivatif fungsi yang diberikan f (x). Jika F (x) adalah salah satu daripada antidivatif f (x), maka apa-apa antiderivatif fungsi ini diperoleh dengan menambah malar kepada F (x): F (x) + C. Grafik fungsi y \u003d F (x) + C diperoleh daripada graf y \u003d F (x) dengan pergeseran di sepanjang paksi Oy. Dengan memilih C, adalah mustahil untuk memastikan bahawa grafik antiderivatif melalui titik tertentu. Mari kita perhatikan peraturan untuk mencari antidivatif. Ingat bahawa operasi mencari derivatif untuk fungsi tertentu dipanggil pembezaan. Operasi terbalik mencari antiderivatif untuk fungsi tertentu dipanggil mengintegrasikan(dari perkataan Latin "Pulihkan"). Jadual antiderivatif untuk beberapa fungsi, anda boleh menulis menggunakan jadual derivatif. Contohnya, mengetahui itu (cos x) "\u003d -sin x, kita dapat (-cos x) "\u003d sin x, dari mana ia mengikuti semua fungsi primitif dosa x ditulis sebagai -cos x + Cdi mana Dengan- berterusan. Pertimbangkan beberapa makna antiderivatif. 1) Fungsi: x p, p ≠ -1. Antiderivatif: (x p + 1) / (p + 1) + C. 2) Fungsi: 1 / x, x\u003e 0. Antiderivatif: ln x + C. 3) Fungsi: x p, p ≠ -1. Antiderivatif: (x p + 1) / (p + 1) + C. 4) Fungsi: e x. Antiderivatif: e x + C. 5) Fungsi: dosa x. Antiderivatif: -cos x + C. 6) Fungsi: (kx + b) p, p ≠ -1, k ≠ 0. Antiderivatif: (((kx + b) p + 1) / k (p + 1)) + C. 7) Fungsi: 1 / (kx + b), k ≠ 0. Antiderivatif: (1 / k) ln (kx + b) + C. 8) Fungsi: e kx + b, k ≠ 0. Antiderivatif: (1 / k) e kx + b + C. 9) Fungsi: sin (kx + b), k ≠ 0. Antiderivatif: (-1 / k) cos (kx + b). 10)
Fungsi: cos (kx + b), k ≠ 0.Antiderivatif: (1 / k) sin (kx + b). Peraturan Integrasi boleh didapati dengan menggunakan peraturan pembezaan. Mari kita pertimbangkan beberapa peraturan. Biarkan F (x) dan G (x) - antidivatif, masing-masing fungsi f (x)dan g (x)pada selang tertentu. Kemudian: 1) fungsi F (x) ± G (x) adalah fungsi primitif f (x) ± g (x); 2) fungsi aF (x)adalah fungsi primitif af (x). laman web, dengan penyalinan penuh atau separa bahan, pautan kepada sumber diperlukan. Penyelesaian integral adalah tugas yang mudah, tetapi hanya untuk golongan elit. Artikel ini adalah untuk mereka yang ingin belajar untuk memahami integral, tetapi tidak tahu apa-apa tentang mereka atau hampir apa-apa. Integral ... Kenapa diperlukan? Bagaimana untuk mengiranya? Apakah integral yang pasti dan tidak pasti? Jika satu-satunya penggunaan integral yang anda ketahui adalah untuk mendapatkan sesuatu yang berguna dari tempat yang sukar dijangkau dengan cara mencengkam dalam bentuk lencana penting, maka selamat datang! Ketahui bagaimana untuk menyelesaikan integral dan mengapa anda tidak boleh melakukannya tanpa ia. Kami mengkaji konsep "integral"Integrasi dikenali di Mesir purba. Sudah tentu, tidak dalam bentuk modennya, tetapi masih. Sejak itu, ahli matematik telah menulis banyak buku tentang topik ini. Terutama dibezakan Newton dan Leibniz tetapi intipati perkara tidak berubah. Bagaimana untuk memahami integral dari awal? Tiada jalan! Untuk memahami topik ini, anda masih memerlukan pengetahuan asas tentang asas analisis matematik. Ini adalah maklumat asas yang akan anda temukan di blog kami. Tidak pentingMarilah kita mempunyai beberapa fungsi f (x) .
Dalam erti kata lain, integral adalah derivatif yang berlawanan atau yang bersifat antiteratif. Dengan cara ini, tentang cara membaca dalam artikel kami.
Suatu primitif wujud untuk semua fungsi yang berterusan. Juga, tanda tetap sering ditambah kepada antidivatif, kerana derivatif fungsi yang berbeza secara berterusan. Proses mencari integral dipanggil integrasi. Contoh mudah:
Agar tidak sentiasa mengira primitives fungsi asas, ia adalah mudah untuk mengurangkan mereka ke meja dan menggunakan nilai yang sedia dibuat:
Terlalu pentingApabila berurusan dengan konsep yang penting, kita berhadapan dengan kuantiti tak terbatas. Integral akan membantu mengira kawasan angka, jisim badan tidak berperikemanusiaan, jalan yang bergerak dengan pergerakan yang tidak merata, dan banyak lagi. Perlu diingat bahawa integral ialah jumlah bilangan tak terhingga yang sangat besar. Sebagai contoh, bayangkan graf fungsi. Bagaimana untuk mencari kawasan angka yang dibatasi oleh graf fungsi?
Menggunakan integral! Kami membahagikan trapezoid curvilinear, terhad oleh paksi koordinat dan graf fungsi, ke segmen infinitesimal. Oleh itu, angka tersebut akan dibahagikan kepada lajur nipis. Jumlah kawasan lajur akan menjadi kawasan trapezoid. Tetapi ingat bahawa pengiraan sedemikian akan memberikan hasil anggaran. Walau bagaimanapun, segmen yang lebih kecil dan sempit, lebih tepat pengiraan. Sekiranya kita mengurangkan sehingga setakat panjangnya akan menjadi sifar, maka jumlah segmen-segmen akan cenderung ke kawasan angka tersebut. Ini adalah integral yang pasti, yang ditulis seperti ini:
By the way! Pembaca kami kini mempunyai diskaun sebanyak 10% Kaedah untuk mengira integral untuk patung-patungSifat-sifat integral tidak terbatasBagaimana untuk menyelesaikan integral tidak terbatas? Di sini kita menganggap sifat-sifat integral tidak terbatas, yang berguna dalam menyelesaikan contoh.
Sifat-sifat integral pasti
Kami telah mengetahui bahawa integral tertentu adalah batas jumlah. Tetapi bagaimana untuk mendapatkan nilai khusus ketika menyelesaikan contoh? Untuk ini, ada formula Newton-Leibniz:
Contoh-contoh integral menyelesaikanDi bawah ini kita pertimbangkan beberapa contoh untuk mencari integral tidak terbatas. Kami mencadangkan bahawa anda secara bebas memahami selok-belok penyelesaian, dan jika sesuatu tidak jelas, tanya soalan dalam komen.
Untuk menyatukan bahan, tonton video tentang bagaimana integral diselesaikan dalam amalan. Jangan putus asa jika integral tidak diberikan dengan serta-merta. Tanya, dan mereka akan memberitahu anda tentang pengiraan integral segala yang mereka tahu sendiri. Dengan bantuan kami, mana-mana triple atau curvilinear yang terpasang di permukaan tertutup akan menjadi kekuatan anda. Fungsi F (x ) dipanggil antiderivatif untuk fungsi f (x) pada selang yang diberikan, jika untuk semua x dari selang waktu ini persamaan dipegang F "(x ) = f(x ) . Sebagai contoh, fungsi itu F (x) \u003d x 2 f (x ) = 2x sejak itu F "(x) \u003d (x 2 )" = 2x \u003d f (x). ◄ Harta utama antidivatif itu Jika F (x) - antidivatif untuk fungsi f (x) pada selang yang diberikan, maka fungsi itu f (x) mempunyai banyak primitif, dan semua primitif ini boleh ditulis sebagai F (x) + Cdi mana Dengan Adakah pemalar sewenang-wenangnya.
Kaedah untuk pengiraan antiderivatif
Tidak pentingTidak penting dari fungsi f (x) dipanggil ungkapan F (x) + C, iaitu keseluruhan kesemua antidivatif fungsi tertentu f (x) . Integral tidak ketara ditunjukkan sebagai berikut: ∫ f (x) dx \u003d F (x) + C , f (x)- dipanggil fungsi integrasi ; f (x) dx - dipanggil integrand ; x - dipanggil pembolehubah integrasi ; F (x) - salah satu antidivatif f (x) ; Dengan Adakah pemalar sewenang-wenangnya. Contohnya ∫ 2 x dx \u003dx 2 + Dengan , ∫ cosx dx \u003ddosa x + Dengan dan sebagainya. ◄ Perkataan "integral" berasal daripada perkataan Latin integer , yang bermaksud "dipulihkan." Dengan mengandaikan integral tidak terhad daripada 2 x , kita semacam memulihkan fungsi x 2 yang derivatifnya 2 x . Pemulihan fungsi dari derivatifnya, atau, secara puratanya, pencarian untuk integral yang tidak pasti melebihi integrand tertentu, dipanggil mengintegrasikan fungsi ini. Integrasi ialah kebalikan dari pembezaan. Untuk mengesahkan bahawa integrasi dilakukan dengan betul, cukup untuk membezakan hasilnya dan mendapatkan integrasi. Ciri-ciri utama integral tidak terbatas
(∫ f (x) dx )" \u003d f (x) . ∫ k · f (x) dx = k · ∫ f (x) dx . ∫ ( f (x) ± g (x ) ) dx = ∫ f (x) dx ± ∫ g (x ) dx . ∫ f ( k x + b) dx = 1 / k F (k x +b ) + C . Jadual antidivatif dan integral tidak terbatas
Terlalu pentingBiarkan di antara [a; b] fungsi yang berterusan ditakrifkan y \u003d f (x) kemudian pasti penting dari a ke b fungsi f (x) dipanggil kenaikan primitif F (x) fungsi ini, iaitu. $$ \\ int_ (a) ^ (b) f (x) dx \u003d F (x) | (_a ^ b) \u003d ~~ F (a) -F (b). $$ Nombor adan b dipanggil dengan sewajarnya lebih rendah dan atas had integrasi. Kaedah-kaedah asas untuk mengira integral tertentu 1. \\ (\\ int_ (a) ^ (a) f (x) dx \u003d 0 \\); 2. \\ (\\ int_ (a) ^ (b) f (x) dx \u003d - \\ int_ (b) ^ (a) f (x) dx \\); 3. \\ (\\ int_ (a) ^ (b) kf (x) dx \u003d k \\ int_ (a) ^ (b) f (x) dx, \\ k - pemalar; Dx \u003d \\ int_ (a) ^ (b) f (x) dx ± \\ int_ (a) ^ (b) g (x) dx \\); 5. \\ (\\ int_ (a) ^ (b) f (x) dx \u003d \\ int_ (a) ^ (c) f (x) dx + \\ int_ (c) ^ (b) f (x) dx \\); 6. \\ (\\ int _ (- a) ^ (a) f (x) dx \u003d 2 \\ int_ (0) ^ (a) f (x) dx \\), di mana f (x) - walaupun berfungsi; 7. \\ (\\ int _ (- a) ^ (a) f (x) dx \u003d 0 \\), di mana f (x) Adakah fungsi ganjil. Catatan . Dalam semua kes, diandaikan bahawa pengintegrasian adalah berintegrasi berbanding selang berangka yang sempadannya adalah batas integrasi. Makna geometri dan fizikal yang penting
Jumlah pusingan badan
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Baca: |
|---|
Baru
- Apa yang memecahkan baron "kaku"?
- Ahli pergerakan Putih
- Jalan Suvorov dan pasukan ke tanah air mereka
- Fungsi F (x) dipanggil antiderivatif untuk fungsi f (x) jika F` (x) \u003d f (x) atau dF (x) \u003d f (x) dx
- Program pengurangan frasa darjah
- Istilah yang serupa, pengurangan mereka, contohnya
- Pengembara Rusia lazarev
- Menyelesaikan persamaan kuadrat tidak lengkap
- Penyelesaian persamaan kuadratik, formula akar, contohnya
- Pesawat menyelaras (Gred 6) - Pasar raya pengetahuan








 Bari Alibasov dan Kumpulan Integral
Bari Alibasov dan Kumpulan Integral