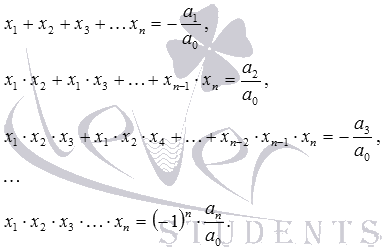Bahagian tapak
Pilihan editor:
- Apakah perbezaannya?
- Mandela Nelson - biografi
- Biografi orang terkenal di China
- 1 koordinat pesawat
- Pesawat koordinat kosong
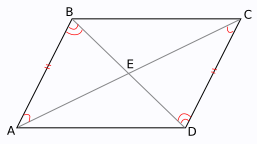
- Apakah sudut luaran parallelogram?
- Bagaimana untuk mencari bilangan peraturan peratus
- Persamaan tangen kepada graf fungsi
- Valery yakovlevich bruce berfungsi
- Persamaan parabola kubik
Pengiklanan
| Jumlah akar persamaan kuadratik. Bagaimana untuk mencari jumlah akar persamaan |
|
Di antara akar dan koefisien persamaan kuadratik, sebagai tambahan kepada rumus akar, terdapat hubungan lain yang berguna yang diberikan teorem Vieta. Dalam artikel ini, kami memberi kenyataan dan bukti teorem Vieta untuk persamaan kuadratik. Seterusnya, kita anggap teorem terbalik kepada teorem Vieta. Selepas itu, kita menganalisis penyelesaian contoh yang paling ciri. Akhirnya, kami menulis formula Vieta yang menentukan hubungan antara akar sebenar persamaan algebra ijazah n dan pekali. Navigasi halaman. Teorem Vieta, pernyataan, buktiDari formula akar persamaan kuadratik a · x 2 + b · x + c \u003d 0 dari bentuk, di mana D \u003d b 2 -4 · a · c, hubungan x 1 + x 2 \u003d -b / a, x 1 · x 2 \u003d c / a. Keputusan ini disahkan. teorem Vieta: Teorem Jika x 1 dan x 2 adalah akar persamaan kuadratik a · x 2 + b · x + c \u003d 0, maka jumlah akar adalah sama dengan nisbah pekali b dan yang diambil dengan tanda bertentangan, dan hasil akar adalah sama dengan nisbah pekali c dan a, iaitu, . Bukti. Bukti teorem Vieta dijalankan mengikut skema berikut: kita menyusun jumlah dan hasil akar persamaan kuadratik dengan menggunakan formula akar yang terkenal, maka kita mengubah ekspresi yang dihasilkan dan memastikan bahawa masing-masing adalah -b / a dan c / a. Mari kita mulakan dengan jumlah akar, buatkannya. Sekarang kita membawa pecahan kepada penyebut biasa, kita ada. Dalam pengangka pecahan yang diperoleh, selepas itu :. Akhirnya, selepas 2, kita dapat. Ini membuktikan hubungan pertama teorem Vieta untuk jumlah akar persamaan kuadratik. Kami melangkah ke tempat yang kedua. Kami mengarang hasil akar persamaan kuadratik :. Menurut kaedah pendaraban pecahan, produk terakhir boleh ditulis sebagai. Sekarang kita melipatgandakan kurungan oleh kurungan dalam pengangka, tetapi lebih cepat untuk meruntuhkan produk ini oleh formula perbezaan persegijadi. Selanjutnya, ingat, lakukan peralihan seterusnya. Dan kerana diskriminasi persamaan kuadratik sepadan dengan rumus D \u003d b 2 -4 · a · c, kita boleh menggantikan b2 -4 · a · c dalam pecahan terakhir dan bukannya D, kita dapati. Selepas membuka kurungan dan mengurangkan istilah seperti itu, kami tiba di pecahan, dan pengurangannya dengan 4 · a memberikan. Ini membuktikan hubungan kedua teorem Vieta untuk produk akar. Jika kita menghilangkan penjelasan, maka bukti teorem Vieta akan mengambil bentuk ringkas: Ia hanya perlu diperhatikan bahawa untuk diskriminasi sama dengan sifar, persamaan kuadratik mempunyai satu akar. Walau bagaimanapun, jika kita menganggap bahawa persamaan dalam kes ini mempunyai dua akar yang sama, maka kesamaan dari teorem Vieta juga dipegang. Sesungguhnya, bagi D \u003d 0 punca persamaan kuadratik kemudian, dan, dan sejak D \u003d 0, iaitu, b 2 -4 · a · c \u003d 0, dari mana b 2 \u003d 4 · a · c, maka. Dalam amalan, teorem Vieta paling sering digunakan berhubung dengan persamaan kuadratik (dengan pekali tertinggi yang sama dengan 1) dari bentuk x 2 + p · x + q \u003d 0. Kadang-kadang ia dirumuskan untuk persamaan kuadrat seperti ini, yang tidak membatasi kesamaan, kerana mana-mana persamaan kuadratik dapat digantikan dengan persamaan yang sama dengan membagi kedua-dua bahagiannya dengan nombor bukan sifar a. Kami memberikan kenyataan teorem Vieta yang sepadan: Teorem Jumlah akar persamaan kuadrat dikurangkan x 2 + p · x + q \u003d 0 adalah sama dengan pekali pada x yang diambil dengan tanda yang bertentangan, dan hasil akar adalah istilah percuma, iaitu x 1 + x 2 \u003d -p, x 1 · x 2 \u003d q. Teorem songsang dari teorem VietaKenyataan kedua teorem Vieta yang diberikan dalam perenggan terdahulu menunjukkan bahawa jika x 1 dan x 2 adalah akar persamaan kuadrat dikurangkan x 2 + p · x + q \u003d 0, maka hubungan x 1 + x 2 \u003d -p, x 1 · x 2 \u003d q. Sebaliknya, dari hubungan bertulis x 1 + x 2 \u003d -p, x 1 · x 2 \u003d q ia mengikuti bahawa x 1 dan x 2 adalah akar persamaan kuadratik x 2 + p · x + q \u003d 0. Dengan kata lain, kenyataan yang bertentangan dengan teorem Vieta adalah benar. Kami merumuskannya dalam bentuk teorem dan membuktikannya. Teorem Jika nombor x 1 dan x 2 sedemikian rupa sehingga x 1 + x 2 \u003d -p dan x 1 · x 2 \u003d q, maka x 1 dan x 2 adalah akar persamaan kuadratik x 2 + p · x + q \u003d 0. Bukti. Selepas menggantikan pekali p dan q dalam persamaan x 2 + p · x + q \u003d 0 hingga x 1 dan x 2, ia diubah menjadi persamaan yang setara. Kami menggantikan nombor x 1 ke persamaan yang dihasilkan bukannya x, kita mempunyai kesamaan x 1 2 - (x 1 + x 2) x 1 + x 1 x 2 \u003d 0, yang bagi mana-mana x 1 dan x 2 mewakili kesamaan angka sebenar 0 \u003d 0, sejak x 1 2 - (x 1 + x 2) x 1 + x 1 x 2 \u003d x 1 2 -x 1 2 -x 2 x 1 + x 1 x 2 \u003d 0. Oleh itu, x 1 adalah akar persamaan x 2 - (x 1 + x 2) x + x 1 x 2 \u003d 0, yang bermaksud bahawa x 1 adalah akar persamaan x 2 + p · x + q \u003d 0 bersamaan dengannya. Jika dalam persamaan x 2 - (x 1 + x 2) x + x 1 x 2 \u003d 0 gantikan x untuk nombor x 2, maka kita memperoleh kesamaan x 2 2 - (x 1 + x 2) x 2 + x 1 x 2 \u003d 0. Ini adalah kesaksamaan yang benar, sejak x 2 2 - (x 1 + x 2) x 2 + x 1 x 2 \u003d x 2 2 -x 1 · x 2 -x 2 2 + x 1 · x 2 \u003d 0. Oleh itu, x 2 juga merupakan akar persamaan x 2 - (x 1 + x 2) x + x 1 x 2 \u003d 0, dan karenanya persamaan x 2 + p · x + q \u003d 0. Ini melengkapkan bukti teorem terbalik kepada teorem Vieta. Contoh menggunakan teorem VietaSudah tiba masanya untuk membincangkan penggunaan praktikal teorem Vieta dan teorem terbalik. Dalam bahagian ini, kami membincangkan penyelesaian kepada beberapa contoh yang paling biasa. Kami mula dengan menggunakan teorem terbalik ke teorem Vieta. Ia mudah digunakan untuk memeriksa sama ada kedua-dua nombor adalah akar persamaan kuadrat yang diberi. Dalam kes ini, jumlah dan perbezaan mereka dikira, selepas itu kesahihan perhubungan diperiksa. Jika kedua-dua hubungan ini dipegang, maka dengan teorem terbalik kepada teorem Vieta, disimpulkan bahawa bilangan ini adalah akar persamaan. Jika sekurang-kurangnya satu hubungan tidak puas, maka angka-angka ini bukanlah akar persamaan kuadratik. Pendekatan ini boleh digunakan dalam menyelesaikan persamaan kuadrat untuk mengesahkan akar yang ditemui. Contohnya. Mana antara pasangan nombor 1) x 1 \u003d -5, x 2 \u003d 3, atau 2), atau 3) adalah sepasang akar persamaan kuadratik 4 · x 2 -16 · x + 9 \u003d 0? Penyelesaian. Koefisien persamaan kuadratik yang diberikan 4 · x 2 -16 · x + 9 \u003d 0 ialah a \u003d 4, b \u003d -16, c \u003d 9. Menurut teorem Vieta, jumlah akar persamaan kuadratik sepadan dengan -b / a, iaitu, 16/4 \u003d 4, dan hasil akar harus sama dengan c / a, iaitu 9/4. Sekarang kita mengira jumlah dan hasil angka dalam setiap tiga pasangan yang diberikan, dan membandingkannya dengan nilai-nilai yang baru diperolehi. Dalam kes pertama, kita mempunyai x 1 + x 2 \u003d -5 + 3 \u003d -2. Nilai yang diperolehi adalah berbeza daripada 4, oleh itu, pengesahan selanjutnya tidak dapat dijalankan, dan oleh teorem terbalik kepada teorem Vieta, kita dapat dengan segera menyimpulkan bahawa sepasang nombor pertama bukan sepasang akar persamaan kuadrat yang diberikan. Kami lulus ke kes kedua. Di sini, iaitu, keadaan pertama berpuas hati. Kami periksa syarat kedua :, nilai yang diperolehi berbeza dari 9/4. Oleh itu, pasangan nombor kedua bukan sepasang akar persamaan kuadratik. Kes terakhir kekal. Di sini dan. Kedua-dua syarat tersebut dipenuhi, oleh itu, nombor-nombor ini x 1 dan x 2 adalah akar persamaan kuadrat yang diberikan. Jawapannya ialah: Teorem terbalik kepada teorem Vieta dalam amalannya boleh digunakan untuk memilih akar persamaan kuadratik. Biasanya memilih keseluruhan akar persamaan kuadratik yang diberi dengan koefisien integer, seperti dalam kes lain ia agak sukar dilakukan. Pada masa yang sama, mereka menggunakan hakikat bahawa jika jumlah dua nombor adalah sama dengan pekali kedua persamaan kuadratik yang diambil dengan tanda tolak, dan hasil angka ini adalah sama dengan istilah bebas, maka angka-angka ini adalah akar persamaan kuadratik ini. Kita akan berurusan dengan ini menggunakan contoh. Ambil persamaan kuadrat x 2 -5 · x + 6 \u003d 0. Untuk nombor x 1 dan x 2 menjadi akar persamaan ini, dua kesamaan x 1 + x 2 \u003d 5 dan x 1 · x 2 \u003d 6 mesti dipenuhi. Ia tetap untuk mengambil nombor tersebut. Dalam kes ini, ini agak mudah dilakukan: 2 dan 3 adalah nombor sedemikian, kerana 2 + 3 \u003d 5 dan 2 · 3 \u003d 6. Jadi, 2 dan 3 adalah akar persamaan kuadratik ini. Teorem terbalik kepada teorem Vieta amat sesuai untuk mencari akar kedua persamaan kuadrat yang dikurangkan apabila salah satu akar sudah diketahui atau jelas. Dalam kes ini, akar kedua ditemui dari mana-mana hubungan. Sebagai contoh, ambil persamaan kuadratik 512 × 2 -509 × -3 \u003d 0. Adalah mudah untuk melihat di sini bahawa unit adalah akar persamaan, kerana jumlah pekali persamaan kuadratik ini adalah sifar. Jadi x 1 \u003d 1. Akar kedua x 2 boleh dijumpai, contohnya, dari hubungan x 1 · x 2 \u003d c / a. Kami mempunyai 1 x 2 \u003d -3 / 512, dari mana x 2 \u003d -3 / 512. Oleh itu, kita menentukan kedua-dua akar persamaan kuadratik: 1 dan -3/512. Sudah jelas bahawa pemilihan akar dinasihatkan hanya dalam kes-kes yang paling mudah. Dalam kes lain, untuk mencari akar, anda boleh menggunakan formula akar persamaan kuadratik melalui diskriminasi. Satu lagi aplikasi praktikal teorem, kebalikan dari teorem Vieta, adalah untuk menyusun persamaan kuadratik untuk akar diberi x 1 dan x 2. Untuk melakukan ini, sudah cukup untuk mengira jumlah akar, yang memberikan pekali x dengan tanda bertentangan persamaan kuadrat dikurangkan, dan hasil akarnya, yang memberikan istilah percuma. Contohnya. Tulis persamaan kuadrat yang akar adalah nombor -11 dan 23. Penyelesaian. Nyatakan x 1 \u003d -11 dan x 2 \u003d 23. Kami mengira jumlah dan produk nombor-nombor ini: x 1 + x 2 \u003d 12 dan x 1 · x 2 \u003d -253. Oleh itu, bilangan ini adalah akar persamaan kuadrat yang dikurangkan dengan pekali kedua -12 dan istilah bebas -253. Iaitu, x 2 -12 · x - 253 \u003d 0 adalah persamaan yang dikehendaki. Jawapannya ialah: x 2 -12 x - 253 \u003d 0. Teorema Vieta sangat sering digunakan dalam menyelesaikan masalah yang berkaitan dengan tanda-tanda akar persamaan kuadratik. Bagaimana teorem Vieta berkaitan dengan tanda-tanda akar persamaan kuadrat dikurangkan x 2 + p · x + q \u003d 0? Kami memberikan dua kenyataan yang sepadan:
Kenyataan ini mengikuti dari formula x 1 · x 2 \u003d q, serta peraturan untuk mendarabkan nombor positif dan negatif dengan tanda-tanda yang berbeza. Pertimbangkan contoh permohonan mereka. Contohnya. R dia positif. Dengan menggunakan formula diskriminasi, kita dapati D \u003d (r + 2) 2 -4 · 1 · (r - 1) \u003d r 2 + 4 · r + 4-4 · r + 4 \u003d r 2 +8, nilai ungkapan r2 +8 adalah positif untuk mana-mana r sebenar, jadi D\u003e 0 untuk mana-mana r nyata. Oleh itu, persamaan kuadratik awal mempunyai dua akar untuk sebarang nilai sebenar parameter r. Sekarang cari apabila akar mempunyai tanda yang berbeza. Sekiranya tanda-tanda akarnya berbeza, maka produk mereka adalah negatif, dan oleh teorem Vieta hasil akar persamaan kuadrat dikurangkan adalah sama dengan istilah bebas. Oleh itu, kita berminat dengan nilai r yang mana r - 1 adalah percuma. Oleh itu, untuk mencari nilai r yang menarik minat kita, kita mesti menyelesaikan ketidaksamaan linear r - 1<0 , откуда находим r<1 . Jawapannya ialah: di r<1 . Formula VietaDi atas, kami bercakap tentang teorem Vieta untuk persamaan kuadratik dan menganalisis hubungan yang disahkan olehnya. Tetapi terdapat formula yang mengaitkan akar dan koefisien sebenar bukan sahaja persamaan kuadrat, tetapi juga persamaan kubik, persamaan kuadrat empat, dan secara umum, persamaan algebra darjah n. Mereka dipanggil formula Vieta. Kami menulis formula Vieta untuk persamaan algebra derajat n bentuk, dan kami mengandaikan bahawa ia mempunyai akar sebenar x 1, x 2, ..., x n (di antara mereka mungkin ada yang kebetulan): Dapatkan formula Vieta yang membolehkan teorem polynomial pemfaktaran linear, serta definisi polinomial yang sama melalui persamaan semua pekali yang sepadan. Jadi polinomial dan penguraiannya menjadi faktor linear bentuk adalah sama. Membuka kurungan dalam kerja terakhir dan menyamakan pekali yang sepadan, kami memperoleh formula Vieta. Khususnya, untuk n \u003d 2, kita mempunyai formula Vieta yang biasa untuk persamaan kuadratik. Untuk persamaan kubik, formula Vieta mempunyai bentuk Ia hanya dapat diperhatikan bahawa di sebelah kiri formula Vieta adalah yang dipanggil asas polinomial simetri. Rujukan
Menentukan jumlah akar persamaan adalah salah satu langkah yang perlu dalam menyelesaikan persamaan kuadratik (persamaan bentuk ax² + bx + c \u003d 0, di mana eksponen a, b, dan c adalah nombor sewenang-wenang, lebih-lebih lagi 0) dengan sokongan untuk teorem Vieta. Manual arahan1. Tulis persamaan kuadratik sebagai ax² + bx + c \u003d 0 Contoh: Persamaan awal: 12 + x² \u003d 8x Persamaan yang ditulis dengan betul: x² - 8x + 12 \u003d 0 2. Terangkan teorem Vieta, yang mana jumlah akar persamaannya sama dengan nombor "b" yang diambil dengan tanda yang bertentangan, dan produknya sama dengan nombor "c." Contoh: Dalam persamaan yang dipertimbangkan, b \u003d -8, c \u003d 12, masing-masing: x1 + x2 \u003d 8 × 1 * x2 \u003d 12 3. Ketahui jika nombor yang betul atau negatif adalah akar persamaan. Jika kedua-dua produk dan jumlah akar adalah nombor positif, semua akar adalah nombor yang betul. Jika hasil akar betul, dan jumlah akarnya adalah nombor negatif, maka kedua-dua akar adalah negatif. Jika hasil akar adalah negatif, maka satu akar mempunyai tanda "+" dan yang lain mempunyai tanda "-". Dalam hal ini, gunakan peraturan tambahan: "Jika jumlah akar adalah bilangan positif, akar yang lebih besar juga positif, dan jika jumlah akarnya nombor negatif adalah lebih besar dalam akar nilai mutlak adalah negatif. "Contoh: Dalam persamaan yang dipertimbangkan, kedua-dua jumlah dan produk adalah nombor yang betul: 8 dan 12, jadi kedua-dua akar adalah nombor positif. 4. Selesaikan sistem persamaan yang dihasilkan dengan memilih akar. Contohnya: x1 * x2 \u003d 12 Cocok pasangan akar, masing-masing, 12 dan 1, 6 dan lebih baik untuk memulakan pemilihan dengan faktor, dan kemudian, untuk memeriksa, menggantikan sepasang faktor dalam persamaan kedua dan periksa sama ada jumlah akar ini sepadan dengan penyelesaiannya. 2, 4 dan 3 Periksa pasangan yang dihasilkan dengan sokongan untuk persamaan x1 + x2 \u003d 8. Pasangan 12 + 1 ≠ 86 + 2 \u003d 84 + 3 ≠ 8 Oleh itu, akar persamaannya ialah angka 6 dan 8. Persamaan disebut persamaan bentuk f (x, y, ...) \u003d g (x, y, ..), di mana f dan g adalah fungsi satu atau beberapa pembolehubah. Untuk menemui akar persamaan ialah untuk mencari satu set argumen di mana persamaan ini dipegang.
Anda perlukan
Manual arahan1. Mungkin anda mempunyai persamaan bentuk: x + 2 \u003d x / 5. Untuk memulakan, kami memindahkan semua komponen kesamaan ini dari sebelah kanan ke kiri, sambil menukar tanda komponen ke sebaliknya. Sifar kekal di sebelah kanan persamaan ini, iaitu, kita mendapatkan yang berikut: x + 2-x / 5 \u003d 0. 2. Kami memberikan istilah yang serupa. Kami mendapat yang berikut: 4x / 5 + 2 \u003d 0. 3. Selanjutnya dari persamaan yang dikurangkan diperolehi kita mencari istilah yang tidak diketahui, dalam kes ini x. Nilai hasil pembolehubah yang tidak diketahui akan menjadi penyelesaian kepada persamaan awal. Dalam kes ini, kita mendapat yang berikut: x \u003d -2.5. Video berkaitan Beri perhatian! Nasihat berguna Teorem Vieta menetapkan sambungan langsung antara akar (x1 dan x2) dan eksponen (b dan c, d) bagi persamaan jenis bx2 + cx + d \u003d 0. Dengan bantuan teorem ini dibenarkan, tanpa menentukan makna akar, untuk mengira jumlah mereka, berani bercakap, dalam fikiran. Tidak ada yang sukar, perkara utama adalah mengetahui beberapa peraturan.
Anda perlukan
Manual arahan1. Bawa persamaan kuadratik dalam kajian ke bentuk piawai, supaya semua eksponen masuk dalam urutan menurun, iaitu pada mulanya ijazah tertinggi adalah x2, dan pada akhirnya ijazah sifar ialah x0. Persamaan mengambil bentuk: b * x2 + c * x1 + d * x0 \u003d b * x2 + c * x + d \u003d 0. 2. Semak bukannya negatif dari diskriminasi. Pemeriksaan ini diperlukan untuk memastikan persamaan mempunyai akar. D (diskriminasi) mengambil bentuk: D \u003d c2 - 4 * b * d. Terdapat beberapa pilihan. D - diskriminasi - betul, yang bermaksud persamaan mempunyai dua akar. D - sama dengan sifar, ia mengikuti dari ini bahawa terdapat akar, tetapi ia adalah dwi, \u200b\u200biaitu x1 \u003d x2. D adalah negatif, untuk kursus dalam algebra sekolah keadaan ini bermakna tidak ada akar, untuk matematik yang lebih tinggi ada akar, tetapi mereka kompleks. 3. Tentukan jumlah akar persamaan. Menggunakan teorem Vieta, ini mudah dilakukan: b * x2 + c * x + d \u003d 0. Jumlah akar persamaan adalah berkadar terus dengan "-c" dan berkadar songsang dengan "b" eksponen. Iaitu, x1 + x2 \u003d -c / b. Tentukan produk akar berdasarkan pernyataan - hasil akar persamaan itu berkadar terus dengan "d" dan berkadar songsang dengan penunjuk "b": x1 * x2 \u003d d / b. Beri perhatian! Nasihat berguna Sekiranya, dengan menggantikan nombor dalam persamaan, persamaan yang betul diperolehi, bilangan tersebut dipanggil akar. Akar mungkin betul, negatif dan sifar. Di antara setiap set akar persamaan, maksimum dan minimum dibezakan.
Manual arahan1. Cari semua akar persamaan, di antara mereka memilih negatif, jika ada. Katakanlah, persamaan kuadrat 2x? -3x + 1 \u003d 0 diberikan. Terapkan formula untuk mencari akar persamaan kuadratik: x (1,2) \u003d / 2 \u003d / 2 \u003d / 2, maka x1 \u003d 2, x2 \u003d 1. Adalah mudah untuk melihat bahawa tidak ada yang negatif di kalangan mereka. 2. Ia juga mungkin untuk menemui akar persamaan kuadratik menggunakan teorem Vieta. Menurut teorem ini, x1 + x1 \u003d -b, x1? X2 \u003d c, dimana b dan c ialah indeks persamaan x? + Bx + c \u003d 0, masing-masing. Memohon teorem ini, ia dibenarkan untuk tidak mengira diskriminasi b? -4ac, yang dalam sesetengah kes boleh memudahkan tugas. 3. Sekiranya eksponen di x walaupun dalam persamaan kuadratik, ia dibenarkan untuk tidak menggunakan asas, tetapi formula ringkas untuk mencari akar. Jika formula asas kelihatan seperti x (1,2) \u003d [- b ±? (B? -4ac)] / 2a, maka dalam bentuk ringkas maka ditulis seperti ini: x (1,2) \u003d [- b / 2 ±? b? / 4-ac)] / a. Jika tidak ada istilah percuma dalam persamaan kuadratik, ia agak mudah untuk mengalihkan x keluar dari kurungan. Dan kadang-kadang bahagian kiri ditambahkan ke persegi penuh: x? + 2x + 1 \u003d (x + 1)?. 4. Terdapat jenis persamaan yang tidak memberikan nombor satu, tetapi banyak penyelesaian. Beri persamaan trigonometrik. Jadi, hasilnya kepada persamaan 2sin? (2x) + 5sin (2x) -3 \u003d 0 adalah x \u003d? / 4+? K, di mana k adalah integer. Iaitu, apabila menggantikan nilai integer bagi parameter k, argumen x akan memenuhi persamaan yang diberi. 5. Dalam masalah trigonometri, mungkin diperlukan untuk mengesan semua akar negatif atau yang paling tinggi negatif. Dalam menyelesaikan masalah tersebut, penalaran logik atau kaedah induksi matematik digunakan. Gantikan beberapa nilai integer untuk k dalam ungkapan x \u003d? / 4+? K dan perhatikan bagaimana argumen berkelakuan. By the way, akar negatif terbesar dalam persamaan sebelumnya ialah x \u003d -3? / 4 pada k \u003d 1. Video berkaitan Beri perhatian! Nasihat berguna Jumlah akar persamaan kuadratik adalah sama dengan pekali kedua dengan tanda bertentangan, dan hasil akar adalah sama dengan istilah bebas. (Ingat: persamaan kuadrat dikurangkan ialah persamaan di mana pekali pertama adalah 1). Penjelasan: Biarkan persamaan kuadratik kapak 2 +bx +c \u003d 0 mempunyai akar x 1 dan x 2. Kemudian oleh teorem Vieta: Contoh 1: Persamaan di atas x 2 - 7x + 10 \u003d 0 mempunyai akar 2 dan 5. Jumlah akar adalah 7, dan produk adalah 10. Dan dalam persamaan kita, pekali kedua ialah -7, dan istilah percuma ialah 10. Oleh itu, jumlah akar adalah sama dengan pekali kedua dengan tanda yang bertentangan, dan hasil akar adalah sama dengan istilah bebas. Seringkali terdapat persamaan kuadratik yang boleh dikira dengan mudah menggunakan teorem Vieta - lebih-lebih lagi, lebih mudah untuk mengira mereka dengan bantuannya. Ini boleh diverifikasi dengan mudah dalam contoh sebelumnya dan dalam perkara berikut. Contoh 2 Selesaikan persamaan kuadratik x 2 – 2x – 24 = 0. Penyelesaian. Kami menggunakan teorem Vieta dan menuliskan dua identiti: x 1 x 2 = –24 x 1 + x 2 = 2 Kami memilih faktor-faktor tersebut untuk -24 supaya jumlahnya sama dengan 2. Selepas beberapa pemikiran, kita dapati: 6 dan -4. Semak: 6 · (- 4) \u003d -24. 6 + (– 4) = 6 – 4 = 2. Seperti yang anda perhatikan, dalam amalan, inti teorem Vieta adalah faktor faktor bebas ke dalam faktor-faktor tersebut, jumlahnya bersamaan dengan pekali kedua dengan tanda yang bertentangan. Faktor-faktor ini akan menjadi akar. Oleh itu, akar persamaan kuadrat kita ialah 6 dan -4. Jawapannya ialah: x 1 = 6, x 2 = –4. Contoh 3 Kami menyelesaikan persamaan kuadrat 3x 2 + 2x - 5 \u003d 0. Di sini kita tidak berurusan dengan persamaan kuadratik yang diberikan. Tetapi persamaan sedemikian juga boleh diselesaikan menggunakan teorem Vieta jika pekali mereka seimbang - sebagai contoh, jika jumlah pekali pertama dan ketiga bersamaan dengan yang kedua dengan tanda bertentangan. Penyelesaian. Koefisien persamaan seimbang: jumlah terma pertama dan ketiga bersamaan dengan yang kedua dengan tanda bertentangan: 3 + (–5) = –2. Menurut teorem Vieta x 1 + x 2 \u003d -2/3 Kita perlu mencari dua nombor yang jumlahnya adalah -2/3, dan produk -5/3. Nombor-nombor ini akan menjadi akar persamaan. Nombor pertama segera ditebak: ini adalah 1. Lagipun, dengan x \u003d 1 persamaan menjadi pengurangan penambahan paling mudah: 3/3 + x 2 \u003d -2/3. Kami menyelesaikan persamaan mudah: x 2 \u003d -2/3 - 3/3. Jawab: x 1 \u003d 1; x 2 \u003d -5/3 Contoh 4: Menyelesaikan persamaan kuadrat 7 x 2 – 6x – 1 = 0. Penyelesaian: Satu akar dikesan dengan segera - ia bergegas terus ke mata: x 1 \u003d 1 (kerana aritmetik mudah didapati: 7 - 6 - 1 \u003d 0). Koefisien persamaan seimbang: jumlah yang pertama dan ketiga bersamaan dengan yang kedua dengan tanda bertentangan: Selaras dengan teorem Vieta, kami menyusun dua identiti (walaupun dalam kes ini salah satu daripada mereka cukup): x 1 x 2 = –1/7 Kami menggantikan nilai x 1 ke mana-mana dua ungkapan ini dan mencari x 2: x 2 = –1/7: 1 = –1/7 Jawapannya ialah: x 1 = 1; x 2 = –1/7 Diskriminasi persamaan kuadrat dikurangkan. Diskriminasi persamaan kuadrat dikurangkan dapat dikira oleh formula umum dan oleh yang mudah: PadaD \u003d 0, akar persamaan yang diberikan boleh dikira dengan formula: Sekiranya D< 0, то уравнение не имеет корней. Jika D \u003d 0, maka persamaan mempunyai satu akar. Jika D\u003e 0, maka persamaan mempunyai dua akar. |
| Baca: |
|---|
Baru
- Apa yang memecahkan baron "kaku"?
- Ahli pergerakan Putih
- Jalan Suvorov dan pasukan ke tanah air mereka
- Fungsi F (x) dipanggil antiderivatif untuk fungsi f (x) jika F` (x) \u003d f (x) atau dF (x) \u003d f (x) dx
- Program pengurangan frasa darjah
- Istilah yang serupa, pengurangan mereka, contohnya
- Pengembara Rusia lazarev
- Menyelesaikan persamaan kuadrat tidak lengkap
- Penyelesaian persamaan kuadratik, formula akar, contohnya
- Pesawat menyelaras (Gred 6) - Pasar raya pengetahuan