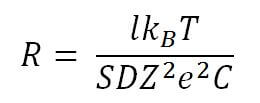Site sections
Editor's Choice:
- Expansion joints in buildings
- Chaber - what is it and its purpose
- Sharpening wood cutters: manual work, using grinding wheels and a grinding machine
- Belts and sandriks, crackers and volutes - secret codes of architecture on the example of the old Saratov Sandriks in architecture
- Surface grit - tooling work
- Maximum load on the balcony slab: how much can a balcony withstand in a panel house?
- Projects: symbols on drawings for water supply and sewage
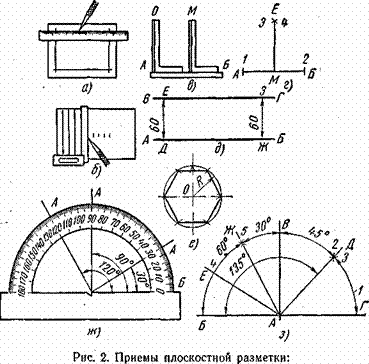
- Marking and marking details How to mark the details with curved contours
- Tools for slotting Tools for slotting
- Tools for chiseling Slotting tools
Advertising
| Movable and fixed unit. Simple mechanisms. Block Blocks giving the gain in power |
|
Bibliographic description: Shumeiko A.V., Vetashenko O. G. The modern view on the simple “block” mechanism, studied in physics textbooks for the 7th grade // Young Scientist. ?? 2016. ?? №2. ?? Pp. 106-113..07.2019).
Physics textbooks for the 7th grade when studying a simple block mechanism interpret differently how to gain in force when lifting cargo from using this mechanism, for example: in peryshkin textbook BUT. V. gain in strength is achieved with using the wheels of the block on which the lever forces act, and in the Gendenstein textbook L. E. The same winnings are obtained with by means of a cable, on which the force of a cable acts. Different textbooks, different subjects and different forces - to get a win in force, when lifting cargo. Therefore, the purpose of this article is to search for objects and forces with by means of which winning in force, when lifting cargo simple mechanism block. Keywords: First, we will review and compare how we get a gain in power, when lifting a load with a simple block mechanism, in the physics textbooks for the 7th grade, for this purpose we will place excerpts from textbook textbooks with the same concepts, for clarity, in the table.
Let us summarize the acquaintance and comparison of texts and drawings in textbooks: Evidence of obtaining a prize in the textbook A.V. Pyoryshkina is carried out on the wheel of the block and the acting force is the force of the lever; when lifting the fixed block does not give the gain in power, and the movable block gives a gain in strength of 2 times. There is no mention of the cable on which the load is hanging on the fixed block and the movable block with the load. On the other hand, in E. E. Gendenshteyn’s textbook, proof of gain in strength is carried out on a cable on which a load or moving unit with load is hanging and the acting force is the force of the cable tension; when lifting a load, the stationary block may give a gain of 2 times, and there is no mention of the lever on the block wheel. A search for literature describing how to get a gain in power with a block and a cable led to the “Elementary textbook of physics” edited by academician G. S. Landsberg, in §84. Simple machines on pages 1668-175 describes: "a simple block, double block, gate, polyspast and differential block". Indeed, by its design, “a double block gives a gain in strength, when lifting a load, due to the difference in the length of the radii of the blocks”, with which the load is lifted, and “a polyspast gives a gain in strength, when lifting a load, due to the rope , on several parts of which, the load hangs. ” Thus, it was possible to find out why they give a gain in strength, when lifting a load, separately a block and a cable (rope), but it was not possible to find out how the block and the cable interact with each other and transfer the weight of the load to each other, since the load can be suspended on the cable , and the cable is thrown over the block or the load can hang on the block, and the block hangs on the cable. It turned out that the tension force of the cable is constant and acts along the entire length of the cable, therefore the transfer of the weight of the load by the cable to the block will be at each point of contact between the cable and the block, and the transfer of the weight of the load suspended on the block - the rope. To clarify the interaction of the unit with the cable, we will conduct experiments on gaining the gain in power by the movable unit, while lifting the load, using the equipment of the school physics office: dynamometers, laboratory units and a set of loads in 1H (102 g). We will start the experiments with the movable block, because we have three different versions of getting the gain in power by this block. The first version is “Fig. 180. The movable block as a lever with unequal shoulders "- textbook A. V. Pyryshkina, the second" Fig.24.5 ... two identical tension forces of the cable F ", - according to the textbook of L. E. Gendenshtein and finally the third" Fig.145.Polispast " . The lifting of the load by the movable tackle cage on several parts of the same rope - according to G. S. Landsberg’s textbook Experience number 1. "Fig.183"
For the experiment number 1, getting the gain in power on the movable block “lever with unequal shoulders OAV pic.180” according to the textbook A. V. Peryshkin, on the movable block “pic.183” position 1, draw a lever with unequal shoulders OAB, like in “ris.180”, and we will begin lifting the load from position 1 to position 2. At the same instant, the block starts rotation, counterclockwise, around its axis at point A, and point B - the end of the lever that the lift is going through, beyond the semicircle, on which the cable around the bottom of the movable block. The point O is the point of support of the lever, which must be fixed, goes down, see “Fig.183” - position 2, i.e. the lever with unequal arms OAV changes as a lever with equal arms (the same paths pass points O and B). On the basis of the data obtained in experiment No. 1 on changes in the position of the OAB lever on the movable block when lifting the load from position 1 to position 2, it can be concluded that the representation of the movable block as a lever with unequal shoulders in "Fig.180", when lifting cargo, with the rotation of the block around its axis, corresponds to a lever with equal shoulders, which does not give a gain in strength, when lifting the load. Experience number 2 will begin with attaching dynamometers to the ends of the cable, on which we will hang the movable block with a weight of 102 g, which corresponds to a gravity of 1 N. We fix one end of the cable on the suspension, and for the second end of the cable we will lift the load on the movable block. Before the lift, the readings of both dynamometers at 0.5 N, first lifting the readings of the dynamometer for which the lift took place, changed to 0.6 N, and remained so during the lift, after the lifting was completed, the readings returned to 0.5 N. The readings of the dynamometer fixed for a fixed suspension did not change during the ascent and remained equal to 0.5 N. Let us analyze the results of the experiment:
We will compare the analysis of the experiment number 2 with the versions of textbooks about getting a gain in force by 2 times the moving block. Let us begin with the statement in L. E. E. Gendenshtein’s textbook "... that three forces are applied to the block: the weight of the load P, directed downwards, and two identical tension forces of the cable, directed upwards (Fig.24.5)". It would be more accurate to say that the weight of the load in “fig. 14.5 ”was divided into two parts of the cable, before and after the block, since the tension force of the cable is one. It remains to analyze the signature under the "ris.181" from the textbook A. A. Pyoryshkin. "Combination of mobile and fixed blocks - a polyspast." The description of the device and the gain in power, when lifting the load, the polyspast is given in the Elementary textbook of physics, ed. G. S. Lansberg where it is said: "Each piece of the rope between the blocks will act on the moving load with the force T, and all pieces of the rope will act with the force nT, where n is the number of separate sections of the rope connecting both parts of the block." It turns out that if we apply the gain in strength “with a rope connecting both parts” of the polyspast from the elementary physics textbook of Landsberg G. S. 180 "would be a mistake. After analyzing four textbooks of physics, we can conclude that the existing description of how to obtain gain in power by a simple mechanism does not correspond to the real situation and therefore requires a new description of the operation of a simple block mechanism. Simple lifting mechanism consists of a block and a cable (rope or chain). The blocks of this lifting mechanism are divided into: by design for simple and complex; according to the method of lifting the load on the mobile and stationary. Acquaintance with the construction of blocks will begin with simple block, which is a wheel rotating around its axis, with a groove around the circumference for a cable (rope, chain) in Fig. 1 and it can be regarded as an equal-arm lever whose arms are equal to the radius of the wheel: OA = OB = r. Such a block does not give a gain in strength, but allows you to change the direction of movement of the cable (ropes, chains).
Double block consists of two blocks of different radii, rigidly bonded to each other and mounted on a common axis of Fig.2. The radii of the blocks r1 and r2 are different and, when lifting the load, act as a lever with unequal shoulders, and the gain in power will be equal to the ratio of the lengths of the radii of the block of larger diameter to the block of smaller diameter F = P · r1 / r2. Gateway consists of a cylinder (drum) and a handle attached to it, which acts as a large-diameter block. The gain in power given by the collar is determined by the ratio of the radius of the circumference R described by the handle to the radius of the cylinder r on which the rope is wound F = P · r / R. Let us turn to the method of lifting loads in blocks. From the description of the design, all the blocks have an axis around which they rotate. If the axis of the block is fixed and does not rise or fall when lifting loads, then this block is called fixed blocksimple block, double block, gate. Have rolling blockthe axis rises and falls with the load of Fig.10 and it is intended mainly to eliminate the cable bending at the point of load suspension. Let's get acquainted with the device and the method of lifting the load with the second part of a simple lifting mechanism - this is a cable, rope or chain. The cable is twisted of steel wires, the rope is twisted of threads or strands, and the chain consists of links connected to each other. Ways of suspension of the cargo and getting the gain in force, when lifting the load, by cable: In fig. 4 the load is fixed at one end of the cable and if you lift the load beyond the other end of the cable, then to lift this load you need a little more force than the weight of the load, since a simple block of gain does not give F = R. In Figure 5, the worker’s load lifts himself up by the cable, which bends around the simple block, at one end of the first part of the cable is fixed the seat on which the worker sits, and for the second part of the cable, the worker lifts himself with a force 2 times less than his weight because the weight of the worker was divided into two parts of the cable, the first - from the seat to the block, and the second - from the block to the hands of the worker F = P / 2.
In Figure 6, the load is lifted by two workers for two cables and the weight of the load is distributed equally between the cables and therefore each worker will lift the load with a force of half the weight of the load F = P / 2. In Figure 7, workers lift a load that hangs on two parts of the same cable and the weight of the load is distributed equally between the parts of this cable (as between two cables) and each worker will lift the load with a force equal to half the weight of the load F = P / 2. In Figure 8, the end of the cable, for which one of the workers lifted the load, was fixed on a fixed suspension, and the weight of the load was divided into two parts of the cable and when the worker lifted the load on the second end of the cable, the force with which the worker would lift the load twice less than the weight of the load F = P / 2 and the lifting of the load will be 2 times slower. In Figure 9, the load hangs on 3 parts of one cable, one end of which is fixed and the gain in power, when lifting the load, will be equal to 3, since the weight of the load will be divided into three parts of the cable F = P / 3. To eliminate the bend and reduce the friction force in the place of suspension of the load, a simple block is installed and the force required to lift the load has not changed, since a simple block does not give gains in Fig.10 and Fig.11, and the block itself will be called moving unit, since the axis of this block rises and falls with the load.
Theoretically, the load can be hung on an unlimited number of parts of one cable, but practically limited to six parts and such a lifting mechanism is called polyspast, which consists of a fixed and movable cages with simple blocks, which alternately bend around the cable, one end fixed to the stationary holder, and the load lifting is done at the second end of the cable. The gain in force depends on the number of parts of the cable between the fixed and movable holders, as a rule it is 6 parts of the cable and the gain in power 6 times. The article discusses the real interaction between the blocks and the cable when lifting the load. The existing practice in determining that “a fixed block does not give a gain in strength, and a movable block gives a gain of 2 times” mistakenly interpreted the interaction of the cable and the block in the lifting mechanism and did not reflect the whole diversity of the block design, which led to the development of one-sided erroneous ideas about block. Compared with the existing volumes of material for the study of a simple block mechanism, the volume of the article increased by 2 times, but this allowed to clearly and efficiently explain the processes occurring in a simple lifting mechanism, not only for students, but also for teachers. Literature:
Keywords: block, double block, fixed block, movable block, polyspast.. Annotation: Physics textbooks for the 7th grade when studying a simple mechanism block differently interpret how to gain a gain when lifting a load using this mechanism, for example: in the textbook A. Perryshkin textbook, the gain in strength is achieved using the wheel of a block that is acted upon by a lever; and in the E. L. Gendenshtein textbook, the same gain is obtained with the help of a cable, which is acted upon by a cable tension force. Different textbooks, different subjects and different forces - to get a gain in strength, while lifting the load. Therefore, the purpose of this article is to search for objects and forces, with the help of which the gain in power is obtained, when a load is lifted by a simple block mechanism. 4.1. Static elements 4.1.7. Some simple mechanisms: blocks Devices designed to move (lift, lower) loads with the help of a wheel and a thread thrown over it, to which some force is applied, are called blocks. Distinguish between fixed and moving blocks. The blocks are intended for moving a weight of P → with the help of the force F → applied to the rope thrown over the wheel. For any type of blocks (motionless and mobile) the condition of balance is satisfied: d 1 F = d 2 P, where d 1 is the shoulder of the force F → applied to the rope; d 2 is the shoulder of the force P → (the weight of the load moved by this block). AT fixed block (fig. 4.8) the shoulders of the forces F → and P → are identical and equal to the radius of the block: d 1 = d 2 = R, therefore, the power modules are equal to each other: F = P. Fig. 4.8 With the help of a fixed block, a body with weight P → can be moved by applying a force F →, the value of which coincides with the value of the weight of the load. In the movable block (fig. 4.9) the shoulders of the forces F → and P → are different: d 1 = 2R and d 2 = R, where d 1 is the shoulder of the force F → applied to the rope; d 2 is the shoulder of force P → (the weight of the load moved by this unit), therefore, the power modules obey equality: Fig. 4.9 With the help of the movable block, the body with the weight P → can be moved by applying a force F → which is half the size of the weight of the load. Blocks allow you to move the body some distance:
However, both mobile and fixed blocks do not give a win in work: how many times we win in strength, so many times we lose in the distance (“golden rule” of mechanics). Example 22. The system consists of two weightless blocks: one mobile and one fixed. A weight of 0.40 kg is suspended from the axis of the moving unit and touches the floor. Some force is applied to the free end of the rope, thrown over the fixed block, as shown in the figure. Under the action of this force, the load rises from the state of rest to a height of 4.0 m in 2.0 s. Find the modulus of force applied to the rope. 2 T → ′ + P → = m a →, 2 T ′ - m g = m a, a = 2 F - m g m. The distance covered by the load coincides with its height above the floor surface and is related to the time of its movement by the formula or taking into account the expression for the acceleration module h = a t 2 2 = (2 F - m g) t 2 2 m. Express from here the desired force: F = m (h t 2 + g 2) and calculate its value: F = 0.40 (4.0 (2.0) 2 + 10 2) = 2.4 N. Example 23. The system consists of two weightless blocks: one mobile and one fixed. Some weight is suspended from the axis of the fixed block as shown in the figure. Under the action of a constant force applied to the free end of the rope, the load begins to move with constant acceleration and moves up to a distance of 3.0 m in 2.0 seconds. During the movement of the load applied force develops an average power of 12 watts. Find the mass of the load. Decision . The forces acting on the movable and fixed blocks are shown in the figure. Two forces T → (on both sides of the block) act on the fixed block from the side of the rope; under the action of these forces, the forward movement of the block is absent. Each of these forces is equal to the force F → applied to the end of the rope: Three forces act on the movable block: two tension forces of the rope T → ′ (on both sides of the block) and the weight of the load P → = m g →; under the action of the indicated forces, the block (together with the load suspended on it) moves upward with acceleration. We write the second law of Newton for the movable unit in the form: 2 T → ′ + P → = m a →, or projected on a coordinate axis directed vertically upwards, 2 T ′ - m g = m a, where T 'is the modulus of the tension force of the rope; m is the mass of the load (the mass of the movable unit with the load); g is the module of the acceleration of gravity; a is the unit acceleration module (the load has the same acceleration, therefore, we will speak about the acceleration of the load). The modulus of the rope tension force T ′ is equal to the modulus of force T: therefore, the load acceleration modulus is determined by the expression a = 2 F - m g m. On the other hand, the acceleration of the load is determined by the formula for the distance traveled: where t is the time of movement of the cargo. Equality 2 F - m g m = 2 S t 2 allows you to get an expression for the modulus of the applied force: F = m (S t 2 + g 2). The load moves uniformly accelerated, therefore the module of its speed is determined by the expression v = at, and the average speed - 〈V〉 = S t = a t 2. The average power developed by the applied force is determined by the formula 〈N〉 = F 〈v〉, or taking into account expressions for the modulus of force and average speed: 〈N〉 = m a (2 S + g t 2) 4 t. From here we express the desired mass: m = 4 t 〈N〉 a (2 S + g t 2). Substitute in the formula for the expression for acceleration (a = 2S / t 2): m = 2 t 3 〈N〉 S (2 S + g t 2) and make the calculation: m = 2 ⋅ (2.0) 3 ⋅ 12 3.0 (2 ⋅ 3.0 + 10 (2.0) 2) ≈ 1.4 kg. Report on the implementation of the research assignment “Study of the system of blocks giving a gain of 2, 3, 4 times” 7th grade students. Secondary school number 76, Yaroslavl Work theme: Study of the system of blocks giving a gain of 2, 3, 4 times. Objective: Applying a system of blocks, get a gain in force of 2, 3, 4 times. Equipment: movable and fixed blocks, tripods, feet with clutches, loads, rope. Work plan: Study the theoretical material on the topic “Simple mechanisms. Blocks "; Assemble and give a description of the installations - block systems giving a gain of 2, 3, 4 times. Analysis of the results of the experiment; Conclusion "A little bit about the blocks" In modern technology, lifting mechanisms are widely used, irreplaceable components of which can be called simple mechanisms. Among them, the most ancient inventions of mankind are blocks. The ancient Greek scientist Archimedes eased the labor of man by giving him a gain in strength when using his invention, and taught him to change the direction of the force. A block is a wheel with a groove around the circumference for a rope or chain whose axis is rigidly attached to a wall or ceiling beam. Lifting devices usually use not one, but several blocks. The system of blocks and cables designed to increase the load capacity is called a chain hoist. In physics lessons, we study a mobile and fixed block. Using a fixed block, you can change the direction of the force. A mobile unit - reduce gives a gain in strength of 2 times.Fixed block Archimedes regarded as equal-lever. The moment of force acting on one side of the fixed block is equal to the moment of force applied on the other side of the block. The forces creating these moments are the same. A moving unit Archimedes took for unequal arms. Regarding the center of rotation, there are moments of forces that must be equal in equilibrium. Block drawings: 2. Assembling installations - block systems, giving a gain in strength of 2, 3 and 4 times. In the work we use the loadwhose weight is 4 N (Fig.3). Fig. 3 Using mobile and fixed blocks, our team assembled the following installations: Block system giving a gain of 2 times (Fig.4 and Fig.5). In this system of blocks, mobile and fixed blocks are used. This combination gives you double the winnings. Therefore, to the point A you need to apply a force equal to half the weight of the load. Pic.4
Pic.5
The photo (Fig.5) shows that this installation gives a gain of 2 times, the dynamometer shows a force approximately equal to 2 N. There are two ropes from the load. We do not take into account the weight of the blocks. Block system giving 3 times the gain . Fig.6 and Fig.7 In this system of blocks, two mobile and fixed blocks are used. Such a combination gives a gain of three times. The principle of operation of our installation with a multiplicity of 3 (3 times gain in power) looks as shown in the figure. The end of the rope is mounted on the platform, then the rope is thrown over the fixed block. Once again - through the mobile unit, which holds the platform with the load. Then pull the rope through another fixed block. This type of mechanism gives a gain in strength of 3 times, it is an odd option. We use a simple rule: how many ropes come from the load, such is our gain in strength. In the length of the rope, we lose exactly as many times as it turns out the gain in power. Pic.6
Pic.7
Fig.8
The photograph (Fig. 8) shows that the dynamometer shows a force approximately equal to 1.5 N. The error gives the weight of the moving unit and the platform. From the load comes three ropes. Block system giving 4 times the gain . In this system of blocks, two mobile and two fixed blocks are used. This combination gives you a four-fold gain. (Fig.9 and Fig.10). Fig. 9
Pic.10
The photo (Fig.10) shows that this installation gives a gain of 4 times the strength, the dynamometer shows a force approximately equal to 1 N. There are four ropes from the load. Conclusion: The system of mobile and fixed blocks, consisting of ropes and blocks, allows you to win in effective strength with a loss in length. We use the simple rule - the golden rule of mechanics: how many ropes come from the load, this is our gain in strength. In the length of the rope, we lose exactly as many times as it turns out the gain in power. Thanks to this golden rule of mechanics, it is possible to lift loads of large mass without making great efforts. Knowing this rule, you can create a system of blocks - a tackle, allowing you to win in force the nth number of times. Therefore, blocks and block systems are widely used in various areas of our life. Pfixed and fixed blocks are widely used in the transmission mechanisms of cars. In addition, the blocks are used by builders to lift large and small loads (for example, when repairing the external facades of buildings, builders often work in a cradle that can move between floors. After finishing work on the floor, workers can quickly move the cradle to the floor above, using with only their own strength). Blocks are so widespread because of the simplicity of their assembly and ease of working with them. Let us assume for now that the mass of the block and cable, as well as the friction in the block, can be neglected. In this case, the force of the cable tension can be considered the same in all its parts. In addition, the cable will be considered inextensible, and its mass - negligible. Fixed blockA fixed unit is used to change the direction of the force. In fig. 24.1, and it is shown how to change the direction of the force with the help of a fixed block to the opposite. However, it can be used to change the direction of the force as you please. Draw a diagram of the use of a fixed block, with which you can rotate the direction of the force by 90 °. Does a fixed block win in strength? Let's consider it on the example shown in fig. 24.1, a. The cable is pulled by the force applied by the fisherman to the free end of the cable. The tension force of the cable remains constant along the cable, therefore, from the side of the cable, the load (fish) is of the same magnitude as the force. Therefore, a fixed block does not give a gain in power. When using a fixed block, the load rises by the same amount as the end of the cable, to which the fisherman applies force. This means that using a fixed block, we do not win or lose on the way. Movable blockWe put the experienceLifting the load with the help of a light movable block, we note that if the friction is low, then for lifting the load it is necessary to apply a force that is about 2 times less than the weight of the load (fig. 24.3). Thus, the mobile unit gives a gain in force of 2 times. Fig. 24.3. When using a rolling block, we win 2 times in strength, but as many times we lose on the way. However, for a double gain in power, you have to pay the same loss on the way: in order to lift a load, for example, by 1 meter, you have to lift the end of a cable thrown over the block by 2 meters. The fact that the mobile unit gives a double gain in strength can be proved without resorting to experience (see below the section “Why does the mobile unit give a gain in strength twice?”). Most often, simple mechanisms are used to gain the gain in power. That is, a smaller force to move more in comparison with her weight. In this case, the gain in power is not achieved "for free." The cost to pay for it is a loss in distance, that is, a greater movement is required than without using a simple mechanism. However, when the forces are limited, the “exchange” of the distance for the force is beneficial. Movable and fixed blocks are some of the types of simple mechanisms. In addition, they are a modified lever, which is also a simple mechanism. Fixed block does not give a gain in strength, it simply changes the direction of its application. Imagine that you need to lift a heavy load up the rope. You will have to pull it up. But if you use a fixed block, you will have to pull it down while the load goes up. In this case, it will be easier for you, since the necessary strength will be made up of muscle strength and your weight. Without the use of a fixed block, it would be necessary to apply the same force, but it would be achieved solely at the expense of muscle strength. The fixed block is a wheel with a chute for the rope. The wheel is fixed, it can rotate around its axis, but can not move. The ends of the rope (cable) hang down, a load is attached to one, and a force is applied to the other. If you pull the cable down, the load rises. Since there is no gain in force, there is no loss in distance. At what distance the load will rise, at the same distance it is necessary to lower the rope. Using rolling block gives a gain in strength twice (ideally). This means that if the weight of the load is F, then in order to lift it, you must apply the force F / 2. The movable unit consists of all of the same wheel with a chute for the cable. However, there is fixed one end of the cable, and the wheel is movable. The wheel moves with the load. The weight of the load is the force directed downwards. It is balanced by two upward forces. One creates a support to which the cable is attached, and the other pulling the cable. The tension force of the cable is the same on both sides, which means that the weight of the load is equally distributed among them. Therefore, each of the forces is 2 times less than the weight of the load. In real situations, the gain in force is less than 2 times, since the lifting force is partially “spent” on the weight of the rope and block, as well as friction. The moving block, giving almost double the gain in power, gives a double loss in distance. In order to raise the load to a certain height h, it is necessary that the ropes on each side of the block decrease to this height, that is, the total is 2h. Usually use combinations of fixed and mobile blocks - tackles. They allow you to get a gain in strength and direction. The more moving blocks in a chain block, the greater will be the gain in power. |
Popular:
New
- Markup definition. Planar marking. Types of markup. Questions for self-test
- Pipe bending machines Various variations of pipe bending machine
- Safety during filing
- What should be the sharpening angle of the scriber
- Drawing on preparation of contours of future product
- Modern ways of cutting metal and its defects
- Kerner - so that the drill does not slip off!
- Objects of inanimate nature Examples of the influence of inanimate nature factors on plants
- Finishing joinery
- Block breakdown in AutoCAD - simple and effective teams from practitioners