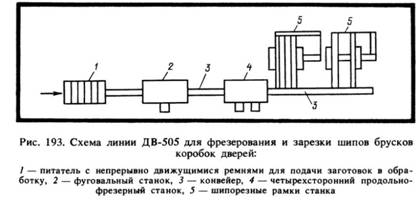
Site sections
Editor's Choice:
- Court decision on recovery from the management company of the amount of damage to the gulf of the apartment
- Living room and children in the same room: options for partitions
- Top sofa upholstery rating: customer reviews
- Expansion joints in buildings
- Chaber - what is it and its purpose
- Sharpening wood cutters: manual work, using grinding wheels and a grinding machine
- Belts and sandriks, crackers and volutes - secret codes of architecture on the example of the old Saratov Sandriks in architecture
- Surface grit - tooling work
- Maximum load on the balcony slab: how much can a balcony withstand in a panel house?
- Projects: symbols on drawings for water supply and sewage
Advertising
| A series of scales of increase and decrease. Placement of images on the drawings. The scale of the drawings. Training spatial imagination |
|
The scale of the drawing is the ratio of its linear dimensions to the actual size of the depicted object. This makes it possible to judge the parameters of the object in question. Using natural dimensions in the preparation of the drawing is not always possible. There are several reasons for this:
In such cases, the images are drawn reduced or enlarged. Standard scalesScale reduction include:
The first number indicates that the scale of the image is two times smaller than the size of the object. In the case when the part or mechanism is small, other designations are used: 2: 1, 2.5: 1, 5: 1, 10: 1. Also, an increase is made 20, 40, 50 and 100 times. How to determine the scaleTo correctly determine the scale of the drawings in accordance with GOST, it is necessary to know the parameters of the part or mechanism. If the object is large, then it can be reduced by dividing by the numbers presented. An example is a double resize. If a part reduced by half will fit on a sheet of paper for a drawing, then the scale is 1: 2. Any item that needs to be depicted can be measured by standard methods (using a ruler, for example), in order to transfer them to paper. The same thing happens when creating something based on a drawing. According to the specified scale, the exact dimensions are determined. Mainly drawings are used:
Resizing allows you to work on designing an object on a small paper surface, which simplifies the process. If the scale of a certain section of the drawing is different (as happens during construction), then a designation with the required number is put near it. When creating drawings, many students make mistakes due to lack of experience and knowledge. To avoid this, it is enough to order the services of our company. Experts will quickly complete the work, which will allow you to get a good grade and see an example of a quality drawing. In addition, we can order the implementation of a term paper, a thesis or an essay that will be done strictly within the stipulated time frame. Why it is necessary to follow GOSTThe document regulating the application of inscriptions, tables, as well as technical requirements, highlights the rules by which the drawing up of each drawing takes place according to certain standards. This contributes to the creation of graphic information that is understandable for any engineer or builder who uses it in their professional activities. Careful reading of the documents will allow for the correct presentation of the information and the scale of the drawings. GOST 2.302-68 * contains the following rules:
Compliance with all these rules will allow you to create a drawing that meets all the requirements and therefore will be convenient for use. Change No. 2 was adopted by the Interstate Council for Standardization, Metrology and Certification (Minutes No. 17 of June 22, 2000)
Change No. 3 was adopted by the Interstate Council for Standardization, Metrology and Certification by correspondence (Minutes No. 23 of February 28, 2006) INTERSTATE STANDARD
* Edition (August 2007) with Amendments No. 1, 2, 3, approved in February 1980, December 2000, June 2006 (IUS 4-80, 3-2001, 9-2006) Approved by the Decree of the Committee of Standards, Measures and Measuring Instruments under the Council of Ministers of the USSR No. 752 of May 28, 1968 Introduction date set 01.01.71 1. This standard establishes the scale of images and their designation on the drawings of all industries and construction. The standard does not apply to drawings obtained by photographing, as well as to illustrations in print publications, etc. (Revised Edition No. 2). 2a In this standard, the following terms are used with the corresponding definitions: scale: The ratio of the linear size of the segment in the drawing to the corresponding linear size of the same segment in nature; actual size scale: Scale with a 1: 1 ratio; zoom scale:Scale with a ratio greater than 1: 1 (2: 1, etc.); zoom out: Scale with a ratio less than 1: 1 (1: 2, etc.). (Enteredin addition, Mod. № 2). 2. The scale of the images in the drawings should be selected from the following row: 3. When designing master plans for large objects, it is allowed to use scales of 1: 2000; 1: 5000; 1: 10,000; 1: 20,000; 1: 25,000; 1: 50,000. 4. In necessary cases it is allowed to apply scales of increase (100 n): 1, where p - integer. 5. The scale indicated in the designated main inscription of the drawing shall be designated as 1: 1; 1: 2; 2: 1, etc. Documents in electronic form in their requisite part must contain props, indicating the accepted scale of the image. When outputting documents in electronic form on paper, the image scale should correspond to the specified one. (Revised Edition, Rev. No. 3). GOST 2.302-68 Group T52 INTERSTATE STANDARD Unified system for design documentation SCALE Unified system for design documentation. Scales MKS 01.100.01 Introduction date 1971-01-01
The following countries voted for the adoption of the amendment by the national authorities: AZ, AM, BY, KZ, KG, MD, RU, TJ, TM, UZ, UA [alpha-2 codes for MK (ISO 3166) 004] 1. This standard establishes the scale of images and their designation on the drawings of all industries and construction. 2a In this standard, the following terms are used with the corresponding definitions: 2. The scale of the images in the drawings should be selected from the following row:
3. When designing master plans for large objects, it is allowed to use scales of 1: 2000; 1: 5000; 1: 10,000; 1: 20,000; 1: 25,000; 1: 50,000. 4. In necessary cases it is allowed to apply magnification scales (100): 1, where is an integer. 5. The scale indicated in the designated main inscription of the drawing shall be designated as 1: 1; 1: 2; 2: 1, etc. INTRODUCTION Topographic map is a reduced generalized image of the terrain, showing the elements using the system of conventional signs. 6.1. TYPES OF TOPOGRAPHIC MAPSWhen mapping and plans, the horizontal projections of the segments are depicted on paper in a reduced form. The extent of this decrease is characterized by scale. Map scale (plan) - the ratio of the length of the line on the map (plan) to the length of the horizontal distance of the corresponding line of the terrain m = l K: d M The scale of the image of small areas on the entire topographic map is almost constant. With small angles of inclination of the physical surface (on the plain), the length of the horizontal projection of the line is very little different from the length of the inclined line. In these cases, the length scale ratio of the line length on the map to the length of the corresponding line on the ground can be considered. The scale is indicated on the maps in different versions. 6.1.1. Numerical scale Numerical scale expressed as a fraction with a numerator equal to 1(aliquot fraction). Or Denominator M Numerical scale shows the degree of reduction of the lengths of lines on the map (plan) with respect to the lengths of the corresponding lines on the ground. By comparing the numerical scales, larger is called the one whose denominator is less. Example. Decision. note to the fact that the numerical scale is an abstract value that does not have specific units of measurement.If the numerator of a fraction is expressed in centimeters, then the denominator will have the same units of measurement, i.e. centimeters for exampleA scale of 1:25 000 means that one centimeter of a map corresponds to 25,000 centimeters of terrain, or 1 inch of a map corresponds to 25,000 inches of terrain. To meet the needs of the economy, science and defense of the country, maps of various scales are needed. Standard scales are defined for state topographic maps, forest management tablets, forestry plans and afforestation plans. scale series(tab. 6.1, 6.2). Scale Topographic Maps Table 6.1.
Previously, this series included scales of 1: 300,000, and 1: 2,000. 6.1.2. Named scaleNamed Scale
called a verbal expression of numerical scale. Under the numerical scale on the topographic map there is an inscription explaining how many meters or kilometers in the area corresponds to one centimeter of the map. for example, on the map under the numerical scale of 1:50 000 it is written: “500 meters in 1 centimeter”. The number 500 in this example is named scale value
. Example. The named scale of the map is “2 kilometers in 1 centimeter”. The length of the segment on the map lК= 6.3 cm. Determine the horizontal position of the line on the ground. To avoid mathematical calculations and speed up the work on the map, use graphic scale . There are two such scales: linear and transverse . Linear scaleTo build a linear scale, choose the original segment, convenient for this scale. This source segment ( but) called base of scale (Fig. 6.1).
The base is laid on a straight line the required number of times, the leftmost base is divided into parts (segment b), to be smallest linear scale divisions
. The distance on the ground, which corresponds to the smallest division of the linear scale, is called linear scale accuracy
.
Lateral scaleFor more accurate measurements use transverse by scale (Fig. 6.2, b).
To build it on a straight line segment, lay several bases of scale ( a). Usually the length of the base is 2 cm or 1 cm. At the points obtained, perpendiculars are set to the line. AB and draw ten parallel lines through them at regular intervals. The upper left base at the top and bottom is divided into 10 equal segments and connected by oblique lines. The zero point of the lower base is connected to the first point. WITH top base and so on. Get a series of parallel oblique lines, which are called transversals.
How to use the transverse scale:
The accuracy of measuring the length of a line using a transverse scale is estimated at half the price of its smallest division. 6.2. VARIETY OF GRAPHIC SCALES6.2.1. Transition scaleSometimes in practice you have to use a map or aerial photograph, the scale of which is not standard. For example, 1:17 500, i.e. 1 cm on the map correspond to 175 m on the ground. If we construct a linear scale with a base of 2 cm, then the smallest division of the linear scale will be 35 m. Digitization of such a scale causes difficulties in the production of practical work. Example. It is required to calculate the length of the base corresponding to 400 m for a 1:17 500 map (175 meters per centimeter). Having decided the proportion, we conclude: the base of the transition scale in centimeters is equal to the size of the segment on the ground in meters divided by the value of the named scale in meters. The length of the base in our case If we now build a transverse scale with the base length but= 2.29 cm, then one division of the left base will correspond to 40 m (Fig. 6.3).
For more accurate measurements on maps and plans, build a transverse scale. 6.2.2. Scale stepsUse this scale to determine the distances measured in steps during the eye survey. The principle of constructing and using the scale of steps is similar to the transition scale. The basis of the scale of steps is calculated so that it corresponds to a round number of steps (pairs, triples) - 10, 50, 100, 500. Example. The known distance of 100 m is measured in steps. 137 steps were passed in the forward direction, and in the reverse direction - 139 steps. Calculate the average length of one step. Shsr = 200/276 = 0.72 m. It is convenient to work with a linear scale, when the scale line is marked in 1 - 3 cm, and the divisions are signed with a round number (10, 20, 50, 100). Obviously, the value of one step of 0.72 m on any scale will have extremely small values. For a scale of 1: 2,000, the segment on the plan will be 0.72 / 2,000 = 0.00036 m or 0.036 cm. Ten steps, at an appropriate scale, will be expressed by a segment of 0.36 cm. The most convenient basis for these conditions, according to the author, there will be a value of 50 steps: 0.036 × 50 = 1.8 cm. The length of the base for 50 steps on a scale of 1: 2,000 with a length of one step equal to 72 cm will be:
6.3. SCALE ACCURACYScale accuracy
(maximum accuracy of the scale) is a segment of the horizontal line, corresponding to 0.1 mm on the plan. The value of 0.1 mm to determine the accuracy of the scale is taken due to the fact that this is the minimum segment that a person can distinguish with the naked eye. The accuracy of the scale allows to solve two important tasks:
It is almost accepted that the length of the segment on the plan or map can be estimated with an accuracy of 0.2 mm. The horizontal distance on the ground, corresponding in this scale to 0.2 mm (0.02 cm) on the plan, is called graphic accuracy of scale
. Graphic accuracy of determining distances on a plan or map can only be achieved using a transverse scale.. 6.4. DETERMINATION OF UNKNOWN SCALE OF THE CARDIn cases when for any reason the scale is absent on the map (for example, cut off when glued together), it can be determined in one of the following ways.
For example, the coordinate lines are designated by the numbers 28, 30, 32, etc. (along the western frame) and 06, 08, 10 (along the southern frame). It is clear that the lines are drawn after 2 km. The distance on the map between adjacent lines is 2 cm. From this it follows that 2 cm on the map correspond to 2 km on the ground, and 1 cm on the map - 1 km on the terrain (named scale). This means that the scale of the map will be 1: 100,000 (1 kilometer in 1 centimeter).
A 1: 1 000 000 (millionth) map sheet is indicated by one of the letters of the Latin alphabet and one of the numbers from 1 to 60. The system of map designations of larger scales is based on the nomenclature of sheets of a million map and can be represented by the following scheme: 1: 1,000,000 - N-37 Depending on the location of the map sheet, the letters and numbers that make up its nomenclature will be different, but the order and number of letters and numbers in the nomenclature of a sheet of a map of a given scale will always be the same.
For example, it is known that the distance from n. Kuvechino to the lake. Deep 5 km. Measuring this distance on the map, got 4.8 cm. Then
One minute of the arc of the meridian (on the eastern or western frame) corresponds to the terrain a distance of 1852 m (nautical mile). Knowing this, you can determine the scale of the map as well as by the known distance between two terrain objects. 6.5. TECHNIQUE OF MEASURING AND DELAYING DISTANCES ON THE MAPTo measure the distances on the map, use a millimeter scale or a scale bar, a caliper meter, and for measuring curved lines - a curvimeter. 6.5.1. Measurement distances millimeter rulerMeasure the distance between the specified points on the map with an accuracy of 0.1 cm with a millimeter ruler. The resulting number of centimeters should be multiplied by the value of the named scale. For flat terrain, the result will correspond to the distance in the terrain in meters or kilometers. 6.5.2. Distance measurement by a caliperWhen measuring the distance in a straight line, the compass needles are set at the end points, then, without changing the compass solution, the distance is counted on a linear or transverse scale. In the case when the compass solution exceeds the length of the linear or transverse scale, the integer number of kilometers is determined by the squares of the coordinate grid, and the remainder is determined by the usual order of scale.
For length broken line
consistently measure the length of each of its links, and then summarize their values. Such lines are also measured by increasing the caliper solution.
Long curved pieces measured on chords with compass steps (see fig. 6.6, b). The compass pitch, equal to an integer of hundreds or tens of meters, is set using a transverse or linear scale. When rearranging the caliper legs along the measured line in the directions shown in fig. 6.6, b arrows, consider steps. The total length of the A 1 C 1 line is the sum of the A 1 B 1 segment, equal to the step size multiplied by the number of steps, and the B 1 C 1 residue measured on a transverse or linear scale. 6.5.3. Distance Measurement with a Curvimeter Curve segments are measured by a mechanical (fig. 6.7) or electronic (fig. 6.8) gauge.
First, turn the wheel by hand, set the arrow on the zero division, then roll the wheel on the measured line. The counting on the dial against the end of the hand (in centimeters) is multiplied by the scale of the map and get the distance on the ground. Digital odometer (fig. 6.7.) Is a high-precision, easy-to-use instrument. The curvimeter includes architectural and engineering functions and has a handy display for reading information. This device can handle metric and Anglo-American (feet, inches, etc.) values, which allows you to work with any maps and drawings. You can enter the most commonly used type of measurement, and the instrument will automatically translate scale measurements.
To improve the accuracy and reliability of the results, it is recommended that all measurements be carried out twice - in the forward and reverse directions. In case of insignificant differences of the measured data, the arithmetic average of the measured values is taken as the final result. 6.5.4. Recalculate horizontal distance to slant rangeIt should be remembered that as a result of measuring distances using maps, the lengths of the horizontal projections of the lines (d) are obtained, and not the lengths of the lines on the earth's surface (S) (Fig. 6.9).
The actual distance on an inclined surface can be calculated by the formula:
where d is the length of the horizontal projection of the line S; The length of the line on a topographic surface can be determined using the table (Table 6.3) of the relative magnitudes of the corrections to the length of the horizontal distance (in%). Table 6.3
Terms of use table 1. The first row of the table (0 dozen) shows the relative magnitudes of the corrections at tilt angles from 0 ° to 9 °, in the second - from 10 ° to 19 °, in the third - from 20 ° to 29 °, in the fourth - from 30 ° up to 39 °. Example. On the topographic map, the length of the horizontal distance is 1735 m, the angle of inclination of the topographic surface is 7 ° 15 ′. In the table, the relative magnitudes of the amendments are given for whole degrees. Therefore, for 7 ° 15 "it is necessary to determine the nearest large and the nearest smaller values multiple to one degree - 8º and 7º: For 60 ′, the correction is 0.23%; Relative correction for tilt angle 7 ° 15 " At small angles of inclination (less than 4 ° - 5 °) the difference in the length of the inclined line and its horizontal projection is very small and may not be taken into account. 6.6. MEASUREMENT OF AREAS BY MAPDetermination of the areas of plots using topographic maps is based on a geometric relationship between the area of the figure and its linear elements. The scale of the area is equal to the square of the linear scale. Graphic, analytical, and instrumental methods are used to measure areas using maps. The use of one or another method of measurement is due to the shape of the area to be measured, a given accuracy of measurement results, the required speed of data acquisition and the availability of the necessary instruments. 6.6.1. Measurement of land area with straight edgesWhen measuring the area of a plot with rectilinear boundaries, the plot is divided into simple geometric figures, the area of each of them is measured by a geometric method, and by summing the areas of individual sections calculated taking into account the scale of the map, the total area of the object is obtained. 6.6.2. Measurement of the area with a curved contourAn object with a curvilinear contour is divided into geometric shapes, preliminarily straightening the borders in such a way that the sum of the cut-off areas and the sum of the surpluses mutually compensate each other (Fig. 6.10). The measurement results will be, to some extent, approximate.
Fig. 6.10. Straightening the curved boundaries of the site and 6.6.3. Measurement of the area of a complex configurationMeasurement of land areas having a complicated irregular configuration more often produced with the help of palettes and planimeters, which gives the most accurate results. Net palette It is a transparent plate with a grid of squares (Fig. 6.11).
The palette is applied to the contour to be measured and the number of cells and their parts trapped inside the contour is counted. Fractions of incomplete squares are estimated by eye, therefore, to improve the accuracy of measurements, small squares with small squares (with a side of 2 to 5 mm) are used. Before working on this map, determine the area of a single cell. Where: but -the side of the square, expressed on the scale of the map; To improve accuracy, the area is determined several times with an arbitrary permutation of the used pallet in any position, including with rotation relative to its original position. For the final value of the area take the arithmetic average of the measurement results. In addition to grid pallets, point and parallel pallets are used, which are transparent plates with etched dots or lines. The points are placed in one of the corners of the grid cells with a known division price, then the grid lines are removed (Fig. 6.12).
The weight of each point is equal to the price of pallet division. The area of the measured area is determined by counting the number of points trapped inside the contour, and multiply this number by the weight of the point. P = h∑l Measurement areas of significant plots produced by cards using planimeter.
Planimeter is used to determine the area mechanically. The polar planimeter is widespread (Fig. 6.14). It consists of two levers - pole and bypass. Determining the area of the contour planimeter is reduced to the following steps. Fixing the pole and setting the needle of the bypass lever at the starting point of the contour, take a count. Then the bypass spire is carefully guided along the contour to the starting point and a second count is taken. The difference in readings will give the contour area in the planimeter divisions. Knowing the absolute price of division planimeter, determine the area of the contour.
6.6.4. Calculating the area of a polygon by the coordinates of its vertices
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
y i (x i-1 - x i + 1) |
||||
|---|---|---|---|---|
Double area in m 2 |
SUM (D2: D6) |
|||
Area in hectares |
||||
In table 6.5 we see the results of the calculations.
Table 6.5.
y i (x i-1 -x i + 1) |
||||
|---|---|---|---|---|
Double area in m 2 |
||||
Area in hectares |
||||
6.7. EYE DIMENSIONS ON THE MAP
In the practice of cartometric work, eye measurements are widely used, which give approximate results. However, the ability to eye to determine on a map the distance, direction, area, slope steepness and other characteristics of objects contributes to mastering the skills of a proper understanding of the cartographic image. The accuracy of eye definitions increases with experience. Vision skills prevent gross errors in measurements with instruments.To determine the length of linear objects on the map, it is necessary to visually compare the magnitude of these objects with kilometer grid segments or linear scale divisions.
To determine the area of objects as a kind of palette, square kilometer grids are used. Each square of the grid of maps of scales 1:10 000 - 1:50 000 on the terrain corresponds to 1 km 2 (100 hectares), the scale 1: 100 000 - 4 km 2, 1: 200 000 - 16 km 2.
Accuracy of quantitative definitions on the map, with the development of the eye, is 10-15% of the measured value.
Video
Scaling tasksTasks and questions for self-control
- What elements are included in the mathematical basis of maps?
- Expand the concepts: “scale”, “horizontal distance”, “numerical scale”, “linear scale”, “accuracy of scale”, “base of scale”.
- What is the named map scale and how to use it?
- What is the transverse scale of the map, for what purpose is it intended?
- What is the transverse scale of the map considered normal?
- What is the scale of topographic maps and forest management tablets used in Ukraine?
- What is the transition scale of the map?
- How is the basis of the transition scale calculated? Previous
The scale is the ratio of the linear dimensions of the image in the drawing to its actual size.
The scale of the images and their designation on the drawings sets GOST 2.302-68 (table 5.3). The scale indicated in the designated main inscription of the drawing should be designated as 1: 1; 1: 2; 1: 4; 2: 1; 5: 1; etc.
Table 5.3 - Scale Drawings
When designing master plans for large objects, it is allowed to use scales of 1: 2000; 1: 5000; 1: 10,000; 1: 20,000; 1: 25,000; 1: 50,000.
5.3 Main title.
Each sheet is framed, the line of which is separated from the three sides of the format by 5 mm from the left side by 20 mm. On the frame line in the lower right corner of the format have the main inscription in accordance with GOST 2.104-68. On A4 sheets, the main inscription is placed only along the short side. The type and thickness of lines in drawings, diagrams and graphs must comply with GOST 2.303-68. Drawings of the design documentation of the project are performed with a pencil. Schemes, graphs, tables are allowed to perform black ink (paste). All inscriptions in the drawing field, dimensional numbers, filling in the main inscription shall be made only in drawing font according to GOST 2.304-81.
Thematic titles on the sheets do not depict, since the name of the contents of the sheet is indicated in the title block. In cases where the sheet with one inscription contains several independent images (poster material), separate images or parts of the text are provided with headings.
The main inscription on the first sheets of drawings and diagrams must comply with form 1, in text design documents - form 2 and form 2a on subsequent sheets. It is allowed to apply form 2a on subsequent sheets of drawings and diagrams.
The angular inscription for drawings and diagrams is located in accordance with Figure 5.1. Filled with turning the sheet 180 o or 90 o.
Figure 5.1 – Layout of the main inscription on various drawings
In the columns of the main inscription, figures 5.2, 5.3, 5.4, indicate:
- in column 1 - the name of the product or its component: the name of the schedule or scheme, as well as the name of the document, if a cipher is assigned to this document. The name should be short and recorded in the nominative singular. If it consists of several words, then a noun is put in the first place, for example: “Threshing drum”, “Safety clutch”, etc. It is allowed to record in this column the name of the contents of the sheet in the manner adopted in the technical literature, for example: “Economic indicators”, “Process map”, etc .;
- in column 2 - the designation of the document (drawing, graphics, diagrams, specifications, etc.);
- in column 3 - the designation of the material (the column is filled only on the drawings of parts). The designation includes the name, brand and standard or technical conditions of the material. If the material stamp contains its abbreviated name “St”, “MF”, then the name of this material is not indicated.
Figure 5.2 - Form No. 1
Figure 5.3 - Form No. 2
Figure 5.4 - Form number 2a
Examples of recording material:
- СЧ 25 GOST 1412-85 (gray cast iron, 250 - ultimate tensile strength in MPa);
- KCh 30-6 GOST 1215-79 (ductile iron, 300 is the ultimate tensile strength in MPa, 6 is the relative elongation in%);
- HF 60 GOST 7293-85 (high-strength cast iron, 600 is the tensile strength in MPa);
- St 3 GOST 380-94 (carbon steel of ordinary quality, 3-serial number of steel);
- Steel 20 GOST 1050-88 (carbon steel, structural quality, 20- carbon content in hundredths of a percent);
- Steel 30 KNZA GOST 4543-71 (alloyed structural steel, 30- carbon content in hundredths of a percent, chromium is not more than 1.5%, nickel is 3%, A is high-quality);
- Steel U8G GOST 1425-90 (tool carbon steel, 8 - carbon content in tenths of a percent; G - high content of manganese);
- Br04TS4S17 GOST 613-79 (bronze is deformable, O- tin 4%, Z-zinc 4%, C-lead 17%);
- BrА9Mts2 GOST 18175-78 (tinless bronze  pressure treated, A-aluminum 9%, manganese 2%);
pressure treated, A-aluminum 9%, manganese 2%);
- LTs38Mts2S2 GOST 17711-93 (cast brass, zinc 38%, manganese 2%, lead 2%);
- AL2 GOST 1583-89 (aluminum casting alloy, 2-serial number of the alloy);
- AK4M2TS6 GOST 1583-93 (aluminum alloy casting, silicon 4%, copper 2%, zinc 6%);
- AMts GOST 4784-74 (aluminum alloy deformable, manganese 1.0 ... 1.6%).
In the manufacture of parts from the range:
- Square  (from a bar of a square profile with a side size of 40 mm square according to GOST 2591-88, steel grade 20 according to GOST 1050-88);
(from a bar of a square profile with a side size of 40 mm square according to GOST 2591-88, steel grade 20 according to GOST 1050-88);
- Hexagon 
 (from hot-rolled steel hexagonal profile according to GOST 2579-88 conventional rolling accuracy, with the size of the inscribed circle - the size of "turnkey" - 22 mm, steel grade 25 according to GOST 1050-88);
(from hot-rolled steel hexagonal profile according to GOST 2579-88 conventional rolling accuracy, with the size of the inscribed circle - the size of "turnkey" - 22 mm, steel grade 25 according to GOST 1050-88);
- A circle  (hot-rolled round steel of usual rolling accuracy in diameter of 20 mm according to GOST 2590-88, steel grade St 3 according to GOST 380-94, supplied as per technical requirements of GOST 535-88);
(hot-rolled round steel of usual rolling accuracy in diameter of 20 mm according to GOST 2590-88, steel grade St 3 according to GOST 380-94, supplied as per technical requirements of GOST 535-88);
- Strip 
 (strip steel 10 mm thick with a width of 70 mm according to GOST 103-76, steel grade St 3 according to GOST 380-94, supplied as per technical requirements of GOST 535-88);
(strip steel 10 mm thick with a width of 70 mm according to GOST 103-76, steel grade St 3 according to GOST 380-94, supplied as per technical requirements of GOST 535-88);
- Corner  (angular ravnopolochnaya steel size 50x3 mm according to GOST 8509-86, steel grade St 3 according to GOST 380-94, the usual rolling accuracy B, supplied to the technical requirements of GOST 535-88);
(angular ravnopolochnaya steel size 50x3 mm according to GOST 8509-86, steel grade St 3 according to GOST 380-94, the usual rolling accuracy B, supplied to the technical requirements of GOST 535-88);
- I-beam  (I-beam hot-rolled number 30 according to GOST 8239-89 of increased accuracy (B), steel grade St 5 according to GOST 380-94, supplied to the technical requirements of GOST 535-88);
(I-beam hot-rolled number 30 according to GOST 8239-89 of increased accuracy (B), steel grade St 5 according to GOST 380-94, supplied to the technical requirements of GOST 535-88);
- Pipe 20x2.8 GOST 3262-75 (non-galvanized ordinary pipe of conventional manufacturing accuracy, unmeasured length, with a conditional passage of 20 mm, wall thickness of 2.8 mm, without thread and without coupling);
- Pipe Ts-R-20x2.8 - 6000 GOST 3262-75 (pipe with a zinc coating of increased manufacturing accuracy, measuring length 6000 mm, with a conditional passage of 20 mm, with thread);
- Pipe  (seamless steel pipe of standard manufacturing accuracy according to GOST 8732-78, with an outer diameter of 70 mm, a wall thickness of 3.5 mm, a multiple of 1250 mm, steel grade 10, manufactured according to group B of GOST 8731-87);
(seamless steel pipe of standard manufacturing accuracy according to GOST 8732-78, with an outer diameter of 70 mm, a wall thickness of 3.5 mm, a multiple of 1250 mm, steel grade 10, manufactured according to group B of GOST 8731-87);
- Pipe  (seamless steel pipe according to GOST 8732-78 with an inner diameter of 70 mm, wall thickness 16 mm, unmeasured length, steel of grade 20, category 1, manufactured in group A, GOST 8731-87);
(seamless steel pipe according to GOST 8732-78 with an inner diameter of 70 mm, wall thickness 16 mm, unmeasured length, steel of grade 20, category 1, manufactured in group A, GOST 8731-87);
- Column 4 - the letter assigned to this document according to GOST 2.103-68, depending on the nature of the work in the form of a project. The graph is filled from the left cell:
–Y - training document;
–DPP - diploma project documentation;
–DR - thesis documentation;
–KP - course project documentation;
–KR - coursework documentation;
- Column 5 - product mass (in kg) according to GOST 2.110-95; on the drawings of parts and assembly drawings indicate the theoretical or actual weight of the product (in kg) without indicating the units of measure.
It is allowed to specify the mass in other units of measurement, indicating them, for example, 0.25 g, 15 tons.
In drawings made on several sheets, the mass is indicated only on the first one.
On the dimensional and installation drawings, as well as on the drawings of parts of prototypes and individual production it is allowed not to specify the mass;
- Column 6 - scale (supplied in accordance with GOST 2.302-68).
If the assembly drawing is carried out on two or more sheets and the images on separate sheets are made on a scale different from that indicated in the main inscription of the first sheet, column 6 of the main inscription on these sheets is not filled out;
- Column 7 - the serial number of the sheet (on documents consisting of one sheet, the column is not filled).
Column 8 - the total number of sheets of the document (the column is filled only on the first sheet).
Column 9 - the name or the distinguishing index of the enterprise issuing the document (since the department on which the graduation project is carried out is ciphered in column 2 - the designation of the document, in this column it is necessary to put down the name of the institute and group code). For example: “PGSHA gr. To-51 ";
- Column 10 - the nature of the work performed by the person signing the document. In the thesis project graph is filled, starting from the top line with the following abbreviations:
- "Developed";
- "Consult";
- “Hands. etc.";
- “Head. Kaf. "
- "N. kontr.".
- Column 11 - the name of the persons who signed the document;
- Column 12 - the signatures of persons whose names are indicated in column 2. Signatures of the persons who developed this document and those responsible for the standard control are mandatory;
- Column 13 - the date of signing the document;
| Read: |
|---|
Popular:
New
- Open lesson "editing, bending"
- Installation of staircases and platforms: general information
- Repair of pipes of water supply in the apartment Repair of steel pipes
- Markup definition. Planar marking. Types of markup. Questions for self-test
- Pipe bending machines Various variations of pipe bending machine
- Safety during filing
- What should be the sharpening angle of the scriber
- Drawing on preparation of contours of future product
- Modern ways of cutting metal and its defects
- Kerner - so that the drill does not slip off!


















 (6.3)
(6.3) (6.4)
(6.4)