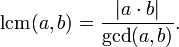Odseki spletnega mesta
Izbira urednikov:
Oglaševanje
| Najmanj skupno večkratnik 2. Kako najti najmanjši skupni večkratnik števil. Iskanje NOC prek GCD |
|
Toda številna naravna števila so v celoti razdeljena tudi na druga naravna števila. Na primer: Število 12 je razdeljeno z 1, 2, 3, 4, 6, 12; Število 36 je razdeljeno z 1, 2, 3, 4, 6, 12, 18, 36. Številke, na katere je število v celoti razdeljeno (za 12 je 1, 2, 3, 4, 6 in 12), se imenujejo delitve števila. Naravni delilnik števil a je naravno število, ki deli dano število a brez sledu. Pokliče se naravno število, ki ima več kot dva delitelja sestavljen . Upoštevajte, da imata številki 12 in 36 skupne delitve. Te številke so: 1, 2, 3, 4, 6, 12. Največji od deliteljev teh števil je 12. Skupni delitelj dveh danih števil a in b je število, s katerim sta obe dani številki deljivi brez preostalih ain b. Skupni večkratnik več številk se imenuje število, ki se deli na vsako od teh številk. Na primer, števila 9, 18 in 45 imajo skupni večkratnik 180. Toda 90 in 360 sta tudi njuna skupna množica. Med vsemi j-skupnimi množicami je vedno najmanjši, v tem primeru 90. To številko imenujemo najmanjšiskupno večkratnik (NOC). NOC je vedno naravno število, ki mora biti večje od največjega števila, za katero je določeno. Najmanj skupnega večkratnika (NLC). LastnostiKomunikativnost: Združljivost:
Zlasti, če in so številke ob istem številu, potem: Najmanj skupni večkratnik dveh celih števil min n je delitelj vseh drugih skupnih večkratnikov min n. Poleg tega veliko skupnih množic m, n sovpada z množico večkratnikov za NOC ( m, n). Asimptotiko za lahko izrazimo v smislu številnih teoretičnih funkcij. Torej Čebiševa funkcija . In tudi: To izhaja iz definicije in lastnosti funkcije Landau g (n). Kar izhaja iz zakona razdelitve praštevil. Iskanje najmanjšega skupnega večkratnika (LCL).NOC ( a, b) se lahko izračuna na več načinov: 1. Če je znan največji skupni delitelj, lahko uporabite njegov odnos z NOC:
2. Naj bo znana kanonična faktorizacija obeh števil:
kje p 1, ..., p k - različne preproste številke in d 1, ..., d k in e 1, ..., e k - celovita števila, ki niso negativna (lahko so ničle, če ustrezni prime ni v razširitvi). Nato NOC ( a,b) se izračuna po formuli: Z drugimi besedami, razširitev LCL vsebuje vse glavne dejavnike, ki se pojavijo v vsaj eni razgradnji števil a, bin vzemimo največji od obeh dejavnikov tega faktorja. Primer: Izračun najmanjšega skupnega večkratnika več številk je mogoče zmanjšati na več zaporednih izračunov NOC dveh števil: Pravilo. Če želite najti NOC več številk, morate: - razdeliti števila na osnovne faktorje; - največjo razgradnjo prenesemo v faktorje želenega produkta (zmnožek dejavnikov največjega danega števila) in nato dodamo faktorje iz razkroja drugih števil, ki se ne pojavijo v prvem številu ali so v njem manjkrat; - dobljeni produkt glavnih faktorjev bo NOC danih števil. Vsaka dve ali več naravnih števil ima svoj NOC. Če številke med seboj niso več ali če pri razširitvi nimajo enakih faktorjev, je njihov LCL enak zmnožku teh števil.
Preprosti faktorji 28 (2, 2, 7), dopolnjeni s faktorjem 3 (številke 21), bo dobljeni produkt (84) najmanjše število, deljeno z 21 in 28.
Preprosti faktorji največjega števila 30, dopolnjeni s faktorjem 5 števila 25, dobljeni produkt 150 je večji od največjega števila 30 in je razdeljen z vsemi danimi številkami. To je najmanjši možni izdelek (150, 250, 300 ...), na katerega so vsa navedena števila večkratna.
Števila 2,3,11,37 so enostavna, zato je njihov LCL enak zmnožku danih števil. Pravilo. Če želite izračunati NOC primerov, morate vse te številke pomnožiti med seboj. Druga možnost: Če želite najti najmanjši skupni večkratnik (LCL) več številk, ki jih potrebujete: 1) predstavljajo vsako številko kot rezultat svojih glavnih faktorjev, na primer: 504 \u003d 2 · 2 · 2 · 3 · 3 · 7, 2) zapišite stopnje vseh glavnih faktorjev: 504 \u003d 2 · 2 · 2 · 3 · 3 · 7 \u003d 2 3 · 3 2 · 7 1, 3) napišite vse enostavne delitelje (faktorje) vsake od teh številk; 4) izbrati največjo stopnjo vsakega od njih, ki jih najdemo v vseh razširitvah teh števil; 5) pomnožiti te stopnje. Primer . Poiščite številke NOC: 168, 180 in 3024. Rešitev . 168 \u003d 2 · 2 · 2 · 3 · 7 \u003d 2 3 · 3 1 · 7 1, 180 \u003d 2 · 2 · 3 · 3 · 5 \u003d 2 2 · 3 2 · 5 1, 3024 \u003d 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 \u003d 2 4 · 3 3 · 7 1. Iz vseh preprostih delitev napišemo največje stopnje in jih pomnožimo: NOC \u003d 2 4 · 3 3 · 5 1 · 7 1 \u003d 15120. Druga številka: b \u003d Ločilo bitov Brez ločevalnega prostora "" Rezultat: Največji skupni delitelj GCD ( a,b)=6 Najmanj skupni večkratni NOC ( a,b)=468 Pokliče se največje pozitivno celo število, s katerim sta števila a in b deljiva brez preostalih največji skupni dejavnik (GCD) teh številk. Imenuje se GCD (a, b), (a, b), gcd (a, b) ali hcf (a, b). Najmanj skupnih več (NOC) dveh celih števil a in b je najmanjše pozitivno celo število, ki ga delimo z a in b brez preostanka. Imenuje se NOC (a, b) ali lcm (a, b). Imenujemo se cela števila a in b medsebojno preprostače nimajo skupnih dejavnikov razen +1 in −1. Največji skupni dejavnikNaj dobimo dve pozitivni številki a 1 in a 2 1). Potrebno je najti skupnega delitelja teh števil, tj. najti takšno številko λ ki deli številke a 1 in a 2 hkrati. Opisujemo algoritem. 1) V tem članku bo beseda številka razumljena kot celo število. Naj a 1 ≥ a 2 in naj kje m 1 , a 3 nekaj celih števil a 3 <a 2 (preostanek delitve) a 1 naprej a 2 naj bo manj a 2). Predpostavimo, da λ deli a 1 in a 2 nato λ deli m 1 a 2 in λ deli a 1 −m 1 a 2 =a 3 (Izjava 2 člena "Delljivost števil. Znak delitve"). Iz tega sledi, da vsak skupni delitelj a 1 in a 2 je skupni delitelj a 2 in a 3. Velja tudi obratno, če λ skupni dejavnik a 2 in a 3 potem m 1 a 2 in a 1 =m 1 a 2 +a 3 so razdeljene tudi na λ . Od tod skupni delitelj a 2 in a 3 obstaja tudi skupni delitelj a 1 in a 2 Od takrat a 3 <a 2 ≤a 1, potem lahko rečemo, da je rešitev problema iskanja skupnega delitelja števil a 1 in a 2 se zmanjša na enostavnejši problem iskanja skupnega delitelja števil a 2 in a 3 . Če a 3 ≠ 0, potem jih lahko razdelimo a 2 naprej a 3. Potem
kje m 1 in a 4 nekaj celih števil, ( a 4 preostanek delitve a 2 naprej a 3 (a 4 <a 3)). S podobnim sklepanjem sklepamo, da so skupni delitelji števil a 3 in a 4 se ujemajo s skupnimi delilniki števil a 2 in a 3 in tudi s skupnimi delilniki a 1 in a 2 Od takrat a 1 , a 2 , a 3 , a 4, ... številk, ki se nenehno zmanjšujejo, in ker je med njimi končno število celih števil a 2 in 0, nato na nekem koraku n, preostanek delitve a n naprej a n + 1 bo nič ( a n + 2 \u003d 0).
Vsak skupni delitelj λ številke a 1 in a 2 tudi delilnik števil a 2 in a 3 , a 3 in a 4 , .... a n in a n + 1. Res je tudi obratno, skupni delitelji števil a n in a n + 1 so tudi delitelji števil a n - 1 in a n, ...., a 2 in a 3 , a 1 in a 2 Toda skupni delitelj števil a n in a n + 1 je število a n + 1, ker a n in a n + 1 delimo s a n + 1 (spomnite se tega a n + 2 \u003d 0). Zato a n + 1 je tudi delilnik števil a 1 in a 2 . Upoštevajte, da je številka a n + 1 je največji od deliteljev števil a n in a n + 1, saj je največji delitelj a n + 1 je sam a n + 1. Če a n + 1 lahko predstavljamo kot zmnožek celih števil, potem so ta števila tudi skupni delitelji števil a 1 in a 2 Številka a n + 1 se imenuje največji skupni dejavnik številke a 1 in a 2 . Številke a 1 in a 2 sta lahko tako pozitivna kot negativna števila. Če je eno od števil nič, potem bo največji skupni delitelj teh števil enak absolutni vrednosti drugega števila. Največji skupni delitelj ničelnih števil ni definiran. Imenuje se zgornji algoritem evklidov algoritemnajti največji skupni delitelj dveh celih števil. Primer iskanja največjega skupnega delitelja dveh številPoiščite največji skupni faktor obeh števil 630 in 434.
V koraku 5 je preostali delitev 0. Torej je največji skupni delitelj števil 630 in 434 14. Upoštevajte, da sta številki 2 in 7 tudi deljivki števil 630 in 434. Vzajemno preproste številkeOpredelitev 1. Naj bo največji skupni delitelj števil a 1 in a 2 je enak ena. Potem se te številke pokličejo medsebojno preproste številkenima skupnega delitelja. Izrek 1. Če a 1 in a 2 sta vzporedni številki in λ neko številko, nato kateri koli skupni delitelj števil λa 1 in a 2 je tudi skupni delilnik števil λ in a 2 . Dokaz. Razmislite o evklidskem algoritmu za iskanje največjega skupnega delitelja števil a 1 in a 2 (glej zgoraj).
Iz pogojev izrek izhaja, da je največji skupni delitelj števil a 1 in a 2 in zato a n in a n + 1 je 1. t.j. a n + 1 \u003d 1. Pomnožite vse te enakosti s λ torej
Naj bo skupni dejavnik a 1 λ in a 2 jesti δ . Potem δ je dejavnik pri a 1 λ , m 1 a 2 λ in v a 1 λ -m 1 a 2 λ =a 3 λ (glej "Delljivost števil", predlog 2). Naprej δ je dejavnik pri a 2 λ in m 2 a 3 λ in je torej dejavnik pri a 2 λ -m 2 a 3 λ =a 4 λ . Obrazložitev, zato smo prepričani v to δ je dejavnik pri a n - 1 λ in m n - 1 a n λ , in zato v a n - 1 λ −m n - 1 a n λ =a n + 1 λ . Od takrat a n + 1 \u003d 1, torej δ je dejavnik pri λ . Od tod tudi številka δ je skupni delilnik števil λ in a 2 . Upoštevamo posebne primere izrek 1. Posledica 1. Naj a in c primesi so relativno b. Potem njihov izdelek ac je primeren v primerjavi z b. Res. Iz izrek 1 ac in b imajo enake skupne delitelje kot c in b. Toda številke c in b medsebojno preprosta, tj. imajo en skupni faktor 1. Nato ac in b imajo tudi en sam skupni faktor 1. Zato ac in b medsebojno preprosta. Posledica 2. Naj a in b coprime številke in naj b deli ak. Potem b deli in k. Res. Iz pogoja izjave ak in b imajo skupnega delitelja b. Na podlagi teorema 1 je dr. b mora biti skupni delitelj b in k. Zato b deli k. Potek 1 lahko posplošimo. Posledica 3. 1. Pustite številke a 1 , a 2 , a 3 , ..., a m prime glede na število b. Potem a 1 a 2 , a 1 a 2 a 3 , ..., a 1 a 2 a 3 ··· a m, produkt teh števil je glavni glede na število b. 2. Imejmo dve vrstici števil
tako, da je vsako število v prvi vrstici prvo glede na vsako številko v drugi vrstici. Nato izdelek Najti je treba takšne številke, ki jih je mogoče deliti z vsako od teh številk. Če je število deljivo s a 1, potem ima obliko sa 1 kam s neko število. Če q je največji skupni delitelj števil a 1 in a 2 nato kje s 1 je nekaj celih števil. Potem je najmanjši skupni večkratnik a 1 in a 2 . a 1 in a 2 sta coprime, potem je najmanj pogosti večkratnik števil a 1 in a 2: Najti morate najmanjši skupni večkratnik teh številk. Iz zgoraj navedenega izhaja, da je katero koli več število a 1 , a 2 , a 3 mora biti večkratnik ε in a 3, in obratno. Naj bo najmanj pogosto več števil ε in a 3 jesti ε 1. Nato sledi več številk a 1 , a 2 , a 3 , a 4 mora biti večkratnik števil ε 1 in a 4. Naj bo najmanj pogosto več števil ε 1 in a 4 jesti ε 2 Tako smo ugotovili, da so vse več številk a 1 , a 2 , a 3 ,...,a m sovpadajo z večkratniki nekega določenega števila ε n, ki se imenuje najmanjši skupni večkratnik danih števil. V posebnem primeru, ko številke a 1 , a 2 , a 3 ,...,a m so coprime, potem je najmanj pogosti večkratnik števil a 1 , a 2, kot je prikazano zgoraj, ima obliko (3). Nadalje, odkar a 3 primera glede na številke a 1 , a 2 nato a 3 prime glede na število a 1 a 2 (Dodatek 1). Torej najmanj pogosti večkratnik a 1 ,a 2 ,a 3 je število a 1 a 2 a 3. Če se trdimo na podoben način, pridemo do naslednjih trditev. Odobritev 1. Najmanj skupni večkratnik medsebojno prime a 1 , a 2 , a 3 ,...,a m je enak njihovemu izdelku a 1 a 2 a 3 ··· a m. Odobritev 2. Katera koli številka, ki jo je mogoče deliti z vsako prvo število a 1 , a 2 , a 3 ,...,a m se deli tudi z njihovim izdelkom a 1 a 2 a 3 ··· a m. Opredelitev Pokliče se največje pozitivno celo število, ki je deljivo brez preostalih števil a in b največji skupni dejavnik (GCD) te številke. Poiščite največji skupni delitelj števil 24 in 35. Opredelitev Naravne številke se imenujejo medsebojno preprostače je njihov največji skupni faktor (GCD) 1. Največji skupni dejavnik (GCD) je mogoče najti, ne da bi napisali vse delitve danih števil. Faktorja števila 48 in 36 dobimo: Da bi našli največji skupni dejavnik Če so vsa dana števila deljena z enim od njih, potem je to število največji skupni dejavnik dane številke. Najmanj skupnih večkratnikov (NLC)Opredelitev Najmanj skupnih večkratnikov (NLC) pozitivna cela števila a in b sta najmanjši pozitivni celi številki, ki sta večkratnik a in b. Najmanjši skupni večkratnik (LCL) števil 75 in 60 je mogoče najti brez zapisovanja zaporednih večkratnikov teh števil. Da bi to naredili, razdelimo 75 in 60 na preproste faktorje: 75 \u003d 3 * 5 * 5 in 60 \u003d 2 * 2 * 3 * 5. Najdejo se tudi najmanj pogosti večkratniki za tri ali več števil. Do najti najmanj pogosto več več naravnih števil, je potrebno: Upoštevajte, da če je ena od teh števil deljena z vsemi drugimi številkami, potem je to število najmanjši skupni večkratnik teh števil. Pitagora (VI stoletje pred našim štetjem) in njegovi učenci so preučevali vprašanje delitve števil. Število, ki je enako vsoti vseh njegovih deliteljev (brez samega števila), so poimenovali popolno število. Na primer, števila 6 (6 \u003d 1 + 2 + 3), 28 (28 \u003d 1 + 2 + 4 + 7 + 14) so \u200b\u200bpopolna. Naslednja popolna števila so 496, 8128, 33 550 336. Pitagorejci so poznali samo prva tri popolna števila. Četrti - 8128 - je postal znan v 1. stoletju. n e. Petega - 33.550.336 - so našli v XV stoletju. Do leta 1983 je bilo znanih že 27 popolnih številk. Toda znanstveniki do zdaj ne vedo, ali obstajajo neparna popolna števila, ali obstaja največje popolno število. Učenci dobijo veliko nalog iz matematike. Med njimi so težave s takšno formulacijo zelo pogoste: obstajata dva pomena. Kako najti najmanjši skupni večkratnik za dane številke? Potrebno je biti sposoben izvajati takšne naloge, saj pridobljene spretnosti uporabljamo za delo z ulomki z različnimi imenovalci. V članku bomo analizirali, kako najti NOC in osnovne pojme. Preden najdete odgovor na vprašanje, kako najti NOC, se morate odločiti za izraz multi. Najpogosteje je ubeseditev tega pojma naslednja: večkratnik neke vrednosti A se imenuje naravno število, ki ga bo deljivo z A. Brez preostalih 8, 12, 16, 20 in tako naprej, do potrebne meje, bo večkratnik 4. Še več, število delitev za določeno vrednost je lahko omejeno in neskončno veliko večkratnikov. Tudi za naravne vrednote obstaja enaka vrednost. To je kazalnik, ki se nanje deli brez sledu. Ko bomo obravnavali koncept najmanjše vrednosti za določene kazalnike, bomo nadaljevali z iskanjem.
Poiščite NOCNajmanjši večkratnik dveh ali več kazalnikov je najmanjše naravno število, ki se v celoti deli z vsemi navedenimi številkami. Obstaja več načinov, kako najti takšno vrednost., upoštevajte naslednje metode:
Zdaj vemo, kakšna je splošna metodologija za iskanje najmanjše vrednosti za dve, tri ali več vrednosti. Vendar pa obstajajo zasebne metode.pomaga pri iskanju NOC, če prejšnji ne pomagajo. Kako najti GCD in NOC. Zasebni načini iskanjaKot pri katerem koli matematičnem odseku obstajajo posebni primeri iskanja NOC, ki pomagajo v posebnih situacijah:
Posebni primeri so manj pogosti kot standardni primeri. Toda zahvaljujoč njim se lahko naučite delati z frakcijami različnih stopenj zapletenosti. To še posebej velja za frakcije.kjer obstajajo različni imenovalci.
Nekaj \u200b\u200bprimerovOglejmo si nekaj primerov, s pomočjo katerih lahko razumemo načelo, da najdemo najmanj več:
Zahvaljujoč primerom lahko razumete, kako se nahaja NOC, kakšne so nianse in kakšen je pomen takšnih manipulacij.
Ugotovite, da je NOC veliko lažje, kot se morda sprva zdi. Za to se uporablja tako preprosto razkroj kot množenje preprostih vrednosti med seboj. Sposobnost dela s tem odsekom matematike pomaga pri nadaljnjem preučevanju matematičnih tem, zlasti frakcij različnih stopenj zahtevnosti. Ne pozabite občasno reševati primerov z različnimi metodami, to razvije logični aparat in vam omogoča, da se spomnite številnih izrazov. Naučite se načinov iskanja takšnega kazalca in lahko boste dobro sodelovali s preostalimi matematičnimi razdelki. Zabavajte se pri učenju matematike! VideoTa videoposnetek vam bo pomagal razumeti in si zapomniti, kako najti najmanjši skupni večkratnik. Nadaljujemo z razpravo o najmanj običajnem večkratniku, ki smo ga začeli v razdelku "NOC - najmanjši skupni večkratnik, definicija, primeri". V tej temi bomo pogledali načine za iskanje NOC za tri ali več številk, preučili bomo vprašanje, kako najti NOC negativnega števila. Yandex.RTB R-A-339285-1 Izračun najmanjšega skupnega večkratnika (NLC) skozi GCDPovezavo najmanj skupnega večkratnika smo že vzpostavili z največjim skupnim deliteljem. Zdaj se bomo naučili, kako določiti NOC prek GCD. Najprej ugotovimo, kako to storiti za pozitivne številke. Opredelitev 1 Najmanjši skupni večkratnik lahko najdemo z uporabo največjega skupnega faktorja s formulo NOC (a, b) \u003d a · b: GCD (a, b). Primer 1 Najti morate številki 126 in 70 NOC. Rešitev Vzamemo a \u003d 126, b \u003d 70. Vrednosti v formuli nadomestimo za izračun najmanjšega skupnega večkratnika z največjim skupnim deliteljem LCL (a, b) \u003d a · b: GCD (a, b). Poiščite GCD številk 70 in 126. Za to potrebujemo Evklidov algoritem: 126 \u003d 70 · 1 + 56, 70 \u003d 56 · 1 + 14, 56 \u003d 14 · 4, torej GCD (126 , 70) = 14 . Izračunamo NOC: NOC (126, 70) \u003d 12670: GCD (126, 70) \u003d 12670: 14 \u003d 630. Odgovor je: NOC (126, 70) \u003d 630. Primer 2 Poiščite trkanje števil 68 in 34. Rešitev NOD v tem primeru ni težko nevtralizirati, saj je 68 razdeljeno na 34. Najmanjši skupni večkratnik izračunamo po formuli: NOC (68, 34) \u003d 68 · 34: GCD (68, 34) \u003d 68 · 34: 34 \u003d 68. Odgovor je: NOC (68, 34) \u003d 68. V tem primeru smo uporabili pravilo iskanja najmanjšega skupnega večkratnika za pozitivna cela števila a in b: če je prvo število deljivo z drugim, potem bo LCM teh števil enak prvemu številu. Iskanje NOC z razvrščanjem števil v glavne dejavnikeZdaj pa poglejmo način, kako najti NOC, ki temelji na dekompoziciji števil v osnovne dejavnike. Opredelitev 2 Če želimo najti najmanj pogosto množico, moramo izvesti več preprostih korakov:
Ta metoda iskanja najmanjšega skupnega večkratnika temelji na enakosti NOC (a, b) \u003d a · b: GCD (a, b). Če pogledate formulo, postane jasno: produkt števk a in b je enak zmnožku vseh dejavnikov, ki sodelujejo pri razširitvi teh dveh števil. Poleg tega je GCD dveh števil enak zmnožku vseh osnovnih faktorjev, ki so hkrati prisotni v faktorizaciji teh dveh števil. Primer 3 Imamo dve številki 75 in 210. Razvrstimo jih lahko tako: 75 \u003d 3 · 5 · 5 in 210 \u003d 2 · 3 · 5 · 7. Če sestavimo produkt vseh faktorjev dveh izvornih števil, dobimo: 2 · 3 · 3 · 5 · 5 · 5 · 7. Če izvzamemo skupne faktorje za obe številki, 3 in 5, dobimo izdelek naslednje oblike: 2 · 3 · 5 · 5 · 7 \u003d 1050. To delo bo naš NOC za številki 75 in 210. Primer 4 Poiščite NOC števil 441 in 700 razdelitev obeh števil v osnovne dejavnike. Rešitev Poiščite vse osnovne faktorje števil, ki so navedeni v pogoju: 441 147 49 7 1 3 3 7 7 700 350 175 35 7 1 2 2 5 5 7 Dobimo dve verigi števil: 441 \u003d 3 · 3 · 7 · 7 in 700 \u003d 2 · 2 · 5 · 5 · 7. Rezultat vseh dejavnikov, ki so sodelovali pri razgradnji teh številk, bo izgledal tako: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 · 7. Poiščite skupne dejavnike. To je številka 7. Izvzamemo ga iz splošnega dela: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7. Izkaže se, da je NOC (441, 700) \u003d 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 \u003d 44 100. Odgovor je: NOC (441, 700) \u003d 44 100. Naj navedemo še eno formulacijo metode za iskanje LCL z dekompozicijo števil v primarne faktorje. Opredelitev 3 Pred tem smo iz skupnega števila dejavnikov izključili skupne faktorje za obe številki. Zdaj bomo storili drugače:
Primer 5 Vrnimo se k številkama 75 in 210, za katere smo v enem od prejšnjih primerov že iskali NOC. Razdelimo jih na glavne dejavnike: 75 \u003d 3 · 5 · 5 in 210 \u003d 2 · 3 · 5 · 7. Na produkt dejavnikov 3, 5 in 5 številke 75 dodajo manjkajoče faktorje 2 in 7 številke 210. Dobili smo: 2 · 3 · 5 · 5 · 7.To je NOC števil 75 in 210. Primer 6 Izračunati je treba številki NOC 84 in 648. Rešitev Števila iz pogoja razdelimo na glavne faktorje: 84 \u003d 2 · 2 · 3 · 7 in 648 \u003d 2 · 2 · 2 · 3 · 3 · 3 · 3. Dodajte izdelku dejavnikov 2, 2, 3 in 7
84 manjkajočih dejavnikov 2, 3, 3 in Odgovor je: NOC (84, 648) \u003d 4.536. Iskanje NOC treh ali več številkNe glede na to, s koliko številkami se ukvarjamo, bo algoritem naših dejanj vedno enak: zaporedoma bomo našli NOC dveh števil. Za ta primer obstaja izrek. Izrek 1 Recimo, da imamo cela števila a 1, 2, ..., a k. NOC m k te številke najdemo v zaporednem izračunu m 2 \u003d NOC (a 1, a 2), m 3 \u003d NOC (m 2, a 3), ..., m k \u003d NOC (m k - 1, a k). Zdaj bomo razmislili, kako lahko izrek uporabimo za reševanje konkretnih problemov. Primer 7 Izračunati je treba najmanjši skupni večkratnik od štirih števil 140, 9, 54 in 250 . Rešitev Uvedemo zapis: a 1 \u003d 140, a 2 \u003d 9, a 3 \u003d 54, a 4 \u003d 250. Za začetek izračunamo m 2 \u003d NOC (a 1, a 2) \u003d NOC (140, 9). Uporabljamo Evklidov algoritem za izračun GCD števil 140 in 9: 140 \u003d 9 · 15 + 5, 9 \u003d 5 · 1 + 4, 5 \u003d 4 · 1 + 1, 4 \u003d 1 · 4. Dobimo: GCD (140, 9) \u003d 1, NOC (140, 9) \u003d 140 · 9: GCD (140, 9) \u003d 140 · 9: 1 \u003d 1.260. Zato je m 2 \u003d 1.260. Zdaj po istem algoritmu izračunamo m 3 \u003d NOC (m 2, a 3) \u003d NOC (1,260, 54). Med izračuni dobimo m 3 \u003d 3.780. Ostaja nam, da izračunamo m 4 \u003d NOC (m 3, a 4) \u003d NOC (3 780, 250). Sledimo istemu algoritmu. Dobimo m 4 \u003d 94 500. NOC štirih števil iz pogojev primera je 94500. Odgovor je: NOC (140, 9, 54, 250) \u003d 94 500. Kot lahko vidite, so izračuni preprosti, vendar precej zamudni. Če želite prihraniti čas, lahko greste po drugi poti. Opredelitev 4 Ponujamo vam naslednji algoritem ukrepov:
Primer 8 Najti je treba NOC petih števil 84, 6, 48, 7, 143. Rešitev Vseh petih števil razdelimo na enostavne faktorje: 84 \u003d 2 · 2 · 3 · 7, 6 \u003d 2 · 3, 48 \u003d 2 · 2 · 2 · 2 · 3, 7, 143 \u003d 11 · 13. Preštevilčne številke, to je število 7, se ne razgrajujejo v osnovne faktorje. Takšna števila sovpadajo z njihovo faktorizacijo. Zdaj vzemite produkt glavnih faktorjev 2, 2, 3 in 7 od 84 in jim dodajte manjkajoče faktorje druge številke. Število 6 razdelimo na 2 in 3. Ti dejavniki so že v izdelku prve številke. Zato jih izpustimo. Še naprej dodajamo manjkajoče dejavnike. Preidemo na številko 48, od produkta glavnih faktorjev, od katerih vzamemo 2 in 2. Nato dodamo osnovni faktor 7 četrtega in faktorja 11 in 13 petega. Dobimo: 2 · 2 · 2 · 2 · 3 · 7 · 11 · 13 \u003d 48 048. To je najmanjši skupni večkratnik petih številk virov. Odgovor je: NOC (84, 6, 48, 7, 143) \u003d 48 048. Iskanje najmanjšega skupnega večkratnika negativnih številDa bi našli najmanjši skupni večkratnik negativnih števil, je treba te številke najprej nadomestiti s številkami z nasprotnim znakom in nato opraviti izračune z zgornjimi algoritmi. Primer 9 NOC (54, - 34) \u003d NOC (54, 34) in NOC (- 622, - 46, - 54, - 888) \u003d NOC (622, 46, 54, 888). Takšna dejanja so dopustna zaradi dejstva, da če to sprejmemo a in - a - nasprotne številke, Primer 10 Treba je izračunati NOC negativnih števil − 145 in − 45 . Rešitev Številke bomo zamenjali − 145 in − 45 na nasprotne številke 145 in 45 . Zdaj po algoritmu izračunamo NOC (145, 45) \u003d 145 · 45: GCD (145, 45) \u003d 145 · 45: 5 \u003d 1 305, pri čemer smo predhodno določili GCD z uporabo evklidskega algoritma. Razumemo, da je NOC števil 145 in − 45 enako 1 305 . Odgovor je: NOC (- 145, - 45) \u003d 1 305. Če v besedilu opazite napako, jo izberite in pritisnite Ctrl + Enter |
| Preberi: |
|---|
Priljubljeno:
Rešitev najpreprostejših trigonometričnih neenakosti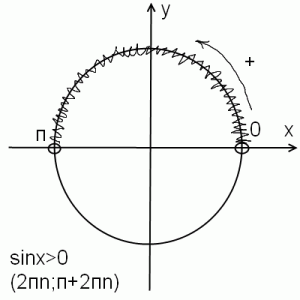
|
Novo
- Kaj je pokvarilo "krutega" barona?
- Član gibanja White
- Pot Suvorova in ekipe v domovino
- Funkcijo F (x) imenujemo antideriva za funkcijo f (x), če je F` (x) \u003d f (x) ali dF (x) \u003d f (x) dx
- Program za zmanjšanje deleža stopinj
- Podobni izrazi, njihovo zmanjšanje, primeri
- Ruski popotniki lazarev
- Reševanje nepopolnih kvadratnih enačb
- Rešitev kvadratnih enačb, formula korenin, primeri
- Koordinatna ravnina (6. razred) - Hipermarket znanja




 .
. .
. .
.