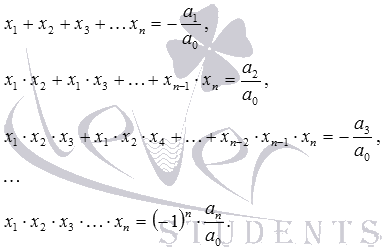|
To metodološko gradivo je samo za referenco in se nanaša na široko paleto tem. Članek ponuja pregled grafov osnovnih osnovnih funkcij in obravnava najpomembnejše vprašanje - kako hitro in hitro sestaviti grafikon. Študij višje matematike brez poznavanja grafov osnovnih elementarnih funkcij bo težaven, zato je zelo pomembno, da si zapomnite, kako izgledajo grafi parabole, hiperbole, sinusa, kosinusa itd., Zapomnite si nekatere vrednosti funkcij. Prav tako bomo govorili o nekaterih lastnostih glavnih funkcij. Ne pretvarjam se, da je gradivo popolno in znanstveno temeljito, poudarek bo predvsem na praksi - tistih, s katerimi se morate soočiti dobesedno na vsakem koraku, v kateri koli temi višje matematike. Lestvice za lutke? Lahko bi to rekli.
Po priljubljenem povpraševanju bralcev vsebino, ki jo je mogoče klikniti:
Poleg tega je na to temo še kratek povzetek.
- obvlada 16 vrst grafov, ko je preučil ŠEST strani!
Resno, šest, tudi sam sem bil presenečen. Ta zbirka vsebuje izboljšano grafiko in je na voljo za nominalno plačilo, ogledate si lahko demo različico. Datoteko je priročno natisniti tako, da so grafi vedno pri roki. Hvala za podporo projektu!
In takoj začnemo:
Kako sestaviti koordinatne osi?
V praksi študentke skoraj vedno izvajajo preskusne naloge v ločenih zvezkih, položenih v kletko. Zakaj preveriti oznako? Konec koncev je delo načeloma mogoče opraviti na listih A4. Celica je potrebna samo za kakovostne in natančne risbe oblikovanja.
Vsaka risba grafikona funkcije se začne s koordinatnimi osi.
Risbe so dvodimenzionalne in tridimenzionalne.
Najprej razmislimo o dvodimenzionalnem primeru kartezijanski pravokotni koordinatni sistem:
1) Narišemo koordinatne osi. Os je poklicana os abscese
in os je ordinatna os
. Vedno jih skušamo narisati čeden in nekrivljen. Puščice prav tako ne bi smele spominjati na brado Papa Carla.
2) Osi podpišemo z velikimi črkami "X" in "igrek". Ne pozabite podpisati osi.
3) Lestvico nastavimo vzdolž osi: narišite nič in dve. Pri izvajanju risbe je najprimernejša in pogosto srečana lestvica: 1 enota \u003d 2 celici (risba na levi strani) - če je mogoče, se lepite nanjo. Vendar se občasno zgodi, da risba ne ustreza na zvezku - potem pomanjšamo: 1 enota \u003d 1 celica (risba na desni). Redko je, vendar se zgodi, da je treba obseg risbe še bolj zmanjšati (ali povečati)
NE "piskajte iz mitraljeza" ... -5, -4, -3, -1, 0, 1, 2, 3, 4, 5,…. Kajti koordinatna ravnina ni spomenik Descartesu in študent ni golob. Stavili smo nič in dve aksialni enoti. Včasih namesto enot, je primerno "zaznati" druge vrednosti, na primer "dve" na osi absces in "tri" na osi ordinate - in ta sistem (0, 2 in 3) bo tudi enotno določil koordinatno mrežo.
Ocenjene dimenzije risbe je najbolje oceniti PRED risbo. Torej, na primer, če naloga zahteva, da narišete trikotnik z vrhovi ,,, potem je jasno, da priljubljena lestvica 1 enote \u003d 2 celici ne bo delovala. Zakaj? Poglejmo poanto - tukaj moramo izmeriti petnajst centimetrov navzdol in risba očitno ne bo ustrezala (ali komaj prilegala) na list zvezka. Zato takoj izberite manjšo lestvico 1 enote \u003d 1 celica.
Mimogrede, približno centimetre in celice za prenosnike. Ali drži, da 30 tetradnih celic vsebuje 15 centimetrov? Izmerite v zvezku za zanimanje 15 centimetrov z ravnilom. V ZSSR je bilo to morda res ... Zanimivo je, da če merite te iste centimetre vodoravno in navpično, bodo rezultati (v celicah) drugačni! Strogo gledano sodobni zvezki niso česani, ampak pravokotni. Morda se bo to zdelo neumnost, toda na primer risanje kroga s parom kompasov v takšnih razmerah je zelo neprijetno. Iskreno povedano, v takih trenutkih začnete razmišljati o pravilnosti tovariša Stalina, ki je v tovarne poslal tovorna vozila, da ne omenjam domače avtomobilske industrije, padajočih letal ali eksplodirajočih elektrarn.
Ko že govorimo o kakovosti ali kratkem priporočilu o pisarniških izdelkih. Danes je večina zvezkov v prodaji, ne da bi rekli slabe besede, popolnoma homogenih. Iz razloga, da se zmočijo, in to ne samo iz gela, ampak tudi iz kemičnih svinčnikov! Shranite na papirju. Priporočam uporabo zvezkov Arkhangelsk celuloze in papirnice (18 listov, kletka) ali Pyaterochka za registracijske teste, čeprav so dražji. Priporočljivo je izbrati gel pisalo, tudi najcenejši kitajski gel pisalo je veliko boljši od kemičnega svinčnika, ki razmaže ali vleče papir. Edini "tekmovalni" kemični svinčnik v mojem spominu je Erich Krause. Piše jasno, lepo in vztrajno - s polno jedro, s skoraj prazno.
Izbirno: V članku je prikazan vid pravokotnega koordinatnega sistema skozi oči analitične geometrije Linearna (ne) odvisnost vektorjev. Osnova vektorjev, podrobne informacije o koordinatnih četrtinah najdete v drugem odstavku lekcije Linearne neenakosti.
Tridimenzionalni ovitek
Tu je skoraj vse enako.
1) Narišemo koordinatne osi. Standard: aplikativna os
- usmerjena navzgor, os - usmerjena desno, os - levo navzdol strogo pod kotom 45 stopinj.
2) Os podpišemo.
3) Lestvico smo postavili vzdolž osi. Lestvica osi - polovica velikosti drugih osi. Upoštevajte tudi, da sem na desni risbi uporabil nestandardni "serif" vzdolž osi (ta možnost je bila že omenjena zgoraj). Z mojega vidika je bolj natančen, hitrejši in bolj estetsko prijeten - ni vam treba pogledati pod mikroskopom na sredino celice in enoto »izrisati« tik ob izvoru.
Ko delate tridimenzionalno risbo, ponovno - dajte prednost lestvici
1 enota \u003d 2 celici (risba na levi strani).
Za kaj vse veljajo ta pravila? Za njihovo kršenje obstajajo pravila. Kaj bom zdaj storil. Dejstvo je, da bom poznejše risbe članka naredil jaz v Excelu, koordinatne osi pa bodo z vidika pravilne zasnove videti nepravilno. Vse grafe bi lahko narisal z roko, toda dejansko bi jih narisal kot grozno nenaklonjen Excel bi jih narisal veliko bolj natančno.
Grafi in osnovne lastnosti elementarnih funkcij
Linearna funkcija je podana z enačbo. Graf linearne funkcije je neposredni. Za izgradnjo črte je dovolj, da poznate dve točki.
Primer 1
Sestavite funkcijski graf. Poiščite dve točki. Za eno od točk je ugodno izbrati nič.
Če torej
Vzemimo še kakšno točko, na primer 1.
Če torej
Ko končate naloge, so koordinate točk običajno povzete v tabeli:
In same vrednosti se izračunajo ustno ali na osnutku kalkulatorja.
Najdemo dve točki, izvedemo risbo:
Pri risanju vedno podpisujemo grafiko.
Ne bo odveč priklicati posameznih primerov linearne funkcije:
Opazite, kako sem uredil napise, podpisov ne smete napačno razumeti, ko preučujete risbo. V tem primeru je bilo skrajno nezaželeno, da bi podpis postavili blizu presečišča črt ali desno spodaj med grafoma.
1) Linearna funkcija obrazca () se imenuje neposredna sorazmernost. Na primer,. Graf neposredne sorazmernosti vedno prehaja skozi izvor. Tako je gradnja proge poenostavljena - poiščite le eno točko.
2) Enačba obrazca definira ravno črto, vzporedno z osjo, predvsem sama os je dana z enačbo. Graf funkcije je sestavljen takoj, ne da bi našli nobene točke. To pomeni, da je zapis treba razumeti na naslednji način: "igra je vedno enaka –4, za katero koli vrednost x."
3) Enačba obrazca definira ravno črto, vzporedno z osjo, predvsem sama os je dana z enačbo. Graf funkcije je prav tako sestavljen takoj. Zapis je treba razumeti na naslednji način: "X je vedno, za katero koli vrednost igralca enak 1".
Nekateri se bodo vprašali, zakaj se spomnite 6. razreda ?! Tako je, morda je tako, le skozi leta prakse sem spoznal ducat študentov, ki jih je mučila naloga, da ustvarijo urnik, kot je.
Gradnja ravne črte je najpogostejši ukrep pri risanju.
Ravno črto podrobno preučimo med analitično geometrijo, tisti, ki to želijo, pa se lahko sklicujejo na članek Enačba premice na ravnini.
Graf kvadratne, kubične funkcije, graf polinoma
Parabola. Kvadratni graf funkcije  () je parabola. Razmislite o znanem primeru:
Spomnimo se nekaterih lastnosti funkcije.
Torej, rešitev naše enačbe: - ravno na tem mestu se nahaja vrh parabole. Zakaj je tako, lahko najdete v teoretičnem članku o izpeljanki in lekciji o ekstremnih funkcijah. Medtem izračunamo ustrezno vrednost "igre":
Torej je točka v točki
Zdaj najdemo druge točke, medtem ko drzno uporabljamo simetrijo parabole. Treba je opozoriti, da funkcija  – niti nevendar kljub temu nihče ni preklical simetrije parabole.
Kako najti preostale točke, mislim, da bo to jasno iz končne mize:
Anfisa Čehova lahko ta algoritem gradnje figurativno imenuje "shuttle" ali načelo "naprej in nazaj".
Izvedimo risbo:
Iz pregledanih grafov se prikliče še en uporaben znak:
Za kvadratno funkcijo  () velja naslednje:
Če, potem so veje parabole usmerjene navzgor.
Če, potem so veje parabole usmerjene navzdol.
Poglobljeno znanje o krivulji lahko dobite v lekciji Hiperbola in Parabola.
Kubična parabola je nastavljena s funkcijo. Tukaj je risba, znana iz šole:
Naštejemo glavne lastnosti funkcije
Funkcijski graf
Predstavlja eno od vej parabole. Izvedimo risbo:
Glavne lastnosti funkcije:
V tem primeru je os navpična asimptota
za zaplet hiperbole na.
VELIKO napaka bo, če pri malomarnosti dovolimo presečitev grafa z asimptoto.
Tudi enostranske meje nam povejo to hiperbolo ni omejeno od zgoraj in ni omejeno od spodaj.
Preučujemo funkcijo v neskončnosti: to je, če začnemo hoditi vzdolž osi levo (ali desno) v neskončnost, potem bodo "igre" vitek neskončno blizu približati se ničli in temu primerno tudi vejam hiperbole neskončno blizu približajte se osi.
Torej os je vodoravna asimptota
za funkcijski graf, če „X“ teži k plus ali minus neskončnost.
Funkcija je čudnoin je torej hiperbola glede na izvor simetrična. To dejstvo je razvidno iz risbe, poleg tega pa je analitično enostavno preverjeno:  .
Graf funkcije forme () predstavlja dve veji hiperbole.
Če, potem se hiperbola nahaja v prvem in tretjem četrtnem koordinatu (glej sliko zgoraj).
Če, potem se hiperbola nahaja v drugem in četrtem koordinatnem četrtletju.
Navedene pravilnosti prebivanja hiperbole ni težko analizirati z vidika geometrijskih transformacij grafov.
Primer 3
Zgradite pravo vejo hiperbole
Uporabljamo točkovno konstrukcijsko metodo, pri čemer je koristno izbrati vrednosti, tako da se v celoti delijo:
Izvedimo risbo:
Leva veja hiperbole ne bo težko zgraditi, tu bo pomagala nenavadno delovanje. V grobem gledano v tabelo točne konstrukcije miselno dodajte minus vsaki številki, postavite ustrezne točke in narišite drugo vejo.
Podrobne geometrijske informacije o obravnavani črti najdete v članku Hyperbola in Parabola.
Graf eksponentne funkcije
V tem razdelku bom takoj razmislil o eksponentni funkciji, saj je v težavah višje matematike v 95% primerov eksponent.
Spominjam vas, da je to neracionalna številka: potrebna bo pri sestavljanju urnika, ki ga bom pravzaprav zgradil brez slovesnosti. Tri točke so verjetno dovolj:
Funkcijski graf pustimo pri miru, o tem pa kasneje.
Glavne lastnosti funkcije:
Grafi funkcij so v osnovi enaki itd.
Moram reči, da je drugi primer v praksi manj pogost, vendar se zgodi, zato se mi je zdelo potrebno vključiti v ta članek.
Graf logaritmične funkcije
Razmislite o funkciji z naravnim logaritmom.
Naredimo točkovno risbo:
Če ste pozabili, kaj je logaritem, si oglejte šolske knjige.
Glavne lastnosti funkcije:
Področje uporabe: 
Razpon vrednosti:
Funkcija ni omejena od zgoraj:  , čeprav počasi, toda veja logaritma sega do neskončnosti.
Preučujemo vedenje funkcije blizu ničle na desni:  . Torej os je navpična asimptota
za funkcijski graf z "x", ki teži k nič na desni.
Bodite prepričani, da poznate in si zapomnite značilno vrednost logaritma: .
Graf logaritma je v osnovi enak na dnu: ,, (decimalni logaritem na podlagi osnove 10) itd. Poleg tega je večja osnova, bolj nežen bo razpored.
Ne bomo obravnavali primera; ne spomnim se nečesa, ko sem zadnjič sestavil urnik s takim razlogom. In logaritem se zdi zelo redek gost pri višjih matematičnih težavah.
Za konec bom povedal še eno dejstvo: Eksponentna funkcija in logaritmična funkcijaAli sta dve medsebojno obratni funkciji. Če natančno pogledate graf logaritma, lahko vidite, da gre za isti eksponent, le malo drugače se nahaja.
Grafi trigonometričnih funkcij
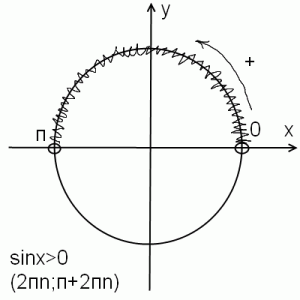
S čim se začnejo trigonometrične muke v šoli? Prav. S sinusom
Načrtujemo funkcijo
Ta vrstica se imenuje sinusni val.
Spominjam vas, da je "pi" iracionalna številka:, in v trigonometriji iz njega puha v očeh.
Glavne lastnosti funkcije:
Ta funkcija je periodično z obdobjem. Kaj to pomeni? Poglejmo segment. Na levi in \u200b\u200bdesni strani se neskončno ponavlja popolnoma isti kos grafa.
Področje uporabe:, torej za vsako vrednost "X" obstaja sinusna vrednost.
Razpon vrednosti: Funkcija je omejeno:, torej vse "igre" sedijo strogo v segmentu.
To se ne zgodi: ali natančneje, zgodi se, vendar navedene enačbe nimajo rešitve. |
Parabola. Graf kvadratne funkcije () je parabola. Razmislite o kanoničnem primeru:
Spomnimo se nekaterih lastnosti funkcije.
Obseg je poljubno realno število (poljubna x-vrednost). Kaj to pomeni? Ne glede na to, katero točko na osi izberemo - za vsakim "X" je točka parabole. Matematično je zapisano tako:. Obseg katere koli funkcije običajno označujemo z ali. Črka označuje niz resničnih številk ali, poenostavljeno, "poljubnega X" (ko se delo izvaja v zvezku, pišejo ne kodrasto črko, temveč krepko črko R).
Obseg vrednosti je niz vseh vrednosti, ki jih lahko sprejme spremenljivka predvajalnika. V tem primeru: - niz vseh pozitivnih vrednosti, vključno z ničlo. Obseg vrednosti običajno označujemo z ali.
Funkcija je celo. Če je funkcija enakomerna, je njen graf simetričen glede na os. To je zelo uporabna lastnost, ki močno poenostavi izdelavo grafa, kar bomo kmalu videli. Analitično je parnost funkcije izražena s pogojem. Kako preveriti katero koli funkcijo za parnost? V enačbi je treba nadomestiti. V primeru parabole je pregled videti tako: to pomeni, da je funkcija enakomerna.
Funkcija ni omejeno od zgoraj. Analitično je lastnost zapisana tako:. Mimogrede, tukaj je primer geometrijskega pomena meje funkcije: če gremo vzdolž osi (levo ali desno) do neskončnosti, se bodo veje parabole (vrednosti "predvajanja" neomejeno dvigale na "plus neskončnost".
Na omejitve učnih funkcij zaželeno je razumeti geometrijski pomen meje.
Ni naključje, da sem lastnosti funkcije podrobno naslikal, vse zgoraj naštete stvari je koristno vedeti in si zapomniti pri načrtovanju funkcij, pa tudi pri raziskovanju funkcijskih grafov.
Primer 2
Plot funkcija 
.
V tem primeru bomo pogledali pomembno tehnično vprašanje: Kako hitro zgraditi parabolo? Pri praktičnih nalogah se zelo pogosto pojavlja potreba po risanju parabole, zlasti pri računanju območje figure z uporabo določenega integral. Zato je priporočljivo, da se naučite risati hitro, z minimalno izgubo časa. Predlagam naslednji algoritem za gradnjo.
Najprej najdemo vrh parabole. Če želite to narediti, vzemite prvo izpeljanko in jo izenačite z ničlo:
Če so derivati \u200b\u200bslabi, si preberite lekcijo. Kako najti izpeljanko?
Torej, rešitev naše enačbe: - ravno na tem mestu se nahaja vrh parabole. Izračunamo ustrezno vrednost "igre":
Torej je točka v točki
Zdaj najdemo druge točke, medtem ko drzno uporabljamo simetrijo parabole. Treba je opozoriti, da funkcija – niti nevendar kljub temu nihče ni preklical simetrije parabole.
Kako najti preostale točke, mislim, da bo to jasno iz končne mize:
Ta algoritem za gradnjo lahko figurativno imenujemo "shuttle". Mogoče vsi ne razumejo bistva shuttlea, potem pa vas za primerjavo opomnim na dobro znano TV oddajo "tudy-syudy z Anfiso Čehovo".
Izvedimo risbo:
Iz pregledanih grafov se prikliče še en uporaben znak:
Za kvadratno funkcijo () velja naslednje:
Če, potem so veje parabole usmerjene navzgor.
Če, potem so veje parabole usmerjene navzdol.
Kubična parabola
Kubična parabola je nastavljena s funkcijo. Tukaj je risba, znana iz šole:
Naštejemo glavne lastnosti funkcije
Področje uporabe - poljubno resnično število:
Razpon vrednosti je poljubno realno število:.
Funkcija je čudno. Če je funkcija liha, je njen graf simetričen glede na izvor. Analitično se čudnost funkcije izrazi s pogojem 
. Izvedemo preverjanje kubične funkcije, pri čemer namesto "X" nadomestimo "minus X":
, potem je funkcija liha.
Funkcija ni omejeno. V jeziku omejitev funkcij lahko to zapišemo na naslednji način:
Učinkovitejša je tudi izdelava kubične parabole s pomočjo algoritma "shuttle" Anfise Čehove:
Zagotovo ste opazili, v čem se še kaže čudnost funkcije. Če bi to ugotovili 
, potem pri izračunu ni več treba ničesar šteti, to samodejno napišite. Ta funkcija velja za vsako nenamerno funkcijo.
Zdaj pa se pogovorimo o polinomnih grafih.
Graf katerega koli polinoma tretje stopnje 
() ima v osnovi naslednjo obliko:
V tem primeru je koeficient na najvišji stopnji, zato je graf obrnjen. Načeloma so grafi polinomov pete, sedme, devete in druge lihe stopnje v bistvu enake oblike. Višja kot je stopnja, bolj vmesni je „zagibulin“.
Polinomi 4., 6. in drugih enakomernih stopenj imajo graf bistveno naslednje oblike:
To znanje je uporabno pri pregledu funkcijskih grafov.
Funkcijski graf
Izvedimo risbo:
Glavne lastnosti funkcije:
Področje uporabe:
Razpon vrednosti:
Se pravi, da je funkcijski graf popolnoma v prvi koordinatni četrtini.
Funkcija ni omejeno od zgoraj. Ali z uporabo omejitve: 
Pri konstruiranju najpreprostejših grafov s koreninami je primeren tudi točkast način gradnje, medtem ko je ugodno izbrati takšne vrednosti "X", da se koren popolnoma izvleče:
Pravzaprav želim na primer razčleniti več primerov s koreninami, vendar so veliko manj pogosti. Osredotočim se na bolj pogoste primere in, kot kaže praksa, nekaj takega, kot je treba graditi veliko pogosteje. Če je potrebno ugotoviti, kako izgledajo grafikoni z drugimi koreninami, priporočam, da pogledate v šolski učbenik ali matematični referenčni učbenik.
Graf hiperbole
Spet se spomnite trivialne "šolske" hiperbole.
Izvedimo risbo:
Glavne lastnosti funkcije:
Področje uporabe:
Razpon vrednosti:
Vnos pomeni: "vsako resnično število brez nič"
V določeni točki funkcija trpi neskončno prekinitev. Ali pa z uporabo enostranskiomejitve:,. Pogovorimo se malo o enostranskih mejah. Vstop pomeni, da mi neskončno blizu približevanje osi ničli levo. Kako se obnaša urnik? Spusti se na minus neskončnosti, neskončno blizu približevanje osi. To dejstvo je zapisano preko omejitve. Podobno vpis pomeni, da tudi mi neskončno blizu približevanje osi ničli na desni. V tem primeru se veja hiperbole dvigne za plus neskončnost, neskončno blizu približevanje osi. Ali na kratko:.
vrsta
kje Z drugimi besedami, kubično funkcijo določa polinom tretje stopnje.
Analitične lastnosti
Uporaba
Kubična parabola se včasih uporablja za izračun prehodne krivulje v prometu, saj je njen izračun veliko enostavnejši od konstrukcije klotoida.
Glej tudi
Napišite recenzijo na članek "Kubična funkcija"
Opombe
Literatura
- L. S. Pontryagin, // "Kvant", 1984, št. 3.
- I. N. Bronstein, K. A. Semendjajev, "Priročnik matematike", Založba Znanost, M. 1967, str. 84
Odlomek o kubni funkciji
"No, tam, za karkoli ..."
V tem času je Petja, na katerega ni bil nihče pozoren, pristopil k očetu in, ves rdeč, zlomljen, nato oster, nato s tankim glasom rekel:
"No, očka, zagotovo bom rekel - in tudi mama, kot hočete - zagotovo bom rekla, da me boste spustili v vojaško službo, ker ne morem ... to je vse ..."
Grofica je z grozo pogledala v nebo, stisnila roke in se jezno obrnila proti možu.
- Tako sem se strinjal! Rekla je.
Toda grof je takoj opomogel od svojega navdušenja.
"No, no," je rekel. - Tu je še bojevnik! Pustite neumnosti: učiti se morate.
- Ni neumno, oče. Obolenski Fedya je mlajši od mene in tudi gre, in kar je najpomembneje, vseeno se ne morem ničesar naučiti zdaj, ko ... - Petja se je ustavila, zardela od znoja in rekla isto: - kadar je očetova v nevarnosti.
- Polno, polno, neumno ...
"Zakaj, sami ste rekli, da bomo vse žrtvovali."
"Petsa, rečem ti, utihni," je zavpil grof in se ozrl na ženo, ki je, bleda, s fiksnimi očmi pogledala na manjšega sina.
"In pravim vam." Torej bo Pyotr Kirillovich rekel ...
- Povem vam - neumnost, mleko se še ni posušilo, ampak hoče v vojaško službo! No, no, povem vam, - in grof je, vzel s seboj papirje, ki jih je verjetno prebral v svoji študiji pred počitkom, šel iz sobe.
- Pyotr Kirillovič, no, dajmo kadit ...
Pierra je bilo nerodno in neodločno. Natašine nenavadno bleščeče in živahne oči so ga nenehno, več kot ljubeče obračale, pripeljale v to stanje.
"Ne, mislim, da grem domov ..."
- Kako iti domov, ampak si hotel imeti večer z nami ... In to se je redko začelo dogajati. In ta je moja ... - je dobrohotno rekel grof in pokazal na Natašo, - samo z vami je bila vesela ...
- Ja, pozabil sem ... Definitivno se moram vrniti domov ... Zadeve ... - nagnjeno je rekel Pierre.
"No, zbogom," je rekel Earl in popolnoma zapustil sobo.
"Zakaj odhajaš?" Zakaj se razburite? Zakaj? .. - je vprašal Pierre Natasha in ga kljubovalno gledal v oči.
"Ker te ljubim! Hotel je povedati, a tega ni rekel, zardeval je do solz in spustil pogled.
"Ker je bolje, da vas manj obiskujem ... Ker ... ne, to je samo moj posel."
Zakaj? ne, povej mi, - je odločno začela Nataša in nenadoma utihnila. Oba sta se začudeno pogledala in zmedena. Poskušal se je zasmehniti, a ni mogel: njegov nasmeh je izrazil trpljenje, on pa je tiho poljubil njeno roko in šel ven.
Pierre se je sam odločil, da ne bo več pri Rostovih. Petica je po odločni zavrnitvi, ki jo je prejel, šel v svojo sobo in tam, zaprl se je pred vsemi, grenko zajokal. Vsi so delali, kot da niso ničesar opazili, ko je prišel na čaj tih in mračen, s solznimi očmi.
Naslednji dan je prišel cesar. Več ljudi na dvorišču Rostov je pustilo ogled kralja. Zjutraj se je Petja dolgo oblekel, si česal lase in si urejal ovratnike, kot pri velikih. Zrcal se je pred ogledalom, naredil kretnje, skomignil in na koncu, ne da bi nikomur povedal, si nadel kapo in zapustil hišo z zadnje verande, trudi se, da je ne bi opazil. Petja se je odločil, da gre naravnost do mesta, kjer je suveren, in neposredno razloži nekemu komorniku (Petja je menil, da je suveren vedno obkrožen s komorniki), da je on, grof Rostov, kljub mladosti hotel služiti svoji domovini, da mladost ne more biti ovira za vdanost in da je pripravljen ... Petja je, ko se je pripravljal, pripravil veliko čudovitih besed, ki jih bo povedal komorniku.
Parabola. Graf kvadratne funkcije () je parabola. Razmislite o kanoničnem primeru:
Spomnimo se nekaterih lastnosti funkcije.
Obseg je poljubno realno število (poljubna x-vrednost). Kaj to pomeni? Ne glede na to, katero točko na osi izberemo - za vsakim "X" je točka parabole. Matematično je zapisano tako:. Obseg katere koli funkcije običajno označujemo z ali. Črka označuje niz resničnih številk ali, poenostavljeno, "poljubnega X" (ko se delo izvaja v zvezku, pišejo ne kodrasto črko, temveč krepko črko R).
Obseg vrednosti je niz vseh vrednosti, ki jih lahko sprejme spremenljivka predvajalnika. V tem primeru: - niz vseh pozitivnih vrednosti, vključno z ničlo. Obseg vrednosti običajno označujemo z ali.
Funkcija je celo. Če je funkcija enakomerna, je njen graf simetričen glede na os. To je zelo uporabna lastnost, ki močno poenostavi izdelavo grafa, kar bomo kmalu videli. Analitično je parnost funkcije izražena s pogojem. Kako preveriti katero koli funkcijo za parnost? V enačbi je treba nadomestiti. V primeru parabole je pregled videti tako: to pomeni, da je funkcija enakomerna.
Funkcija ni omejeno od zgoraj. Analitično je lastnost zapisana tako:. Mimogrede, tukaj je primer geometrijskega pomena meje funkcije: če gremo vzdolž osi (levo ali desno) do neskončnosti, se bodo veje parabole (vrednosti "predvajanja" neomejeno dvigale na "plus neskončnost".
Na omejitve učnih funkcij zaželeno je razumeti geometrijski pomen meje.
Ni naključje, da sem lastnosti funkcije podrobno naslikal, vse zgoraj naštete stvari je koristno vedeti in si zapomniti pri načrtovanju funkcij, pa tudi pri raziskovanju funkcijskih grafov.
Primer 2
Plot funkcija 
.
V tem primeru bomo pogledali pomembno tehnično vprašanje: Kako hitro zgraditi parabolo? Pri praktičnih nalogah se potreba po risanju parabole pojavi zelo pogosto, zlasti pri izračunu površine figure z uporabo določenega integral. Zato je priporočljivo, da se naučite risati hitro, z minimalno izgubo časa. Predlagam naslednji algoritem za gradnjo.
Najprej najdemo vrh parabole. Če želite to narediti, vzemite prvo izpeljanko in jo izenačite z ničlo:
Če so derivati \u200b\u200bslabi, si preberite lekcijo. Kako najti izpeljanko?
Torej, rešitev naše enačbe: - ravno na tem mestu se nahaja vrh parabole. Izračunamo ustrezno vrednost "igre":
Torej je točka v točki
Zdaj najdemo druge točke, medtem ko drzno uporabljamo simetrijo parabole. Treba je opozoriti, da funkcija – niti nevendar kljub temu nihče ni preklical simetrije parabole.
Kako najti preostale točke, mislim, da bo to jasno iz končne mize:
Ta algoritem za gradnjo lahko figurativno imenujemo "shuttle". Mogoče vsi ne razumejo bistva shuttlea, potem pa vas za primerjavo opomnim na dobro znano TV oddajo "tudy-syudy z Anfiso Čehovo".
Izvedimo risbo:
Iz pregledanih grafov se prikliče še en uporaben znak:
Za kvadratno funkcijo () velja naslednje:
Če, potem so veje parabole usmerjene navzgor.
Če, potem so veje parabole usmerjene navzdol.
Kubična parabola
Kubična parabola je nastavljena s funkcijo. Tukaj je risba, znana iz šole:
Naštejemo glavne lastnosti funkcije
Področje uporabe - poljubno resnično število:
Razpon vrednosti je poljubno realno število:.
Funkcija je čudno. Če je funkcija liha, je njen graf simetričen glede na izvor. Analitično se čudnost funkcije izrazi s pogojem 
. Izvedemo preverjanje kubične funkcije, pri čemer namesto "X" nadomestimo "minus X":
, potem je funkcija liha.
Funkcija ni omejeno. V jeziku omejitev funkcij lahko to zapišemo na naslednji način:
Učinkovitejša je tudi izdelava kubične parabole s pomočjo algoritma "shuttle" Anfise Čehove:
Zagotovo ste opazili, v čem se še kaže čudnost funkcije. Če bi to ugotovili 
, potem pri izračunu ni več treba ničesar šteti, to samodejno napišite. Ta funkcija velja za vsako nenamerno funkcijo.
Zdaj pa se pogovorimo o polinomnih grafih.
Graf katerega koli polinoma tretje stopnje 
() ima v osnovi naslednjo obliko:
V tem primeru je koeficient na najvišji stopnji, zato je graf obrnjen. Načeloma so grafi polinomov pete, sedme, devete in druge lihe stopnje v bistvu enake oblike. Višja kot je stopnja, bolj vmesni je „zagibulin“.
Polinomi 4., 6. in drugih enakomernih stopenj imajo graf bistveno naslednje oblike:
To znanje je uporabno pri pregledu funkcijskih grafov.
Funkcijski graf
Izvedimo risbo:
Glavne lastnosti funkcije:
Področje uporabe:
Razpon vrednosti:
Se pravi, da je funkcijski graf popolnoma v prvi koordinatni četrtini.
Funkcija ni omejeno od zgoraj. Ali z uporabo omejitve: 
Pri konstruiranju najpreprostejših grafov s koreninami je primeren tudi točkast način gradnje, medtem ko je ugodno izbrati takšne vrednosti "X", da se koren popolnoma izvleče:
Funkcijo y \u003d x ^ 2 imenujemo kvadratna funkcija. Graf kvadratne funkcije je parabola. Splošen pogled na parabolo je prikazan na spodnji sliki.
Kvadratna funkcija
Slika 1. Splošni pogled parabole
Kot je razvidno iz grafa, je simetrično glede na os Oy. Os Oy imenujemo os simetrije parabole. To pomeni, da če na grafu narišete črto, vzporedno z osjo Ox nad to osjo. Nato bo čez dve točki prešla parabolo. Oddaljenost od teh točk do osi Oy bo enaka.
Os simetrije deli graf parabole na dva dela. Ti deli se imenujejo veje parabole. In točka parabole, ki leži na osi simetrije, se imenuje vrhova parabole. To pomeni, da os simetrije prehaja skozi vrh parabole. Koordinate te točke (0; 0).
Osnovne lastnosti kvadratne funkcije
1. Za x \u003d 0, y \u003d 0 in y\u003e 0 za x0
2. Kvadratna funkcija v svoji točki doseže najmanjšo vrednost. Ymin pri x \u003d 0; Upoštevati je treba tudi, da največja vrednost funkcije ne obstaja.
3. Funkcija se v intervalu zmanjšuje (-∞; 0] in v intervalu poveča)
