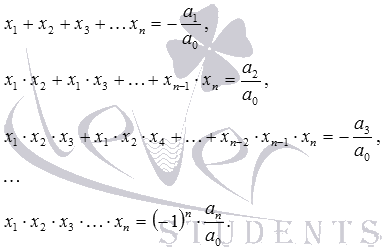Odseki spletnega mesta
Izbira urednikov:
Oglaševanje
| Vsota korenin kvadratne enačbe. Kako najti vsoto korenin enačbe |
|
Med koreni in koeficienti kvadratne enačbe poleg korenskih formul obstajajo tudi drugi koristni odnosi vietajev izrek. V tem članku podajamo trditev in dokaz teorema Viete za kvadratno enačbo. Nato štejemo izrek, ki je obraten teoremu Viete. Po tem analiziramo rešitve najbolj značilnih primerov. Na koncu napišemo formule Vieta, ki definirajo odnos med resničnimi koreninami algebarska enačba stopnjo n in njenimi koeficienti. Navigacija po strani. Vieta izrek, izjava, dokazIz formul korenin kvadratne enačbe a · x 2 + b · x + c \u003d 0 obrazca, kjer je D \u003d b 2 −4 · a · c, razmerja x 1 + x 2 \u003d −b / a, x 1 · x 2 \u003d c / a Ti rezultati so potrjeni. vietajev izrek: Izrek Če x 1 in x 2 sta korenini kvadratne enačbe a · x 2 + b · x + c \u003d 0, potem je vsota korenin enaka razmerju koeficientov b in vzet z nasprotnim znakom, produkt korenin pa je enak razmerju koeficientov c in a, to je . Dokaz. Dokaz Vieta izrekamo po naslednji shemi: sestavimo vsoto in produkt korenin kvadratne enačbe z dobro znanimi korenskimi formulami, nato pretvorimo nastale izraze in se prepričamo, da sta −b / a in c / a. Začnimo z vsoto korenin, dopolnimo jo. Zdaj uvajamo ulomke v skupni imenovalec, ki ga imamo. V števcu dobljenega ulomka, za katerim:. Končno po 2 dobimo. To dokazuje prvo razmerje izrek Viete za vsoto korenin kvadratne enačbe. Preidemo na drugo. Sestavimo rezultat korenin kvadratne enačbe:. V skladu s pravilom množenja frakcij lahko zadnji izdelek zapišemo kot. Zdaj pomnožimo oklepaje z oklepaji v števcu, vendar hitreje ta izdelek zrušimo za formula kvadratne razliketako. Nadalje, spominjanje, izvedite naslednji prehod. In ker diskriminator kvadratne enačbe ustreza formuli D \u003d b 2 −4 · a · c, lahko v zadnji frakciji namesto D nadomestimo b 2 −4 · a · c, dobimo. Po odpiranju oklepajev in zmanjšanju takšnih izrazov pridemo do ulomaka in zmanjšanja za 4 · a daje. To dokazuje drugo razmerje izrek Vieta za produkt korenin. Če izpustimo razlage, bo dokaz teorema Viete v lakonski obliki: Omenimo le, da ima kvadratura enačba za razlikovalno enoto nič. Če pa predpostavimo, da ima enačba v tem primeru dve enaki korenini, velja tudi enakost iz teorema Vieta. Dejansko je za D \u003d 0 koren kvadratne enačbe potem in, in ker je D \u003d 0, torej b 2 -4 · a · c \u003d 0, od koder je b 2 \u003d 4 · a · c, potem. V praksi se teorem Vieta najpogosteje uporablja glede na kvadratno enačbo (z najvišjim koeficientom enakim 1) oblike x 2 + p · x + q \u003d 0. Včasih je oblikovan za tovrstne kvadratne enačbe, ki ne omejujejo splošnosti, saj lahko katero koli kvadratno enačbo nadomestimo z enakovredno enačbo tako, da oba njena dela delimo z ničelnim številom a. Podamo ustrezen stavek izrek Vieta: Izrek Vsota korenin zmanjšane kvadratne enačbe x 2 + p · x + q \u003d 0 je enaka koeficientu pri x, vzeti z nasprotnim znakom, produkt korenin pa je prosti izraz, to je x 1 + x 2 \u003d −p, x 1 · x 2 \u003d q. Inverzni teorem VietaDruga trditev iz teorema Viete iz prejšnjega odstavka kaže, da če sta x 1 in x 2 korenine zmanjšane kvadratne enačbe x 2 + p · x + q \u003d 0, potem je razmerja x 1 + x 2 \u003d −p, x 1 · x 2 \u003d q. Po drugi strani iz zapisanih razmerij x 1 + x 2 \u003d −p, x 1 · x 2 \u003d q izhaja, da sta x 1 in x 2 korenine kvadratne enačbe x 2 + p · x + q \u003d 0. Z drugimi besedami, trditev, nasprotno Vietaovemu izrekanju, drži. Formuliramo ga v obliki izrekanja in ga dokažemo. Izrek Če sta številki x 1 in x 2 taki, da sta x 1 + x 2 \u003d −p in x 1 · x 2 \u003d q, sta x 1 in x 2 korenine kvadratne enačbe x 2 + p · x + q \u003d 0. Dokaz. Po zamenjavi koeficientov p in q v enačbi x 2 + p · x + q \u003d 0 do x 1 in x 2 se pretvori v enakovredno enačbo. Število x 1 nadomestimo v dobljeno enačbo namesto x, imamo enakost x 1 2 - (x 1 + x 2) x 1 + x 1 x 2 \u003d 0, ki za kateri koli x 1 in x 2 predstavlja resnično številčno enakost 0 \u003d 0, saj x 1 2 - (x 1 + x 2) x 1 + x 1 x 2 \u003d x 1 2 −x 1 2 −x 2 x 1 + x 1 x 2 \u003d 0. Zato je x 1 koren enačbe x 2 - (x 1 + x 2) x + x 1 x 2 \u003d 0, kar pomeni, da je x 1 koren enačbe x 2 + p · x + q \u003d 0, ki mu ustreza. Če v enačbi x 2 - (x 1 + x 2) x + x 1 x 2 \u003d 0 nadomestimo x za število x 2, potem dobimo enakost x 2 2 - (x 1 + x 2) x 2 + x 1 x 2 \u003d 0. To je resnična enakost, saj x 2 2 - (x 1 + x 2) x 2 + x 1 x 2 \u003d x 2 2 −x 1 · x 2 −x 2 2 + x 1 · x 2 \u003d 0. Zato je x 2 tudi koren enačbe x 2 - (x 1 + x 2) x + x 1 x 2 \u003d 0in s tem enačbe x 2 + p · x + q \u003d 0. S tem je dokončan dokaz teorema, obratno v teorem Vieta. Primeri uporabe teorema VietaČas je za pogovor o praktični uporabi teorema Vieta in njegovega obratnega izrekanja. V tem razdelku obravnavamo rešitve nekaterih najpogostejših primerov. Začnemo z uporabo teorema, obratnega na izrek Viete. Prikladno je uporabiti za preverjanje, ali sta ti dve številki korenine dane kvadratne enačbe. V tem primeru se izračuna njihova vsota in razlika, po kateri se preveri veljavnost razmerij. Če oba razmerja držita, potem lahko na podlagi teorema, obratnega Vietaovemu teoremu, sklepamo, da so ta števila korenine enačbe. Če vsaj eden od odnosov ni zadovoljen, potem ta števila niso korenine kvadratne enačbe. Ta pristop je mogoče uporabiti pri reševanju kvadratnih enačb za preverjanje najdenih korenin. Primer. Kateri od parov števil 1) x 1 \u003d −5, x 2 \u003d 3 ali 2) ali 3) je par korenin kvadratne enačbe 4 · x 2 −16 · x + 9 \u003d 0? Rešitev. Koeficienti dane kvadratne enačbe 4 · x 2 −16 · x + 9 \u003d 0 so a \u003d 4, b \u003d −16, c \u003d 9. Po Vietaovem izrekanju mora biti vsota korenin kvadratne enačbe enaka −b / a, to je 16/4 \u003d 4, produkt korenin pa naj bo enak c / a, to je 9/4. Zdaj izračunamo vsoto in zmnožek števil v vsakem od treh danih parov ter jih primerjamo s pravkar pridobljenimi vrednostmi. V prvem primeru imamo x 1 + x 2 \u003d −5 + 3 \u003d −2. Dobljena vrednost je drugačna od 4, zato nadaljnjega preverjanja ni mogoče izvesti in po izreku, ki je obratno Vieteovemu izrekanju, lahko takoj ugotovimo, da prvi par številk ni par korenin dane kvadratne enačbe. Preidemo na drugi primer. Tu je torej prvi pogoj izpolnjen. Preverimo drugi pogoj:, dobljena vrednost se razlikuje od 9/4. Zato drugi par številk ni par korenin kvadratne enačbe. Zadnji primer ostaja. Tu in. Oba pogoja sta izpolnjena, zato sta ti številki x 1 in x 2 korenini dane kvadratne enačbe. Odgovor je: Teoreme, obratne na izrek Viete, lahko v praksi uporabimo za izbiro korenin kvadratne enačbe. Običajno poberemo celotne korenine danih kvadratnih enačb s celimi koeficienti, kot je to v drugih primerih precej težko. Hkrati uporabljajo dejstvo, da če je vsota dveh števil enaka drugemu koeficientu kvadratne enačbe, vzeti z znakom minus, in zmnožek teh števil je enak prosti izraz, potem so ta števila korenine te kvadratne enačbe. S tem se bomo lotili na primeru. Vzemimo kvadratno enačbo x 2 −5 · x + 6 \u003d 0. Da sta številki x 1 in x 2 koreni te enačbe, morata biti izpolnjeni dve enačbi x 1 + x 2 \u003d 5 in x 1 · x 2 \u003d 6. Še vedno je treba pobrati takšne številke. V tem primeru je to povsem enostavno: 2 in 3 sta taki številki, saj sta 2 + 3 \u003d 5 in 2 · 3 \u003d 6. Tako sta 2 in 3 korenine te kvadratne enačbe. Teorema, obratna teoremu Vieta, je še posebej priročna za iskanje drugega korena zmanjšane kvadratne enačbe, kadar je ena od korenin že znana ali očitna. V tem primeru najdemo drugo korenino iz katerega koli od odnosov. Za primer vzemimo kvadratno enačbo 512 × 2 −509 × −3 \u003d 0. Tukaj je enostavno opaziti, da je enota koren enačbe, saj je vsota koeficientov te kvadratne enačbe enaka nič. Torej x 1 \u003d 1. Drugi koren x 2 lahko najdemo na primer iz razmerja x 1 · x 2 \u003d c / a. Imamo 1 x 2 \u003d −3 / 512, od kod x 2 \u003d −3 / 512. Tako smo določili obe koreni kvadratne enačbe: 1 in −3/512. Jasno je, da je izbira korenin priporočljiva le v najpreprostejših primerih. V drugih primerih lahko uporabite koreninske formule kvadratne enačbe s pomočjo diskriminatorja, če želite najti korenine. Druga praktična uporaba teorema, inverzna izrek Viete, je sestavljanje kvadratnih enačb za dani koreni x 1 in x 2. Če želite to narediti, je dovolj izračunati vsoto korenin, ki daje koeficient x z nasprotnim znakom zmanjšane kvadratne enačbe in zmnožek korenin, ki daje prosti izraz. Primer. Napišite kvadratno enačbo, katere koreni sta številki −11 in 23. Rešitev. Označimo x 1 \u003d −11 in x 2 \u003d 23. Izračunamo vsoto in produkt teh števil: x 1 + x 2 \u003d 12 in x 1 · x 2 \u003d −253. Zato so te številke korenine zmanjšane kvadratne enačbe z drugim koeficientom −12 in prostim izrazom −253. To pomeni, da je x 2 −12 · x - 253 \u003d 0 želena enačba. Odgovor je: x 2 −12 x - 253 \u003d 0. Vietajev izrek se zelo pogosto uporablja pri reševanju problemov, povezanih z znaki korenin kvadratnih enačb. Kako je Vietajev izrek povezan z znaki korenin reducirane kvadratne enačbe x 2 + p · x + q \u003d 0? Podamo dve ustrezni izjavi:
Te izjave izhajajo iz formule x 1 · x 2 \u003d q, kot tudi pravila za množenje pozitivnih, negativnih števil in števil z različnimi znaki. Razmislite o primerih njihove uporabe. Primer. R je pozitiven. Z razlikovalno formulo najdemo D \u003d (r + 2) 2 −4 · 1 · (r - 1) \u003d r 2 + 4 · r + 4−4 · r + 4 \u003d r 2 +8, vrednost izraza r 2 +8 je pozitivna za kateri koli resnični r, zato je D\u003e 0 za kateri koli resnični r. Zato ima začetna kvadratna enačba dve realni vrednosti parametra r. Zdaj ugotovite, kdaj imajo korenine drugačne znake. Če so znaki korenin različni, potem je njihov produkt negativen, in po teoremu Vieta je produkt korenin zmanjšane kvadratne enačbe enak prosti pojmu. Zato nas zanimajo tiste vrednosti r, pri katerih je prosti izraz r - 1 negativen. Tako, da bi našli vrednosti r, ki nas zanimajo, moramo reši linearno neenakost r - 1<0 , откуда находим r<1 . Odgovor je: pri r<1 . Vieta FormulasZgoraj smo govorili o izreku Vieta za kvadratno enačbo in analizirali odnose, ki jih potrjuje. Obstajajo pa formule, ki povezujejo resnične korenine in koeficiente ne samo kvadratnih enačb, temveč tudi kubičnih enačb, enačb štiričlanske stopnje in na splošno oz. algebarske enačbe stopnja n. Pokličejo se formule Vieta. Vieta napišemo formule za algebrsko enačbo stopnje n forme in domnevamo, da ima n resničnih korenin x 1, x 2, ..., x n (med njimi so morda naključna): Pridobite formule Vieta omogoča polinomni teorem linearne faktoriacije, pa tudi definicijo enakih polinomov z enakostjo vseh njihovih ustreznih koeficientov. Torej polinom in njegova razgradnja na linearne faktorje oblike sta enaka. Odpiranje oklepajev v zadnjem delu in enačenje ustreznih koeficientov dobimo formule Vieta. Zlasti za n \u003d 2 imamo že znane formule Viete za kvadratno enačbo. Za kubično enačbo imajo formule Vieta obliko Omenimo le, da so na levi strani formule Vieta tako imenovani osnovni simetrični polinomi. Reference
Določitev vsote korenin enačbe je eden od potrebnih korakov pri reševanju kvadratnih enačb (enačbe oblike ax² + bx + c \u003d 0, kjer so eksponenti a, b in c poljubna števila, poleg tega a? 0) s podporo za izrek Viete. Navodila za uporabo1. Kvadratno enačbo zapišite kot ax² + bx + c \u003d 0 Primer: Začetna enačba: 12 + x² \u003d 8x Pravilno zapisana enačba: x² - 8x + 12 \u003d 0 2. Uporabite teorem Vieta, po katerem je vsota korenin enačbe enaka številu "b" z nasprotnim znakom, njihov produkt pa je enak številki "c". Primer: V obravnavani enačbi je b \u003d -8, c \u003d 12 oziroma: x1 + x2 \u003d 8 × 1 ∗ x2 \u003d 12 3. Ugotovite, ali so pravilna ali negativna števila korenine enačb. Če sta izdelek in vsota korenin pozitivna števila, so vse korenine pravilno število. Če je produkt korenin pravilen in je seštevek korenin negativno število, potem sta obe korenini negativni. Če je produkt korenin negativen, potem ima en koren znak "+", drugi pa znak "-". V tem primeru uporabite dodatno pravilo: "Če je vsota korenin pozitivno število, je tudi večja korenina pozitivna in če je vsota korenin negativno število je večje v absolutni vrednosti, koren je negativen. “Primer: V obravnavani enačbi sta vsota in zmnožek pravilni številki: 8 in 12, tako da sta oba korena pozitivna števila. 4. Reši nastali sistem enačb z izbiro korenin. Udobneje bo selekcijo začeti s faktorji in nato, če želite preveriti, zamenjati kateri koli par faktorjev v drugi enačbi in preveriti, ali vsota teh korenin ustreza rešitvi Primer: x1 ∗ x2 \u003d 12 Primernih parov korenin sta 12 in 1, 6 in 2, 4 in 3 Preverite nastale pare s podporo za enačbo x1 + x2 \u003d 8. Parovi 12 + 1 ≠ 86 + 2 \u003d 84 + 3 ≠ 8 Ustrezno so korenine enačbe števil 6 in 8. Enačba se imenuje enakost oblike f (x, y, ...) \u003d g (x, y, ..), kjer sta f in g funkciji ene ali več spremenljivk. Odkriti koren enačbe pomeni odkriti niz argumentov, v katerih ta enakost velja.
Potrebovali boste
Navodila za uporabo1. Morda imate enačbo oblike: x + 2 \u003d x / 5. Za začetek prenesemo vse sestavine te enakosti z desne na levo, hkrati pa spremenimo znak komponente v nasprotno. Na desni strani te enačbe ostane ničla, torej dobimo naslednje: x + 2-x / 5 \u003d 0. 2. Podamo enake izraze. Dobimo naslednje: 4x / 5 + 2 \u003d 0. 3. Nadalje iz dobljene zmanjšane enačbe najdemo neznan izraz, v tem primeru x. Nastala vrednost neznane spremenljivke bo rešitev začetne enačbe. V tem primeru dobimo naslednje: x \u003d -2,5. Sorodni videoposnetki Bodite pozorni! Koristni nasvet Vietajev izrek vzpostavlja neposredno povezavo med koreninami (x1 in x2) in eksponentami (b in c, d) enačbe tipa bx2 + cx + d \u003d 0. S tem izrekom je mogoče, ne da bi določili pomen korenin, v mislih izračunati njihovo vsoto. Nič ni težko, glavna stvar je poznati nekatera pravila.
Potrebovali boste
Navodila za uporabo1. Kvadratno enačbo spravi v standardno obliko, tako da gredo vsi eksponenti v padajočem vrstnem redu, to je sprva najvišja stopnja x2, na koncu pa ničelna stopnja x0. Enačba ima obliko: b * x2 + c * x1 + d * x0 \u003d b * x2 + c * x + d \u003d 0. 2. Preverite negativnost diskriminatorja. To preverjanje je potrebno za zagotovitev, da ima enačba korenine. D (diskriminatorno) ima obliko: D \u003d c2 - 4 * b * d. Obstaja več možnosti. D - diskriminatorno - pravilno, kar pomeni, da ima enačba dve korenini. D - je enak nič, iz tega sledi, da obstaja korenina, vendar je dvojna, torej x1 \u003d x2. D je negativen, za tečaj šolske algebre to stanje pomeni, da ni korenin, za višjo matematiko so korenine, vendar so zapletene. 3. Določite seštevek korenin enačbe. S teoremom Vieta je to enostavno storiti: b * x2 + c * x + d \u003d 0. Vsota korenin enačbe je neposredno sorazmerna s »–c« in obratno sorazmerna s eksponentom »b«. Namreč, x1 + x2 \u003d -c / b. Določite zmnožek korenin v skladu z izjavo - produkt korenin enačbe je neposredno sorazmeren z "d" in obratno sorazmeren kazalcu "b": x1 * x2 \u003d d / b. Bodite pozorni! Koristni nasvet Če z zamenjavo števila v enačbi dobimo pravilno enakost, se takšno število imenuje koren. Korenine so lahko pravilne, negativne in ničelne. Med vsakim nizom korenin enačbe ločimo največ in minimum.
Navodila za uporabo1. Poiščite vse korenine enačbe, med njimi izberite negativne, če obstajajo. Naj bo, recimo, dana kvadratna enačba 2x? -3x + 1 \u003d 0. Uporabite formulo za iskanje korenin kvadratne enačbe: x (1,2) \u003d / 2 \u003d / 2 \u003d / 2, potem je x1 \u003d 2, x2 \u003d 1. Lahko je opaziti, da med njimi ni negativnih. 2. Prav tako je mogoče odkriti korenine kvadratne enačbe s pomočjo izrek Vieta. V skladu s tem izrekom je x1 + x1 \u003d -b, x1? X2 \u003d c, kjer sta b in c indeksa enačbe x? + Bx + c \u003d 0. Z uporabo tega izrekanja ni dovoljeno izračunati diskriminatornega b? -4ac, kar lahko v nekaterih primerih nalogo zelo poenostavi. 3. Če je eksponent pri x celo v kvadratni enačbi, lahko za iskanje korenin uporabimo ne osnovno, temveč skrajšano formulo. Če je osnovna formula videti kot x (1,2) \u003d [- b ±? (B? -4ac)] / 2a, se v skrajšani obliki zapiše takole: x (1,2) \u003d [- b / 2 ±? ( b? / 4-ac)] / a. Če v kvadratni enačbi ni prostega izraza, je premik x iz oklepajev dokaj enostavno. In občasno se levi del doda v polni kvadrat: x? + 2x + 1 \u003d (x + 1)?. 4. Obstajajo vrste enačb, ki ne dajejo ne enega števila, temveč celega števila rešitev. Povejte trigonometrične enačbe. Torej, rezultat enačbe 2sin? (2x) + 5sin (2x) -3 \u003d 0 je x \u003d? / 4+? K, kjer je k celo število. To pomeni, da bo pri zamenjavi katere koli celostne vrednosti parametra k argument x izpolnil dano enačbo. 5. Pri trigonometričnih težavah bo morda treba odkriti vse negativne korenine ali največ negativnih. Pri reševanju takšnih problemov se uporablja logično sklepanje ali metoda matematične indukcije. Nadomestite več celih vrednosti za k v izrazu x \u003d? / 4+? K in opazujte, kako se argument obnaša. Mimogrede, največji negativni koren v prejšnji enačbi bo x \u003d -3? / 4 pri k \u003d 1. Sorodni videoposnetki Bodite pozorni! Koristni nasvet Vsota korenin kvadratne enačbe je enaka drugemu koeficientu z nasprotnim znakom, produkt korenin pa je prosti izraz. (Spomnimo: zmanjšana kvadratna enačba je enačba, kjer je prvi koeficient 1). Pojasnilo: Naj bo kvadratna enačba sekira 2 +bx +c \u003d 0 ima korenine x 1 in x 2 Potem po teoremu Vieta: Primer 1: Zgornja enačba x 2 - 7x + 10 \u003d 0 ima korenini 2 in 5. Vsota korenin je 7, izdelek pa 10. In v naši enačbi je drugi koeficient -7, prosti izraz pa 10. Tako je vsota korenin enaka drugemu koeficientu z nasprotnim znakom, produkt korenin pa je prosti izraz. Precej pogosto obstajajo kvadratne enačbe, ki jih je mogoče enostavno izračunati s pomočjo teorema Vieta - še več, lažje jih je izračunati z njegovo pomočjo. To je mogoče enostavno preveriti tako v prejšnjem primeru kot v naslednjem. Primer 2 Rešite kvadratno enačbo x 2 – 2x – 24 = 0. Rešitev. Uporabljamo izrek Vieta in zapišemo dve identiteti: x 1 x 2 = –24 x 1 + x 2 = 2 Takšne faktorje izberemo za –24, tako da je njihova vsota enaka 2. Po premisleku ugotovimo: 6 in –4. Preveri: 6 · (- 4) \u003d –24. 6 + (– 4) = 6 – 4 = 2. Kot ste opazili, je v praksi bistvo Vieta teorema prosti izraz v takih faktorjih, katerih vsota je enaka drugemu koeficientu z nasprotnim znakom. Ti dejavniki bodo korenine. Zato so korenine naše kvadratne enačbe 6 in –4. Odgovor je: x 1 = 6, x 2 = –4. Primer 3 Rešimo kvadratno enačbo 3x 2 + 2x - 5 \u003d 0. Tukaj ne obravnavamo dane kvadratne enačbe. Toda takšne enačbe lahko rešimo tudi z izrekom Viete, če so njihovi koeficienti uravnoteženi - na primer, če je vsota prvega in tretjega koeficienta enaka drugemu z nasprotnim znakom. Rešitev. Koeficienti enačbe so uravnoteženi: vsota prvega in tretjega stavka je enaka drugemu z nasprotnim znakom: 3 + (–5) = –2. Po teoremu Vieta x 1 + x 2 \u003d –2/3 Najti moramo dve številki, katerih vsota je –2/3, in produkt –5/3. Ta števila bodo korenine enačbe. Prvo število takoj ugibamo: to je 1. Konec koncev se s x \u003d 1 enačba spremeni v najpreprostejše seštevanje-odštevanje: 3/3 + x 2 \u003d –2/3. Rešimo preprosto enačbo: x 2 \u003d –2/3 - 3/3 Odgovor: x 1 \u003d 1; x 2 \u003d –5/3 Primer 4: Rešite kvadratno enačbo 7 x 2 – 6x – 1 = 0. Rešitev: En koren je zaznan takoj - rine direktno v oči: x 1 \u003d 1 (ker dobimo preprosto aritmetiko: 7 - 6 - 1 \u003d 0). Koeficienti enačbe so uravnoteženi: vsota prvega in tretjega sta enaka drugemu z nasprotnim znakom: V skladu s teoremom Vieta sestavimo dve identiteti (čeprav je v tem primeru ena od njih dovolj): x 1 x 2 = –1/7 Vrednost x 1 nadomestimo s katerim koli od teh dveh izrazov in najdemo x 2: x 2 = –1/7: 1 = –1/7 Odgovor je: x 1 = 1; x 2 = –1/7 Razlikovalec reducirane kvadratne enačbe. Razlikovalnik zmanjšane kvadratne enačbe lahko izračunamo tako s splošno formulo kot poenostavljeno: NaD \u003d 0, korenine dane enačbe lahko izračunamo po formuli: Če je D< 0, то уравнение не имеет корней. Če je D \u003d 0, potem ima enačba en koren. Če je D\u003e 0, potem ima enačba dve korenini. |
| Preberi: |
|---|
Priljubljeno:
Rešitev najpreprostejših trigonometričnih neenakosti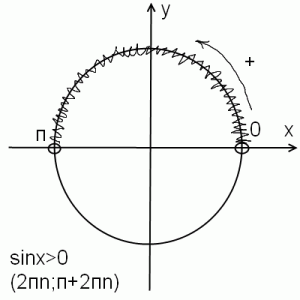
|
Novo
- Kaj je pokvarilo "krutega" barona?
- Član gibanja White
- Pot Suvorova in ekipe v domovino
- Funkcijo F (x) imenujemo antideriva za funkcijo f (x), če je F` (x) \u003d f (x) ali dF (x) \u003d f (x) dx
- Program za zmanjšanje deleža stopinj
- Podobni izrazi, njihovo zmanjšanje, primeri
- Ruski popotniki lazarev
- Reševanje nepopolnih kvadratnih enačb
- Rešitev kvadratnih enačb, formula korenin, primeri
- Koordinatna ravnina (6. razred) - Hipermarket znanja