Paralelogram je štirikotnik z nasprotnimi stranicami, ki so dvojno vzporedne. Ta definicija že zadostuje, saj iz nje sledijo preostale lastnosti paralelograma in se dokazujejo v obliki izrek.

Glavne lastnosti paralelograma so:

• paralelogram je konveksni štirikotnik;
• v paralelogramu sta nasprotni strani enaki v parih;
• paralelogram ima v parih nasprotne kote;
• diagonale paralelograma se delijo na polovico s presečiščem.

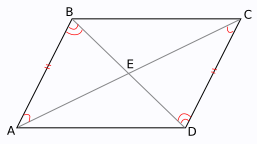
Parallelogram - konveksni štirikotnik

Najprej dokažemo izrek, da paralelogram je izbočen štirikotnik. Poligon je izbočen, ne glede na to, katera stran je razširjena na ravno črto, bodo vse druge strani poligona na eni strani te črte.

Naj navedemo paralelogram ABCD, v katerem je AB nasprotna stran za CD, BC pa nasprotna stran za AD. Potem iz definicije paralelograma sledi, da je AB || CD, BC || AD.

Vzporedni segmenti nimajo skupnih točk, ne sekajo se. To pomeni, da CD leži na eni strani AB. Ker segment BC povezuje točko B odseka AB s točko C segmenta CD, segment AD pa povezuje druge točke AB in CD, odseka BC in AD prav tako ležita na isti strani premice AB, kjer leži CD. Tako vse tri strani - CD, BC, AD - ležijo na eni strani AB.

Podobno je dokazano, da glede na druge strani paralelograma druge tri strani ležijo na eni strani.

Nasproti strani in koti so enaki

Ena od lastnosti paralelograma je ta v paralelogramu sta nasprotni strani in nasprotni koti v parih enaki. Na primer, če je dan paralelogram ABCD, potem ima AB \u003d CD, AD \u003d BC, ∠A \u003d ∠C, ∠B \u003d ∠D. Ta izrek je dokazan na naslednji način.

Paralelogram je štirikotnik. Torej ima dve diagonali. Ker je paralelogram konveksni štirikotnik, ga kateri koli od njih deli na dva trikotnika. Razmislite o trikotniku ABC in ADC v paralelogramu ABCD, dobljenem z risanjem diagonale AC.

Ti trikotniki imajo skupno eno stran - AC. Kot BCA je enak kotu CAD, navpičen s vzporednima BC in AD. Kotoma BAC in ACD sta enako navpična z vzporednima AB in CD. Zato je ∆ABC \u003d ∆ADC pod dvema kotoma in stranjo med njimi.

V teh trikotnikov stran AB ustreza stranski CD, stran BC pa AD. Zato sta AB \u003d CD in BC \u003d AD.

Kot B ustreza kotu D, to je ∠B \u003d ∠D. Kot paralelograma A je vsota dveh kotov - - BAC in iCAD. Kot C je enak consistsBCA in ∠ACD. Ker sta para kotov enaka drug drugemu, potem je ∠A \u003d ∠C.

Tako je dokazano, da sta v paralelogramu nasprotni strani in koti enaki.

Diagonale razpolovimo

Ker je paralelogram izbočen štirikotnik, potem ima dve diagonali in se sekata. Naj dobimo paralelogram ABCD, njegova diagonali AC in BD se presekata v točki E. Razmislimo o trikotniku ABE in CDE, ki ju tvorita.

Za te trikotnike sta strani AB in CD enaki kot nasprotni strani paralelograma. Kot ABE je enak kotu CDE, ki leži navzkrižno z vzporednima črtama AB in CD. Iz istega razloga je ∠BAE \u003d ∠DCE. Zato je ∆ABE \u003d ∆CDE pod dvema kotoma in stranjo med njimi.

Opazite lahko tudi, da sta kota AEB in CED navpična, torej tudi enaka drug drugemu.

Ker sta trikotnika ABE in CDE enaka drug drugemu, so vsi njihovi ustrezni elementi enaki. Stranska AE prvega trikotnika ustreza strani CE drugega, kar pomeni AE \u003d CE. Podobno je BE \u003d DE. Vsak par enakih segmentov sestavlja diagonalo paralelograma. Tako je dokazano, da diagonale paralelograma so na polovici razdeljene s presečiščem.

Paralelogram je štirikotnik, v katerem sta nasprotni strani vzporedni, to je, da ležita na vzporednih črtah (slika 1).

  Izrek 1 O lastnosti strani in kotov paralelograma.   V paralelogramu sta nasprotni strani enaki, nasprotni koti so enaki, vsota kotov, ki mejijo na eno stran paralelograma, pa je 180 °.

Dokaz. V tem paralelogramu ABCD narišemo diagonalo AC in dobimo dva trikotnika ABC in ADC (slika 2).

Ti trikotniki so enaki, saj so ∠ 1 \u003d ∠ 4, ∠ 2 \u003d ∠ 3 (ležijo vogali navzkrižno za vzporedne črte), stran zvočnika pa je pogosta. Iz enakosti Δ ABC \u003d Δ ADC izhaja, da je AB \u003d CD, BC \u003d AD, ∠ B \u003d ∠ D. Vsota kotov, ki mejijo na eno stran, na primer kota A in D, je 180 ° kot enostranska z vzporednimi črtami. Izrek je dokazan.

Opomba. Enakost nasprotnih strani paralelograma pomeni, da so odseki vzporednih, odrezani z vzporednikom, enaki.

Ugotovitev 1. Če sta dve premici vzporedni, so vse točke ene premice na isti razdalji od druge.

Dokaz. Pravzaprav naj bo || b (slika 3).

Iz katere koli dve točki B in C črte b povlecite pravokotni BA in CD na črko a. Ker je AB || CD, potem je figura ABCD paralelogram in zato je AB \u003d CD.

Razdalja med dvema vzporednima črtama je razdalja od poljubne točke ene od premic do druge črte.

Glede na dokazano je enaka dolžini pravokotne črte od neke točke ene od vzporednih črt do druge črte.

Primer 1   Obseg paralelograma je 122 cm. Ena od njegovih strani je 25 cm večja od druge. Poiščite stranice paralelograma.

Rešitev.   Po teoremu 1 sta nasprotni strani paralelograma enaki. Eno stran paralelograma označimo s x, drugo pa z y. Potem s pogojem $$ \\ left \\ (\\ začetek (matrica) 2x + 2y \u003d 122 \\\\ x - y \u003d 25 \\ konec (matrica) \\ desno. $$ Rešitev tega sistema dobimo x \u003d 43, y \u003d 18. Tako Tako so stranice paralelograma 18, 43, 18 in 43 cm.

Primer 2

Rešitev.   Pogoj problema naj ustreza sliki 4.

AB označimo s x, BC pa z y. Pod pogojem je obod paralelograma 10 cm, to je 2 (x + y) \u003d 10 ali x + y \u003d 5. Obod trikotnika ABD je 8 cm. In ker je AB + AD \u003d x + y \u003d 5, potem je BD \u003d 8 - 5 \u003d 3. Torej BD \u003d 3 cm.

Primer 3   Poiščite kote paralelograma, pri čemer veste, da je eden od njih 50 ° večji od drugega.

Rešitev.   Stanje problema naj ustreza sliki 5.

Merimo stopnjo kota A s x. Nato je stopinska mera kota D x + 50 °.

Kotoma BAD in ADC sta enostranski notranji z vzporednima ravnima AB in DC ter seantnim AD. Potem bo vsota teh poimenovanih kotov 180 °, tj.
  x + x + 50 ° \u003d 180 °, ali x \u003d 65 °. Tako je ∠ A \u003d ∠ C \u003d 65 °, a ∠ B \u003d ∠ D \u003d 115 °.

Primer 4   Strani paralelograma so 4,5 dm in 1,2 dm. Z vrha akutnega kota se nariše bisektor. Na katere dele se deli večja stran paralelograma?

Rešitev.   Stanje problema naj ustreza sliki 6.

AE je bisektor akutnega kota paralelograma. Zato je ∠ 1 \u003d ∠ 2.

ŠTIRI RAGONI.

§43. PARALELOGRAMI.

1. Opredelitev paralelograma.

Če prečkamo par vzporednih črt z drugim parom vzporednih črt, dobimo štirikotnik, v katerem sta nasprotni strani parno vzporedni.

V štirikotnikov ABDC in EFNM (slika 224) BD || AC in AB || CD;
  EF || MN in EM || Fn

Štirikotnik, v katerem sta nasprotni strani dvojno vzporedni, se imenuje paralelogram.

2. Lastnosti paralelograma.

Izrek. Diagonala paralelograma ga deli na dva enaka trikotnika.

Naj bo paralelogram ABDC (slika 225), v katerem je AB || CD in AC || BD.

Dokazati je treba, da ga diagonala deli na dva enaka trikotnika.

Diagonalo CB narišemo v paralelogramu ABDC. Dokažimo to /\   CAB \u003d /\   CDB

CB stran je običajna za te trikotnike; /   ABC \u003d /   BCD, kot notranji križno ležeči koti z vzporednima AB in CD in sekantnim CB; /   DIA \u003d /   CBD, kot tudi navznoter ležeči koti pri vzporednih AC in BD in seantnem CB (§ 38).

Od tod /\   CAB \u003d /\   CDB

Na enak način je mogoče dokazati, da diagonala AD deli paralelogram na dva enaka trikotnika ACD in ABD.

Posledice. 1 . Nasprotni koti paralelograma so enaki drug drugemu.

/   A \u003d /   D, to izhaja iz enakosti trikotnikov CAB in CDB.
  Podobno in /   C \u003d /   B.

2. Nasproti strani paralelograma sta enaki drug drugemu.

AB \u003d CD in AC \u003d BD, saj so to stranice enakih trikotnikov in ležijo pod enakimi koti.

Izrek 2 Diagonale paralelograma na mestu njihovega presečišča so razdeljene na polovico.

Naj bosta BC in AD diagonali paralelograma ABDC (slika 226). Dokazujemo, da je AO \u003d OD in CO \u003d OB.

Če želite to narediti, primerjajte na primer nekaj parov nasprotno nameščenih trikotnikov /\   AOW in /\   COD.

V teh trikotnih AB \u003d CD kot nasprotnih straneh paralelograma;
/ 1 = / 2, kot notranji koti ležijo navzkrižno med vzporednima AB in CD ter seantom AD;
/ 3 = / 4 iz istega razloga, saj je AB || CD in CB sta njuna sekvenca (§ 38).

Iz tega sledi /\   AOW \u003d /\   COD. In v enakovrednih trikotnikovh pod enakimi koti ležijo enake stranice. Zato je AO \u003d OD in CO \u003d OB.

Izrek 3 Vsota kotov, ki mejijo na eno stran paralelograma, je 2 d .

Dokažite se.

3. Znaki paralelograma.

Izrek Če sta nasprotni strani štirikotnika enaki v parih, je ta štirikotnik paralelogram.

V štirikotniku pustimo AB \u003d С (slika 227) AB \u003d CD in AC \u003d ВD. Dokazujemo, da je pod tem pogojem AB || CD in AC || BD, to je štirikotnik ABDC - paralelogram.
Odsek povežite s katero koli dve nasprotni točki tega štirikotnika, na primer C in B. Štirikotnik ABDC je razdeljen na dva enaka trikotnika: /\   CAB in /\   CDB Dejansko je njihova stran CB pogosta, AB \u003d CD in AC \u003d BD pod pogojem. Torej so tri strani enega trikotnika torej enake trem stranem drugega /\   CAB \u003d /\   CDB

Zato sta enaka kota v enakih trikotnih nasproti enakim stranicam
/ 1 = / 2 in / 3 = / 4.

Kot 1. in 2. kota sta navznoter ležeča kota na presečišču črt AB in CD premice CB. Zato je AB || CD

Na enak način sta kota 3. in 4. notranjega ležečega kota na presečišču črt CA in BD premice CB, torej CA || BD (§ 35).

Tako sta nasprotni strani štirikotnika ABDC dvojno vzporedni, torej je paralelogram, kot je potrebno.

Izrek 2 Če sta dve nasprotni strani štirikotnika enaki in vzporedni, je ta štirikotnik paralelogram.

V štirikotnik pustimo ABDC AB \u003d CD in AB || CD Dokažimo, da je pod temi pogoji štirikotni paralelogram ABDC (slika 228).

Vrhovi C in B povežemo z odsekom CB, zaradi vzporednosti premic AB in CD sta kota 1 in 2 kot vogala v notranjosti, ki ležita navzkrižno, enaka (§ 38).
  Potem je trikotnik CAB enak trikotniku CDB, saj je njihova stran CB običajna oz.
  AB \u003d CD po predpostavki izrek in / 1 = / 2 kot dokazano. Iz enakosti teh trikotnikov izhaja enakost kotov 3 in 4, saj ležijo nasproti enakim stranem v enakih trikotnikih.

Toda kota 3 in 4 sta notranja ležeča kota, ki sta nastala na presečišču črt AC in BD premice CB, torej AC || BD (§ 35), tj. Štirikotnik
  ABDC-paralelogram.

Vaje.

1. Dokažite, da če so diagonale štirikotnika na mestu njihovega presečišča razdeljene na polovico, potem je ta štirikotnik paralelogram.

2. Dokažite, da je štirikotnik, pri katerem je vsota notranjih kotov, ki mejijo na vsako od obeh sosednjih strani, enaka 2 dobstaja paralelogram.

3. Sestavite paralelogram na dveh straneh in kot med njima:

a) z uporabo paralelizma nasprotnih strani paralelograma;
   b) z uporabo enakosti nasprotnih strani paralelograma.

4. Sestavite paralelogram na dveh sosednjih straneh in diagonali.

5. Sestavite paralelogram vzdolž njegovih dveh diagonal in kota med njima.

6. Sestavite paralelogram vzdolž njegove strani in dveh diagonal.

Tako kot v evklidski geometriji sta točka in ravna črta glavna elementa teorije ravnin, tako je paralelogram ena ključnih figur konveksnih štirikotnikov. Iz njega kot niti iz kroglice pritekajo pojmi „pravokotnik“, „kvadrat“, „romb“ in druge geometrijske količine.

Vkontakte

Opredelitev paralelograma

Konveksni štirikotnik,   sestavljen iz segmentov, katerih vsak par je vzporeden, je v geometriji znan kot paralelogram.

Klasični paralelogram izgleda kot štirikotnik ABCD. Strani se imenujejo osnove (AB, BC, CD in AD), pravokotna črta iz katere koli točke na stran nasproti te točke se imenuje višina (BE in BF), črte AC in BD pa imenujemo diagonali.

Pozor!   Kvadrat, romb in pravokotnik so posebni primeri paralelograma.

Strani in koti: značilnosti razmerja

Ključne značilnosti na splošno   vnaprej določeno z notacijo, jih dokazuje teorem. Te lastnosti so naslednje:

1. Stranke, ki so nasprotne, so v parih enake.
2. Koti, ki se nahajajo drug proti drugemu, so enaki v parih.

Dokaz: upoštevajte ∆ABC in ∆ADC, ki ju dobite zaradi ločitve štirikotnika ABCD premice AC. ∠BCA \u003d ∠CAD in ∠BAC \u003d ∠ACD, saj sta AC skupna zanje (navpični koti za BC || AD in AB || CD). Iz tega sledi: ∆ABC \u003d ∆ADC (drugi znak enakosti trikotnikov).

Segmenta AB in BC v ∆ABC parno ustrezata črtama CD in AD v ∆ADC, kar pomeni njuno identiteto: AB \u003d CD, BC \u003d AD. Tako ∠B ustreza ∠D in so enaki. Ker so ∠A \u003d ∠BAC + ∠CAD, ∠C \u003d ∠BCA + ∠ACD, ki so tudi parno enaki, potem je ∠A \u003d ∠C. Lastnost je dokazana.

Značilnosti diagonale figure

Glavni simptomteh paralelogramskih črt: presečišče jih deli na polovico.

Dokaz: Naj bo T. E presečišče diagonale AC in BD na sliki ABCD. Tvorijo dva sorazmerna trikotnika - ∆ABE in ∆CDE.

AB \u003d CD, saj so nasprotni. Glede na črte in sekante sta ∠ABE \u003d ∠CDE in ∠BAE \u003d ∠DCE.

Po drugem kriteriju enakosti je ΔABE \u003d ΔCDE. To pomeni, da sta elementa ∆ABE in ∆CDE: AE \u003d CE, BE \u003d DE in sta hkrati sorazmerna dela AC in BD. Lastnost je dokazana.

Značilnosti sosednjih vogalov

Na sosednjih straneh je vsota kotov 180 °, saj ležijo na eni strani vzporednih črt in sekant. Za štirikotnik ABCD:

∠A + ∠B \u003d ∠C + ∠D \u003d ∠A + ∠D \u003d ∠B + ∠C \u003d 180º

Lastnosti bisektorjev:

1.   , spuščeni na eno stran, so pravokotni;
2. nasprotni vrhovi imajo vzporedne bisektorje;
3. trikotnik, ki ga dobimo z držanjem bisektorja, bodo enake.

Določanje značilnih značilnosti paralelograma po izrek

Značilnosti te številke izhajajo iz njenega glavnega izrekanja, ki navaja naslednje: štirikotnik se šteje za paralelogramv primeru, da se njegove diagonale sekajo, in ta točka jih razdeli na enake segmente.

Dokaz: Predpostavimo, da v T. E sekata premici AC in BD štirikotnika ABCD. Ker sta ∠AED \u003d ∠BEC in AE + CE \u003d AC BE + DE \u003d BD, ∆AED \u003d ∆BEC (s prvim znakom enakosti trikotnikov). Se pravi, ∠EAD \u003d ∠ECB. So tudi notranji prečni koti sekanca AC za ravne črte AD in BC. Tako po definiciji paralelizma - AD || Pr. Podobna lastnost linij BC in CD je tudi izhodna. Izrek je dokazan.

Izračun površine slike

Območje te številke   ki jih najdemo z več metodamiena najpreprostejših: pomnožitev višine in osnove, na katero je vlečena.

Dokaz: črpamo pravokotni BE in CF iz točki B in C. ∆ABE in ∆DCF sta enaki, saj sta AB \u003d CD in BE \u003d CF. ABCD je izometričen s pravokotnikom EBCF, saj so sestavljeni iz proporcionalnih številk: S ABE in S EBCD, pa tudi S DCF in S EBCD. Iz tega sledi, da je območje te geometrijske figure enako pravokotniku:

S ABCD \u003d S EBCF \u003d BE × BC \u003d BE × AD.

Za določitev splošne formule območja paralelograma označimo višino kot hbin na stran b. V skladu s tem:

Drugi načini iskanja območja

Površinski izračuni skozi stranice paralelograma in kotaki jih tvorijo je druga znana metoda.

,

Spr-ma - območje;

a in b sta njegovi strani

α je kot med odsekoma a in b.

Ta metoda praktično temelji na prvi, vendar v primeru, da ni znana. vedno odreže pravi trikotnik, katerega parametri so trigonometrične identitete, to je. Preoblikovanje odnosa dobimo. V enačbi prve metode nadomestimo višino s tem izdelkom in pridobimo dokaz veljavnosti te formule.

Skozi diagonale paralelograma in kota oz.   ki jih ustvarijo na križišču, najdete tudi območje.

Dokaz: AC in BD, ki se sekata, tvorita štiri trikotnike: ABE, BEC, CDE in AED. Njihova vsota je enaka površini tega štirikotnika.

Območje vsakega od teh ∆ lahko najdemo za izrazom, kjer je a \u003d BE, b \u003d AE, ∠γ \u003d ∠AEB. Od takrat se v izračunih uporablja ena sama vrednost sinusa. Tako je. Ker je AE + CE \u003d AC \u003d d 1 in BE + DE \u003d BD \u003d d 2, se formula formule zmanjša na:

.

Uporaba v vektorski algebri

Značilnosti sestavnih delov tega štirikotnika so našle uporabo v vektorski algebri, in sicer: dodajanje dveh vektorjev. Pravilo paralelograma določa, da če imajo vektorje   in   ne   kolinearna, potem bo njihova vsota enaka diagonali te številke, katere osnove ustrezajo tem vektorjem.

Dokaz: iz poljubno izbranega začetka - tj. - konstruiramo vektorje in. Nato konstruiramo paralelogram OASV, kjer sta segmenta OA in OB strani. Tako OS leži na vektorju ali vsoti.

Formule za izračun parametrov paralelograma

Podatki za identiteto so pod naslednjimi pogoji:

1. a in b, α sta strani in kot med njima;
2. d 1 in d 2, γ sta diagonali na mestu njihovega presečišča;
3. h a in h b sta višini, spuščeni na straneh a in b;

Parameter	Formula
Iskanje strank
vzdolž diagonale in kosinusa kota med njimi
diagonalno in stransko
skozi višino in nasprotni vrh
Iskanje dolžine diagonale
ob straneh in velikosti vrha med njimi

Paralelogram je štirikotnik, katerega nasprotni strani sta vzporedni, tj. ležite na vzporednih črtah

Lastnosti paralelograma:
Izrek 22.   Nasproti strani paralelograma sta enaki.
   Dokaz. V paralelogramu ABCD narišemo diagonalo AC. Trikotnika ACD in ACB sta enaka, saj imata skupni stranski AC in dva para enakih kotov. poleg nje: ∠ САВ \u003d ∠ АСD, ∠ АСВ \u003d kot DAC (kot ležeči vogali z vzporednima črtama AD in BC). Zato sta AB \u003d CD in BC \u003d AD, kot ustrezni strani enakih trikotnikov, ipd. Iz enakosti teh trikotnikov izhaja tudi enakost ustreznih kotov trikotnikov:
Izrek 23.   Nasprotni koti paralelograma so: ∠ A \u003d ∠ C in ∠ B \u003d ∠ D.
   Enakost prvega para izhaja iz enakosti trikotnikov ABD in CBD, drugega pa - ABC in ACD.
Izrek 24.   Sosednji vogali paralelograma, tj. koti, ki mejijo na eno stran, segajo do 180 stopinj.
   To je zato, ker gre za notranje enostranske vogale.
Izrek 25.   Diagonale paralelograma se na mestu njihovega presečišča delijo na polovico.
   Dokaz. Upoštevajte trikotnike BOC in AOD. Po prvi lastnosti AD \u003d BC ∠ OAD \u003d ∠ WWS in ∠ ODA \u003d ∠ WWS kot leži navzkrižno z vzporednima črtama AD in BC. Zato so trikotniki BOC in AOD enaki vzdolž strani in vogalov, ki so zraven nje. Zato BO \u003d OD in AO \u003d OS, kot ustrezni strani enakih trikotnikov, ipd.

Znaki paralelograma
Izrek 26.   Če sta nasprotni strani štirikotnika dvojno enaki, je to paralelogram.
Dokaz. Naj bodo stranice AD \u200b\u200bin BC, AB in CD štirikotnika ABCD enake (slika 2). Narišite diagonalni zvočnik. Trikotnik ABC in ACD sta enaka na treh straneh. Potem sta kota BAC in DCA enaka in je zato AB vzporeden s CD. Vzporednost strani zrakoplova in AD izhaja iz enakosti kotov CAD in ACB.
Izrek 27.   Če sta nasprotna kota štirikotnika dvojno enaka, je to paralelogram.
   Pustimo ∠ A \u003d ∠ C in ∠ B \u003d ∠ D. Ker ∠ A + ∠ B + ∠ C + ∠ D \u003d 360 °, potem sta ∠ A + ∠ B \u003d 180 ° in strani AD in BC sta vzporedni (z znakom vzporednih črt). Dokazujemo tudi vzporednost strani AB in CD in sklepamo, da je ABCD po definiciji paralelogram.
Izrek 28.   Če sosednji vogali štirikotnika, tj. koti, ki mejijo na eno stran, so skupaj 180 stopinj, potem je paralelogram.
   Če notranji enostranski koti seštevajo do 180 stopinj, so ravne črte vzporedne. Torej AB para CD in BC paral AD. Četrkotnik se po definiciji izkaže kot paralelogram.
Izrek 29.   Če so diagonale štirikotnika v presečišču na polovici medsebojno razdeljene, je štirikotnik paralelogram.
   Dokaz. Če je AO \u003d OS, BO \u003d OD, sta trikotnika AOD in BOC enaka, saj imata v zgornjem delu O enake (navpične) kote, pritrjene med pari enakih strani. Iz enakosti trikotnikov sklepamo, da sta AD in BC enaka. Strani AB in CD sta prav tako enaki, štirikotnik pa se izkaže, da je paralelogram glede na funkcijo 1.
Izrek 30.   Če ima štirikotnik par enakih strani, vzporednih med seboj, je to paralelogram.
   Naj bodo stranice AB in CD vzporedne in enake v štirikotniku ABCD. Narišite diagonali AC in BD. Vzporednost teh črt pomeni enakost ležečih kotov ABO \u003d CDO in BAO \u003d OCD. Trikotnika ABO in CDO sta na strani in vogalih poleg nje enaka. Zato je AO \u003d OS, BO \u003d OD, tj. diagonale se delijo presečišče na polovico in štirikotnik se po funkciji 4 izkaže kot paralelogram.

V geometriji so upoštevani posebni primeri paralelograma.