Odseki spletnega mesta
Izbira urednikov:
Oglaševanje
| Kako najti antiderivno funkcijo na neki točki. Funkcijo F (x) imenujemo antideriva za funkcijo f (x), če je F` (x) \u003d f (x) ali dF (x) \u003d f (x) dx |
|
Namen:
Matematična analiza je zbirka odsekov matematike, namenjena preučevanju funkcij in njihovim posploševanjem po metodah diferencialnih in integralnih izračunov. Če smo do zdaj preučevali odsek matematične analize, imenovan diferencialni izračun, katerega bistvo je preučevanje funkcij v "majhnem". I.e. raziskava funkcije v dovolj majhnih soseskah vsake definicijske točke. Ena od operacij diferenciacije je iskanje izpeljanke (diferenciala) in njegova uporaba pri preučevanju funkcij. Prav tako pomemben je obratni problem. Če je vedenje funkcije v bližini vsake točke njene definicije znano, potem kako obnoviti funkcijo kot celoto, tj. na celotnem področju njegove definicije. Ta naloga je predmet preučevanja tako imenovanega integralnega računa. Integracija je obratna diferenciacija. Ali obnovitev funkcije f (x) iz danega izvoda f` (x). Latinska beseda "integro" pomeni obnovo. Primer št. 1. Naj bo (x) `\u003d 3x 2. Rešitev: Na podlagi pravila diferenciacije je enostavno uganiti, da je f (x) \u003d x 3, ker (x 3), \u003d 3x 2 Ker je izpeljanka vsakega od njih 3x2. (Izvedba konstante je 0). Vse te funkcije se med seboj razlikujejo s konstantnim izrazom. Zato lahko splošno rešitev problema zapišemo v obliki f (x) \u003d x 3 + C, kjer je C katero koli stalno realno število. Kliče se katera koli od najdenih funkcij f (x) POMEMBNO za funkcijo F` (x) \u003d 3x 2 Opredelitev
Funkcijo F (x) imenujemo antideriva za funkcijo f (x) v določenem intervalu J, če je za vse x iz tega intervala F` (x) \u003d f (x). Torej je funkcija F (x) \u003d x 3 antideriva za f (x) \u003d 3x 2 na (- ∞; ∞). Kot smo že opazili, ima ta funkcija neskončno število antideritivov (glej primer št. 1). Primer št. 2
Funkcija F (x) \u003d x je antideriva za vse f (x) \u003d 1 / x na intervalu (0; +), ker za vse x iz tega intervala velja enakost. Primer št. 3.
Funkcija F (x) \u003d tg3x je antideriva za f (x) \u003d 3 / cos3x v intervalu (-n / 2;
n / a 2), Primer št. 4
Funkcija F (x) \u003d 3sin4x + 1 / x-2 je antideriva za f (x) \u003d 12cos4x-1 / x 2 na intervalu (0; ∞) Predavanje 2. Tema: antideriva. Glavna lastnost primitivne funkcije. Pri preučevanju antiderivativa se bomo zanašali na naslednjo trditev. Znak konstantnosti funkcije: Če je izvod Ψ (x) funkcije na intervalu J enak 0, potem je funkcija Ψ (x) na tem intervalu konstantna. To izjavo je mogoče prikazati geometrijsko. Znano je, da je Ψ` (x) \u003d tanα, γ α-kot naklona tangenta na grafu funkcije Ψ (x) v točki z absceso x 0. Če je Ψ` (υ) \u003d 0 v kateri koli točki intervala J, potem tgα \u003d 0 δ za katero koli tangento na grafu funkcije Ψ (x). To pomeni, da je tangenta na grafu funkcije na kateri koli točki vzporedna z osjo absces. Zato na prikazanem intervalu grafikon funkcije Ψ (x) sovpada z ravnim odsekom y \u003d C. Torej je funkcija f (x) \u003d c konstantna na intervalu J, če je f '(x) \u003d 0 na tem intervalu. Dejansko lahko za poljubni x 1 in x 2 iz intervala J po izrek o povprečni vrednosti funkcije zapišemo: Izrek: (glavna lastnost primitivne funkcije) Če je F (x) eden od antiderivov za funkcijo f (x) na intervalu J, potem ima množica vseh antierivatov te funkcije obliko: F (x) + C, kjer je C poljubno realno število. Dokaz: Naj bo F` (x) \u003d f (x), potem (F (x) + C) `\u003d F` (x) + C` \u003d f (x), za x Є J. Primer: Poiščite niz antiderivov funkcije f (x) \u003d cos x. Narišite grafe prvih treh. Rešitev: Sin x je eno izmed antideriva za funkcijo f (x) \u003d cos x F 1 (x) \u003d Sin x-1 Geometrijska ilustracija: Graf katerega koli antiderivativa F (x) + C lahko dobimo iz grafa antiderivativa F (x) z uporabo vzporednega prenosa r (0; c). Primer: Za funkcijo f (x) \u003d 2x poiščite antideriva, katerega graf prehaja skozi T.M (1; 4) Rešitev: F (x) \u003d x 2 + C je množica vseh antiderivov, F (1) \u003d 4 - pod pogojem problema. Antideriva. Primitivno je s primerom enostavno razumeti. Vzemite funkcijo y \u003d x 3. Kot vemo iz prejšnjih razdelkov, ki izhajajo iz x 3 je 3 x 2: (x 3)" = 3x 2 . Zato iz funkcije y \u003d x 3 dobimo novo funkcijo: ob = 3x 2 . To je: funkcija y \u003d x 3 je primitiven za funkcijo ob = 3x 2 . Opredelitev antideriva: V našem primeru ( x 3)" = 3x 2 torej y \u003d x 3 - antideriva za ob = 3x 2 . Integracija Kot veste, postopek iskanja izpeljanke glede na določeno funkcijo imenujemo diferenciacija. In obratno delovanje imenujemo integracija. Pojasnjevalni primer: ob = 3x 2 + greh x. Rešitev: Vemo, da je antideriva za 3 x 2 je x 3 . Antideriva za greh x je –cos x. Dodajte dva antideriva in dobite antideriva za določeno funkcijo: y \u003d x 3 + (–kozije x), y \u003d x 3 - cos x. Odgovor je: Pojasnjevalni primer: Poiščite antideriva za funkcijo ob \u003d 2 greh x. Rešitev: Opažamo, da je k \u003d 2. Antideriva za greh x je –cos x. Zato za funkcijo ob \u003d 2 greh x antiderivativa je funkcija ob \u003d –2 cos x. Pojasnjevalni primer: Poiščite antideriva za funkcijo y \u003d greh 2 x. Rešitev: Opazite to k \u003d 2. Antideriva za greh x je –cos x. Pri iskanju antideriva za funkcijo uporabljamo svojo formulo y \u003d cos 2 x: 1 cos 2 x cos 2 x
Pojasnjevalni primer. Vzemite funkcijo iz prejšnjega primera: y \u003d greh 2 x. Za to funkcijo imajo vsi primitivi obliko: cos 2 x Pojasnilo. Vzemite prvo vrstico. To se glasi takole: če je funkcija y \u003d f ( x) je 0, potem je antideriva za to 1. Zakaj? Ker je izpeljanka enote enaka nič: 1 "\u003d 0. Preostale vrstice se berejo v istem vrstnem redu. Kako zapisati podatke iz tabele? Vzemite osmo vrstico: (-kos x) "\u003d greh x Drugi del napišemo z znakom izpeljanke, nato z znakom enakosti in izpeljanko. Beremo: antideriva za funkcijo greh x je -cos funkcija x. Ali pa: -cos funkcija x je primitiven za funkcijo greh x. Razmislite o premiku točke po ravni črti. Pustite pravočasno t točka je že od začetka gibanja prehodila pot s (t). Nato trenutna hitrost v (t) enak izvodu funkcije s (t) to je v (t) \u003d s "(t). V praksi se pojavi obratna težava: za določeno hitrost točke v (t) najti njeno pot s (t), tj. najti takšno funkcijo s (t) katerega izpeljanka je v (t). Funkcija s (t) taka, da s "(t) \u003d v (t)se imenujejo primitivne funkcije v (t). Na primer, če v (t) \u003d atkje ampakJe dano število, potem je funkcija Funkcija F (x) imenovana antiderivativna funkcija f (x)v določenem intervalu, če sploh xiz te vrzeli F "(x) \u003d f (x). Na primer funkcija F (x) \u003d sin xje primitivna funkcija f (x) \u003d cos x,od takrat (sin x) "\u003d cos x; funkcijo F (x) \u003d x 4/4je primitivna funkcija f (x) \u003d x 3od takrat (x 4/4) "\u003d x 3. Razmislite o težavi. Izziv. Dokažite, da so funkcije x 3/3, x 3/3 + 1, x 3/3 - 4 antideriva iste funkcije f (x) \u003d x 2. Rešitev. 1) Označimo F 1 (x) \u003d x 3/3, potem je F "1 (x) \u003d 3 ∙ (x 2/3) \u003d x 2 \u003d f (x). 2) F 2 (x) \u003d x 3/3 + 1, F "2 (x) \u003d (x 3/3 + 1)" \u003d (x 3/3) "+ (1)" \u003d x 2 \u003d f ( x). 3) F 3 (x) \u003d x 3/3 - 4, F "3 (x) \u003d (x 3/3 - 4)" \u003d x 2 \u003d f (x). Na splošno je vsaka funkcija x 3/3 + C, kjer je C konstanta, primitivna funkcije x 2. To izhaja iz dejstva, da je izvod konstante enak nič. Ta primer pokaže, da je za določeno funkcijo njeno antideriva določeno dvoumno. Naj bosta F 1 (x) in F 2 (x) dve antierivati \u200b\u200biste funkcije f (x). Potem je F 1 "(x) \u003d f (x) in F" 2 (x) \u003d f (x). Izvod njihove razlike g (x) \u003d F 1 (x) - F 2 (x) je enak nič, saj je g "(x) \u003d F" 1 (x) - F "2 (x) \u003d f (x) - f (x) \u003d 0. Če je g "(x) \u003d 0 na določenem intervalu, potem je tangenta na grafu funkcije y \u003d g (x) v vsaki točki tega intervala vzporedna z osjo Ox. Zato je graf funkcije y \u003d g (x) ravna premica, vzporedna z osjo Ox, t. npr. g (x) \u003d C, kjer je C konstanta. Iz enakosti g (x) \u003d C, g (x) \u003d F 1 (x) - F 2 (x) sledi, da je F 1 (x) \u003d F 2 (x) + C Torej, če je funkcija F (x) na nekem intervalu antideriva funkcije f (x), potem so vsi antiderivati \u200b\u200bf (x) zapisani v obliki F (x) + C, kjer je C poljubna konstanta. Upoštevajte grafe vseh antiderivov določene funkcije f (x). Če je F (x) eden od antiderivov f (x), potem katero koli antideriva to funkcijo dobimo z dodajanjem konstante F (x): F (x) + C. Iz grafa dobimo grafe funkcij y \u003d F (x) + C. y \u003d F (x) s premikom vzdolž osi Oy. Z izbiro C je mogoče zagotoviti, da antiderivativni graf prehaja skozi dano točko. Bodimo pozorni na pravila za iskanje antideritivov. Spomnimo se, da se imenuje operacija iskanja izvoda za dano funkcijo diferenciacija. Pokliče se obratna operacija iskanja antideriva za določeno funkcijo povezovanje(iz latinske besede "Obnovi"). Antiderivativna tabela za nekatere funkcije lahko sestavite s tabelo izpeljank. Na primer, vedeti to (cos x) "\u003d -sin x, dobimo (-cos x) "\u003d sin x, od koder sledi, da vse primitivne funkcije greh x so zapisani kot -cos x + Ckje Z- konstanta. Razmislite o nekaterih pomenih antideritivov. 1) Funkcija: x p, p ≠ -1. Antideriva: (x p + 1) / (p + 1) + C. 2) Funkcija: 1 / x, x\u003e 0. Antideriva: ln x + C 3) Funkcija: x p, p ≠ -1. Antideriva: (x p + 1) / (p + 1) + C. 4) Funkcija: e x. Antideriva: e x + C 5) Funkcija: greh x. Antideriva: -cos x + C 6) Funkcija: (kx + b) p, p ≠ -1, k ≠ 0. Antideriva: (((kx + b) p + 1) / k (p + 1)) + C. 7) Funkcija: 1 / (kx + b), k ≠ 0. Antideriva: (1 / k) ln (kx + b) + C. 8) Funkcija: e kx + b, k ≠ 0. Antideriva: (1 / k) e kx + b + C. 9) Funkcija: sin (kx + b), k ≠ 0. Antideriva: (-1 / k) cos (kx + b). 10)
Funkcija: cos (kx + b), k ≠ 0.Antideriva: (1 / k) sin (kx + b). Pravila vključevanja je mogoče dobiti z uporabo pravila diferenciacije. Razmislimo o nekaterih pravilih. Naj F (x) in G (x) - antideriva oziroma funkcije f (x)in g (x)v določenem intervalu. Nato: 1) funkcijo F (x) ± G (x) je primitivna funkcija f (x) ± g (x); 2) funkcijo aF (x)je primitivna funkcija af (x). spletnega mesta, s popolnim ali delnim kopiranjem gradiva je potrebna povezava do vira. Reševanje integralov je lahka naloga, vendar le za elito. Ta članek je namenjen tistim, ki se želijo naučiti razumeti integrale, vendar o njih ne vedo ničesar ali skoraj nič. Integral ... Zakaj je to potrebno? Kako izračunati? Kaj so določeni in nedoločni integrali? Če je edina uporaba sestavine, ki jo poznate, pridobiti nekaj koristnega iz težko dostopnih krajev s kavljem v obliki integralne značke, potem dobrodošli! Preberite, kako rešiti integrale in zakaj brez tega ne morete. Preučujemo koncept "integralnega"Integracija je bila znana že v starem Egiptu. Seveda ne v svoji sodobni obliki, a vseeno. Od takrat so matematiki napisali veliko knjig na to temo. Posebej odlikuje Newton in Leibniz toda bistvo stvari se ni spremenilo. Kako razumeti integrale od nič? Ni šans! Če želite razumeti to temo, še vedno potrebujete osnovno znanje o osnovah matematične analize. To so temeljne informacije, ki jih boste našli na našem blogu. Neomejen integralNaj imamo nekaj funkcije f (x) .
Z drugimi besedami, integral je izpeljanka nasprotno ali antideriva. Mimogrede, o tem, kako brati v našem članku.
Za vse neprekinjene funkcije obstaja primitiv. Prav tako se antiderivatu pogosto doda stalni znak, saj se izpeljani funkciji, ki se razlikujeta s konstanto, ujemata. Postopek iskanja integrala se imenuje integracija. Preprost primer:
Da ne bomo stalno izračunavali primitivov osnovnih funkcij, jih je priročno zmanjšati v tabelo in uporabiti že pripravljene vrednosti:
Določen integralKo obravnavamo koncept integral, imamo opravka z neskončno majhnimi količinami. Integral bo pomagal izračunati površino figure, maso nehomogenega telesa, pot, ki jo je prehodil z neenakomernim gibanjem, in še veliko več. Ne smemo pozabiti, da je integral vsota neskončno velikega števila neskončno majhnih izrazov. Kot primer si predstavljajte graf funkcije. Kako najti območje figure, omejeno s funkcijskim grafom?
Uporaba integral! Zakrivljeni trapez, omejen s koordinatnimi osmi in funkcijskim grafom, razdelimo na neskončno majhne segmente. Tako bo slika razdeljena na tanke stolpce. Vsota površin stolpcev bo površina trapeza. Toda ne pozabite, da bo takšen izračun prinesel približen rezultat. Toda manjši in ožji so segmenti, natančnejši je izračun. Če jih zmanjšamo do te mere, da bo dolžina nagnjena k nič, potem seštevek površin odsekov nagiba na površino figure. To je dokončen integral, ki je napisan tako:
Mimogrede! Naši bralci imajo zdaj 10% popust Pravila za izračun integralov za lutkeLastnosti nedoločenega integralKako rešiti nedoločen integral? Tukaj razmislimo o lastnostih nedoločenega integral, ki so uporabne pri reševanju primerov.
Lastnosti določenega integral
Ugotovili smo že, da je določen integral meja vsote. Toda kako pridobiti določeno vrednost pri reševanju primera? Za to obstaja formula Newton-Leibniz:
Primeri reševanja integralovSpodaj bomo obravnavali več primerov iskanja nedoločenih integralov. Predlagamo, da samostojno razumete pretanke rešitve, in če nekaj ni jasno, postavite vprašanja v komentarjih.
Če želite utrditi gradivo, si oglejte videoposnetek o tem, kako se integrali rešujejo v praksi. Ne obupajte, če integral ni dan takoj. Vprašajte, in povedali vam bodo o izračunu integralov vsega, kar sami vedo. Z našo pomočjo bo kateri koli trojni ali krivočelni del nad zaprto površino postal vaša moč. Funkcija F (x ) klical antideriva za funkcijo f (x) v določenem intervalu, če sploh x iz tega intervala velja enakost F "(x ) = f(x ) . Na primer funkcija F (x) \u003d x 2 f (x ) = 2x od takrat F "(x) \u003d (x) 2 )" = 2x \u003d f (x). ◄ Glavna lastnost antideriva Če F (x) - antideriva za delovanje f (x) v določenem intervalu, potem funkcija f (x) ima neskončno veliko primitivov in vsi ti primitivi se lahko zapišejo kot F (x) + Ckje Z Je samovoljna konstanta.
Pravila za izračun antiderivatov
Neomejen integralNeomejen integral iz funkcije f (x) imenovan izraz F (x) + Ctj. celoto vseh antideritivov določene funkcije f (x) . Neomejen integral je označen tako: ∫ f (x) dx \u003d F (x) + C , f (x)- pokliče integrand funkcija ; f (x) dx - pokliče integrand ; x - pokliče integracijska spremenljivka ; F (x) - eno izmed antideritivov f (x) ; Z Je samovoljna konstanta. Na primer ∫ 2 x dx \u003dx 2 + Z , ∫ cosx dx \u003dgreh x + Z in tako naprej. ◄ Beseda "integral" izvira iz latinske besede celo število , kar pomeni "obnovljeno." Ob predpostavki, da je nedoločen integral 2 x , nekako obnovimo funkcijo x 2 katerega izpeljanka je 2 x . Ponovna vzpostavitev funkcije iz njene izpeljane ali, kar je podobno, iskanje nedoločenega integralnega v danem integrandu, se imenuje povezovanje to funkcijo. Integracija je obratna diferenciacija, da bi preverili, ali je integracija pravilno izvedena, je dovolj, da rezultat diferenciramo in dobimo integrand. Glavne lastnosti nedoločenega integral
(∫ f (x) dx )" \u003d f (x) . ∫ k · f (x) dx = k · ∫ f (x) dx . ∫ ( f (x) ± g (x) ) ) dx = ∫ f (x) dx ± ∫ g (x ) dx . ∫ f ( k x + b) dx = 1 / k F (k x +b ) + C . Tabela antiderivov in nedoločenih integralov
Določen integralPustite vmes [a; b] določena neprekinjena funkcija y \u003d f (x) torej določen integral od a do b funkcije f (x) imenovan primitivni prirast F (x) te funkcije, tj. $$ \\ int_ (a) ^ (b) f (x) dx \u003d F (x) | (_a ^ b) \u003d ~~ F (a) -F (b). $$ Številke ain b se imenujejo v skladu s tem nižje in vrh meje integracije. Osnovna pravila za izračun določenega integral 1. \\ (\\ int_ (a) ^ (a) f (x) dx \u003d 0 \\); 2. \\ (\\ int_ (a) ^ (b) f (x) dx \u003d - \\ int_ (b) ^ (a) f (x) dx \\); 3. \\ (\\ int_ (a) ^ (b) kf (x) dx \u003d k \\ int_ (a) ^ (b) f (x) dx, \\) kjer k - konstanta; 4. \\ (\\ int_ (a) ^ (b) (f (x) ± g (x)) dx \u003d \\ int_ (a) ^ (b) f (x) dx ± \\ int_ (a) ^ (b) g (x) dx \\); 5. \\ (\\ int_ (a) ^ (b) f (x) dx \u003d \\ int_ (a) ^ (c) f (x) dx + \\ int_ (c) ^ (b) f (x) dx \\); 6. \\ (\\ int _ (- a) ^ (a) f (x) dx \u003d 2 \\ int_ (0) ^ (a) f (x) dx \\), kjer f (x) - enakomerna funkcija; 7. \\ (\\ int _ (- a) ^ (a) f (x) dx \u003d 0 \\), kjer f (x) Je liho delovanje. Opomba . V vseh primerih se domneva, da so integrali integrirani v številskih intervalih, katerih meje so meje integracije. Geometrični in fizični pomen določenega integral
Telesna prostornina vrtenja
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Preberi: |
|---|
Priljubljeno:
Rešitev najpreprostejših trigonometričnih neenakosti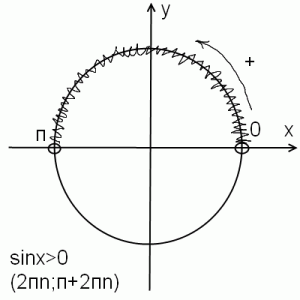
|
Novo
- Kaj je pokvarilo "krutega" barona?
- Član gibanja White
- Pot Suvorova in ekipe v domovino
- Funkcijo F (x) imenujemo antideriva za funkcijo f (x), če je F` (x) \u003d f (x) ali dF (x) \u003d f (x) dx
- Program za zmanjšanje deleža stopinj
- Podobni izrazi, njihovo zmanjšanje, primeri
- Ruski popotniki lazarev
- Reševanje nepopolnih kvadratnih enačb
- Rešitev kvadratnih enačb, formula korenin, primeri
- Koordinatna ravnina (6. razred) - Hipermarket znanja








 Bari Alibasov in skupina Integral
Bari Alibasov in skupina Integral