Odseki spletnega mesta
Izbira urednikov:
Oglaševanje
| Algoritem za iskanje enačbe tangente na funkcijskem grafu. Enačba tangente v grafu funkcije |
|
Vaša zasebnost nam je pomembna. Zaradi tega smo razvili Pravilnik o zasebnosti, ki opisuje, kako uporabljamo in shranjujemo vaše podatke. Prosimo, preberite našo politiko zasebnosti in nas obvestite, če imate kakršna koli vprašanja. Zbiranje in uporaba osebnih podatkovOsebni podatki se nanašajo na podatke, ki jih je mogoče uporabiti za identifikacijo določene osebe ali za vzpostavitev stika z njim. Od osebnih podatkov vas lahko prosimo, da kadar koli stopite v stik z nami. Spodaj je nekaj primerov vrst osebnih podatkov, ki jih lahko zbiramo, in kako jih lahko uporabljamo. Katere osebne podatke zbiramo:
Kako uporabljamo vaše osebne podatke:
Razkritje tretjim osebamInformacije, ki smo jih prejeli od vas, ne razkrivamo tretjim osebam. Izjeme:
Varstvo osebnih podatkovSprejemamo varnostne ukrepe - vključno z upravnimi, tehničnimi in fizičnimi -, da zaščitimo vaše osebne podatke pred izgubo, tatvino in zlorabo ter pred nepooblaščenim dostopom, razkritjem, spreminjanjem in uničenjem. Ohranjanje zasebnosti na ravni vašega podjetjaDa bi zagotovili, da so vaši osebni podatki varni, svojim zaposlenim sporočamo pravila zaupnosti in varnosti ter strogo spremljamo izvajanje ukrepov za zaupnost. Ta matematični program najde enačbo tangente v grafu funkcije \\ (f (x) \\) v uporabniško določeni točki \\ (a \\). Program ne prikazuje samo tangentne enačbe, ampak prikazuje tudi postopek reševanja problema. Ta spletni kalkulator je lahko uporabnikom srednje šole pri pripravi na preizkuse in izpite, staršem pri preverjanju znanja pred izpitom nadzor nad rešitvijo mnogih problemov iz matematike in algebre. Ali pa je morda predrago, če bi najeli mentorja ali kupili nove učbenike? Ali pa želite, da domače naloge iz matematike ali algebre opravite čim hitreje? V tem primeru lahko uporabite tudi naše programe s podrobno rešitev. Tako lahko sami izvajate usposabljanje in / ali usposabljanje mlajših bratov ali sester, hkrati pa se bo izboljšala stopnja izobrazbe na področju nalog. Če morate najti izpeljanko funkcije, imamo za to nalogo najti izpeljanko. Če niste seznanjeni s pravili za vnašanje funkcij, priporočamo, da se seznanite z njimi. Vnesite izraz za funkcijo \\ (f (x) \\) in številko \\ (a \\) Poiščite enačbo tangenta Ugotovljeno je bilo, da se nekateri skripti, potrebni za rešitev te težave, niso naložili in program morda ne bo deloval. Da se rešitev prikaže, morate omogočiti JavaScript. Tu so navodila, kako v brskalniku omogočiti JavaScript. Ker Veliko je ljudi, ki želijo težavo rešiti, vaša prošnja je bila na vrsti. Če ti opazil napako v rešitvi, o tem lahko pišete v obrazcu za povratne informacije. Naše igre, uganke, emulatorji: Malo teorije.Koeficient črte kotaSpomnimo, da je graf linearne funkcije \\ (y \u003d kx + b \\) premica. Kliče se število \\ (k \u003d tg \\ alfa \\) neposreden naklon, kot \\ (\\ alfa \\) je kot med to premico in osjo Ox Če \\ (k\u003e 0 \\), potem \\ (0 Če \\ (kOn enačba tangenta na grafu funkcije Če točka M (a; f (a)) spada v graf funkcije y \u003d f (x) in če se na tej točki lahko nariše tangenta, ki ni pravokotna na absciso na graf funkcije, potem iz geometrijskega pomena izpeljanke izhaja, da je kotni koeficient tangente enak f "(a). Nato bomo razvili algoritem za sestavljanje enačbe tangent na grafu katere koli funkcije. Naj bo funkcija y \u003d f (x) in točka M (a; f (a)) podana na grafu te funkcije; naj se ve, da obstaja f "(a). Sestavimo enačbo tangenta na grafu določene funkcije v dani točki. Ta enačba ima kot enačba katere koli ravne črte, ki ni vzporedna z ordinatno osjo obliko y \u003d kx + b, zato je težava najti vrednosti koeficientov k in b. Vse je jasno s kotnim koeficientom k: znano je, da je k \u003d f "(a). Za izračun vrednosti b uporabimo dejstvo, da želena premica prehaja skozi točko M (a; f (a)). To pomeni, da če nadomestimo koordinate točke M v enačbo premice dobimo pravilno enakost: \\ (f (a) \u003d ka + b \\), to je \\ (b \u003d f (a) - ka \\). Ostane nadomestitev najdenih vrednosti koeficientov k in b v enačbi premice: Prejeli smo enačba tangente v grafu funkcije \\ (y \u003d f (x) \\) v točki \\ (x \u003d a \\). Algoritem za iskanje enačbe tangenta na grafu funkcije \\ (y \u003d f (x) \\) Vaša zasebnost nam je pomembna. Zaradi tega smo razvili Pravilnik o zasebnosti, ki opisuje, kako uporabljamo in shranjujemo vaše podatke. Prosimo, preberite našo politiko zasebnosti in nas obvestite, če imate kakršna koli vprašanja. Zbiranje in uporaba osebnih podatkovOsebni podatki se nanašajo na podatke, ki jih je mogoče uporabiti za identifikacijo določene osebe ali za vzpostavitev stika z njim. Od osebnih podatkov vas lahko prosimo, da kadar koli stopite v stik z nami. Spodaj je nekaj primerov vrst osebnih podatkov, ki jih lahko zbiramo, in kako jih lahko uporabljamo. Katere osebne podatke zbiramo:
Kako uporabljamo vaše osebne podatke:
Razkritje tretjim osebamInformacije, ki smo jih prejeli od vas, ne razkrivamo tretjim osebam. Izjeme:
Varstvo osebnih podatkovSprejemamo varnostne ukrepe - vključno z upravnimi, tehničnimi in fizičnimi -, da zaščitimo vaše osebne podatke pred izgubo, tatvino in zlorabo ter pred nepooblaščenim dostopom, razkritjem, spreminjanjem in uničenjem. Ohranjanje zasebnosti na ravni vašega podjetjaDa bi zagotovili, da so vaši osebni podatki varni, svojim zaposlenim sporočamo pravila zaupnosti in varnosti ter strogo spremljamo izvajanje ukrepov za zaupnost. Članek podrobno razloži definicije, geometrijski pomen izpeljanke z grafičnim zapisom. Upoštevali bomo enačbo tangentne črte s primeri, poiskali enačbe tangente na krivuljah 2 reda. Yandex.RTB R-A-339285-1 Opredelitev 1 Kot naklona ravne črte y \u003d k x + b je kot α, ki se meri iz pozitivne smeri osi x do premca y \u003d k x + b v pozitivni smeri. Na sliki je smer x označena z zeleno puščico in v obliki zelenega loka, kot naklona pa z rdečim lokom. Modra črta se nanaša na črto. Opredelitev 2 Kotni koeficient premice y \u003d k x + b se imenuje numerični koeficient k. Kotni koeficient je enak naklonu premice, z drugimi besedami, k \u003d t g α.
Sekant je črta, ki poteka skozi 2 točki funkcije f (x). Z drugimi besedami, sekant je ravna črta, ki jo potegnemo skozi kateri koli dve točki grafa dane funkcije.
Na sliki je razvidno, da je AB sekant, f (x) pa črna krivulja, α rdeč lok, kar pomeni kot naklona sekante. Ko je kotni koeficient ravne črte enak tangentu kota nagiba, je jasno, da lahko tangenta desnega trikotnika ABC najdemo z razmerjem nasprotne noge in sosednje. Opredelitev 4 Dobimo formulo za iskanje vrste sekant: k \u003d tg α \u003d BCAC \u003d f (x B) - fx A x B - x A, kjer so absces točk A in B vrednosti x A, x B in f (x A), f (x B) vrednosti deluje na teh točkah. Očitno je naklon sekant določen z enačbo k \u003d f (x B) - f (x A) x B - x A ali k \u003d f (x A) - f (x B) x A - x B, in enačba mora biti zapisano kot y \u003d f (x B) - f (x A) x B - x A x - x A + f (x A) oz. Seant graf deli vizualno na 3 dele: levo od točke A, od A do B, desno od B. Na spodnji sliki je razvidno, da obstajajo tri sekance, ki se štejejo za naključne, torej so postavljene s podobno enačbo.
Po definiciji je jasno, da črta in njen sekant v tem primeru sovpadata. Seant lahko večkrat prečka graf določene funkcije. Če obstaja enačba oblike y \u003d 0 za sekant, potem je število presečišč s sinusoidom neskončno. Opredelitev 5 Tangenta na grafu funkcije f (x) pri x 0; f (x 0) je premica, ki poteka skozi dano točko x 0; f (x 0), z odsekom, ki ima veliko x vrednosti blizu x 0. Primer 1 Podrobno razmislite o spodnjem primeru. Potem je jasno, da se v točki s koordinatami (1; 2) premica, definirana s funkcijo y \u003d x + 1, šteje za tangentno na y \u003d 2 x. Za jasnost je treba upoštevati grafe z vrednostmi, ki so blizu (1; 2). Funkcija y \u003d 2 x je označena s črno, modra črta je tangenta, rdeča pika je presečišče.
Očitno se y \u003d 2 x združi s črto y \u003d x + 1. Za določitev tangente je treba upoštevati vedenje tangente A B z neskončnim pristopom točke B do točke A. Za jasnost predstavljamo sliko.
Sekant AB, označen z modro črto, se nagiba k položaju samega tangente, kot naklona sekanta α pa se začne nagibati pod kotom nagiba tangenta α x. Opredelitev 6 Tangenta na grafu funkcije y \u003d f (x) v točki A je mejni položaj sesanca A B pri B, ki teži k A, to je B → A. Zdaj se obrnemo na upoštevanje geometričnega pomena izpeljane funkcije na neki točki. Preidimo na obravnavo sekantnega AB v funkciji f (x), kjer sta A in B s koordinatama x 0, f (x 0) in x 0 + ∆ x, f (x 0 + ∆ x) in ∆ x označena kot prirastek argumenta . Zdaj bo funkcija dobila obliko ∆ y \u003d ∆ f (x) \u003d f (x 0 + ∆ x) - f (∆ x). Za jasnost navajamo primer.
Razmislimo o dobljenem pravem trikotniku A B C. Za rešitev uporabimo definicijo tangent, torej dobimo razmerje ∆ y ∆ x \u003d t g α. Iz definicije tangente izhaja, da je lim Δ x → 0 Δ y Δ x \u003d t g α x. S pravilom izpeljanke v točki imamo, da se izpeljanka f (x) v točki x 0 imenuje meja razmerij prirasta funkcije do prirasta argumenta, kjer je ∆ x → 0, potem označujemo kot f (x 0) \u003d lim ∆ x → 0 ∆ y ∆ x . Iz tega sledi, da je f "(x 0) \u003d lim Δ x → 0 Δ y Δ x \u003d t g α x \u003d k x, kjer je k x označen s tangento kot kotni koeficient. To pomeni, da dobimo, da f '(x) lahko obstaja v točki x 0, poleg tega pa tudi tangenta na dani graf funkcije v stični točki, ki je enaka x 0, f 0 (x 0), kjer je vrednost kotnega koeficienta tangenta v točki enaka izpeljani v točki x 0. Potem dobimo, da je k x \u003d f "(x 0). Geometrični pomen izpeljane funkcije na neki točki je podan koncept obstoja tangente na grafu v isti točki. Za pisanje enačbe katere koli črte na ravnini je potrebno imeti kotni koeficient s točko, skozi katero gre. Njegova oznaka se v križišču vzame kot x 0. Enačba tangenta na grafu funkcije y \u003d f (x) v točki x 0, f 0 (x 0) ima obliko y \u003d f "(x 0) · x - x 0 + f (x 0). To pomeni, da lahko končna vrednost izpeljane f "(x 0) določa položaj tangente, to je navpično, pod pogojem, da je x x x x 0 + 0 f" (x) \u003d ∞ in lim x → x 0 - 0 f "(x ) \u003d ∞ ali sploh ne pod pogojem lim x → x 0 + 0 f "(x) ≠ lim x → x 0 - 0 f" (x). Lokacija tangente je odvisna od vrednosti njenega kotnega koeficienta kx \u003d f "(x 0). Ko je vzporedno z osjo x, dobimo kk \u003d 0, ko je vzporedno s k o - kx \u003d ∞, oblika tangentne enačbe x \u003d x 0 pa se poveča kot kx\u003e 0, se zmanjša pri kx< 0 . Primer 2 V točki s koordinatami (1; 3) z določitvijo kota naklona sestavite enačbo tangenta na grafu funkcije y \u003d e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3. Rešitev S hipotezo imamo, da je funkcija določena za vsa realna števila. Dobimo, da je točka s koordinatami, ki jih poda pogoj (1; 3), tangentna točka, potem je x 0 \u003d - 1, f (x 0) \u003d - 3. Najti je treba izpeljanko na točki z vrednostjo - 1. To dobimo y "\u003d ex + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3" \u003d \u003d ex + 1 "+ x 3 3" - 6 - 3 3 x "- 17 - 3 3" \u003d ex + 1 + x 2 - 6 - 3 3 y "(x 0) \u003d y" (- 1) \u003d e - 1 + 1 + - 1 2 - 6 - 3 3 \u003d 3 3 Vrednost f '(x) na mestu tangente je nagib tangente, ki je enak naklonu. Potem je k x \u003d t g α x \u003d y "(x 0) \u003d 3 3 Iz tega sledi, da je α x \u003d a r c t g 3 3 \u003d π 6 Odgovor je:tangenta enačba ima obliko y \u003d f "(x 0) · x - x 0 + f (x 0) y \u003d 3 3 (x + 1) - 3 y \u003d 3 3 x - 9 - 3 3 Za jasnost dajemo primer v grafični ilustraciji. Črna barva se uporablja za graf izvirne funkcije, modra barva je slika tangente, rdeča pika je točka dotika. Slika desno prikazuje povečan pogled.
Primer 3 Ugotovite, ali v grafu določene funkcije obstaja tangenta Rešitev S hipotezo imamo, da se domenska definicija določene funkcije šteje za množico vseh realnih števil. Obrnimo se k iskanju izpeljanke y "\u003d 3 · x - 1 5 + 1" \u003d 3 · 1 5 · (x - 1) 1 5 - 1 \u003d 3 5 · 1 (x - 1) 4 5 Če je x 0 \u003d 1, potem f '(x) ni določen, vendar so meje zapisane kot lim x → 1 + 0 3 5 · 1 (x - 1) 4 5 \u003d 3 5 · 1 (+ 0) 4 5 \u003d 3 5 1 + 0 \u003d + ∞ in lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 \u003d 3 5 · 1 (- 0) 4 5 \u003d 3 5 · 1 + 0 \u003d + ∞, kar pomeni obstoj navpična tangenta na (1; 1). Odgovor je: enačba ima obliko x \u003d 1, kjer bo naklon kota π 2. Zaradi jasnosti upodabljajte grafično.
Primer 4 Poiščite točke grafa funkcije y \u003d 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, kjer
Rešitev Treba je biti pozoren na obseg. S hipotezo imamo, da je funkcija določena na množici vseh realnih števil. Odpremo modul in rešimo sistem z intervali x ∈ - ∞; 2 in [- 2; + ∞). To dobimo y \u003d - 1 15 x 3 + 18 x 2 + 105 x + 176, x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12, x ∈ [- 2; + ∞) Treba je razlikovati funkcijo. To imamo y "\u003d - 1 15 x 3 + 18 x 2 + 105 x + 176", x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [- 2; + ∞) ⇔ y" \u003d - 1 5 (x 2 + 12 x + 35), x ∈ - ∞; - 2 1 5 x 2 - 4 x + 3, x ∈ [- 2; + ∞) Kadar je x \u003d - 2, izpeljanka ne obstaja, ker enosmerne meje na tej točki niso enake: lim x → - 2 - 0 y "(x) \u003d lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 \u003d - 1 5 (- 2) 2 + 12 (- 2) + 35 \u003d - 3 lim x → - 2 + 0 y "(x) \u003d lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) \u003d 1 5 - 2 2 - 4 - 2 + 3 \u003d 3 Izračunamo vrednost funkcije v točki x \u003d - 2, kjer dobimo to
Ko je x ∈ - ∞; - 2, potem - 1 5 (x 2 + 12 x + 35) \u003d 0, za x ∈ (- 2; + ∞) dobimo 1 5 (x 2 - 4 x + 3) \u003d 0. 1 5 (x 2 + 12 x + 35) \u003d 0 D \u003d 12 2 - 4 · 35 \u003d 144 - 140 \u003d 4 x 1 \u003d - 12 + 4 2 \u003d - 5 ∈ - ∞; - 2 x 2 \u003d - 12 - 4 2 \u003d - 7 ∈ - ∞; - 2 1 5 (x 2 - 4 x + 3) \u003d 0 D \u003d 4 2 - 4 · 3 \u003d 4 x 3 \u003d 4 - 4 2 \u003d 1 ∈ - 2; + ∞ x 4 \u003d 4 + 4 2 \u003d 3 ∈ - 2; + ∞ Izračunamo ustrezne vrednosti funkcij y 1 \u003d y - 5 \u003d 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 \u003d 8 5 y 2 \u003d y (- 7) \u003d 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 \u003d 4 3 y 3 \u003d y (1) \u003d 1 15 1 + 2 3 - 4 5 · 1 2 - 16 5 · 1 - 26 5 + 3 1 + 2 \u003d 8 5 y 4 \u003d y (3) \u003d 1 15 3 + 2 3 - 4 5 · 3 2 - 16 5 · 3 - 26 5 + 3 3 + 2 \u003d 4 3 Od tod - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 veljajo za iskane točke v funkcijskem grafu. Razmislite o grafičnem prikazu rešitve.
Črna črta je funkcijski graf, rdeče pike so točke dotika.
Prva enačba nima korenin, saj je diskriminator manj kot nič. To pišemo 1 5 x 2 + 12 x + 35 \u003d 8 5 x 2 + 12 x + 43 \u003d 0 D \u003d 12 2 - 4 · 43 \u003d - 28< 0 Druga enačba ima torej dve resnični korenini 1 5 (x 2 - 4 x + 3) \u003d 8 5 x 2 - 4 x - 5 \u003d 0 D \u003d 4 2 - 4 · (- 5) \u003d 36 x 1 \u003d 4 - 36 2 \u003d - 1 ∈ - 2; + ∞ x 2 \u003d 4 + 36 2 \u003d 5 ∈ - 2; + ∞ Pojdimo na iskanje vrednosti funkcije. To dobimo y 1 \u003d y (- 1) \u003d 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 \u003d 4 15 y 2 \u003d y (5) \u003d 1 15 5 + 2 3 - 4 5 · 5 2 - 16 5 · 5 - 26 5 + 3 5 + 2 \u003d 8 3 Točke z vrednostmi - 1; 4 15, 5; 8 3 so točke, v katerih so tangente vzporedne z premico y \u003d 8 5 x + 4. Odgovor je:črna črta je graf funkcije, rdeča črta je graf y \u003d 8 5 x + 4, modra črta je tangent v točkah - 1; 4 15, 5; 8 3.
Za določene funkcije je lahko neskončno število tangent. Primer 5 Napišite enačbe vseh razpoložljivih tangentnih funkcij y \u003d 3 cos 3 2 x - π 4 - 1 3, ki so nameščene pravokotno na ravno y \u003d - 2 x + 1 2. Rešitev Za sestavljanje enačbe tangenta je potrebno najti koeficient in koordinate tangente, ki temeljijo na pogoju pravokotnosti črt. Opredelitev je naslednja: produkt kotnih koeficientov, ki so pravokotni na ravne črte, je enak - 1, to pomeni, da je zapisan kot k x · k ⊥ \u003d - 1. Iz pogoja imamo, da je kotni koeficient pravokoten na ravno črto in je enak k ⊥ \u003d - 2, potem je k x \u003d - 1 k ⊥ \u003d - 1 - 2 \u003d 1 2. Zdaj morate najti koordinate točk dotika. Poiskati morate x, po katerem je njegova vrednost za dano funkcijo. Upoštevajte, da iz geometrijskega pomena izpeljanke v točki To dobimo y "(x 0) \u003d 3 cos 3 2 x 0 - π 4 - 1 3" \u003d 3 · - sin 3 2 x 0 - π 4 · 3 2 x 0 - π 4 "\u003d \u003d - 3 · sin 3 2 x 0 - π 4 · 3 2 \u003d - 9 2 · sin 3 2 x 0 - π 4 ⇒ kx \u003d y "(x 0) ⇔ - 9 2 · sin 3 2 x 0 - π 4 \u003d 1 2 ⇒ sin 3 2 x 0 - π 4 \u003d - 1 9 Ta trigonometrična enačba bo uporabljena za izračun ordinat tačk. 3 2 x 0 - π 4 \u003d a r c sin - 1 9 + 2 πk ali 3 2 x 0 - π 4 \u003d π - a r c sin - 1 9 + 2 πk 3 2 x 0 - π 4 \u003d - a r c sin 1 9 + 2 πk ali 3 2 x 0 - π 4 \u003d π + a r c sin 1 9 + 2 πk x 0 \u003d 2 3 π 4 - a r c sin 1 9 + 2 πk ali x 0 \u003d 2 3 5 π 4 + a r c sin 1 9 + 2 πk, k ∈ Z Z je množica celih števil. Najdene x točke dotika. Zdaj morate iti na iskanje vrednosti y: y 0 \u003d 3 cos 3 2 x 0 - π 4 - 1 3 y 0 \u003d 3 · 1 - sin 2 3 2 x 0 - π 4 - 1 3 ali y 0 \u003d 3 · - 1 - sin 2 3 2 x 0 - π 4 - 1 3 y 0 \u003d 3 · 1 - - 1 9 2 - 1 3 ali y 0 \u003d 3 · - 1 - - 1 9 2 - 1 3 y 0 \u003d 4 5 - 1 3 ali y 0 \u003d - 4 5 + 1 3 Iz tega sledi, da je 2 3 π 4 - a r c sin 1 9 + 2 πk; 4 5 - 1 3, 2 3 5 π 4 + a r c sin 1 9 + 2 πk; - 4 5 + 1 3 so točke dotika. Odgovor je: potrebne enačbe zapišemo kot y \u003d 1 2 x - 2 3 π 4 - lok sin 1 9 + 2 πk + 4 5 - 1 3, y \u003d 1 2 x - 2 3 5 π 4 + lok sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z Za vizualno sliko upoštevajte funkcijo in tangento na koordinatni črti. Na sliki je razvidno, da se lokacija funkcije giblje med [- 10; 10], kjer je črna črta graf funkcije, so modre črte tangent, ki so pravokotne na dano črto oblike y \u003d - 2 x + 1 2. Rdeče pike so točke dotika.
Kanonične enačbe krivulj drugega reda niso edinstvene funkcije. Enačbe tangente zanje so sestavljene po dobro znanih shemah. Tangenta na krogZa določitev kroga s središčem na x c e n t e r; y c e n t e r in s polmerom R se uporablja formula x - x c e n t e r 2 + y - y c e n t e r 2 \u003d R 2. To enakost lahko zapišemo kot združitev dveh funkcij: y \u003d R 2 - x - x c e n t e r 2 + y c e n t e r y \u003d - R 2 - x - x c e n t e r 2 + y c e n t e r Prva funkcija je nameščena na vrhu, druga pa na dnu, kot je prikazano na sliki.
Sestaviti enačbo kroga v točki x 0; y 0, ki se nahaja v zgornjem ali spodnjem polkrogu, najdemo enačbo grafa funkcije oblike y \u003d R 2 - x - x c e n t e r 2 + y c e n t e r ali y \u003d - R 2 - x - x c e n t e r 2 + y c e n t e r na navedeni točki. Ko v točkah x c e n t e r; y c e n t e r + R in x c e n t e r; y c e n t e r - R, tangente lahko damo z enačbami y \u003d y c e n t e r + R in y \u003d y c e n t e r - R in v točkah x c e n t e r + R; y c e n t e r in
Tangenta do elipseKadar ima elipsa središče na točki x c e n t e r; y c e n t t r r s pol osi a in b, potem ga lahko določimo z enačbo x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 \u003d 1. Elipso in krog lahko označimo s kombinacijo dveh funkcij, in sicer: zgornje in spodnje pol-elipse. Potem to dobimo y \u003d b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y \u003d - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r
Če so tangente nameščene na konicah elipse, so vzporedne približno x ali približno y. Spodaj za jasnost razmislite na sliki.
Primer 6 Napišite enačbo tangenta na elipso x - 3 2 4 + y - 5 2 25 \u003d 1 v točkah s x, ki je enaka x \u003d 2. Rešitev Treba je najti kontaktne točke, ki ustrezajo vrednosti x \u003d 2. Nadomestimo obstoječo enačbo elipse in dobimo x - 3 2 4 x \u003d 2 + y - 5 2 25 \u003d 1 1 4 + y - 5 2 25 \u003d 1 ⇒ y - 5 2 \u003d 3 4 · 25 ⇒ y \u003d ± 5 3 2 + 5 Potem 2; 5 3 2 + 5 in 2; - 5 3 2 + 5 so točke dotika, ki pripadajo zgornji in spodnji pol elipsi. Nadaljujemo z iskanjem in reševanjem enačbe elipse glede na y. To dobimo x - 3 2 4 + y - 5 2 25 \u003d 1 y - 5 2 25 \u003d 1 - x - 3 2 4 (y - 5) 2 \u003d 25 · 1 - x - 3 2 4 y - 5 \u003d ± 5 · 1 - x - 3 2 4 y \u003d 5 ± 5 2 4 - x - 3 2 Očitno je zgornja pol-elipsa nastavljena s funkcijo oblike y \u003d 5 + 5 2 4 - x - 3 2, spodnja y \u003d 5 - 5 2 4 - x - 3 2. Uporabljamo standardni algoritem, da sestavimo enačbo tangente na grafu funkcije v točki. Pišemo, da je enačba za prvo tangento v točki 2; 5 3 2 + 5 bo imel obliko y "\u003d 5 + 5 2 4 - x - 3 2" \u003d 5 2 · 1 2 4 - (x - 3) 2 · 4 - (x - 3) 2 "\u003d \u003d - 5 2 · x - 3 4 - ( x - 3) 2 ⇒ y "(x 0) \u003d y" (2) \u003d - 5 2 · 2 - 3 4 - (2 - 3) 2 \u003d 5 2 3 ⇒ y \u003d y "(x 0) · x - x 0 + y 0 ⇔ y \u003d 5 2 3 (x - 2) + 5 3 2 + 5 Dobimo, da je enačba druge tangenta z vrednostjo v točki y "\u003d 5 - 5 2 4 - (x - 3) 2" \u003d - 5 2 · 1 2 4 - (x - 3) 2 · 4 - (x - 3) 2 "\u003d \u003d 5 2 · x - 3 4 - (x - 3) 2 ⇒ y "(x 0) \u003d y" (2) \u003d 5 2 · 2 - 3 4 - (2 - 3) 2 \u003d - 5 2 3 ⇒ y \u003d y "(x 0) · x - x 0 + y 0 ⇔ y \u003d - 5 2 3 (x - 2) - 5 3 2 + 5 Grafično se tangente označijo na naslednji način:
Hiperbola tangentaKadar ima hiperbola središče na točki x c e n t e r; y c e n t e r in točki x c e n t e r + α; y c e n t e r in x c e n t e r - α; y c e n t e r, pride do neenakosti x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 \u003d 1, če je s točki x c e n t e r; y c e n t e r + b in x c e n t e r; y c e n t t e r - b, potem ga definiramo z neenakostjo x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 \u003d - 1.
Hiperbolo lahko predstavljamo kot dve kombinirani funkciji obrazca y \u003d ba · (x - xcenter) 2 - a 2 + ycentery \u003d - ba · (x - xcenter) 2 - a 2 + ycenter ali y \u003d ba · (x - xcenter) 2 + a 2 + ycentery \u003d - ba (x - xcenter) 2 + a 2 + ycenter
V prvem primeru imamo, da so tangente vzporedne z σ, v drugem pa vzporedne z σ. Iz tega sledi, da je za iskanje enačbe tangente s hiperbolo potrebno ugotoviti, kateri funkciji pripada tangentna točka. Da bi to določili, je treba enačbe nadomestiti in jih preveriti glede identitete. Primer 7 Naredimo enačbo tangenta na hiperbolo x - 3 2 4 - y + 3 2 9 \u003d 1 v točki 7; - 3 3 - 3. Rešitev Potrebno je preoblikovati zapis rešitve za iskanje hiperbole z uporabo 2 funkcij. To dobimo x - 3 2 4 - y + 3 2 9 \u003d 1 ⇒ y + 3 2 9 \u003d x - 3 2 4 - 1 ⇒ y + 3 2 \u003d 9 x - 3 2 4 - 1 ⇒ y + 3 \u003d 3 2 x - 3 2 - 4 in l in y + 3 \u003d - 3 2 · x - 3 2 - 4 ⇒ y \u003d 3 2 · x - 3 2 - 4 - 3 y \u003d - 3 2 · x - 3 2 - 4 - 3 Ugotoviti je treba, kateri funkciji pripada dana točka s koordinatami 7; - 3 3 - 3. Očitno je za preverjanje prve funkcije potrebno y (7) \u003d 3 2 · (7 - 3) 2 - 4 - 3 \u003d 3 3 - 3 ≠ - 3 3 - 3, potem točka ne pripada grafu, saj enakost ne drži. Za drugo funkcijo imamo, da je y (7) \u003d - 3 2 · (7 - 3) 2 - 4 - 3 \u003d - 3 3 - 3 ≠ - 3 3 - 3, kar pomeni, da točka pripada danemu grafu. Od tod je treba poiskati kotni koeficient. To dobimo y "\u003d - 3 2 · (x - 3) 2 - 4 - 3" \u003d - 3 2 · x - 3 (x - 3) 2 - 4 ⇒ kx \u003d y "(x 0) \u003d - 3 2 · x 0 - 3 x 0 - 3 2 - 4 x 0 \u003d 7 \u003d - 3 2 · 7 - 3 7 - 3 2 - 4 \u003d - 3 Odgovor je: tangentna enačba je lahko predstavljena kot y \u003d - 3 · x - 7 - 3 3 - 3 \u003d - 3 · x + 4 3 - 3 Vizualno prikazan na naslednji način:
Parabolična tangentaZa sestavljanje enačbe tangenta na parabolo y \u003d ax 2 + bx + c v točki x 0, y (x 0) morate uporabiti standardni algoritem, potem bo enačba dobila obliko y \u003d y "(x 0) · x - x 0 + y ( x 0) Takšna tangenta v točki je vzporedna z o x. Parabolo x \u003d a y 2 + b y + c je treba dati kot združitev dveh funkcij. Zato moramo rešiti enačbo za y. To dobimo x \u003d ay 2 + za + c ⇔ ay 2 + za + c - x \u003d 0 D \u003d b 2 - 4 a (c - x) y \u003d - b + b 2 - 4 a (c - x) 2 ay \u003d - b - b 2 - 4 a (c - x) 2 a Grafično prikazujemo, kako:
Če želite izvedeti pripadnost točke x 0, y (x 0) funkciji, nežno ukrepajte po standardnem algoritmu. Takšna tangenta bo vzporedna z y glede na parabolo. Primer 8 Enačbo tangenta zapišemo v graf x - 2 y 2 - 5 y + 3, ko imamo tangentni kot 150 °. Rešitev Rešitev začnemo tako, da parabolo predstavljamo kot dve funkciji. To dobimo 2 y 2 - 5 y + 3 - x \u003d 0 D \u003d (- 5) 2 - 4 · (- 2) · (3 - x) \u003d 49 - 8 xy \u003d 5 + 49 - 8 x - 4 y \u003d 5 - 49 - 8 x - 4 Vrednost kotnega koeficienta je enaka vrednosti izpeljane v točki x 0 te funkcije in je enaka tangentu kota naklona. Dobili smo: k x \u003d y "(x 0) \u003d t g α x \u003d t g 150 ° \u003d - 1 3 Od tod določimo vrednost x za točke dotika. Prva funkcija bo zapisana kot y "\u003d 5 + 49 - 8 x - 4" \u003d 1 49 - 8 x ⇒ y "(x 0) \u003d 1 49 - 8 x 0 \u003d - 1 3 ⇔ 49 - 8 x 0 \u003d - 3 Očitno ni pravih korenin, saj so dobile negativno vrednost. Sklepamo, da tangenta s kotom 150 ° za takšno funkcijo ne obstaja. Druga funkcija bo zapisana kot y "\u003d 5 - 49 - 8 x - 4" \u003d - 1 49 - 8 x ⇒ y "(x 0) \u003d - 1 49 - 8 x 0 \u003d - 1 3 ⇔ 49 - 8 x 0 \u003d - 3 x 0 \u003d 23 4 ⇒ y (x 0) \u003d 5 - 49 - 8 · 23 4 - 4 \u003d - 5 + 3 4 Imamo, da so točke tangenta 23 4; - 5 + 3 4. Odgovor je: tangentna enačba ima obliko y \u003d - 1 3x - 23 4 + - 5 + 3 4 Grafično prikazujemo to na naslednji način:
Če v besedilu opazite napako, jo izberite in pritisnite Ctrl + Enter
Toda kaj se zgodi, če izpeljanka pri x 0 ne obstaja? Možni sta dve možnosti:
Tangenta enačbaVsaka nevertikalna črta je podana z enačbo oblike y \u003d kx + b, kjer je k kotni koeficient. Tangenta ni izjema in za sestavljanje njene enačbe v neki točki x 0 je dovolj, da poznamo vrednost funkcije in izpeljanke na tej točki. Naj bo podana funkcija y \u003d f (x), ki ima na odseku izpeljanko y \u003d f '(x). Nato lahko v kateri koli točki x 0 ∈ (a; b) tangenta nariše na graf te funkcije, ki ga poda enačba: y \u003d f '(x 0) · (x - x 0) + f (x 0) Tu je f '(x 0) vrednost izpeljane v točki x 0, f (x 0) pa vrednost same funkcije.
Enačba tangenta je y \u003d f '(x 0) · (x - x 0) + f (x 0). Točka x 0 \u003d 2 nam je dana, vendar bo treba izračunati vrednosti f (x 0) in f '(x 0). Najprej poiščite vrednost funkcije. Tu je vse enostavno: f (x 0) \u003d f (2) \u003d 2 3 \u003d 8;
Tokrat ne bomo podrobno opisali vsakega dejanja - navedli bomo le ključne korake. Imamo: f (x 0) \u003d f (π / 2) \u003d 2sin (π / 2) + 5 \u003d 2 + 5 \u003d 7; Tangenta enačba: y \u003d 0 · (x - π / 2) + 7 ⇒ y \u003d 7 V slednjem primeru se je črta izkazala za vodoravno, ker njegov kotni koeficient k \u003d 0. S tem ni nič narobe - le naleteli smo na skrajno točko. |
| Preberi: |
|---|
Priljubljeno:
Rešitev najpreprostejših trigonometričnih neenakosti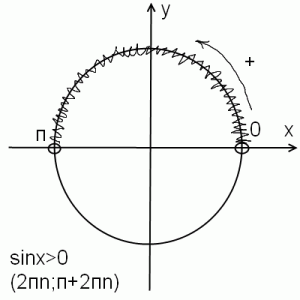
|
Novo
- Kaj je pokvarilo "krutega" barona?
- Član gibanja White
- Pot Suvorova in ekipe v domovino
- Funkcijo F (x) imenujemo antideriva za funkcijo f (x), če je F` (x) \u003d f (x) ali dF (x) \u003d f (x) dx
- Program za zmanjšanje deleža stopinj
- Podobni izrazi, njihovo zmanjšanje, primeri
- Ruski popotniki lazarev
- Reševanje nepopolnih kvadratnih enačb
- Rešitev kvadratnih enačb, formula korenin, primeri
- Koordinatna ravnina (6. razred) - Hipermarket znanja