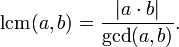Odseki spletnega mesta
Izbira urednikov:
Oglaševanje
| Kako preveriti kvadratno enačbo. Rešitev kvadratnih enačb, formula korenin, primeri. Kvadratna enačba s parametrom |
|
V tem članku obravnavamo rešitev nepopolnih kvadratnih enačb. Najprej pa ponovimo, kaj enačbe imenujemo kvadratne. Enačba oblike ax 2 + bx + c \u003d 0, kjer je x spremenljivka, koeficienti a, b in c pa nekatera števila, in ≠ 0, imenujemo kvadrat. Ker vidimo, da koeficient pri x 2 ni enak nič, zato so lahko koeficienti pri x ali prosti izraz enaki nič, v tem primeru dobimo nepopolno kvadratno enačbo. Nepopolne kvadratne enačbe so tri vrste: 1) Če je b \u003d 0, c ≠ 0, potem je os 2 + c \u003d 0; 2) Če je b ≠ 0, c \u003d 0, potem je os 2 + bx \u003d 0; 3) Če je b \u003d 0, c \u003d 0, potem je os 2 \u003d 0.
Za rešitev enačbe prenesemo prosti izraz s desno stran enačbe os 2 \u003d ‒s. Ker je ≠ 0, obe strani enačbe delimo z a, potem je x 2 \u003d ‒s / a. Če je ‒с / а\u003e 0, potem ima enačba dve korenini x \u003d ± √ (–c / a). Če ‒c / a< 0, то это уравнение решений не имеет. Более наглядно решение данных уравнений представлено на схеме. Poskusimo ugotoviti primere, kako rešiti takšne enačbe. Primer 1. Rešimo enačbo 2x 2 - 32 \u003d 0. Odgovor: x 1 \u003d - 4, x 2 \u003d 4. Primer 2. Rešimo enačbo 2x 2 + 8 \u003d 0. Odgovor: enačba nima rešitve.
Da rešimo enačbo ax 2 + bx \u003d 0, jo faktoriramo, torej oklepaj x, dobimo x (ax + b) \u003d 0. Izdelek je nič, če je vsaj eden od faktorjev nič. Potem je x \u003d 0 ali ax + b \u003d 0. Rešimo enačbo ax + b \u003d 0, dobimo ax \u003d - b, od kod x \u003d - b / a. Enačba oblike ax 2 + bx \u003d 0 ima vedno dva korena x 1 \u003d 0 in x 2 \u003d - b / a. Poglejte, kako na diagramu izgleda rešitev takšnih enačb. Svoje znanje popravljamo na konkretnem primeru. Primer 3. Rešimo enačbo 3x 2 - 12x \u003d 0. x (3x - 12) \u003d 0 x \u003d 0 ali 3x - 12 \u003d 0 Odgovor: x 1 \u003d 0, x 2 \u003d 4.
Če je os 2 \u003d 0, potem je x 2 \u003d 0. Enačba ima dva enaka korena x 1 \u003d 0, x 2 \u003d 0. Za jasnost upoštevajte shemo. Pri reševanju primera 4 bomo preverili, ali enačbe te oblike rešujemo zelo preprosto. Primer 4 Rešimo enačbo 7x 2 \u003d 0. Odgovor: x 1, 2 \u003d 0. Ni vedno takoj jasno, kakšno nepopolno kvadratno enačbo moramo rešiti. Razmislite o naslednjem primeru. Primer 5 Reši enačbo
Obe strani enačbe pomnožimo s skupnim imenovalcem, to je 30
Skrajšajte 5 (5x 2 + 9) - 6 (4x 2 - 9) \u003d 90. Oklepaji 25x 2 + 45 - 24x 2 + 54 \u003d 90. Podamo podobno Premaknite se 99 z leve strani enačbe v desno in spremenite znak v nasprotno Odgovor: korenin ni. Preučili smo, kako se rešujejo delne kvadratne enačbe. Upam, da zdaj s takšnimi nalogami ne boste imeli težav. Bodite previdni pri določanju vrste nepopolne kvadratne enačbe, potem boste uspeli. Če imate vprašanja na to temo, se prijavite na moje lekcije, težave bomo rešili skupaj. spletnega mesta, s popolnim ali delnim kopiranjem gradiva je potrebna povezava do vira. Nadaljevanje teme »Reševanje enačb« vas bo v tem članku seznanilo s kvadratnimi enačbami. Vse bomo podrobno preučili: bistvo in pojem kvadratne enačbe, postavili bomo spremljajoče izraze, analizirali bomo rešitev rešitve za nepopolne in popolne enačbe, seznanili se bomo s korensko formulo in diskriminatorno, vzpostavili bomo razmerje med koreninami in koeficienti in seveda dali jasno rešitev praktičnih primerov. Yandex.RTB R-A-339285-1 Kvadratna enačba, njene vrsteOpredelitev 1Kvadratna enačba Ali je enačba zapisana kot a x 2 + b x x + c \u003d 0kje x - spremenljivka, a, b in c - nekaj številk, medtem ko ane nič. Pogosto kvadratne enačbe imenujemo tudi enačbe druge stopnje, saj je v bistvu kvadratna enačba algebrska enačba druge stopnje. Navajamo primer za ponazoritev dane definicije: 9 · x 2 + 16 · x + 2 \u003d 0; 7,5 x 2 + 3, 1 x + 0, 11 \u003d 0 itd. So kvadratne enačbe. Opredelitev 2 Številke a, b in c Ali so koeficienti kvadratne enačbe a x 2 + b x x + c \u003d 0, koeficient a nosi ime prvega, višjega ali koeficient pri x 2, b - drugi koeficient ali koeficient pri x, in c imenovan svobodni član. Na primer v kvadratni enačbi 6 x 2 - 2 x 11 \u003d 0 višji koeficient je 6, drugi koeficient je − 2 , in prost termin je − 11 . Bodite pozorni na dejstvo, da ko koeficienti bin / ali c sta negativna, potem se uporabi kratek zapis zapisa oblike 6 x 2 - 2 x 11 \u003d 0pa ne 6 x 2 + (- 2) x + (- 11) \u003d 0. Pojasnimo tudi ta vidik: če so koeficienti a in / ali b so enaki 1 ali − 1 , potem morda ne bodo izrecno sodelovali pri pisanju kvadratne enačbe, kar je razloženo s posebnostmi pisanja navedenih numeričnih koeficientov. Na primer v kvadratni enačbi y 2 - y + 7 \u003d 0 višji koeficient je 1, drugi koeficient pa − 1 . Zmanjšane in neredduirane kvadratne enačbeGlede na vrednost prvega koeficienta se kvadratne enačbe delijo na reducirane in nereduktivne. Opredelitev 3 Kvadratna enačba Je kvadratna enačba, kjer je vodilni koeficient 1. Pri drugih vrednostih najvišjega koeficienta se kvadratna enačba ne zmanjša. Navajamo primere: zmanjšajo se kvadratne enačbe x 2 - 4 · x + 3 \u003d 0, x 2 - x - 4 5 \u003d 0, v katerih je najvišji koeficient 1. 9 x 2 - x - 2 \u003d 0 - neredducirana kvadratna enačba, pri čemer se prvi koeficient razlikuje od 1 . Kakršno koli neredducirano kvadratno enačbo lahko spremenimo v zmanjšano enačbo, če oba dela delimo na prvi koeficient (enakovredno preoblikovanje). Preoblikovana enačba bo imela enake korenine kot dana neurejena enačba ali pa sploh nima korenin. Upoštevanje konkretnega primera nam bo omogočilo, da jasno pokažemo izvajanje prehoda iz neredduirane kvadratne enačbe na dano. Primer 1 Podana je enačba: 6x2 + 18x - 7 \u003d 0 . Potrebno je pretvoriti izvirno enačbo v dani obrazec. Rešitev Po zgornji shemi delimo oba dela prvotne enačbe z vodilnim koeficientom 6. Nato dobimo: (6 · x 2 + 18 · x - 7): 3 \u003d 0: 3, in to je isto kot: (6 * x 2): 3 + (18 * x): 3 - 7: 3 \u003d 0 in nadalje: (6: 6) x 2 + (18: 6) x - 7: 6 \u003d 0. Od tod: x 2 + 3 x - 1 1 6 \u003d 0. Tako dobimo enačbo, ki je enaka dani. Odgovor je: x 2 + 3 x - 1 1 6 \u003d 0. Popolne in nepopolne kvadratne enačbeObrnimo se k definiciji kvadratne enačbe. V njej smo to razjasnili a ≠ 0. Podoben pogoj je nujen za enačbo a x 2 + b x x + c \u003d 0 je bil ravno kvadrat, ker kdaj a \u003d 0 v bistvu pretvori v linearno enačbo bx + c \u003d 0. V primeru, ko koeficienti b in cso enake nič (kar je možno, posamično in skupaj), kvadratna enačba se imenuje nepopolna. Opredelitev 4 Nepopolna kvadratna enačba Ali je takšna kvadratna enačba a x 2 + b x x + c \u003d 0,kjer je vsaj eden od koeficientov bin c(ali oboje) je nič. Popolna kvadratna enačba - kvadratna enačba, v kateri vsi numerični koeficienti niso enaki nič. Pogovorimo se, zakaj so te vrste kvadratnih enačb dobile takšna imena. Pri b \u003d 0 ima kvadratna enačba obliko a x 2 + 0 x x c \u003d 0to je isto kot a x 2 + c \u003d 0. Na c \u003d 0 kvadratna enačba se zapiše kot a x 2 + b x x 0 \u003d 0kar je enakovredno a x 2 + b x \u003d 0. Na b \u003d 0 in c \u003d 0 enačba bo imela obliko a x 2 \u003d 0. Dobljene enačbe se od polne kvadratne enačbe razlikujejo po tem, da njihovi levi deli ne vsebujejo niti izraza s spremenljivko x, niti prostega izraza ali obojega hkrati. Pravzaprav je to dejstvo po tej vrsti enačb dobilo ime - nepopolno. Na primer, x 2 + 3 · x + 4 \u003d 0 in - 7 · x 2 - 2 · x + 1, 3 \u003d 0 so polne kvadratne enačbe; x 2 \u003d 0, - 5 x 2 \u003d 0; 11x 2 + 2 \u003d 0, - x 2 - 6x \u003d 0 so nepopolne kvadratne enačbe. Reševanje nepopolnih kvadratnih enačbZgornja definicija omogoča razlikovanje naslednjih vrst nepopolnih kvadratnih enačb:
Razmislimo o zaporedju rešitve vsake vrste nepopolnih kvadratnih enačb. Rešitev enačbe a · x 2 \u003d 0Kot že omenjeno, koeficienti ustrezajo tej enačbi b in cenako nič. Enačba a x 2 \u003d 0 možno je pretvoriti v enačbo, ki je enakovredna njej x 2 \u003d 0ki jo dobimo tako, da obe strani prvotne enačbe delimo s številom ani enako nič. Očitno dejstvo je, da je koren enačbe x 2 \u003d 0 nič zato 0 2 = 0 . Ta enačba nima drugih korenin, kar je razloženo z lastnostmi stopnje: za poljubno število strni enaka nič, neenakost je resnična p 2\u003e 0, iz česar izhaja, da s p ≠ 0 enakost p 2 \u003d 0nikoli ne bo dosežen. Opredelitev 5 Tako za nepopolno kvadratno enačbo a · x 2 \u003d 0 obstaja enkraten koren x \u003d 0. Primer 2 Na primer, rešimo nepopolno kvadratno enačbo - 3 x 2 \u003d 0. Enačba mu je enakovredna x 2 \u003d 0njen edini koren je x \u003d 0, potem ima izvirna enačba en sam koren - nič. Na kratko je odločitev sprejeta na naslednji način: - 3 x 2 \u003d 0, x 2 \u003d 0, x \u003d 0. Rešitev enačbe a · x 2 + c \u003d 0Naslednji korak je reševanje nepopolnih kvadratnih enačb, kjer je b \u003d 0, c ≠ 0, torej enačbe obrazca a x 2 + c \u003d 0. To enačbo transformiramo tako, da izraz premaknemo iz enega dela enačbe v drugega, spremenimo znak v nasprotno in oba dela enačbe delimo s številom, ki ni enako nič:
Naše preobrazbe so enakovredne, tako da je dobljena enačba enakovredna izvirniku in to dejstvo omogoča sklep o koreninah enačbe. Iz kakšnih pomenov a in cvrednost izraza je odvisna od c a: lahko ima znak minus (na primer, če a \u003d 1 in c \u003d 2, nato - c a \u003d - 2 1 \u003d - 2) ali znak plus (na primer, če a \u003d - 2 in c \u003d 6, potem - c a \u003d - 6 - 2 \u003d 3); ni nič, ker c ≠ 0. Poglejmo se na situacijah, ko - c a< 0 и - c a > 0 . V primeru, ko - c a< 0 , уравнение x 2 = - c a не будет иметь корней. Утверждая это, мы опираемся на то, что квадратом любого числа является число неотрицательное. Из сказанного следует, что при - c a < 0 ни для какого числа str enakost p 2 \u003d - c a ne more biti resnična. Vse je drugače, ko - c a\u003e 0: zapomni si kvadratni koren in postalo bo očitno, da bo koren enačbe x 2 \u003d - c a število - c a, saj je - c a 2 \u003d - c a. Lahko je razumeti, da je število - - c a - tudi koren enačbe x 2 \u003d - c a: res, - - c a 2 \u003d - c a. Enačba ne bo imela drugih korenin. To lahko pokažemo z nasprotno metodo. Najprej označimo korenine, ki smo jih našli zgoraj x 1 in - x 1. Predpostavimo, da ima enačba x 2 \u003d - c a tudi koren x 2ki se razlikuje od korenin x 1 in - x 1. To vemo, namesto v enačbo x njegove korenine, enačbo spremenimo v pošteno številčno enakost. Za x 1 in - x 1 zapišemo: x 1 2 \u003d - c a in za x 2 - x 2 2 \u003d - c a. Na podlagi lastnosti numeričnih enakosti odštejemo eno pravo enakost od drugega pojma z izrazom, kar nam daje: x 1 2 - x 2 2 \u003d 0. Z akcijskimi lastnostmi s številkami napišite zadnjo enakost kot (x 1 - x 2) · (x 1 + x 2) \u003d 0. Znano je, da je produkt dveh števil enak nič in samo, če je vsaj eno od števil nič. Iz zgoraj navedenega izhaja, da x 1 - x 2 \u003d 0 in / ali x 1 + x 2 \u003d 0ista stvar x 2 \u003d x 1 in / ali x 2 \u003d - x 1. Prišlo je do očitnega nasprotja, saj se je sprva strinjalo, da je koren enačbe x 2 drugačen od x 1 in - x 1. Torej smo dokazali, da enačba nima korenin razen x \u003d - c a in x \u003d - - c a. Vse zgornje trditve povzamemo. Opredelitev 6 Nepopolna kvadratna enačba a x 2 + c \u003d 0 enakovredna enačbi x 2 \u003d - c a, ki:
Navajamo primere reševanja enačb a x 2 + c \u003d 0. Primer 3 Podana je kvadratna enačba 9 x 2 + 7 \u003d 0.Treba je najti rešitev zanjo. Rešitev Prosti izraz prenesemo na desno stran enačbe, potem enačba dobi obliko 9 x 2 \u003d - 7. Odgovor je: enačba 9 x 2 + 7 \u003d 0nima korenin. Primer 4 Rešiti je treba enačbo - x 2 + 36 \u003d 0. Rešitev Premaknite 36 na desno stran: - x 2 \u003d - 36. Odgovor je: x \u003d 6 ali x \u003d - 6. Rešitev enačbe a · x 2 + b · x \u003d 0Analiziramo tretjo vrsto nepopolnih kvadratnih enačb, kadar c \u003d 0. Da bi našli rešitev nepopolne kvadratne enačbe a x 2 + b x \u003d 0, uporabljamo metodo faktorizacije. S polinomom na levi strani enačbe razdeli faktor tako, da se izračuna skupni faktor x. Ta korak bo omogočil pretvorbo izvirne nepopolne kvadratne enačbe v njen ekvivalent x · (a · x + b) \u003d 0. In ta enačba je enakovredna množici enačb x \u003d 0 in a x + b \u003d 0. Enačba a x + b \u003d 0 linearni in njegov koren: x \u003d - b a. Opredelitev 7 Torej nepopolna kvadratna enačba a x 2 + b x \u003d 0 bo imel dve korenini x \u003d 0 in x \u003d - b a. Kot primer pritrdite material. Primer 5 Najti moramo rešitev enačbe 2 3 · x 2 - 2 2 7 · x \u003d 0. Rešitev Vzemi ven x iz oklepajev in dobite enačbo x · 2 3 · x - 2 2 7 \u003d 0. Ta enačba je enakovredna enačbam x \u003d 0 in 2 3x - 2 2 7 \u003d 0. Zdaj je potrebno rešiti dobljeno linearno enačbo: 2 3 · x \u003d 2 2 7, x \u003d 2 2 7 2 3. Na kratko napišemo rešitev enačbe na naslednji način: 2 3 · x 2 - 2 2 7 · x \u003d 0 x · 2 3 · x - 2 2 7 \u003d 0 x \u003d 0 ali 2 3 x - 2 2 7 \u003d 0 x \u003d 0 ali x \u003d 3 3 7 Odgovor je: x \u003d 0, x \u003d 3 3 7. Razlikovalna, formula korenin kvadratne enačbeČe želite najti rešitev kvadratnih enačb, obstaja koreninska formula: Opredelitev 8 x \u003d - b ± D 2 · a, kjer D \u003d b 2 - 4 Ali je tako imenovana diskriminatorka kvadratne enačbe. Pojem x \u003d - b ± D 2 · v bistvu pomeni, da je x 1 \u003d - b + D 2 · a, x 2 \u003d - b - D 2 · a. Koristno bo razumeti, kako je nastala ta formula in kako jo uporabiti. Izpeljava formule za korenine kvadratne enačbeSoočimo se z izzivom reševanja kvadratne enačbe a x 2 + b x x + c \u003d 0. Izvedemo številne enakovredne transformacije:
Tako smo prišli do enačbe x + b 2 · a 2 \u003d b 2 - 4 · a · c 4 · a 2, kar je enako prvotni enačbi a x 2 + b x x + c \u003d 0. Rešitev takšnih enačb smo analizirali v prejšnjih odstavkih (rešitev nepopolnih kvadratnih enačb). Že pridobljene izkušnje omogočajo sklep glede korenin enačbe x + b 2 · a 2 \u003d b 2 - 4 · a · c 4 · a 2:
Iz tega je razviden edini koren x \u003d - b 2 · a;
Sklepati je mogoče, da je prisotnost ali odsotnost korenin enačbe x + b 2 · a 2 \u003d b 2 - 4 · a · c 4 · a 2 (in zato izvirna enačba) odvisna od znaka izraza b 2 - 4 · a · c 4 · 2, posneta na desni. In znak tega izraza je podan z znakom številčnika, (imenovalca 4 · a 2 bo vedno pozitiven), torej znak izražanja b 2 - 4 · a · c. Na ta izraz b 2 - 4 · a · c ime je podano - razlikovalnik kvadratne enačbe in črka D je opredeljena kot njegova poimenovanje. Tu lahko napišete bistvo diskriminatorja - po njegovi vrednosti in podpisom sklepajo, ali bo imela kvadratna enačba resnične korenine, in če je odgovor, kakšno je število korenin - ena ali dve. Vrnemo se k enačbi x + b 2 · a 2 \u003d b 2 - 4 · a · c 4 · a 2. Ponovno ga napišemo z oznako diskriminatorja: x + b 2 · a 2 \u003d D 4 · a 2. Ponovno oblikujemo zaključke: Opredelitev 9
Rezultat našega sklepanja je bil izpeljava formule za korenine kvadratne enačbe: x \u003d - b + D 2 · a, x \u003d - b - D 2 · a, diskriminatorno D izračunano po formuli D \u003d b 2 - 4. Te formule omogočajo določitev obeh pravih korenin z diskriminacijo, večjo od nič. Kadar je diskriminator nič, bo uporaba obeh formul dala enak koren kot edina rešitev kvadratne enačbe. V primeru, ko je diskriminator negativen, ko poskušamo uporabiti korensko formulo kvadratne enačbe, se soočamo s potrebo po izločanju kvadratnega korena negativnega števila, kar nas bo popeljalo izven obsega resničnih števil. Če je diskriminator negativen, kvadratna enačba ne bo imela pravih korenin, možen pa je par zapletenih konjugiranih korenin, določenih z istimi koreninskimi formulami, ki smo jih dobili. Algoritem za reševanje kvadratnih enačb s korenskimi formulamiKvadratno enačbo je mogoče rešiti tako, da takoj uporabimo korensko formulo, v bistvu pa po potrebi poiščemo zapletene korenine. V večini primerov je običajno mišljeno iskanje ne zapletenih, temveč resničnih korenin kvadratne enačbe. Potem je optimalno, preden uporabimo formule korenin kvadratne enačbe, najprej določiti diskriminatorno in se prepričati, da ni negativna (sicer sklepamo, da enačba nima pravih korenin) in nato nadaljujemo z izračunom vrednosti korenin. Zgornja obrazložitev omogoča oblikovanje algoritma za reševanje kvadratne enačbe. Opredelitev 10 Za reševanje kvadratne enačbe a x 2 + b x x + c \u003d 0potrebno:
Upoštevajte, da kadar je diskriminator nič, lahko uporabite formulo x \u003d - b ± D 2 · a, bo dala enak rezultat kot formula x \u003d - b 2 · a. Poglejmo nekaj primerov. Primeri reševanja kvadratnih enačbPodajamo rešitev primerov za različne vrednosti diskriminatornega. Primer 6 Poiskati je treba korenine enačbe x 2 + 2 x - 6 \u003d 0. Rešitev Zapišemo numerične koeficiente kvadratne enačbe: a \u003d 1, b \u003d 2 in c \u003d - 6. Nato delujemo po algoritmu, tj. nadaljujemo z izračunom diskriminatornega, za katerega nadomestimo koeficiente a, b in c v diskriminatorni formuli: D \u003d b 2 - 4 · a · c \u003d 2 2 - 4 · 1 · (- 6) \u003d 4 + 24 \u003d 28. Torej, dobili smo D\u003e 0, kar pomeni, da bo imela izvirna enačba dve resnični korenini. x \u003d - 2 ± 2 · 7 2 x \u003d - 2 + 2 · 7 2 ali x \u003d - 2 - 2 · 7 2 x \u003d - 1 + 7 ali x \u003d - 1 - 7 Odgovor je: x \u003d - 1 + 7, x \u003d - 1 - 7. Primer 7 Potrebno je rešiti kvadratno enačbo - 4x 2 + 28x - 49 \u003d 0. Rešitev Opredelite diskriminatorno: D \u003d 28 2 - 4 · (- 4) · (- 49) \u003d 784 - 784 \u003d 0. S to razlikovalno vrednostjo bo imela začetna enačba le en koren, določen s formulo x \u003d - b 2 · a. x \u003d - 28 2 · (- 4) x \u003d 3, 5 Odgovor je: x \u003d 3, 5. Primer 8 Rešiti je treba enačbo 5y 2 + 6y + 2 \u003d 0 Rešitev Številčni koeficienti te enačbe bodo: a \u003d 5, b \u003d 6 in c \u003d 2. Te vrednosti uporabimo za iskanje diskriminatornega: D \u003d b 2 - 4 · a · c \u003d 6 2 - 4 · 5 · 2 \u003d 36 - 40 \u003d - 4. Izračunana diskriminacija je negativna, zato prvotna kvadratna enačba nima pravih korenin. V primeru, ko je naloga navesti zapletene korenine, uporabimo korensko formulo z izvajanjem dejanj s kompleksnimi števili: x \u003d - 6 ± 4 4 · 5, x \u003d - 6 + 2 · i 10 ali x \u003d - 6 - 2 · i 10, x \u003d - 3 5 + 1 5 · i ali x \u003d - 3 5 - 1 5 · i. Odgovor je: ni veljavnih korenin; zapletene korenine so naslednje: - 3 5 + 1 5 · i, - 3 5 - 1 5 · i. V šolskem učnem načrtu ni standardne zahteve po iskanju zapletenih korenin, zato, če je med rešitvijo diskriminatorna opredeljena kot negativna, se takoj zapiše odgovor, da pravih korenin ni. Korenska formula za enake koeficienteKoreninska formula x \u003d - b ± D 2 · a (D \u003d b 2 - 4 · a · c) omogoča pridobitev še ene bolj kompaktne formule, ki omogoča iskanje rešitev kvadratnih enačb z enakomernim koeficientom pri x (ali s koeficientom oblike 2 · n, na primer, 2 · 3 ali 14 · ln 5 \u003d 2 · 7 · ln 5). Pokažimo, kako izhaja ta formula. Naloga najdemo rešitev kvadratne enačbe a · x 2 + 2 · n · x + c \u003d 0. Delujemo po algoritmu: določimo diskriminatorno D \u003d (2 · n) 2 - 4 · a · c \u003d 4 · n 2 - 4 · a · c \u003d 4 · (n 2 - a · c) in nato uporabimo korensko formulo: x \u003d - 2 · n ± D 2 · a, x \u003d - 2 · n ± 4 · n 2 - a · c 2 · a, x \u003d - 2 · n ± 2 n 2 - a · c 2 · a, x \u003d - n ± n 2 - a Izraz n 2 - a · c označimo kot D 1 (včasih ga označimo z D "). Formula korenin kvadratne enačbe, ki je obravnavana z drugim koeficientom 2 n, ima obliko: x \u003d - n ± D 1 a, kjer je D 1 \u003d n 2 - a · c. Lahko je videti, da je D \u003d 4 · D 1 ali D 1 \u003d D 4. Z drugimi besedami, D1 je četrtina diskriminatornega. Očitno je znak D 1 enak znaku D, kar pomeni, da lahko znak D 1 služi tudi kot pokazatelj prisotnosti ali odsotnosti korenin kvadratne enačbe. Opredelitev 11 Zato je za rešitev kvadratne enačbe z drugim koeficientom 2 n potrebno:
Primer 9 Rešiti je potrebno kvadratno enačbo 5 · x 2 - 6 · x - 32 \u003d 0. Rešitev Drugi koeficient dane enačbe je lahko predstavljen kot 2 · (- 3). Nato damo dano kvadratno enačbo kot 5 · 2 + 2 · (- 3) · x - 32 \u003d 0, kjer je a \u003d 5, n \u003d - 3 in c \u003d - 32. Izračunamo četrti del diskriminatorne: D 1 \u003d n 2 - a · c \u003d (- 3) 2 - 5 · (- 32) \u003d 9 + 160 \u003d 169. Nastala vrednost je pozitivna, kar pomeni, da ima enačba dve resnični korenini. Določimo jih po ustrezni korenski formuli: x \u003d - n ± D 1 a, x \u003d - - 3 ± 169 5, x \u003d 3 ± 13 5, x \u003d 3 + 13 5 ali x \u003d 3 - 13 5 x \u003d 3 1 5 ali x \u003d - 2 Izračune bi bilo mogoče uporabiti po običajni formuli korenin kvadratne enačbe, vendar bi bila v tem primeru rešitev bolj okorna. Odgovor je: x \u003d 3 1 5 ali x \u003d - 2. Poenostavitev oblike kvadratnih enačbVčasih je mogoče optimizirati obliko prvotne enačbe, kar bo poenostavilo postopek izračuna korenin. Na primer, kvadratna enačba 12 · x 2 - 4 · x - 7 \u003d 0 je očitno bolj priročna za reševanje kot 1200 · x 2 - 400 · x - 700 \u003d 0. Pogosteje poenostavitev oblike kvadratne enačbe poteka z dejanji množenja ali deljenja obeh njenih delov na določeno število. Zgoraj smo na primer poenostavili zapis enačbe 1200 · x 2 - 400 · x - 700 \u003d 0, dobljen z deljenjem obeh njegovih delov na 100. Takšna transformacija je mogoča, kadar koeficienti kvadratne enačbe niso sočasni. Nato običajno razdelijo obe strani enačbe na največji skupni delitelj absolutnih vrednosti njegovih koeficientov. Kot primer uporabimo kvadratno enačbo 12 · x 2 - 42 · x + 48 \u003d 0. Določimo GCD absolutnih vrednosti njegovih koeficientov: GCD (12, 42, 48) \u003d GCD (GCD (12, 42), 48) \u003d GCD (6, 48) \u003d 6. Obe strani izvirne kvadratne enačbe delimo s 6 in dobimo enakovredno kvadratno enačbo 2 · x 2 - 7 · x + 8 \u003d 0. Z množenjem obeh strani kvadratne enačbe se navadno izločijo delni koeficienti. V tem primeru pomnožite z najmanj običajnim večkratnikom imenovalcev njegovih koeficientov. Na primer, če je vsak del kvadratne enačbe 1 6 · x 2 + 2 3 · x - 3 \u003d 0 pomnožen z NOC (6, 3, 1) \u003d 6, potem bo zapisan v enostavnejši obliki x 2 + 4 · x - 18 \u003d 0. Za zaključek ugotavljamo, da se skoraj vedno znebimo minusov s prvim koeficientom kvadratne enačbe, pri čemer spremenimo znake vsakega člana enačbe, kar dosežemo z množenjem (ali deljenjem) obeh delov na -1. Na primer, iz kvadratne enačbe - 2 · x 2 - 3 · x + 7 \u003d 0, lahko preidete na njeno poenostavljeno različico 2 · x 2 + 3 · x - 7 \u003d 0. Razmerje med koreninami in koeficientiFormula korenin kvadratnih enačb x \u003d - b ± D 2 · že znana nam izraža korenine enačbe v smislu njenih numeričnih koeficientov. Na podlagi te formule lahko določimo druga razmerja med koreninami in koeficienti. Najbolj znane in uporabne so formule iz teorema Vieta: x 1 + x 2 \u003d - b a in x 2 \u003d c a. Zlasti za dano kvadratno enačbo je vsota korenin drugi koeficient z nasprotnim znakom, produkt korenin pa je prosti izraz. Na primer po obliki kvadratne enačbe 3 · x 2 - 7 · x + 22 \u003d 0 je mogoče takoj ugotoviti, da je vsota njegovih korenin 7 3 in produkt korenin 22 3. Najdete lahko tudi številne druge relacije med koreninami in koeficienti kvadratne enačbe. Na primer, vsoto kvadratov korenin kvadratne enačbe lahko izrazimo s koeficienti: x 1 2 + x 2 2 \u003d (x 1 + x 2) 2 - 2 · x 1 · x 2 \u003d - ba 2 - 2 · ca \u003d b 2 a 2 - 2 · ca \u003d b 2 - 2 · a · ca 2 Če v besedilu opazite napako, jo izberite in pritisnite Ctrl + Enter Kvadratne enačbe se pogosto pojavljajo med reševanjem različnih problemov fizike in matematike. V tem članku bomo pogledali, kako rešiti te enakosti na univerzalen način "s pomočjo diskriminatornih." V članku so tudi primeri uporabe pridobljenega znanja. O katerih enačbah bomo razpravljali?Spodnja slika prikazuje formulo, v kateri je x neznana spremenljivka, latinični znaki a, b, c pa nekaj znanih števil. Vsak od teh simbolov se imenuje koeficient. Kot lahko vidite, je številka "a" pred spremenljivko x na kvadrat. To je najvišja stopnja predstavljenega izraza, zato jo imenujemo kvadratna enačba. Pogosto uporabite drugo ime: enačba drugega reda. Vrednost sama po sebi je kvadratni koeficient (stoječ kvadrat s spremenljivko), b je linearni koeficient (zraven spremenljivke je dvignjen na prvo moč) in na koncu je število c svoboden izraz. Upoštevajte, da je oblika enačbe, ki je prikazana na zgornji sliki, običajni klasični kvadratni izraz. Poleg nje obstajajo tudi druge enačbe drugega reda, v katerih so koeficienti b, c lahko nič. Kadar je naloga rešiti obravnavano enakost, to pomeni, da je treba najti takšne vrednosti spremenljivke x, ki bi jo zadovoljile. Tukaj je treba najprej pozabiti naslednje: ker je najvišja stopnja x 2, ta vrsta izražanja ne more imeti več kot 2 rešitvi. To pomeni, da če bi pri reševanju enačbe našli 2 vrednosti x, ki ju izpolnjujeta, potem ste lahko prepričani, da ne obstaja 3. številka, nadomestitev katere namesto x bi bila enakost tudi resnična. Rešitve enačbe v matematiki imenujejo korenine. Metode reševanja enačb drugega redaReševanje takšnih enačb zahteva poznavanje neke teorije o njih. V šolskem tečaju algebre so obravnavane 4 različne metode reševanja. Naštejemo jih:
Prednost prve metode je njena preprostost, vendar je ni mogoče uporabiti za vse enačbe. Druga metoda je univerzalna, vendar nekoliko okorna. Tretja metoda je značilna po prepoznavnosti, vendar ni vedno priročna in uporabna. In končno, uporaba diskriminatorne enačbe je univerzalen in dokaj enostaven način za iskanje korenin absolutno katere koli enačbe drugega reda. Torej bo članek upošteval samo njega. Formula za pridobitev korenin enačbeObrnimo se k splošni obliki kvadratne enačbe. Zapišemo ga: a * x² + b * x + c \u003d 0. Pred uporabo metode reševanja "prek diskriminatornega" je treba enakost vedno pripeljati v pisno obliko. Se pravi, mora biti sestavljen iz treh izrazov (ali manj, če je b ali c 0). Na primer, če obstaja izraz: x²-9 * x + 8 \u003d -5 * x + 7 * x², potem morate najprej vse člane prenesti na eno stran enakosti in v enakih stopnjah dodati izraze, ki vsebujejo spremenljivko x. V tem primeru bo ta operacija pripeljala do naslednjega izraza: -6 * x²-4 * x + 8 \u003d 0, kar je enako enačbi 6 * x² + 4 * x-8 \u003d 0 (tukaj smo levo in desno stran pomnožili z -1) .  V zgornjem primeru je a \u003d 6, b \u003d 4, c \u003d -8. Upoštevajte, da so vsi člani obravnavane enakosti vedno sešteti, tako da če se pojavi znak "-", potem to pomeni, da je ustrezni koeficient negativen, kot je število c v tem primeru.  Ko smo preučili ta trenutek, se preidemo na samo formulo, ki omogoča pridobitev korenin kvadratne enačbe. Ima pogled, ki je predstavljen na spodnji fotografiji.  Kot je razvidno iz tega izraza, vam omogoča, da dobite dve korenini (bodite pozorni na znak "±"). Če želite to narediti, je dovolj, da koeficiente b, c in a nadomestimo. Koncept diskriminatornegaV prejšnjem odstavku smo dali formulo, ki omogoča hitro reševanje katere koli enačbe drugega reda. V njej se radikalni izraz imenuje diskriminatorno, torej D \u003d b²-4 * a * c. Zakaj je ta del formule izoliran in ali sploh ima svoje ime? Dejstvo je, da diskriminator povezuje vse tri koeficiente enačbe v en sam izraz. Slednje dejstvo pomeni, da v celoti vsebuje podatke o koreninah, ki jih lahko izrazimo z naslednjim seznamom:
Naloga določitve diskriminatornega Podajamo preprost primer, kako najti diskriminatorja. Naj bo dana ta enakost: 2 * x² - 4 + 5 * x-9 * x² \u003d 3 * x-5 * x² + 7. Pripeljemo ga v standardni obrazec, dobimo: (2 * x²-9 * x² + 5 * x²) + (5 * x-3 * x) + (- 4-7) \u003d 0, od koder pridemo do enakosti: -2 * x² + 2 * x-11 \u003d 0. Tukaj je a \u003d -2, b \u003d 2, c \u003d -11. Zdaj lahko uporabimo imenovano formulo za diskriminatorno: D \u003d 2² - 4 * (- 2) * (- 11) \u003d -84. Nastala številka je odgovor na nalogo. Ker je diskriminator v primeru manj kot nič, lahko rečemo, da ta kvadratna enačba nima pravih korenin. Samo številke kompleksnega tipa bodo njegova rešitev. Primer neenakosti skozi diskriminatornoRešujemo probleme nekoliko drugačne vrste: podana je enakost -3 * x²-6 * x + c \u003d 0. Poiskati je treba vrednosti c, za katere je D\u003e 0. V tem primeru sta znana le dva od treh koeficientov, zato ne bo delovalo, da bi izračunali natančno vrednost diskriminatorne, je pa znano, da je pozitivna. Slednje dejstvo uporabljamo pri sestavljanju neenakosti: D \u003d (-6) ²-4 * (- 3) * c\u003e 0 \u003d\u003e 36 + 12 * c\u003e 0. Rešitev nastale neenakosti vodi do rezultata: c\u003e -3. Preverite nastalo številko. Če želite to narediti, izračunajte D za 2 primera: c \u003d -2 in c \u003d -4. Število -2 izpolnjuje rezultat (-2\u003e -3), ustrezni diskriminacijski dobi vrednost: D \u003d 12\u003e 0. Število -4 pa ne izpolnjuje neenakosti (-4. Tako bodo vsa števila c, večja od -3, izpolnila pogoj. Primer reševanja enačbePredstavljamo problem, ki ni samo v iskanju diskriminatornega, temveč tudi v reševanju enačbe. Poiskati je treba korenine za enakost -2 * x² + 7-9 * x \u003d 0. V tem primeru je diskriminator enaka naslednji vrednosti: D \u003d 81-4 * (- 2) * 7 \u003d 137. Nato so korenine enačbe definirane na naslednji način: x \u003d (9 ± √137) / (- 4). To so natančne vrednosti korenin, če izračunamo približno koren, potem dobimo številke: x \u003d -5,176 in x \u003d 0,676. Geometrijski problemRešili bomo težavo, ki zahteva ne le sposobnost izračunavanja diskriminatorjev, temveč tudi uporabo veščin abstraktnega razmišljanja in znanje o tem, kako narediti kvadratne enačbe. Bob je imel odejo velikosti 5 x 4 metre. Fant mu je hotel obšiti po obodu neprekinjen trak iz lepe tkanine. Kako debel bo ta trak, če se ve, da ima Bob 10 m² tkanine.  Naj ima trak debelino x m, potem bo površina tkanine vzdolž dolge strani odeje (5 + 2 * x) * x, in ker sta 2 dolgi strani, imamo: 2 * x * (5 + 2 * x). Na kratki strani bo površina prišiti tkanine 4 * x, saj sta na teh dveh straneh 2, dobimo vrednost 8 * x. Upoštevajte, da je bila vrednost 2 * x dodana na dolgi strani, ko se je dolžina odeje povečala za to število. Skupna površina tkanine, prišiti na odejo, je 10 m². Zato dobimo enakost: 2 * x * (5 + 2 * x) + 8 * x \u003d 10 \u003d\u003e 4 * x² + 18 * x-10 \u003d 0. Za ta primer je diskriminator: D \u003d 18²-4 * 4 * (- 10) \u003d 484. Njegov koren je 22. S formulo najdemo želene korenine: x \u003d (-18 ± 22) / (2 * 4) \u003d (- 5; 0,5). Očitno je, da je od obeh korenin pogoj težave primeren le s številko 0,5. Tako bo trak iz tkanine, ki ga Bob prišiti na odejo, imel širino 50 cm. V sodobni družbi je sposobnost izvajanja dejanj z enačbami, ki vsebujejo kvadratno spremenljivko, uporabna na številnih področjih dejavnosti in se v praksi pogosto uporablja v znanstvenem in tehničnem razvoju. Dokaz tega je gradnja morskih in rečnih plovil, letal in raket. S takšnimi izračuni se določijo usmeritve gibanja različnih teles, vključno s vesoljskimi predmeti. Primeri reševanja kvadratnih enačb najdejo uporabo ne le v ekonomskem napovedovanju, načrtovanju in gradnji stavb, temveč tudi v najbolj običajnih vsakdanjih okoliščinah. Potrebni so lahko pri pohodništvu, športu, v trgovinah pri nakupovanju in v drugih zelo pogostih situacijah. Izraz razdelite na sestavne dejavnikeStopnja enačbe je določena z najvišjo stopnjo spremenljivke, ki jo dani izraz vsebuje. Če je enak 2, potem takšno enačbo imenujemo kvadrat. Če so izraženi v jeziku formul, potem te izraze, ne glede na to, kako izgledajo, vedno lahko pripeljemo v obliko, kadar levo stran izraza sestavljajo trije izrazi. Med njimi: os 2 (to je spremenljivka, kvadratna s koeficientom), bx (neznan brez kvadrata s svojim koeficientom) in c (prosta komponenta, torej navadna številka). Vse to na desni strani je enako 0. V primeru, da takemu polinomu manjka eden od njegovih sestavnih delov, z izjemo sekire 2, ga imenujemo nepopolna kvadratna enačba. Najprej je treba upoštevati primere rešitve takšnih problemov, vrednost spremenljivk, v katerih ni težko najti. Če je izraz videti tako, da sta izraza v izrazu na desni strani dva, natančneje ax 2 in bx, je x najlažje najti tako, da spremenljivko postavimo iz oklepajev. Zdaj bo naša enačba videti takole: x (ax + b). Nadalje postane očitno, da je bodisi x \u003d 0, bodisi je naloga zmanjšana na iskanje spremenljivke iz naslednjega izraza: ax + b \u003d 0. Navedeno narekuje ena od lastnosti množenja. Pravilo pravi, da produkt dveh faktorjev daje 0 le, če je eden od njiju enak nič. Primerx \u003d 0 ali 8x - 3 \u003d 0 Kot rezultat dobimo dva korena enačbe: 0 in 0,375. Te vrste enačbe lahko opišejo gibanje teles pod dejstvom gravitacije, ki se je začelo premikati od določene točke, vzete kot izvor. Tu ima matematični zapis takšno obliko: y \u003d v 0 t + gt 2/2. Če nadomestite potrebne vrednosti, izenačite desno 0 in poiščete morebitne neznanke, lahko ugotovite čas, ki preteče od trenutka, ko telo naraste, dokler ne pade, in številne druge količine. Toda o tem bomo govorili kasneje.
Faktorizacija izrazaZgoraj opisano pravilo omogoča reševanje teh težav v bolj zapletenih primerih. Razmislite o primerih reševanja kvadratnih enačb te vrste. X 2 - 33x + 200 \u003d 0 Ta kvadratni trinom je končan. Najprej pretvorite izraz in ga faktorite. Obstajata dva: (x-8) in (x-25) \u003d 0. Posledično imamo dve korenini 8 in 25. Primeri reševanja kvadratnih enačb v 9. razredu omogočajo, da s to metodo poiščemo spremenljivko v izrazih ne le drugega, temveč celo tretjega in četrtega reda. Na primer: 2x 3 + 2x 2 - 18x - 18 \u003d 0. Pri razvrščanju desne strani spremenljivke dobimo tri, torej (x + 1), (x-3) in (x + 3). Posledično postane očitno, da ima ta enačba tri korenine: -3; -1; 3. Ekstrakcija kvadratnega korenaDrugi primer nepopolne enačbe drugega reda je izraz v jeziku črk, ki so predstavljeni tako, da je desna stran zgrajena iz komponent ax 2 in c. Tukaj, za pridobitev vrednosti spremenljivke, se prosti izraz prenese na desno stran, nato pa se kvadratni koren izvleče z obeh strani enakosti. Treba je opozoriti, da tudi v tem primeru običajno obstajata dva korena enačbe. Izjema so lahko samo enakosti, ki ne vsebujejo izraza c, kjer je spremenljivka enaka nič, in tudi različice izrazov, ko se desna stran izkaže za negativno. V zadnjem primeru rešitve sploh ne obstajajo, saj zgornjih dejanj ni mogoče izvesti s koreninami. Upoštevati je treba primere rešitev takšnih kvadratnih enačb. V tem primeru so korenine enačbe števil -4 in 4. Izračun zemljiščPotreba po takšnih izračunih se je pojavila že v starih časih, saj je bil razvoj matematike v veliki meri posledica potrebe po določitvi površin in oboda zemljišč z največjo natančnostjo.
Primeri z reševanjem kvadratnih enačb, ki temeljijo na tovrstnih problemih, bi morali razmišljati o nas. Recimo, da obstaja pravokoten kos zemlje, katerega dolžina je 16 metrov večja od širine. Če je znano, da je njegova površina 612 m 2, je treba najti dolžino, širino in obod mesta. Da se lotimo poslovanja, najprej sestavimo potrebno enačbo. Širino odseka označimo s x, potem bo njegova dolžina (x + 16). Iz zapisanega izhaja, da območje določimo z izrazom x (x + 16), ki je glede na pogoj našega problema 612. To pomeni, da je x (x + 16) \u003d 612. Rešitve popolnih kvadratnih enačb in ta izraz je ravno to, ni mogoče storiti na enak način. Zakaj? Čeprav leva stran še vedno vsebuje dva faktorja, produkt le-teh sploh ni 0, zato se tukaj uporabljajo druge metode. DiskriminatornoNajprej bomo naredili potrebne transformacije, potem bo izgled tega izraza izgledal takole: x 2 + 16x - 612 \u003d 0. To pomeni, da smo dobili izraz v obliki, ki ustreza prej navedenemu standardu, kjer je a \u003d 1, b \u003d 16, c \u003d -612. To je lahko primer reševanja kvadratnih enačb s pomočjo diskriminatornih. Tukaj so potrebni izračuni narejeni po shemi: D \u003d b 2 - 4ac. Ta pomožna vrednost ne omogoča le iskanja želenih količin v enačbi drugega reda, temveč določa število možnih možnosti. V primeru D\u003e 0 sta dva; za D \u003d 0 obstaja en koren. V primeru D<0, никаких шансов для решения у уравнения вообще не имеется. O koreninah in njihovi formuliV našem primeru je diskriminatorna: 256 - 4 (-612) \u003d 2704. To kaže, da odgovor na naš problem obstaja. Če poznate k, je treba rešitev kvadratnih enačb nadaljevati po spodnji formuli. Omogoča vam izračun korenin.
To pomeni, da v predstavljenem primeru: x 1 \u003d 18, x 2 \u003d -34. Druga možnost v tej dilemi ne more biti rešitev, saj velikosti zemljišča ni mogoče izmeriti v negativnih vrednostih, zato je x (torej širina ploskve) 18 m. Zato izračunamo dolžino: 18 + 16 \u003d 34 in obod 2 (34+ 18) \u003d 104 (m 2). Primeri in nalogeNadaljujemo s študijem kvadratnih enačb. Primeri in podrobna rešitev več njih bodo podani spodaj. 1) 15x 2 + 20x + 5 \u003d 12x 2 + 27x + 1 Vse prenesemo na levo stran enakosti, naredimo preobrazbo, torej dobimo obliko enačbe, ki jo običajno imenujemo standard, in jo enačimo z ničlo. 15x 2 + 20x + 5 - 12x 2 - 27x - 1 \u003d 0 Če jih sestavimo skupaj, določimo diskriminatorno: D \u003d 49 - 48 \u003d 1. Zato bo naša enačba imela dve korenini. Izračunamo jih po zgornji formuli, kar pomeni, da bo prvi od njih 4/3, drugi pa 1. 2) Zdaj bomo razkrili uganke drugačne vrste. Ugotovite, ali so tukaj korenine x 2 - 4x + 5 \u003d 1? Da dobimo izčrpen odgovor, zmanjšamo polinom na ustrezno znano obliko in izračunamo diskriminatorje. V tem primeru rešitev kvadratne enačbe ni potrebna, ker bistvo problema sploh ni v tem. V tem primeru je D \u003d 16 - 20 \u003d -4, kar pomeni, da korenin resnično ni. Teorem VietaKvadratne enačbe je priročno rešiti s pomočjo zgornjih formul in različno, ko se kvadratni koren izvleče iz vrednosti slednjih. Vendar to ni vedno tako. Vendar pa obstaja veliko načinov za pridobitev vrednosti spremenljivk v tem primeru. Primer: rešitve kvadratnih enačb po izreku Vieta. Ime je dobila po tem, da je živela v 16. stoletju v Franciji in si ustvarila sijajno kariero zahvaljujoč matematičnemu talentu in povezavam na dvoru. Njegov portret lahko vidimo v članku.
Vzorec, ki ga je opazil slavni Francoz, je bil naslednji. Dokazal je, da so korenine enačbe številčno enake -p \u003d b / a, njihov produkt pa ustreza q \u003d c / a. Zdaj razmislite o določenih nalogah. 3x 2 + 21x - 54 \u003d 0 Zaradi preprostosti preoblikujemo izraz: x 2 + 7x - 18 \u003d 0 S pomočjo teorema Vieta bomo dobili naslednje: vsota korenin je -7, njihov produkt pa -18. Od tod dobimo, da so korenine enačbe števil -9 in 2. Po opravljenem preverjanju se bomo prepričali, ali se te vrednosti spremenljivk res ujemajo v izraz. Graf in enačba parabolePojma kvadratne funkcije in kvadratne enačbe sta tesno povezana. Primeri tega so že bili podani že prej. Zdaj pa si oglejmo nekaj matematičnih ugank nekoliko podrobneje. Vizualiziramo lahko katero koli enačbo opisanega tipa. Podobna odvisnost, narisana v grafu, se imenuje parabola. Različne vrste so predstavljene na spodnji sliki.
Vsaka parabola ima točko, torej točko, iz katere izhajajo njene veje. Če je\u003e 0, gredo visoko v neskončnost, in ko a<0, они рисуются вниз. Простейшим примером подобной зависимости является функция y = x 2 . В данном случае в уравнении x 2 =0 неизвестное может принимать только одно значение, то есть х=0, а значит существует только один корень. Это неудивительно, ведь здесь D=0, потому что a=1, b=0, c=0. Выходит формула корней (точнее одного корня) квадратного уравнения запишется так: x = -b/2a. Vizualne slike funkcij pomagajo rešiti vse enačbe, tudi kvadratne. Ta metoda se imenuje grafična. In vrednost spremenljivke x je koordinata absces na točkah, kjer premica grafa preseka z 0x. Koordinate vrhov lahko najdemo s pravkar dano formulo x 0 \u003d -b / 2a. In, če nadomestite dobljeno vrednost v začetni enačbi funkcije, lahko najdete y 0, to je drugo koordinatno točko parabole, ki spada v ordinatno os. Presečišče vej parabole z abscesoPrimerov z rešitvijo kvadratnih enačb je veliko, vendar obstajajo splošni vzorci. Upoštevaj jih. Jasno je, da je presek grafa z osjo 0x za a\u003e 0 mogoč le, če y 0 prevzame negativne vrednosti. In za a<0 координата у 0 должна быть положительна. Для указанных вариантов D>0. V nasprotnem primeru D<0. А когда D=0, вершина параболы расположена непосредственно на оси 0х. Po urniku parabole lahko določite tudi korenine. Tudi obratno je. To pomeni, če ni enostavno dobiti vizualne slike kvadratne funkcije, lahko desno stran izraza izenačite na 0 in rešite nastalo enačbo. In če poznamo presečišča z 0x osjo, je lažje risati. Iz zgodovineZ uporabo enačb, ki vsebujejo kvadratno spremenljivko, v starih časih niso le matematično izračunali in določali območja geometrijskih oblik. Predhodniki so potrebovali takšne izračune za grandiozna odkritja na področju fizike in astronomije, pa tudi za izdelavo astroloških napovedi.
Kot kažejo sodobni znanstveniki, so bili prebivalci Babilona med prvimi, ki so rešili kvadratne enačbe. Zgodilo se je štiri stoletja pred prihodom naše dobe. Seveda so se njihovi izračuni bistveno razlikovali od trenutno sprejetih in izkazali so se za veliko bolj primitivne. Na primer, mezopotamijski matematiki niso imeli pojma o obstoju negativnih števil. Prav tako niso bili seznanjeni z drugimi subtilnostmi tistih, ki jih pozna vsak šolar našega časa. Morda celo prej kot babilonski znanstveniki, indijski modreci Baudhayama so se ukvarjali z reševanjem kvadratnih enačb. Zgodilo se je približno osem stoletij pred Kristusovim prihodom. Res je, enačbe drugega reda, katerih rešitve je navedel, so bile najpreprostejše. Poleg njega so takšna vprašanja v antiki zanimala kitajska matematika. V Evropi so kvadratne enačbe začeli reševati šele na začetku XIII stoletja, kasneje pa so jih pri svojih delih uporabili tako veliki znanstveniki, kot so Newton, Descartes in mnogi drugi. Upam, da se boste s tem člankom naučili najti korenine polne kvadratne enačbe. S pomočjo diskriminatornih rešujejo le popolne kvadratne enačbe, za reševanje nepopolnih kvadratnih enačb pa se uporabljajo druge metode, ki jih boste našli v članku »Reševanje nepopolnih kvadratnih enačb«. Katere kvadratne enačbe imenujemo popolne? Je enačbe oblike ax 2 + b x + c \u003d 0, kjer koeficienti a, b in c niso enaki nič. Torej, za reševanje celotne kvadratne enačbe moramo izračunati diskriminatorno D. D \u003d b 2 - 4ac. Glede na pomen diskriminatornega odgovora zapišemo. Če je diskriminator negativno število (D< 0),то корней нет. Če je diskriminator enak nič, potem je x \u003d (-b) / 2a. Kadar je diskriminator pozitivno število (D\u003e 0), potem je x 1 \u003d (-b - √D) / 2a in x 2 \u003d (-b + √D) / 2a. Na primer. Reši enačbo x 2 - 4x + 4 \u003d 0. D \u003d 4 2 - 4 · 4 \u003d 0 x \u003d (- (-4)) / 2 \u003d 2 Odgovor: 2. Rešite enačbo 2 x 2 + x + 3 \u003d 0. D \u003d 1 2 - 4 · 2 · 3 \u003d - 23 Odgovor: korenin ni. Rešite enačbo 2 x 2 + 5x - 7 \u003d 0. D \u003d 5 2 - 4 · 2 · (–7) \u003d 81 x 1 \u003d (-5 - 81) / (2 · 2) \u003d (-5 - 9) / 4 \u003d - 3,5 x 2 \u003d (-5 + 81) / (2 · 2) \u003d (-5 + 9) / 4 \u003d 1 Odgovor: - 3,5; 1. Predstavljajte si torej rešitev popolnih kvadratnih enačb s vezjem na sliki 1. S pomočjo teh formul lahko rešite katero koli celotno kvadratno enačbo. To morate samo skrbno spremljati enačba je bila napisana kot standardni polinom ampak x 2 + bx + c, sicer lahko naredite napako. Na primer, v zapisu enačbe x + 3 + 2x 2 \u003d 0 se lahko napačno odloči, da a \u003d 1, b \u003d 3 in c \u003d 2. Nato D \u003d 3 2 - 4 · 1 · 2 \u003d 1 in potem ima enačba dva korena. In to ne drži. (Glej rešitev zgornjega primera 2). Če enačba torej ni napisana z polinomom standardne oblike, mora biti najprej polna kvadratna enačba zapisana z polinomom standardne oblike (na prvem mestu naj bo monom z najvišjo eksponentno t.j. ampak x 2 potem z manj – bxin nato svoboden član s Pri reševanju kvadratne enačbe in kvadratne enačbe z enakomernim koeficientom v drugem izrazu lahko uporabimo druge formule. Seznanimo se s temi formulami. Če je v polni kvadratni enačbi z drugim pojmom koeficient enakomeren (b \u003d 2k), potem lahko enačbo rešimo s formulami, prikazanimi na diagramu slike 2. Celotna kvadratna enačba se imenuje zmanjšana, če je koeficient x 2 enako enotnosti in enačba ima obliko x 2 + px + q \u003d 0. Takšno enačbo lahko damo za rešitev ali dobimo z deljenjem vseh koeficientov, enačbo s koeficientom ampakstoji ob x 2 . Slika 3 prikazuje diagram rešitve zmanjšanega kvadrata Primer. Reši enačbo 3x 2 + 6x - 6 \u003d 0. Rešimo to enačbo s pomočjo formul na sliki 1. D \u003d 6 2 - 4 · 3 · (- 6) \u003d 36 + 72 \u003d 108 √D \u003d √108 \u003d √ (36 · 3) \u003d 6√3 x 1 \u003d (-6 - 6√3) / (2 · 3) \u003d (6 (-1 - √ (3))) / 6 \u003d –1 - √3 x 2 \u003d (-6 + 6√3) / (2 · 3) \u003d (6 (-1+ √ (3))) / 6 \u003d –1 + √3 Odgovor: –1 - √3; –1 + √3 Opazite lahko, da je koeficient x v tej enačbi enakomerno število, to je b \u003d 6 ali b \u003d 2k, od kod je k \u003d 3. Nato bomo enačbo poskusili rešiti s pomočjo formul, prikazanih na diagramu slike D 1 \u003d 3 2 - 3 · (- 6 ) \u003d 9 + 18 \u003d 27 √ (D 1) \u003d √27 \u003d √ (9 · 3) \u003d 3√3 x 1 \u003d (-3 - 3√3) / 3 \u003d (3 (-1 - √ (3))) / 3 \u003d - 1 - √3 x 2 \u003d (-3 + 3√3) / 3 \u003d (3 (-1 + √ (3))) / 3 \u003d - 1 + √3 Odgovor: –1 - √3; –1 + √3. Če opazimo, da so vsi koeficienti v tej kvadratni enačbi deljivi s 3 in izvedemo delitev, dobimo zmanjšano kvadratno enačbo x 2 + 2x - 2 \u003d 0 To enačbo rešimo s pomočjo formul za zmanjšano kvadratno enačbo D 2 \u003d 2 2 - 4 · (- 2) \u003d 4 + 8 \u003d 12 √ (D 2) \u003d √12 \u003d √ (4 · 3) \u003d 2√3 x 1 \u003d (-2 - 2√3) / 2 \u003d (2 (-1 - √ (3))) / 2 \u003d - 1 - √3 x 2 \u003d (-2 + 2√3) / 2 \u003d (2 (-1+ √ (3))) / 2 \u003d - 1 + √3 Odgovor: –1 - √3; –1 + √3. Kot lahko vidite, smo pri reševanju te enačbe z uporabo različnih formul dobili enak odgovor. Zato, ko ste dobro obvladali formule, prikazane na diagramu slike 1, lahko vedno rešite katero koli popolno kvadratno enačbo. spletnega mesta, s popolnim ali delnim kopiranjem gradiva je potrebna povezava do vira. |
| Preberi: |
|---|
Priljubljeno:
Rešitev najpreprostejših trigonometričnih neenakosti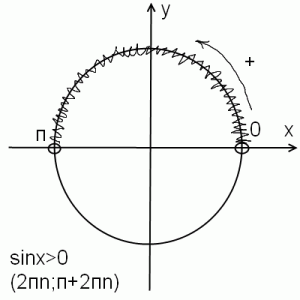
|
Novo
- Kaj je pokvarilo "krutega" barona?
- Član gibanja White
- Pot Suvorova in ekipe v domovino
- Funkcijo F (x) imenujemo antideriva za funkcijo f (x), če je F` (x) \u003d f (x) ali dF (x) \u003d f (x) dx
- Program za zmanjšanje deleža stopinj
- Podobni izrazi, njihovo zmanjšanje, primeri
- Ruski popotniki lazarev
- Reševanje nepopolnih kvadratnih enačb
- Rešitev kvadratnih enačb, formula korenin, primeri
- Koordinatna ravnina (6. razred) - Hipermarket znanja











 enačbe. Kot primer bomo uporabili formule, obravnavane v tem članku.
enačbe. Kot primer bomo uporabili formule, obravnavane v tem članku. enačbe slika 3.
enačbe slika 3.