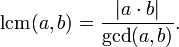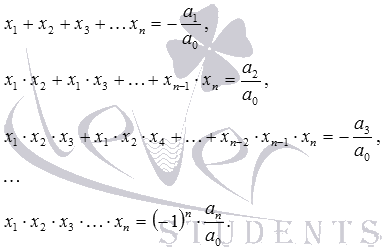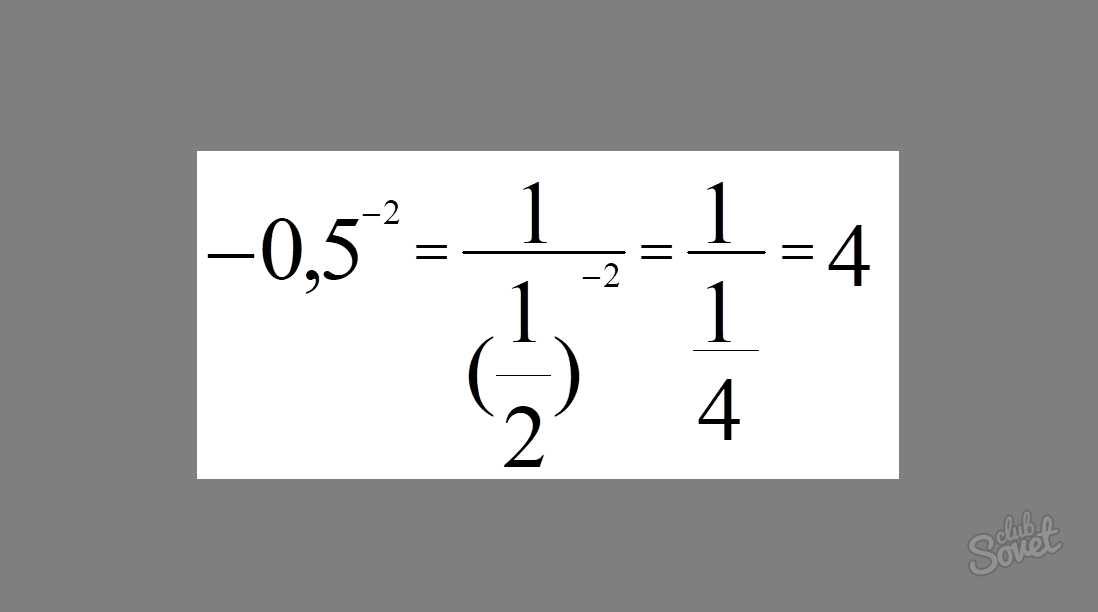Odseki spletnega mesta
Izbira urednikov:
Oglaševanje
| Pravila kvadratne enačbe. Rešitev nepopolnih kvadratnih enačb. Nepopolne kvadratne enačbe |
|
Nadaljevanje teme »Reševanje enačb« vas bo v tem članku seznanilo s kvadratnimi enačbami. Vse bomo podrobno preučili: bistvo in pojem kvadratne enačbe, postavili bomo spremljajoče izraze, analizirali bomo rešitev rešitve za nepopolne in popolne enačbe, seznanili se bomo s korensko formulo in diskriminatorno, vzpostavili bomo razmerje med koreninami in koeficienti in seveda dali jasno rešitev praktičnih primerov. Yandex.RTB R-A-339285-1 Kvadratna enačba, njene vrsteOpredelitev 1Kvadratna enačba Ali je enačba zapisana kot a x 2 + b x x + c \u003d 0kje x - spremenljivka, a, b in c - nekaj številk, medtem ko ane nič. Pogosto kvadratne enačbe imenujemo tudi enačbe druge stopnje, saj je v bistvu kvadratna enačba algebrska enačba druge stopnje. Navajamo primer za ponazoritev dane definicije: 9 · x 2 + 16 · x + 2 \u003d 0; 7,5 x 2 + 3, 1 x + 0, 11 \u003d 0 itd. So kvadratne enačbe. Opredelitev 2 Številke a, b in c Ali so koeficienti kvadratne enačbe a x 2 + b x x + c \u003d 0, koeficient a nosi ime prvega, višjega ali koeficient pri x 2, b - drugi koeficient ali koeficient pri x, in c imenovan svobodni član. Na primer v kvadratni enačbi 6 x 2 - 2 x 11 \u003d 0 višji koeficient je 6, drugi koeficient je − 2 , in prost termin je − 11 . Bodite pozorni na dejstvo, da ko koeficienti bin / ali c sta negativna, potem se uporabi kratek zapis zapisa oblike 6 x 2 - 2 x 11 \u003d 0pa ne 6 x 2 + (- 2) x + (- 11) \u003d 0. Pojasnimo tudi ta vidik: če so koeficienti a in / ali b so enaki 1 ali − 1 , potem morda ne bodo izrecno sodelovali pri pisanju kvadratne enačbe, kar je razloženo s posebnostmi pisanja navedenih numeričnih koeficientov. Na primer v kvadratni enačbi y 2 - y + 7 \u003d 0 višji koeficient je 1, drugi koeficient pa − 1 . Zmanjšane in neredduirane kvadratne enačbeGlede na vrednost prvega koeficienta se kvadratne enačbe delijo na reducirane in nereduktivne. Opredelitev 3 Kvadratna enačba Je kvadratna enačba, kjer je vodilni koeficient 1. Pri drugih vrednostih najvišjega koeficienta se kvadratna enačba ne zmanjša. Navajamo primere: zmanjšajo se kvadratne enačbe x 2 - 4 · x + 3 \u003d 0, x 2 - x - 4 5 \u003d 0, v katerih je najvišji koeficient 1. 9 x 2 - x - 2 \u003d 0 - neredducirana kvadratna enačba, pri čemer se prvi koeficient razlikuje od 1 . Kakršno koli neredducirano kvadratno enačbo lahko spremenimo v zmanjšano enačbo, če oba dela delimo na prvi koeficient (enakovredno preoblikovanje). Preoblikovana enačba bo imela enake korenine kot dana neurejena enačba ali pa sploh nima korenin. Upoštevanje konkretnega primera nam bo omogočilo, da jasno pokažemo izvajanje prehoda iz neredduirane kvadratne enačbe na dano. Primer 1 Podana je enačba: 6x2 + 18x - 7 \u003d 0 . Potrebno je pretvoriti izvirno enačbo v dani obrazec. Rešitev Po zgornji shemi delimo oba dela prvotne enačbe z vodilnim koeficientom 6. Nato dobimo: (6 · x 2 + 18 · x - 7): 3 \u003d 0: 3, in to je isto kot: (6 * x 2): 3 + (18 * x): 3 - 7: 3 \u003d 0 in nadalje: (6: 6) x 2 + (18: 6) x - 7: 6 \u003d 0. Od tod: x 2 + 3 x - 1 1 6 \u003d 0. Tako dobimo enačbo, ki je enaka dani. Odgovor je: x 2 + 3 x - 1 1 6 \u003d 0. Popolne in nepopolne kvadratne enačbeObrnimo se k definiciji kvadratne enačbe. V njej smo to razjasnili a ≠ 0. Podoben pogoj je nujen za enačbo a x 2 + b x x + c \u003d 0 je bil ravno kvadrat, ker kdaj a \u003d 0 v bistvu pretvori v linearno enačbo bx + c \u003d 0. V primeru, ko koeficienti b in cso enake nič (kar je možno, posamično in skupaj), kvadratna enačba se imenuje nepopolna. Opredelitev 4 Nepopolna kvadratna enačba Ali je takšna kvadratna enačba a x 2 + b x x + c \u003d 0,kjer je vsaj eden od koeficientov bin c(ali oboje) je nič. Popolna kvadratna enačba - kvadratna enačba, v kateri vsi numerični koeficienti niso enaki nič. Pogovorimo se, zakaj so te vrste kvadratnih enačb dobile takšna imena. Pri b \u003d 0 ima kvadratna enačba obliko a x 2 + 0 x x c \u003d 0to je isto kot a x 2 + c \u003d 0. Na c \u003d 0 kvadratna enačba se zapiše kot a x 2 + b x x 0 \u003d 0kar je enakovredno a x 2 + b x \u003d 0. Na b \u003d 0 in c \u003d 0 enačba bo imela obliko a x 2 \u003d 0. Dobljene enačbe se od polne kvadratne enačbe razlikujejo po tem, da njihovi levi deli ne vsebujejo niti izraza s spremenljivko x, niti prostega izraza ali obojega hkrati. Pravzaprav je to dejstvo po tej vrsti enačb dobilo ime - nepopolno. Na primer, x 2 + 3 · x + 4 \u003d 0 in - 7 · x 2 - 2 · x + 1, 3 \u003d 0 so polne kvadratne enačbe; x 2 \u003d 0, - 5 x 2 \u003d 0; 11x 2 + 2 \u003d 0, - x 2 - 6x \u003d 0 so nepopolne kvadratne enačbe. Reševanje nepopolnih kvadratnih enačbZgornja definicija omogoča razlikovanje naslednjih vrst nepopolnih kvadratnih enačb:
Razmislimo o zaporedju rešitve vsake vrste nepopolnih kvadratnih enačb. Rešitev enačbe a · x 2 \u003d 0Kot že omenjeno, koeficienti ustrezajo tej enačbi b in cenako nič. Enačba a x 2 \u003d 0 možno je pretvoriti v enačbo, ki je enakovredna njej x 2 \u003d 0ki jo dobimo tako, da obe strani prvotne enačbe delimo s številom ani enako nič. Očitno dejstvo je, da je koren enačbe x 2 \u003d 0 nič zato 0 2 = 0 . Ta enačba nima drugih korenin, kar je razloženo z lastnostmi stopnje: za poljubno število strni enaka nič, neenakost je resnična p 2\u003e 0, iz česar izhaja, da s p ≠ 0 enakost p 2 \u003d 0nikoli ne bo dosežen. Opredelitev 5 Tako za nepopolno kvadratno enačbo a · x 2 \u003d 0 obstaja enkraten koren x \u003d 0. Primer 2 Na primer, rešimo nepopolno kvadratno enačbo - 3 x 2 \u003d 0. Enačba mu je enakovredna x 2 \u003d 0njen edini koren je x \u003d 0, potem ima izvirna enačba en sam koren - nič. Na kratko je odločitev sprejeta na naslednji način: - 3 x 2 \u003d 0, x 2 \u003d 0, x \u003d 0. Rešitev enačbe a · x 2 + c \u003d 0Naslednji korak je reševanje nepopolnih kvadratnih enačb, kjer je b \u003d 0, c ≠ 0, torej enačbe obrazca a x 2 + c \u003d 0. To enačbo transformiramo tako, da izraz premaknemo iz enega dela enačbe v drugega, spremenimo znak v nasprotno in oba dela enačbe delimo s številom, ki ni enako nič:
Naše preobrazbe so enakovredne, tako da je dobljena enačba enakovredna izvirniku in to dejstvo omogoča sklep o koreninah enačbe. Iz kakšnih pomenov a in cvrednost izraza je odvisna od c a: lahko ima znak minus (na primer, če a \u003d 1 in c \u003d 2, nato - c a \u003d - 2 1 \u003d - 2) ali znak plus (na primer, če a \u003d - 2 in c \u003d 6, potem - c a \u003d - 6 - 2 \u003d 3); ni nič, ker c ≠ 0. Poglejmo se na situacijah, ko - c a< 0 и - c a > 0 . V primeru, ko - c a< 0 , уравнение x 2 = - c a не будет иметь корней. Утверждая это, мы опираемся на то, что квадратом любого числа является число неотрицательное. Из сказанного следует, что при - c a < 0 ни для какого числа str enakost p 2 \u003d - c a ne more biti resnična. Vse je drugače, ko - c a\u003e 0: zapomni si kvadratni koren in postalo bo očitno, da bo koren enačbe x 2 \u003d - c a število - c a, saj je - c a 2 \u003d - c a. Lahko je razumeti, da je število - - c a - tudi koren enačbe x 2 \u003d - c a: res, - - c a 2 \u003d - c a. Enačba ne bo imela drugih korenin. To lahko pokažemo z nasprotno metodo. Najprej označimo korenine, ki smo jih našli zgoraj x 1 in - x 1. Predpostavimo, da ima enačba x 2 \u003d - c a tudi koren x 2ki se razlikuje od korenin x 1 in - x 1. To vemo, namesto v enačbo x njegove korenine, enačbo spremenimo v pošteno številčno enakost. Za x 1 in - x 1 zapišemo: x 1 2 \u003d - c a in za x 2 - x 2 2 \u003d - c a. Na podlagi lastnosti numeričnih enakosti odštejemo eno pravo enakost od drugega pojma z izrazom, kar nam daje: x 1 2 - x 2 2 \u003d 0. Z akcijskimi lastnostmi s številkami napišite zadnjo enakost kot (x 1 - x 2) · (x 1 + x 2) \u003d 0. Znano je, da je produkt dveh števil enak nič in samo, če je vsaj eno od števil nič. Iz zgoraj navedenega izhaja, da x 1 - x 2 \u003d 0 in / ali x 1 + x 2 \u003d 0ista stvar x 2 \u003d x 1 in / ali x 2 \u003d - x 1. Prišlo je do očitnega nasprotja, saj se je sprva strinjalo, da je koren enačbe x 2 drugačen od x 1 in - x 1. Torej smo dokazali, da enačba nima korenin razen x \u003d - c a in x \u003d - - c a. Vse zgornje trditve povzamemo. Opredelitev 6 Nepopolna kvadratna enačba a x 2 + c \u003d 0 enakovredna enačbi x 2 \u003d - c a, ki:
Navajamo primere reševanja enačb a x 2 + c \u003d 0. Primer 3 Podana je kvadratna enačba 9 x 2 + 7 \u003d 0.Treba je najti rešitev zanjo. Rešitev Prosti izraz prenesemo na desno stran enačbe, potem enačba dobi obliko 9 x 2 \u003d - 7. Odgovor je: enačba 9 x 2 + 7 \u003d 0nima korenin. Primer 4 Rešiti je treba enačbo - x 2 + 36 \u003d 0. Rešitev Premaknite 36 na desno stran: - x 2 \u003d - 36. Odgovor je: x \u003d 6 ali x \u003d - 6. Rešitev enačbe a · x 2 + b · x \u003d 0Analiziramo tretjo vrsto nepopolnih kvadratnih enačb, kadar c \u003d 0. Da bi našli rešitev nepopolne kvadratne enačbe a x 2 + b x \u003d 0, uporabljamo metodo faktorizacije. S polinomom na levi strani enačbe razdeli faktor tako, da se izračuna skupni faktor x. Ta korak bo omogočil pretvorbo izvirne nepopolne kvadratne enačbe v njen ekvivalent x · (a · x + b) \u003d 0. In ta enačba je enakovredna množici enačb x \u003d 0 in a x + b \u003d 0. Enačba a x + b \u003d 0 linearni in njegov koren: x \u003d - b a. Opredelitev 7 Torej nepopolna kvadratna enačba a x 2 + b x \u003d 0 bo imel dve korenini x \u003d 0 in x \u003d - b a. Kot primer pritrdite material. Primer 5 Najti moramo rešitev enačbe 2 3 · x 2 - 2 2 7 · x \u003d 0. Rešitev Vzemi ven x iz oklepajev in dobite enačbo x · 2 3 · x - 2 2 7 \u003d 0. Ta enačba je enakovredna enačbam x \u003d 0 in 2 3x - 2 2 7 \u003d 0. Zdaj je potrebno rešiti dobljeno linearno enačbo: 2 3 · x \u003d 2 2 7, x \u003d 2 2 7 2 3. Na kratko napišemo rešitev enačbe na naslednji način: 2 3 · x 2 - 2 2 7 · x \u003d 0 x · 2 3 · x - 2 2 7 \u003d 0 x \u003d 0 ali 2 3 x - 2 2 7 \u003d 0 x \u003d 0 ali x \u003d 3 3 7 Odgovor je: x \u003d 0, x \u003d 3 3 7. Razlikovalna, formula korenin kvadratne enačbeČe želite najti rešitev kvadratnih enačb, obstaja koreninska formula: Opredelitev 8 x \u003d - b ± D 2 · a, kjer D \u003d b 2 - 4 Ali je tako imenovana diskriminatorka kvadratne enačbe. Pojem x \u003d - b ± D 2 · v bistvu pomeni, da je x 1 \u003d - b + D 2 · a, x 2 \u003d - b - D 2 · a. Koristno bo razumeti, kako je nastala ta formula in kako jo uporabiti. Izpeljava formule za korenine kvadratne enačbeSoočimo se z izzivom reševanja kvadratne enačbe a x 2 + b x x + c \u003d 0. Izvedemo številne enakovredne transformacije:
Tako smo prišli do enačbe x + b 2 · a 2 \u003d b 2 - 4 · a · c 4 · a 2, kar je enako prvotni enačbi a x 2 + b x x + c \u003d 0. Rešitev takšnih enačb smo analizirali v prejšnjih odstavkih (rešitev nepopolnih kvadratnih enačb). Že pridobljene izkušnje omogočajo sklep glede korenin enačbe x + b 2 · a 2 \u003d b 2 - 4 · a · c 4 · a 2:
Iz tega je razviden edini koren x \u003d - b 2 · a;
Sklepati je mogoče, da je prisotnost ali odsotnost korenin enačbe x + b 2 · a 2 \u003d b 2 - 4 · a · c 4 · a 2 (in zato izvirna enačba) odvisna od znaka izraza b 2 - 4 · a · c 4 · 2, posneta na desni. In znak tega izraza je podan z znakom številčnika, (imenovalca 4 · a 2 bo vedno pozitiven), torej znak izražanja b 2 - 4 · a · c. Na ta izraz b 2 - 4 · a · c ime je podano - razlikovalnik kvadratne enačbe in črka D je opredeljena kot njegova poimenovanje. Tu lahko napišete bistvo diskriminatorja - po njegovi vrednosti in podpisom sklepajo, ali bo imela kvadratna enačba resnične korenine, in če je odgovor, kakšno je število korenin - ena ali dve. Vrnemo se k enačbi x + b 2 · a 2 \u003d b 2 - 4 · a · c 4 · a 2. Ponovno ga napišemo z oznako diskriminatorja: x + b 2 · a 2 \u003d D 4 · a 2. Ponovno oblikujemo zaključke: Opredelitev 9
Rezultat našega sklepanja je bil izpeljava formule za korenine kvadratne enačbe: x \u003d - b + D 2 · a, x \u003d - b - D 2 · a, diskriminatorno D izračunano po formuli D \u003d b 2 - 4. Te formule omogočajo določitev obeh pravih korenin z diskriminacijo, večjo od nič. Kadar je diskriminator nič, bo uporaba obeh formul dala enak koren kot edina rešitev kvadratne enačbe. V primeru, ko je diskriminator negativen, ko poskušamo uporabiti korensko formulo kvadratne enačbe, se soočamo s potrebo po izločanju kvadratnega korena negativnega števila, kar nas bo popeljalo izven obsega resničnih števil. Če je diskriminator negativen, kvadratna enačba ne bo imela pravih korenin, možen pa je par zapletenih konjugiranih korenin, določenih z istimi koreninskimi formulami, ki smo jih dobili. Algoritem za reševanje kvadratnih enačb s korenskimi formulamiKvadratno enačbo je mogoče rešiti tako, da takoj uporabimo korensko formulo, v bistvu pa po potrebi poiščemo zapletene korenine. V večini primerov je običajno mišljeno iskanje ne zapletenih, temveč resničnih korenin kvadratne enačbe. Potem je optimalno, preden uporabimo formule korenin kvadratne enačbe, najprej določiti diskriminatorno in se prepričati, da ni negativna (sicer sklepamo, da enačba nima pravih korenin) in nato nadaljujemo z izračunom vrednosti korenin. Zgornja obrazložitev omogoča oblikovanje algoritma za reševanje kvadratne enačbe. Opredelitev 10 Za reševanje kvadratne enačbe a x 2 + b x x + c \u003d 0potrebno:
Upoštevajte, da kadar je diskriminator nič, lahko uporabite formulo x \u003d - b ± D 2 · a, bo dala enak rezultat kot formula x \u003d - b 2 · a. Poglejmo nekaj primerov. Primeri reševanja kvadratnih enačbPodajamo rešitev primerov za različne vrednosti diskriminatornega. Primer 6 Poiskati je treba korenine enačbe x 2 + 2 x - 6 \u003d 0. Rešitev Zapišemo numerične koeficiente kvadratne enačbe: a \u003d 1, b \u003d 2 in c \u003d - 6. Nato delujemo po algoritmu, tj. nadaljujemo z izračunom diskriminatornega, za katerega nadomestimo koeficiente a, b in c v diskriminatorni formuli: D \u003d b 2 - 4 · a · c \u003d 2 2 - 4 · 1 · (- 6) \u003d 4 + 24 \u003d 28. Torej, dobili smo D\u003e 0, kar pomeni, da bo imela izvirna enačba dve resnični korenini. x \u003d - 2 ± 2 · 7 2 x \u003d - 2 + 2 · 7 2 ali x \u003d - 2 - 2 · 7 2 x \u003d - 1 + 7 ali x \u003d - 1 - 7 Odgovor je: x \u003d - 1 + 7, x \u003d - 1 - 7. Primer 7 Potrebno je rešiti kvadratno enačbo - 4x 2 + 28x - 49 \u003d 0. Rešitev Opredelite diskriminatorno: D \u003d 28 2 - 4 · (- 4) · (- 49) \u003d 784 - 784 \u003d 0. S to razlikovalno vrednostjo bo imela začetna enačba le en koren, določen s formulo x \u003d - b 2 · a. x \u003d - 28 2 · (- 4) x \u003d 3, 5 Odgovor je: x \u003d 3, 5. Primer 8 Rešiti je treba enačbo 5y 2 + 6y + 2 \u003d 0 Rešitev Številčni koeficienti te enačbe bodo: a \u003d 5, b \u003d 6 in c \u003d 2. Te vrednosti uporabimo za iskanje diskriminatornega: D \u003d b 2 - 4 · a · c \u003d 6 2 - 4 · 5 · 2 \u003d 36 - 40 \u003d - 4. Izračunana diskriminacija je negativna, zato prvotna kvadratna enačba nima pravih korenin. V primeru, ko je naloga navesti zapletene korenine, uporabimo korensko formulo z izvajanjem dejanj s kompleksnimi števili: x \u003d - 6 ± 4 4 · 5, x \u003d - 6 + 2 · i 10 ali x \u003d - 6 - 2 · i 10, x \u003d - 3 5 + 1 5 · i ali x \u003d - 3 5 - 1 5 · i. Odgovor je: ni veljavnih korenin; zapletene korenine so naslednje: - 3 5 + 1 5 · i, - 3 5 - 1 5 · i. V šolskem učnem načrtu ni standardne zahteve po iskanju zapletenih korenin, zato, če je med rešitvijo diskriminatorna opredeljena kot negativna, se takoj zapiše odgovor, da pravih korenin ni. Korenska formula za enake koeficienteKoreninska formula x \u003d - b ± D 2 · a (D \u003d b 2 - 4 · a · c) omogoča pridobitev še ene bolj kompaktne formule, ki omogoča iskanje rešitev kvadratnih enačb z enakomernim koeficientom pri x (ali s koeficientom oblike 2 · n, na primer, 2 · 3 ali 14 · ln 5 \u003d 2 · 7 · ln 5). Pokažimo, kako izhaja ta formula. Naloga najdemo rešitev kvadratne enačbe a · x 2 + 2 · n · x + c \u003d 0. Delujemo po algoritmu: določimo diskriminatorno D \u003d (2 · n) 2 - 4 · a · c \u003d 4 · n 2 - 4 · a · c \u003d 4 · (n 2 - a · c) in nato uporabimo korensko formulo: x \u003d - 2 · n ± D 2 · a, x \u003d - 2 · n ± 4 · n 2 - a · c 2 · a, x \u003d - 2 · n ± 2 n 2 - a · c 2 · a, x \u003d - n ± n 2 - a Izraz n 2 - a · c označimo kot D 1 (včasih ga označimo z D "). Formula korenin kvadratne enačbe, ki je obravnavana z drugim koeficientom 2 n, ima obliko: x \u003d - n ± D 1 a, kjer je D 1 \u003d n 2 - a · c. Lahko je videti, da je D \u003d 4 · D 1 ali D 1 \u003d D 4. Z drugimi besedami, D1 je četrtina diskriminatornega. Očitno je znak D 1 enak znaku D, kar pomeni, da lahko znak D 1 služi tudi kot pokazatelj prisotnosti ali odsotnosti korenin kvadratne enačbe. Opredelitev 11 Zato je za rešitev kvadratne enačbe z drugim koeficientom 2 n potrebno:
Primer 9 Rešiti je potrebno kvadratno enačbo 5 · x 2 - 6 · x - 32 \u003d 0. Rešitev Drugi koeficient dane enačbe je lahko predstavljen kot 2 · (- 3). Nato damo dano kvadratno enačbo kot 5 · 2 + 2 · (- 3) · x - 32 \u003d 0, kjer je a \u003d 5, n \u003d - 3 in c \u003d - 32. Izračunamo četrti del diskriminatorne: D 1 \u003d n 2 - a · c \u003d (- 3) 2 - 5 · (- 32) \u003d 9 + 160 \u003d 169. Nastala vrednost je pozitivna, kar pomeni, da ima enačba dve resnični korenini. Določimo jih po ustrezni korenski formuli: x \u003d - n ± D 1 a, x \u003d - - 3 ± 169 5, x \u003d 3 ± 13 5, x \u003d 3 + 13 5 ali x \u003d 3 - 13 5 x \u003d 3 1 5 ali x \u003d - 2 Izračune bi bilo mogoče uporabiti po običajni formuli korenin kvadratne enačbe, vendar bi bila v tem primeru rešitev bolj okorna. Odgovor je: x \u003d 3 1 5 ali x \u003d - 2. Poenostavitev oblike kvadratnih enačbVčasih je mogoče optimizirati obliko prvotne enačbe, kar bo poenostavilo postopek izračuna korenin. Na primer, kvadratna enačba 12 · x 2 - 4 · x - 7 \u003d 0 je očitno bolj priročna za reševanje kot 1200 · x 2 - 400 · x - 700 \u003d 0. Pogosteje poenostavitev oblike kvadratne enačbe poteka z dejanji množenja ali deljenja obeh njenih delov na določeno število. Zgoraj smo na primer poenostavili zapis enačbe 1200 · x 2 - 400 · x - 700 \u003d 0, dobljen z deljenjem obeh njegovih delov na 100. Takšna transformacija je mogoča, kadar koeficienti kvadratne enačbe niso sočasni. Nato običajno razdelijo obe strani enačbe na največji skupni delitelj absolutnih vrednosti njegovih koeficientov. Kot primer uporabimo kvadratno enačbo 12 · x 2 - 42 · x + 48 \u003d 0. Določimo GCD absolutnih vrednosti njegovih koeficientov: GCD (12, 42, 48) \u003d GCD (GCD (12, 42), 48) \u003d GCD (6, 48) \u003d 6. Obe strani izvirne kvadratne enačbe delimo s 6 in dobimo enakovredno kvadratno enačbo 2 · x 2 - 7 · x + 8 \u003d 0. Z množenjem obeh strani kvadratne enačbe se navadno izločijo delni koeficienti. V tem primeru pomnožite z najmanj običajnim večkratnikom imenovalcev njegovih koeficientov. Na primer, če je vsak del kvadratne enačbe 1 6 · x 2 + 2 3 · x - 3 \u003d 0 pomnožen z NOC (6, 3, 1) \u003d 6, potem bo zapisan v enostavnejši obliki x 2 + 4 · x - 18 \u003d 0. Za zaključek ugotavljamo, da se skoraj vedno znebimo minusov s prvim koeficientom kvadratne enačbe, pri čemer spremenimo znake vsakega člana enačbe, kar dosežemo z množenjem (ali deljenjem) obeh delov na -1. Na primer, iz kvadratne enačbe - 2 · x 2 - 3 · x + 7 \u003d 0, lahko preidete na njeno poenostavljeno različico 2 · x 2 + 3 · x - 7 \u003d 0. Razmerje med koreninami in koeficientiFormula korenin kvadratnih enačb x \u003d - b ± D 2 · že znana nam izraža korenine enačbe v smislu njenih numeričnih koeficientov. Na podlagi te formule lahko določimo druga razmerja med koreninami in koeficienti. Najbolj znane in uporabne so formule iz teorema Vieta: x 1 + x 2 \u003d - b a in x 2 \u003d c a. Zlasti za dano kvadratno enačbo je vsota korenin drugi koeficient z nasprotnim znakom, produkt korenin pa je prosti izraz. Na primer po obliki kvadratne enačbe 3 · x 2 - 7 · x + 22 \u003d 0 je mogoče takoj ugotoviti, da je vsota njegovih korenin 7 3 in produkt korenin 22 3. Najdete lahko tudi številne druge relacije med koreninami in koeficienti kvadratne enačbe. Na primer, vsoto kvadratov korenin kvadratne enačbe lahko izrazimo s koeficienti: x 1 2 + x 2 2 \u003d (x 1 + x 2) 2 - 2 · x 1 · x 2 \u003d - ba 2 - 2 · ca \u003d b 2 a 2 - 2 · ca \u003d b 2 - 2 · a · ca 2 Če v besedilu opazite napako, jo izberite in pritisnite Ctrl + Enter Nepopolna kvadratna enačba se od klasičnih (popolnih) enačb razlikuje po tem, da so njeni faktorji ali prosti izraz enaki nič. Graf takšnih funkcij je parabola. Glede na splošni videz jih delimo v 3 skupine. Načela rešitve za vse vrste enačb so enaka. Pri določanju vrste nepopolnega polinoma ni nič zapletenega. Z ilustrativnimi primeri najbolje razmislite o glavnih razlikah:
Slednji primer je precej teoretična možnost in se nikoli ne pojavi pri nalogah za preverjanje znanja, saj je edina resnična vrednost spremenljivke x v izrazu enaka nič. V prihodnosti bomo upoštevali metode in primere reševanja nepopolnih kvadratnih enačb 1) in 2) vrst. Splošni algoritem iskanja spremenljivk in primeri rešitevNe glede na vrsto enačbe se algoritem rešitve zmanjša na naslednje korake:
Nepopolne enačbe najlažje rešimo tako, da levo stran odštejemo in v desni pustimo ničlo. Tako se formula za nepopolno kvadratno enačbo za iskanje korenin zmanjša na izračun vrednosti x za vsak faktor. Naučimo se tega rešiti le v praksi, zato razmislimo o konkretnem primeru iskanja korenin nepopolne enačbe: Kot lahko vidite, je v tem primeru b \u003d 0. Faktor z levo stranjo in dobite izraz: 4 (x - 0,5) ⋅ (x + 0,5) \u003d 0. Očitno je izdelek enak nič, če je vsaj eden od dejavnikov nič. Vrednosti spremenljivke x1 \u003d 0,5 in (ali) x2 \u003d -0,5 izpolnjujejo podobne zahteve. Za enostavno in hitro obvladovanje naloge faktorjiranja kvadratnega trinomala se je treba spomniti naslednje formule: Če izraz nima prostega izraza, je naloga močno poenostavljena. Dovolj bo le, da poiščete in povežete skupni imenovalec. Za jasnost razmislite o primeru, kako rešiti nepopolne kvadratne enačbe oblike ax2 + bx \u003d 0. Spremenite spremenljivko x iz oklepajev in dobite naslednji izraz: x ⋅ (x + 3) \u003d 0. V skladu z logiko sklepamo, da je x1 \u003d 0 in x2 \u003d -3. Tradicionalni način reševanja in nepopolnih kvadratnih enačbKaj se bo zgodilo, če bomo uporabili razlikovalno formulo in poskušali najti korenine polinoma s koeficienti, ki so enaki nič? Vzemimo primer iz zbirke značilnih nalog za USE iz matematike 2017, rešili ga bomo s pomočjo standardnih formul in metode faktorizacije. 7x 2 - 3x \u003d 0. Izračunamo vrednost diskriminatorjev: D \u003d (-3) 2 - 4 ⋅ (-7) ⋅ 0 \u003d 9. Izkaže se, da ima polinom dve korenini: Zdaj rešite enačbo s faktoringom in primerjajte rezultate. X ⋅ (7x + 3) \u003d 0, 2) 7x + 3 \u003d 0, Kot lahko vidite, obe metodi dajeta enak rezultat, vendar se je reševanje enačbe z drugo metodo izkazalo veliko lažje in hitreje. Teorem VietaToda kaj storiti z najljubšim izrekom Viete? Ali lahko to metodo uporabimo z nepopolnim trinomilom? Poskusimo razumeti vidike redukcije nepopolnih enačb na klasično obliko ax2 + bx + c \u003d 0. Pravzaprav je v tem primeru mogoče uporabiti izrek Viete. Potrebno je le, da izraz spravite v splošno obliko in nadomestite manjkajoče izraze z ničlo. Na primer, za b \u003d 0 in a \u003d 1, da bi odpravili verjetnost zmede, nalogo napišite v obliki: ax2 + 0 + c \u003d 0. Nato lahko razmerje vsote in produkta korenin in faktorjev polinoma izrazimo takole:
Teoretični izračuni pomagajo spoznati bistvo vprašanja in vedno zahtevajo razvijanje veščin za reševanje določenih problemov. Spet se obrnemo na referenčni seznam značilnih nalog za izpit in poiščemo primeren primer: Izraz zapišemo v obliki, ki je priročna za uporabo teorema Vieta: x 2 + 0 - 16 \u003d 0. Naslednji korak je ustvariti sistem pogojev:
Očitno sta korenina kvadratnega polinoma x 1 \u003d 4 in x 2 \u003d -4. Zdaj pa trenirajmo, da enačbo spravimo v splošno obliko. Vzemimo naslednji primer: 1/4 × x 2 - 1 \u003d 0 Da bi uporabili izrek Vieta na izraz, se je treba znebiti frakcije. Levo in desno stran pomnožimo s 4 in pogledamo rezultat: x2–4 \u003d 0. Nastalo enakost je pripravljeno rešiti s teoremom Vieta, vendar je veliko lažje in hitreje odgovor dobiti preprosto s premikanjem c \u003d 4 na desno stran enačbe: x2 \u003d 4. Če povzamemo, je treba reči, da je najboljši način za reševanje nepopolnih enačb faktorizacija, je najpreprostejša in najhitrejša metoda. Če naletite na težave pri iskanju korenin, se lahko obrnete na tradicionalno metodo iskanja korenin s pomočjo diskriminatornih. Sodelujemo z kvadratne enačbe. To so zelo priljubljene enačbe! V najbolj splošni obliki je kvadratna enačba videti takole: Na primer:
Tukaj ampak =1; b = 3; c = -4
Tukaj ampak =2; b = -0,5; c = 2,2
Tukaj ampak =-3; b = 6; c = -18 No, razumeš ... Kako rešiti kvadratne enačbe? Če je pred vami kvadratna enačba v tej obliki, potem je vse že preprosto. Zapomni si magično besedo diskriminatorno . Redki srednješolec te besede ni slišal! Stavek "odloči se diskriminatorno" vzbuja zaupanje in je spodbuden. Ker vam ni treba čakati na trike od diskriminatornega! Je enostavno in brez težav ravnati. Torej, formula za iskanje korenin kvadratne enačbe izgleda tako:
Izraz pod znakom korena je zelo enak diskriminatorno. Kot lahko vidite, za iskanje x uporabimo samo a, b in c. I.e. koeficienti iz kvadratne enačbe. Samo nežno nadomestite vrednosti a, b in c v to formulo in razmislite. Namestnik s svojimi znaki! Na primer za prvo enačbo ampak =1; b = 3; c \u003d -4. Tako pišemo: Primer je skoraj rešen:
To je vse. Kateri primeri so možni pri uporabi te formule? Samo trije primeri. 1. Diskriminator je pozitiven. To pomeni, da lahko iz njega izvlečete korenino. Dober koren se pridobiva, ali slab - drugo vprašanje. Pomembno je, da se načeloma pridobi. Potem ima vaša kvadratna enačba dve korenini. Dve različni rešitvi. 2. Diskriminator je nič. Potem imate eno rešitev. Strogo gledano, to ni en koren, ampak dve enaki. Toda to igra vlogo pri neenakostih, tam bomo zadevo podrobneje preučili. 3. Diskriminator je negativen. Iz negativnega števila se kvadratni koren ne izvleče. No, ok. To pomeni, da ni rešitev. Vse je zelo preprosto. In kaj, mislite, da ne morete zmotiti? No, ja ... Recimo, da moramo rešiti tak primer:
Tukaj a \u003d -6; b \u003d -5; c \u003d -1 Recimo, da veste, da le redko prejmete odgovore. Pa ne bodi len. Pisanje dodatne vrstice bo trajalo 30 sekund in število napak močno pade. Tako pišemo podrobno, z vsemi oklepaji in znaki:
Zdi se, da je neverjetno težko tako skrbno barvati. A le zdi se. Poskusite. No, ali pa izberite. Kateri je boljši, hiter ali pravi? Poleg tega vas bom osrečil. Čez nekaj časa ni treba vse tako skrbno barvati. Sama se bo pravilno izkazala. Še posebej, če uporabljate spodaj opisane praktične tehnike. Ta zlobni primer s kopico minusov se bo rešil enostavno in brez napak! Torej kako rešiti kvadratne enačbe skozi diskriminatorno smo se spomnili. Ali naučeno, kar tudi ni slabo. Znati določiti a, b in c. Veš kako previdno nadomestite jih v korenski formuli in previdno šteje rezultat. Razumete, da je tu ključna beseda previdno? Vendar so pogosto kvadratne enačbe videti nekoliko drugače. Na primer takole:
Je nepopolne kvadratne enačbe . Rešimo jih lahko tudi z diskriminacijo. Samo ugotoviti morate, kakšni so tukaj enaki a, b in c. Ste se zavedali? V prvem primeru a \u003d 1; b \u003d -4; ampak c? Sploh ga ni! No ja, kajne. V matematiki to pomeni c \u003d 0 ! To je vse. Namesto tega v formuli nadomestimo nič c in uspelo nam bo. Podobno je z drugim primerom. Samo nič tukaj ni s, in b ! Toda nepopolne kvadratne enačbe je mogoče rešiti veliko lažje. Brez diskriminatornih. Razmislite o prvi nepopolni enačbi. Kaj je mogoče storiti tam na levi strani? X lahko postavite iz oklepajev! Vzemimo ga ven.
In kaj od tega? In dejstvo, da je izdelek takrat enak nič in le, če je kateri koli od dejavnikov enak nič! Ne verjamete? No, potem si omislite dve ne-nič številki, ki bota, pomnoženi z ničlo, dali! To je vse. To bodo korenine naše enačbe. Oboje ustreza. Če katero koli izmed njih nadomestimo s prvotno enačbo, dobimo pravilno identiteto 0 \u003d 0. Kot vidite, je rešitev veliko preprostejša kot skozi diskriminatorno. Drugo enačbo je mogoče rešiti tudi preprosto. Premaknite se 9 na desno. Dobili smo: Ostane še ekstrakt korenine 9 in to je to. Izkazalo se bo:
Tudi dve korenini . x \u003d +3 in x \u003d -3. Tako so rešene vse nepopolne kvadratne enačbe. Bodisi tako, da x postavimo iz oklepaja ali preprosto prestavimo številko v desno, čemur sledi izvleček korena. Zdaj pa upoštevajte praktične tehnike, ki močno zmanjšajo število napak. Prav tiste zaradi nepazljivosti, za katere se potem zgodi, da so boleče in žaljive ... Prvi sprejem. Ne bodite leni, preden rešite kvadratno enačbo, da jo pripeljete do standardne oblike. Kaj to pomeni?
Ne hitite, da napišete formulo korenin! Kvote boste gotovo mešali a, b in c. Primer pravilno sestavite. Najprej X na kvadrat, nato brez kvadrata, nato prosti član. Takole:
In spet ne hitite! Minus pred X v kvadratu vas lahko razjezi. Pozabiti je enostavno ... Znebite se minus. Kako? Da, kot je bilo poučeno v prejšnji temi! Celo enačbo je potrebno pomnožiti z -1. Dobili smo:
In zdaj lahko varno zapišete formulo za korenine, upoštevajte diskriminatorno in dopolnite primer. Naredite sami. Morali bi dobiti korenine 2 in -1. Sprejem drugega. Preverite korenine! Po izreku Vieta. Ne bojte se, vse bom razložil! Preverite zadnji enačba. I.e. tisto, s katero smo zapisali korensko formulo. Če (kot v tem primeru) koeficient a \u003d 1Preverjanje korenin je enostavno. Dovolj je, da jih pomnožimo. Morali bi dobiti prost termin, tj. v našem primeru -2. Upoštevajte, ne 2, ampak -2! Brezplačni član s svojim znakom
. Če se to ni izšlo, pomeni, da so se nekje zmešali. Poiščite napako. Če se bo izšlo, morate položiti korenine. Zadnji in zadnji pregled. Morali bi dobiti koeficient b s nasproti
poznan. V našem primeru -1 + 2 \u003d +1. Koeficient bki je pred x -1. Torej, to je v redu! Tretji sprejem. Če ima vaša enačba delne koeficiente, se znebite ulomkov! Enačbo pomnožimo s skupnim imenovalcem, kot je opisano v prejšnjem razdelku. Ko delajo z deli napake, se zaradi nekega razloga povzpnejo ... Mimogrede, obljubil sem, da bom hudoben zgled poenostavil s kopico minusov. Prosim! Tu je.
Da se ne bi zmedli v minusih, enačbo pomnožimo z -1. Dobili smo:
To je vse! Odločanje je užitek! Torej, če povzamem temo. Praktični nasveti: 1. Pred rešitvijo pripeljemo kvadratno enačbo v standardni obrazec, jo sestavimo prav. 2. Če je pred x-kvadratom negativen koeficient, ga odpravimo tako, da celotno enačbo pomnožimo z -1. 3. Če so koeficienti delni, ulomke odpravimo tako, da celotno enačbo pomnožimo z ustreznim faktorjem. 4. Če je kvadrat kvadrata čist, koeficient je enak enoti, je rešitev mogoče enostavno preveriti z izrekom Vieta. Naredi! Delne enačbe. DLD. Nadaljujemo obvladovanje enačbe. Že vemo, kako delati z linearnimi in kvadratnimi enačbami. Zadnji pogled je ostal - delne enačbe. Ali pa jih imenujejo tudi veliko bolj trdno - delno racionalne enačbe. Je eno in isto. Delne enačbe. Kot že ime pove, so v teh enačbah nujno prisotni ulomki. Toda ne le ulomki, ampak frakcije, ki jih imamo neznan v imenovalcu. Vsaj v enem. Na primer:
Spomnim se, če samo v imenovalcih številke, to so linearne enačbe. Kako se odločiti delne enačbe? Najprej se znebite frakcij! Po tem se enačba najpogosteje spremeni v linearno ali kvadratno. In potem vemo, kaj storiti ... V nekaterih primerih se lahko spremeni v identiteto, na primer 5 \u003d 5 ali napačen izraz, na primer 7 \u003d 2. A to se redko zgodi. Spodaj ga bom omenil. Toda kako se znebiti frakcij !? Zelo preprosto. Uporaba vseh enakih transformacij. Celo enačbo moramo pomnožiti z istim izrazom. Tako, da so vsi imenovalci zmanjšani! Vse bo takoj postalo lažje. Razložim s primerom. Rešimo enačbo: Kako so se učili v osnovnih razredih? Vse prenesemo v eno smer, pripeljemo do skupnega imenovalca itd. Pozabi kot nočna mora! To morate storiti, ko dodate ali odštejete frakcijske izraze. Ali pa delajte z neenakostmi. In v enačbah takoj pomnožimo obe strani z izrazom, ki nam bo dal priložnost, da zmanjšamo vse imenovalce (tj. V bistvu s skupnim imenovalcem). In kaj je ta izraz? Na levi strani zmanjšamo imenovalec, množenje s x + 2 . In na desni morate pomnožiti z 2. Zato je treba enačbo pomnožiti z 2 (x + 2). Pomnoži:
To je običajno množenje ulovov, vendar bom podrobno napisal:
Upoštevajte, oklepaja še ne odprem (x + 2)! Tako kot celoto zapišem:
Leva stran je v celoti zmanjšana (x + 2), in v desni 2. Kaj je bilo potrebno! Po zmanjšanju dobimo linearno enačba: In to enačbo bodo rešili vsi! x \u003d 2. Rešimo še en primer, nekoliko bolj zapleten:
Če se spomnimo, da je 3 \u003d 3/1, in 2x \u003d 2x /1, lahko napišete:
In spet se znebimo tistega, kar v resnici ne maramo - od frakcij. Vidimo, da morate imenovalec zmanjšati s x, če množico pomnožite s (x - 2). In enote nam niso ovira. No, pomnožite se. Po vsem levo stran in vse desna stran:
Spet oklepaji (x - 2) Ne razkrijem. Delam z oklepajem kot celoto, kot da bi šlo za eno samo številko! To je treba vedno storiti, sicer se nič ne bo zmanjšalo.
Z občutkom globokega zadovoljstva smo posekali (x - 2) in dobite enačbo brez frakcij v ravnilu! In zdaj odpremo oklepaje: Podobne damo, vse prenesemo na levo stran in dobimo:
Klasična kvadratna enačba. Toda minus pred nami ni dober. Vedno se ga lahko znebite tako, da pomnožite ali delite na -1. Če pa natančno pogledate primer, boste opazili, da je najbolje to enačbo razdeliti na -2! Z enim naletom bo minus izginil in kvote bodo lepše! Delite z -2. Na levi strani - izraz, in na desni - samo delite z ničjo na -2, nič in dobite:
Rešujemo ga skozi diskriminatorno in preverjamo s teoremom Vieta. Dobimo x \u003d 1 in x \u003d 3. Dve korenini. Kot lahko vidite, je v prvem primeru enačba po transformaciji postala linearna, tukaj pa - kvadratna. Dogaja se, da se po odstranitvi frakcij zmanjšajo vsi X-ji. Ostaja nekaj kot 5 \u003d 5. To pomeni, da x je lahko kateri koli. Karkoli že bo, se bo še vedno pogodilo. In res je, 5 \u003d 5. Toda potem, ko se znebite frakcij, se lahko izkaže, da so popolnoma neresnične, tip 2 \u003d 7. In to pomeni, da to brez rešitev! Pri katerem koli x se izkaže za neresnico. Uresničil glavno rešitev delne enačbe? Je preprost in logičen. Izvirni izraz spremenimo tako, da izgine vse, kar nam ni všeč. Ali pa se vmešava. V tem primeru gre za frakcije. Na enak način bomo storili z vsemi vrstami zapletenih primerov z logaritmi, sinusi in drugimi grozotami. Mi smo vedno vsega se bomo znebili. Vendar moramo spremeniti izvirni izraz v smer, ki jo potrebujemo po pravilih, da ... Razvoj tega je priprava na izpit iz matematike. Torej mojster. Zdaj se bomo naučili, kako obiti enega od glavne zasede na izpitu! Najprej pa poglejmo, če se vanj zapleteš ali ne. Poglejmo preprost primer:
Stvar je že znana, oba dela pomnožimo s (x - 2)dobimo:
Opomni z oklepaji (x - 2) delamo kot z enim, integralnim izrazom!
Tu nisem napisal enotnosti v imenovalcih, to je trdno ... In nisem imenoval oklepajev v imenovalcih, razen x - 2 nič ni, ne znaš risati. Skrajšajte:
Odpremo oklepaje, vse premaknemo v levo, damo podobne:
Odločimo se, preverimo, dobimo dve korenini. x \u003d 2 in x \u003d 3. Super. Predpostavimo, da naloga piše, da napišemo koren ali njihovo vsoto, če je več korenin. Kaj bomo napisali? Če se odločite, da je odgovor 5, ste so bili v zasedi. In naloga ne bo štela vase. Delovali so zaman ... Pravilen odgovor je 3. Kaj je narobe ?! In poskusite narediti pregled. Nadomestite neznane vrednosti v vir primer. In če s x \u003d 3 vse skupaj bo čudovito raslo, dobili smo 9 \u003d 9, potem pa na x \u003d 2 dobili delitev z ničlo! Česar se kategorično ne da. Pomeni x \u003d 2 ne gre za rešitev in se v odgovoru ne upošteva. To je tako imenovana zunanja ali presežna korenina. Samo spustimo ga. Končni koren je eden. x \u003d 3. Kako pa ?! - slišim ogorčene vzklike. Naučili so nas, da enačbo lahko pomnožimo z izrazom! To je identična transformacija! Da, enako. Pod majhnim pogojem - izrazom, s katerim množimo (delimo) - ničelna vrednost. A x - 2 ob x \u003d 2 enako nič! Torej je vse pošteno. In kaj zdaj storiti ?! Ne pomnožite z izrazom? Vsakokrat preverite? Spet nerazumljivo! Miren Brez panike! V teh težkih razmerah nas bodo rešile tri čarobne črke. Vem, kaj si mislila. Prav! Je DLD . Območje veljavnih vrednosti. Upam, da se boste s tem člankom naučili najti korenine polne kvadratne enačbe. S pomočjo diskriminatornih rešujejo le popolne kvadratne enačbe, za reševanje nepopolnih kvadratnih enačb pa se uporabljajo druge metode, ki jih boste našli v članku »Reševanje nepopolnih kvadratnih enačb«. Katere kvadratne enačbe imenujemo popolne? Je enačbe oblike ax 2 + b x + c \u003d 0, kjer koeficienti a, b in c niso enaki nič. Torej, za reševanje celotne kvadratne enačbe moramo izračunati diskriminatorno D. D \u003d b 2 - 4ac. Glede na pomen diskriminatornega odgovora zapišemo. Če je diskriminator negativno število (D< 0),то корней нет. Če je diskriminator enak nič, potem je x \u003d (-b) / 2a. Kadar je diskriminator pozitivno število (D\u003e 0), potem je x 1 \u003d (-b - √D) / 2a in x 2 \u003d (-b + √D) / 2a. Na primer. Reši enačbo x 2 - 4x + 4 \u003d 0. D \u003d 4 2 - 4 · 4 \u003d 0 x \u003d (- (-4)) / 2 \u003d 2 Odgovor: 2. Rešite enačbo 2 x 2 + x + 3 \u003d 0. D \u003d 1 2 - 4 · 2 · 3 \u003d - 23 Odgovor: korenin ni. Rešite enačbo 2 x 2 + 5x - 7 \u003d 0. D \u003d 5 2 - 4 · 2 · (–7) \u003d 81 x 1 \u003d (-5 - 81) / (2 · 2) \u003d (-5 - 9) / 4 \u003d - 3,5 x 2 \u003d (-5 + 81) / (2 · 2) \u003d (-5 + 9) / 4 \u003d 1 Odgovor: - 3,5; 1. Predstavljajte si torej rešitev popolnih kvadratnih enačb s vezjem na sliki 1. S pomočjo teh formul lahko rešite katero koli celotno kvadratno enačbo. To morate samo skrbno spremljati enačba je bila napisana kot standardni polinom ampak x 2 + bx + c, sicer lahko naredite napako. Na primer, v zapisu enačbe x + 3 + 2x 2 \u003d 0 se lahko napačno odloči, da a \u003d 1, b \u003d 3 in c \u003d 2. Nato D \u003d 3 2 - 4 · 1 · 2 \u003d 1 in potem ima enačba dva korena. In to ne drži. (Glej rešitev zgornjega primera 2). Če enačba torej ni napisana z polinomom standardne oblike, mora biti najprej polna kvadratna enačba zapisana z polinomom standardne oblike (na prvem mestu naj bo monom z najvišjo eksponentno t.j. ampak x 2 potem z manj – bxin nato svoboden član s Pri reševanju kvadratne enačbe in kvadratne enačbe z enakomernim koeficientom v drugem izrazu lahko uporabimo druge formule. Seznanimo se s temi formulami. Če je v polni kvadratni enačbi z drugim pojmom koeficient enakomeren (b \u003d 2k), potem lahko enačbo rešimo s formulami, prikazanimi na diagramu slike 2. Celotna kvadratna enačba se imenuje zmanjšana, če je koeficient x 2 enako enotnosti in enačba ima obliko x 2 + px + q \u003d 0. Takšno enačbo lahko damo za rešitev ali dobimo z deljenjem vseh koeficientov, enačbo s koeficientom ampakstoji ob x 2 . Slika 3 prikazuje diagram rešitve zmanjšanega kvadrata Primer. Reši enačbo 3x 2 + 6x - 6 \u003d 0. Rešimo to enačbo s pomočjo formul na sliki 1. D \u003d 6 2 - 4 · 3 · (- 6) \u003d 36 + 72 \u003d 108 √D \u003d √108 \u003d √ (36 · 3) \u003d 6√3 x 1 \u003d (-6 - 6√3) / (2 · 3) \u003d (6 (-1 - √ (3))) / 6 \u003d –1 - √3 x 2 \u003d (-6 + 6√3) / (2 · 3) \u003d (6 (-1+ √ (3))) / 6 \u003d –1 + √3 Odgovor: –1 - √3; –1 + √3 Opazite lahko, da je koeficient x v tej enačbi enakomerno število, to je b \u003d 6 ali b \u003d 2k, od kod je k \u003d 3. Nato bomo enačbo poskusili rešiti s pomočjo formul, prikazanih na diagramu slike D 1 \u003d 3 2 - 3 · (- 6 ) \u003d 9 + 18 \u003d 27 √ (D 1) \u003d √27 \u003d √ (9 · 3) \u003d 3√3 x 1 \u003d (-3 - 3√3) / 3 \u003d (3 (-1 - √ (3))) / 3 \u003d - 1 - √3 x 2 \u003d (-3 + 3√3) / 3 \u003d (3 (-1 + √ (3))) / 3 \u003d - 1 + √3 Odgovor: –1 - √3; –1 + √3. Če opazimo, da so vsi koeficienti v tej kvadratni enačbi deljivi s 3 in izvedemo delitev, dobimo zmanjšano kvadratno enačbo x 2 + 2x - 2 \u003d 0 To enačbo rešimo s pomočjo formul za zmanjšano kvadratno enačbo D 2 \u003d 2 2 - 4 · (- 2) \u003d 4 + 8 \u003d 12 √ (D 2) \u003d √12 \u003d √ (4 · 3) \u003d 2√3 x 1 \u003d (-2 - 2√3) / 2 \u003d (2 (-1 - √ (3))) / 2 \u003d - 1 - √3 x 2 \u003d (-2 + 2√3) / 2 \u003d (2 (-1+ √ (3))) / 2 \u003d - 1 + √3 Odgovor: –1 - √3; –1 + √3. Kot lahko vidite, smo pri reševanju te enačbe z uporabo različnih formul dobili enak odgovor. Zato, ko ste dobro obvladali formule, prikazane na diagramu slike 1, lahko vedno rešite katero koli popolno kvadratno enačbo. blog.site, s popolnim ali delnim kopiranjem gradiva je treba navesti vir. Kvadratna enačba - je rešena preprosto! * Nadalje v besedilu "KU".Prijatelji, zdi se, da bi bilo pri matematiki morda lažje kot reševanje takšne enačbe. A nekaj mi je govorilo, da so mnogi imeli težave z njim. Odločila sem se, da vidim koliko prikazov na zahtevo mesečno odda Yandex. Evo, kaj se je zgodilo, poglejte:
Kaj to pomeni? To pomeni, da približno 70.000 ljudi mesečno išče te podatke, kakšne ima to veze s poletjem in kaj se bo zgodilo sredi šolskega leta - prošenj bo dvakrat več. To ni presenetljivo, saj ti fantje in dekleta, ki so že dolgo končali šolo in se pripravljajo na izpit, iščejo te podatke, pa tudi šolarji si ga prizadevajo osvežiti v spominu. Kljub temu, da obstaja veliko spletnih mest, ki vam povedo, kako rešiti to enačbo, sem se odločil, da bom prispeval in objavil gradivo. Prvič, želim, da obiskovalci na to zahtevo pridejo na mojo spletno stran; drugič, v drugih člankih bom glede govora "KU" podal povezavo do tega članka; tretjič, o njegovi rešitvi vam bom povedal malo več, kot je običajno navedeno na drugih spletnih mestih. Začnimo!Vsebina članka: Kvadratna enačba je enačba oblike:
kjer so koeficienti a,b in c sta poljubna števila, ≠ 0. V šolskem tečaju je gradivo podano v naslednji obliki - razdelitev enačb v tri razrede je pogojno opravljeno: 1. Imejte dve korenini. 2. * Imejte samo eno korenino. 3. nimajo korenin. Tu je vredno omeniti, da nimajo veljavnih korenin Kako se izračunajo korenine? Preprosto! Izračunamo diskriminatorno. V tej "strašljivi" besedi se skriva zelo preprosta formula:
Osnovne formule so naslednje:
* Te formule je treba znati na pamet. Takoj lahko posnamete in se odločite: Primer:
1. Če je D\u003e 0, potem ima enačba dve korenini. 2. Če je D \u003d 0, potem ima enačba en koren. 3. Če je D< 0, то уравнение не имеет действительных корней. Poglejmo enačbo:
Ob tej priložnosti, ko je diskriminator nič, šolski tečaj pravi, da se dobi ena korenina, tukaj je devet. Tako je, ampak je ... To stališče je nekoliko nekoliko napačno. Pravzaprav se izkaže, da sta dve korenini. Da, ne bodite presenečeni, dobite dve enaki korenini in če želite biti matematično natančni, v odgovor zapišite dve korenini: x 1 \u003d 3 x 2 \u003d 3 Toda to je majhna digresija. V šoli lahko posnamete in rečete, da je koren ena. Zdaj naslednji primer:
Kot vemo, koren ni izvlečen iz negativne številke, zato v tem primeru ni rešitve. To je celoten postopek odločanja. Kvadratna funkcija. Pokaže, kako rešitev izgleda geometrijsko. To je izjemno pomembno za razumevanje (v prihodnosti bomo v enem od člankov podrobno analizirali rešitev kvadratne neenakosti). To je funkcija obrazca:
kjer sta x in y spremenljivki a, b, c so podane številke in ≠ 0 Graf je parabola:
Se pravi, da se reši kvadratna enačba z "y", ki je enaka nič, najdemo presečišča parabole z osjo x. Te točke so lahko dve (diskriminatorno pozitivne), ena (diskriminatorna enako nič) in nobena (diskriminatorno negativna). Podrobnosti o kvadratni funkciji lahko vidimo članek Inne Feldman. Upoštevajte naslednje primere: Primer 1: Reši 2x 2 +8 x–192=0 a \u003d 2 b \u003d 8 c \u003d –192 D \u003d b 2 –4ac \u003d 8 2 –4 ∙ 2 ∙ (–192) \u003d 64 + 1536 \u003d 1600
Odgovor: x 1 \u003d 8 x 2 \u003d –12 * Lahko smo takoj razdelili levo in desno stran enačbe za 2, torej poenostavili. Izračuni bodo enostavnejši. Primer 2: Da se odločim x 2–22 x + 121 \u003d 0 a \u003d 1 b \u003d –22 c \u003d 121 D \u003d b 2 –4ac \u003d (- 22) 2 –4 ∙ 1 ∙ 121 \u003d 484–484 \u003d 0
Dobili smo, da je x 1 \u003d 11 in x 2 \u003d 11 V odgovor je dovoljeno napisati x \u003d 11. Odgovor: x \u003d 11 Primer 3: Da se odločim x 2 –8x + 72 \u003d 0 a \u003d 1 b \u003d –8 c \u003d 72 D \u003d b 2 –4ac \u003d (- 8) 2 –4 ∙ 1 ∙ 72 \u003d 64–288 \u003d –224 Diskriminator je negativen, rešitve ni v realnem številu. Odgovor: ni rešitve Diskriminator je negativen. Obstaja rešitev! Tu se bomo osredotočili na reševanje enačbe v primeru, ko dobimo negativno diskriminacijo. Ali veste kaj o kompleksnih številkah? Tu ne bom podrobno govoril o tem, zakaj in od kod so prišli ter kakšna je njihova specifična vloga in potreba po matematiki, to je tema za velik ločen članek. Koncept kompleksnega števila. Malo teorije. Kompleksno število z je število obrazca z \u003d a + bi kjer sta a in b realna števila, je tako imenovana imaginarna enota. a + bi Je ENOTNO ŠTEVILO, ne dodajanje. Izmišljena enota je enaka korenu minus ena:
Zdaj razmislite o enačbi:
Imam dve konjugatni korenini. Nepopolna kvadratna enačba. Razmislite o posebnih primerih, ko je koeficient "b" ali "c" enak nič (ali sta oba enaka nič). Zlahka jih rešujejo brez diskriminatorjev. Primer 1. Koeficient b \u003d 0. Enačba ima obliko:
Pretvori: Primer: 4x 2 –16 \u003d 0 \u003d\u003e 4x 2 \u003d 16 \u003d\u003e x 2 \u003d 4 \u003d\u003e x 1 \u003d 2 x 2 \u003d –2 Primer 2. Koeficient c \u003d 0. Enačba ima obliko:
Pretvarjanje, faktoriziranje:
* Izdelek je enak nič, če je vsaj eden od faktorjev enak nič. Primer: 9x 2 –45x \u003d 0 \u003d\u003e 9x (x - 5) \u003d 0 \u003d\u003e x \u003d 0 ali x - 5 \u003d 0 x 1 \u003d 0 x 2 \u003d 5 Primer 3. Koeficienti b \u003d 0 in c \u003d 0.
Tu je jasno, da bo rešitev enačbe vedno x \u003d 0. Uporabne lastnosti in vzorci koeficientov. Obstajajo lastnosti, ki vam omogočajo reševanje enačb z velikimi koeficienti. ampakx 2 + bx+ c=0 enakost velja a + b + c \u003d 0,torej
- če za koeficiente enačbe ampakx 2 + bx+ c=0 enakost velja a + c \u003db, torej
Te lastnosti pomagajo rešiti določeno vrsto enačbe. Primer 1: 5001 x 2 –4995 x – 6=0 Vsota koeficientov je 5001+ ( – 4995)+(– 6) \u003d 0, kar pomeni
Primer 2: 2501 x 2 +2507 x+6=0 Izpolnjena je enakost a + c \u003db, pomeni
Vzorci koeficientov. 1. Če je v enačbi os 2 + bx + c \u003d 0 koeficient "b" enak (a 2 +1) in koeficient "c" je številčno enak koeficientu "a", potem so njegove korenine enake
os 2 + (a 2 +1) ∙ x + a \u003d 0 \u003d\u003e x 1 \u003d –a x 2 \u003d –1 / a. Primer. Razmislite o enačbi 6x 2 + 37x + 6 \u003d 0. x 1 \u003d –6 x 2 \u003d –1/6. 2. Če je v enačbi os 2 - bx + c \u003d 0 koeficient "b" enak (a 2 +1), koeficient "c" pa je številčno enak koeficientu "a", potem so njegove korenine enake
os 2 - (a 2 +1) ∙ x + a \u003d 0 \u003d\u003e x 1 \u003d a x 2 \u003d 1 / a. Primer. Razmislite o enačbi 15x2 –226x +15 \u003d 0. x 1 \u003d 15 x 2 \u003d 1/15. 3. Če v enačbios 2 + bx - c \u003d koeficient "b" je enako (a 2 - 1) in koeficient "c" številčno enak koeficientu "a", potem so njegove korenine enake
sekira 2 + (a 2 -1) ∙ x - a \u003d 0 \u003d\u003e x 1 \u003d - a x 2 \u003d 1 / a. Primer. Razmislite o enačbi 17x 2 + 288x - 17 \u003d 0. x 1 \u003d - 17 x 2 \u003d 1/17. 4. Če je v enačbi os 2 - bx - c \u003d 0 koeficient "b" enak (a 2 - 1) in koeficient c je številčno enak koeficientu "a", potem so njegove korenine enake
os 2 - (a 2 –1) ∙ x - a \u003d 0 \u003d\u003e x 1 \u003d a x 2 \u003d - 1 / a. Primer. Vzemimo enačbo 10x 2 - 99x –10 \u003d 0. x 1 \u003d 10 x 2 \u003d - 1/10 Vieta izrek. Vietajev izrek je poimenovan po slovitem francoskem matematiku Francoisu Vieti. Z uporabo teorema Vieta lahko izrazimo vsoto in produkt korenin poljubnega KU glede na njegove koeficiente. 45 = 1∙45 45 = 3∙15 45 = 5∙9. Število 14 daje le 5 in 9. To so korenine. Z določeno veščino s pomočjo predstavljenega izrek lahko takoj rešite številne kvadratne enačbe. Vietajev izrek. priročno je, da lahko po reševanju kvadratne enačbe na običajen način (skozi diskriminatorno) preverimo pridobljene korenine. Priporočam, da to počnete vedno. METODA RAVNANJA S to metodo se koeficient "a" pomnoži s prostim izrazom, kot da se "prenese" nanjo, zato se imenuje način "prenosa".Ta metoda se uporablja, kadar je enostavno najti korenine enačbe z izrekom Vieta in, kar je najpomembneje, kadar je diskriminator natančen kvadrat. Če ampak± b + c≠ 0, potem se uporablja metoda prenosa, na primer: 2x 2 – 11x +5 = 0 (1) => x 2 – 11x +10 = 0 (2) Z izrekom Viete v enačbi (2) je enostavno določiti, da je x 1 \u003d 10 x 2 \u003d 1 Dobljene korenine enačbe moramo razdeliti na 2 (saj je x 2 "vrgel" dva), dobimo x 1 \u003d 5 x 2 \u003d 0,5. Kakšna je utemeljitev? Poglejte, kaj se zgodi. Razlikovalniki enačb (1) in (2) sta enaki: Če pogledate korenine enačb, dobite le različne imenovalce, rezultat pa je odvisen od koeficienta pri x 2:
Druga (spremenjena) korenina se izkaže 2-krat več. Zato se rezultat deli z 2. * Če prenesemo tri, potem rezultat razdelimo na 3 itd. Odgovor: x 1 \u003d 5 x 2 \u003d 0,5 V ur-ie in izpit. Na kratko bom povedal o njegovem pomenu - ODLOČITI SE boste morali hitro in brez razmišljanja, koren in diskriminatorne formule morate poznati na pamet. Zelo veliko nalog, ki so del nalog USE, se zmanjša na reševanje kvadratne enačbe (vključno z geometrijskimi). Kaj je vredno opozoriti! 1. Oblika enačbe je lahko "implicitna". Na primer, možen je naslednji vnos: 15+ 9x 2 - 45x \u003d 0 ali 15x + 42 + 9x 2 - 45x \u003d 0 ali 15 -5x + 10x 2 \u003d 0. Morate ga spraviti v standardni obrazec (da se ne boste zmedli pri odločanju). 2. Ne pozabite, da je x neznana količina in jo lahko označimo s katero koli drugo črko - t, q, p, h in drugimi. |
| Preberi: |
|---|
Priljubljeno:
Rešitev najpreprostejših trigonometričnih neenakosti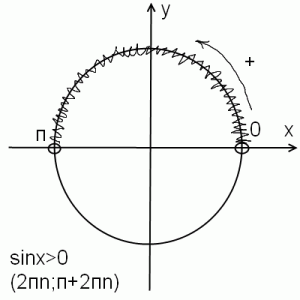
|
Novo
- Kaj je pokvarilo "krutega" barona?
- Član gibanja White
- Pot Suvorova in ekipe v domovino
- Funkcijo F (x) imenujemo antideriva za funkcijo f (x), če je F` (x) \u003d f (x) ali dF (x) \u003d f (x) dx
- Program za zmanjšanje deleža stopinj
- Podobni izrazi, njihovo zmanjšanje, primeri
- Ruski popotniki lazarev
- Reševanje nepopolnih kvadratnih enačb
- Rešitev kvadratnih enačb, formula korenin, primeri
- Koordinatna ravnina (6. razred) - Hipermarket znanja


















 enačbe. Kot primer bomo uporabili formule, obravnavane v tem članku.
enačbe. Kot primer bomo uporabili formule, obravnavane v tem članku. enačbe slika 3.
enačbe slika 3.