Opće teoreme govornika sustava tijela. Teoremi na kretanju središta mase, o promjeni količine kretanja, o promjeni glavne točke količine kretanja, o promjeni kinetičke energije. Načela Dalamberta i mogućih pokreta. Opća jednadžba govornika. Lagrange jednadžbe.

Opći teoremi čvrste dinamike i tijela sustava

Teoremi općih govornika - Ovo je teorem na kretanju središta mase mehanički sustav, Teorem na promjeni u količini pokreta, teorem o promjeni u glavnom trenutku broja kretanja (kinetički trenutak) i teorema na promjeni kinetičke energije mehaničkog sustava.

Teorem na kretanju središta mehaničkog sustava mase

Teorem na kretanju središta mase.
Proizvod masovnog sustava za ubrzanje njegovog središta mase jednaka je vektorskoj zbroj svih vanjskih sila koje djeluju na sustav:
.

Ovdje m je masa sustava:
;
c - ubrzanje središta masovnog sustava:
;
v C - Speed \u200b\u200bCenter sustav:
;
r c - Vektor radijusa (koordinate) Centar masovnog sustava:
;
- koordinate (u odnosu na fiksni centar) i masu bodova iz koje se sustav sastoji.

Teorem o promjeni količine kretanja (impuls)

Pokret sustava (impuls) Jednako tako, masa cjelokupnog sustava na brzini njegovog središta mase ili količine količine kretanja (zbroj impulsa) pojedinih točaka ili dijelova komponenti sustava:
.

Teorem na promjeni u količini kretanja u diferencijalnom obliku.
Vrijeme derivata na količini pokreta (impulsa) sustava jednak je vektorskoj zbroj svih vanjskih sila koje djeluju na sustav:
.

Teorem o promjeni iznosa kretanja u cjelovitim oblicima.
Promjena količine pokreta (pulsa) sustava za određeno vremensko razdoblje jednak je zbroju impulsa vanjske čvrstoće u istom vremenskom razdoblju:
.

Zakon očuvanja količine kretanja (impuls).
Ako zbroj svih vanjskih sila koje djeluju na sustav je nula, tada će vektor pokreta sustava biti konstantan. To jest, sve njegove projekcije na osi koordinata spasit će konstantne vrijednosti.

Ako je količina projekcija vanjskih sila na koje ili osi jednaka nuli, tada će biti konstantna projekcija broja pokreta sustava na ovoj osi.

Teorem na promjeni u glavnoj točki iznosa kretanja (teorem trenutaka)

Glavno vrijeme kretanja sustava u odnosu na ovaj centar o naziva se vrijednost jednaka vektoj zbroj trenutaka kretanja svih točaka sustava u odnosu na ovaj centar:
.
Ovdje kvadratni nosači označavaju vektorsku umjetnost.

Očaravajući sustavi

Dalje ispod teorema odnosi se na slučaj kada mehanički sustav ima fiksnu točku ili os, koja je osigurana u odnosu na inertijskog referentnog sustava. Na primjer, tijelo pričvršćeno na sferični ležaj. Ili sustav tijela koji se kreću oko fiksnog centra. Također može biti fiksna os oko koje se tijelo rotira ili sustav tijela. U ovom slučaju, pod trenucima potrebno je razumjeti trenutke impulsa i sila na fiksnu os.

Teorem na promjeni u glavnoj točki iznosa kretanja (teorem trenutaka)
Vrijeme derivata od glavne točke u količini pokreta sustava u odnosu na određeni stacionarni centar o jednak je zbroju trenutaka svih vanjskih sila sustava u odnosu na isto središte.

Zakon o održavanju glavnog trenutka broja kretanja (trenutak impulsa).
Ako je zbroj trenutaka svih vanjskih sila vezanih za sustav u odnosu na ovaj fiksni centar O je nula, tada će glavni trenutak količine kretanja sustava u odnosu na ovaj centar biti trajan. To jest, sve njegove projekcije na osi koordinata spasit će konstantne vrijednosti.

Ako je zbroj trenutaka vanjskih sila u odnosu na određenu stacionarnu os nula, onda će se trenutak broja kretanja sustava u odnosu na ovu osovinu biti konstantna.

Proizvoljne sustave

Sljedeći teorem ima univerzalnu prirodu. Primjenjivo je na fiksne sustave i slobodno kretanje. U slučaju fiksnih sustava, morate uzeti u obzir reakcije veza u fiksnim točkama. Razlikuje se od prethodnog teorema činjenicom da umjesto fiksne točke o, potrebno je uzeti središte sustava mase C.

Teorem trenutaka u odnosu na središte mase
Vrijeme dobivene od glavne točke u količini pokreta sustava u odnosu na središte mase C jednaka je zbroju trenutaka svih vanjskih sila sustava u odnosu na isto središte.

Zakon očuvanja trenutka impulsa.
Ako je zbroj trenutaka svih vanjskih sila vezanih za sustav u odnosu na središte mase C je nula, onda će glavni trenutak količine kretanja sustava u odnosu na ovaj centar biti konstantan. To jest, sve njegove projekcije na osi koordinata spasit će konstantne vrijednosti.

Trenutak tijela inercije

Ako se tijelo okreće oko osi Z S kutnom brzinom ω z, tada se njegov trenutak kretanja (kinetički trenutak) u odnosu na z osi određuje formulom:
L z \u003d j z ω z,
gdje je J z trenutak inercije tijela u odnosu na z osi.

Trenutak inercije tijela u odnosu na z osi Određeno formulom:
,
Gdje je H K udaljenost od točke mase M na osi Z.
Za tankog prstena masenog m i radijusa R ili cilindra, masa je distribuirana kroz štap,
J z \u003d m r 2 .
Za kruti homogeni prsten ili cilindar,
.

Steiner-Guigens teorem.
Neka CZ - os koja prolazi kroz središte tijela tijela, oz - osa paralelna s njom. Tada su trenuci inercije tijela u odnosu na ove osi povezane s odnosom:
J oz \u003d j cz + m a 2 ,
gdje je m tjelesna težina; A - udaljenost između osi.

Više općenito :
,
Gdje je inercija tenzor.
Ovdje je vektor proveden iz centra mase tijela do točke s masom M K.

Teorem o promjeni kinetičke energije

Neka tijelo mase M izvede translacijski i rotacijski pokret s kutnom brzinom ω oko određene Z osi. Tada je kinetička energija tijela određena formulom:
,
gdje je v C brzina kretanja središta mase tijela;
J CZ je trenutak inercije tijela u odnosu na osovinu koja prolazi kroz središte mase tijela paralelno s osi rotacije. Smjer osi rotacije može varirati s vremenom. Navedena formula daje trenutnu vrijednost kinetičke energije.

Teorem o promjeni kinetičke energije sustava u diferencijalnom obliku.
Diferencijal (prirast) kinetičke energije sustava na neki od njezinih pokreta jednak je količini razlika u radu na ovom kretanju svih vanjskih i unutarnjih sila vezanih za sustav:
.

Teorem na promjeni kinetičke energije sustava u cjelovitim oblicima.
Promjena kinetičke energije sustava na nekim od njezina kretanja jednaka je zbroju rada na ovom kretanju svih vanjskih i unutarnjih sila vezanih uz sustav:
.

Rad koji snaga čini jednak je skalarskom proizvodu vektora čvrstoće i beskrajno malih pokreta točke njegove primjene:
,
To jest, proizvod modula F i DS vektora na kosinuznog kuta između njih.

Rad koji je trenutak snaga jednak je skalarskom proizvodu vektora zakretnog momenta i beskonačno mali kut rotacije:
.

Načelo dalambera

Suština načela Dalambera je zadatak govornika smanjiti statične zadatke. Za to se pretpostavlja (ili je unaprijed poznato) da tijelo sustava ima određene (kutni) ubrzanja. Dalje, inercija se uvodi i (ili) trenutke sila inercije, koji su jednaki u veličini i obrnuto u smjeru sila i trenutaka snaga, koje bi, prema zakonima mehaničara, stvorili određene ubrzanja ili kutni ubrzanja

Razmotrite primjer. Put u tijelu počinio je translacijski pokret i vanjske sile. Zatim pretpostavljamo da te sile stvaraju ubrzanje središta masovnog sustava. Prema teoremu na kretanju središta masa, središte mase tijela imalo bi isto ubrzanje, ako je moć djelovala na tijelu. Dalje, uvozimo moć inercije:
.
Nakon toga, zadatak govornika:
.
;
.

Za rotacijsko gibanje dolazi na isti način. Neka se tijelo okreće oko osi Z i postoje vanjski trenuci M e ZK za to. Pretpostavljamo da ti trenutci stvaraju kutni ubrzanje ε z. Dalje, uvozimo trenutak inercije snage m i \u003d - j z z z. Nakon toga, zadatak govornika:
.
Pretvara se u zadatak statičkog:
;
.

Načelo mogućih pokreta

Načelo mogućih pokreta koristi se za rješavanje statičkih zadataka. U nekim zadacima daje kraće rješenje nego izraditi jednadžbe jednadžbe. To se posebno odnosi na sustave s vezama (na primjer, tijela povezane niti i blokovima) koji se sastoje od mnogih tijela.

Načelo mogućih pokreta.
Za ravnotežu mehaničkog sustava s idealnim vezama, potrebno je i dovoljno da je zbroj elementarnog rada svih aktivnih sila koji djeluju na njega s bilo kojim mogućim pokretom sustava bio je nula.

Moguće kretanje sustava - Ovo je mali pokret u kojem se ne narušavaju veze na sustavu.

Idealne veze - To su veze koje ne čine rad prilikom premještanja sustava. Točnije, količinu posla koji se obavljaju sami priključci kada se sustav kreće je nula.

Opća jednadžba govornika (načelo Dalambera - Lagrange)

Načelo Dalamber - Lagrange je Udruga načela Dalamberta s načelom mogućih pokreta. To jest, pri rješavanju problema dinamike, uvodemo sile inecije i smanjili zadatak statike koje rješavamo uz pomoć načela mogućih pokreta.

Načelo Dalambera - Lagrange.
Prilikom premještanja mehaničkog sustava s idealnim vezama u svakom trenutku, zbroj elementarnog rada svih priključenih aktivnih sila i sve inercijalne sile na bilo kojem mogućem kretanju sustava je nula:
.
Ova jednadžba se zove ukupnu jednadžbu govornika.

Lagrange jednadžbe

Generalizirane koordinate Q. 1, Q 2, ..., q n - Ovo je kombinacija N vrijednosti koje nedvosmisleno određuju položaj sustava.

Broj generaliziranih koordinata N podudara se s brojem stupnjeva slobode sustava.

Generalizirane brzine - To su izvedeni iz generaliziranih koordinata vremena t.

Generalizirane snage Q. 1, Q 2, ..., q n .
Razmotrite moguće kretanje sustava, u kojem će koordinata Q K dobiti kretanje ΔQ k. Preostale koordinate ostaju nepromijenjene. Neka δA K bude posao koji obavljaju vanjske sile s takvim potezom. Zatim
ΔA K \u003d Q K ΔQ K, ili
.

Ako se, s mogućim kretanjem sustava mijenjaju sve koordinate, rad na vanjske sile s takvim potezom ima oblik:
ΔA \u003d P. 1 ΔQ 1 + Q 2 ΔQ 2 + ... + q n ΔQ n.
Tada su generalizirane sile djelomične derivate od pokreta:
.

Za potencijalne sile s potencijalnim π,
.

Lagrange jednadžbe - To su jednadžbe mehaničkog sustava u generaliziranim koordinatama:

Ovdje je kinetička energija. To je funkcija generaliziranih koordinata, brzina i, možda, vrijeme. Stoga je njegov privatni derivat također funkcija generaliziranih koordinata, brzina i vremena. Zatim je potrebno uzeti u obzir da su koordinate i brzine funkcije vremena. Stoga, da biste pronašli potpuni derivat u vremenu, morate primijeniti pravilo diferencijacije složene funkcije:
.

Reference:
S. M. Targ, Kratki tečaj Teorijska mehanika, "viša škola", 2010.

Predavanje 3. Teoremi općih govornika

Dinamika materijalnih točakato je važan dio teoretske mehanike. Ovdje se uglavnom smatra zadacima kretanja mehaničkih sustava (sustavi materijalnih točaka) s konačnim brojem stupnjeva slobode - maksimalni broj neovisnih parametara koji određuju položaj sustava. Glavna zadaća dinamike sustava je proučavanje prometnih zakona čvrst i mehaničkih sustava.

Najjednostavniji pristup proučavanju kretanja sustava koji se sastoji od N. Materijalne točke, koji se spuštaju na razmatranje kretanja svakog pojedinog mjesta sustava. U isto vrijeme, moraju se odrediti sve sile koje djeluju na svakoj točki sustava, uključujući i snagu interakcije između točaka.

Određivanje ubrzanja svake točke u skladu s drugim Newtonskim zakonom (1.2), dobivamo za svaku točku tri skakarna diferencijalna prava drugog pokreta drugog reda, tj. 3 N. diferencijalni zakon kretanja za cijeli sustav.

Da biste pronašli jednadžbe kretanja mehaničkog sustava u skladu s određenim silama i početnim uvjetima za svaku točku sustava, potrebno je integrirati diferencijalne zakone. Ovaj zadatak je težak čak iu slučaju dvaju materijalnih točaka, koji se kreću samo pod djelovanjem interakcijskih snaga pod pravom svjetske atrakcije (zadatak dvaju tijela), te je izuzetno težak u slučaju triju mjesnih mjesta ( zadatak triju tijela).

Stoga je potrebno pronaći takve metode za rješavanje problema koji bi doveli do riješenih jednadžbi i dali ideju o kretanju mehaničkog sustava. Opće teoreme govornika, što su posljedica diferencijalnih prometnih zakona, omogućuju vam da izbjegnete složenost koja proizlazi iz integracije i dobije potrebne rezultate.

3. 1. Opći komentari

Točke mehaničkog sustava bit će numerirane indeksima i., j., k. itd., Koji pokreću sve vrijednosti 1, 2, 3… N.gdje N. - broj točaka sustava. Fizičke količine povezane s k.- Point je označen istim indeksom kao i točkom. Na primjer, radijus-vektor i brzina ekspresna k.točka.

Za svaku od točaka sustava postoje prednosti dvostrukog porijekla: prvo, sile čiji izvori leže izvan sustava koji se zove vanjski snage i označene; Drugo, snage na dijelu drugih točaka ovog sustava, nazvane unutrašnji snage i označene. Domaće snage zadovoljavaju Newtonov treći zakon. Razmotrite najjednostavnija svojstva unutarnjih sila koje djeluju na cijeli mehanički sustav u svakome.

Prvo vlasništvo. Geometrijski zbroj svih unutarnjih sila sustava (glavni vektor unutarnjih sila) je nula.

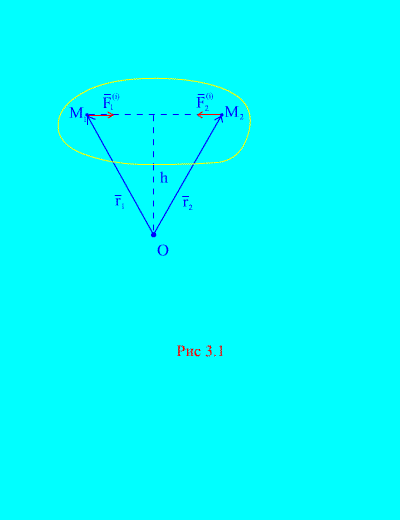
Doista, ako razmislite o bilo kojoj dvije proizvoljne točke sustava, na primjer i (Sl. 3.1)onda za njih jer Snage djelovanja i protuzakoniranja uvijek su jednake modulu, djeluju uz jednu liniju djelovanja u suprotnom smjeru, koji povezuje interakciju bodova. Glavni vektor unutarnjih sila sastoji se od parova sila interakcijskih točaka, dakle

(3.1)

Drugog objekta. Geometrijska suma trenutaka svih unutarnjih sila u odnosu na proizvoljnu točku prostora je nula.

Razmotriti sustav trenutaka snaga i točku OKO(Sl. 3.1), Od (Sl. 3.1), to je jasno

,

jer Obje snage imaju ista ramena i suprotne smjerove vektorskih trenutaka. Glavni trenutak domaće ovlasti OKO Sastoji se od vektorske količine takvih izraza i nula je. Stoga,

Neka se vanjske i unutarnje sile djeluju na mehanički sustav koji se sastoji od N. Bodovi (Sl. 3.2), Ako je svaka točka sustava pričvršćena na automatske vanjske sile i dobivene sve unutarnje sile, onda za bilo koji k.- Ako se točka sustava može izvršiti diferencijalne jednadžbe kretanja. Sve takve jednadžbe će N.:

iu projekcijama za fiksne osi koordinata 3 N.:

(3.4)

Vektorske jednadžbe (3.3) ili ekvivalentne skakarne jednadžbe (3.4) zastupljene su diferencijalnim zakonima kretanja materijalnih točaka cijelog sustava. Ako se sve točke kreću paralelno s jednom ravninom ili jednom ravnom linijom, broj jednadžbi (3.4) u prvom slučaju će 2 N.Drugi N..

Primjer 1. Dva masa opterećenja i međusobno su povezani s nerazumnim kabelom, perkcked kroz blok (Sl. 3.3), Zanemarivanje frikcijskih sila, kao i masu bloka i kabela, kako bi se odredio zakon tereta i napetosti kabela.

Odluka, Sustav se sastoji od dva materijalna tijela (vezana uz neprofitabilnu kabel) koja se kreće paralelno s jednom osi x. Pišemo diferencijalne zakone kretanja u projekcijama na osi h. Za svako tijelo.

Neka se desni teret spusti s ubrzanjem, a zatim će lijevo opterećenje rasti s ubrzanjem. Mentalno pušten s priključka (kabel) i zamijeniti ga reakcijama i (Sl. 3.3), S obzirom na slobodno tijelo, učinit ćemo diferencijalne zakone kretanja u projekciji na osi h. (Ovo se odnosi na napetost niti su unutarnje sile, a težina robe - vanjski):

Jer (tijela su povezana s nerazumnim kabelom), dobivamo

Rješavanje tih jednadžbi u vezi ubrzanja i napetosti kabela T., dobiti

.

Imajte na umu da napetost kabela nije jednaka čvrstoće odgovarajućeg tereta.

3. 2. Teorem masovnog centra

Poznato je da se kruti i mehanički sustav u ravnini mogu premjestiti vrlo teške. Do prvog teorema na kretanju tijela i mehaničkog sustava može se postići kako slijedi: bacanje k.l. Subjekt koji se sastoji od mnogih pričvršćenih krutina. Jasno je da će letjeti na Paraboli. To se pokazalo prilikom proučavanja kretanja točke. Međutim, sada objekt nije točka. Ona se okreće, shacks tijekom procesa leta oko određenog učinkovitog centra, koji se kreće uz Parabolu. Prvi teorem o kretanju složenih predmeta sugerira da je određeni učinkovit centar središte mase premještanja. Središte mase se ne mora nužno nalazi u samom tijelu, može se lagati i negdje izvan njega.

Teorema. Središte mase mehaničkog sustava kreće se kao materijalna točka mase jednaka masi cijelog sustava, na koju se primjenjuju sve vanjske sile na sustav.

Da biste dokazali teoremu, ponovno napišite diferencijalne zakone kretanja (3.3) u sljedećem obliku:

(3.5)

gdje N. - broj točaka sustava.

Pomičući jednadžbu međusobno:

(ali)

Položaj središta masovnog mehaničkog sustava u odnosu na odabrani koordinatni sustav određen je formulom (2.1): Gdje M.- masovni sustav. Zatim lijevo dio Jednakost (a) bit će zabilježena

Prvi iznos koji je stajao u pravom dijelu jednakosti (a) jednak je glavnom vektoru vanjskih sila, a potonji od imovine unutarnjih sila je nula. Zatim jednakost (a), uzimajući u obzir (b) prepisivanje

, (3.6)

oni. produkt masovnog sustava za ubrzanje središta mase jednak je geometrijskoj zbroj svih vanjskih sila koje djeluju na sustav.

Iz jednadžbe (3.6) slijedi da unutarnje sile izravno ne utječu na kretanje središta mase. Međutim, u nekim slučajevima, razlog za izgled vanjskih sila vezanih za sustav. Dakle, unutarnje sile koje vode do rotacije vožnji kotača automobila uzrokuju vanjsku spojku da se nanosi na šipku kotača.

Primjer 2. Mehanizam koji se nalazi u vertikalnoj ravnini montiran je na horizontalnu glatku ravninu i pričvršćena je na to čvrsto fiksirano s površinom šipki DO i L. (Sl. 3.4).

Radijus diska 1 R. Tako. Disk 2 masa m. i radijus r. vezan s ručicom, dugo R.+ r. U točki S 2, Krivoship se rotira s konstantnim

kutna brzina. U početnom trenutku krivopotiranje je zauzelo pravo vodoravni položaj, Zanemarivanje mase ručice, odrediti najveće horizontalne i vertikalne napore koje djeluju na barovima ako je ukupna masa kreveta i kotača 1 jednaka M. Također razmotrite ponašanje mehanizma u odsutnosti šipki.

Odluka, Sustav se sastoji od dvije mase ( N.=2 ): još uvijek disk 1 iz kreveta i pokretnog diska 2. Pošaljite osovinu w.kroz središte gravitacije fiksnog diska okomito, osi h.- duž horizontalne ravnine.

Pišemo teoremu o kretanju središta mase (3.6) u koordinatnom obliku

Vanjske sile ovog sustava su: težina kreveta i stacionarni disk - Mg., Težina mobilnog diska - mg., - Ukupna reakcija horizontalne vijake je normalna potpuna reakcija ravnine. Stoga,

Tada će zakoni pokreta (b) prepisati

Izračunajte koordinate središta mase mehaničkog sustava:

; (d)

kao što se može vidjeti (Sl. 3.4), , , (kut rotacije crpke), , Zamjena ovih izraza u (d) i izračunavanje drugih derivata t. Iz toga, dobivamo to

(e)

Zamjena (c) i (d) u \u200b\u200b(b), nalazimo

Horizontalni tlak koji djeluje na barovima ima najveći i najmanji smisao kada cos. = 1 Prema tome, tj.

Mehanizam tlaka horizontalna ravnina ima najveći i najmanji smisao kada grijeh. prema tome, tj.

U stvari, prva zadaća dinamike je riješena: prema poznatim jednadžbama kretanja središta masovnog sustava (E), obnovljene su sile koje sudjeluju u pokretu.

U odsutnosti barova K. i L. (Sl. 3.4)Mehanizam može početi odskočiti preko horizontalne ravnine. To će se dogoditi kada, tj. Kada slijedi da je kutna brzina rotacije ručice, u kojoj se mehanizam odskakuje, treba zadovoljiti jednakost

.

3. 3. Zakon o konzerviranju kretanja središta mase

Ako glavni vektor vanjskih sila djeluje na sustav je nula, tj. , onda van(3.6) Slijedi da je ubrzanje središta mase nula, stoga je brzina središta mase konstantna u modulu i smjeru. Ako je, posebno, u početnom trenutku, središte mase je sam, on počiva cijelo vrijeme dok glavni vektor vanjskih sila je nula.

Iz ove teorema postoji nekoliko posljedica.

· Jedne unutarnje sile ne mogu se mijenjati po prirodi masovnog centra sustava.

· Ako je glavni vektor vanjskih sila koje djeluje na sustav je nula, onda je središte mase sami ili se kreće ravnomjerno i ravno.

· Ako je projekcija glavnog vektora vanjskih sila sustava na neku fiksnu osovinu nula, tada se projekcija brzine sustava masovnog centra ne mijenja na ovoj osi.

· Par sila vezanih za krutinu ne može promijeniti kretanje njegovog središta mase (može samo uzrokovati rotaciju tijela oko središta masa).

Razmotrite primjer koji ilustrira zakon o konzerviranju kretanja središta mase.

Primjer 3. Dvije pošiljke od masa i povezane su neprofitabilnom nit, blokirane kroz blok (Sl. 3.5)Skinuo je klin M.Klin se oslanja na glatku horizontalnu ravninu. U početnom trenutku sustav je bio sam. Pronađite kretanje klina u ravnini pri spuštanju prvog tereta na visinu N. Zanemarit ćemo blok i nit.

Odluka. Vanjske sile koje djeluju na klin zajedno s teretima su gravitacijske snage i Mg., kao i normalna reakcija glatke horizontalne površine N. Zbog toga,

Budući da je u početnom trenutku sustav bio sam, imamo.

Izračunajte koordinatu središta mase sustava u i tada t. 1 Kada teži težina g. Kune na visini H..

Za sada:

,

gdje H.- Prema tome, koordinate središta mase tereta težine g, G i klin vaganje M.g..

Pretpostavimo da će klin kretati u pozitivnom smjeru osi VOL. Po veličini L.Ako težina težine ide dolje na visinu N.Onda za trenutak

jer učitava zajedno s klinom L. Pravo, a teret se pomiče na udaljenost duž klina prema gore. Od tada nakon izračuna dobivamo

.

3.4. Broj pokreta sustava

3.4.1. Izračun broja pokreta sustava

Broj kretanja materijalne točke je vektorska vrijednost jednaka proizvodu točke točke na vektoru njegove brzine

Jedinica mjerenja količine kretanja -

Broj gibanja mehaničkog sustava naziva se vektorski iznos količine kretanja pojedinih točaka sustava, tj.

gdje N. - broj točaka sustava.

Broj kretanja mehaničkog sustava može se izraziti masovnim sustavom M.i masu brzine. Stvarno,

oni. Količina kretanja sustava jednak je masi cijelog sustava na brzini njezine središnje mase.Smjer se podudara s smjerom (Sl. 3.6)

U projekcijama o pravokutnim sjekovima imaju

gdje, - izbočine brzine masovnog sustava.

Ovdje M.- masa mehaničkog sustava; ne mijenja kada se sustav kreće.

Ovi rezultati su posebno prikladni za korištenje pri izračunavanju količine krutog kretanja.

Iz formule (3.7) može se vidjeti da ako se mehanički sustav kreće tako da njegovo središte mase ostaje fiksno, količina pokreta sustava ostaje jednak nuli.

3.4.2. Elementarni i puni puls snage

Učinak sile na materijalnu točku tijekom vremena dT. Može se karakterizirati elementarnim impulsom. Pune impulsne snage u to vrijeme t., ili poticajne sile određene formulom

ili u projekcijama o koordinatama osi

(3.8a)

Jedinicu impulsne snage.

3.4.3. Teorem na promjeni broja pokreta sustava

Neka se vanjske i unutarnje sile primjenjuju na točke sustava. Zatim za svaku točku sustava možete primijeniti diferencijalne zakone kretanja (3.3), što znači da :

.

Zbrajajući sve točke sustava, dobivamo

Vlasništvo unutarnjih snaga i po definiciji imati

(3.9)

Množenjem oba dijela ove jednadžbe dT., Dobivam teoremu o promjeni količine kretanja u diferencijalnom obliku:

, (3.10)

oni. diferencijal količine kretanja mehaničkog sustava jednaka je vektorskoj zbroj elementarnih impulsa svih vanjskih sila koje djeluju na točku mehaničkog sustava.

Računanje integrala iz oba dijela (3.10) u vremenu od 0 do t., Dobivamo teorem u krajnjoj ili integralnoj obliku

(3.11)

U projekcijama o koordinatnim osima imat ćemo

Promjena broja mehaničkog sustava tijekom vremenat.jednak vektoru svih impulsa vanjskih sila koje djeluju na točku mehaničkog sustava u isto vrijeme.

Primjer 4. Masa tereta m. spušta se niz nagnutu ravninu iz stanja odmora pod djelovanjem sile F., Proporcionalno vrijeme: gdje (Sl. 3.7), Koja će brzina okrenuti tijelo t. sekundi nakon početka kretanja, ako je koeficijent klizanja tereta na nagnutom ravnini jednak f..

Odluka. Prikazati snagu priloženu teretu: mg. - snaga opterećenja, N. - normalna reakcija ravnine - silu trenja klizanja tereta u ravninu i. Smjer svih sila je prikazan (Sl. 3.7).

Usmjeramo osovinu h. Uz nagnutu ravninu. Pišemo teorem o promjeni iznosa kretanja (3.11) u projekciji na osi h.:

(ali)

Pod uvjetom, jer U početnom trenutku, teret je bio u mirovanju. Zbroj projekcija impulsa svih sila na osi X je jednaka

Stoga,

,

.

3.4.4. Zakoni održavanja količine kretanja

Zakoni o očuvanju dobivaju se kao posebni slučajevi teorema na promjeni u iznosu od kretanja. Mogući su dva posebna slučaja.

· Ako se vektorski zbroj svih vanjskih sila primjenjuje na sustav je nula, tj. zatim iz teorema slijedi (3.9) , što ,

oni. Ako je glavni vektor vanjskih sila sustava nula, onda je broj pokreta sustava stalno velik i smjer.

· Ako je projekcija glavnog vektora vanjskih sila na bilo koji koordinatna os jednaka nuli, na primjer, Oh, tj. , onda je projekcija količine kretanja na ovoj osi trajna.

Razmotrite primjer primjene zakona očuvanja iznosa kretanja.

Primjer 5. Balistički klatno je masovno tijelo suspendirano na dugu nit (Sl. 3.8).

Metak masa se kreće pri brzini Vlan I pada u fiksno tijelo, zaglavi u njemu, a tijelo odstupa. Što je bila brzina metka ako je tijelo porasla na visinu h. ?

Odluka. Neka tijelo s zaglavljenim metkom stekao brzinu. Zatim, koristeći zakon očuvanja količine kretanja u interakciji dvaju tijela, možete snimati .

Brzina se može izračunati primjenom zakona očuvanja mehaničke energije , Zatim. Kao rezultat toga, pronađeno

.

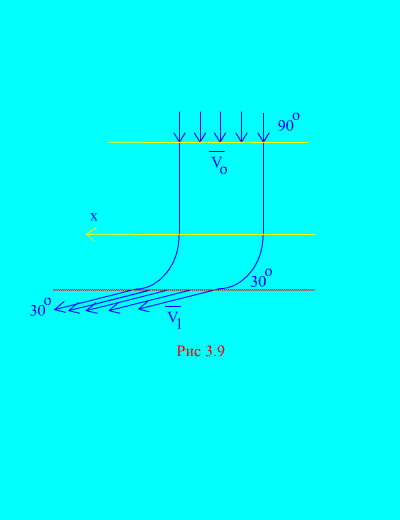
Primjer 6., Voda ulazi u fiksnog kanala (Sl. 3.9) varijabilni poprečni presjek brzinom pod kutom do horizonta; područje poprečnog presjeka kanala na ulazu; Brzina vode na izlazu iz kanala i čini kut s horizontom.

Odredite horizontalnu komponentu reakcije koju voda ima na zidovima kanala. Gustoća vode .

Odluka. Mi ćemo odrediti horizontalnu komponentu reakcije reaktivnog reaktivnog zidova kanala na vodi. Ova sila je jednaka modulu i suprotno znaku željene sile. Imamo, prema (3.11a),

, (ali)

Mi izračunavamo masu volumena tekućine koja ulazi u kanal za T:

Vrijednost RAV 0 se zove druga masa je masa tekućine koja teče kroz bilo koji presjek cijevi po jedinici vremena.

Ista količina vode ostavlja kanal u isto vrijeme. Početna i konačna brzina prikazana je u stanju.

Izračunavamo desnu stranu jednakosti (a) koja određuje količinu projekcija na horizontalnoj osi vanjskih sila koje se primjenjuju na sustav (voda). Jedina horizontalna sila je horizontalna komponenta jednake reakcije zidova R X., Ova sila s stalnim pokretima vode je konstantna. stoga

, (u)

Zamjena (b) i (c) u (a), dobivamo

3.5. Sustav kinetičkog trenutka

3.5.1. Glavno vrijeme pokreta sustava

Neka - točka radijusa-vektor mase sustava u odnosu na neku točku A, nazvana središtem (Sl. 3.10).

Trenutak pokreta (kinetički trenutak) Što se tiče središta A.zove se vektor , definiran formulom

. (3.12)

U isto vrijeme, vektor usmjereno okomito na avion prolazeći kroz središte ALIi vektor .

Trenutak količine kretanja (kinetički trenutak) u odnosu na osto se zove projekcija na ovoj osima trenutka broja kretanja točke u odnosu na bilo koji centar odabranog na ovoj osi.

Glavni trenutak broja kretanja (kinetički trenutak) sustava u odnosu na centar anazvao je veličinu

(3.13)

Glavno vrijeme pokreta (kinetički trenutak) u odnosu na osnazvana projekcija na ovoj osi glavne točke broja pokreta sustava u odnosu na bilo koju odabranu na ovom Središnja os.

3.5.2. Kinetički zakretni moment rotirajuće krutine u odnosu na os rotacije

Kompatibilna nepomična točka OKOtijelo leži na osi rotacije OKOz, s početkom koordinatnog sustava Ohuzčije se osi rotiraju s tijelom (Sl. 3.11), Dopustiti biti radijus-vektor točke tijela u odnosu na početak koordinata, njegove projekcije na osi su označene. Vektor projekcije kutna brzina Tijela na istim osi označavamo 0, 0, ().

Ministarstvo prosvjete i znanosti Ruska Federacija

Savezna državna proračunska ustanova visokog stručnog obrazovanja

"Kuban državni tehnološki sveučilište"

Teorijska mehanika

Dinamika Dijela

Odobren od strane uredništva

sveučilišno vijeće kao

tutorial

Krasnodar

UDC 531.1 / 3 (075)

Teorijska mehanika. Dio 2. Dinamika: tutorial / l.i.dyko; Kuban. država Tekhnol.un-t. Krasnodar, 2011. 123 s.

ISBN 5-230-06865-5

Prikazani su u kratkom obliku teorijskog materijala, primjeri rješavanja problema su dani, od kojih većina odražava stvarna pitanja tehnologije, pozornost se posvećuje izbor racionalne metode rješenja.

Dizajniran za prvostupnike po dopisivanju i udaljenim oblicima obuke, transportnih i inženjerskih smjerova.

Stol. 1 bolestan. 68 bibliograd. 20 imena.

Znanstveni urednik Cand.tehn. Nauk, izv. V.f. Melnikov

Recenzenti: Odjel za teorijsku mehaniku i teoriju mehanizama i strojeva Kubanskog agrarskog sveučilišta u prof. Fm Canarev; Izvanredni profesor Odjela za teoretsku mehaniku Kubana Državnog tehnološkog sveučilišta M.E. Beznačajan

Ispisuje se odlukom uredništva i izdavačkog vijeća Kubanskog državnog tehnološkog sveučilišta.

Ispis

ISBN 5-230-06865-5 Kubbda 1998.

Predgovor

Ovaj vodič namijenjen je studentima korespondencije formiranje građevinskih, transportnih i inženjerskih specijaliteta, ali se može koristiti u proučavanju odjeljka "dinamika" teoretske mehanike studenata s učenicima drugih specijaliteta, kao i studenata dana oblik obuke u samostalnom radu.

Priručnik je sastavljen u skladu s trenutnim programom teorijske mehanike, pokriva sva pitanja glavnog dijela tečaja. Svaki odjeljak sadrži kratki teorijski materijal, opremljen ilustracijama i metodičnim smjernicama za njegovu uporabu pri rješavanju zadataka. U priručniku je rastavljen odluka od 30 zadataka koji odražavaju stvarna pitanja tehnologije i odgovarajuće kontrolne zadatke za odlučiti, Za svaki zadatak prikazan je dizajn shema, jasno ilustrirajuće rješenje. Odlučujuća odluka udovoljava zahtjevima za registraciju kontrole radnih studenata.

Autor izražava duboku zahvalnost nastavnicima Odjela za teorijsku mehaniku i teoriju mehanizama i strojeva Kubanskog agrarnog sveučilišta za puno posla na preispitivanju udžbenika, kao i učitelje Odjela za teorijsku mehaniku Kubana državnog tehnološkog Sveučilište za vrijedne komentare i savjete o pripremi udžbenika za objavljivanje.

Svi kritički komentari i želje će biti prihvaćen od strane autora s zahvalnošću i kasnije.

Uvod

Dinamika je najvažniji dio teorijske mehanike. Najspecifičniji zadaci koji se u inženjerskoj praksi pripadaju dinamici. Koristeći zaključke statika i kinematike, dinamika uspostavlja opće zakone kretanja materijalnih tijela pod djelovanjem primijenjenih snaga.

Najjednostavniji materijalni objekt je materijalna točka. Za materijalnu točku možete uzeti materijalno tijelo bilo kojeg oblika, čije se veličine u problemu koji se razmatra može zanemariti. Za materijalnu točku možete uzeti tijelo konačnih veličina ako je razlika u kretanju njegovih točaka za ovaj zadatak nije značajna. To se događa kada su veličine tijela male u usporedbi s udaljenostima koje prolaze bodove tijela. Svaka čestica kruteća može se smatrati materijalnom točkom.

Sile pričvršćene na točku ili materijalno tijelo, u dinamici se procjenjuju na njihovom dinamičnom učinku, to jest, prema tome kako mijenjaju karakteristike pokreta materijalnih objekata.

Kretanje materijalnih objekata tijekom vremena provodi se u prostoru u odnosu na određeni referentni sustav. U klasičnoj mehanici na temelju Newtonova aksioma, prostor se smatra trodimenzionalnim, njegova svojstva ne ovise o materijalnim objektima koji se kreću u njemu. Položaj točke u takvom prostoru određuje se tri koordinata. Vrijeme se ne odnosi na prostor i kretanje materijalnih objekata. Smatra se istim za sve referentne sustave.

Zakoni govornika opisuju kretanje materijalnih objekata u odnosu na apsolutne osi koordinata, uvjetno usvojenih za fiksno. Početak apsolutnog koordinatnog sustava prihvaća se u središtu sunca, a osi se šalju na udaljene, uvjetno ne-pokretne zvijezde. Prilikom rješavanja mnogih tehničkih zadataka, koordinatne osi povezane sa Zemljom mogu se smatrati uvjetno pokretnim.

Parametri mehaničkog kretanja materijalnih objekata u dinamici utvrđuju se matematičkim zaključcima od osnovnih zakona klasične mehanike.

Prvi zakon (zakon inercije):

Materijalna točka zadržava stanje mirovanja ili ujednačenog i pravocrtnog pokreta dok se ne pokaže djelovanje bilo koje snage iz tog stanja.

Ujednačeno i pravocrtno kretanje točke nazivaju se pokretom inercije. Pochka je poseban slučaj inercije, kada je brzina točke nula.

Svaka materijalna točka ima inerciju, tj. Nastoji sačuvati stanje mirovanja ili ujednačenog pravocrtanog pokreta. Referentni sustav, s obzirom na koji se obavlja zakon inercije, zove se inercija, a kretanje promatrano u odnosu na ovaj sustav naziva se apsolutno. Svaki referentni sustav koji obavlja u odnosu na inercijskog sustava translacijski ravni i ujednačen kretanja također će biti inercijalni sustav.

Drugi zakon (osnovni zakon dinamike):

Ubrzanje materijalne točke u odnosu na inercijskog referentnog sustava proporcionalan je sili pričvršćenoj na točku i podudara se s silom prema:
.

Temeljnog zakona, dinamika slijedi da je na snazi
ubrzanje
, Masa točke karakterizira stupanj otpornosti na točku promjene u brzini, tj. Je li mjera inertnosti materijalne točke.

Treći zakon (Zakon o djelovanju i nevladi):

Snage s kojima se dva tijela djeluju jednaka modulu i usmjerene su duž jedne ravno na suprotne strane.

Snage, koje se nazivaju akcija i oporba, su priložene različita tijela I stoga uravnotežen sustav ne formira.

Četvrti zakon (Zakon o neovisnosti snage):

Uz istodobno djelovanje nekoliko sila, ubrzanje materijalne točke jednaka je geometrijskoj količini ubrzanja koja bi imala točku pod djelovanjem svake sile odvojeno:

gdje
,
,…,
.

(Mehanički sustavi) - IV opcija

1. Glavna jednadžba dinamike materijalne točke, kao što je poznato, izražena je jednadžbom. Diferencijalne jednadžbe Pokreti proizvoljnih točaka ne-free mehanički sustav prema dva načina za podjelu sila mogu se zabilježiti u dva oblika:

(1) Gdje je k \u003d 1, 2, 3, ..., n je broj točaka materijalnog sustava.

(2)

gdje - masa K-SO-a; - Radijus vektora K-SO-a je dana (aktivna) sila koja djeluje na K-TH jednu ili dobivene sve aktivne sile koje djeluju na K-TH. - rezultirajuće sile reakcija veza koje djeluju na K-TH; - rezultirajuće unutarnje sile koje djeluju na K-TH; - jednakost vanjskih sila koje djeluju na K-TH.

Uz pomoć jednadžbi (1) i (2), možete nastojati odlučiti i prve i druge zadatke govornika. Međutim, rješenje drugog zadatka dinamike sustava je vrlo komplicirana ne samo s matematičkog stajališta, već i zato što se suočavamo s temeljnim poteškoćama. Sastoje se u činjenici da je i za sustav (1) i za sustav (2) broj jednadžbi značajno manje broj Nepoznato.

Dakle, ako se koristi (1), zatim poznat po drugom (obrnutom) zadatku govornika će biti i, a nepoznanici će biti. Jednadžbe vektor će biti " n."I nepoznato -" 2n ".

Ako nastavite od sustava jednadžbi (2), onda je poznat i dio vanjskih sila. Zašto dio? Činjenica je da vanjska čvrstoća uključuje vanjske reakcije veza koje su nepoznate. Osim toga, također će biti nepoznanici.

Tako je, kako je sustav (1) i sustav (2) otključan. Potrebno je dodati jednadžbe, s obzirom na jednadžbe linkova i moguće je nametnuti neka ograničenja na samim spojevima. Što učiniti?

Ako nastavimo od (1), onda možete ići na način da sastavite jednadžbe prve vrste Lagrangea. Ali ovaj put nije racionalan jer jednostavno zadatak (manje stupnjeva slobode), teže sa stajališta matematike da ga riješi.

Onda obraćamo pozornost na sustav (2), gdje - su uvijek nepoznati. Prvi korak pri rješavanju sustava je eliminirati ove nepoznanice. Trebalo bi ga imati na umu da se obično ne zanimaju unutarnje sile kada se sustav kreće, to jest, kada se sustav kreće, ne morate znati kako se svaka točka sustava kreće, ali dovoljno je znati kako je sustav općenito.

Dakle, ako različiti putevi Isključiti iz sustava (2) nepoznate sile, dobivamo neke odnose, tj. Neki se pojavljuju opće karakteristike Za sustav, znanje o tome omogućuje suditi kako se sustav kreće općenito. Te karakteristike unose takozvane opće teoreme Dinamika. Četiri takve teoreme:

1. Teorem O. moving centar mehaničkog sustava mase;

2. Teorem ob. promjena broja mehaničkim sustavom;

3. Teorem ob. promijenite kinetički trenutak mehaničkog sustava;

4. Teorem ob. promijenite kinetičku energiju mehaničkog sustava.