Vietnes sadaļas
Redaktora izvēle:
- Lietišķā komunikācija pa tālruni
- Iesniegums darba laika grafika maiņai - paraugs
- Kādi maksājumi pienākas darbiniekam pēc atlaišanas
- Par ko jūs varat apbalvot darbiniekus: kādam jābūt prēmiju iemesla formulējumam
- Noteikumi saziņai ar klientiem pa tālruni
- Kā ievērot biroja etiķeti
- basmati rīsu recepte basmati gatavošana
- Atlaide (prēmija) obligācijai
- Virsstundu darba iesaistīšanās kārtība
- Basmati rīsu recepte Basmati rīsi Vai man vajadzētu izskalot?
Reklāma
| Vienkārši un ne pārāk veidi, kā aprēķināt kuba sakni. Sakņu ekstrakcija: metodes, piemēri, risinājumi |
|
Skaitļa x n-tā sakne ir nenegatīvs skaitlis z, kas, paaugstinot līdz n-tam pakāpei, kļūst par x. Saknes definīcija ir iekļauta aritmētisko pamatoperāciju sarakstā, ar kuru mēs iepazināmies bērnībā. Matemātiskais apzīmējums"Sakne" nāk no latīņu vārda radix, un mūsdienās vārds "radikāls" tiek izmantots kā šī matemātiskā termina sinonīms. Kopš 13. gadsimta matemātiķi saknes izvilkšanas darbību ir apzīmējuši ar burtu r ar horizontālu joslu virs radikālas izteiksmes. 16. gadsimtā tika ieviests apzīmējums V, kas pamazām nomainīja zīmi r, bet horizontālā līnija tika saglabāta. Ir viegli drukāt tipogrāfijā vai rakstīt ar roku, bet iekšā elektroniskās publikācijas un programmēšanas izplatība burtu apzīmējums sakne - kv. Šajā rakstā mēs apzīmēsim kvadrātsaknes. KvadrātsakneSkaitļa x kvadrātveida radikālis ir skaitlis z, kas, reizinot ar sevi, kļūst par x. Piemēram, ja mēs reizinām 2 ar 2, mēs iegūstam 4. Divi šajā gadījumā ir kvadrātsakne no četriem. Reiziniet 5 ar 5, iegūstam 25, un tagad mēs jau zinām izteiksmes sqrt(25) vērtību. Mēs varam reizināt un -12 ar -12 un iegūt 144, un radikāls 144 būs gan 12, gan -12. Acīmredzot kvadrātsaknes var būt gan pozitīvi, gan negatīvi skaitļi. Atrisināšanai svarīgs ir šādu sakņu savdabīgais duālisms kvadrātvienādojumi, tāpēc, meklējot atbildes šādās problēmās, jānorāda abas saknes. Pieņemot lēmumu algebriskās izteiksmes tiek izmantotas aritmētiskās kvadrātsaknes, tas ir, tikai to pozitīvās vērtības. Skaitļus, kuru kvadrātsaknes ir veseli skaitļi, sauc par perfektiem kvadrātiem. Ir vesela šādu skaitļu virkne, kuras sākums izskatās šādi: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256… Citu skaitļu kvadrātsaknes ir iracionāli skaitļi. Piemēram, sqrt(3) = 1.73205080757... un tā tālāk. Šis skaitlis ir bezgalīgs un nav periodisks, kas rada zināmas grūtības šādu radikāļu aprēķināšanā. Skolas matemātikas kursā teikts, ka no negatīviem skaitļiem nevar ņemt kvadrātsaknes. Kā mēs mācāmies vidusskolas matemātiskās analīzes kursā, to var un vajag darīt - tieši tam ir nepieciešami kompleksie skaitļi. Tomēr mūsu programma ir izstrādāta, lai iegūtu reālās sakņu vērtības, tāpēc tā neaprēķina pat radikāļus no negatīviem skaitļiem. kuba sakneSkaitļa x kubiskais radikālis ir skaitlis z, kuru reizinot ar sevi trīs reizes, tiek iegūts skaitlis x. Piemēram, ja mēs reizinām 2 × 2 × 2, mēs iegūstam 8. Tāpēc divi ir astoņu kuba sakne. Reiziniet četras reizes ar sevi un iegūstiet 4 × 4 × 4 = 64. Acīmredzot četri ir skaitļa 64 kuba sakne. Ir bezgalīga skaitļu virkne, kuras kubiskie radikāļi ir veseli skaitļi. Tās sākums izskatās šādi: 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744… Pārējiem skaitļiem kuba saknes ir neracionāli skaitļi. Atšķirībā no kvadrātveida radikāļiem, kuba saknes, tāpat kā jebkuru nepāra sakni, var ņemt no negatīviem skaitļiem. Tas viss ir par skaitļiem mazāks par nulli. Mīnuss ar mīnusu dod plusu - no skolas sola zināms noteikums. Mīnus reiz pluss padara mīnusu. Ja negatīvus skaitļus reizinat nepāra reižu skaitu, tad arī rezultāts būs negatīvs, tāpēc izņemiet nepāra radikāli no negatīvs skaitlis nekas mūs neliedz. Tomēr kalkulatora programma darbojas citādi. Faktiski saknes iegūšana nozīmē paaugstināšanu uz apgriezto jaudu. Kvadrātsakne tiek uzskatīta par paaugstināšanu līdz 1/2, bet kubs - 1/3. Formulu paaugstināšanai līdz jaudai 1/3 var apgriezt un izteikt kā 2/6. Rezultāts ir tāds pats, taču šādu sakni nav iespējams iegūt no negatīva skaitļa. Tādējādi mūsu kalkulators aprēķina aritmētiskās saknes tikai no pozitīviem skaitļiem. N-tā sakneŠāds grezns radikāļu aprēķināšanas veids ļauj noteikt jebkuras pakāpes saknes no jebkuras izteiksmes. Varat iegūt skaitļa kuba piekto sakni vai skaitļa 19. radikāli uz 12. Tas viss ir eleganti īstenots kā paaugstināšana attiecīgi ar jaudu 3/5 vai 12/19. Apsveriet piemēruKvadrātveida diagonāleKvadrāta diagonāles neracionalitāti zināja senie grieķi. Viņi saskārās ar plakana kvadrāta diagonāles aprēķināšanas problēmu, jo tā garums vienmēr ir proporcionāls divu kvadrātsaknei. Diagonāles garuma noteikšanas formula ir iegūta no un galu galā ir šāda: d = a × sqrt(2). Izmantojot mūsu kalkulatoru, noteiksim kvadrātveida radikāli no diviem. Šūnā "Skaitlis (x)" ievadīsim vērtību 2, bet šūnā "Jauda (n)" arī 2. Rezultātā iegūstam izteiksmi sqrt (2) = 1,4142. Tādējādi kvadrāta diagonāles aptuvenai aplēsei pietiek ar tā malu reizināt ar 1,4142. SecinājumsRadikāla meklēšana ir standarta aritmētiska darbība, bez kuras nav nepieciešami zinātniski vai projektēšanas aprēķini. Protams, mums nav jānosaka saknes, lai risinātu ikdienas problēmas, taču mūsu tiešsaistes kalkulators noteikti noderēs skolēniem vai studentiem, lai pārbaudītu mājasdarbus algebrā vai aprēķinos. Ir pienācis laiks izjaukt sakņu ekstrakcijas metodes. Tie ir balstīti uz sakņu īpašībām, jo īpaši uz vienādību, kas attiecas uz jebkuru nenegatīvu skaitli b. Tālāk mēs savukārt apsvērsim galvenās sakņu ieguves metodes. Sāksim ar vienkāršāko gadījumu – sakņu izvilkšanu no naturāliem skaitļiem, izmantojot kvadrātu tabulu, kubu tabulu utt. Ja kvadrātu, kubu u.c. nav pie rokas, ir loģiski izmantot saknes iegūšanas metodi, kas ietver saknes skaitļa sadalīšanu vienkāršos faktoros. Atsevišķi ir vērts pakavēties pie tā, kas ir iespējams saknēm ar nepāra eksponentiem. Visbeidzot, apsveriet metodi, kas ļauj secīgi atrast saknes vērtības ciparus. Sāksim. Izmantojot kvadrātu tabulu, kubu tabulu utt.Vienkāršākajos gadījumos kvadrātu, kubu uc tabulas ļauj iegūt saknes. Kas ir šīs tabulas? Veselu skaitļu kvadrātu tabula no 0 līdz 99 (ieskaitot) sastāv no divām zonām. Tabulas pirmā zona atrodas uz pelēka fona, atlasot noteiktu rindu un noteiktu kolonnu, tā ļauj izveidot skaitli no 0 līdz 99. Piemēram, atlasīsim rindu ar 8 desmitiem un kolonnu ar 3 vienībām, ar to mēs nofiksējām skaitli 83. Otrā zona aizņem pārējo tabulu. Katra tā šūna atrodas noteiktas rindas un noteiktas kolonnas krustpunktā un satur atbilstošā skaitļa kvadrātu no 0 līdz 99. Mūsu izvēlētās 8 desmitnieku rindas un viena 3. kolonnas krustpunktā atrodas šūna ar skaitli 6889, kas ir skaitļa 83 kvadrāts. Kubu tabulas, skaitļu ceturto pakāpju tabulas no 0 līdz 99 un tā tālāk ir līdzīgas kvadrātu tabulai, tikai tās otrajā zonā satur kubus, ceturtās pakāpes utt. atbilstošos skaitļus. Kvadrātu, kubu, ceturtās pakāpes tabulas utt. ļauj iegūt kvadrātsaknes, kubsaknes, ceturtās saknes utt. attiecīgi no skaitļiem šajās tabulās. Izskaidrosim to pielietošanas principu sakņu ieguvē. Pieņemsim, ka no skaitļa a ir jāizvelk n-tās pakāpes sakne, savukārt skaitlis a ir ietverts n-to grādu tabulā. Saskaņā ar šo tabulu mēs atrodam skaitli b tādu, ka a=b n . Tad Kā piemēru parādīsim, kā 19683. gada kuba sakne tiek iegūta, izmantojot kuba tabulu. Mēs atrodam kubu tabulā skaitli 19 683, no tā secinām, ka šis skaitlis ir skaitļa 27 kubs, tāpēc Skaidrs, ka n-to grādu tabulas ir ļoti ērtas, iegūstot saknes. Taču tās bieži vien nav pa rokai, un to sastādīšana prasa noteiktu laiku. Turklāt bieži vien ir nepieciešams iegūt saknes no skaitļiem, kas nav ietverti attiecīgajās tabulās. Šādos gadījumos ir jāizmanto citas sakņu iegūšanas metodes. Saknes skaitļa sadalīšana pirmfaktorosDiezgan ērts veids, kā iegūt sakni no naturālā skaitļa (ja, protams, sakne ir iegūta), ir sadalīt saknes skaitli pirmfaktoros. Viņa būtība ir šāda: pēc tam ir diezgan viegli attēlot to kā grādu ar vēlamo indikatoru, kas ļauj iegūt saknes vērtību. Paskaidrosim šo punktu. No naturāla skaitļa a izņem n-tās pakāpes sakni, un tā vērtība ir vienāda ar b. Šajā gadījumā vienādība a=b n ir patiesa. Skaitli b kā jebkuru naturālu skaitli var attēlot kā visu tā pirmfaktoru p 1 , p 2 , …, pm reizinājumu formā p 1 p 2 pm , un saknes skaitli a šajā gadījumā attēlo kā (p 1 p 14 ... pm) n . Tā kā skaitļa sadalīšana pirmfaktoros ir unikāla, tad saknes skaitļa a sadalīšana pirmfaktoros izskatīsies šādi (p 1 ·p 2 ·…·pm) n , kas ļauj aprēķināt saknes vērtību kā . Ņemiet vērā, ka, ja saknes skaitļa a faktorizāciju nevar attēlot formā (p 1 ·p 2 ·…·p m) n , tad n-tās pakāpes sakne no šāda skaitļa a netiek pilnībā izvilkta. Ar to nodarbosimies, risinot piemērus. Piemērs. Paņemiet kvadrātsakni no 144 . Risinājums. Ja pievēršamies iepriekšējā rindkopā dotajai kvadrātu tabulai, skaidri redzams, ka 144=12 2 , no kuras ir skaidrs, ka 144 kvadrātsakne ir 12 . Bet, ņemot vērā šo punktu, mēs esam ieinteresēti, kā sakne tiek iegūta, sadalot saknes numuru 144 primārajos faktoros. Apskatīsim šo risinājumu. Sadalīsimies 144 uz galvenajiem faktoriem: Tas ir, 144=2 2 2 2 3 3 . Pamatojoties uz iegūto sadalīšanos, var veikt šādas pārvērtības: 144 = 2 2 2 2 3 3 = (2 2) 2 3 2 = (2 2 3) 2 = 12 2. Sekojoši, Izmantojot sakņu pakāpes un īpašību īpašības, risinājumu varētu formulēt nedaudz savādāk: . Atbilde: Lai konsolidētu materiālu, apsveriet vēl divu piemēru risinājumus. Piemērs. Aprēķiniet saknes vērtību. Risinājums. Saknes skaitļa 243 pirmfaktorizācija ir 243=3 5 . Pa šo ceļu, Atbilde: Piemērs. Vai saknes vērtība ir vesels skaitlis? Risinājums. Lai atbildētu uz šo jautājumu, sadalīsim saknes skaitli galvenajos faktoros un pārbaudīsim, vai to var attēlot kā vesela skaitļa kubu. Mums ir 285 768=2 3 3 6 7 2 . Iegūtais sadalījums nav attēlots kā vesela skaitļa kubs, jo pakāpe galvenais faktors 7 nav reizināts ar trīs. Tāpēc kuba sakne 285 768 netiek ņemta pilnībā. Atbilde: Nē. Sakņu iegūšana no daļskaitļiemIr pienācis laiks izdomāt, no kā tiek iegūta sakne daļskaitlis. Daļējās saknes skaitli rakstīsim kā p/q . Saskaņā ar koeficienta saknes īpašību šāda vienādība ir patiesa. No šīs vienlīdzības izriet frakcijas saknes noteikums: Daļas sakne ir vienāda ar skaitītāja saknes dalījuma ar saucēja sakni. Apskatīsim piemēru saknes iegūšanai no frakcijas. Piemērs. Kas ir kvadrātsakne no kopējā frakcija 25/169 . Risinājums. Saskaņā ar kvadrātu tabulu mēs atklājam, ka sākotnējās daļas skaitītāja kvadrātsakne ir 5, bet saucēja kvadrātsakne ir 13. Tad Atbilde: Decimāldaļas vai jaukta skaitļa sakne tiek iegūta pēc saknes skaitļu aizstāšanas ar parastajām daļām. Piemērs. Ņemiet decimāldaļas 474.552 kubsakni. Risinājums. Iedomājieties oriģinālu decimālzīme parastās daļas veidā: 474,552=474552/1000. Tad Atbilde:
Negatīvā skaitļa saknes izvilkšanaAtsevišķi ir vērts pakavēties pie sakņu iegūšanas no negatīviem skaitļiem. Pētot saknes, mēs teicām, ka, ja saknes eksponents ir nepāra skaitlis, tad zem saknes zīmes var atrasties negatīvs skaitlis. Mēs piešķīrām šādiem apzīmējumiem šādu nozīmi: negatīvam skaitlim −a un nepāra eksponentam saknes 2 n−1, mums ir Apskatīsim risinājuma piemēru. Piemērs. Atrodiet saknes vērtību. Risinājums. Mēs pārveidojam sākotnējo izteiksmi tā, lai zem saknes zīmes tas izrādītos pozitīvs skaitlis: Šeit ir risinājuma kopsavilkums: Atbilde:
Bitu pagrieziena saknes vērtības atrašanaIN vispārējs gadījums zem saknes ir skaitlis, kuru, izmantojot iepriekš apspriestos paņēmienus, nevar attēlot kā jebkura skaitļa n-to pakāpi. Bet tajā pašā laikā ir jāzina dotās saknes vērtība vismaz līdz noteiktai zīmei. Šajā gadījumā, lai iegūtu sakni, varat izmantot algoritmu, kas ļauj secīgi iegūt pietiekami vēlamā skaitļa ciparu vērtības. Pirmais šī algoritma solis ir noskaidrot, kas ir vissvarīgākais saknes vērtības bits. Lai to izdarītu, skaitļus 0, 10, 100, ... secīgi paaugstina līdz pakāpei n, līdz tiek iegūts skaitlis, kas pārsniedz saknes skaitli. Tad skaitlis, ko iepriekšējā solī paaugstinājām līdz pakāpei n, norādīs atbilstošo augstāko secību. Piemēram, izvilkšanas laikā apsveriet šo algoritma darbību kvadrātsakne no pieciem. Mēs ņemam skaitļus 0, 10, 100, ... un saliekam tos kvadrātā, līdz iegūstam skaitli, kas ir lielāks par 5 . Mums ir 0 2 = 0<5 , 10 2 =100>5 , kas nozīmē, ka nozīmīgākais cipars būs vienību cipars. Šī bita, kā arī zemāko bitu vērtība tiks atrasta nākamajās sakņu ekstrakcijas algoritma darbībās. Visas sekojošās algoritma darbības ir vērstas uz saknes vērtības secīgu precizēšanu, jo tiek atrastas vēlamās saknes vērtības nākamo ciparu vērtības, sākot no augstākās un pārejot uz zemāko. . Piemēram, saknes vērtība pirmajā solī ir 2 , otrajā - 2,2 , trešajā - 2,23 un tā tālāk 2,236067977 ... . Aprakstīsim, kā tiek atrastas bitu vērtības. Bitu atrašana tiek veikta, uzskaitot to iespējamās vērtības 0, 1, 2, ..., 9. Šajā gadījumā paralēli tiek aprēķinātas atbilstošo skaitļu n-tās pakāpes, un tās tiek salīdzinātas ar saknes skaitli. Ja kādā posmā pakāpes vērtība pārsniedz radikālo skaitli, tad tiek uzskatīts, ka ir atrasta iepriekšējai vērtībai atbilstošā cipara vērtība, un tiek veikta pāreja uz nākamo saknes ekstrakcijas algoritma soli, ja tas nenotiek, tad šī cipara vērtība ir 9 . Izskaidrosim visus šos punktus, izmantojot to pašu piemēru, kā iegūt kvadrātsakni no pieci. Vispirms atrodiet vienību cipara vērtību. Mēs atkārtosim vērtības 0, 1, 2, …, 9, attiecīgi aprēķinot 0 2 , 1 2 , …, 9 2, līdz iegūsim vērtību, kas ir lielāka par radikālo skaitli 5. Visi šie aprēķini ir ērti parādīti tabulas veidā: Tātad vienību cipara vērtība ir 2 (jo 2 2<5
, а 2 3 >pieci). Pāriesim pie desmitās vietas vērtības atrašanas. Šajā gadījumā skaitļus 2.0, 2.1, 2.2, ..., 2.9 salīdzināsim kvadrātā, salīdzinot iegūtās vērtības ar saknes skaitli 5: Kopš 2.2 2<5
, а 2,3 2 >5 , tad desmitās vietas vērtība ir 2 . Varat turpināt simtdaļas vērtības atrašanu: Tātad atrasts nākamā vērtība sakne no pieci, tas ir vienāds ar 2,23. Un tāpēc jūs varat turpināt atrast vērtības tālāk: 2,236, 2,2360, 2,23606, 2,236067, … . Lai konsolidētu materiālu, mēs analizēsim saknes ekstrakciju ar simtdaļu precizitāti, izmantojot aplūkoto algoritmu. Pirmkārt, mēs definējam vecāko ciparu. Lai to izdarītu, skaitļus 0, 10, 100 utt. līdz iegūstam skaitli, kas ir lielāks par 2151.186 . Mums ir 0 3 = 0<2 151,186 , 10 3 =1 000<2151,186 , 100 3 =1 000 000>2 151.186 , tātad nozīmīgākais cipars ir desmiti cipars. Definēsim tā vērtību. Kopš 103<2 151,186
, а 20 3 >2 151,186 , tad desmitcipara vērtība ir 1 . Pāriesim pie vienībām. Tādējādi vienas vietas vērtība ir 2 . Pāriesim pie desmit. Tā kā pat 12.9 3 ir mazāks par radikālo skaitli 2 151.186 , tad desmitās vietas vērtība ir 9 . Atliek veikt pēdējo algoritma soli, tas mums dos saknes vērtību ar nepieciešamo precizitāti. Šajā posmā saknes vērtība tiek atrasta līdz simtdaļām: Noslēdzot šo rakstu, es vēlos teikt, ka ir daudz citu veidu, kā iegūt saknes. Bet lielākajai daļai uzdevumu pietiek ar tiem, kurus mēs pētījām iepriekš. Bibliogrāfija.
Inženiertehniskais kalkulators tiešsaistēMēs steidzamies ikvienam iepazīstināt ar bezmaksas inženierijas kalkulatoru. Ar to jebkurš students var ātri un, pats galvenais, ērti veikt dažāda veida matemātiskos aprēķinus tiešsaistē. Kalkulators ir ņemts no vietnes - web 2.0 zinātniskais kalkulatorsVienkāršs un ērti lietojams inženiertehniskais kalkulators ar neuzkrītošu un intuitīvu saskarni patiesi noderēs visplašākajam interneta lietotāju lokam. Tagad, kad jums ir nepieciešams kalkulators, apmeklējiet mūsu vietni un izmantojiet bezmaksas inženierijas kalkulatoru. Inženiertehniskais kalkulators var veikt gan vienkāršas aritmētiskas darbības, gan diezgan sarežģītus matemātiskos aprēķinus. Web20calc ir inženierijas kalkulators, kuram ir milzīgs skaits funkciju, piemēram, kā aprēķināt visas elementārās funkcijas. Kalkulators atbalsta arī trigonometriskās funkcijas, matricas, logaritmus un pat diagrammu veidošanu. Neapšaubāmi, Web20calc interesēs to cilvēku grupu, kas, meklējot vienkāršus risinājumus, meklētājprogrammās ieraksta vaicājumu: tiešsaistes matemātiskais kalkulators. Bezmaksas tīmekļa lietojumprogramma palīdzēs jums uzreiz aprēķināt jebkuras matemātiskas izteiksmes rezultātu, piemēram, atņemt, saskaitīt, dalīt, iegūt sakni, palielināt līdz pakāpei utt. Izteiksmē var izmantot paaugstināšanas, saskaitīšanas, atņemšanas, reizināšanas, dalīšanas, procentuālās, PI konstantes darbības. Sarežģītiem aprēķiniem jāizmanto iekavas. Inženiertehniskā kalkulatora īpašības:1. aritmētiskās pamatoperācijas; Inženiertehniskais kalkulators ļauj izmantot dažādas matemātiskas funkcijas:Sakņu (kvadrātsaknes, kubiksaknes, kā arī n-tās pakāpes saknes) ekstrakcija; Šajā inženiertehniskajā kalkulatorā ir iekļauts arī lielumu kalkulators ar iespēju konvertēt fiziskos lielumus dažādām mērīšanas sistēmām – datora mērvienībām, attālumam, svaram, laikam utt. Izmantojot šo funkciju, jūs varat uzreiz pārvērst jūdzes kilometros, mārciņas kilogramos, sekundes stundās utt. Lai veiktu matemātiskos aprēķinus, vispirms attiecīgajā laukā ievadiet matemātisko izteiksmju secību, pēc tam noklikšķiniet uz vienādības zīmes un skatiet rezultātu. Vērtības var ievadīt tieši no tastatūras (šim nolūkam kalkulatora apgabalam jābūt aktīvam, tāpēc būs lietderīgi ievietot kursoru ievades laukā). Cita starpā datus var ievadīt, izmantojot paša kalkulatora pogas. Lai izveidotu grafikus ievades laukā, ierakstiet funkciju, kā norādīts piemēra laukā, vai izmantojiet īpaši šim nolūkam paredzēto rīkjoslu (lai to atvērtu, noklikšķiniet uz pogas ar ikonu diagrammas formā). Lai konvertētu vērtības, nospiediet Unit, lai strādātu ar matricām - Matrix. Pirms kalkulatoru parādīšanās skolēni un skolotāji ar roku aprēķināja kvadrātsaknes. Ir vairāki veidi, kā manuāli aprēķināt skaitļa kvadrātsakni. Daži no tiem piedāvā tikai aptuvenu risinājumu, citi sniedz precīzu atbildi. SoļiGalvenā faktorizācija
Saknes skaitli faktoros, kas ir kvadrātskaitļi. Atkarībā no saknes numura jūs saņemsiet aptuvenu vai precīzu atbildi. Kvadrātskaitļi ir skaitļi, no kuriem var ņemt visu kvadrātsakni. Faktori ir skaitļi, kurus reizinot, tiek iegūts sākotnējais skaitlis. Piemēram, skaitļa 8 faktori ir 2 un 4, jo 2 x 4 = 8, skaitļi 25, 36, 49 ir kvadrātskaitļi, jo √25 = 5, √36 = 6, √49 = 7. Kvadrātveida koeficienti ir faktori, kas ir kvadrātskaitļi. Vispirms mēģiniet faktorizēt saknes skaitli kvadrātveida faktoros. Instrukcija Lai palielinātu skaitli līdz 1/3, ievadiet šo skaitli, pēc tam noklikšķiniet uz barošanas pogas un ievadiet aptuveno vērtību no 1/3 līdz 0,333. Šī precizitāte ir pietiekama lielākajai daļai aprēķinu. Taču aprēķinu precizitāti ir ļoti vienkārši uzlabot – vienkārši pievienojiet tik daudz tripletu, cik ietilps kalkulatora indikatorā (piemēram, 0,3333333333333333). Pēc tam nospiediet pogu "=". Lai aprēķinātu trešo sakni, izmantojot datoru, palaidiet programmu Windows kalkulators. Trešās pakāpes saknes aprēķināšanas procedūra ir pilnīgi līdzīga iepriekš aprakstītajai. Vienīgā atšķirība ir eksponēšanas pogas dizainā. Kalkulatora virtuālajā tastatūrā tas ir apzīmēts kā "x^y". Trešās pakāpes sakni var aprēķināt arī programmā MS Excel. Lai to izdarītu, ievadiet "=" jebkurā šūnā un atlasiet ikonu "ievietot" (fx). Parādītajā logā atlasiet funkciju "DEGREE" un noklikšķiniet uz pogas "OK". Parādītajā logā ievadiet tā skaitļa vērtību, kuram vēlaties aprēķināt trešās pakāpes sakni. Sadaļā "Grādi" ievadiet skaitli "1/3". Sastādiet numuru 1/3 tieši šādā formā - kā parastu. Pēc tam noklikšķiniet uz pogas "OK". Tabulas šūnā, kurā tā tika izveidota, parādīsies dotā skaitļa kuba sakne. Ja trešās pakāpes sakne ir jāaprēķina pastāvīgi, tad nedaudz uzlabojiet iepriekš aprakstīto metodi. Kā numuru, no kura vēlaties iegūt sakni, norādiet nevis pašu numuru, bet gan tabulas šūnu. Pēc tam katru reizi ievadiet šajā šūnā sākotnējo skaitli - tā kuba sakne parādīsies šūnā ar formulu. Saistītie video
Piezīme Secinājums. Šajā rakstā tika aplūkotas dažādas metodes kuba saknes vērtību aprēķināšanai. Izrādījās, ka kuba saknes vērtības var atrast ar iterācijas metodi, var arī tuvināt kuba sakni, palielināt skaitli līdz 1/3 pakāpei, meklēt saknes vērtības trešās pakāpes, izmantojot Microsoft Office Excel, iestatot formulas šūnās. Noderīgs padoms Īpaši bieži tiek izmantotas otrās un trešās pakāpes saknes, un tāpēc tām ir īpaši nosaukumi. Kvadrātsakne: šajā gadījumā eksponents parasti tiek izlaists, un termins "sakne", nenorādot pakāpi, visbiežāk nozīmē kvadrātsakni. Praktiskais sakņu aprēķins Algoritms n-tās pakāpes saknes atrašanai. Kvadrātsaknes un kubsaknes parasti tiek nodrošinātas visos kalkulatoros. Avoti:
Saknes atrašanas operācija trešais grāds parasti sauc par "kubiskās" saknes ekstrakciju, un tas sastāv no tāda reāla skaitļa atrašanas, kuru veidojot kubā, tiks iegūta vērtība, kas vienāda ar saknes skaitli. Jebkuras aritmētiskās saknes ekstrakcijas darbība grāds n ir ekvivalents paaugstināšanas darbībai līdz jaudai 1/n. Praksē ir vairāki veidi, kā aprēķināt kuba sakni. |
Populārs:
Konusa tilpums, tā aprēķins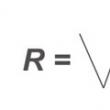
|
Jauns
- Ko nozīmē sāpināt lauvas lepnumu
- Glāžu piramīda: šampanieša glāžu piramīda ar savām rokām Kā izveidot šampanieša piramīdu
- Tējas maisiņu izgatavošana Kā pagatavot tējas maisiņus
- Kā stilīgi ģērbties skolai: vispārīgi ieteikumi Tagad uzziniet, ko spēj šis mazais skapis
- Kā moderni ģērbties skolā: stilīgs izskats Tagad paskatieties, ko spēj šis mazais drēbju skapis
- Noderīgas un kaitīgas ķiploku īpašības grūtniecības laikā Jūs varat ēst ķiplokus grūtniecēm
- Kandidoze grūtniecības vidū Strazda ārstēšana grūtniecēm otrajā trimestrī
- Kā tikt galā ar miegainību grūtniecības laikā, ja esat darbā
- Vārda Anna nozīme Ko vārds Anna nozīmē meitenei
- Ko bērnam vajadzētu darīt pusotra gada vecumā Ko mazulis var izdarīt 1 gada vecumā



 . Tas pabeidz saknes ekstrakciju no parastās frakcijas 25/169.
. Tas pabeidz saknes ekstrakciju no parastās frakcijas 25/169. . Atliek izvilkt kuba saknes, kas atrodas iegūtās frakcijas skaitītājā un saucējā. Jo
. Atliek izvilkt kuba saknes, kas atrodas iegūtās frakcijas skaitītājā un saucējā. Jo  .
.
 . Tagad
. Tagad  . Mēs piemērojam noteikumu par saknes izņemšanu no parastās frakcijas:
. Mēs piemērojam noteikumu par saknes izņemšanu no parastās frakcijas:  . Atliek aprēķināt saknes iegūtās frakcijas skaitītājā un saucējā:
. Atliek aprēķināt saknes iegūtās frakcijas skaitītājā un saucējā:  .
.
 .
.
 .
.











