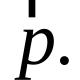Tamsayı ifadesi, toplama, çıkarma ve çarpma işlemlerini kullanan sayılardan ve değişmez değişkenlerden oluşan matematiksel bir ifadedir. Tamsayılar ayrıca sıfır dışında herhangi bir sayıya bölmeyi içeren ifadeleri de içerir.

Kesirli rasyonel ifade kavramı

Kesirli ifade, sayı ve harf değişkenleriyle yapılan toplama, çıkarma ve çarpma işlemlerinin yanı sıra, sıfıra eşit olmayan bir sayıya bölme işlemlerini de içeren, harf değişkenli ifadelere bölmeyi de içeren matematiksel bir ifadedir.

Rasyonel ifadelerin tamamı tam ve kesirli ifadelerdir. Rasyonel denklemler sol ve sağ taraflarının rasyonel ifadeler olduğu denklemlerdir. Rasyonel bir denklemde sol ve sağ taraflar tamsayı ifadeleri ise, o zaman böyle bir rasyonel denkleme tamsayı denir.

Rasyonel bir denklemde sol veya sağ taraflar kesirli ifadelerse, böyle bir rasyonel denkleme kesirli denir.

Kesirli rasyonel ifade örnekleri

1. x-3/x = -6*x+19

2. (x-4)/(2*x+5) = (x+7)/(x-2)

3. (x-3)/(x-5) + 1/x = (x+5)/(x*(x-5))

Kesirli rasyonel denklemi çözme şeması

1. Denklemde yer alan tüm kesirlerin ortak paydasını bulun.

2. Denklemin her iki tarafını ortak bir paydayla çarpın.

3. Ortaya çıkan denklemin tamamını çözün.

4. Kökleri kontrol edin ve ortak paydayı ortadan kaldıranları hariç tutun.

Kesirli rasyonel denklemleri çözdüğümüz için kesirlerin paydalarında değişkenler olacaktır. Bu onların ortak payda olacağı anlamına gelir. Ve algoritmanın ikinci noktasında ortak bir paydayla çarpıyoruz, o zaman yabancı kökler görünebilir. Ortak paydanın sıfıra eşit olacağı nokta, onunla çarpmanın anlamsız olacağı anlamına gelir. Bu nedenle sonunda elde edilen kökleri kontrol etmek gerekir.

Bir örneğe bakalım:

Kesirli rasyonel denklemi çözün: (x-3)/(x-5) + 1/x = (x+5)/(x*(x-5)).

sadık kalacağız genel şema: Öncelikle tüm kesirlerin ortak paydasını bulalım. x*(x-5) elde ederiz.

Her kesri ortak bir paydayla çarpın ve elde edilen denklemin tamamını yazın.

(x-3)/(x-5) * (x*(x-5))= x*(x+3);
1/x * (x*(x-5)) = (x-5);
(x+5)/(x*(x-5)) * (x*(x-5)) = (x+5);
x*(x+3) + (x-5) = (x+5);

Ortaya çıkan denklemi basitleştirelim. Şunu elde ederiz:

x^2+3*x + x-5 - x - 5 =0;
x^2+3*x-10=0;

Basit, indirgenmiş ikinci dereceden bir denklem elde ederiz. herhangi biriyle çözüyoruz bilinen yöntemler x=-2 ve x=5 köklerini elde ederiz.

Şimdi elde edilen çözümleri kontrol ediyoruz:

-2 ve 5 sayılarını ortak paydada değiştirin. x=-2'de ortak payda x*(x-5) kaybolmaz, -2*(-2-5)=14. Bu, -2 sayısının orijinal kesirli rasyonel denklemin kökü olacağı anlamına gelir.

x=5'te ortak payda x*(x-5) sıfır olur. Dolayısıyla bu sayı orijinal kesirli rasyonel denklemin kökü değildir, çünkü sıfıra bölünme olacaktır.

İkinci dereceden denklemlerin nasıl çözüleceğini zaten öğrendik. Şimdi çalışılan yöntemleri rasyonel denklemlere genişletelim.

Rasyonel ifade nedir? Bu kavramla zaten karşılaştık. Rasyonel ifadeler sayılar, değişkenler, bunların güçleri ve matematiksel işlem sembollerinden oluşan ifadelerdir.

Buna göre rasyonel denklemler aşağıdaki formdaki denklemlerdir: burada - rasyonel ifadeler.

Daha önce yalnızca doğrusal denklemlere indirgenebilecek rasyonel denklemleri değerlendiriyorduk. Şimdi ikinci dereceden denklemlere indirgenebilecek rasyonel denklemleri ele alalım.

Örnek 1

Denklemi çözün: .

Çözüm:

Bir kesir ancak ve ancak payı 0'a eşitse ve paydası 0'a eşit değilse 0'a eşittir.

Aşağıdaki sistemi elde ediyoruz:

Sistemin ilk denklemi ikinci dereceden bir denklemdir. Çözmeden önce tüm katsayılarını 3'e bölelim. Bunu elde ederiz:

İki kök elde ediyoruz: ; .

2 hiçbir zaman 0'a eşit olmadığından iki koşulun karşılanması gerekir: . Yukarıda elde edilen denklemin köklerinin hiçbiri, ikinci eşitsizliği çözerken elde edilen değişkenin geçersiz değerleriyle çakışmadığı için her ikisi de bu denklemin çözümüdür.

Cevap:.

Öyleyse rasyonel denklemleri çözmek için bir algoritma formüle edelim:

1. Tüm terimleri, sağ taraf 0 olacak şekilde sol tarafa taşıyın.

2. Sol tarafı dönüştürün ve basitleştirin, tüm kesirleri azaltın ortak payda.

3. Ortaya çıkan kesri aşağıdaki algoritmayı kullanarak 0'a eşitleyin: .

4. Birinci denklemde elde edilen kökleri yazın ve cevapta ikinci eşitsizliği sağlayın.

Başka bir örneğe bakalım.

Örnek 2

Denklemi çözün: .

Çözüm

En başta, 0 sağda kalacak şekilde tüm terimleri sola kaydırırız:

Şimdi denklemin sol tarafını ortak bir paydaya getirelim:

Bu denklem sisteme eşdeğerdir:

Sistemin ilk denklemi ikinci dereceden bir denklemdir.

Bu denklemin katsayıları: . Diskriminantı hesaplıyoruz:

İki kök elde ediyoruz: ; .

Şimdi ikinci eşitsizliği çözelim: Faktörlerden hiçbiri 0'a eşit değilse, faktörlerin çarpımı 0'a eşit değildir.

İki koşulun karşılanması gerekir: . İlk denklemin iki kökünden yalnızca birinin uygun olduğunu bulduk - 3.

Cevap:.

Bu dersimizde rasyonel ifadenin ne olduğunu hatırladık ve ikinci dereceden denklemlere indirgenebilen rasyonel denklemlerin nasıl çözüleceğini öğrendik.

Bir sonraki derste rasyonel denklemlere gerçek durumların modelleri olarak bakacağız ve ayrıca hareket problemlerine bakacağız.

Referanslar

1. Bashmakov M.I. Cebir, 8. sınıf. - M.: Eğitim, 2004.
2. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. ve diğerleri Cebir, 8. 5. baskı. - M.: Eğitim, 2010.
3. Nikolsky S.M., Potapov M.A., Reshetnikov N.N., Shevkin A.V. Cebir, 8. sınıf. için öğretici eğitim kurumları. - M.: Eğitim, 2006.

1. Festival pedagojik fikirler "Açık ders" ().
2. School.xvatit.com ().
3. Rudocs.exdat.com ().

Ev ödevi

hakkında konuşmaya devam edelim denklem çözme. Bu yazımızda bu konuyu detaylı olarak ele alacağız. rasyonel denklemler ve tek değişkenli rasyonel denklemlerin çözüm ilkeleri. Öncelikle hangi tür denklemlere rasyonel denildiğini bulalım, tam rasyonel ve kesirli rasyonel denklemlerin tanımını verelim ve örnekler verelim. Daha sonra rasyonel denklemleri çözmek için algoritmalar elde edeceğiz ve elbette gerekli tüm açıklamalarla birlikte tipik örneklerin çözümlerini ele alacağız.

Sayfada gezinme.

Belirtilen tanımlara dayanarak, birkaç rasyonel denklem örneği veriyoruz. Örneğin, x=1, 2·x−12·x 2 ·y·z 3 =0, ,'nin tümü rasyonel denklemlerdir.

Gösterilen örneklerden, rasyonel denklemlerin ve diğer türdeki denklemlerin tek değişkenli veya iki, üç vb. olabileceği açıktır. değişkenler. Aşağıdaki paragraflarda tek değişkenli rasyonel denklemlerin çözümünden bahsedeceğiz. İki değişkenli denklemleri çözme ve çok sayıda olmaları özel ilgiyi hak ediyor.

Rasyonel denklemler bilinmeyen değişken sayısına bölünmesinin yanı sıra tamsayı ve kesirli olarak da ayrılırlar. İlgili tanımları verelim.

Tanım.

Rasyonel denklem denir tüm, eğer hem sol hem de sağ tarafları tamsayı rasyonel ifadeler ise.

Tanım.

Rasyonel bir denklemin parçalarından en az biri kesirli bir ifade ise, böyle bir denklem denir. kesirli rasyonel(veya kesirli rasyonel).

Tam denklemlerin bir değişkene göre bölmeyi içermediği açıktır; aksine, kesirli rasyonel denklemler zorunlu olarak bir değişkene (veya paydadaki bir değişkene) bölmeyi içerir. Yani 3 x+2=0 ve (x+y)·(3·x 2 −1)+x=−y+0,5– bunlar tam rasyonel denklemlerdir, her iki parçası da tam ifadelerdir. A ve x:(5 x 3 +y 2)=3:(x−1):5 kesirli rasyonel denklem örnekleridir.

Bu noktayı bitirirken, şu ana kadar bilinen lineer denklemlerin ve ikinci dereceden denklemlerin tamamen rasyonel denklemler olduğuna dikkat edelim.

Denklemlerin tamamını çözme

Denklemlerin tamamını çözmenin temel yaklaşımlarından biri onları eşdeğer denklemlere indirgemektir. cebirsel denklemler. Bu her zaman denklemin aşağıdaki eşdeğer dönüşümleri gerçekleştirilerek yapılabilir:

• ilk olarak orijinal tamsayı denkleminin sağ tarafındaki ifade ile sol tarafa aktarılır. karşıt işaret sağ tarafta sıfır almak için;
• Bundan sonra denklemin sol tarafında ortaya çıkan standart form.

Sonuç, orijinal tamsayı denklemine eşdeğer bir cebirsel denklemdir. Böylece, en basit durumlarda denklemlerin tamamının çözülmesi, doğrusal veya ikinci dereceden denklemlerin çözümüne indirgenir ve genel durum– n dereceli bir cebirsel denklemi çözmek. Açıklık sağlamak için, örneğin çözümüne bakalım.

Örnek.

Tüm denklemin köklerini bulun 3·(x+1)·(x−3)=x·(2·x−1)−3.

Çözüm.

Tüm bu denklemin çözümünü eşdeğer bir cebirsel denklemin çözümüne indirgeyelim. Bunun için öncelikle ifadeyi sağ taraftan sola aktarıyoruz ve bunun sonucunda denkleme ulaşıyoruz. 3·(x+1)·(x−3)−x·(2·x−1)+3=0. İkinci olarak, sol tarafta oluşan ifadeyi gerekli işlemleri yaparak standart formun bir polinomuna dönüştürüyoruz: 3·(x+1)·(x−3)−x·(2·x−1)+3= (3 x+3) (x−3)−2 x 2 +x+3= 3 x 2 −9 x+3 x−9−2 x 2 +x+3=x 2 −5 x−6. Böylece orijinal tamsayı denkleminin çözümü çözüme indirgenir. ikinci dereceden denklem x 2 −5 x−6=0 .

Diskriminantını hesaplıyoruz D=(−5) 2 −4·1·(−6)=25+24=49 pozitiftir, bu da denklemin iki gerçek kökü olduğu anlamına gelir; bunu ikinci dereceden bir denklemin kökleri formülünü kullanarak buluruz:

Tamamen emin olmak için hadi yapalım Denklemin bulunan köklerinin kontrol edilmesi. İlk önce kök 6'yı kontrol ederiz, orijinal tamsayı denkleminde x değişkeni yerine onu kullanırız: 3·(6+1)·(6−3)=6·(2·6−1)−3 63=63 aynıdır. Bu geçerli bir sayısal denklemdir, dolayısıyla x=6 aslında denklemin köküdür. Şimdi −1 kökünü kontrol edersek, elimizde 3·(−1+1)·(−1−3)=(−1)·(2·(−1)−1)−3, buradan, 0=0 . X=−1 olduğunda orijinal denklem de doğru bir sayısal eşitliğe dönüşür, dolayısıyla x=−1 aynı zamanda denklemin köküdür.

Cevap:

6 , −1 .

Burada ayrıca "tüm denklemin derecesi" teriminin, bir denklemin tamamının cebirsel bir denklem biçiminde temsil edilmesiyle ilişkili olduğuna da dikkat edilmelidir. İlgili tanımı verelim:

Tanım.

Tüm denklemin gücü eşdeğer cebirsel denklemin derecesi denir.

Bu tanıma göre önceki örnekteki denklemin tamamı ikinci dereceye sahiptir.

Bu, tek bir şey olmasa bile, tüm rasyonel denklemleri çözmenin sonu olabilirdi…. Bilindiği gibi, derecenin ikincinin üzerinde olduğu cebirsel denklemlerin çözümü önemli zorluklarla ilişkilidir ve dördüncü derecenin üzerinde olan denklemler için hiçbir genel kök formülü yoktur. Bu nedenle üçüncü, dördüncü ve daha fazla denklemin tamamını çözmek için yüksek derecelerÇoğu zaman başka çözüm yöntemlerine başvurmak zorunda kalırsınız.

Bu gibi durumlarda rasyonel denklemlerin tamamının çözümüne dayalı bir yaklaşım çarpanlara ayırma yöntemi. Bu durumda aşağıdaki algoritmaya uyulur:

• Öncelikle denklemin sağ tarafında bir sıfır olmasını sağlarlar; bunun için denklemin tamamının sağ tarafındaki ifadeyi sola aktarırlar;
• daha sonra sol tarafta ortaya çıkan ifade, birkaç faktörün çarpımı olarak sunulur ve bu da birkaç basit denklem dizisine geçmemize olanak tanır.

Bir denklemin tamamını çarpanlara ayırma yoluyla çözmek için verilen algoritma şunları gerektirir: detaylı açıklamaörnek olarak.

Örnek.

Denklemin tamamını çöz (x 2 −1)·(x 2 −10·x+13)= 2 x (x 2 −10 x+13) .

Çözüm.

Öncelikle her zamanki gibi ifadeyi denklemin sağ tarafından sol tarafına aktarıyoruz, işareti değiştirmeyi unutmadan, şunu elde ediyoruz: (x 2 −1)·(x 2 −10·x+13)− 2 x (x 2 −10 x+13)=0 . Burada, ortaya çıkan denklemin sol tarafını standart formda bir polinom haline dönüştürmenin tavsiye edilmeyeceği oldukça açıktır, çünkü bu, formun dördüncü derecesinin cebirsel bir denklemini verecektir. x 4 −12 x 3 +32 x 2 −16 x−13=0çözümü zor olan bir durumdur.

Öte yandan, ortaya çıkan denklemin sol tarafında x 2 −10 x+13'ü bir çarpım olarak sunabileceğimiz açıktır. Sahibiz (x 2 −10 x+13) (x 2 −2 x−1)=0. Ortaya çıkan denklem orijinal denklemin tamamına eşdeğerdir ve bu da iki ikinci dereceden denklem x 2 −10·x+13=0 ve x 2 −2·x−1=0 ile değiştirilebilir. Bir diskriminant aracılığıyla bilinen kök formüllerini kullanarak köklerini bulmak zor değildir; kökler eşittir. Bunlar orijinal denklemin istenen kökleridir.

Cevap:

Ayrıca rasyonel denklemlerin tamamını çözmek için de faydalıdır yeni bir değişken ekleme yöntemi. Bazı durumlarda derecesi orijinal denklemin tamamının derecesinden daha düşük olan denklemlere geçmenize olanak tanır.

Örnek.

Rasyonel bir denklemin gerçek köklerini bulun (x 2 +3 x+1) 2 +10=−2 (x 2 +3 x−4).

Çözüm.

Tüm bu rasyonel denklemi cebirsel bir denkleme indirgemek, en hafif deyimle, pek iyi bir fikir değil, çünkü bu durumda rasyonel kökleri olmayan dördüncü dereceden bir denklemi çözme ihtiyacı duyacağız. Bu nedenle başka bir çözüm aramanız gerekecek.

Burada yeni bir y değişkeni tanıtabileceğinizi ve x 2 +3·x ifadesini bununla değiştirebileceğinizi görmek kolaydır. Bu değiştirme bizi tüm (y+1) 2 +10=−2·(y−4) denklemine götürür; bu, −2·(y−4) ifadesini sol tarafa taşıdıktan ve ardından ifadeyi dönüştürdükten sonra burada oluşan ikinci derece denklem y 2 +4·y+3=0'a indirgenir. Bu denklemin y=−1 ve y=−3 köklerini bulmak kolaydır, örneğin Vieta teoreminin tersi olan teoreme göre seçilebilirler.

Şimdi yeni bir değişken ekleme yönteminin ikinci kısmına, yani ters değiştirme işlemine geçiyoruz. Ters değiştirme işlemini gerçekleştirdikten sonra, x 2 +3 x=−1 ve x 2 +3 x=−3 olmak üzere iki denklem elde ederiz; bunlar x 2 +3 x+1=0 ve x 2 +3 x+3 olarak yeniden yazılabilir. =0 . İkinci dereceden bir denklemin kökleri formülünü kullanarak ilk denklemin köklerini buluruz. İkinci dereceden denklemin ise diskriminantı negatif olduğundan gerçek kökleri yoktur (D=3 2 −4·3=9−12=−3 ).

Cevap:

Genel olarak, yüksek dereceli denklemlerin tamamıyla uğraşırken her zaman araştırmaya hazır olmalıyız. standart dışı yöntem veya bunları çözmek için yapay bir yöntem.

Kesirli rasyonel denklemleri çözme

İlk olarak, p(x) ve q(x)'in tamsayı rasyonel ifadeler olduğu kesirli rasyonel denklemlerin nasıl çözüleceğini anlamak faydalı olacaktır. Daha sonra diğer kesirli rasyonel denklemlerin çözümünün belirtilen türdeki denklemlerin çözümüne nasıl indirgeneceğini göstereceğiz.

Denklemi çözmeye yönelik bir yaklaşım şu ifadeye dayanmaktadır: v'nin sıfır olmayan bir sayı olduğu u/v sayısal kesri (aksi takdirde tanımsız olan ile karşılaşırız), ancak ve ancak payının şu şekilde olması durumunda sıfıra eşittir: sıfıra eşitse, ancak ve ancak u=0 ise olur. Bu ifade sayesinde denklemin çözümü, p(x)=0 ve q(x)≠0 olmak üzere iki koşulun yerine getirilmesine indirgenir.

Bu sonuç aşağıdakilere karşılık gelir kesirli rasyonel denklemi çözmek için algoritma. Formun kesirli rasyonel denklemini çözmek için ihtiyacınız olan şey

• p(x)=0 rasyonel denkleminin tamamını çözün;
• ve bulunan her kök için q(x)≠0 koşulunun karşılanıp karşılanmadığını kontrol edin;
• eğer doğruysa bu kök orijinal denklemin köküdür;
• eğer karşılanmazsa bu kök yabancıdır, yani orijinal denklemin kökü değildir.

Kesirli bir rasyonel denklemi çözerken duyurulan algoritmayı kullanmanın bir örneğine bakalım.

Örnek.

Denklemin köklerini bulun.

Çözüm.

Bu kesirli rasyonel bir denklemdir ve şu şekildedir: p(x)=3·x−2, q(x)=5·x 2 −2=0.

Bu tür kesirli rasyonel denklemlerin çözümüne yönelik algoritmaya göre, öncelikle 3 x−2=0 denklemini çözmemiz gerekir. Bu doğrusal denklem, kökü x=2/3'tür.

Geriye bu kökü kontrol etmek, yani 5 x 2 −2≠0 koşulunu karşılayıp karşılamadığını kontrol etmek kalıyor. 5 x 2 −2 ifadesinde x yerine 2/3 sayısını koyarsak ve elde ederiz. Koşul karşılanmıştır, dolayısıyla x=2/3 orijinal denklemin köküdür.

Cevap:

2/3 .

Kesirli bir rasyonel denklemin çözümüne biraz farklı bir açıdan yaklaşabilirsiniz. Bu denklem, orijinal denklemin x değişkeni üzerindeki p(x)=0 tamsayı denklemine eşdeğerdir. Yani buna bağlı kalabilirsiniz kesirli rasyonel denklemi çözmek için algoritma :

• p(x)=0 denklemini çözün;
• x değişkeninin ODZ'sini bulun;
• kabul edilebilir değerlerin bölgesine ait kökleri alın - bunlar orijinal kesirli rasyonel denklemin istenen kökleridir.

Örneğin bu algoritmayı kullanarak kesirli bir rasyonel denklemi çözelim.

Örnek.

Denklemi çözün.

Çözüm.

Öncelikle ikinci dereceden x 2 −2·x−11=0 denklemini çözüyoruz. Kökleri çift ikinci katsayı için kök formülü kullanılarak hesaplanabilir, elimizdeki D 1 =(−1) 2 −1·(−11)=12, Ve .

İkinci olarak orijinal denklem için x değişkeninin ODZ'sini buluyoruz. x 2 +3·x≠0 olan ve x·(x+3)≠0 ile aynı olan tüm sayılardan oluşur; dolayısıyla x≠0, x≠−3.

Geriye ilk adımda bulunan köklerin ODZ'ye dahil edilip edilmediğini kontrol etmek kalıyor. Açıkçası evet. Bu nedenle orijinal kesirli rasyonel denklemin iki kökü vardır.

Cevap:

ODZ'nin bulunması kolaysa bu yaklaşımın ilkinden daha karlı olduğunu ve özellikle p(x) = 0 denkleminin köklerinin irrasyonel veya rasyonel olması ancak oldukça büyük bir paya sahip olması durumunda özellikle faydalı olduğunu unutmayın. /veya payda, örneğin, 127/1101 ve −31/59. Bunun nedeni, bu tür durumlarda q(x)≠0 koşulunun kontrol edilmesinin önemli miktarda hesaplama çabası gerektirmesi ve ODZ kullanılarak yabancı köklerin hariç tutulmasının daha kolay olmasıdır.

Diğer durumlarda, denklemi çözerken, özellikle p(x) = 0 denkleminin kökleri tamsayı olduğunda, verilen algoritmalardan ilkini kullanmak daha karlı olur. Yani, ODZ'yi bulup denklemi çözmek yerine, hemen tüm p(x)=0 denkleminin köklerini bulmak ve ardından q(x)≠0 koşulunun onlar için karşılanıp karşılanmadığını kontrol etmek tavsiye edilir. Bu ODZ'de p(x)=0. Bunun nedeni, bu gibi durumlarda kontrol etmenin genellikle DZ'yi bulmaktan daha kolay olmasıdır.

Belirtilen nüansları göstermek için iki örneğin çözümünü ele alalım.

Örnek.

Denklemin köklerini bulun.

Çözüm.

İlk önce tüm denklemin köklerini bulalım (2 x−1) (x−6) (x 2 −5 x+14) (x+1)=0, kesrin payı kullanılarak oluşturulur. Sol taraf bu denklemin bir çarpımıdır ve sağ tarafı sıfırdır, bu nedenle denklemleri çarpanlara ayırma yoluyla çözme yöntemine göre bu denklem dört denklemden oluşan bir diziye eşdeğerdir 2 x−1=0 , x−6=0 , x 2 −5 x+14= 0 , x+1=0 . Bu denklemlerden üçü doğrusal, biri ikinci derecedendir; bunları çözebiliriz. İlk denklemden x=1/2, ikinciden - x=6, üçüncüden - x=7, x=−2, dördüncüden - x=−1 buluyoruz.

Bulunan köklerle, orijinal denklemin sol tarafındaki kesirin paydasının kaybolup kaybolmadığını kontrol etmek oldukça kolaydır, ancak tam tersine ODZ'yi belirlemek o kadar basit değildir, çünkü bunun için çözmeniz gerekecek beşinci derecenin cebirsel denklemi. Bu nedenle, kökleri kontrol etmek adına ODZ'yi bulmayı bırakacağız. Bunu yapmak için ifadedeki x değişkeni yerine bunları birer birer değiştiriyoruz. x 5 −15 x 4 +57 x 3 −13 x 2 +26 x+112, değiştirmeden sonra elde edilenleri sıfırla karşılaştırın: (1/2) 5 −15·(1/2) 4 + 57·(1/2) 3 −13·(1/2) 2 +26·(1/2)+112= 1/32−15/16+57/8−13/4+13+112= 122+1/32≠0 ;
6 5 −15·6 4 +57·6 3 −13·6 2 +26·6+112= 448≠0 ;
7 5 −15·7 4 +57·7 3 −13·7 2 +26·7+112=0;
(−2) 5 −15·(−2) 4 +57·(−2) 3 −13·(−2) 2 + 26·(−2)+112=−720≠0 ;
(−1) 5 −15·(−1) 4 +57·(−1) 3 −13·(−1) 2 + 26·(−1)+112=0 .

Dolayısıyla, 1/2, 6 ve −2 orijinal kesirli rasyonel denklemin istenen kökleridir ve 7 ve −1 ise yabancı köklerdir.

Cevap:

1/2 , 6 , −2 .

Örnek.

Kesirli bir rasyonel denklemin köklerini bulun.

Çözüm.

İlk önce denklemin köklerini bulalım (5 x 2 −7 x−1) (x−2)=0. Bu denklem iki denklemden oluşan bir diziye eşdeğerdir: kare 5 x 2 −7 x−1=0 ve doğrusal x−2=0. İkinci dereceden bir denklemin kökleri formülünü kullanarak iki kök buluruz ve ikinci denklemden x=2 elde ederiz.

X'in bulunan değerlerinde paydanın sıfıra gidip gitmediğini kontrol etmek oldukça tatsızdır. Ve orijinal denklemde x değişkeninin izin verilen değerlerinin aralığını belirlemek oldukça basittir. Bu nedenle ODZ üzerinden hareket edeceğiz.

Bizim durumumuzda, orijinal kesirli rasyonel denklemin x değişkeninin ODZ'si, x 2 +5·x−14=0 koşulunun karşılandığı sayılar dışındaki tüm sayılardan oluşur. Bu ikinci dereceden denklemin kökleri x=−7 ve x=2'dir ve bundan ODZ hakkında bir sonuç çıkarıyoruz: tüm x'lerden oluşur, öyle ki .

Geriye bulunan köklerin ve x=2'nin kabul edilebilir değerler aralığına ait olup olmadığını kontrol etmek kalır. Kökler aittir, dolayısıyla orijinal denklemin kökleridir ve x=2 ait değildir, dolayısıyla yabancı bir köktür.

Cevap:

Ayrıca kesirli rasyonel denklem formundaki payda bir sayının olduğu, yani p(x)'in bir sayı ile temsil edildiği durumlar üzerinde ayrıca durmak faydalı olacaktır. Aynı zamanda

• eğer bu sayı sıfır değilse, o zaman denklemin kökleri yoktur, çünkü bir kesir ancak ve ancak payı sıfıra eşitse sıfıra eşittir;
• bu sayı sıfırsa denklemin kökü ODZ'den herhangi bir sayıdır.

Örnek.

Çözüm.

Denklemin sol tarafındaki kesrin payı sıfırdan farklı bir sayı içerdiğinden herhangi bir x için bu kesrin değeri sıfır olamaz. Dolayısıyla bu denklemin kökleri yoktur.

Cevap:

kök yok.

Örnek.

Denklemi çözün.

Çözüm.

Bu kesirli rasyonel denklemin sol tarafındaki kesrin payı sıfır içerir, dolayısıyla bu kesrin değeri, anlamlı olduğu herhangi bir x için sıfırdır. Başka bir deyişle, bu denklemin çözümü bu değişkenin ODZ'sinden herhangi bir x değeridir.

Geriye bu kabul edilebilir değer aralığını belirlemek kalıyor. x 4 +5 x 3 ≠0 olan tüm x değerlerini içerir. x 4 +5 x 3 =0 denkleminin çözümleri 0 ve −5'tir, çünkü bu denklem x 3 (x+5)=0 denklemine eşdeğerdir ve bu da iki x denkleminin birleşimine eşdeğerdir 3 =0 ve x +5=0, bu köklerin görülebildiği yerden. Bu nedenle kabul edilebilir değerlerin istenen aralığı, x=0 ve x=−5 dışında herhangi bir x'tir.

Dolayısıyla, kesirli bir rasyonel denklemin sıfır ve eksi beş dışında herhangi bir sayıdan oluşan sonsuz sayıda çözümü vardır.

Cevap:

Son olarak, keyfi biçimdeki kesirli rasyonel denklemlerin çözümü hakkında konuşmanın zamanı geldi. r(x)=s(x) şeklinde yazılabilirler; burada r(x) ve s(x) rasyonel ifadelerdir ve bunlardan en az biri kesirlidir. İleriye baktığımızda, çözümlerinin zaten bize tanıdık gelen formdaki denklemlerin çözülmesine bağlı olduğunu varsayalım.

Bir terimin denklemin bir kısmından ters işaretli diğer kısmına aktarılmasının eşdeğer bir denklem oluşturduğu bilinmektedir, dolayısıyla r(x)=s(x) denklemi r(x)−s(x) denklemine eşdeğerdir. )=0.

Ayrıca bu ifadeye eşit olan herhangi bir ifadenin mümkün olduğunu da biliyoruz. Böylece r(x)−s(x)=0 denkleminin sol tarafındaki rasyonel ifadeyi her zaman formun özdeş eşit rasyonel kesrine dönüştürebiliriz.

Dolayısıyla, orijinal kesirli rasyonel denklem r(x)=s(x)'ten denkleme geçiyoruz ve bunun çözümü, yukarıda öğrendiğimiz gibi, p(x)=0 denkleminin çözümüne indirgeniyor.

Ancak burada, r(x)−s(x)=0 ile ve ardından p(x)=0 ile değiştirilirken, x değişkeninin izin verilen değerlerinin aralığının genişleyebileceği gerçeğini hesaba katmak gerekir. .

Sonuç olarak, ulaştığımız orijinal r(x)=s(x) denklemi ile p(x)=0 denklemi eşit olmayabilir ve p(x)=0 denklemini çözerek kökleri elde edebiliriz. bunlar orijinal r(x)=s(x) denkleminin yabancı kökleri olacaktır. Bir kontrol yaparak veya bunların orijinal denklemin ODZ'sine ait olup olmadığını kontrol ederek yabancı kökleri tanımlayabilir ve cevaba dahil etmeyebilirsiniz.

Bu bilgileri şöyle özetleyelim r(x)=s(x) kesirli rasyonel denklemini çözmek için algoritma. Kesirli rasyonel denklem r(x)=s(x)'i çözmek için şunlara ihtiyacınız vardır:

• İfadeyi sağ taraftan ters işaretle hareket ettirerek sağdaki sıfırı alın.
• Denklemin sol tarafında kesirler ve polinomlarla işlemler gerçekleştirin, böylece onu formun rasyonel bir kesirine dönüştürün.
• p(x)=0 denklemini çözün.
• Yabancı kökleri orijinal denklemde değiştirerek veya orijinal denklemin ODZ'sine ait olduklarını kontrol ederek tanımlayın ve ortadan kaldırın.

Daha fazla netlik sağlamak için, kesirli rasyonel denklemlerin çözüm zincirinin tamamını göstereceğiz:
.

Verilen bilgi bloğunu açıklığa kavuşturmak için çözüm sürecinin ayrıntılı bir açıklamasıyla birlikte birkaç örneğin çözümlerine bakalım.

Örnek.

Kesirli rasyonel denklemi çözün.

Çözüm.

Az önce elde edilen çözüm algoritmasına göre hareket edeceğiz. Ve önce terimleri denklemin sağ tarafından sola kaydırıyoruz, sonuç olarak denkleme geçiyoruz.

İkinci adımda, ortaya çıkan denklemin sol tarafındaki kesirli rasyonel ifadeyi kesir formuna dönüştürmemiz gerekiyor. Bunu yapmak için rasyonel kesirleri ortak bir paydaya indiririz ve ortaya çıkan ifadeyi basitleştiririz: . Böylece denkleme geliyoruz.

Bir sonraki adımda −2·x−1=0 denklemini çözmemiz gerekiyor. x=−1/2'yi buluyoruz.

Bulunan −1/2 sayısının orijinal denklemin yabancı bir kökü olup olmadığını kontrol etmek kalır. Bunu yapmak için orijinal denklemdeki x değişkeninin VA'sını kontrol edebilir veya bulabilirsiniz. Her iki yaklaşımı da gösterelim.

Kontrol ederek başlayalım. Orijinal denklemde x değişkeni yerine −1/2 sayısını koyarsak aynı şeyi elde ederiz: −1=−1. Değiştirme doğru sayısal eşitliği verir, dolayısıyla x=−1/2 orijinal denklemin köküdür.

Şimdi algoritmanın son noktasının ODZ üzerinden nasıl gerçekleştirildiğini göstereceğiz. Orijinal denklemin kabul edilebilir değerleri aralığı -1 ve 0 dışındaki tüm sayılar kümesidir (x=−1 ve x=0'da kesirlerin paydaları sıfırdır). Önceki adımda bulunan x=−1/2 kökü ODZ'ye aittir, dolayısıyla x=−1/2 orijinal denklemin köküdür.

Cevap:

−1/2 .

Başka bir örneğe bakalım.

Örnek.

Denklemin köklerini bulun.

Çözüm.

Kesirli bir rasyonel denklemi çözmemiz gerekiyor, hadi algoritmanın tüm adımlarını izleyelim.

İlk önce terimi sağ taraftan sola kaydırırız, şunu elde ederiz.

İkinci olarak sol tarafta oluşan ifadeyi dönüştürüyoruz: . Sonuç olarak x=0 denklemine ulaşıyoruz.

Kökü bellidir; sıfırdır.

Dördüncü adımda, bulunan kökün orijinal kesirli rasyonel denkleme yabancı olup olmadığını bulmaya devam ediyor. Orijinal denklemde yerine konulduğunda ifade elde edilir. Açıkçası sıfıra bölmeyi içerdiği için mantıklı değil. Buradan 0'ın yabancı bir kök olduğu sonucuna vardık. Bu nedenle orijinal denklemin kökleri yoktur.

7, bu da Denklem'e yol açar. Buradan, sol taraftaki paydadaki ifadenin sağ taraftaki paydadaki ifadeye eşit olması gerektiği sonucuna varabiliriz. Şimdi üçlünün her iki tarafından da çıkarıyoruz: . Benzetme yoluyla, nereden ve daha ileri.

Kontrol, bulunan her iki kökün de orijinal kesirli rasyonel denklemin kökleri olduğunu gösterir.

Cevap:

Referanslar.

• Cebir: ders kitabı 8. sınıf için. genel eğitim kurumlar / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; tarafından düzenlendi S. A. Telyakovsky. - 16. baskı. - M.: Eğitim, 2008. - 271 s. : hasta. - ISBN 978-5-09-019243-9.
• Mordkoviç A.G. Cebir. 8. sınıf. 2 saat içinde Bölüm 1. Genel eğitim kurumlarının öğrencileri için ders kitabı / A. G. Mordkovich. - 11. baskı, silindi. - M.: Mnemosyne, 2009. - 215 s.: hasta. ISBN 978-5-346-01155-2.
• Cebir: 9. sınıf: eğitici. genel eğitim için kurumlar / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; tarafından düzenlendi S. A. Telyakovsky. - 16. baskı. - M.: Eğitim, 2009. - 271 s. : hasta. - ISBN 978-5-09-021134-5.

Basitçe söylemek gerekirse bunlar, paydasında en az bir değişkenin bulunduğu denklemlerdir.

Örneğin:

\(\frac(9x^2-1)(3x)\) \(=0\)
\(\frac(1)(2x)+\frac(x)(x+1)=\frac(1)(2)\)
\(\frac(6)(x+1)=\frac(x^2-5x)(x+1)\)

Örnek Olumsuz kesirli rasyonel denklemler:

\(\frac(9x^2-1)(3)\) \(=0\)
\(\frac(x)(2)\) \(+8x^2=6\)

Kesirli rasyonel denklemler nasıl çözülür?

Kesirli rasyonel denklemler hakkında hatırlamanız gereken en önemli şey, onları yazmanız gerektiğidir. Ve kökleri bulduktan sonra kabul edilebilirlik açısından kontrol ettiğinizden emin olun. Aksi takdirde yabancı kökler ortaya çıkabilir ve kararın tamamı yanlış kabul edilecektir.

Kesirli rasyonel denklemi çözmek için algoritma:

ODZ'yi yazın ve “çözün”.

Denklemdeki her terimi ortak paydayla çarpın ve elde edilen kesirleri iptal edin. Paydalar kaybolacak.

Parantezleri açmadan denklemi yazınız.

Ortaya çıkan denklemi çözün.

Bulunan kökleri ODZ ile kontrol edin.

Cevabınıza 7. adımdaki testi geçen kökleri yazın.

Algoritmayı ezberlemeyin, 3-5 tane çözülmüş denklem kendiliğinden hatırlanacaktır.

Örnek . Kesirli rasyonel denklemi çözün \(\frac(x)(x-2) - \frac(7)(x+2)=\frac(8)(x^2-4)\)

Çözüm:

Cevap: \(3\).

Örnek . Kesirli rasyonel denklemin köklerini bulun \(=0\)

Çözüm:

Cevap: \(\frac(1)(2)\).

“Polinomlu rasyonel denklemler” en sık karşılaşılan konulardan biridir. test görevleri Matematikte Birleşik Devlet Sınavı. Bu nedenle tekrar etmekte fayda var özel ilgi. Pek çok öğrenci diskriminant bulma, göstergeleri sağdan sola aktarma ve denklemi ortak paydaya getirme sorunuyla karşı karşıya kalıyor ve bu nedenle bu tür görevleri tamamlamak zorluklara neden oluyor. Web sitemizdeki Birleşik Devlet Sınavına hazırlanırken rasyonel denklemleri çözmek, her türlü karmaşıklıktaki sorunlarla hızlı bir şekilde başa çıkmanıza ve testi başarıyla geçmenize yardımcı olacaktır.

Birleşik Matematik Sınavına başarıyla hazırlanmak için Shkolkovo eğitim portalını seçin!

Bilinmeyenleri hesaplama kurallarını bilmek ve kolayca elde etmek doğru sonuçlar, çevrimiçi hizmetimizi kullanın. Shkolkovo portalı, hazırlık için gerekli her şeyi içeren türünün tek örneği bir platformdur. Birleşik Devlet Sınavı materyalleri. Öğretmenlerimiz tüm matematik kurallarını sistematize edip anlaşılır bir biçimde sundular. Ek olarak, okul çocuklarını, temeli sürekli güncellenen ve genişletilen standart rasyonel denklemleri çözme konusunda ellerini denemeye davet ediyoruz.

Teste daha etkili bir hazırlık için, özel yöntemimizi izlemenizi ve kuralları tekrarlayıp basit problemleri çözerek başlamanızı, yavaş yavaş daha karmaşık problemlere geçmenizi öneririz. Böylece mezun kendisi için en zor konuları belirleyebilecek ve bunları incelemeye odaklanabilecektir.

Bugün Shkolkovo ile son teste hazırlanmaya başlayın, sonuçların gelmesi uzun sürmeyecek! En çok seç kolay örnekönerilenlerden. İfadeyi hızlı bir şekilde öğrendiyseniz daha fazlasına geçin. zor görev. Bu şekilde bilginizi matematikteki USE görevlerini uzmanlık düzeyinde çözme noktasına kadar geliştirebilirsiniz.

Eğitim yalnızca Moskova'dan mezun olanlar için değil, diğer şehirlerden gelen okul çocukları için de geçerlidir. Örneğin, günde birkaç saatinizi portalımızda çalışarak geçirin; çok yakında her türlü karmaşıklıktaki denklemlerle başa çıkabileceksiniz!