Teorem umum dinamik sistem badan. Teorem tentang gerakan pusat jisim, tentang mengubah momentum, tentang mengubah momen utama momentum, tentang mengubah tenaga kinetik. Prinsip D'Alembert dan kemungkinan anjakan. Persamaan am dinamik. Persamaan Lagrange.

Teorem umum dinamik jasad tegar dan sistem jasad

Teorem umum dinamik ialah teorem tentang gerakan pusat jisim sistem mekanikal, teorem tentang perubahan jumlah gerakan, teorem tentang perubahan momen utama momentum sudut (momentum sudut) dan teorem tentang perubahan tenaga kinetik sistem mekanikal.

Teorem mengenai gerakan pusat jisim sistem mekanikal

Teorem tentang gerakan pusat jisim.
Hasil darab jisim sistem dengan pecutan pusat jisimnya adalah sama dengan jumlah vektor semua daya luar yang bertindak ke atas sistem:
.

Di sini M ialah jisim sistem:
;
a C - pecutan pusat jisim sistem:
;
v C ialah kelajuan pusat jisim sistem:
;
r C - vektor jejari (koordinat) pusat jisim sistem:
;
- koordinat (berbanding dengan pusat tetap) dan jisim titik yang membentuk sistem.

Teorem tentang perubahan jumlah gerakan (momentum)

Jumlah pergerakan (impuls) sistem adalah sama dengan hasil darab jisim keseluruhan sistem dengan kelajuan pusat jisimnya atau jumlah momentum (jumlah impuls) titik atau bahagian individu yang membentuk sistem:
.

Teorem tentang perubahan momentum dalam bentuk pembezaan.
Terbitan masa bagi momentum (momentum) sistem adalah sama dengan jumlah vektor semua daya luar yang bertindak ke atas sistem:
.

Teorem tentang perubahan momentum dalam bentuk kamiran.
Perubahan dalam momentum (impuls) sistem dalam tempoh masa tertentu adalah sama dengan jumlah impuls daya luar dalam tempoh masa yang sama:
.

Hukum kekekalan momentum (momentum).
Jika jumlah semua daya luar yang bertindak pada sistem adalah sama dengan sifar, maka vektor momentum sistem akan tetap. Iaitu, semua unjurannya pada paksi koordinat akan mengekalkan nilai malar.

Jika jumlah unjuran daya luar pada mana-mana paksi adalah sama dengan sifar, maka unjuran momentum sistem pada paksi ini akan tetap.

Teorem tentang perubahan momen utama momentum (teorem momen)

Momen utama momentum sistem berkenaan dengan pusat O tertentu dipanggil nilai yang sama dengan jumlah vektor momen kuantiti gerakan semua titik sistem berbanding pusat ini:
.
Di sini, kurungan segi empat sama menunjukkan hasil silang.

Sistem tetap

Teorem berikut merujuk kepada kes apabila sistem mekanikal mempunyai titik atau paksi tetap, yang ditetapkan relatif kepada kerangka rujukan inersia. Sebagai contoh, badan tetap dengan galas sfera. Atau sistem badan yang bergerak di sekitar pusat tetap. Ia juga boleh menjadi paksi tetap di mana badan atau sistem badan berputar. Dalam kes ini, momen harus difahami sebagai momen impuls dan daya relatif kepada paksi tetap.

Teorem tentang perubahan momen utama momentum (teorem momen)
Terbitan masa bagi momentum sudut utama sistem berbanding beberapa pusat tetap O adalah sama dengan jumlah momen semua daya luar sistem berbanding pusat yang sama.

Hukum kekekalan momentum sudut utama (momentum sudut).
Jika jumlah momen semua daya luar yang digunakan pada sistem berbanding dengan pusat tetap O yang diberikan adalah sama dengan sifar, maka momentum sudut utama sistem berbanding pusat ini akan tetap. Iaitu, semua unjurannya pada paksi koordinat akan mengekalkan nilai malar.

Jika jumlah momen daya luar berkenaan dengan beberapa paksi tetap adalah sama dengan sifar, maka momen momentum sistem berkenaan dengan paksi ini akan tetap.

Sistem sewenang-wenangnya

Teorem seterusnya adalah universal. Ia boleh digunakan untuk kedua-dua sistem tetap dan yang bergerak bebas. Dalam kes sistem berlabuh, adalah perlu untuk mengambil kira tindak balas ikatan pada titik berlabuh. Ia berbeza daripada teorem sebelumnya kerana bukannya titik tetap O, seseorang harus mengambil pusat jisim C sistem.

Teorem Momen Pusat Jisim
Terbitan masa bagi momentum sudut utama sistem berbanding pusat jisim C adalah sama dengan jumlah momen semua daya luar sistem berbanding pusat yang sama.

Hukum kekekalan momentum sudut.
Jika jumlah momen semua daya luar yang digunakan pada sistem berbanding pusat jisim C adalah sama dengan sifar, maka momentum sudut utama sistem berbanding pusat ini akan tetap. Iaitu, semua unjurannya pada paksi koordinat akan mengekalkan nilai malar.

Momen inersia badan

Jika badan berputar mengelilingi paksi z dengan halaju sudut ω z, maka momentum sudutnya (momentum sudut) berbanding paksi z ditentukan oleh formula:
L z = J z ω z,
di mana J z ialah momen inersia badan berbanding paksi z.

Momen inersia jasad terhadap paksi-z ditentukan oleh formula:
,
di mana h k ialah jarak dari titik berjisim m k ke paksi z.
Untuk gelang nipis berjisim M dan jejari R atau silinder yang jisimnya diagihkan ke atas rimnya,
J z = M R 2 .
Untuk cincin atau silinder seragam pepejal,
.

Teorem Steiner-Huygens.
Biarkan Cz ialah paksi yang melalui pusat jisim badan, Oz paksi selari dengannya. Kemudian momen inersia badan mengenai paksi ini dikaitkan dengan nisbah:
J Oz = J Cz + M a 2 ,
di mana M ialah berat badan; a ialah jarak antara paksi.

Dalam lebih kes am :
,
di manakah tensor inersia badan.
Berikut ialah vektor yang dilukis dari pusat jisim badan ke titik dengan jisim m k.

Teorem tentang perubahan tenaga kinetik

Biarkan jasad berjisim M melakukan gerakan translasi dan putaran dengan halaju sudut ω mengelilingi beberapa paksi z. Kemudian tenaga kinetik badan ditentukan oleh formula:
,
di mana v C ialah kelajuan pergerakan pusat jisim badan;
J Cz - momen inersia jasad terhadap paksi yang melalui pusat jisim jasad selari dengan paksi putaran. Arah paksi putaran boleh berubah mengikut masa. Formula yang ditentukan memberikan nilai serta-merta tenaga kinetik.

Teorem tentang perubahan tenaga kinetik sistem dalam bentuk pembezaan.
Perbezaan (kenaikan) tenaga kinetik sistem untuk beberapa anjakannya adalah sama dengan jumlah pembezaan kerja pada anjakan semua daya luaran dan dalaman yang digunakan pada sistem:
.

Teorem tentang perubahan tenaga kinetik sistem dalam bentuk kamiran.
Perubahan dalam tenaga kinetik sistem dengan beberapa anjakannya adalah sama dengan jumlah kerja pada anjakan ini semua daya luaran dan dalaman yang digunakan pada sistem:
.

Kerja yang dilakukan oleh kuasa, adalah sama dengan hasil skalar bagi vektor daya dan anjakan tak terhingga bagi titik penggunaannya:
,
iaitu hasil darab nilai mutlak vektor F dan ds dengan kosinus sudut di antara keduanya.

Kerja yang dilakukan oleh momen kuasa, adalah sama dengan hasil kali skalar bagi vektor momen dan sudut putaran tak terhingga:
.

Prinsip D'Alembert

Intipati prinsip d'Alembert adalah untuk mengurangkan masalah dinamik kepada masalah statik. Untuk ini, diandaikan (atau diketahui terlebih dahulu) bahawa badan sistem mempunyai pecutan (sudut) tertentu. Seterusnya, daya inersia dan (atau) momen daya inersia diperkenalkan, yang sama magnitud dan bertentangan arah dengan daya dan momen daya, yang, menurut undang-undang mekanik, akan mewujudkan pecutan atau pecutan sudut tertentu.

Mari kita lihat contoh. Dalam perjalanan, badan membuat gerakan ke hadapan dan kuasa luar bertindak ke atasnya. Selanjutnya, kami menganggap bahawa daya ini mewujudkan pecutan pusat jisim sistem. Mengikut teorem tentang gerakan pusat jisim, pusat jisim suatu jasad akan mempunyai pecutan yang sama jika daya bertindak ke atas jasad itu. Seterusnya, kami memperkenalkan daya inersia:
.
Selepas itu, masalah dinamik:
.
;
.

Untuk gerakan berputar, teruskan dengan cara yang sama. Biarkan badan berputar mengelilingi paksi z dan momen luar daya M e zk bertindak ke atasnya. Kami menganggap bahawa detik-detik ini mencipta pecutan sudut ε z. Seterusnya, kami memperkenalkan momen daya inersia M И = - J z ε z. Selepas itu, masalah dinamik:
.
Berubah menjadi tugas statik:
;
.

Prinsip anjakan yang mungkin

Prinsip anjakan yang mungkin digunakan untuk menyelesaikan masalah statik. Dalam beberapa masalah, ia memberikan penyelesaian yang lebih pendek daripada persamaan keseimbangan. Ini terutama berlaku untuk sistem dengan kekangan (contohnya, sistem badan yang disambungkan oleh benang dan blok), yang terdiri daripada banyak badan

Prinsip anjakan yang mungkin.
Untuk keseimbangan sistem mekanikal dengan kekangan yang ideal, adalah perlu dan mencukupi bahawa jumlah kerja asas semua daya aktif yang bertindak ke atasnya untuk sebarang kemungkinan anjakan sistem adalah sama dengan sifar.

Kemungkinan pergerakan sistem- ini adalah anjakan kecil, yang tidak memutuskan sambungan yang dikenakan pada sistem.

Sambungan yang sempurna- ini adalah sambungan yang tidak melakukan kerja apabila sistem dialihkan. Lebih tepat lagi, jumlah kerja yang dilakukan oleh pautan itu sendiri apabila sistem bergerak adalah sama dengan sifar.

Persamaan am dinamik (d'Alembert - prinsip Lagrange)

Prinsip d'Alembert-Lagrange ialah gabungan prinsip d'Alembert dengan prinsip anjakan yang mungkin. Iaitu, apabila menyelesaikan masalah dinamik, kami memperkenalkan daya inersia dan mengurangkan masalah kepada masalah statik, yang kami selesaikan menggunakan prinsip anjakan yang mungkin.

D'Alembert - Prinsip Lagrange.
Apabila sistem mekanikal dengan kekangan ideal bergerak pada setiap saat masa, jumlah kerja asas semua daya aktif yang digunakan dan semua daya inersia pada sebarang kemungkinan anjakan sistem adalah sama dengan sifar:
.
Persamaan ini dipanggil persamaan am dinamik.

Persamaan Lagrange

Koordinat umum q 1, q 2, ..., q n ialah koleksi nilai n yang secara unik menentukan kedudukan sistem.

Bilangan koordinat umum n bertepatan dengan bilangan darjah kebebasan sistem.

Kelajuan umum ialah terbitan koordinat umum berkenaan dengan masa t.

Daya am Q 1, Q 2, ..., Q n .
Pertimbangkan kemungkinan pergerakan sistem, di mana koordinat q k akan menerima pergerakan δq k. Selebihnya koordinat kekal tidak berubah. Biarkan δA k ialah kerja yang dilakukan oleh daya luar semasa anjakan sedemikian. Kemudian
δA k = Q k δq k, atau
.

Jika, dengan kemungkinan pergerakan sistem, semua koordinat berubah, maka kerja yang dilakukan oleh daya luar semasa pergerakan sedemikian mempunyai bentuk:
δA = Q 1 δq 1 + Q 2 δq 2 + ... + Q n δq n.
Kemudian daya umum ialah terbitan separa bagi kerja pada anjakan:
.

Untuk kuasa yang berpotensi dengan potensi Π,
.

Persamaan Lagrange ialah persamaan gerakan sistem mekanikal dalam koordinat umum:

Di sini T ialah tenaga kinetik. Ia adalah fungsi koordinat umum, halaju, dan mungkin masa. Oleh itu, terbitan separanya juga merupakan fungsi koordinat umum, halaju dan masa. Selanjutnya, anda perlu mengambil kira bahawa koordinat dan kelajuan adalah fungsi masa. Oleh itu, untuk mencari jumlah terbitan masa, adalah perlu untuk menggunakan peraturan untuk membezakan fungsi kompleks:
.

Rujukan:
S. M. Targ, Kursus pendek mekanik teori, "Sekolah Tinggi", 2010.

Kuliah 3. Teorem umum dinamik

Dinamik sistem titik material adalah bahagian penting dalam mekanik teori. Ia terutamanya berkaitan dengan masalah pergerakan sistem mekanikal (sistem titik material) dengan bilangan darjah kebebasan yang terhingga - bilangan maksimum parameter bebas yang menentukan kedudukan sistem. Tugas utama dinamik sistem adalah untuk mengkaji undang-undang gerakan padu dan sistem mekanikal.

Pendekatan paling mudah untuk mengkaji gerakan sistem, yang terdiri daripada N mata material, untuk dikurangkan kepada mempertimbangkan pergerakan setiap titik individu sistem. Dalam kes ini, semua daya yang bertindak pada setiap titik sistem mesti ditentukan, termasuk daya interaksi antara titik.

Menentukan pecutan setiap titik mengikut undang-undang kedua Newton (1.2), kita memperoleh bagi setiap titik tiga hukum pembezaan tertib kedua skalar gerakan, i.e. 3 N undang-undang pembezaan pergerakan untuk keseluruhan sistem.

Untuk mencari persamaan gerakan sistem mekanikal untuk daya yang diberikan dan keadaan awal bagi setiap titik sistem, hukum pembezaan yang terhasil mesti disepadukan. Masalah ini sukar walaupun dalam kes dua titik material yang bergerak hanya di bawah tindakan daya interaksi mengikut undang-undang tarikan sejagat (masalah dua badan), dan amat sukar dalam kes tiga titik berinteraksi (masalah tiga badan).

Oleh itu, adalah perlu untuk mencari kaedah untuk menyelesaikan masalah yang akan membawa kepada persamaan yang boleh diselesaikan dan memberi gambaran tentang gerakan sistem mekanikal. Teorem umum dinamik, sebagai akibat daripada undang-undang pembezaan gerakan, membolehkan mengelakkan kerumitan yang timbul daripada penyepaduan dan mendapatkan keputusan yang diperlukan.

3. 1. Ucapan am

Titik sistem mekanikal akan dinomborkan dengan indeks i, j, k dan seterusnya yang dijalankan melalui semua nilai 1, 2, 3… N, di mana N Merupakan bilangan mata dalam sistem. Kuantiti fizik yang berkaitan dengan k-titik ke-ditandakan oleh indeks yang sama dengan titik. Sebagai contoh, nyatakan vektor jejari dan halaju, masing-masing k titik ke.

Untuk setiap titik sistem, daya asal dua kali bertindak: pertama, daya yang sumbernya terletak di luar sistem, dipanggil luaran pasukan dan ditetapkan; kedua, kuasa dari titik lain sistem ini, dipanggil dalaman pasukan dan ditetapkan. Daya dalaman memenuhi undang-undang ketiga Newton. Mari kita pertimbangkan sifat termudah bagi daya dalaman yang bertindak ke atas keseluruhan sistem mekanikal di mana-mana keadaannya.

Harta pertama. Jumlah geometri semua daya dalaman sistem (vektor utama daya dalaman) adalah sama dengan sifar.

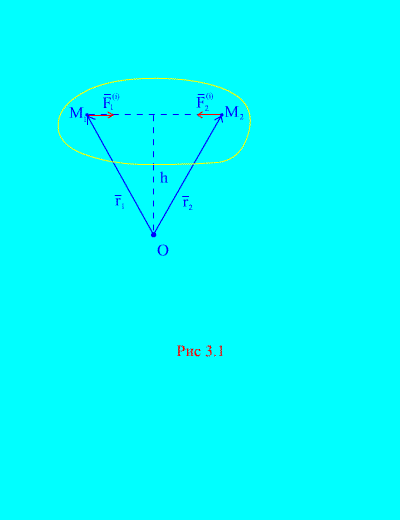
Sesungguhnya, jika kita mempertimbangkan mana-mana dua titik sewenang-wenangnya sistem, sebagai contoh, dan (rajah 3.1), kemudian untuk mereka sejak daya tindakan dan tindak balas sentiasa sama dalam magnitud, mereka bertindak sepanjang satu garis tindakan dalam arah yang bertentangan, yang menghubungkan titik-titik yang berinteraksi. Vektor utama daya dalaman terdiri daripada pasangan daya titik berinteraksi, oleh itu

(3.1)

Harta kedua. Jumlah geometri momen semua daya dalaman berbanding dengan titik arbitrari dalam ruang ialah sifar.

Pertimbangkan sistem momen daya dan relatif kepada titik O(rajah 3.1)... daripada (rajah 3.1)... itu jelas

,

sejak kedua-dua daya mempunyai bahu yang sama dan arah yang bertentangan dengan momen vektor. Perkara utama kuasa dalaman relatif kepada titik O terdiri daripada jumlah vektor bagi ungkapan tersebut dan bersamaan dengan sifar. Oleh itu,

Biarkan daya luaran dan dalaman bertindak ke atas sistem mekanikal yang terdiri daripada N mata (rajah 3.2)... Jika paduan daya luar dan paduan semua daya dalaman digunakan pada setiap titik sistem, maka bagi mana-mana k-titik ke- sistem, anda boleh mengarang persamaan pembezaan gerakan. Akan ada sejumlah persamaan tersebut N:

dan dalam unjuran pada paksi tetap koordinat 3 N:

(3.4)

Persamaan vektor (3.3) atau persamaan skalar setara (3.4) mewakili hukum pembezaan pergerakan titik bahan bagi keseluruhan sistem. Jika semua titik bergerak selari dengan satu satah atau satu garis lurus, maka bilangan persamaan (3.4) dalam kes pertama ialah 2 N, pada yang kedua N.

Contoh 1. Dua pemberat berat dan disambungkan oleh kabel yang tidak dapat dipanjangkan yang dilemparkan ke atas blok (rajah 3.3)... Mengabaikan daya geseran, serta jisim blok dan kabel, menentukan hukum pergerakan beban dan ketegangan kabel.

Penyelesaian... Sistem ini terdiri daripada dua badan bahan (disambungkan dengan kabel yang tidak boleh dipanjangkan) yang bergerak selari dengan satu paksi NS. Mari kita tuliskan hukum pembezaan gerakan dalam unjuran pada paksi NS untuk setiap badan.

Biarkan berat kanan turun dengan pecutan, maka berat kiri akan naik dengan pecutan. Kami secara mental membebaskan diri daripada sambungan (kabel) dan menggantikannya dengan reaksi dan (rajah 3.3)... Dengan mengandaikan jasad itu bebas, kami menyusun hukum pembezaan pergerakan dalam unjuran ke paksi NS(bermaksud bahawa ketegangan benang adalah daya dalaman, dan berat pemberat adalah luaran):

Oleh kerana dan (badan disambungkan dengan kabel yang tidak boleh dipanjangkan), kami memperoleh

Menyelesaikan persamaan ini untuk pecutan dan ketegangan kabel T, kita mendapatkan

.

Perhatikan bahawa ketegangan kabel tidak sama dengan graviti beban yang sepadan.

3. 2. Teorem tentang gerakan pusat jisim

Adalah diketahui bahawa badan tegar dan sistem mekanikal dalam pesawat boleh bergerak dengan agak kompleks. Teorem pertama tentang gerakan jasad dan sistem mekanikal boleh dicapai seperti berikut: baling K.-L. objek yang terdiri daripada banyak jasad tegar yang bercantum antara satu sama lain. Ia adalah jelas bahawa ia akan terbang dalam parabola. Ini didedahkan ketika mengkaji pergerakan titik. Walau bagaimanapun, kini objek itu bukan titik. Ia berpusing, bergoyang semasa penerbangan mengelilingi beberapa pusat berkesan, yang bergerak di sepanjang parabola. Teorem pertama mengenai gerakan objek kompleks mengatakan bahawa pusat berkesan tertentu ialah pusat jisim objek yang bergerak. Pusat jisim tidak semestinya terletak di dalam badan itu sendiri; ia juga boleh terletak di suatu tempat di luarnya.

Teorem. Pusat jisim sistem mekanikal bergerak seperti titik bahan dengan jisim yang sama dengan jisim keseluruhan sistem, di mana semua daya luar yang bertindak ke atas sistem digunakan.

Untuk membuktikan teorem, kita menulis semula hukum pembezaan gerakan (3.3) dalam bentuk berikut:

(3.5)

di mana N Merupakan bilangan mata dalam sistem.

Mari kita tambahkan persamaan dalam sebutan antara satu sama lain:

(a)

Kedudukan pusat jisim sistem mekanikal relatif kepada sistem koordinat yang dipilih ditentukan oleh formula (2.1): di mana M Adalah jisim sistem. Kemudian sebelah kiri kesamaan (a) akan ditulis

Jumlah pertama di sebelah kanan kesamaan (a) adalah sama dengan vektor utama daya luaran, dan yang terakhir, dengan sifat daya dalaman, adalah sama dengan sifar. Kemudian kesamaan (a), dengan mengambil kira (b), akan ditulis semula

, (3.6)

mereka. hasil darab jisim sistem dengan pecutan pusat jisimnya adalah sama dengan jumlah geometri semua daya luar yang bertindak ke atas sistem.

Daripada persamaan (3.6) ia menunjukkan bahawa daya dalaman tidak secara langsung mempengaruhi gerakan pusat jisim. Walau bagaimanapun, dalam beberapa kes, ia adalah sebab untuk kemunculan daya luaran yang digunakan pada sistem. Oleh itu, daya dalaman memacu roda pemanduan kereta ke dalam putaran menyebabkan daya lekatan luaran dikenakan pada rim roda untuk bertindak ke atasnya.

Contoh 2. Mekanisme, yang terletak dalam satah menegak, dipasang pada satah licin mendatar dan dilekatkan padanya oleh bar yang dipasang tegar pada permukaan KEPADA dan L (rajah 3.4).

Jejari cakera 1 R tidak bergerak. Jisim cakera 2 m dan jejari r diikat dengan engkol, panjang R+ r pada titik C 2... Engkol berputar pada pemalar

halaju sudut. Pada saat awal, engkol menduduki sebelah kanan kedudukan mendatar... Dengan mengabaikan jisim engkol, tentukan daya mendatar dan menegak yang paling besar yang bertindak pada palang, jika jumlah jisim katil dan roda 1 adalah sama dengan M. Juga pertimbangkan kelakuan mekanisme jika tiada bar.

Penyelesaian... Sistem ini terdiri daripada dua jisim ( N=2 ): cakera pegun 1 dengan katil dan cakera alih 2. Mari kita arahkan paksi di melalui pusat graviti cakera pegun secara menegak ke atas, paksi NS- sepanjang satah mendatar.

Mari kita tuliskan teorem tentang gerakan pusat jisim (3.6) dalam bentuk koordinat

Daya luaran sistem ini ialah: berat katil dan cakera pegun - Mg, berat cakera bergerak - mg, ialah jumlah tindak balas mendatar bolt; ialah jumlah tindak balas normal satah. Oleh itu,

Kemudian undang-undang gerakan (b) akan ditulis semula

Mari kita hitung koordinat pusat jisim sistem mekanikal:

; (G)

seperti yang dilihat daripada (rajah 3.4), , , (sudut engkol), ... Menggantikan ungkapan ini dalam (d) dan mengira terbitan kali kedua t daripada,, kita dapat itu

(e)

Menggantikan (c) dan (e) dalam (b), kita dapati

Tekanan mendatar yang bertindak pada bar mempunyai nilai tertinggi dan terendah apabila cos = 1 masing-masing, i.e.

Tekanan mekanisme pada satah mendatar mempunyai nilai terbesar dan terkecil apabila dosa masing-masing, i.e.

Malah, masalah pertama dinamik telah diselesaikan: mengikut persamaan gerakan terkenal pusat jisim sistem (e), daya yang terlibat dalam gerakan itu dipulihkan.

Dengan ketiadaan bar K dan L (rajah 3.4), mekanisme mungkin mula melantun di atas satah mendatar. Ini akan berlaku apabila, i.e. apabila, ia berikutan bahawa halaju sudut putaran engkol, di mana mekanisme melantun, mesti memenuhi kesamaan

.

3. 3. Hukum kekekalan gerakan pusat jisim

Jika vektor utama daya luaran yang bertindak pada sistem adalah sifar, i.e. kemudian dari(3.6)ia berikutan bahawa pecutan pusat jisim adalah sifar, oleh itu, halaju pusat jisim adalah malar dalam magnitud dan arah. Jika, khususnya, pada saat awal pusat jisim berada dalam keadaan rehat, maka ia berada dalam keadaan rehat sepanjang masa sehingga vektor utama daya luar adalah sama dengan sifar.

Beberapa akibat berikutan daripada teorem ini.

· Daya dalaman sahaja tidak boleh mengubah sifat gerakan pusat jisim sistem.

· Jika vektor utama daya luar yang bertindak ke atas sistem adalah sifar, maka pusat jisim berada dalam keadaan rehat atau bergerak secara seragam dan lurus.

· Jika unjuran vektor utama daya luaran sistem pada beberapa paksi tetap adalah sama dengan sifar, maka unjuran halaju pusat jisim sistem pada paksi ini tidak berubah.

· Sepasang daya yang dikenakan pada jasad tegar tidak boleh mengubah pergerakan pusat jisimnya (ia hanya boleh menyebabkan badan berputar mengelilingi pusat jisim).

Mari kita pertimbangkan contoh yang menggambarkan undang-undang pemuliharaan gerakan pusat jisim.

Contoh 3. Dua pemberat adalah jisim dan disambungkan oleh benang yang tidak dapat dipanjangkan yang dilemparkan ke atas bongkah itu (rajah 3.5) dipasang pada baji dengan jisim M. Baji terletak pada satah mendatar yang licin. Pada saat awal, sistem dalam keadaan tenang. Cari anjakan baji di sepanjang satah apabila berat pertama diturunkan ke ketinggian N. Abaikan jisim bongkah dan benang.

Penyelesaian. Daya luaran yang bertindak pada baji bersama-sama dengan pemberat ialah daya graviti, dan Mg, serta tindak balas normal permukaan mendatar licin N. Oleh itu,

Memandangkan pada mulanya sistem berada dalam keadaan rehat, kami ada.

Mari kita mengira koordinat pusat jisim sistem pada dan pada masa ini t 1 apabila beban berat g turun ke ketinggian H.

Buat masa ini:

,

di mana , , NS- masing-masing, koordinat pusat jisim beban seberat g, g dan berat baji Mg.

Katakan baji pada saat masa bergerak ke arah positif paksi lembu mengikut jumlah L jika berat turun ke ketinggian N. Kemudian, buat masa ini

sejak beban bersama baji akan bergerak ke L ke kanan, dan beban akan bergerak ke atas sepanjang baji. Sejak, selepas pengiraan kita dapat

.

3.4. Kuantiti Pergerakan Sistem

3.4.1. Mengira jumlah pergerakan sistem

Kuantiti pergerakan titik bahan ialah kuantiti vektor yang sama dengan hasil darab jisim titik dengan vektor halajunya

Unit pergerakan -

Kuantiti gerakan sistem mekanikal dipanggil jumlah vektor kuantiti gerakan titik individu sistem, i.e.

di mana N Merupakan bilangan mata dalam sistem.

Jumlah pergerakan sistem mekanikal boleh dinyatakan dalam sebutan jisim sistem M dan kelajuan pusat jisim. sungguh,

mereka. momentum sistem adalah sama dengan hasil darab jisim keseluruhan sistem dengan kelajuan pusat jisimnya. Hala tuju sama dengan arah (rajah 3.6)

Dalam unjuran ke paksi segi empat tepat, kita ada

di mana,, ialah unjuran halaju pusat jisim sistem.

Di sini M- jisim sistem mekanikal; tidak berubah apabila sistem bergerak.

Keputusan ini amat berguna apabila mengira kuantiti pergerakan jasad tegar.

Ia boleh dilihat daripada formula (3.7) bahawa jika sistem mekanikal bergerak supaya pusat jisimnya kekal pegun, maka momentum sistem itu kekal sifar.

3.4.2. Dorongan daya asas dan penuh

Tindakan daya pada titik material dari semasa ke semasa dt boleh dicirikan oleh impuls asas. Dorongan penuh kuasa dari semasa ke semasa t, atau impuls daya, ditentukan oleh formula

atau dalam unjuran kepada koordinat paksi

(3.8a)

Unit daya impuls ialah.

3.4.3. Teorem mengenai perubahan dalam jumlah gerakan sistem

Biarkan daya luaran dan dalaman digunakan pada titik-titik sistem. Kemudian untuk setiap titik sistem seseorang boleh menggunakan hukum pembezaan gerakan (3.3), dengan mengambil kira bahawa :

.

Menjumlahkan semua mata sistem, kita dapat

Dengan harta kuasa dalaman dan mengikut takrifan kita ada

(3.9)

Mendarab kedua-dua belah persamaan ini dengan dt, kita memperoleh teorem tentang perubahan momentum dalam bentuk pembezaan:

, (3.10)

mereka. pembezaan momentum sistem mekanikal adalah sama dengan jumlah vektor bagi impuls asas semua daya luaran yang bertindak pada titik sistem mekanikal.

Mengira kamiran kedua-dua belah (3.10) sepanjang masa dari 0 hingga t, kita memperoleh teorem dalam bentuk terhingga atau kamiran

(3.11)

Dalam unjuran ke paksi koordinat, kita akan mempunyai

Perubahan dalam jumlah pergerakan sistem mekanikal dari semasa ke semasat, adalah sama dengan jumlah vektor semua impuls daya luar yang bertindak pada titik-titik sistem mekanikal untuk masa yang sama.

Contoh 4. Berat jisim m menuruni satah condong dari keadaan rehat di bawah tindakan daya F, berkadar dengan masa: di mana (rajah 3.7)... Apakah kelajuan yang akan diperolehi oleh badan t beberapa saat selepas permulaan pergerakan, jika pekali geseran gelongsor beban pada satah condong ialah f.

Penyelesaian. Mari kita gambarkan daya yang dikenakan pada beban: mg - daya graviti beban, N Adakah tindak balas normal satah, ialah daya geseran gelongsor beban pada satah, dan. Arah semua kuasa digambarkan dalam (rajah 3.7).

Mari kita arahkan paksi NS sepanjang satah condong ke bawah. Mari kita tuliskan teorem tentang perubahan momentum (3.11) dalam unjuran pada paksi NS:

(a)

Dengan syarat, sejak pada saat awal masa, beban berada dalam keadaan rehat. Jumlah unjuran impuls semua daya pada paksi-x ialah

Oleh itu,

,

.

3.4.4. Undang-undang pemuliharaan momentum

Undang-undang pemuliharaan diperoleh sebagai kes khas teorem tentang perubahan momentum. Dua kes khas mungkin.

· Jika jumlah vektor semua daya luar yang digunakan pada sistem adalah sifar, i.e. , maka teorem itu membayangkan (3.9) , apa ,

mereka. jika vektor utama daya luaran sistem adalah sama dengan sifar, maka momentum sistem adalah malar dalam magnitud dan arah.

· Jika unjuran vektor utama daya luaran ke mana-mana paksi koordinat adalah sama dengan sifar, sebagai contoh, Oh, i.e. , maka unjuran momentum pada paksi ini adalah malar.

Mari kita pertimbangkan contoh penggunaan undang-undang pengekalan momentum.

Contoh 5. Bandul balistik ialah badan berjisim yang digantung oleh benang panjang (rajah 3.8).

Peluru dengan jisim bergerak dengan laju V dan jatuh ke dalam badan yang tidak bergerak, tersangkut di dalamnya, dan badan itu terpesong. Berapakah kelajuan peluru itu jika badan naik ke ketinggian h ?

Penyelesaian. Biarkan badan dengan peluru yang tersekat mendapat kelajuan. Kemudian, menggunakan undang-undang pemuliharaan momentum dalam interaksi dua jasad, kita boleh menulis .

Kelajuan boleh dikira menggunakan undang-undang pemuliharaan tenaga mekanikal ... lepas tu . Akibatnya, kita dapati

.

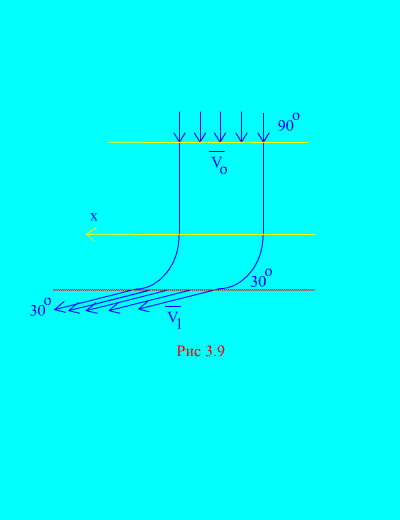
Contoh 6... Air memasuki saluran tetap (rajah 3.9) bahagian berubah-ubah dengan kelajuan pada sudut ke ufuk; kawasan keratan rentas saluran di pintu masuk; halaju air di pintu keluar dari saluran dan membuat sudut dengan ufuk.

Tentukan komponen mendatar bagi tindak balas yang terdapat pada air pada dinding saluran. Ketumpatan air .

Penyelesaian. Kami akan menentukan komponen mendatar tindak balas dinding saluran kepada air. Daya ini adalah sama dalam magnitud dan bertentangan dalam tanda dengan daya yang diperlukan. Kami mempunyai, menurut (3.11a),

... (a)

Kami mengira jisim isipadu cecair yang memasuki saluran semasa masa t:

Nilai rАV 0 dipanggil jisim kedua - jisim cecair yang mengalir melalui mana-mana bahagian paip per unit masa.

Jumlah air yang sama meninggalkan terusan pada masa yang sama. Kelajuan awal dan akhir diberikan dalam keadaan.

Mari kita hitung bahagian kanan kesamaan (a) yang menentukan jumlah unjuran pada paksi mendatar daya luar yang dikenakan pada sistem (air). Satu-satunya daya mendatar ialah komponen mendatar bagi tindak balas dinding yang terhasil R x... Daya ini malar pada aliran air yang tetap. sebab tu

... (v)

Menggantikan (b) dan (c) dalam (a), kita perolehi

3.5. Momen kinetik sistem

3.5.1. Momen momentum utama sistem

Biarkan vektor jejari titik dengan jisim sistem berbanding beberapa titik A, dipanggil pusat (rajah 3.10).

Momentum sudut (momen kinetik) titik berbanding pusat A dipanggil vektor , ditentukan oleh formula

. (3.12)

Selain itu, vektor diarahkan berserenjang dengan satah yang melalui pusat A dan vektor .

Momentum sudut (momentum sudut) sesuatu titik berbanding paksi dipanggil unjuran pada paksi momentum sudut titik relatif kepada mana-mana pusat yang dipilih pada paksi tertentu.

Momen utama momentum (momen kinetik) sistem berbanding pusat A dipanggil nilai

(3.13)

Momen utama momentum (momen kinetik) sistem mengenai paksi dipanggil unjuran pada paksi ini bagi momen utama sistem berbanding mana-mana yang dipilih pada sesuatu tertentu paksi tengah.

3.5.2. Momen kinetik jasad tegar berputar tentang paksi putaran

Titik tetap yang serasi O badan berbaring di atas paksi putaran Oz, dengan asal sistem koordinat Oohz, yang paksinya akan berputar dengan badan (rajah 3.11)... Biarkan vektor jejari suatu titik jasad berbanding dengan asalan, dan nyatakan unjurannya pada paksi dengan,,. Unjuran vektor halaju sudut jasad pada paksi yang sama kita nyatakan dengan 0, 0, ().

Kementerian Pendidikan dan Sains Persekutuan Russia

Institusi Pendidikan Bajet Negeri Persekutuan Pendidikan Profesional Tinggi

"Universiti Teknologi Negeri Kuban"

Mekanik teori

Penceramah bahagian 2

Diluluskan oleh Editorial dan Penerbitan

majlis universiti sebagai

panduan belajar

Krasnodar

UDC 531.1 / 3 (075)

Mekanik teori. Bahagian 2. Dinamik: Buku Teks / LI Draiko; Cuba. negeri technol.un-t. Krasnodar, 2011.123 p.

ISBN 5-230-06865-5

Bahan teori dibentangkan dalam bentuk ringkas, contoh penyelesaian masalah diberikan, kebanyakannya mencerminkan isu teknikal sebenar, perhatian diberikan kepada pilihan penyelesaian yang rasional.

Ia bertujuan untuk sarjana muda surat-menyurat dan bentuk latihan jarak jauh dalam pembinaan, pengangkutan dan kejuruteraan mekanikal.

Tab. 1 Rajah. 68 Bibliografi. 20 tajuk

Editor saintifik, Calon Sains Teknikal, Prof. V.F. Melnikov

Penyemak: Ketua Jabatan Mekanik Teori dan Teori Mekanisme dan Mesin Universiti Agraria Kuban prof. F.M. Kanarev; Profesor Madya Jabatan Mekanik Teoretikal Universiti Teknologi Negeri Kuban M.E. berbilang

Diterbitkan oleh keputusan Majlis Editorial dan Penerbitan Universiti Teknologi Negeri Kuban.

Cetak semula

ISBN 5-230-06865-5 KubGTU 1998

Kata pengantar

Buku teks ini bertujuan untuk pelajar surat-menyurat kepakaran pembinaan, pengangkutan dan kejuruteraan mekanikal, tetapi boleh digunakan semasa mempelajari bahagian "Dinamik" kursus mekanik teori oleh pelajar surat-menyurat kepakaran lain, serta pelajar sepenuh masa dalam kerja bebas.

Manual ini disusun mengikut program semasa kursus mekanik teori, merangkumi semua isu bahagian utama kursus. Setiap bahagian mengandungi bahan teori pendek, disediakan dengan ilustrasi dan garis panduan untuk kegunaannya dalam menyelesaikan masalah. Manual berkenaan dengan penyelesaian 30 masalah, mencerminkan isu teknikal sebenar dan tugasan kawalan yang sepadan keputusan bebas... Untuk setiap tugas, skema pengiraan dibentangkan yang menggambarkan penyelesaian dengan jelas. Reka bentuk penyelesaian memenuhi keperluan untuk reka bentuk kertas ujian pelajar separuh masa.

Penulis merakamkan setinggi-tinggi penghargaan kepada guru-guru Jabatan Mekanik Teori dan Teori Mekanisme dan Mesin Universiti Agraria Kuban atas kerja hebat mereka dalam menyemak buku teks, serta kepada guru-guru Jabatan Mekanik Teori Negeri Kuban. Universiti Teknologi untuk komen dan nasihat berharga tentang penyediaan buku teks untuk penerbitan.

Segala komen dan cadangan yang kritikal akan diterima dengan penuh rasa terima kasih oleh penulis pada masa akan datang.

pengenalan

Dinamik adalah cabang mekanik teori yang paling penting. Kebanyakan masalah khusus dalam amalan kejuruteraan adalah berkaitan dengan dinamik. Dengan menggunakan kesimpulan statik dan kinematik, dinamik menetapkan undang-undang umum pergerakan badan bahan di bawah tindakan daya gunaan.

Objek material yang paling mudah ialah titik material. Badan material dalam bentuk apa pun boleh diambil sebagai titik material, yang dimensinya boleh diabaikan dalam masalah yang sedang dipertimbangkan. Badan dengan dimensi terhingga boleh dianggap sebagai titik material jika perbezaan dalam gerakan titiknya tidak penting untuk masalah tertentu. Ini berlaku apabila dimensi badan adalah kecil berbanding dengan jarak yang dilalui oleh titik-titik badan. Setiap zarah pepejal boleh dianggap sebagai titik bahan.

Daya yang dikenakan pada titik atau badan material dinilai dalam dinamik dengan kesan dinamiknya, iaitu, dengan cara ia mengubah ciri-ciri gerakan objek material.

Pergerakan objek material dalam perjalanan masa berlaku di ruang relatif kepada kerangka rujukan tertentu. Dalam mekanik klasik, berdasarkan aksiom Newton, ruang dianggap tiga dimensi, sifatnya tidak bergantung pada objek material yang bergerak di dalamnya. Kedudukan titik dalam ruang tersebut ditentukan oleh tiga koordinat. Masa tidak dikaitkan dengan ruang dan pergerakan objek material. Ia dianggap sama untuk semua bingkai rujukan.

Undang-undang dinamik menerangkan pergerakan objek material berhubung dengan paksi mutlak koordinat, secara konvensional diambil sebagai tidak bergerak. Asal usul sistem koordinat mutlak diambil di pusat Matahari, dan paksi diarahkan ke bintang yang jauh dan tidak bergerak secara konvensional. Apabila menyelesaikan banyak masalah teknikal, paksi koordinat yang dikaitkan dengan Bumi boleh dianggap tidak bergerak secara konvensional.

Parameter pergerakan mekanikal objek bahan dalam dinamik ditentukan melalui potongan matematik daripada undang-undang asas mekanik klasik.

Undang-undang pertama (hukum inersia):

Titik material mengekalkan keadaan rehat atau gerakan seragam dan rectilinear sehingga tindakan mana-mana daya akan membawanya keluar dari keadaan ini.

Pergerakan seragam dan rectilinear sesuatu titik dipanggil gerakan inersia. Rehat ialah kes khas gerakan inersia apabila kelajuan sesuatu titik adalah sifar.

Mana-mana titik material adalah lengai, iaitu, ia bertujuan untuk mengekalkan keadaan rehat atau gerakan rectilinear seragam. Rangka rujukan yang berkaitan dengan mana hukum inersia dipenuhi dipanggil inersia, dan gerakan yang diperhatikan berhubung dengan bingkai ini dipanggil mutlak. Sebarang kerangka rujukan yang membuat translasi rectilinear dan gerakan seragam berbanding dengan bingkai inersia juga akan menjadi bingkai inersia.

Undang-undang kedua (undang-undang asas dinamik):

Pecutan titik material berbanding sistem rujukan inersia adalah berkadar dengan daya yang dikenakan pada titik dan bertepatan dengan daya dalam arah:
.

Daripada undang-undang asas dinamik ia mengikutinya dengan daya
pecutan
... Jisim titik mencirikan darjah rintangan titik kepada perubahan halajunya, iaitu, ia adalah ukuran inersia titik bahan.

Undang-undang ketiga (hukum tindakan dan tindak balas):

Daya yang mana dua jasad bertindak antara satu sama lain adalah sama besarnya dan diarahkan sepanjang satu garis lurus dalam arah yang bertentangan.

Daya yang dipanggil tindakan dan tindak balas dikenakan badan yang berbeza dan oleh itu tidak membentuk sistem yang seimbang.

Undang-undang keempat (undang-undang kebebasan tindakan kuasa):

Dengan tindakan serentak beberapa daya, pecutan titik material adalah sama dengan jumlah geometri pecutan yang akan ada pada titik di bawah tindakan setiap daya secara berasingan:

, di mana
,
,…,
.

(SISTEM MEKANIKAL) - Pilihan IV

1. Persamaan asas bagi dinamik titik material, seperti yang diketahui, dinyatakan oleh persamaan. Persamaan Pembezaan pergerakan titik sewenang-wenangnya sistem mekanikal bukan bebas mengikut dua kaedah pembahagian daya boleh ditulis dalam dua bentuk:

(1) , dengan k = 1, 2, 3,…, n ialah bilangan titik sistem bahan.

(2)

di manakah jisim titik k-th; ialah vektor jejari bagi titik k-th, ialah daya (aktif) yang diberikan yang bertindak pada titik k-th atau paduan semua daya aktif yang bertindak pada titik k-th. - paduan daya tindak balas ikatan, bertindak pada titik ke-k; - paduan daya dalaman yang bertindak pada titik ke-k; ialah paduan daya luar yang bertindak pada titik ke-k.

Menggunakan persamaan (1) dan (2), seseorang boleh berusaha untuk menyelesaikan kedua-dua masalah dinamik pertama dan kedua. Walau bagaimanapun, penyelesaian masalah kedua dinamik untuk sistem menjadi sangat rumit bukan sahaja dari sudut pandangan matematik, tetapi juga kerana kita berhadapan dengan kesukaran asas. Mereka terdiri daripada fakta bahawa kedua-dua untuk sistem (1) dan untuk sistem (2) bilangan persamaan adalah ketara kurang bilangan tidak diketahui.

Jadi, jika kita menggunakan (1), maka dinamik akan diketahui untuk masalah kedua (terbalik) dan dan akan tidak diketahui. Persamaan vektor akan menjadi " n", Dan tidak diketahui -" 2n ".

Jika kita meneruskan dari sistem persamaan (2), maka beberapa daya luar juga diketahui. Mengapa berpisah? Hakikatnya ialah kuasa luar juga termasuk tindak balas luaran ikatan, yang tidak diketahui. Di samping itu, yang tidak diketahui juga akan.

Oleh itu, kedua-dua sistem (1) dan sistem (2) TIDAK DITUTUP. Ia adalah perlu untuk menambah persamaan, dengan mengambil kira persamaan kekangan, dan mungkin anda masih perlu mengenakan beberapa sekatan ke atas kekangan itu sendiri. Apa nak buat?

Jika kita meneruskan dari (1), maka kita boleh mengikuti laluan merangka persamaan Lagrange jenis pertama. Tetapi jalan ini tidak rasional kerana apa tugas yang lebih mudah(sedikit darjah kebebasan), semakin sukar dari sudut matematik untuk menyelesaikannya.

Kemudian mari kita perhatikan sistem (2), di mana - sentiasa tidak diketahui. Langkah pertama dalam menyelesaikan sistem adalah untuk menghapuskan yang tidak diketahui ini. Perlu diingat bahawa, sebagai peraturan, kita tidak berminat dengan daya dalaman apabila sistem bergerak, iaitu, apabila sistem bergerak, tidak perlu mengetahui bagaimana setiap titik sistem bergerak, tetapi ia adalah cukup untuk mengetahui bagaimana sistem secara keseluruhan bergerak.

Jadi kalau cara yang berbeza mengecualikan daya yang tidak diketahui daripada sistem (2), maka kita memperoleh beberapa hubungan, iaitu, beberapa Ciri umum untuk sistem, pengetahuan yang memungkinkan untuk menilai bagaimana sistem bergerak secara umum. Ciri-ciri ini diperkenalkan menggunakan apa yang dipanggil teorem am pembesar suara. Terdapat empat teorem sedemikian:

1. Teorem tentang pergerakan pusat jisim sistem mekanikal;

2. Teorem tentang mengubah momentum sistem mekanikal;

3. Teorem tentang perubahan momentum sudut sistem mekanikal;

4. Teorem tentang perubahan dalam tenaga kinetik sistem mekanikal.