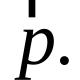«Մարդու մեծությունը մտածելու կարողության մեջ է»:
Բլեզ Պասկալ.

Դասի նպատակները.

1) Ուսումնական– ուսանողներին ծանոթացնել միատարր հավասարումների հետ, դիտարկել դրանց լուծման մեթոդները և նպաստել նախկինում ուսումնասիրված եռանկյունաչափական հավասարումների տեսակների լուծման հմտությունների զարգացմանը:

2) Զարգացնող- զարգացնել ուսանողների ստեղծագործական գործունեությունը, նրանց ճանաչողական գործունեությունը, տրամաբանական մտածողությունը, հիշողությունը, խնդրահարույց իրավիճակում աշխատելու կարողությունը, հասնել իրենց մտքերը ճիշտ, հետևողականորեն, ռացիոնալ արտահայտելու կարողությանը, ընդլայնել ուսանողների մտահորիզոնը և բարձրացնել նրանց մաթեմատիկական մակարդակը. մշակույթը։

3) Ուսումնական- զարգացնել ինքնակատարելագործման ցանկություն, աշխատասիրություն, զարգացնել մաթեմատիկական նշումներ գրագետ և ճշգրիտ կատարելու կարողություն, ակտիվություն զարգացնել, օգնել խթանել հետաքրքրությունը մաթեմատիկայի նկատմամբ:

Դասի տեսակը.համակցված.

Սարքավորումներ:

1. Դակիչ քարտեր վեց ուսանողների համար:
2. Քարտեր անկախ և անհատական ​​աշխատանքուսանողներ.
3. «Եռանկյունաչափական հավասարումների լուծում», «Թվային միավորի շրջան»:
4. Էլեկտրականացված եռանկյունաչափության աղյուսակներ.
5. Ներկայացում դասի համար (Հավելված 1).

Դասի առաջընթաց

1. Կազմակերպչական փուլ (2 րոպե)

Փոխադարձ ողջույններ; ստուգել ուսանողների պատրաստվածությունը դասին ( աշխատավայր, տեսքը); ուշադրության կազմակերպում.

Ուսուցիչը ուսանողներին պատմում է դասի թեման, նպատակները (սլայդ 2)և բացատրում է, որ դասի ընթացքում կօգտագործվեն գրասեղանների վրա դրված թերթիկները:

2. Տեսական նյութի կրկնություն (15 րոպե)

Դակիչ քարտի առաջադրանքներ(6 հոգի) . Աշխատանքային ժամանակը բռունցքով հարվածված քարտերով – 10 րոպե (Հավելված 2)

Խնդիրներ լուծելով՝ ուսանողները կսովորեն, թե որտեղ են օգտագործվում եռանկյունաչափական հաշվարկները: Ստացվում են հետևյալ պատասխանները՝ եռանկյունավորում (տեխնիկա, որը թույլ է տալիս աստղագիտության մեջ չափել մոտակա աստղերի հեռավորությունները), ակուստիկա, ուլտրաձայնային, տոմոգրաֆիա, գեոդեզիա, ծածկագրություն։

(սլայդ 5)

Ճակատային հետազոտություն.

1. Ո՞ր հավասարումներն են կոչվում եռանկյունաչափական:
2. Եռանկյունաչափական հավասարումների ի՞նչ տեսակներ գիտեք:
3. Ո՞ր հավասարումներն են կոչվում ամենապարզ եռանկյունաչափական հավասարումներ:
4. Ո՞ր հավասարումներն են կոչվում քառակուսի եռանկյունաչափական:
5. Ձևակերպե՛ք a-ի արկսինի սահմանումը.
6. Ձևակերպե՛ք a-ի աղեղի կոսինուսի սահմանումը.
7. Ձևակերպե՛ք a-ի արկտանգենսի սահմանումը.
8. Ձևակերպե՛ք a թվի աղեղային կոտանգենսի սահմանումը.

Խաղ «Գուշակիր կոդավորված բառը»

Բլեզ Պասկալը մի անգամ ասել է, որ մաթեմատիկան այնքան լուրջ գիտություն է, որ չպետք է բաց թողնել այն մի փոքր ավելի զվարճալի դարձնելու հնարավորությունը։ Դրա համար առաջարկում եմ խաղալ։ Օրինակները լուծելուց հետո որոշիր գաղտնագրված բառը կազմելու համար օգտագործվող թվերի հաջորդականությունը: Լատիներեն այս բառը նշանակում է «սինուս»: (սլայդ 3)

2) աղեղ tg (-√3)

4) tg (arc cos (1/2))

5) tg (arc ctg √3)

Պատասխան՝ «Թեքվել»

Խաղ «Վերացական մաթեմատիկոս»»

Էկրանի վրա նախագծված են բանավոր աշխատանքի առաջադրանքները.

Ստուգեք, որ հավասարումները ճիշտ են լուծված:(ճիշտ պատասխանը հայտնվում է սլայդում ուսանողի պատասխանից հետո): (սլայդ 4)

Տնային առաջադրանքների ստուգում.

Ուսուցիչը սահմանում է բոլոր աշակերտների կողմից տնային առաջադրանքների կատարման ճիշտությունը և տեղեկացվածությունը. բացահայտում է գիտելիքների բացերը. բարելավում է սովորողների գիտելիքները, հմտությունները և կարողությունները պարզ եռանկյունաչափական հավասարումների լուծման ոլորտում.

1 հավասարում. Աշակերտը մեկնաբանում է հավասարման լուծումը, որի տողերը հայտնվում են սլայդի վրա՝ մեկնաբանության հերթականությամբ): (սլայդ 6)

√3tg2x = 1;

tg2x =1/√3;

2х= արկտան 1/√3 +πn, n ∈Զ.

2х= π/6 +πn, n ∈Զ.

x= π/12 + π/2 n, n ∈Զ.

2 հավասարում. Լուծում հգրատախտակին գրված ուսանողներին:

2 մեղք 2 x + 3 cosx = 0:

3. Նոր գիտելիքների թարմացում (3 րոպե)

Աշակերտները, ուսուցչի խնդրանքով, վերհիշում են եռանկյունաչափական հավասարումների լուծման ուղիները: Նրանք ընտրում են այն հավասարումները, որոնք արդեն գիտեն լուծել, անվանում են հավասարման լուծման մեթոդը և ստացված արդյունքը։ . Պատասխանները հայտնվում են սլայդում: (սլայդ 7) .

Նոր փոփոխականի ներմուծում.

Թիվ 1. 2sin 2 x – 7sinx + 3 = 0:

Թող sinx = t, ապա.

2t 2 – 7t + 3 = 0:

Ֆակտորիզացիա:

№2. 3sinx cos4x – cos4x = 0;

сos4x(3sinx – 1) = 0;

cos4x = 0 կամ 3 sinx – 1 = 0; ...

Թիվ 3. 2 sinx – 3 cosx = 0,

Թիվ 4. 3 մեղք 2 x – 4 sinx cosx + cos 2 x = 0:

Ուսուցիչ:Դուք դեռ չգիտեք, թե ինչպես լուծել վերջին երկու տեսակի հավասարումները: Նրանք երկուսն էլ նույն տեսակն են: Դրանք չեն կարող կրճատվել sinx կամ cosx ֆունկցիաների հավասարման: Կանչվում են միատարր եռանկյունաչափական հավասարումներ.Բայց միայն առաջինը - միատարր հավասարումառաջին աստիճանի, իսկ երկրորդը երկրորդ աստիճանի միատարր հավասարում է։ Այսօր դասի ընթացքում մենք կծանոթանանք նման հավասարումների և կսովորենք, թե ինչպես լուծել դրանք։

4. Նոր նյութի բացատրություն (25 րոպե)

Ուսուցիչը ուսանողներին տալիս է միատարր եռանկյունաչափական հավասարումների սահմանումներ և ներկայացնում դրանց լուծման մեթոդներ:

Սահմանում. a sinx + b cosx =0 ձևի հավասարումը, որտեղ a ≠ 0, b ≠ 0 կոչվում է. առաջին աստիճանի միատարր եռանկյունաչափական հավասարում.(սլայդ 8)

Նման հավասարման օրինակ է թիվ 3 հավասարումը։ Մենք կգրենք այն ընդհանուր տեսարանհավասարեցնել և վերլուծել այն:

a sinx + b cosx = 0:

Եթե ​​cosx = 0, ապա sinx = 0:

-Կարո՞ղ է նման իրավիճակ լինել։

- Ոչ: Մենք հակասություն ենք ստացել հիմնական եռանկյունաչափական ինքնության հետ:

Սա նշանակում է cosx ≠ 0: Եկեք կատարենք տերմին առ անդամ բաժանում cosx-ով.

a tgx + b = 0

tgx = –b / a- ամենապարզ եռանկյունաչափական հավասարումը:

Եզրակացություն:Միատարր եռանկյունաչափական հավասարումներառաջին աստիճանը լուծվում է հավասարման երկու կողմերը cosx-ի (sinx) բաժանելով:

Օրինակ. 2 sinx – 3 cosx = 0,

Որովհետև cosx ≠ 0, ապա

tgx = 3/2 ;

x = արկտան (3/2) +πn, n ∈Z.

Սահմանում. a sin 2 x + b sinx cosx + c cos 2 x = 0 ձևի հավասարումը, որտեղ a ≠ 0, b ≠ 0, c ≠ 0 կոչվում է. երկրորդ աստիճանի եռանկյունաչափական հավասարում. (սլայդ 8)

Նման հավասարման օրինակ է թիվ 4 հավասարումը։ Եկեք գրենք հավասարման ընդհանուր ձևը և վերլուծենք այն:

a sin 2 x + b sinx cosx + c cos 2 x = 0:

Եթե ​​cosx = 0, ապա sinx = 0:

Կրկին մենք հակասություն ստացանք հիմնական եռանկյունաչափական ինքնությանը:

Սա նշանակում է cosx ≠ 0: Եկեք կատարենք տերմին առ անդամ բաժանում cos 2 x-ով:

իսկ tg 2 x + b tgx + c = 0 հավասարում է, որը վերածվում է քառակուսի:

Եզրակացություն. ՕհԵրկրորդ աստիճանի միատարր եռանկյունաչափական հավասարումները լուծվում են հավասարման երկու կողմերը cos 2 x-ի բաժանելով (sin 2 x):

Օրինակ. 3 մեղք 2 x – 4 sinx cosx + cos 2 x = 0:

Որովհետև cos 2 x ≠ 0, ապա

3tg 2 x – 4 tgx + 1 = 0 (Հրավիրեք ուսանողին գնալ գրատախտակ և ինքնուրույն լրացնել հավասարումը):

Փոխարինում՝ tgx = y: 3y 2 – 4 y + 1 = 0

D = 16 – 12 = 4

y 1 = 1 կամ y 2 = 1/3

tgx = 1 կամ tgx = 1/3

x = արկտան (1/3) + πn, n ∈Z:

x = arctan1 + πn, n ∈Z.

x = π/4 + πn, n ∈Z.

5. Սովորողների կողմից նոր նյութի ըմբռնումը ստուգելու փուլ (1ր.)

Ընտրեք տարօրինակը.

sinx = 2cosx; 2sinx + cosx = 2;

√3sinx + cosx = 0; մեղք 2 x – 2 sinx cosx + 4cos 2 x = 0;

4cosx + 5sinx = 0; √3sinx – cosx = 0:

(սլայդ 9)

6. Նոր նյութի համախմբում (24ր).

Աշակերտները պատասխանողների հետ միասին լուծում են գրատախտակի վրա դրված հավասարումները նոր նյութ. Առաջադրանքները գրված են սլայդի վրա՝ աղյուսակի տեսքով։ Հավասարում լուծելիս բացվում է սլայդի նկարի համապատասխան մասը։ 4 հավասարումների լրացման արդյունքում ուսանողներին ներկայացվում է մաթեմատիկոսի դիմանկարը, ով էական ազդեցություն է ունեցել եռանկյունաչափության զարգացման վրա։ (աշակերտները կճանաչեն Ֆրանսուա Վիետայի դիմանկարը՝ մեծ մաթեմատիկոս, ով մեծ ներդրում է ունեցել եռանկյունաչափության մեջ, հայտնաբերել է կրճատված քառակուսի հավասարման արմատների հատկությունը և զբաղվել գաղտնագրությամբ) . (սլայդ 10)

1) √3sinx + cosx = 0,

Որովհետև cosx ≠ 0, ապա

√3tgx + 1 = 0;

tgx = –1/√3;

x = արկտան (–1/√3) + πn, n ∈Z.

x = –π/6 + πn, n ∈Z.

2) մեղք 2 x – 10 sinx cosx + 21cos 2 x = 0:

Որովհետև cos 2 x ≠ 0, ապա tg 2 x – 10 tgx + 21 = 0

Փոխարինում: tgx = y.

y 2 – 10 y + 21 = 0

y 1 = 7 կամ y 2 = 3

tgx = 7 կամ tgx = 3

x = arctan7 + πn, n ∈Z

x = arctan3 + πn, n ∈Z

3) մեղք 2 2x – 6 sin2x cos2x + 5cos 2 2x = 0:

Որովհետև cos 2 2x ≠ 0, ապա 3tg 2 2x – 6tg2x +5 = 0

Փոխարինում: tg2x = y.

3y 2 – 6y + 5 = 0

D = 36 – 20 = 16

y 1 = 5 կամ y 2 = 1

tg2x = 5 կամ tg2x = 1

2х = arctan5 + πn, n ∈Z

x = 1/2 արկտան5 + π/2 n, n ∈Z

2х = arctan1 + πn, n ∈Z

x = π/8 + π/2 n, n ∈Z

4) 6sin 2 x + 4 sin(π-x) cos(2π-x) = 1:

6sin 2 x + 4 sinx cosx = 1.

6sin 2 x + 4 sinx cosx – sin 2 x – cos 2 x = 0:

5sin 2 x + 4 sinx cosx – cos 2 x = 0:

Որովհետև cos 2 x ≠0, ապա 5tg 2 x + 4 tgx –1 = 0

Փոխարինում: tg x = y.

5у 2 + 4у – 1 = 0

D = 16 + 20 = 36

y 1 = 1/5 կամ y 2 = –1

tg x = 1/5 կամ tg x = –1

x = arctan1/5 + πn, n ∈Z

x = արկտան (–1) + πn, n ∈Z

x = –π/4 + πn, n ∈Z

Լրացուցիչ (քարտի վրա).

Լուծե՛ք հավասարումը և, առաջարկված չորսից ընտրելով մեկ տարբերակ, գուշակե՛ք այն մաթեմատիկոսի անունը, ով ստացել է կրճատման բանաձևերը.

2sin 2 x – 3 sinx cosx – 5cos 2 x = 0:

Հնարավոր պատասխաններ.

x = arctan2 + 2πn, n ∈Z x = –π/2 + πn, n ∈Z – Պ. Չեբիշև

x = արկտան 12,5 + 2πn, n ∈Z x = –3π/4 + πn, n ∈Z – Էվկլիդես

x = արկտան 5 + πn, n ∈Z x = –π/3 + πn, n ∈Z – Սոֆյա Կովալևսկայա

x = arctan2.5 + πn, n ∈Z x = –π/4 + πn, n ∈Z – Լեոնհարդ Էյլեր

Ճիշտ պատասխան՝ Լեոնհարդ Էյլեր։

7. Տարբերակված անկախ աշխատանք (8ր.)

Մեծ մաթեմատիկոսն ու փիլիսոփան ավելի քան 2500 տարի առաջ մտածելու կարողությունները զարգացնելու միջոց է առաջարկել։ «Մտածելը սկսվում է զարմանքից», - ասաց նա: Այսօր մենք բազմիցս տեսել ենք, որ այս խոսքերը ճիշտ են։ Ավարտելով անկախ աշխատանք 2 տարբերակի վրա՝ դուք կկարողանաք ցույց տալ, թե ինչպես եք յուրացրել նյութը և պարզել այս մաթեմատիկոսի անունը։ Համար ինքնուրույն աշխատանքօգտագործեք թերթիկները, որոնք գտնվում են ձեր սեղաններին: Դուք ինքներդ կարող եք ընտրել առաջարկված երեք հավասարումներից մեկը: Բայց հիշեք, որ լուծելով համապատասխան հավասարումը դեղին գույնԴուք կարող եք ստանալ միայն «3»՝ լուծելով կանաչ գույնին համապատասխանող հավասարումը «4», կարմիրը՝ «5»: (Հավելված 3)

Դժվարության ինչ մակարդակ էլ որ ընտրեն ուսանողները, հետո ճիշտ որոշումՀավասարման առաջին տարբերակում ստացվում է «ԱՐԻՍՏ» բառը, երկրորդը՝ «ՀՅՈՒՐԱՆՈՑ»: Սլայդի վրայի բառն է՝ «ԱՐԻՍՏ-ՀՅՈՒՐԱՆՈՑ»: (սլայդ 11)

Ստուգման են ներկայացվում ինքնուրույն աշխատանքով աշխատաթերթերը։ (Հավելված 4)

8. Տնային առաջադրանքների ձայնագրում (1 րոպե)

Դ/զ՝ §7.17. Կազմե՛ք և լուծե՛ք առաջին աստիճանի 2 միատարր և երկրորդ աստիճանի 1 միատարր հավասարումներ (կազմելու համար օգտագործելով Վիետայի թեորեմը): (սլայդ 12)

9. Դասի ամփոփում, գնահատում (2 րոպե)

Ուսուցիչը ևս մեկ անգամ ուշադրություն է հրավիրում հավասարումների այդ տեսակների և այն տեսական փաստերի վրա, որոնք վերհիշվել են դասարանում, և խոսում է դրանք սովորելու անհրաժեշտության մասին։

Ուսանողները պատասխանում են հարցերին.

1. Ի՞նչ տեսակի եռանկյունաչափական հավասարումներ ենք մեզ ծանոթ:
2. Ինչպե՞ս են լուծվում այս հավասարումները:

Ուսուցիչն ամենաշատը նշում է հաջողված աշխատանքառանձին սովորողների դասին տալիս է գնահատականներ.

Երկու անհայտով ոչ գծային հավասարումներ

Սահմանում 1. Թող Ա-ն որոշ չափով լինի թվերի զույգերի հավաքածու (x; y) . Ասում են, որ տրված է Ա բազմությունըթվային ֆունկցիա զերկու փոփոխականներից

x և y, եթե նշված է մի կանոն, որի օգնությամբ A բազմության թվերի յուրաքանչյուր զույգ կապված է որոշակի թվի հետ։ Երկու x և y փոփոխականների z թվային ֆունկցիան նշելը հաճախ էնշել

Այսպիսով. Որտեղ (x , y) զ

Որտեղ (x , y) = - գործառույթից բացի ցանկացած այլ գործառույթ ,

կացին+ըստ+գ

որտեղ a, b, c թվերը տրվում են: Սահմանում 3.Լուծել հավասարումը (2) x; yզանգահարեք մի զույգ համարներով (

), որի համար (2) բանաձևը իսկական հավասարություն է։

Օրինակ 1. Լուծե՛ք հավասարումը

Քանի որ ցանկացած թվի քառակուսին ոչ բացասական է, (4) բանաձևից հետևում է, որ x և y անհայտները բավարարում են հավասարումների համակարգին.

որի լուծումը թվերի զույգ է (6; 3):

Պատասխան՝ (6; 3)

Օրինակ 2. Լուծե՛ք հավասարումը Հետևաբար, (6) հավասարման լուծումն էանսահման թվով զույգ թվեր

(1 + y ; y) ,

բարի

որտեղ y-ն ցանկացած թիվ է:

գծային Սահմանում 4.

Հավասարումների համակարգի լուծում x; yզանգահարեք մի զույգ համարներով (

) , այս համակարգի յուրաքանչյուր հավասարման մեջ դրանք փոխարինելիս ստացվում է ճիշտ հավասարություն։

Երկու հավասարումների համակարգերը, որոնցից մեկը գծային է, ունեն ձև(x , y)

է

Լուծում. Եկեք արտահայտենք անհայտ y-ը (7) համակարգի առաջին հավասարումից x անհայտի միջոցով և ստացված արտահայտությունը փոխարինենք համակարգի երկրորդ հավասարմամբ.

Հավասարման լուծում

x 1 = - 1 , x 2 = 9 .

Հետևաբար,

y 1 = 8 - x 1 = 9 ,
y 2 = 8 - x 2 = - 1 .

Երկու հավասարումների համակարգեր, որոնցից մեկը միատարր է

Երկու հավասարումների համակարգերը, որոնցից մեկը միատարր է, ունեն ձև

որտեղ a, b, c տրված են թվեր, և Երկու հավասարումների համակարգերը, որոնցից մեկը գծային է, ունեն ձև(x , y) – x և y երկու փոփոխականների ֆունկցիա:

Օրինակ 6. Լուծել հավասարումների համակարգ

Լուծում. Լուծենք միատարր հավասարումը

3x 2 + 2xy - y 2 = 0 ,

3x 2 + 17xy + 10y 2 = 0 ,

այն որպես քառակուսային հավասարում անհայտ x-ի նկատմամբ.

.

Դեպքում x = - 5y, համակարգի երկրորդ հավասարումից (11) ստանում ենք հավասարումը

5y 2 = - 20 ,

որը արմատներ չունի։

Դեպքում

(11) համակարգի երկրորդ հավասարումից ստանում ենք հավասարումը

,

որոնց արմատները թվերն են y 1 = 3 , y 2 = - 3 . Այս արժեքներից յուրաքանչյուրի համար գտնելով x-ի համապատասխան արժեքը՝ մենք ստանում ենք համակարգի երկու լուծում՝ (- 2 ; 3), (2 ; - 3) :

Պատասխան՝ (- 2 ; 3), (2 ; - 3)

Այլ տեսակների հավասարումների համակարգերի լուծման օրինակներ

Օրինակ 8. Լուծել հավասարումների համակարգ (MIPT)

Լուծում. Ներկայացնենք նոր անհայտներ u և v, որոնք արտահայտվում են x և y միջոցով՝ համաձայն բանաձևերի.

Համակարգը (12) նոր անհայտներով վերագրելու համար նախ x և y անհայտներն արտահայտում ենք u և v-ով: Համակարգից (13) հետևում է, որ

Եկեք լուծենք գծային համակարգը (14)՝ այս համակարգի երկրորդ հավասարումից հանելով x փոփոխականը։

• Այդ նպատակով մենք կատարում ենք հետևյալ փոխակերպումները համակարգի վրա (14).
• Համակարգի առաջին հավասարումը կթողնենք անփոփոխ.

երկրորդ հավասարումից հանում ենք առաջին հավասարումը և համակարգի երկրորդ հավասարումը փոխարինում ստացված տարբերությամբ։

Արդյունքում համակարգը (14) վերածվում է համարժեք համակարգի

որից մենք գտնում ենք

Օգտագործելով (13) և (15) բանաձևերը, մենք վերագրում ենք բնօրինակ համակարգը (12) ձևով.

Համակարգի առաջին հավասարումը (16) գծային է, ուստի մենք կարող ենք նրանից արտահայտել անհայտ u-ը անհայտ v-ի միջոցով և այս արտահայտությունը փոխարինել համակարգի երկրորդ հավասարմամբ:

1. Այսօր մենք կուսումնասիրենք միատարր եռանկյունաչափական հավասարումները։ Նախ, եկեք նայենք տերմինաբանությանը. ինչ է միատարր եռանկյունաչափական հավասարումը: Այն ունի հետևյալ բնութագրերը.
2. այն պետք է պարունակի մի քանի տերմին.
3. բոլոր պայմանները պետք է ունենան նույն աստիճանը.

Միատարր եռանկյունաչափական ինքնության մեջ ներառված բոլոր գործառույթները պետք է անպայման ունենան նույն արգումենտը:

Լուծման ալգորիթմ

Եկեք ընտրենք պայմանները

Եվ եթե առաջին կետով ամեն ինչ պարզ է, ապա արժե ավելի մանրամասն խոսել երկրորդի մասին: Ի՞նչ է նշանակում ունենալ տերմինների նույն աստիճանը: Դիտարկենք առաջին խնդիրը.

3cosx+5sinx=0

3\cos x+5\sin x=0 Այս հավասարման առաջին անդամն է 3\cos x. Խնդրում ենք նկատի ունենալ, որ այստեղ կա միայն մեկ եռանկյունաչափական ֆունկցիա. cosx\cos x - և ոչ ուրիշ եռանկյունաչափական ֆունկցիաներայստեղ չկա, ուստի այս տերմինի աստիճանը 1 է։ Նույնը երկրորդի դեպքում՝ 5 սինքս 5\sin x - այստեղ կա միայն սինուս, այսինքն՝ այս տերմինի աստիճանը նույնպես հավասար է մեկին։ Այսպիսով, մենք մեր առջև ունենք երկու տարրից բաղկացած ինքնություն, որոնցից յուրաքանչյուրը պարունակում է եռանկյունաչափական ֆունկցիա և միայն մեկը։ Սա առաջին աստիճանի հավասարումն է։

Անցնենք երկրորդ արտահայտությանը.

4մեղք2 x+sin2x−3=0

4((\sin )^(2))x+\sin 2x-3=0

Այս շինարարության առաջին անդամն է 4մեղք2 x 4((\sin )^(2))x.

Այժմ մենք կարող ենք գրել հետևյալ լուծումը.

մեղք2 x=sinx⋅sinx

((\sin )^(2))x=\sin x\cdot \sin x

Այլ կերպ ասած, առաջին անդամը պարունակում է երկու եռանկյունաչափական ֆունկցիա, այսինքն՝ նրա աստիճանը երկու է։ Եկեք զբաղվենք երկրորդ տարրով. sin2x\ sin 2x. Հիշենք այս բանաձեւը՝ կրկնակի անկյան բանաձեւը.

sin2x=2sinx⋅cosx

\sin 2x=2\sin x\cdot \cos x

Եվ կրկին ստացված բանաձեւում մենք ունենք երկու եռանկյունաչափական ֆունկցիա՝ սինուս եւ կոսինուս։ Այսպիսով, շինարարության այս տերմինի հզորության արժեքը նույնպես հավասար է երկուսի։

Անցնենք երրորդ տարրին՝ 3. Մաթեմատիկայի դասընթացից ավագ դպրոցՄենք հիշում ենք, որ ցանկացած թիվ կարելի է բազմապատկել 1-ով, ուստի գրում ենք այն.

˜ 3=3⋅1

Եվ միավորը կարող է գրվել՝ օգտագործելով հիմնական եռանկյունաչափական ինքնությունը հետևյալ ձևով.

1=մեղք2 x⋅ cos2 x

1=((\ sin )^(2))x\cdot ((\cos)^(2))x

Հետևաբար, մենք կարող ենք 3-ը վերաշարադրել հետևյալ կերպ.

3=3(մեղք2 x⋅ cos2 x)=3մեղք2 x+3 cos2 x

3=3\left(((\sin )^(2))x\cdot ((\cos)^(2))x \աջ)=3((\sin )^(2))x+3(( \cos )^(2))x

Այսպիսով, մեր 3-րդ տերմինը բաժանված է երկու տարրի, որոնցից յուրաքանչյուրը միատարր է և ունի երկրորդ աստիճան։ Առաջին տերմինի սինուսը տեղի է ունենում երկու անգամ, երկրորդում կոսինուսը նույնպես երկու անգամ: Այսպիսով, 3-ը կարող է ներկայացվել նաև որպես տերմին երկուսի հզորության աստիճանով:

Նույնը երրորդ արտահայտության դեպքում.

մեղք3 x+ մեղք2 xcosx=2 cos3 x

Եկեք տեսնենք. Առաջին տերմինն է մեղք3 x((\sin )^(3))x-ը երրորդ աստիճանի եռանկյունաչափական ֆունկցիա է։ Երկրորդ տարր - մեղք2 xcosx((\sin )^(2))x\cos x.

մեղք2 ((\sin )^(2))-ը երկու հզորության արժեքով կապ է cosx\cos x-ն առաջին անդամն է: Ընդհանուր առմամբ, երրորդ տերմինը նույնպես ունի երեք հզորության արժեք: Վերջապես, աջ կողմում կա ևս մեկ հղում. 2cos3 x 2((\cos )^(3))x-ը երրորդ աստիճանի տարր է։ Այսպիսով, մենք ունենք երրորդ աստիճանի միատարր եռանկյունաչափական հավասարում։

Մենք ունենք տարբեր աստիճանի երեք ինքնություն գրված: Կրկին ուշադրություն դարձրեք երկրորդ արտահայտությանը. Բնօրինակ արձանագրության մեջ անդամներից մեկը վիճաբանություն ունի 2x 2x. Մենք ստիպված ենք ձերբազատվել այս փաստարկից՝ այն փոխակերպելով կրկնակի անկյան սինուսի բանաձևի միջոցով, քանի որ մեր ինքնության մեջ ներառված բոլոր ֆունկցիաները պետք է անպայման ունենան նույն արգումենտը։ Եվ սա միատարր եռանկյունաչափական հավասարումների պահանջ է։

Օգտագործում ենք հիմնական եռանկյունաչափական ինքնության բանաձևը և գրում վերջնական լուծումը

Պայմանները դասավորել ենք, անցնենք լուծմանը։ Անկախ հզորության աստիճանից, այս տիպի հավասարումների լուծումը միշտ կատարվում է երկու քայլով.

1) ապացուցել դա

cosx≠0

\cos x\ne 0. Դա անելու համար բավական է հիշել հիմնական եռանկյունաչափական ինքնության բանաձևը. (մեղք2 x⋅ cos2 x=1)\left(((\sin )^(2))x\cdot ((\cos)^(2))x=1 \աջ) և փոխարինել այս բանաձևով cosx=0\cos x=0. Մենք կստանանք հետևյալ արտահայտությունը.

մեղք2 x=1sinx=±1

\սկիզբ (հավասարեցնել)& ((\sin )^(2))x=1 \\& \sin x=\pm 1 \\\վերջ (հավասարեցնել)

Ստացված արժեքները փոխարինելով, այսինքն՝ փոխարենը cosx\cos x-ը զրո է, և փոխարենը sinx\sin x — 1 կամ -1, սկզբնական արտահայտության մեջ կստանանք սխալ թվային հավասարություն։ Սա է այն հիմնավորումը, որ

cosx≠0

2) երկրորդ քայլը տրամաբանորեն բխում է առաջինից. Քանի որ

cosx≠0

\cos x\ne 0, մենք կառուցվածքի մեր երկու կողմերն էլ բաժանում ենք cosn x((\cos )^(n))x, որտեղ n n-ն ինքնին միատարր եռանկյունաչափական հավասարման հզորության ցուցիչն է: Ի՞նչ է սա մեզ տալիս.

\[\սկիզբ(զանգված)(·(35)(l))

sinxcosx=tgxcosxcosx=1

\սկիզբ (հավասարեցնել)& \frac(\sin x)(\cos x)=tgx \\& \frac(\cos x)(\cos x)=1 \\\վերջ (հավասարեցնել) \\() \\ \վերջ (զանգված)\]

Դրա շնորհիվ մեր ծանր նախնական շինարարությունը կրճատվում է մինչև հավասարման n n-աստիճան շոշափողի նկատմամբ, որի լուծումը հեշտությամբ կարելի է գրել փոփոխականի փոփոխության միջոցով: Դա ամբողջ ալգորիթմն է: Տեսնենք, թե ինչպես է այն աշխատում գործնականում:

Մենք լուծում ենք իրական խնդիրներ

Առաջադրանք թիվ 1

Եվ եթե առաջին կետով ամեն ինչ պարզ է, ապա արժե ավելի մանրամասն խոսել երկրորդի մասին: Ի՞նչ է նշանակում ունենալ տերմինների նույն աստիճանը: Դիտարկենք առաջին խնդիրը.

3cosx+5sinx=0

Մենք արդեն պարզել ենք, որ սա միատարր եռանկյունաչափական հավասարում է՝ մեկին հավասար հզորության ցուցիչով։ Հետևաբար, առաջին հերթին եկեք պարզենք դա cosx≠0\cos x\ne 0. Ենթադրենք հակառակը, որ

cosx=0→sinx=±1

\cos x=0\ to \sin x=\pm 1.

Ստացված արժեքը փոխարինում ենք մեր արտահայտության մեջ, ստանում ենք.

3⋅0+5⋅(±1) =0±5=0

\սկիզբ (հավասարեցնել)& 3\cdot 0+5\cdot \ձախ(\pm 1 \աջ)=0 \\& \pm 5=0 \\\վերջ (հավասարեցնել)

Սրանից ելնելով կարելի է ասել, որ cosx≠0\cos x\ne 0. Բաժանենք մեր հավասարումը cosx\cos x քանի որ մեր ամբողջ արտահայտությունն ունի մեկ հզորության արժեք: Մենք ստանում ենք.

3(cosxcosx) +5(sinxcosx) =0 3+5tgx=0tgx=− 3 5

\սկիզբ(հավասարեցնել)& 3\ձախ(\frac(\cos x)(\cos x) \աջ)+5\ձախ(\frac(\sin x)(\cos x) \աջ)=0 \\& 3+5tgx=0 \\& tgx=-\frac(3)(5) \\\վերջ (հավասարեցնել)

Սա աղյուսակի արժեք չէ, ուստի պատասխանը կներառի arctgx arctgx:

x=arctg (−3 5 ) + π n,n∈Z

x=arctg\left(-\frac(3)(5) \right)+\text( )\!\!\pi\!\!\text( )n,n\in Z

Քանի որ arctg arctg arctg-ը կենտ ֆունկցիա է, մենք կարող ենք արգումենտից հանել «մինուսը» և դնել arctg-ի դիմաց: Մենք ստանում ենք վերջնական պատասխանը.

x=−arctg 3 5 + π n,n∈Z

x=-arctg\frac(3)(5)+\text( )\!\!\pi\!\!\text( )n,n\in Z

Առաջադրանք թիվ 2

4մեղք2 x+sin2x−3=0

4((\sin )^(2))x+\sin 2x-3=0

Ինչպես հիշում եք, նախքան այն լուծելը, դուք պետք է որոշ փոխակերպումներ կատարեք: Մենք իրականացնում ենք վերափոխումները.

4մեղք2 x+2sinxcosx−3 (մեղք2 x+ cos2 x)=0 4մեղք2 x+2sinxcosx−3 մեղք2 x−3 cos2 x=0մեղք2 x+2sinxcosx−3 cos2 x=0

\սկիզբ (հավասարեցնել)& 4((\sin )^(2)x+2\sin x\cos x-3\left(((\sin )^(2))x+((\cos)^(2 ))x \աջ)=0 \\& 4((\sin )^(2))x+2\sin x\cos x-3((\sin )^(2)x-3(\cos )^(2))x=0 \\& ((\sin )^(2))x+2\sin x\cos x-3((\cos)^(2)x=0 \\\վերջ (հավասարեցնել)

Մենք ստացանք երեք տարրերից բաղկացած կառուցվածք. Առաջին կիսամյակում մենք տեսնում ենք մեղք2 ((\sin )^(2)), այսինքն նրա հզորության արժեքը երկու է: Երկրորդ ժամկետում մենք տեսնում ենք sinx\սին x եւ cosx\cos x - կրկին երկու ֆունկցիա կա, դրանք բազմապատկվում են, ուստի ընդհանուր աստիճանը կրկին երկու է: Երրորդ հղումում մենք տեսնում ենք cos2 x((\cos )^(2))x - նման է առաջին արժեքին:

Ապացուցենք դա cosx=0\cos x=0 այս կառուցման լուծումը չէ: Դա անելու համար ենթադրենք հակառակը.

\[\սկիզբ(զանգված)(·(35)(l))

\cos x=0 \\\sin x=\pm 1 \\1+2\cdot \left(\pm 1 \աջ)\cdot 0-3\cdot 0=0 \\1+0-0=0 \ \1=0 \\\վերջ (զանգված)\]

Մենք դա ապացուցել ենք cosx=0\cos x=0 չի կարող լուծում լինել: Անցնենք երկրորդ քայլին՝ մեր ամբողջ արտահայտությունը բաժանենք վրա cos2 x((\cos )^(2))x. Ինչու քառակուսի: Քանի որ այս միատարր հավասարման հզորության աստիճանը հավասար է երկուսի.

մեղք2 xcos2 x+2sinxcosxcos2 x−3=0 տ է2 x+2tgx−3=0

\սկիզբ(հավասարեցնել)& \frac(((\sin )^(2))x)((\cos)^(2))x)+2\frac(\sin x\cos x)((\ cos )^(2))x)-3=0 \\& t((g)^(2))x+2tgx-3=0 \\\վերջ (հավասարեցնել)

Հնարավո՞ր է այս արտահայտությունը լուծել դիսկրիմինանտի միջոցով: Իհարկե կարող ես։ Բայց ես առաջարկում եմ հիշել թեորեմը. թեորեմի հակադարձՎիետա, և մենք ստանում ենք, որ այս բազմանդամը ներկայացնում ենք երկու պարզ բազմանդամների տեսքով, այն է՝

(tgx+3) (tgx−1) =0tgx=−3→x=−arctg3+ π n,n∈Ztgx=1→x= π 4 + π k,k∈Z

\սկիզբ (հավասարեցնել)& \ձախ (tgx+3 \աջ)\ ձախ (tgx-1 \աջ)=0 \\& tgx=-3\ դեպի x=-arctg3+\տեքստ ( )\!\!\pi\ !\!\text( )n,n\in Z \\& tgx=1\to x=\frac(\text( )\!\!\pi\!\!\text( ))(4)+\ text( )\!\!\pi\!\!\text( )k,k\in Z \\\end(align)

Շատ ուսանողներ հարցնում են՝ արժե՞ ինքնության լուծումների յուրաքանչյուր խմբի համար առանձին գործակիցներ գրել, թե՞ չանհանգստացնել ու ամենուր նույնը գրել։ Անձամբ ես կարծում եմ, որ ավելի լավ ու վստահելի է օգտագործել տարբեր տառեր, որպեսզի եթե լուրջ տեխնիկական համալսարան ընդունվես մաթեմատիկայի լրացուցիչ թեստերով, քննիչները պատասխանի մեջ մեղք չգտնեն։

Առաջադրանք թիվ 3

մեղք3 x+ մեղք2 xcosx=2 cos3 x

((\sin )^(3))x+((\sin )^(2))x\cos x=2((\cos)^(3))x

Մենք արդեն գիտենք, որ սա երրորդ աստիճանի միատարր եռանկյունաչափական հավասարում է, հատուկ բանաձևեր պետք չեն, և մեզանից պահանջվում է ընդամենը տերմինը տեղափոխել։ 2cos3 x 2((\cos)^(3))x դեպի ձախ: Եկեք վերաշարադրենք.

մեղք3 x+ մեղք2 xcosx−2 cos3 x=0

((\sin )^(3))x+((\sin )^(2))x\cos x-2((\cos)^(3))x=0

Մենք տեսնում ենք, որ յուրաքանչյուր տարր պարունակում է երեք եռանկյունաչափական ֆունկցիա, ուստի այս հավասարումն ունի երեք հզորության արժեք: Եկեք լուծենք այն: Առաջին հերթին պետք է դա ապացուցել cosx=0\cos x=0 արմատ չէ.

\[\սկիզբ(զանգված)(·(35)(l))

\cos x=0 \\\sin x=\pm 1 \\\վերջ (զանգված)\]

Եկեք այս թվերը փոխարինենք մեր սկզբնական կառուցման մեջ.

(±1)3 +1⋅0−2⋅0=0 ±1+0−0=0±1=0

\սկիզբ (հավասարեցնել)& ((\ ձախ (\pm 1 \աջ))^(3))+1\cdot 0-2\cdot 0=0 \\& \pm 1+0-0=0 \\& \pm 1=0 \\\վերջ (հավասարեցնել)

Հետևաբար, cosx=0\cos x=0 լուծում չէ։ Մենք դա ապացուցել ենք cosx≠0\cos x\ne 0. Այժմ, երբ մենք դա ապացուցեցինք, եկեք մեր սկզբնական հավասարումը բաժանենք. cos3 x((\cos )^(3))x. Ինչու՞ խորանարդի մեջ: Քանի որ մենք պարզապես ապացուցեցինք, որ մեր սկզբնական հավասարումն ունի երրորդ հզորությունը.

մեղք3 xcos3 x+մեղք2 xcosxcos3 x−2=0 տ Երկու հավասարումների համակարգերը, որոնցից մեկը գծային է, ունեն ձև3 x+t Երկու հավասարումների համակարգերը, որոնցից մեկը գծային է, ունեն ձև2 x−2=0

\սկիզբ(հավասարեցնել)& \frac(((\sin )^(3))x)((\cos)^(3))x)+\frac(((\sin )^(2))x\ cos x)(((\cos)^(3))x)-2=0 \\& t((g)^(3))x+t((g)^(2))x-2=0 \\\վերջ (հավասարեցնել)

Ներկայացնենք նոր փոփոխական.

tgx=t

Եկեք վերաշարադրենք շինարարությունը.

տ3 +տ2 −2=0

((t)^(3))+((t)^(2))-2=0

Մեր առջև խորանարդ հավասարում. Ինչպե՞ս լուծել այն: Սկզբում, երբ ես նոր էի հավաքում այս վիդեո ձեռնարկը, նախատեսում էի նախ խոսել բազմանդամների ֆակտորինգի և այլ տեխնիկայի մասին: Բայց ներս այս դեպքումամեն ինչ շատ ավելի պարզ է. Նայեք մեր տրված ինքնությանը, որի ամենաբարձր աստիճան ունեցող տերմինը 1 է: Բացի այդ, բոլոր գործակիցները ամբողջ թվեր են: Սա նշանակում է, որ մենք կարող ենք օգտագործել Բեզութի թեորեմի հետևանքը, որն ասում է, որ բոլոր արմատները -2 թվի բաժանարարներն են, այսինքն՝ ազատ անդամը։

Հարց է առաջանում՝ ինչի՞ վրա է բաժանվում -2-ը։ Քանի որ 2-ը պարզ թիվ է, տարբերակները շատ չեն: Սրանք կարող են լինել հետևյալ թվերը՝ 1; 2; -1; -2. Բացասական արմատները անմիջապես անհետանում են: Ինչո՞ւ։ Քանի որ երկուսն էլ բացարձակ արժեքով 0-ից մեծ են, հետևաբար տ3 ((t)^(3)) մոդուլով ավելի մեծ կլինի, քան տ2 ((տ)^(2)). Եվ քանի որ խորանարդը կենտ ֆունկցիա է, հետևաբար խորանարդի թիվը կլինի բացասական, և տ2 ((t)^(2)) - դրական, և այս ամբողջ շինարարությունը, հետ t=−1 t=-1 և t=−2 t=-2, չի լինի 0-ից ավելի: Դրանից հանեք -2 և ստացեք 0-ից փոքր թիվ: Եկեք փոխարինենք այս թվերից յուրաքանչյուրը:

˜ t=1→ 1+1−2=0→0=0

˜t=1\to \text( )1+1-2=0\to 0=0

Մենք ստացել ենք ճիշտ թվային հավասարություն։ Հետևաբար, t=1 t=1 արմատն է։

t=2→8+4−2=0→10≠0

t=2\մինչև 8+4-2=0\մինչև 10\ne 0

t=2 t=2 արմատ չէ։

Ըստ հետևության և նույն Բեզութի թեորեմի՝ ցանկացած բազմանդամ, որի արմատն է x0 ((x)_(0)), ներկայացրեք այն ձևով.

Q(x)=(x= x0 )P(x)

Q(x)=(x=((x)_(0)))P(x)

Մեր դեպքում՝ դերում x x-ը փոփոխական է տտ, և դերում x0 ((x)_(0)) 1-ի հավասար արմատ է: Ստանում ենք.

տ3 +տ2 −2=(t−1)⋅P(t)

((t)^(3))+((t)^(2))-2=(t-1)\cdot P(t)

Ինչպես գտնել բազմանդամը Պ (t) P\ձախ (t\աջ): Ակնհայտ է, որ դուք պետք է անեք հետևյալը.

P(t)= տ3 +տ2 −2 t−1

P(t)=\frac(((t)^(3))+((t)^(2))-2)(t-1)

Փոխարինենք.

տ3 +տ2 +0⋅t−2t−1=տ2 +2տ+2

\frac(((t)^(3))+((t)^(2))+0\cdot t-2)(t-1)=((t)^(2))+2t+2

Այսպիսով, մեր սկզբնական բազմանդամը բաժանվում է առանց մնացորդի։ Այսպիսով, մենք կարող ենք վերաշարադրել մեր սկզբնական հավասարությունը հետևյալ կերպ.

(t−1) ( տ2 +2t+2)=0

(t-1)(((t)^(2))+2t+2)=0

Արտադրյալը զրո է, երբ գործոններից առնվազն մեկը զրո է: Մենք արդեն դիտարկել ենք առաջին բազմապատկիչը: Դիտարկենք երկրորդը.

տ2 +2t+2=0

((t)^(2))+2t+2=0

Փորձառու ուսանողները հավանաբար արդեն հասկացել են դա այս դիզայնըարմատներ չունի, բայց եկեք դեռ հաշվարկենք դիսկրիմինանտը։

D=4−4⋅2=4−8=−4

D=4-4\cdot 2=4-8=-4

Տարբերիչը 0-ից փոքր է, հետևաբար արտահայտությունն արմատներ չունի: Ընդհանուր առմամբ, հսկայական շինարարությունը նվազեցվեց սովորական հավասարության.

\[\սկիզբ(զանգված)(·(35)(l))

t=\text( )1 \\tgx=\text( )1 \\x=\frac(\text( )\!\!\pi\!\!\text( ))(4)+\text( ) \!\!\pi\!\!\text( )k,k\in Z \\\ end(array)\]

Եզրափակելով, ես կցանկանայի ավելացնել մի քանի մեկնաբանություն վերջին առաջադրանքի վերաբերյալ.

1. պայմանը միշտ կբավարարվի՞ cosx≠0\cos x\ne 0, և արժե՞ ընդհանրապես իրականացնել այս ստուգումը: Իհարկե, ոչ միշտ: Այն դեպքերում, երբ cosx=0\cos x=0-ը մեր հավասարության լուծումն է, այն պետք է հանենք փակագծերից, այնուհետև փակագծերում կմնա լրիվ միատարր հավասարումը։
2. Ի՞նչ է բազմանդամը բազմանդամի բաժանելը: Իսկապես, դպրոցներից շատերը դա չեն ուսումնասիրում, և երբ աշակերտներն առաջին անգամ են տեսնում նման ձևավորում, նրանք փոքր ցնցում են ապրում: Բայց, փաստորեն, դա պարզ է և հաճելի ողջույն, որը մեծապես հեշտացնում է հավասարումների լուծումը ավելի բարձր աստիճաններ. Իհարկե, դրան նվիրված կլինի առանձին տեսադասընթաց, որը կհրապարակեմ մոտ ապագայում։

Հիմնական կետերը

Միատարր եռանկյունաչափական հավասարումները սիրված թեմա են բոլոր տեսակի համար թեստեր. Դրանք կարելի է լուծել շատ պարզ՝ միայն մեկ անգամ պարապել: Որպեսզի հասկանալի լինի, թե ինչի մասին է խոսքը, ներկայացնենք նոր սահմանում։

Միատարր եռանկյունաչափական հավասարումը այն հավասարումն է, որտեղ յուրաքանչյուր ոչ զրոյական անդամ բաղկացած է նույն թվով եռանկյունաչափական գործոններից: Սրանք կարող են լինել սինուսներ, կոսինուսներ կամ դրանց համակցություններ. լուծման մեթոդը միշտ նույնն է:

Միատարր եռանկյունաչափական հավասարման աստիճանը եռանկյունաչափական գործոնների թիվն է, որոնք ներառված են ոչ զրոյական տերմիններում.

sinx+15 cos x=0

\sin x+15\text( cos )x=0 - 1-ին աստիճանի ինքնություն;

2 sin2x+5sinxcosx−8cos2x=0

2\text( sin)2x+5\sin xcosx-8\cos 2x=0 - 2-րդ աստիճան;

sin3x+2sinxcos2x=0

\sin 3x+2\sin x\cos 2x=0 - 3-րդ աստիճան;

sinx+cosx=1

\sin x+\cos x=1 - և այս հավասարումը միատարր չէ, քանի որ աջ կողմում կա միավոր՝ ոչ զրոյական անդամ, որտեղ եռանկյունաչափական գործակիցներ չկան.

sin2x+2sinx−3=0

\sin 2x+2\sin x-3=0 նույնպես ոչ միատարր հավասարում է։ Տարր sin2x\sin 2x-ը երկրորդ աստիճանի է (քանի որ այն կարող է ներկայացվել

sin2x=2sinxcosx

\sin 2x=2\sin x\cos x), 2սինքս 2\sin x-ն առաջինն է, իսկ 3 տերմինը հիմնականում զրո է, քանի որ դրանում չկան սինուսներ կամ կոսինուսներ:

Լուծման ընդհանուր սխեմա

Լուծման սխեման միշտ նույնն է.

Ենթադրենք, որ cosx=0\cos x=0. Հետո sinx=±1\sin x=\pm 1 - սա բխում է հիմնական ինքնությունից: Եկեք փոխարինենք sinx\սին x եւ cosx\cos x սկզբնական արտահայտության մեջ, և եթե արդյունքը անհեթեթ է (օրինակ՝ արտահայտությունը 5=0 5=0), անցեք երկրորդ կետին;

Մենք ամեն ինչ բաժանում ենք կոսինուսի հզորությամբ՝ cosx, cos2x, cos3x... - կախված է հավասարման հզորության արժեքից։ Ստանում ենք սովորական հավասարություն շոշափողներով, որը կարելի է ապահով լուծել tgx=t-ին փոխարինելուց հետո։

tgx=tԳտնված արմատները կլինեն սկզբնական արտահայտության պատասխանը:

Այս հոդվածում մենք կանդրադառնանք միատարր եռանկյունաչափական հավասարումների լուծման մեթոդին:

Միատարր եռանկյունաչափական հավասարումները ունեն նույն կառուցվածքը, ինչ ցանկացած այլ տեսակի միատարր հավասարումները։ Հիշեցնեմ երկրորդ աստիճանի միատարր հավասարումների լուծման մեթոդը.

Դիտարկենք ձևի միատարր հավասարումներ

Միատարր հավասարումների տարբերակիչ առանձնահատկությունները.

ա) բոլոր միանուններն ունեն նույն աստիճանը,

բ) ազատ տերմինը զրո է,

գ) հավասարումը պարունակում է երկու տարբեր հիմքերով հզորություններ:

Միատարր հավասարումները լուծվում են նմանատիպ ալգորիթմի միջոցով:

Այս տիպի հավասարումը լուծելու համար մենք հավասարման երկու կողմերը բաժանում ենք (կարելի է բաժանել կամ ըստ)

Ուշադրություն. Հավասարման աջ և ձախ կողմերը անհայտ պարունակող արտահայտության վրա բաժանելիս կարող եք արմատներ կորցնել: Հետևաբար, անհրաժեշտ է ստուգել, ​​թե արդյոք այն արտահայտության արմատները, որոնցով մենք բաժանում ենք հավասարման երկու կողմերը, սկզբնական հավասարման արմատներն են։

Եթե ​​այդպես է, ապա մենք գրում ենք այս արմատը, որպեսզի հետագայում չմոռանանք դրա մասին, այնուհետև արտահայտությունը բաժանում ենք սրանով:

Ընդհանուր առմամբ, աջ կողմում զրո ունեցող ցանկացած հավասարում լուծելիս առաջին բանը, որ պետք է անել, ընդլայնվելն է։ ձախ կողմըֆակտորինգի հավասարումներ ըստ ցանկացածի մատչելի ձևով. Եվ հետո յուրաքանչյուր գործոն հավասարեցրեք զրոյի: Այս դեպքում մենք հաստատ արմատները չենք կորցնի։

Այսպիսով, զգուշորեն բաժանեք հավասարման ձախ կողմը տերմին առ անդամ արտահայտության մեջ: Մենք ստանում ենք.

Կրճատենք երկրորդ և երրորդ կոտորակների համարիչն ու հայտարարը.

Ներկայացնենք փոխարինումը.

Մենք ստանում ենք քառակուսային հավասարում:

Եկեք լուծենք քառակուսի հավասարումը, գտնենք ֊ի արժեքները և այնուհետև վերադառնանք սկզբնական անհայտին։

Միատարր եռանկյունաչափական հավասարումներ լուծելիս պետք է հիշել մի քանի կարևոր բան.

1. Կեղծ տերմինը կարող է փոխարկվել սինուսի և կոսինուսի քառակուսու՝ օգտագործելով հիմնական եռանկյունաչափական ինքնությունը.

2. Կրկնակի արգումենտի սինուսը և կոսինուսը երկրորդ աստիճանի միանդամներ են. կրկնակի արգումենտի սինուսը հեշտությամբ կարելի է վերածել սինուսի և կոսինուսի արտադրյալի, իսկ կրկնակի արգումենտի կոսինուսը՝ սինուսի կամ կոսինուսի քառակուսու.

Դիտարկենք միատարր եռանկյունաչափական հավասարումների լուծման մի քանի օրինակ։

1. Եկեք լուծենք հավասարումը.

Սա դասական օրինակԱռաջին աստիճանի միատարր եռանկյունաչափական հավասարում. յուրաքանչյուր միանդամի աստիճանը հավասար է մեկի, ազատ անդամը հավասար է զրոյի։

Նախքան հավասարման երկու կողմերը բաժանելը , դուք պետք է ստուգեք, որ հավասարման արմատները սկզբնական հավասարման արմատները չեն: Ստուգում ենք՝ if , ապա title="sin(x)0">, следовательно их сумма не равна нулю.!}

Բաժանենք հավասարման երկու կողմերը:

Մենք ստանում ենք.

, Որտեղ

, Որտեղ

Պատասխան. , Որտեղ

2. Եկեք լուծենք հավասարումը.

Սա երկրորդ աստիճանի միատարր եռանկյունաչափական հավասարման օրինակ է։ Մենք հիշում ենք, որ եթե մենք կարող ենք հաշվի առնել հավասարման ձախ կողմը, ապա նպատակահարմար է դա անել: Այս հավասարման մեջ մենք կարող ենք հանել. Եկեք սա անենք.

Առաջին հավասարման լուծում՝ , որտեղ

Երկրորդ հավասարումը առաջին աստիճանի միատարր եռանկյունաչափական հավասարումն է։ Այն լուծելու համար հավասարման երկու կողմերը բաժանեք . Մենք ստանում ենք.

Պատասխան՝ որտեղ,

3. Եկեք լուծենք հավասարումը.

Որպեսզի այս հավասարումը «դառնա» միատարր, մենք այն վերածում ենք արտադրյալի և 3 թիվը ներկայացնում ենք որպես սինուսի և կոսինուսի քառակուսիների գումար.

Բոլոր տերմինները տեղափոխենք ձախ, բացենք փակագծերը և ներկայացնենք նմանատիպ տերմիններ։ Մենք ստանում ենք.

Եկեք ֆակտորիզացնենք ձախ կողմը և յուրաքանչյուր գործակից սահմանենք զրոյի.

Պատասխան՝ որտեղ,

4. Եկեք լուծենք հավասարումը.

Մենք տեսնում ենք, թե ինչ կարող ենք հանել փակագծերից։ Եկեք սա անենք.

Յուրաքանչյուր գործոն հավասարեցնենք զրոյի.

Առաջին հավասարման լուծում.

Բնակչության երկրորդ հավասարումը երկրորդ աստիճանի դասական միատարր հավասարումն է։ Հավասարման արմատները սկզբնական հավասարման արմատները չեն, ուստի մենք հավասարման երկու կողմերը բաժանում ենք հետևյալի.

Առաջին հավասարման լուծում.

Երկրորդ հավասարման լուծում.

Դասի թեման՝ «Համասեռ եռանկյունաչափական հավասարումներ».

(10-րդ դասարան)

Թիրախ: ներկայացնել I և II աստիճանների միատարր եռանկյունաչափական հավասարումների հայեցակարգը. ձևակերպել և մշակել I և II աստիճանների միատարր եռանկյունաչափական հավասարումների լուծման ալգորիթմ. սովորեցնել ուսանողներին լուծել I և II աստիճանների միատարր եռանկյունաչափական հավասարումներ. զարգացնել օրինաչափությունները նույնականացնելու և ընդհանրացնելու ունակությունը. խթանել հետաքրքրությունը առարկայի նկատմամբ, զարգացնել համերաշխության և առողջ մրցակցության զգացում:

Դասի տեսակը. նոր գիտելիքների ձևավորման դաս.

Ձև: աշխատել խմբերով.

Սարքավորումներ: համակարգիչ, մուլտիմեդիա տեղադրում

Դասի առաջընթաց

Կազմակերպչական պահ

Ողջույն ուսանողներին, մոբիլիզացնելով ուշադրությունը.

Դասին գիտելիքների գնահատման վարկանիշային համակարգ (ուսուցիչը բացատրում է գիտելիքների գնահատման համակարգը՝ լրացնելով գնահատման թերթիկը ուսուցչի կողմից ուսանողներից ընտրված անկախ փորձագետի կողմից): Դասը ուղեկցվում է շնորհանդեսով։ .

Հիմնական գիտելիքների թարմացում:

Տնային աշխատանքը ստուգվում և գնահատվում է անկախ փորձագետի և խորհրդատուների կողմից դասից առաջ և ավարտվում է միավորների թերթիկը:

Ուսուցիչը ամփոփում է տնային աշխատանքը.

Ուսուցիչ: Շարունակում ենք ուսումնասիրել «Եռանկյունաչափական հավասարումներ» թեման։ Այսօր դասի ընթացքում մենք ձեզ կծանոթացնենք եռանկյունաչափական հավասարումների մեկ այլ տեսակի և դրանց լուծման մեթոդների հետ, հետևաբար մենք կկրկնենք մեր սովորածը: Բոլոր տեսակի եռանկյունաչափական հավասարումներ լուծելիս դրանք կրճատվում են ամենապարզ եռանկյունաչափական հավասարումների լուծմանը։

Ստուգվում են խմբերով կատարված անհատական ​​տնային աշխատանքները: «Ամենապարզ եռանկյունաչափական հավասարումների լուծումները» շնորհանդեսի պաշտպանությունը

(Խմբի աշխատանքը գնահատվում է անկախ փորձագետի կողմից)

Սովորելու մոտիվացիա.

Ուսուցիչ: Մենք անելիքներ ունենք խաչբառը լուծելու համար։ Լուծելով այն՝ մենք կիմանանք նոր տեսակի հավասարումների անվանումը, որը կսովորենք լուծել այսօր դասարանում։

Հարցերը նախագծված են գրատախտակին: Ուսանողները կռահում են, և անկախ փորձագետը նշում է այն ուսանողների միավորները, ովքեր պատասխանում են գնահատականների թերթիկում:

Խաչբառը լուծելով՝ երեխաները կկարդան «միատարր» բառը:

Նոր գիտելիքների յուրացում.

Ուսուցիչ: Դասի թեման է «Համասեռ եռանկյունաչափական հավասարումներ»:

Եկեք գրենք դասի թեման տետրում: Միատարր եռանկյունաչափական հավասարումները լինում են առաջին և երկրորդ աստիճանի։

Եկեք գրենք առաջին աստիճանի միատարր հավասարման սահմանումը: Ես ցույց եմ տալիս այս տիպի հավասարումների լուծման օրինակ, դուք ստեղծում եք առաջին աստիճանի միատարր եռանկյունաչափական հավասարման լուծման ալգորիթմ:

Ձևի հավասարումը Ա sinx + բ cosx = 0 կոչվում է առաջին աստիճանի միատարր եռանկյունաչափական հավասարում:

Դիտարկենք հավասարման լուծումը, երբ գործակիցները ԱԵվ Վտարբերվում են 0-ից:

Օրինակ՝ sinx + cosx = 0

Ռ Հավասարման անդամի երկու կողմերը բաժանելով cosx-ով, ստանում ենք

Ուշադրություն. Դուք կարող եք բաժանել 0-ի միայն այն դեպքում, եթե այս արտահայտությունը ոչ մի տեղ չի վերածվում 0-ի: Եթե ​​կոսինուսը հավասար է 0-ի, ապա սինուսը նույնպես հավասար կլինի 0-ի, հաշվի առնելով, որ գործակիցները տարբերվում են 0-ից, բայց մենք գիտենք, որ սինուսը և կոսինուսը տարբեր կետերում զրոյի են գնում։ Հետեւաբար, այս գործողությունը կարող է իրականացվել այս տեսակի հավասարումը լուծելիս:

Առաջին աստիճանի միատարր եռանկյունաչափական հավասարման լուծման ալգորիթմ. հավասարման երկու կողմերը բաժանել cosx, cosx 0-ով

Ձևի հավասարումը Ա sin mx +բ cos mx = 0կոչվում է նաև առաջին աստիճանի միատարր եռանկյունաչափական հավասարում և լուծում է նաև հավասարման երկու կողմերի բաժանումը կոսինուսով mx:

Ձևի հավասարումը ա մեղք 2 x+բ sinx cosx +գ cos2x = 0կոչվում է երկրորդ աստիճանի միատարր եռանկյունաչափական հավասարում։

Օրինակ : մեղք 2 x + 2sinx cosx – 3cos 2 x = 0

a գործակիցը տարբերվում է 0-ից և հետևաբար, ինչպես նախորդ հավասարումը, cosx-ը հավասար չէ 0-ի, հետևաբար կարող եք օգտագործել հավասարման երկու կողմերը cos 2 x-ով բաժանելու մեթոդը։

Մենք ստանում ենք tg 2 x + 2tgx – 3 = 0

Մենք լուծում ենք՝ ներմուծելով նոր փոփոխական, թող tgx = a, այնուհետև ստանում ենք հավասարումը

a 2 + 2a – 3 = 0

D = 4 – 4 (–3) = 16

a 1 = 1 a 2 = –3

Վերադարձ դեպի փոխարինում

Պատասխան.

Եթե ​​գործակիցը a = 0, ապա հավասարումը կստանա 2sinx cosx – 3cos2x = 0 ձևը, այն լուծում ենք փակագծերից հանելով cosx ընդհանուր գործակիցը։ Եթե ​​c = 0 գործակիցը, ապա հավասարումը ընդունում է sin2x +2sinx cosx = 0 ձևը, այն լուծում ենք փակագծերից հանելով sinx ընդհանուր գործակիցը։ Առաջին աստիճանի միատարր եռանկյունաչափական հավասարման լուծման ալգորիթմ.

Տեսեք, արդյոք հավասարումը պարունակում է asin2 x անդամ:

Եթե ​​asin2 x տերմինը պարունակվում է հավասարման մեջ (այսինքն՝ a 0), ապա հավասարումը լուծվում է՝ հավասարման երկու կողմերը բաժանելով cos2x-ի և այնուհետև ներմուծելով նոր փոփոխական։

Եթե ​​asin2 x տերմինը չի պարունակում հավասարման մեջ (այսինքն a = 0), ապա հավասարումը լուծվում է ֆակտորիզացիայի միջոցով. cosx-ը հանվում է փակագծերից: Նույն կերպ են լուծվում a sin2m x + b sin mx cos mx + c cos2mx = 0 ձևի միատարր հավասարումները.

Միատարր եռանկյունաչափական հավասարումների լուծման ալգորիթմը գրված է 102-րդ էջի դասագրքում։

Ֆիզիկական դաստիարակության րոպե

Միատարր եռանկյունաչափական հավասարումների լուծման հմտությունների ձևավորում

Խնդրի գրքերի բացում էջ 53

1-ին եւ 2-րդ խմբերը որոշում են թիվ 361-վ

3-րդ եւ 4-րդ խմբերը որոշում են թիվ 363-վ

Լուծումը ցույց տվեք գրատախտակին, բացատրեք, լրացրեք: Անկախ փորձագետը գնահատում է.

Օրինակների լուծում թիվ 361-վ խնդրագրքից
sinx – 3cosx = 0
հավասարման երկու կողմերը բաժանում ենք cosx 0-ով, ստանում ենք

թիվ 363-վ
sin2x + sinxcosx – 2cos2x = 0
հավասարման երկու կողմերը բաժանում ենք cos2x-ի, ստանում ենք tg2x + tanx – 2 = 0

լուծել՝ ներմուծելով նոր փոփոխական
թող tgx = a, ապա մենք ստանում ենք հավասարումը
a2 + a – 2 = 0
D = 9
a1 = 1 a2 = –2
վերադարձ դեպի փոխարինում

Անկախ աշխատանք.

Լուծե՛ք հավասարումները։

2 cosx – 2 = 0

2cos2x – 3cosx +1 = 0

3 sin2x + sinx cosx – 2 cos2x = 0

Անկախ աշխատանքի ավարտին նրանք փոխում են աշխատանքը և փոխադարձաբար ստուգում. Ճիշտ պատասխանները նախագծված են գրատախտակին:

Հետո վարձով են տալիս անկախ փորձագետ.

Ինքնասպասարկման լուծում

Ամփոփելով դասը.

Ի՞նչ տեսակի եռանկյունաչափական հավասարումներ ենք սովորել դասարանում:

Առաջին և երկրորդ աստիճանի եռանկյունաչափական հավասարումների լուծման ալգորիթմ.

Տնային աշխատանք. § 20.3 կարդալ. Թիվ 361(դ), 363(բ), լրացուցիչ դժվարություն թիվ 380(ա):

Խաչբառ.

Եթե ​​մուտքագրեք ճիշտ բառեր, ապա կստանաք եռանկյունաչափական հավասարումների տեսակներից մեկի անունը:

Փոփոխականի արժեքը, որը ճիշտ է դարձնում հավասարումը: (արմատ)

Անկյունների չափման միավոր? (Ռադիան)

Թվային գործոն արտադրանքի մեջ: (գործակից)

Մաթեմատիկայի ճյուղ, որն ուսումնասիրում է եռանկյունաչափական ֆունկցիաները։ (Եռանկյունաչափություն)

Ի՞նչ մաթեմատիկական մոդել է անհրաժեշտ եռանկյունաչափական ֆունկցիաները ներմուծելու համար: (Շրջանակ)

Ո՞ր եռանկյունաչափական ֆունկցիան է զույգ։ (Կոսինուս)

Ինչ է կոչվում իսկական հավասարություն: (Ինքնությունը)

Հավասարություն փոփոխականի հետ? (Հավասարում)

Հավասարումներ, որոնք ունեն նույն արմատները. (համարժեք)

Հավասարման արմատների բազմություն ? (Լուծում)

Միավորների թերթիկ

№
n\n

Ուսուցչի ազգանունը, անունը

Տնային աշխատանք

Ներկայացում

Ճանաչողական գործունեություն
ուսումնասիրելով

Հավասարումների լուծում

Անկախ
Աշխատանք

Տնային առաջադրանք – 12 միավոր (տնային աշխատանքի համար նշանակվել է 3 հավասարում 4 x 3 = 12)

Ներկայացում – 1 միավոր

Ուսանողների գործունեություն – 1 պատասխան – 1 միավոր (առավելագույնը 4 միավոր)

Հավասարումների լուծում 1 միավոր

Անկախ աշխատանք – 4 միավոր

Խմբային վարկանիշ.

«5» – 22 միավոր կամ ավելի
«4» – 18 – 21 միավոր
«3» – 12 – 17 միավոր