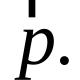Սովորական դիֆերենցիալ հավասարում հավասարում է, որը կապում է անկախ փոփոխականի, այս փոփոխականի անհայտ ֆունկցիայի և տարբեր կարգերի նրա ածանցյալների (կամ դիֆերենցիալների) հետ:

Դիֆերենցիալ հավասարման կարգը կոչվում է դրանում պարունակվող ամենաբարձր ածանցյալի կարգ։

Սովորականներից բացի ուսումնասիրվում են նաև մասնակի դիֆերենցիալ հավասարումներ։ Սրանք անկախ փոփոխականներին առնչվող հավասարումներ են, այս փոփոխականների և դրանց մասնակի ածանցյալների անհայտ ֆունկցիան նույն փոփոխականների նկատմամբ: Բայց մենք միայն կքննարկենք սովորական դիֆերենցիալ հավասարումներ և հետևաբար, հակիրճ լինելու համար բաց կթողնենք «սովորական» բառը։

Օրինակներ դիֆերենցիալ հավասարումներ:

(1) ;

(3) ;

(4) ;

Հավասարումը (1) չորրորդ կարգի է, հավասարումը (2) երրորդ կարգի, (3) և (4) հավասարումները երկրորդ կարգի, հավասարումը (5) առաջին կարգի:

Դիֆերենցիալ հավասարում nՊարտադիր չէ, որ այդ կարգը պարունակի բացահայտ ֆունկցիա՝ նրա բոլոր ածանցյալները՝ առաջինից մինչև n-րդ կարգը և անկախ փոփոխականը: Այն չի կարող պարունակել որոշակի կարգերի բացահայտ ածանցյալներ, ֆունկցիաներ կամ անկախ փոփոխականներ:

Օրինակ, (1) հավասարման մեջ ակնհայտորեն չկան երրորդ և երկրորդ կարգի ածանցյալներ, ինչպես նաև ֆունկցիա. (2) հավասարման մեջ՝ երկրորդ կարգի ածանցյալը և ֆունկցիան. (4) հավասարման մեջ՝ անկախ փոփոխական; (5) հավասարման մեջ՝ ֆունկցիաներ. Միայն (3) հավասարումը պարունակում է բացահայտորեն բոլոր ածանցյալները, ֆունկցիան և անկախ փոփոխականը:

Դիֆերենցիալ հավասարման լուծում յուրաքանչյուր ֆունկցիա կոչվում է y = f(x), երբ փոխարինվում է հավասարման մեջ, այն վերածվում է ինքնության։

Դիֆերենցիալ հավասարման լուծում գտնելու գործընթացը կոչվում է իր ինտեգրում.

Օրինակ 1.Գտե՛ք դիֆերենցիալ հավասարման լուծումը:

Լուծում. Եկեք այս հավասարումը գրենք ձևով. Լուծումը ֆունկցիան իր ածանցյալից գտնելն է: Սկզբնական ֆունկցիան, ինչպես հայտնի է ինտեգրալ հաշվարկից, հակաածանցյալ է, այսինքն.

Սա այն է այս դիֆերենցիալ հավասարման լուծումը . Փոխվում է դրա մեջ Գ, մենք կստանանք տարբեր լուծումներ։ Մենք պարզեցինք, որ կան անսահման թվով լուծումներ առաջին կարգի դիֆերենցիալ հավասարման համար:

Դիֆերենցիալ հավասարման ընդհանուր լուծում nրդ կարգը դրա լուծումն է, որը հստակ արտահայտված է անհայտ ֆունկցիայի նկատմամբ և պարունակում է nանկախ կամայական հաստատուններ, այսինքն.

Օրինակ 1-ի դիֆերենցիալ հավասարման լուծումը ընդհանուր է:

Դիֆերենցիալ հավասարման մասնակի լուծում կոչվում է լուծում, որում կամայական հաստատուններին տրվում են հատուկ թվային արժեքներ:

Օրինակ 2.Գտե՛ք դիֆերենցիալ հավասարման ընդհանուր լուծումը և կոնկրետ լուծումը .

Լուծում. Եկեք ինտեգրենք հավասարման երկու կողմերը մի քանի անգամ, որոնք հավասար են դիֆերենցիալ հավասարման կարգին:

,

.

Արդյունքում ստացանք ընդհանուր լուծում.

տրված երրորդ կարգի դիֆերենցիալ հավասարման։

Հիմա եկեք կոնկրետ լուծում գտնենք նշված պայմաններում: Դա անելու համար փոխարինեք դրանց արժեքները կամայական գործակիցների փոխարեն և ստացեք

.

Եթե, բացի դիֆերենցիալ հավասարումից, սկզբնական պայմանը տրված է ձևով, ապա այդպիսի խնդիր կոչվում է. Կոշի խնդիր . Փոխարինեք արժեքները և հավասարման ընդհանուր լուծման մեջ և գտեք կամայական հաստատունի արժեքը Գ, և այնուհետև գտնված արժեքի հավասարման որոշակի լուծում Գ. Սա է Քոշիի խնդրի լուծումը։

Օրինակ 3.Լուծե՛ք Քոշիի խնդիրը օրինակ 1-ի դիֆերենցիալ հավասարման համար, առարկայից մինչև .

Լուծում. Եկեք փոխարինենք արժեքները սկզբնական վիճակից ընդհանուր լուծման մեջ y = 3, x= 1. Մենք ստանում ենք

Մենք գրում ենք Քոշիի խնդրի լուծումը այս առաջին կարգի դիֆերենցիալ հավասարման համար.

Դիֆերենցիալ հավասարումների լուծումը, նույնիսկ ամենապարզը, պահանջում է լավ ինտեգրման և ածանցյալ հմտություններ, ներառյալ բարդ ֆունկցիաները: Սա կարելի է տեսնել հետևյալ օրինակում.

Օրինակ 4.Գտե՛ք դիֆերենցիալ հավասարման ընդհանուր լուծումը:

Լուծում. Հավասարումը գրված է այնպես, որ դուք կարող եք անմիջապես ինտեգրել երկու կողմերը:

.

Մենք կիրառում ենք փոփոխականի փոփոխությամբ ինտեգրման մեթոդը (փոխարինում): Թող այդպես լինի:

Պահանջվում է վերցնել dxիսկ հիմա՝ ուշադրություն, մենք դա անում ենք ըստ բարդ ֆունկցիայի տարբերակման կանոնների, քանի որ xև կա բարդ գործառույթ («խնձոր» - քաղվածք քառակուսի արմատկամ, ինչ է նույնը, «մեկ կեսը», իսկ «աղացած միսը» իշխանության բարձրացումը հենց արմատի տակ արտահայտված արտահայտությունն է).

Մենք գտնում ենք ինտեգրալը.

Վերադառնալով փոփոխականին x, ստանում ենք.

.

Սա առաջին աստիճանի այս դիֆերենցիալ հավասարման ընդհանուր լուծումն է:

Դիֆերենցիալ հավասարումներ լուծելու համար կպահանջվեն ոչ միայն բարձրագույն մաթեմատիկայի նախորդ բաժինների, այլ նաև տարրական, այսինքն՝ դպրոցական մաթեմատիկայի հմտություններ: Ինչպես արդեն նշվեց, ցանկացած կարգի դիֆերենցիալ հավասարման մեջ չի կարող լինել անկախ փոփոխական, այսինքն՝ փոփոխական x. Այս խնդիրը լուծելու համար կօգնեն դպրոցից չմոռացված (սակայն, կախված նրանից, թե ով) գիտելիքները դպրոցից: Սա հաջորդ օրինակն է։

Դիֆերենցիալ հավասարումներ (DE): Այս երկու բառերը սովորաբար սարսափեցնում են սովորական մարդուն: Դիֆերենցիալ հավասարումները շատ ուսանողների համար կարծես արգելող և դժվար յուրացվող բան են: Uuuuuu... դիֆերենցիալ հավասարումներ, ինչպե՞ս կարող եմ գոյատևել այս ամենը?!

Այս կարծիքն ու այս վերաբերմունքը սկզբունքորեն սխալ է, քանի որ իրականում ԴԻՖԵՐԵՆՑԻԱԼ ՀԱՎԱՍԱՐՈՒՄՆԵՐ - ՊԱՐԶ Է ԵՎ ՆՈՒՅՆԻՍԿ Զվարճալի. Ի՞նչ պետք է իմանաք և կարողանաք անել, որպեսզի սովորեք, թե ինչպես լուծել դիֆերենցիալ հավասարումներ: Դիֆուզները հաջողությամբ ուսումնասիրելու համար դուք պետք է լավ լինեք ինտեգրվելու և տարբերելու մեջ: Որքան լավ են ուսումնասիրված թեմաները Մեկ փոփոխականի ֆունկցիայի ածանցյալԵվ Անորոշ ինտեգրալ, այնքան հեշտ կլինի հասկանալ դիֆերենցիալ հավասարումները։ Ասեմ ավելին, եթե ունես քիչ թե շատ պատշաճ ինտեգրացիոն հմտություններ, ուրեմն թեման համարյա յուրացված է։ Որքան ավելի շատ ինտեգրալներ տարբեր տեսակներդուք գիտեք, թե ինչպես որոշել, այնքան լավ: Ինչո՞ւ։ Քանի որ դուք ստիպված կլինեք շատ ինտեգրվել: Եվ տարբերակել. Նաև խիստ խորհուրդ են տալիսսովորել գտնել անուղղակիորեն նշված ֆունկցիայի ածանցյալ.

Դեպքերի 95%-ում ներս թեստերԱռաջին կարգի դիֆերենցիալ հավասարումների 3 տեսակ կա՝ բաժանելի փոփոխականներով հավասարումներ, որոնց կանդրադառնանք այս դասում; միատարր հավասարումներԵվ գծային անհամասեռ հավասարումներ. Նրանց համար, ովքեր սկսում են ուսումնասիրել դիֆուզերները, խորհուրդ եմ տալիս կարդալ դասերը այս հերթականությամբ: Կան նույնիսկ ավելի հազվադեպ դիֆերենցիալ հավասարումների տեսակներ. հավասարումներ ընդհանուր դիֆերենցիալներում, Բեռնուլիի հավասարումներև մի քանի ուրիշներ: Վերջին երկու տեսակներից ամենակարևորը հավասարումներ են ընդհանուր դիֆերենցիալներում, քանի որ բացի այս դիֆերենցիալ հավասարումից ես համարում եմ. նոր նյութ- մասնավոր ինտեգրում.

Նախ, եկեք հիշենք սովորական հավասարումները. Դրանք պարունակում են փոփոխականներ և թվեր։ Ամենապարզ օրինակը: Ի՞նչ է նշանակում լուծել սովորական հավասարումը: Սա նշանակում է գտնել թվերի հավաքածու, որոնք բավարարում են այս հավասարումը։ Հեշտ է նկատել, որ երեխաների հավասարումը ունի մեկ արմատ. Պարզապես զվարճանալու համար եկեք ստուգենք և փոխարինենք գտնված արմատը մեր հավասարման մեջ.

– ստացվել է ճիշտ հավասարություն, ինչը նշանակում է, որ լուծումը ճիշտ է գտնվել։

Դիֆուզորները նախագծված են մոտավորապես նույն ձևով:

Դիֆերենցիալ հավասարում առաջին կարգը, պարունակում է:
1) անկախ փոփոխական;
2) կախյալ փոփոխական (գործառույթ);
3) ֆունկցիայի առաջին ածանցյալը՝ .

Որոշ դեպքերում առաջին կարգի հավասարումը կարող է բացակայել «x» և/կամ «y»-ից. կարևորգնալ կառավարման սենյակ էրառաջին ածանցյալ, և չկարավելի բարձր կարգի ածանցյալներ – , և այլն:

Ի՞նչ է դա նշանակում։Դիֆերենցիալ հավասարման լուծումը նշանակում է գտնել բազմաթիվ գործառույթներ, որոնք բավարարում են այս հավասարումը։ Գործառույթների այս հավաքածուն կոչվում է դիֆերենցիալ հավասարման ընդհանուր լուծում.

Օրինակ 1

Լուծել դիֆերենցիալ հավասարումը

Ամբողջական զինամթերք. Որտեղի՞ց սկսել լուծել առաջին կարգի դիֆերենցիալ հավասարումը:

Առաջին հերթին, դուք պետք է վերագրեք ածանցյալը մի փոքր այլ ձևով: Եկեք հիշենք ածանցյալի ծանր նշումը. Ածանցյալի այս նշանակումը, հավանաբար, ձեզանից շատերին թվացել է ծիծաղելի և անհարկի, բայց դա այն է, ինչ կանոնակարգում է դիֆուզերներում:

Այսպիսով, առաջին փուլում մենք վերագրում ենք ածանցյալը մեզ անհրաժեշտ ձևով.

Երկրորդ փուլում Միշտտեսնենք, թե դա հնարավոր է առանձին փոփոխականներ?Ի՞նչ է նշանակում տարանջատել փոփոխականները: Կոպիտ ասած. ձախ կողմումմենք պետք է հեռանանք միայն «հույներ», Ա աջ կողմումկազմակերպել միայն «X». Փոփոխականների բաժանումն իրականացվում է «դպրոցական» մանիպուլյացիաների միջոցով՝ դրանք փակագծերից դուրս դնելը, նշանի փոփոխությամբ տերմինները մասից մաս փոխանցելը, համամասնության կանոնի համաձայն գործոնների մասից մաս փոխանցելը և այլն։

Դիֆերենցիալները և լիարժեք բազմապատկիչներ են և ռազմական գործողությունների ակտիվ մասնակիցներ: Քննարկվող օրինակում փոփոխականները հեշտությամբ տարանջատվում են՝ շեղելով գործոնները՝ համաձայն համամասնության կանոնի.

Փոփոխականները առանձնացված են: Ձախ կողմում կան միայն «Y», աջ կողմում՝ միայն «X»:

Հաջորդ փուլն է դիֆերենցիալ հավասարման ինտեգրում. Դա պարզ է, մենք ինտեգրալներ ենք դնում երկու կողմերում.

Իհարկե, պետք է ինտեգրալներ վերցնել։ IN այս դեպքումդրանք աղյուսակային են՝

Ինչպես հիշում ենք, ցանկացած հակաածանցյալին վերագրվում է հաստատուն: Այստեղ երկու ինտեգրալ կա, բայց հաստատունը բավական է մեկ անգամ գրել։ Այն գրեթե միշտ նշանակվում է աջ կողմում:

Խստորեն ասած, ինտեգրալները վերցնելուց հետո դիֆերենցիալ հավասարումը համարվում է լուծված։ Միակ բանը, որ մեր «y»-ը «x»-ով չի արտահայտվում, այսինքն՝ լուծումը ներկայացված է անուղղակիորենձևը. Դիֆերենցիալ հավասարման անուղղակի ձևով լուծումը կոչվում է դիֆերենցիալ հավասարման ընդհանուր ինտեգրալ. Այսինքն՝ սա ընդհանուր ինտեգրալ է։

Այժմ մենք պետք է փորձենք գտնել ընդհանուր լուծում, այսինքն՝ փորձենք հստակ ներկայացնել ֆունկցիան։

Խնդրում ենք հիշել առաջին տեխնիկան, այն շատ տարածված է և հաճախ օգտագործվում է գործնական առաջադրանքներում: Երբ ինտեգրումից հետո լոգարիթմը հայտնվում է աջ կողմում, գրեթե միշտ ցանկալի է հաստատունը գրել նաև լոգարիթմի տակ:

Այսինքն՝ փոխարենգրառումները սովորաբար գրվում են .

Այստեղ դա նույն լիարժեք հաստատունն է, ինչ . Ինչու է դա անհրաժեշտ: Եվ որպեսզի ավելի հեշտ լինի արտահայտել «խաղը»: Մենք օգտագործում ենք լոգարիթմների դպրոցական հատկությունը. . Այս դեպքում.

Այժմ լոգարիթմներն ու մոդուլները կարող են օգտագործվել մաքուր խիղճհեռացնել երկու մասից.

Ֆունկցիան հստակորեն ներկայացված է. Սա է ընդհանուր լուծումը։

Շատ առանձնահատկություններ դիֆերենցիալ հավասարման ընդհանուր լուծումն է:

Տալով հաստատուն տարբեր իմաստներ, դուք կարող եք ստանալ անսահման շատ մասնավոր լուծումներդիֆերենցիալ հավասարում. Գործառույթներից որևէ մեկը և այլն: կբավարարի դիֆերենցիալ հավասարումը.

Երբեմն ընդհանուր լուծումը կոչվում է գործառույթների ընտանիք. IN այս օրինակումընդհանուր լուծում գծային ֆունկցիաների ընտանիք է, ավելի ճիշտ՝ ուղիղ համեմատականության ընտանիք։

Շատ դիֆերենցիալ հավասարումներ բավականին հեշտ է փորձարկել: Սա արվում է շատ պարզ, վերցնում ենք գտնված լուծումը և գտնում ածանցյալը.

Մենք մեր լուծումը և գտնված ածանցյալը փոխարինում ենք սկզբնական հավասարման մեջ.

– ստացվել է ճիշտ հավասարություն, ինչը նշանակում է, որ լուծումը ճիշտ է գտնվել։ Այսինքն, ընդհանուր լուծումը բավարարում է հավասարումը։

Առաջին օրինակի մանրակրկիտ վերանայումից հետո տեղին է պատասխանել դիֆերենցիալ հավասարումների վերաբերյալ մի քանի միամիտ հարցերի:

1)Այս օրինակում մենք կարողացանք առանձնացնել փոփոխականները. Կարո՞ղ է դա միշտ անել:Ոչ, ոչ միշտ: Եվ նույնիսկ ավելի հաճախ, փոփոխականները չեն կարող առանձնացվել: Օրինակ՝ մեջ միատարր առաջին կարգի հավասարումներ, նախ պետք է փոխարինել այն։ Այլ տեսակի հավասարումների դեպքում, օրինակ. գծային անհամասեռ առաջին կարգի հավասարման մեջ, պետք է օգտագործել տարբեր տեխնիկաև ընդհանուր լուծում գտնելու մեթոդները: Բաժանելի փոփոխականներով հավասարումները, որոնք մենք դիտարկում ենք առաջին դասում, դիֆերենցիալ հավասարումների ամենապարզ տեսակն են։

2) Միշտ հնարավո՞ր է ինտեգրել դիֆերենցիալ հավասարումը:Ոչ, ոչ միշտ: Շատ հեշտ է ստեղծել «շքեղ» հավասարում, որը չի կարող ինտեգրվել, բացի այդ, կան ինտեգրալներ, որոնք չեն կարող ընդունվել. Բայց նման DE-ները կարող են լուծվել մոտավորապես հատուկ մեթոդների կիրառմամբ: D'Alembert և Cauchy երաշխիք. ...ու, lurkmore.ru Ես հենց հիմա շատ եմ կարդացել:

3) Այս օրինակում մենք լուծում ստացանք ընդհանուր ինտեգրալի տեսքով . Միշտ հնարավո՞ր է ընդհանուր ինտեգրալից ընդհանուր լուծում գտնել, այսինքն՝ «y»-ը բացահայտ արտահայտել։Ոչ, ոչ միշտ: Օրինակ՝. Դե, ինչպե՞ս կարելի է այստեղ «հունարեն» արտահայտել։ Նման դեպքերում պատասխանը պետք է գրել որպես ընդհանուր ինտեգրալ։ Բացի այդ, երբեմն կարելի է ընդհանուր լուծում գտնել, բայց գրված է այնքան ծանր ու անշնորհք, որ ավելի լավ է պատասխանը թողնել ընդհանուր ինտեգրալի տեսքով.

Մենք չենք շտապի: Մեկ այլ պարզ հեռակառավարման վահանակ և մեկ այլ բնորոշ լուծում:

Օրինակ 2

Գտեք դիֆերենցիալ հավասարման որոշակի լուծում, որը բավարարում է նախնական պայմանը

Ըստ պայմանի՝ պետք է գտնել մասնավոր լուծում DE-ն բավարարում է նախնական պայմանը: Հարցի այս ձեւակերպումը նույնպես կոչվում է Կոշի խնդիր.

Նախ մենք ընդհանուր լուծում ենք գտնում. Հավասարման մեջ «x» փոփոխական չկա, բայց դա չպետք է շփոթի, գլխավորն այն է, որ այն ունի առաջին ածանցյալը:

Մենք վերագրում ենք ածանցյալը ճիշտ ձևով:

Ակնհայտ է, որ փոփոխականները կարելի է առանձնացնել՝ տղաները դեպի ձախ, աղջիկները՝ աջ.

Եկեք ինտեգրենք հավասարումը.

Ստացվում է ընդհանուր ինտեգրալը։ Այստեղ ես աստղանիշով գծել եմ հաստատուն, փաստն այն է, որ շատ շուտով այն կվերածվի մեկ այլ հաստատունի։

Այժմ մենք փորձում ենք ընդհանուր ինտեգրալը վերափոխել ընդհանուր լուծման (ուղղակի արտահայտեք «y»): Եկեք հիշենք հին լավ բաները դպրոցից. . Այս դեպքում.

Ցուցանիշի հաստատունը ինչ-որ կերպ անկոշեր է թվում, ուստի այն սովորաբար իջնում ​​է երկրի վրա: Մանրամասն՝ այսպես է լինում. Օգտագործելով աստիճանների հատկությունը՝ մենք ֆունկցիան վերագրում ենք հետևյալ կերպ.

Եթե ​​հաստատուն է, ապա կա նաև որոշակի հաստատուն, որը մենք նշում ենք տառով.

Հիշեք հաստատունի «վարումը», սա երկրորդ տեխնիկան է, որը հաճախ օգտագործվում է դիֆերենցիալ հավասարումներ լուծելիս:

Այսպիսով, ընդհանուր լուծումը հետևյալն է. Սա էքսպոնենցիալ ֆունկցիաների գեղեցիկ ընտանիք է:

Վերջնական փուլում դուք պետք է գտնեք որոշակի լուծում, որը բավարարում է տվյալ նախնական պայմանը։ Սա նույնպես պարզ է.

Ո՞րն է առաջադրանքը։ Պետք է վերցնել այդպիսինհաստատունի արժեքը, որպեսզի նշված սկզբնական պայմանը բավարարվի:

Այն կարող է ֆորմատավորվել տարբեր ձևերով, բայց սա, հավանաբար, կլինի ամենահստակ ճանապարհը: Ընդհանուր լուծման մեջ «X»-ի փոխարեն մենք փոխարինում ենք զրո, իսկ «Y»-ի փոխարեն՝ երկու.



Այսինքն՝

Ստանդարտ դիզայնի տարբերակ.

Մենք հաստատունի գտած արժեքը փոխարինում ենք ընդհանուր լուծման մեջ.
- սա այն կոնկրետ լուծումն է, որը մեզ անհրաժեշտ է:

Եկեք ստուգենք. Մասնավոր լուծման ստուգումը ներառում է երկու փուլ.

Նախ անհրաժեշտ է ստուգել, ​​թե արդյոք հայտնաբերված լուծումը իսկապես բավարարում է նախնական պայմանը: «X»-ի փոխարեն մենք փոխարինում ենք զրո և տեսնում ենք, թե ինչ է տեղի ունենում.
-Այո, իսկապես, ստացվել է երկու, ինչը նշանակում է, որ նախնական պայմանը բավարարված է։

Երկրորդ փուլն արդեն ծանոթ է. Մենք վերցնում ենք ստացված կոնկրետ լուծումը և գտնում ենք ածանցյալը.

Մենք փոխարինում ենք սկզբնական հավասարման մեջ.

– ստացվել է ճիշտ հավասարություն:

Եզրակացություն. կոնկրետ լուծումը ճիշտ է գտնվել:

Անցնենք ավելի բովանդակալից օրինակների։

Օրինակ 3

Լուծել դիֆերենցիալ հավասարումը

Լուծում:Մենք վերագրում ենք ածանցյալը մեզ անհրաժեշտ ձևով.

Մենք գնահատում ենք՝ հնարավո՞ր է տարանջատել փոփոխականները։ Կարող է. Երկրորդ տերմինը նշանի փոփոխությամբ տեղափոխում ենք աջ կողմ.

Եվ մենք բազմապատկիչները փոխանցում ենք համամասնության կանոնի համաձայն.

Փոփոխականները առանձնացված են, եկեք ինտեգրենք երկու մասերը.

Պետք է զգուշացնեմ, մոտենում է դատաստանի օրը։ Եթե ​​լավ չեք սովորել անորոշ ինտեգրալներ, լուծել են մի քանի օրինակներ, ապա գնալու տեղ չկա, դուք ստիպված կլինեք տիրապետել դրանք հիմա:

Ձախ կողմի ինտեգրալը հեշտ է գտնել Ինտեգրում եռանկյունաչափական ֆունկցիաներ անցյալ տարի:

Աջ կողմում մենք ունենք լոգարիթմ, ըստ իմ առաջին տեխնիկական առաջարկության, այս դեպքում հաստատունը նույնպես պետք է գրվի լոգարիթմի տակ։

Այժմ մենք փորձում ենք պարզեցնել ընդհանուր ինտեգրալը։ Քանի որ մենք ունենք միայն լոգարիթմներ, դրանցից ազատվելը միանգամայն հնարավոր է (և անհրաժեշտ): Մենք հնարավորինս «փաթեթավորում» ենք լոգարիթմները: Փաթեթավորումն իրականացվում է օգտագործելով երեք հատկություններ.

Խնդրում ենք վերաշարադրել այս երեք բանաձևերը ձեր մեջ աշխատանքային գրքույկ, դիֆուզորներ լուծելիս դրանք շատ հաճախ են օգտագործվում։

Ես մանրամասն նկարագրելու եմ լուծումը.

Փաթեթավորումն ավարտված է, հեռացրեք լոգարիթմները.

Հնարավո՞ր է «խաղ» արտահայտել: Կարող է. Անհրաժեշտ է երկու մասերը քառակուսի դնել։ Բայց ձեզ հարկավոր չէ դա անել:

Երրորդ տեխնիկական խորհրդատվություն: Եթե ​​ընդհանուր լուծում ստանալու համար անհրաժեշտ է բարձրանալ իշխանության կամ արմատավորվել, ապա շատ դեպքերումպետք է ձեռնպահ մնալ այս գործողություններից և պատասխանը թողնել ընդհանուր ինտեգրալի տեսքով։ Փաստն այն է, որ ընդհանուր լուծումը հավակնոտ և սարսափելի տեսք կունենա՝ մեծ արմատներով, նշաններով:

Ուստի պատասխանը գրում ենք ընդհանուր ինտեգրալի տեսքով։ Լավ ձևովՀամարվում է, որ այն ներկայացնում է ընդհանուր ինտեգրալը ձևով, այսինքն՝ աջ կողմում, հնարավորության դեպքում, թողնում է միայն հաստատուն։ Դա անելը պարտադիր չէ, բայց պրոֆեսորին հաճոյանալը միշտ էլ ձեռնտու է ;-)

Պատասխան.ընդհանուր ինտեգրալ:

Նշում.Ցանկացած հավասարման ընդհանուր ինտեգրալը կարելի է գրել մեկից ավելի ձևերով։ Այսպիսով, եթե ձեր արդյունքը չի համընկնում նախկինում հայտնի պատասխանի հետ, դա չի նշանակում, որ դուք սխալ եք լուծել հավասարումը:

Ընդհանուր ինտեգրալը նույնպես բավականին հեշտ է ստուգել, ​​գլխավորը գտնել կարողանալն է անուղղակիորեն նշված ֆունկցիայի ածանցյալները. Տարբերակենք պատասխանը.

Մենք երկու տերմիններն էլ բազմապատկում ենք հետևյալով.

Եվ բաժանեք հետևյալի վրա.

Բնօրինակ դիֆերենցիալ հավասարումը ստացվել է ճշգրիտ, ինչը նշանակում է, որ ընդհանուր ինտեգրալը ճիշտ է գտնվել։

Օրինակ 4

Գտեք դիֆերենցիալ հավասարման որոշակի լուծում, որը բավարարում է նախնական պայմանը: Կատարել ստուգում.

Սա օրինակ է անկախ որոշում. Հիշեցնեմ, որ Քոշիի խնդիրը բաղկացած է երկու փուլից.
1) Ընդհանուր լուծում գտնելը.
2) Որոշակի լուծում գտնելը.

Ստուգումն իրականացվում է նաև երկու փուլով (տես նաև Օրինակ 2), անհրաժեշտ է.
1) Համոզվեք, որ հայտնաբերված կոնկրետ լուծումը իսկապես բավարարում է նախնական պայմանը:
2) Ստուգեք, որ կոնկրետ լուծումը ընդհանուր առմամբ բավարարում է դիֆերենցիալ հավասարումը:

Ամբողջական լուծում և պատասխան դասի վերջում։

Օրինակ 5

Գտեք դիֆերենցիալ հավասարման որոշակի լուծում , բավարարելով նախնական պայմանը։ Կատարել ստուգում.

Լուծում:Նախ, եկեք գտնենք ընդհանուր լուծում Այս հավասարումն արդեն պարունակում է պատրաստի դիֆերենցիալներ, ինչը նշանակում է, որ լուծումը պարզեցված է: Մենք առանձնացնում ենք փոփոխականները.

Եկեք ինտեգրենք հավասարումը.

Ձախից ինտեգրալը աղյուսակային է, աջում՝ վերցված ինտեգրալը ֆունկցիան դիֆերենցիալ նշանի տակ ներառելու մեթոդ:

Ընդհանուր ինտեգրալը ստացվել է, հնարավո՞ր է հաջողությամբ արտահայտել ընդհանուր լուծումը։ Կարող է. Մենք կախում ենք լոգարիթմներ.

(Հուսով եմ բոլորը հասկանում են վերափոխումը, նման բաներն արդեն պետք է հայտնի լինեն)

Այսպիսով, ընդհանուր լուծումը հետևյալն է.

Գտնենք տվյալ սկզբնական պայմանին համապատասխան կոնկրետ լուծում։ Ընդհանուր լուծման մեջ «X»-ի փոխարեն մենք փոխարինում ենք զրո, իսկ «Y»-ի փոխարեն՝ երկուսի լոգարիթմը.

Ավելի ծանոթ դիզայն.

Մենք հաստատունի գտնված արժեքը փոխարինում ենք ընդհանուր լուծման մեջ:

Պատասխան.մասնավոր լուծում.

Ստուգում. Նախ, եկեք ստուգենք, արդյոք նախնական պայմանը բավարարված է.
-Ամեն ինչ բզզում է:

Հիմա եկեք ստուգենք, թե արդյոք հայտնաբերված կոնկրետ լուծումն ընդհանրապես բավարարում է դիֆերենցիալ հավասարումը: Գտնել ածանցյալը.

Դիտարկենք սկզբնական հավասարումը. - այն ներկայացված է դիֆերենցիալներով: Ստուգելու երկու եղանակ կա. Գտնված ածանցյալից կարելի է արտահայտել դիֆերենցիալը.

Գտնված կոնկրետ լուծումը և ստացված դիֆերենցիալը փոխարինենք սկզբնական հավասարմամբ :

Մենք օգտագործում ենք հիմնական լոգարիթմական ինքնությունը.

Ստացվում է ճիշտ հավասարություն, ինչը նշանակում է, որ կոնկրետ լուծումը ճիշտ է գտնվել։

Ստուգման երկրորդ մեթոդը հայելային է և ավելի ծանոթ՝ հավասարումից Եկեք արտահայտենք ածանցյալը, դա անելու համար մենք բոլոր կտորները բաժանում ենք հետևյալի.

Եվ փոխակերպված DE-ի մեջ մենք փոխարինում ենք ստացված մասնակի լուծումը և գտնված ածանցյալը։ Պարզեցումների արդյունքում պետք է ստացվի նաև ճիշտ հավասարություն։

Օրինակ 6

Լուծել դիֆերենցիալ հավասարումը. Պատասխանը ներկայացրու ընդհանուր ինտեգրալի տեսքով.

Սա ձեզ համար ինքնուրույն լուծելու օրինակ է, ամբողջական լուծում և պատասխանեք դասի վերջում։

Ի՞նչ դժվարություններ են սպասվում տարանջատելի փոփոխականներով դիֆերենցիալ հավասարումներ լուծելիս:

1) Միշտ չէ, որ ակնհայտ է (հատկապես թեյնիկի համար), որ փոփոխականները կարելի է առանձնացնել: Եկեք դիտարկենք պայմանական օրինակ: Այստեղ պետք է փակագծերից հանել գործոնները և առանձնացնել արմատները՝ . Պարզ է, թե ինչ պետք է անել հաջորդը:

2) Ինտեգրման հետ կապված դժվարություններ: Ինտեգրալները հաճախ ամենապարզը չեն, և եթե կան թերություններ գտնելու հմտություններում անորոշ ինտեգրալ, ապա շատ դիֆուզորների հետ դժվար կլինի։ Բացի այդ, «քանի որ դիֆերենցիալ հավասարումը պարզ է, ուրեմն թող ինտեգրալներն ավելի բարդ լինեն» տրամաբանությունը տարածված է հավաքածուների և ուսումնական ձեռնարկների կազմողների շրջանում:

3) փոխակերպումներ հաստատունով. Ինչպես բոլորն են նկատել, դիֆերենցիալ հավասարումների մեջ հաստատունով կարող եք գրեթե ամեն ինչ անել: Իսկ նման փոխակերպումները միշտ չէ, որ հասկանալի են սկսնակին։ Դիտարկենք մեկ այլ պայմանական օրինակ. . Ցանկալի է բոլոր տերմինները բազմապատկել 2-ով. . Ստացված հաստատունը նաև որոշակի հաստատուն է, որը կարելի է նշանակել հետևյալով. . Այո, և քանի որ աջ կողմում կա լոգարիթմ, ապա նպատակահարմար է հաստատունը վերագրել մեկ այլ հաստատունի տեսքով. .

Դժբախտությունն այն է, որ նրանք հաճախ չեն անհանգստանում ինդեքսներով և օգտագործում են նույն տառը: Եվ արդյունքում լուծման գրառումը ստանում է հետևյալ ձևը.

Սա ի՞նչ դժոխք է։ Կան նաև սխալներ. Ֆորմալ առումով՝ այո։ Բայց ոչ պաշտոնական - սխալ չկա, հասկանալի է, որ հաստատունը փոխարկելիս դեռևս ստացվում է որևէ այլ հաստատուն:

Կամ այս օրինակը, ենթադրենք, որ հավասարումը լուծելու ընթացքում ստացվում է ընդհանուր ինտեգրալ։ Այս պատասխանը տգեղ է թվում, ուստի խորհուրդ է տրվում փոխել բոլոր գործոնների նշանները. . Ձեւականորեն, ձայնագրության համաձայն, կրկին սխալ կա, այն պետք է գրվեր։ Բայց ոչ պաշտոնական հասկացվում է, որ դա դեռևս ինչ-որ այլ հաստատուն է (ավելին, այն կարող է ցանկացած արժեք վերցնել), ուստի հաստատունի նշանը փոխելն իմաստ չունի, և դուք կարող եք օգտագործել նույն տառը:

Ես կփորձեմ խուսափել անզգույշ մոտեցումից, և դեռ դնում եմ տարբեր ցուցանիշներդրանք փոխարկելիս:

Օրինակ 7

Լուծել դիֆերենցիալ հավասարումը. Կատարել ստուգում.

Լուծում:Այս հավասարումը թույլ է տալիս տարանջատել փոփոխականները: Մենք առանձնացնում ենք փոփոխականները.

Եկեք ինտեգրենք.

Այստեղ հաստատունը որպես լոգարիթմ սահմանել պետք չէ, քանի որ դրանից ոչ մի օգտակար բան չի ստացվի։

Պատասխան.ընդհանուր ինտեգրալ:

Ստուգեք՝ տարբերակեք պատասխանը (ներկայացված ֆունկցիա).

Մենք ազատվում ենք կոտորակներից՝ երկու անդամները բազմապատկելով հետևյալով.

Ստացված է սկզբնական դիֆերենցիալ հավասարումը, ինչը նշանակում է, որ ընդհանուր ինտեգրալը ճիշտ է գտնվել։

Օրինակ 8

Գտեք DE-ի որոշակի լուծում:
,

Սա ձեզ համար օրինակ է ինքնուրույն լուծելու համար։ Միակ մեկնաբանությունն այն է, որ այստեղ դուք ստանում եք ընդհանուր ինտեգրալ, և, ավելի ճիշտ ասած, պետք է հնարել ոչ թե կոնկրետ լուծում գտնելու համար, այլ. մասնակի ինտեգրալ. Ամբողջական լուծում և պատասխան դասի վերջում։

Ինչպես արդեն նշվեց, տարանջատելի փոփոխականներով դիֆուզներում հաճախ առաջանում են ոչ ամենապարզ ինտեգրալները: Եվ ահա ևս մի քանի նման օրինակ, որպեսզի դուք ինքնուրույն լուծեք: Բոլորին խորհուրդ եմ տալիս լուծել թիվ 9-10 օրինակները՝ անկախ պատրաստվածության մակարդակից, դա թույլ կտա թարմացնել ինտեգրալներ գտնելու իրենց հմտությունները կամ լրացնել գիտելիքների բացերը։

Օրինակ 9

Լուծել դիֆերենցիալ հավասարումը

Օրինակ 10

Լուծել դիֆերենցիալ հավասարումը

Հիշեք, որ ընդհանուր ինտեգրալ գրելու մեկից ավելի եղանակ կա, և ձեր պատասխանները կարող են տարբեր տեսք ունենալ: տեսքըիմ պատասխանները. Համառոտ լուծում և պատասխաններ դասի վերջում:

Ուրախ առաջխաղացում:

Օրինակ 4:Լուծում: Եկեք ընդհանուր լուծում գտնենք. Մենք առանձնացնում ենք փոփոխականները.


Եկեք ինտեգրենք.



Ընդհանուր ինտեգրալը ստացվել է, մենք փորձում ենք այն պարզեցնել։ Եկեք փաթեթավորենք լոգարիթմները և ազատվենք դրանցից.

I. Սովորական դիֆերենցիալ հավասարումներ

1.1. Հիմնական հասկացություններ և սահմանումներ

Դիֆերենցիալ հավասարումը հավասարում է, որը կապված է անկախ փոփոխականի հետ x, պահանջվող ֆունկցիան yև դրա ածանցյալները կամ դիֆերենցիալները:

Խորհրդանշականորեն դիֆերենցիալ հավասարումը գրված է հետևյալ կերպ.

F(x,y,y")=0, F(x,y,y")=0, F(x,y,y",y",.., y (n))=0

Դիֆերենցիալ հավասարումը կոչվում է սովորական, եթե պահանջվող ֆունկցիան կախված է մեկ անկախ փոփոխականից:

Դիֆերենցիալ հավասարման լուծումկոչվում է ֆունկցիա, որը այս հավասարումը վերածում է ինքնության:

Դիֆերենցիալ հավասարման կարգըայս հավասարման մեջ ներառված ամենաբարձր ածանցյալի կարգն է

Օրինակներ.

1. Դիտարկենք առաջին կարգի դիֆերենցիալ հավասարումը

Այս հավասարման լուծումը y = 5 ln x ֆունկցիան է: Իրոք, փոխարինող y"հավասարման մեջ մենք ստանում ենք ինքնությունը:

Եվ սա նշանակում է, որ y = 5 ln x– ֆունկցիան այս դիֆերենցիալ հավասարման լուծումն է:

2. Դիտարկենք երկրորդ կարգի դիֆերենցիալ հավասարումը y" - 5y" +6y = 0. Ֆունկցիան այս հավասարման լուծումն է։

Իսկապես, .

Փոխարինելով այս արտահայտությունները հավասարման մեջ՝ ստանում ենք.

Եվ սա նշանակում է, որ ֆունկցիան այս դիֆերենցիալ հավասարման լուծումն է։

Դիֆերենցիալ հավասարումների ինտեգրումդիֆերենցիալ հավասարումների լուծումներ գտնելու գործընթացն է։

Դիֆերենցիալ հավասարման ընդհանուր լուծումկոչվում է ձևի ֆունկցիա , որը ներառում է այնքան անկախ կամայական հաստատուններ, որքան հավասարման կարգը։

Դիֆերենցիալ հավասարման մասնակի լուծումկամայական հաստատունների տարբեր թվային արժեքների ընդհանուր լուծումից ստացված լուծում է: Կամայական հաստատունների արժեքները հայտնաբերվում են փաստարկի և ֆունկցիայի որոշակի սկզբնական արժեքներում:

Դիֆերենցիալ հավասարման որոշակի լուծման գրաֆիկը կոչվում է ինտեգրալ կոր.

Օրինակներ

1. Գտեք առաջին կարգի դիֆերենցիալ հավասարման որոշակի լուծում

xdx + ydy = 0, Եթե y= 4 ժամը x = 3.

Լուծում. Ինտեգրելով հավասարման երկու կողմերը՝ մենք ստանում ենք

Մեկնաբանություն. Ինտեգրման արդյունքում ստացված կամայական C հաստատունը կարող է ներկայացվել հետագա փոխակերպումների համար հարմար ցանկացած ձևով։ Այս դեպքում, հաշվի առնելով շրջանագծի կանոնական հավասարումը, հարմար է C կամայական հաստատունը ներկայացնել .

- դիֆերենցիալ հավասարման ընդհանուր լուծում.

Նախնական պայմանները բավարարող հավասարման առանձնահատուկ լուծում y = 4 ժամը x = 3-ը գտնվել է ընդհանուրից՝ նախնական պայմանները փոխարինելով ընդհանուր լուծման մեջ. 3 2 + 4 2 = C 2; C=5.

Փոխարինելով C=5 ընդհանուր լուծման մեջ՝ ստանում ենք x 2 +y 2 = 5 2 .

Սա որոշակի լուծում է դիֆերենցիալ հավասարման, որը ստացվում է ընդհանուր լուծումից տվյալ սկզբնական պայմաններում:

2. Գտե՛ք դիֆերենցիալ հավասարման ընդհանուր լուծումը

Այս հավասարման լուծումը ձևի ցանկացած ֆունկցիա է, որտեղ C-ն կամայական հաստատուն է: Իրոք, փոխարինելով հավասարումների մեջ՝ մենք ստանում ենք՝ , .

Հետևաբար, այս դիֆերենցիալ հավասարումն ունի անսահման թվով լուծումներ, քանի որ C հաստատունի տարբեր արժեքների համար հավասարությունը որոշում է հավասարման տարբեր լուծումներ։

Օրինակ, ուղղակի փոխարինմամբ դուք կարող եք ստուգել, ​​որ գործառույթները հավասարման լուծումներ են։

Խնդիր, որի դեպքում պետք է գտնել հավասարման որոշակի լուծում y" = f(x,y)բավարարում է նախնական պայմանը y (x 0) = y 0, կոչվում է Կոշիի խնդիր։

Հավասարման լուծում y" = f(x,y)նախնական պայմանը բավարարող, y (x 0) = y 0, կոչվում է Քոշիի խնդրի լուծում։

Քոշիի խնդրի լուծումը պարզ երկրաչափական նշանակություն ունի. Իսկապես, ըստ այս սահմանումների, լուծեք Քոշիի խնդիրը y" = f(x,y)հաշվի առնելով, որ y (x 0) = y 0, նշանակում է գտնել հավասարման ինտեգրալ կորը y" = f(x,y)որն անցնում է այս կետը M 0 (x 0,y 0).

II. Առաջին կարգի դիֆերենցիալ հավասարումներ

2.1. Հիմնական հասկացություններ

Առաջին կարգի դիֆերենցիալ հավասարումը ձևի հավասարումն է F(x,y,y") = 0:

Առաջին կարգի դիֆերենցիալ հավասարումը ներառում է առաջին ածանցյալը և չի ներառում ավելի բարձր կարգի ածանցյալներ:

Հավասարում y" = f(x,y)կոչվում է ածանցյալի նկատմամբ լուծված առաջին կարգի հավասարում։

Առաջին կարգի դիֆերենցիալ հավասարման ընդհանուր լուծումը ձևի ֆունկցիա է, որը պարունակում է մեկ կամայական հաստատուն:

Օրինակ.Դիտարկենք առաջին կարգի դիֆերենցիալ հավասարումը:

Այս հավասարման լուծումը ֆունկցիան է։

Իսկապես, փոխարինելով այս հավասարումը իր արժեքով, մենք ստանում ենք

այսինքն 3x=3x

Հետևաբար, ֆունկցիան C ցանկացած հաստատունի հավասարման ընդհանուր լուծումն է։

Գտեք այս հավասարման որոշակի լուծում, որը բավարարում է նախնական պայմանը y(1)=1Նախնական պայմանների փոխարինում x = 1, y = 1հավասարման ընդհանուր լուծման մեջ մենք ստանում ենք, թե որտեղից C=0.

Այսպիսով, մենք ստանում ենք որոշակի լուծում ընդհանուրից՝ այս հավասարման մեջ փոխարինելով ստացված արժեքը C=0- մասնավոր լուծում.

2.2. Դիֆերենցիալ հավասարումներ՝ բաժանելի փոփոխականներով

Բաժանելի փոփոխականներով դիֆերենցիալ հավասարումը ձևի հավասարումն է. y"=f(x)g(y)կամ դիֆերենցիալների միջոցով, որտեղ f(x)Եվ g(y)- նշված գործառույթները:

Նրանց համար y, որի համար , հավասարումը y"=f(x)g(y)համարժեք է հավասարմանը, որում փոփոխականը yառկա է միայն ձախ կողմում, իսկ x փոփոխականը միայն աջ կողմում է: Ասում են՝ «հեղ. y"=f(x)g(yՏարանջատենք փոփոխականները»։

Ձևի հավասարումը կոչվում է տարանջատված փոփոխական հավասարում:

Հավասարման երկու կողմերի ինտեգրում Ըստ x, ստանում ենք G(y) = F(x) + Cհավասարման ընդհանուր լուծումն է, որտեղ G(y)Եվ F(x)– որոշ հակաածանցյալներ, համապատասխանաբար, ֆունկցիաների և f(x), Գկամայական հաստատուն.

Բաժանելի փոփոխականներով առաջին կարգի դիֆերենցիալ հավասարման լուծման ալգորիթմ

Օրինակ 1

Լուծե՛ք հավասարումը y» = xy

Լուծում. Ֆունկցիայի ածանցյալ y"փոխարինել այն

եկեք առանձնացնենք փոփոխականները

Եկեք ինտեգրենք հավասարության երկու կողմերը.

Օրինակ 2

2 տարեկան» = 1- 3x 2, Եթե y 0 = 3ժամը x 0 = 1

Սա տարանջատված փոփոխական հավասարում է: Եկեք պատկերացնենք դա դիֆերենցիալներով։ Դա անելու համար մենք վերագրում ենք այս հավասարումը ձևի մեջ Այստեղից

Ինտեգրելով վերջին հավասարության երկու կողմերը՝ մենք գտնում ենք

Նախնական արժեքների փոխարինում x 0 = 1, y 0 = 3մենք կգտնենք ՀԵՏ 9=1-1+Գ, այսինքն. C = 9:

Հետևաբար, պահանջվող մասնակի ինտեգրալը կլինի կամ

Օրինակ 3

Գրի՛ր կետով անցնող կորի հավասարումը M(2;-3)և ունենալով շոշափում անկյունային գործակիցով

Լուծում. Ըստ պայմանի

Սա բաժանելի փոփոխականներով հավասարում է: Փոփոխականները բաժանելով՝ ստանում ենք.

Ինտեգրելով հավասարման երկու կողմերը՝ մենք ստանում ենք.

Օգտագործելով նախնական պայմանները, x = 2Եվ y = - 3մենք կգտնենք Գ:

Հետևաբար, պահանջվող հավասարումն ունի ձև

2.3. Առաջին կարգի գծային դիֆերենցիալ հավասարումներ

Առաջին կարգի գծային դիֆերենցիալ հավասարումը ձևի հավասարումն է y" = f(x)y + g(x)

Որտեղ f(x)Եվ g(x)- որոշ նշված գործառույթներ:

Եթե g(x)=0ապա գծային դիֆերենցիալ հավասարումը կոչվում է միատարր և ունի ձև. y" = f(x)y

Եթե ​​ապա հավասարումը y" = f(x)y + g(x)կոչվում է տարասեռ:

Գծային միատարր դիֆերենցիալ հավասարման ընդհանուր լուծում y" = f(x)yտրված է բանաձևով՝ որտեղ ՀԵՏ- կամայական հաստատուն:

Մասնավորապես, եթե C = 0,ապա լուծումը y = 0Եթե ​​գծային միատարր հավասարումկարծես յ» = կիՈրտեղ կորոշ հաստատուն է, ապա դրա ընդհանուր լուծումն ունի ձև.

Գծային անհամասեռ դիֆերենցիալ հավասարման ընդհանուր լուծում y" = f(x)y + g(x)տրված է բանաձևով ,

դրանք. հավասար է համապատասխան գծային միատարր հավասարման ընդհանուր լուծման և այս հավասարման առանձին լուծման գումարին։

Ձևի գծային անհամասեռ հավասարման համար y» = kx + b,

Որտեղ կԵվ բ- որոշ թվեր և որոշակի լուծում կլինեն մշտական ​​գործառույթ: Հետևաբար, ընդհանուր լուծումն ունի ձև.

Օրինակ. Լուծե՛ք հավասարումը y" + 2y +3 = 0

Լուծում. Ներկայացնենք հավասարումը ձևով y" = -2y - 3Որտեղ k = -2, b= -3Ընդհանուր լուծումը տրվում է բանաձևով.

Հետևաբար, որտեղ C-ն կամայական հաստատուն է:

2.4. Բեռնուլիի մեթոդով առաջին կարգի գծային դիֆերենցիալ հավասարումների լուծում

Առաջին կարգի գծային դիֆերենցիալ հավասարման ընդհանուր լուծում գտնելը y" = f(x)y + g(x)նվազեցնում է երկու դիֆերենցիալ հավասարումների լուծումն առանձնացված փոփոխականներով՝ օգտագործելով փոխարինումը y=uv, Որտեղ uԵվ v- անհայտ գործառույթներ x. Լուծման այս մեթոդը կոչվում է Բեռնուլիի մեթոդ։

Առաջին կարգի գծային դիֆերենցիալ հավասարման լուծման ալգորիթմ

y" = f(x)y + g(x)

1. Մուտքագրեք փոխարինում y=uv.

2. Տարբերակել այս հավասարությունը y" = u"v + uv"

3. Փոխարինող yԵվ y"այս հավասարման մեջ. u"v + uv" =f(x)uv + g(x)կամ u"v + uv" + f(x)uv = g(x).

4. Հավասարման անդամները խմբավորե՛ք այնպես, որ uհանել այն փակագծերից.

5. Փակագծից, այն հավասարեցնելով զրոյի, գտի՛ր ֆունկցիան

Սա բաժանելի հավասարում է.

Բաժանենք փոփոխականները և ստանանք.

Որտեղ . .

6. Փոխարինեք ստացված արժեքը vհավասարման մեջ (քայլ 4-ից).

և գտե՛ք ֆունկցիան Սա հավասարում է բաժանելի փոփոխականներով.

7. Ընդհանուր լուծումը գրի՛ր ձևով. , այսինքն. .

Օրինակ 1

Գտեք հավասարման կոնկրետ լուծում y" = -2y +3 = 0Եթե y=1ժամը x = 0

Լուծում. Եկեք լուծենք այն փոխարինման միջոցով y=uv,.y" = u"v + uv"

Փոխարինող yԵվ y"այս հավասարման մեջ մենք ստանում ենք

Երկրորդ և երրորդ անդամները խմբավորելով հավասարման ձախ կողմում՝ հանում ենք ընդհանուր գործակիցը u փակագծերից դուրս

Փակագծերում տրված արտահայտությունը հավասարեցնում ենք զրոյի և, լուծելով ստացված հավասարումը, գտնում ենք ֆունկցիան. v = v(x)

Մենք ստանում ենք հավասարում առանձնացված փոփոխականներով։ Եկեք ինտեգրենք այս հավասարման երկու կողմերը. Գտեք ֆունկցիան v:

Փոխարինենք ստացված արժեքը vհավասարման մեջ մենք ստանում ենք.

Սա տարանջատված փոփոխական հավասարում է: Եկեք ինտեգրենք հավասարման երկու կողմերը. Գտնենք ֆունկցիան u = u(x,c) Եկեք ընդհանուր լուծում գտնենք. Եկեք գտնենք սկզբնական պայմաններին բավարարող հավասարման որոշակի լուծում y = 1ժամը x = 0:

III. Բարձր կարգի դիֆերենցիալ հավասարումներ

3.1. Հիմնական հասկացություններ և սահմանումներ

Երկրորդ կարգի դիֆերենցիալ հավասարումը հավասարում է, որը պարունակում է երկրորդ կարգից ոչ բարձր ածանցյալներ: Ընդհանուր դեպքում երկրորդ կարգի դիֆերենցիալ հավասարումը գրվում է հետևյալ կերպ. F(x,y,y,y") = 0

Երկրորդ կարգի դիֆերենցիալ հավասարման ընդհանուր լուծումը ձևի ֆունկցիա է, որը ներառում է երկու կամայական հաստատուն. C 1Եվ Գ 2.

Երկրորդ կարգի դիֆերենցիալ հավասարման որոշակի լուծում կամայական հաստատունների որոշակի արժեքների ընդհանուր լուծումից ստացված լուծումն է: C 1Եվ Գ 2.

3.2. Երկրորդ կարգի գծային միատարր դիֆերենցիալ հավասարումներ հետ հաստատուն գործակիցներ.

Երկրորդ կարգի գծային միատարր դիֆերենցիալ հավասարում հաստատուն գործակիցներովկոչվում է ձևի հավասարում y" + py" +qy = 0, Որտեղ էջԵվ ք- հաստատուն արժեքներ.

Հաստատուն գործակիցներով երկրորդ կարգի միատարր դիֆերենցիալ հավասարումների լուծման ալգորիթմ

1. Դիֆերենցիալ հավասարումը գրի՛ր ձևով. y" + py" +qy = 0.

2. Ստեղծի՛ր նրա բնորոշ հավասարումը, նշելով y"միջոցով r 2, y"միջոցով r, y 1-ում: r 2 + pr + q = 0

Հոդվածի բովանդակությունը

ԴԻՖԵՐԵՆՑԻԱԼ ՀԱՎԱՍԱՐՈՒՄՆԵՐ.Շատերը ֆիզիկական օրենքներ, որոնց ենթակա են որոշակի երևույթներ, գրվում են որոշ մեծությունների միջև որոշակի հարաբերություն արտահայտող մաթեմատիկական հավասարման տեսքով։ Հաճախակի մենք խոսում ենքժամանակի ընթացքում փոփոխվող քանակությունների միջև փոխհարաբերությունների մասին, օրինակ, շարժիչի արդյունավետությունը, որը չափվում է այն հեռավորությամբ, որը մեքենան կարող է անցնել մեկ լիտր վառելիքով, կախված է մեքենայի արագությունից: Համապատասխան հավասարումը պարունակում է մեկ կամ մի քանի ֆունկցիա և դրանց ածանցյալներ և կոչվում է դիֆերենցիալ հավասարում։ (Ժամանակի ընթացքում հեռավորության փոփոխության արագությունը որոշվում է արագությամբ, հետևաբար, արագությունը հեռավորության ածանցյալ է, նմանապես, արագացումը արագության ածանցյալ է, քանի որ արագացումը որոշում է ժամանակի հետ արագության փոփոխության արագությունը): Մեծ արժեք, որը դիֆերենցիալ հավասարումներն ունեն մաթեմատիկայի և հատկապես դրա կիրառման համար, բացատրվում է նրանով, որ բազմաթիվ ֆիզիկական և տեխնիկական խնդիրների ուսումնասիրությունը հանգում է նման հավասարումների լուծմանը։ Դիֆերենցիալ հավասարումները կարևոր դեր են խաղում նաև այլ գիտություններում, ինչպիսիք են կենսաբանությունը, տնտեսագիտությունը և էլեկտրատեխնիկան; իրականում դրանք առաջանում են ամենուր, որտեղ անհրաժեշտ է լինում երևույթների քանակական (թվային) նկարագրությունը (քանի որ. մեզ շրջապատող աշխարհըփոփոխությունները ժամանակի ընթացքում և պայմանները փոխվում են մի վայրից մյուսը):

Օրինակներ.

Հետևյալ օրինակները ավելի լավ պատկերացում են տալիս, թե ինչպես են տարբեր խնդիրներ ձևակերպվում դիֆերենցիալ հավասարումների լեզվով:

1) Որոշ ռադիոակտիվ նյութերի քայքայման օրենքն այն է, որ քայքայման արագությունը համաչափ է այս նյութի առկա քանակին: Եթե x- նյութի քանակությունը ժամանակի որոշակի կետում տ, ապա այս օրենքը կարելի է գրել հետևյալ կերպ.

Որտեղ dx/dtքայքայման արագությունն է, և կ– տվյալ նյութը բնութագրող որոշակի դրական հաստատուն: (Աջ կողմի մինուս նշանը դա ցույց է տալիս xժամանակի ընթացքում նվազում է; գումարած նշանը, որը միշտ ենթադրվում է, երբ նշանը հստակ նշված չէ, դա կնշանակի xժամանակի ընթացքում ավելանում է)

2) Տարայի մեջ ի սկզբանե պարունակում է 100 մ 3 ջրի մեջ լուծված 10 կգ աղ. Եթե մաքուր ջուրրոպեում 1 մ 3 արագությամբ լցվում է տարայի մեջ և հավասարապես խառնվում լուծույթին, և ստացված լուծույթը նույն արագությամբ դուրս է հոսում տարայի մեջ, ապա ինչքա՞ն աղ կլինի տարայի մեջ ցանկացած հաջորդ պահին։ Եթե x- աղի քանակությունը (կգ-ով) տարայի մեջ միաժամանակ տ, ապա ցանկացած պահի տՏարայի մեջ 1 մ 3 լուծույթը պարունակում է x/100 կգ աղ; հետևաբար, աղի քանակը նվազում է x/100 կգ/րոպե, կամ

3) Թող մարմնի վրա զանգվածներ լինեն մԶսպանակի վերջից կասեցված, վերականգնող ուժը գործում է գարնանային լարվածության չափին համաչափ: Թող x- մարմնի շեղման չափը հավասարակշռության դիրքից. Այնուհետև, համաձայն Նյուտոնի երկրորդ օրենքի, որն ասում է, որ արագացումը (երկրորդ ածանցյալը xժամանակով, նշանակված դ 2 x/dt 2) ուժին համաչափ.

Աջ կողմն ունի մինուս նշան, քանի որ վերականգնող ուժը նվազեցնում է աղբյուրի ձգումը:

4) Մարմնի սառեցման օրենքը ասում է, որ մարմնի ջերմության քանակը նվազում է մարմնի ջերմաստիճանի տարբերությանը և միջավայրը. Եթե ​​90°C ջերմաստիճանում տաքացրած մեկ բաժակ սուրճը գտնվում է սենյակում, որտեղ ջերմաստիճանը 20°C է, ապա.

Որտեղ Տ- սուրճի ջերմաստիճանը ժամանակին տ.

5) Բլեֆուսկու նահանգի ԱԳ նախարարը պնդում է, որ Լիլիպուտի կողմից ընդունված սպառազինության ծրագիրը ստիպում է իր երկրին հնարավորինս մեծացնել ռազմական ծախսերը։ Նմանատիպ հայտարարություններ է անում Լիլիպուտի արտաքին գործերի նախարարը։ Ստացված իրավիճակը (իր ամենապարզ մեկնաբանությամբ) կարելի է ճշգրիտ նկարագրել երկու դիֆերենցիալ հավասարումներով։ Թող xԵվ y- Լիլիպուտի և Բլեֆուսկուի սպառազինության ծախսերը. Ենթադրելով, որ Լիլիպուտը մեծացնում է սպառազինության վրա իր ծախսերը Բլեֆուսկուի սպառազինության վրա ծախսերի աճի տեմպերին համաչափ և հակառակը, մենք ստանում ենք.

որտեղ անդամներն են կացինԵվ - կողմիցնկարագրել յուրաքանչյուր երկրի ռազմական ծախսերը, կԵվ լդրական հաստատուններ են: (Այս խնդիրն առաջին անգամ այս կերպ ձևակերպվել է 1939 թվականին Լ. Ռիչարդսոնի կողմից):

Դիֆերենցիալ հավասարումների լեզվով խնդիրը գրվելուց հետո դուք պետք է փորձեք լուծել դրանք, այսինքն. գտե՛ք այն մեծությունները, որոնց փոփոխության արագությունները ներառված են հավասարումների մեջ: Երբեմն լուծումները հայտնաբերվում են հստակ բանաձևերի տեսքով, բայց ավելի հաճախ դրանք կարելի է ներկայացնել միայն մոտավոր ձևով կամ որակական տեղեկատվություն ստանալ դրանց մասին։ Հաճախ կարող է դժվար լինել որոշել, թե արդյոք գոյություն ունի լուծում, էլ ուր մնաց՝ գտնել: Դիֆերենցիալ հավասարումների տեսության կարևոր հատվածը բաղկացած է այսպես կոչված «գոյության թեորեմներից», որոնցում ապացուցված է դիֆերենցիալ հավասարումների այս կամ այն ​​տիպի լուծման գոյությունը։

Ֆիզիկական խնդրի սկզբնական մաթեմատիկական ձևակերպումը սովորաբար պարունակում է պարզեցնող ենթադրություններ. դրանց ողջամիտության չափանիշը կարող է լինել մաթեմատիկական լուծման համապատասխանության աստիճանը առկա դիտարկումների հետ։

Դիֆերենցիալ հավասարումների լուծումներ.

Դիֆերենցիալ հավասարում, օրինակ դի/dx = x/y, բավարարվում է ոչ թե թվով, այլ ֆունկցիայով, այս կոնկրետ դեպքում այնպիսին, որ նրա գրաֆիկը ցանկացած կետում, օրինակ՝ կոորդինատներով կետում (2,3), ունի շոշափում։ լանջին, հավասար է կոորդինատների հարաբերակցությանը (մեր օրինակում 2/3): Սա հեշտ է ստուգել, ​​եթե դուք կառուցում եք մեծ թվովմիավորներ և յուրաքանչյուրից մի կողմ դրեք համապատասխան թեքությամբ կարճ հատված։ Լուծումը կլինի մի ֆունկցիա, որի գրաֆիկը դիպչում է իր յուրաքանչյուր կետին համապատասխան հատվածին: Եթե ​​կան բավարար կետեր և հատվածներ, ապա մենք կարող ենք մոտավորապես ուրվագծել լուծման կորերի ընթացքը (նկար 1-ում ներկայացված են երեք այդպիսի կորեր): Յուրաքանչյուր կետով անցնում է լուծման ճիշտ մեկ կոր yԹիվ 0. Յուրաքանչյուր առանձին լուծում կոչվում է դիֆերենցիալ հավասարման մասնակի լուծում; եթե հնարավոր է գտնել բոլոր կոնկրետ լուծումները պարունակող բանաձեւ (բացառությամբ մի քանի հատուկների), ապա ասում են, որ ընդհանուր լուծում է ստացվել։ Որոշակի լուծումը ներկայացնում է մեկ գործառույթ, մինչդեռ ընդհանուր լուծումը ներկայացնում է դրանց մի ամբողջ ընտանիք: Դիֆերենցիալ հավասարման լուծումը նշանակում է գտնել դրա որոշակի կամ ընդհանուր լուծումը: Մեր դիտարկած օրինակում ընդհանուր լուծումն ունի ձևը y 2 – x 2 = գ, Որտեղ գ- ցանկացած թիվ; (1,1) կետով անցնող որոշակի լուծում ունի ձևը y = xև պարզվում է, թե երբ գ= 0; (2,1) կետով անցնող որոշակի լուծում ունի ձև y 2 – x 2 = 3. Այն պայմանը, որը պահանջում է, որ լուծույթի կորը անցնի, օրինակ, կետով (2,1), կոչվում է նախնական պայման (քանի որ այն նշում է լուծման կորի մեկնարկային կետը):

Կարելի է ցույց տալ, որ (1) օրինակում ընդհանուր լուծումն ունի ձև x = ce –կտ, Որտեղ գ- հաստատուն, որը կարող է որոշվել, օրինակ, նշելով նյութի քանակը տ= 0. Հավասարում օրինակից (2) – հատուկ դեպքհավասարումը օրինակից (1), համապատասխան կ= 1/100: Նախնական վիճակ x= 10 ժամը տ= 0-ը տալիս է որոշակի լուծում x = 10ե –տ/100 . Օրինակ (4) հավասարումն ունի ընդհանուր լուծում Տ = 70 + ce –կտև մասնավոր լուծում 70 + 130 – կտ; արժեքը որոշելու համար կ, անհրաժեշտ են լրացուցիչ տվյալներ։

Դիֆերենցիալ հավասարում դի/dx = x/yկոչվում է առաջին կարգի հավասարում, քանի որ այն պարունակում է առաջին ածանցյալը (դիֆերենցիալ հավասարման կարգը սովորաբար համարվում է դրանում ներառված ամենաբարձր ածանցյալի կարգը): Գործնականում առաջացած առաջին տեսակի դիֆերենցիալ հավասարումների մեծ մասի (թեև ոչ բոլորի) համար յուրաքանչյուր կետով անցնում է լուծման միայն մեկ կոր:

Կան առաջին կարգի դիֆերենցիալ հավասարումների մի քանի կարևոր տեսակներ, որոնք կարող են լուծվել բանաձևերի տեսքով, որոնք պարունակում են միայն տարրական ֆունկցիաներ՝ ուժեր, ցուցիչներ, լոգարիթմներ, սինուսներ և կոսինուսներ և այլն։ Նման հավասարումները ներառում են հետևյալը.

Հավասարումներ բաժանելի փոփոխականներով:

Ձևի հավասարումներ դի/dx = զ(x)/է(y) կարելի է լուծել դիֆերենցիալներով գրելով է(y)դի = զ(x)dxև երկու մասերի ինտեգրում: Ամենավատ դեպքում լուծումը կարող է ներկայացվել հայտնի ֆունկցիաների ինտեգրալների տեսքով։ Օրինակ, հավասարման դեպքում դի/dx = x/yմենք ունենք զ(x) = x, է(y) = y. Ձևի մեջ գրելով ydy = xdxև ինտեգրվելով՝ մենք ստանում ենք y 2 = x 2 + գ. Բաժանելի փոփոխականներով հավասարումները ներառում են (1), (2), (4) օրինակներից ստացված հավասարումները (դրանք կարող են լուծվել վերը նկարագրված եղանակով):

Հավասարումներ ընդհանուր դիֆերենցիալներում.

Եթե ​​դիֆերենցիալ հավասարումն ունի ձևը դի/dx = Մ(x,y)/Ն(x,y), որտեղ ՄԵվ Ներկու տրված ֆունկցիաներ են, ապա այն կարող է ներկայացվել որպես Մ(x,y)dx – Ն(x,y)դի= 0. Եթե ձախ կողմըինչ-որ ֆունկցիայի դիֆերենցիալն է Ֆ(x,y), ապա դիֆերենցիալ հավասարումը կարելի է գրել այսպես dF(x,y) = 0, որը համարժեք է հավասարմանը Ֆ(x,y) = կոնստ. Այսպիսով, հավասարման լուծման կորերը ֆունկցիայի «հաստատուն մակարդակների գծերն են» կամ հավասարումները բավարարող կետերի տեղը։ Ֆ(x,y) = գ. Հավասարում ydy = xdx(նկ. 1) - բաժանելի փոփոխականներով, և նույնը - ընդհանուր դիֆերենցիալներով. վերջինս համոզվելու համար գրում ենք ձևով. ydy – xdx= 0, այսինքն. դ(y 2 – x 2) = 0. Ֆունկցիա Ֆ(x,y) այս դեպքում հավասար է (1/2)( y 2 – x 2); Նրա հաստատուն մակարդակի գծերից մի քանիսը ներկայացված են Նկ. 1.

Գծային հավասարումներ.

Գծային հավասարումները «առաջին աստիճանի» հավասարումներ են. անհայտ ֆունկցիան և նրա ածանցյալները նման հավասարումների մեջ հայտնվում են միայն առաջին աստիճանի: Այսպիսով, առաջին կարգի գծային դիֆերենցիալ հավասարումը ունի ձև դի/dx + էջ(x) = ք(x), որտեղ էջ(x) Եվ ք(x) – գործառույթներ, որոնք կախված են միայն x. Դրա լուծումը միշտ կարելի է գրել՝ օգտագործելով հայտնի ֆունկցիաների ինտեգրալները: Առաջին կարգի դիֆերենցիալ հավասարումների շատ այլ տեսակներ լուծվում են հատուկ տեխնիկայի միջոցով:

Բարձր կարգի հավասարումներ.

Շատ դիֆերենցիալ հավասարումներ, որոնց բախվում են ֆիզիկոսները, երկրորդ կարգի հավասարումներ են (այսինքն՝ երկրորդ ածանցյալներ պարունակող հավասարումներ, օրինակ, օրինակ (3) պարզ ներդաշնակ շարժման հավասարումը։ մդ 2 x/dt 2 = –kx. Ընդհանուր առմամբ, մենք կարող ենք ակնկալել, որ երկրորդ կարգի հավասարումը ունի մասնակի լուծումներ, որոնք բավարարում են երկու պայման. Օրինակ, կարելի է պահանջել, որ լուծման կորը անցնի տվյալ կետով տվյալ ուղղությամբ: Այն դեպքերում, երբ դիֆերենցիալ հավասարումը պարունակում է որոշակի պարամետր (թիվ, որի արժեքը կախված է հանգամանքներից), պահանջվող տիպի լուծումներ գոյություն ունեն միայն այն դեպքում, եթե. որոշակի արժեքներայս պարամետրը: Օրինակ, հաշվի առեք հավասարումը մդ 2 x/dt 2 = –kxև մենք դա կպահանջենք y(0) = y(1) = 0. Ֆունկցիա yє 0-ն ակնհայտորեն լուծում է, բայց եթե այն ամբողջ բազմապատիկ է էջ, այսինքն. կ = մ 2 n 2 էջ 2, որտեղ nամբողջ թիվ է, բայց իրականում միայն այս դեպքում կան այլ լուծումներ, մասնավորապես. y= մեղք npx. Պարամետրերի արժեքները, որոնց համար հավասարումը ունի հատուկ լուծումներ, կոչվում են բնորոշ կամ սեփական արժեքներ. նրանք կարևոր դեր են խաղում բազմաթիվ առաջադրանքներում:

Պարզ ներդաշնակ շարժման հավասարումը հավասարումների կարևոր դասի օրինակ է, այն է՝ հաստատուն գործակիցներով գծային դիֆերենցիալ հավասարումներ։ Ավելին ընդհանուր օրինակ(նաև երկրորդ կարգ) – հավասարում

Որտեղ աԵվ բ- տրված հաստատուններ, զ(x) տրված ֆունկցիա է։ Նման հավասարումներ կարելի է լուծել տարբեր ձևերով, օրինակ՝ օգտագործելով Լապլասի ինտեգրալ փոխակերպումը։ Նույնը կարելի է ասել հաստատուն գործակիցներով ավելի բարձր կարգերի գծային հավասարումների մասին։ Նրանք նույնպես կարևոր դեր են խաղում գծային հավասարումներփոփոխական գործակիցներով:

Ոչ գծային դիֆերենցիալ հավասարումներ.

Անհայտ ֆունկցիաներ պարունակող հավասարումները և դրանց ածանցյալները առաջինից բարձր կամ ավելի բարդ ձևով հզորություններին կոչվում են ոչ գծային: IN վերջին տարիներինդրանք ավելի ու ավելի մեծ ուշադրություն են գրավում: Փաստն այն է, որ ֆիզիկական հավասարումները սովորաբար գծային են միայն առաջին մոտավորության համար. Հետագա և ավելի ճշգրիտ հետազոտությունները, որպես կանոն, պահանջում են ոչ գծային հավասարումների օգտագործում։ Բացի այդ, շատ խնդիրներ ունեն ոչ գծային բնույթ: Քանի որ ոչ գծային հավասարումների լուծումները հաճախ շատ բարդ են և դժվար է ներկայացնել պարզ բանաձևերի միջոցով, զգալի մասը ժամանակակից տեսություննվիրված է նրանց վարքի որակական վերլուծությանը, այսինքն. մեթոդների մշակում, որոնք հնարավորություն են տալիս, առանց հավասարումը լուծելու, ինչ-որ էական բան ասել լուծումների բնույթի մասին որպես ամբողջություն. օրինակ, որ դրանք բոլորը սահմանափակ են, կամ ունեն պարբերական բնույթ, կամ որոշակիորեն կախված են գործակիցները։

Դիֆերենցիալ հավասարումների մոտավոր լուծումներ կարելի է գտնել թվային եղանակով, սակայն դա շատ ժամանակ է պահանջում։ Գերարագ համակարգիչների ի հայտ գալով այս ժամանակը զգալիորեն կրճատվեց, ինչը նոր հնարավորություններ բացեց բազմաթիվ խնդիրների թվային լուծման համար, որոնք նախկինում անլուծելի էին նման լուծման համար:

Գոյության թեորեմներ.

Գոյության թեորեմը այն թեորեմն է, որն ասում է, որ որոշակի պայմաններում տրված դիֆերենցիալ հավասարումն ունի լուծում: Կան դիֆերենցիալ հավասարումներ, որոնք չունեն լուծումներ կամ ունեն դրանցից ավելի շատ, քան սպասվում էր: Գոյության թեորեմի նպատակն է համոզել մեզ, որ տրված հավասարումն իրականում լուծում ունի, և ամենից հաճախ մեզ վստահեցնել, որ այն ունի պահանջվող տիպի ճշգրիտ լուծում: Օրինակ, այն հավասարումը, որը մենք արդեն հանդիպել ենք դի/dx = –2yունի ուղիղ մեկ լուծում, որն անցնում է հարթության յուրաքանչյուր կետով ( x,y), և քանի որ մենք արդեն գտել ենք այդպիսի լուծում, դրանով մենք ամբողջությամբ լուծել ենք այս հավասարումը: Մյուս կողմից, հավասարումը ( դի/dx) 2 = 1 – y 2-ն ունի բազմաթիվ լուծումներ: Նրանց թվում են ուղիղ y = 1, y= –1 և կորեր y= մեղք ( x + գ) Լուծումը կարող է բաղկացած լինել այս ուղիղ գծերի և կորերի մի քանի հատվածներից, որոնք միմյանց մեջ են անցնում շփման կետերում (նկ. 2):

Մասնակի դիֆերենցիալ հավասարումներ.

Սովորական դիֆերենցիալ հավասարումը հայտարարություն է մեկ փոփոխականի անհայտ ֆունկցիայի ածանցյալի մասին: Մասնակի դիֆերենցիալ հավասարումը պարունակում է երկու կամ ավելի փոփոխականների ֆունկցիա և այդ ֆունկցիայի ածանցյալներ առնվազն երկու տարբեր փոփոխականների նկատմամբ:

Ֆիզիկայի մեջ նման հավասարումների օրինակներ են Լապլասի հավասարումը

X, y) շրջանակի ներսում, եթե արժեքները uսահմանող շրջանագծի յուրաքանչյուր կետում նշված: Քանի որ ֆիզիկայում մեկից ավելի փոփոխականների հետ կապված խնդիրները ավելի շուտ կանոն են, քան բացառություն, հեշտ է պատկերացնել, թե որքան մեծ է մասնակի դիֆերենցիալ հավասարումների տեսության թեման:

Տրված է առցանց հաշվիչթույլ է տալիս առցանց լուծել դիֆերենցիալ հավասարումներ: Բավական է մուտքագրել ձեր հավասարումը համապատասխան դաշտում՝ նշելով ֆունկցիայի ածանցյալը ապաստրոֆի միջոցով և սեղմել «լուծել հավասարումը» և հանրաճանաչ WolframAlpha կայքի հիման վրա ներդրված համակարգը մանրամասն կներկայացնի դիֆերենցիալ հավասարման լուծումբացարձակապես անվճար: Դուք կարող եք նաև սահմանել Քոշիի խնդիրը այնպես, որ ամբողջ հավաքածուից հնարավոր լուծումներընտրել տրված սկզբնական պայմաններին համապատասխանող քանորդը. Կոշիի խնդիրը մուտքագրված է առանձին դաշտում։

Դիֆերենցիալ հավասարում

Լռելյայնորեն, ֆունկցիան հավասարման մեջ yփոփոխականի ֆունկցիա է x. Այնուամենայնիվ, դուք կարող եք նշել ձեր սեփական նշանակումը փոփոխականի համար, եթե դուք գրեք, օրինակ, y(t) հավասարման մեջ, հաշվիչը ավտոմատ կերպով կճանաչի դա yփոփոխականից ֆունկցիա կա տ. Հաշվիչի օգնությամբ կարող եք լուծել դիֆերենցիալ հավասարումներցանկացած բարդության և տեսակի՝ միատարր և անհամասեռ, գծային կամ ոչ գծային, առաջին կամ երկրորդ և ավելի բարձր կարգի, բաժանելի կամ անբաժանելի փոփոխականներով հավասարումներ և այլն։ Լուծման տարբերություն. հավասարումը տրված է վերլուծական ձևով, ունի մանրամասն նկարագրություն. Դիֆերենցիալ հավասարումները շատ տարածված են ֆիզիկայում և մաթեմատիկայում: Առանց դրանց հաշվարկի անհնար է լուծել բազմաթիվ խնդիրներ (հատկապես մաթեմատիկական ֆիզիկայում)։

Դիֆերենցիալ հավասարումների լուծման փուլերից մեկը ֆունկցիաների ինտեգրումն է։ Կան դիֆերենցիալ հավասարումների լուծման ստանդարտ մեթոդներ: Անհրաժեշտ է հավասարումները վերածել y և x տարանջատելի փոփոխականներով ձևի և առանձին ինտեգրել առանձնացված ֆունկցիաները։ Դա անելու համար երբեմն պետք է որոշակի փոխարինում կատարվի: