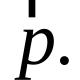Ուշադրություն.
Կան լրացուցիչ
նյութեր 555-րդ հատուկ բաժնում:
Նրանց համար, ովքեր շատ «ոչ շատ ...» են:
Եվ նրանց համար, ովքեր «շատ…»)

Թվաբանական առաջընթացթվերի շարք է, որոնցում յուրաքանչյուր թիվ նույն չափով մեծ է (կամ փոքր) նախորդից։

Այս թեման հաճախ բարդ և անհասկանալի է թվում: Տառերի ինդեքսներ n-րդ կիսամյակառաջընթացներ, առաջընթացի տարբերություններ - այս ամենը ինչ-որ կերպ շփոթեցնող է, այո... Եկեք պարզենք թվաբանական առաջընթացի իմաստը և ամեն ինչ անմիջապես կլավանա:)

Թվաբանական առաջընթացի հայեցակարգը.

Թվաբանական առաջընթացը շատ պարզ և հստակ հասկացություն է։ Դուք կասկածներ ունե՞ք։ Իզուր։) Ինքներդ տես։

Ես կգրեմ թվերի անավարտ շարք.

1, 2, 3, 4, 5, ...

Կարող եք երկարացնել այս շարքը: Ո՞ր թվերն են լինելու հաջորդ՝ հինգից հետո։ Բոլորը... հը..., մի խոսքով, բոլորը կհասկանան, որ հաջորդը լինելու են 6, 7, 8, 9 և այլն թվերը։

Եկեք բարդացնենք խնդիրը. Ես ձեզ տալիս եմ թվերի անավարտ շարք.

2, 5, 8, 11, 14, ...

Դուք կկարողանաք որսալ օրինակը, երկարացնել շարքը և անվանել յոթերորդշարքի համարը?

Եթե ​​հասկացաք, որ այս թիվը 20 է, շնորհավորում ենք։ Ոչ միայն դուք զգացիք հիմնական կետերըթվաբանական առաջընթաց,բայց նաև հաջողությամբ օգտագործեց դրանք բիզնեսում: Եթե ​​չեք հասկացել, կարդացեք:

Այժմ եկեք թարգմանենք հիմնական կետերը սենսացիաներից մաթեմատիկայի:

Առաջին առանցքային կետը.

Թվաբանական առաջընթացը վերաբերում է թվերի շարքին:Սա սկզբում շփոթեցնող է: Մենք սովոր ենք հավասարումներ լուծելու, գրաֆիկներ նկարելու և այդ ամենին... Բայց այստեղ մենք երկարացնում ենք շարքը, գտնում շարքի թիվը...

Դա լավ է: Պարզապես առաջընթացները մաթեմատիկայի նոր ճյուղի հետ առաջին ծանոթությունն են: Բաժինը կոչվում է «Սերիա» և աշխատում է հատուկ թվերի և արտահայտությունների հետ: Ընտելացեք դրան։)

Երկրորդ առանցքային կետը.

Թվաբանական առաջընթացում ցանկացած թիվ տարբերվում է նախորդից նույն չափով։

Առաջին օրինակում այս տարբերությունը մեկն է. Ինչ թիվ էլ վերցնես, նախորդից մեկով ավելի է։ Երկրորդում `երեք: Ցանկացած թիվ երեքով ավելի է նախորդից։ Փաստորեն, հենց այս պահն է մեզ հնարավորություն ըմբռնելու օրինաչափությունը և հաշվարկելու հաջորդ թվերը։

Երրորդ առանցքային կետը.

Այս պահը աչքի չի ընկնում, այո... Բայց շատ, շատ կարևոր է։ Ահա այն. յուրաքանչյուրը առաջընթացի համարըկանգնած է իր տեղում.Կա առաջին թիվը, կա յոթերորդը, կա քառասունհինգերորդը և այլն: Եթե ​​դրանք պատահականորեն խառնեք, օրինակը կվերանա: Թվաբանական առաջընթացը նույնպես կվերանա: Մնում է ընդամենը թվերի շարք:

Ամբողջ իմաստը դա է:

Իհարկե, նոր թեմայում հայտնվում են նոր տերմիններ և նշանակումներ։ Դուք պետք է իմանաք նրանց: Հակառակ դեպքում դուք չեք հասկանա առաջադրանքը: Օրինակ, դուք պետք է որոշեք նման բան.

Գրեք թվաբանական առաջընթացի առաջին վեց անդամները (a n), եթե a 2 = 5, d = -2,5:

Ոգեշնչող?) Նամակներ, որոշ ցուցիչներ... Իսկ առաջադրանքն, ի դեպ, ավելի պարզ լինել չէր կարող։ Պարզապես պետք է հասկանալ տերմինների և նշանակումների իմաստը: Այժմ մենք կյուրացնենք այս գործը և կվերադառնանք առաջադրանքին։

Պայմաններ և նշանակումներ.

Թվաբանական առաջընթացթվերի շարք է, որոնցում յուրաքանչյուր թիվ տարբերվում է նախորդից նույն չափով։

Այս քանակությունը կոչվում է . Եկեք նայենք այս հայեցակարգին ավելի մանրամասն:

Թվաբանական առաջընթացի տարբերություն.

Թվաբանական առաջընթացի տարբերությունայն գումարն է, որով ցանկացած առաջընթացի թիվ ավելիննախորդը.

Մեկը կարևոր կետ. Խնդրում եմ ուշադրություն դարձրեք բառին «ավելին».Մաթեմատիկորեն սա նշանակում է, որ առաջընթացի յուրաքանչյուր թիվ է ավելացնելովթվաբանական առաջընթացի տարբերությունը նախորդ թվին:

Հաշվարկելու համար ասենք երկրորդշարքի համարները, դուք պետք է առաջինհամարը ավելացնելթվաբանական պրոգրեսիայի հենց այս տարբերությունը: Հաշվարկի համար հինգերորդ- տարբերությունն անհրաժեշտ է ավելացնելԴեպի չորրորդ,լավ և այլն:

Թվաբանական առաջընթացի տարբերությունԿարող է լինել դրական,ապա շարքի յուրաքանչյուր թիվ իրական կդառնա ավելի շատ, քան նախորդը:Այս առաջընթացը կոչվում է աճող։Օրինակ.

8; 13; 18; 23; 28; .....

Այստեղ ստացվում է յուրաքանչյուր թիվ ավելացնելովդրական թիվ՝ +5 նախորդին։

Տարբերությունը կարող է լինել բացասական,ապա շարքի յուրաքանչյուր թիվ կլինի ավելի քիչ, քան նախորդը:Այս առաջընթացը կոչվում է (չեք հավատա!) նվազում.

Օրինակ.

8; 3; -2; -7; -12; .....

Այստեղ նույնպես ստացվում է յուրաքանչյուր թիվ ավելացնելովնախորդին, բայց արդեն բացասական թիվ, -5.

Ի դեպ, պրոգրեսիայի հետ աշխատելիս շատ օգտակար է անմիջապես որոշել դրա բնույթը` ավելանում է, թե նվազում: Սա մեծապես օգնում է կողմնորոշվել որոշման մեջ, նկատել ձեր սխալները և ուղղել դրանք, քանի դեռ ուշ չէ:

Թվաբանական առաջընթացի տարբերությունսովորաբար նշվում է տառով դ.

Ինչպես գտնել դ? Շատ պարզ. Շարքի ցանկացած թվից անհրաժեշտ է հանել նախորդհամարը։ հանել. Ի դեպ, հանման արդյունքը կոչվում է «տարբերություն»):

Եկեք սահմանենք, օրինակ. դթվաբանական առաջընթացի ավելացման համար.

2, 5, 8, 11, 14, ...

Վերցնում ենք մեր ուզած շարքի ցանկացած թիվ, օրինակ՝ 11։ Դրանից հանում ենք նախորդ համարըդրանք. 8:

Սա ճիշտ պատասխանն է։ Այս թվաբանական առաջընթացի համար տարբերությունը երեք է:

Դուք կարող եք վերցնել այն առաջընթացի ցանկացած թիվ,քանի որ կոնկրետ առաջընթացի համար դ-միշտ նույնը.Գոնե ինչ-որ տեղ շարքի սկզբում, թեկուզ մեջտեղում, թեկուզ ցանկացած տեղ։ Դուք չեք կարող վերցնել միայն առաջին համարը: Պարզապես այն պատճառով, որ հենց առաջին համարը ոչ մի նախորդ.)

Ի դեպ, դա իմանալով d=3, այս առաջընթացի յոթերորդ թիվը գտնելը շատ պարզ է: Հինգերորդ թվին գումարենք 3 - ստանում ենք վեցերորդը, կլինի 17։ Վեցերորդ թվին գումարենք երեք, ստանում ենք յոթերորդ թիվը՝ քսան։

Եկեք սահմանենք դնվազող թվաբանական առաջընթացի համար.

8; 3; -2; -7; -12; .....

Հիշեցնում եմ, որ, անկախ նշաններից, որոշել դանհրաժեշտ է ցանկացած համարից խլել նախորդը.Ընտրեք առաջընթացի ցանկացած թիվ, օրինակ -7: Նրա նախորդ թիվը -2 է։ Ապա.

d = -7 - (-2) = -7 + 2 = -5

Թվաբանական առաջընթացի տարբերությունը կարող է լինել ցանկացած թիվ՝ ամբողջ, կոտորակային, իռացիոնալ, ցանկացած թիվ։

Այլ տերմիններ և նշանակումներ:

Շարքի յուրաքանչյուր թիվ կոչվում է թվաբանական պրոգրեսիայի անդամ։

Առաջընթացի յուրաքանչյուր անդամ ունի իր համարը.Թվերը խիստ կարգավորված են՝ առանց որևէ հնարքների։ Առաջին, երկրորդ, երրորդ, չորրորդ և այլն: Օրինակ՝ 2, 5, 8, 11, 14, ... երկուսը առաջին անդամն է, հինգը՝ երկրորդը, տասնմեկը՝ չորրորդը, լավ, հասկանում եք...) Խնդրում եմ հստակ հասկացեք. թվերն իրենք ենկարող է լինել բացարձակապես ցանկացած, ամբողջ, կոտորակային, բացասական, ինչ էլ որ լինի, բայց թվերի համարակալում- խիստ կարգով:

Ինչպես գրել առաջընթաց ընդհանուր տեսարան? Հարց չկա։ Շարքի յուրաքանչյուր թիվ գրվում է որպես տառ: Թվաբանական առաջընթացը նշելու համար սովորաբար օգտագործվում է տառը ա. Անդամի համարը նշվում է ներքևի աջ մասում գտնվող ինդեքսով: Մենք գրում ենք տերմիններ՝ բաժանված ստորակետերով (կամ ստորակետերով), այսպես.

ա 1, ա 2, ա 3, ա 4, ա 5, .....

ա 1- սա առաջին համարն է, ա 3- երրորդ և այլն: Ոչ մի շքեղ բան: Այս շարքը կարելի է հակիրճ գրել այսպես. (a n).

Առաջընթացներ են տեղի ունենում վերջավոր և անսահման:

Վերջնականառաջընթաց ունի սահմանափակ քանակությամբանդամներ։ Հինգ, երեսունութ, ինչ էլ որ լինի: Բայց դա վերջավոր թիվ է:

Անսահմանառաջընթաց - ունի անսահման թվով անդամներ, ինչպես կարող եք կռահել:)

Դուք կարող եք գրել վերջնական առաջընթացը նման շարքի միջոցով, բոլոր տերմինները և վերջում մի կետ.

ա 1, ա 2, ա 3, ա 4, ա 5:

Կամ այսպես, եթե անդամները շատ են.

a 1, a 2, ... a 14, a 15:

Կարճ մուտքագրում դուք պետք է լրացուցիչ նշեք անդամների թիվը: Օրինակ (քսան անդամների համար), այսպես.

(a n), n = 20

Անսահման առաջընթացը կարելի է ճանաչել տողի վերջում գտնվող էլիպսիսով, ինչպես այս դասի օրինակներում:

Այժմ դուք կարող եք լուծել առաջադրանքները: Առաջադրանքները պարզ են՝ զուտ թվաբանական առաջընթացի իմաստը հասկանալու համար։

Թվաբանական առաջընթացի առաջադրանքների օրինակներ.

Եկեք մանրամասն նայենք վերը տրված առաջադրանքին.

1. Դուրս գրիր թվաբանական պրոգրեսիայի առաջին վեց անդամները (a n), եթե a 2 = 5, d = -2,5:

Մենք առաջադրանքը թարգմանում ենք հասկանալի լեզվով: Տրված է անվերջ թվաբանական պրոգրեսիա։ Այս առաջընթացի երկրորդ թիվը հայտնի է. ա 2 = 5.Առաջընթացի տարբերությունը հայտնի է. դ = -2,5:Մենք պետք է գտնենք այս առաջընթացի առաջին, երրորդ, չորրորդ, հինգերորդ և վեցերորդ անդամները:

Պարզության համար գրեմ մի շարք՝ ըստ խնդրի պայմանների։ Առաջին վեց ժամկետները, որտեղ երկրորդ անդամը հինգն է.

a 1, 5, a 3, a 4, a 5, a 6,...

ա 3 = ա 2 + դ

Փոխարինել արտահայտության մեջ ա 2 = 5Եվ դ = -2,5. Մի մոռացեք մինուսի մասին:

ա 3=5+(-2,5)=5 - 2,5 = 2,5

Երրորդ ժամկետը ստացվեց երկուսից պակաս. Ամեն ինչ տրամաբանական է. Եթե ​​թիվը մեծ է նախորդից բացասականարժեքը, ինչը նշանակում է, որ թիվն ինքնին պակաս կլինի նախորդից: Առաջընթացը նվազում է. Լավ, եկեք հաշվի առնենք:) Մենք հաշվում ենք մեր շարքի չորրորդ անդամը.

ա 4 = ա 3 + դ

ա 4=2,5+(-2,5)=2,5 - 2,5 = 0

ա 5 = ա 4 + դ

ա 5=0+(-2,5)= - 2,5

ա 6 = ա 5 + դ

ա 6=-2,5+(-2,5)=-2,5 - 2,5 = -5

Այսպիսով, հաշվարկվել են երրորդից վեցերորդ ժամկետները։ Արդյունքը հետևյալ շարքն է.

ա 1, 5, 2.5, 0, -2.5, -5, ....

Մնում է գտնել առաջին տերմինը ա 1Ըստ հայտնի երկրորդ. Սա քայլ է մյուս ուղղությամբ՝ դեպի ձախ։) Այսպիսով՝ թվաբանական առաջընթացի տարբերությունը դչպետք է ավելացվի ա 2, Ա խլել:

ա 1 = ա 2 - դ

ա 1=5-(-2,5)=5 + 2,5=7,5

վերջ։ Առաջադրանքի պատասխան.

7,5, 5, 2,5, 0, -2,5, -5, ...

Ընդ որում, ուզում եմ նշել, որ մենք լուծել ենք այս խնդիրը կրկնվողճանապարհ. Այս սարսափելի բառը նշանակում է միայն պրոգրեսիայի անդամի որոնում ըստ նախորդ (կից) թվի.Ստորև մենք կքննարկենք առաջընթացի հետ աշխատելու այլ եղանակներ:

Այս պարզ առաջադրանքից կարելի է մեկ կարևոր եզրակացություն անել.

Հիշեք.

Եթե ​​մենք գիտենք առնվազն մեկ անդամ և թվաբանական առաջընթացի տարբերությունը, մենք կարող ենք գտնել այս առաջընթացի ցանկացած անդամ:

Հիշու՞մ ես։ Այս պարզ եզրակացությունը թույլ է տալիս լուծել խնդիրների մեծ մասը դպրոցական դասընթացայս թեմայով։ Բոլոր առաջադրանքները պտտվում են շուրջը երեք հիմնականպարամետրեր: թվաբանական պրոգրեսիայի անդամ, առաջընթացի տարբերություն, պրոգրեսիայի անդամի թիվ։Բոլորը.

Իհարկե, բոլոր նախորդ հանրահաշիվները չեղյալ չեն հայտարարվում:) Անհավասարությունները, հավասարումները և այլ բաներ կցվում են պրոգրեսիային: Բայց ըստ բուն առաջընթացի- ամեն ինչ պտտվում է երեք պարամետրի շուրջ.

Որպես օրինակ, եկեք նայենք այս թեմայի վերաբերյալ հայտնի առաջադրանքներին:

2. Վերջավոր թվաբանական պրոգրեսիան գրի՛ր շարքով, եթե n=5, d = 0,4 և a 1 = 3,6։

Այստեղ ամեն ինչ պարզ է. Ամեն ինչ արդեն տրված է։ Դուք պետք է հիշեք, թե ինչպես են հաշվում թվաբանական առաջընթացի անդամները, հաշվեք դրանք և գրեք դրանք: Առաջադրանքի պայմաններում խորհուրդ է տրվում բաց չթողնել բառերը՝ «վերջնական» և « n=5«Որպեսզի չհաշվես, քանի դեռ դեմքդ ամբողջովին կապտած ես:) Այս պրոգրեսում ընդամենը 5 (հինգ) անդամ կա.

a 2 = a 1 + d = 3.6 + 0.4 = 4

a 3 = a 2 + d = 4 + 0.4 = 4.4

ա 4 = ա 3 + d = 4,4 + 0,4 = 4,8

ա 5 = ա 4 + d = 4,8 + 0,4 = 5,2

Մնում է գրել պատասխանը.

3,6; 4; 4,4; 4,8; 5,2.

Մեկ այլ խնդիր.

3. Որոշեք, թե արդյոք 7 թիվը կլինի թվաբանական առաջընթացի անդամ (a n), եթե. ա 1 = 4,1; d = 1.2:

Հմմ... Ո՞վ գիտի: Ինչպե՞ս որոշել ինչ-որ բան:

Ո՞նց-ինչպե՞ս... Շարքի տեսքով գրի՛ր պրոգրեսիան ու տես՝ այնտեղ յոթ կլինի՞, թե՞ ոչ։ Մենք հաշվում ենք.

a 2 = a 1 + d = 4.1 + 1.2 = 5.3

a 3 = a 2 + d = 5.3 + 1.2 = 6.5

ա 4 = ա 3 + դ = 6,5 + 1,2 = 7,7

4,1; 5,3; 6,5; 7,7; ...

Հիմա պարզ երևում է, որ մենք ընդամենը յոթն ենք սայթաքել է 6.5-ի և 7.7-ի միջև: Յոթը չի մտնում մեր թվերի շարքի մեջ, և, հետևաբար, յոթը չի լինի տվյալ առաջընթացի անդամ։

Պատասխան՝ ոչ։

Եվ ահա GIA-ի իրական տարբերակի վրա հիմնված խնդիր.

4. Թվաբանական առաջընթացի մի քանի հաջորդական անդամներ դուրս են գրվում.

...; 15; X; 9; 6; ...

Ահա մի շարք գրված առանց վերջի և սկզբի. Անդամների թվեր չկան, տարբերություն չկա դ. Դա լավ է: Խնդիրը լուծելու համար բավական է հասկանալ թվաբանական առաջընթացի իմաստը։ Եկեք նայենք և տեսնենք, թե ինչ է հնարավոր իմանալայս շարքից? Որո՞նք են երեք հիմնական պարամետրերը:

Անդամների համարներ? Այստեղ ոչ մի թիվ չկա։

Բայց կան երեք թվեր և ուշադրություն: - բառ «հետևողական»վիճակում։ Սա նշանակում է, որ թվերը խիստ կարգավորված են, առանց բացերի։ Այս շարքում երկուսը կա՞ն: հարեւանհայտնի թվեր? Այո, ես ունեմ: Սրանք 9 և 6 են։ Հետևաբար, մենք կարող ենք հաշվարկել թվաբանական առաջընթացի տարբերությունը։ Վեցից հանել նախորդհամարը, այսինքն. ինը:

Մնացել են ընդամենը մանրուքներ։ Ո՞ր թիվը կլինի X-ի նախորդը: Տասնհինգ. Սա նշանակում է, որ X-ը կարելի է հեշտությամբ գտնել պարզ գումարման միջոցով: Թվաբանական առաջընթացի տարբերությունը ավելացրեք 15-ի.

վերջ։ Պատասխան. x=12

Մենք ինքներս ենք լուծում հետևյալ խնդիրները. Նշում. այս խնդիրները հիմնված չեն բանաձևերի վրա: Զուտ թվաբանական առաջընթացի իմաստը հասկանալու համար:) Մենք պարզապես գրում ենք թվերի և տառերի շարք, նայում և պարզում ենք այն:

5. Գտե՛ք թվաբանական պրոգրեսիայի առաջին դրական անդամը, եթե a 5 = -3; d = 1.1.

6. Հայտնի է, որ 5.5 թիվը թվաբանական պրոգրեսիայի անդամ է (a n), որտեղ a 1 = 1.6; d = 1.3. Որոշե՛ք այս անդամի n թիվը։

7. Հայտնի է, որ թվաբանական առաջընթացում a 2 = 4; ա 5 = 15,1: Գտեք 3.

8. Թվաբանական առաջընթացի մի քանի հաջորդական անդամներ դուրս են գրվում.

...; 15.6; X; 3.4; ...

Գտե՛ք x տառով նշված առաջընթացի տերմինը:

9. Գնացքը սկսեց շարժվել կայարանից՝ միատեսակ արագությունը րոպեում 30 մետրով ավելացնելով։ Որքա՞ն կլինի գնացքի արագությունը հինգ րոպեում: Տվեք ձեր պատասխանը կմ/ժամով:

10. Հայտնի է, որ թվաբանական առաջընթացում a 2 = 5; ա 6 = -5. Գտեք 1-ը.

Պատասխաններ (խառնաշփոթ)՝ 7.7; 7.5; 9.5; 9; 0.3; 4.

Ամեն ինչ ստացվե՞լ է։ Զարմանալի! Հետևյալ դասերում կարող եք տիրապետել թվաբանական առաջընթացին ավելի բարձր մակարդակով։

Ամեն ինչ չստացվեց? Խնդիր չկա։ Հատուկ 555 բաժնում այս բոլոր խնդիրները մաս առ մաս բաժանվում են:) Եվ, իհարկե, պարզ. գործնական տեխնիկա, որն անմիջապես ընդգծում է նման խնդիրների լուծումը պարզ, հստակ, մի հայացքով:

Ի դեպ, գնացքի գլուխկոտրուկում կա երկու խնդիր, որոնց վրա մարդիկ հաճախ են սայթաքում. Մեկը զուտ առաջընթացի առումով է, իսկ երկրորդը ընդհանուր է մաթեմատիկայի, և ֆիզիկայի ցանկացած խնդիրների համար: Սա չափերի թարգմանությունն է մեկից մյուսը: Այն ցույց է տալիս, թե ինչպես կարելի է լուծել այս խնդիրները:

Այս դասում մենք նայեցինք թվաբանական առաջընթացի տարրական իմաստին և դրա հիմնական պարամետրերին: Սա բավական է այս թեմայի շուրջ գրեթե բոլոր խնդիրները լուծելու համար։ Ավելացնել դթվերին, շարք գրեք, ամեն ինչ կլուծվի։

Մատների լուծումը լավ է աշխատում շարքի շատ կարճ կտորների համար, ինչպես այս դասի օրինակներում: Եթե ​​շարքն ավելի երկար է, ապա հաշվարկներն ավելի են բարդանում։ Օրինակ, եթե հարցի 9-րդ խնդիրում փոխարինենք «հինգ րոպե»վրա «երեսունհինգ րոպե»խնդիրը զգալիորեն կվատթարանա։)

Եվ կան նաև առաջադրանքներ, որոնք ըստ էության պարզ են, բայց աբսուրդային՝ հաշվարկների առումով, օրինակ.

Տրված է թվաբանական պրոգրեսիա (a n): Գտե՛ք 121 թիվը, եթե a 1 =3 և d=1/6:

Ուրեմն ի՞նչ, մի՞թե մենք 1/6-ը շատ ու շատ անգամ ենք ավելացնելու։ Դուք կարող եք սպանել ինքներդ!

Դուք կարող եք:) Եթե չգիտեք մի պարզ բանաձև, որով կարող եք լուծել այդպիսի առաջադրանքները մեկ րոպեում: Այս բանաձևը կլինի հաջորդ դասին։ Եվ այդ խնդիրը լուծված է այնտեղ։ Մի րոպեում։)

Եթե ​​Ձեզ դուր է գալիս այս կայքը...

Ի դեպ, ես ձեզ համար ևս մի քանի հետաքրքիր կայք ունեմ։)

Դուք կարող եք զբաղվել օրինակներ լուծելով և պարզել ձեր մակարդակը: Փորձարկում ակնթարթային ստուգմամբ: Սովորենք՝ հետաքրքրությամբ։)

Կարող եք ծանոթանալ ֆունկցիաներին և ածանցյալներին։

Դե, ընկերներ, եթե դուք կարդում եք այս տեքստը, ապա ներքին գլխարկ-ապացույցն ինձ ասում է, որ դուք դեռ չգիտեք, թե ինչ է թվաբանական առաջընթացը, բայց դուք իսկապես (ոչ, այսպես. SOOOOO!) ցանկանում եք իմանալ: Ուստի երկար ներածություններով ձեզ չեմ տանջի և անմիջապես կանցնեմ բուն կետին:

Նախ, մի երկու օրինակ. Դիտարկենք թվերի մի քանի հավաքածու.

• 1; 2; 3; 4; ...
• 15; 20; 25; 30; ...
• $\sqrt(2);\ 2\sqrt(2);\ 3\sqrt(2);...$

Ի՞նչ ընդհանուր բան ունեն այս բոլոր հավաքածուները: Առաջին հայացքից՝ ոչինչ։ Բայց իրականում ինչ-որ բան կա. Մասնավորապես. ամեն հաջորդ տարրընույն թվով տարբերվում է նախորդից.

Դատեք ինքներդ։ Առաջին հավաքածուն ուղղակի հաջորդական թվեր են, որոնցից յուրաքանչյուրը մեկով ավելի է նախորդից: Երկրորդ դեպքում հարակից թվերի տարբերությունն արդեն հինգ է, բայց այս տարբերությունը դեռ հաստատուն է։ Երրորդ դեպքում ընդհանրապես արմատներ կան։ Սակայն $2\sqrt(2)=\sqrt(2)+\sqrt(2)$ և $3\sqrt(2)=2\sqrt(2)+\sqrt(2)$, այսինքն. և այս դեպքում յուրաքանչյուր հաջորդ տարր պարզապես ավելանում է $\sqrt(2)$-ով (և մի վախեցեք, որ այս թիվը իռացիոնալ է):

Այսպիսով, բոլոր նման հաջորդականությունները կոչվում են թվաբանական առաջընթացներ: Տանք խիստ սահմանում.

Սահմանում. Թվերի այն հաջորդականությունը, որտեղ յուրաքանչյուր հաջորդը նախորդից տարբերվում է ճիշտ նույն չափով, կոչվում է թվաբանական պրոգրեսիա։ Հենց այն գումարը, որով թվերը տարբերվում են, կոչվում է պրոգրեսիայի տարբերություն և ամենից հաճախ նշվում է $d$ տառով։

Նշում. $\left(((a)_(n)) \right)$-ն ինքնին առաջընթացն է, $d$-ը դրա տարբերությունն է:

Եվ ընդամենը մի քանի կարևոր նշում. Նախ, առաջընթացը միայն դիտարկվում է պատվիրել էթվերի հաջորդականությունը. դրանք թույլատրվում է կարդալ խիստ այն հաջորդականությամբ, որով դրանք գրված են, և ուրիշ ոչինչ: Թվերը չեն կարող վերադասավորվել կամ փոխանակվել:

Երկրորդ, հաջորդականությունն ինքնին կարող է լինել կամ վերջավոր կամ անվերջ: Օրինակ, բազմությունը (1; 2; 3) ակնհայտորեն վերջավոր թվաբանական պրոգրեսիա է: Բայց եթե դուք ինչ-որ բան գրում եք ոգով (1; 2; 3; 4; ...) - սա արդեն անսահման առաջընթաց է: Չորսից հետո էլիպսիսը կարծես հուշում է, որ դեռ շատ թվեր են սպասվում: Օրինակ՝ անսահման շատ:

Կցանկանայի նաև նշել, որ առաջընթացները կարող են աճել կամ նվազել: Մենք արդեն տեսել ենք աճողներ՝ նույն հավաքածուն (1; 2; 3; 4; ...): Ահա նվազող առաջընթացի օրինակներ.

• 49; 41; 33; 25; 17; ...
• 17,5; 12; 6,5; 1; −4,5; −10; ...
• $\sqrt(5);\ \sqrt(5)-1;\ \sqrt(5)-2;\ \sqrt(5)-3;...$

Լավ, լավ. վերջին օրինակը կարող է չափազանց բարդ թվալ: Բայց մնացածը, կարծում եմ, հասկանում ես։ Այսպիսով, մենք ներկայացնում ենք նոր սահմանումներ.

Սահմանում. Թվաբանական առաջընթացը կոչվում է.

1. աճում է, եթե յուրաքանչյուր հաջորդ տարրը մեծ է նախորդից.
2. նվազում, եթե, ընդհակառակը, յուրաքանչյուր հաջորդ տարր պակաս է նախորդից:

Բացի այդ, կան, այսպես կոչված, «ստացիոնար» հաջորդականություններ. դրանք բաղկացած են նույն կրկնվող թվից: Օրինակ, (3; 3; 3; ...):

Մնում է միայն մեկ հարց. ինչպե՞ս տարբերել աճող առաջընթացը նվազողից: Բարեբախտաբար, այստեղ ամեն ինչ կախված է միայն $d$ թվի նշանից, այսինքն. առաջընթացի տարբերություններ.

1. Եթե ​​$d \gt 0$, ապա առաջընթացը մեծանում է.
2. Եթե ​​$d \lt 0$, ապա առաջընթացն ակնհայտորեն նվազում է.
3. Վերջապես, կա $d=0$ դեպք - այս դեպքում ամբողջ առաջընթացը կրճատվում է միանման թվերի անշարժ հաջորդականության՝ (1; 1; 1; 1; ...) և այլն:

Փորձենք հաշվարկել $d$ տարբերությունը վերը նշված երեք նվազող առաջընթացների համար: Դա անելու համար բավական է վերցնել ցանկացած երկու հարակից տարր (օրինակ՝ առաջինը և երկրորդը) և ձախ կողմի թիվը հանել աջ կողմի թվից։ Այն այսպիսի տեսք կունենա.

• 41−49=−8;
• 12−17,5=−5,5;
• $\sqrt(5)-1-\sqrt(5)=-1$:

Ինչպես տեսնում ենք, բոլորի մեջ երեք դեպքտարբերությունն իրականում բացասական է ստացվել։ Եվ հիմա, երբ մենք քիչ թե շատ պարզել ենք սահմանումները, ժամանակն է պարզել, թե ինչպես են նկարագրվում առաջընթացները և ինչ հատկություններ ունեն դրանք:

Առաջընթացի պայմանները և կրկնության բանաձևը

Քանի որ մեր հաջորդականության տարրերը հնարավոր չէ փոխանակել, դրանք կարող են համարակալվել.

\[\left(((a)_(n)) \աջ)=\ձախ\(((a)_(1)),\ ((a)_(2)),((a)_(3 )),... \ճիշտ\)\]

Այս հավաքածուի առանձին տարրերը կոչվում են պրոգրեսիայի անդամներ: Դրանք նշվում են թվով՝ առաջին անդամ, երկրորդ անդամ և այլն։

Բացի այդ, ինչպես արդեն գիտենք, առաջընթացի հարևան տերմինները կապված են բանաձևով.

\[((a)_(n))-((a)_(n-1))=d\Աջ սլաք ((a)_(n))=((a)_(n-1))+d \]

Մի խոսքով, պրոգրեսիայի $n$th անդամը գտնելու համար դուք պետք է իմանաք $n-1$th անդամը և $d$ տարբերությունը: Այս բանաձևը կոչվում է կրկնվող, քանի որ դրա օգնությամբ դուք կարող եք գտնել ցանկացած թիվ միայն իմանալով նախորդը (և իրականում բոլոր նախորդները): Սա շատ անհարմար է, ուստի կա ավելի խորամանկ բանաձև, որը նվազեցնում է ցանկացած հաշվարկ մինչև առաջին տերմինը և տարբերությունը.

\[((a)_(n))=((a)_(1))+\ձախ(n-1 \աջ)d\]

Դուք հավանաբար արդեն հանդիպել եք այս բանաձեւին. Նրանք սիրում են այն տալ բոլոր տեսակի տեղեկատու գրքերում և լուծումների գրքերում: Իսկ մաթեմատիկայի ցանկացած խելամիտ դասագրքում այն ​​առաջիններից է։

Այնուամենայնիվ, ես առաջարկում եմ ձեզ մի փոքր պարապել:

Առաջադրանք թիվ 1. Գրի՛ր $\left((a)_(n)) \right)$ թվաբանական պրոգրեսիայի առաջին երեք անդամները, եթե $((a)_(1))=8,d=-5$։

Լուծում. Այսպիսով, մենք գիտենք $((a)_(1))=8$ առաջին անդամը և $d=-5$ պրոգրեսիայի տարբերությունը: Եկեք օգտագործենք հենց նոր տրված բանաձևը և փոխարինենք $n=1$, $n=2$ և $n=3$:

\[\սկիզբ(հավասարեցնել) & ((a)_(n))=((a)_(1))+\ձախ(n-1 \աջ)d; \\ & ((a)_(1))=((a)_(1))+\ձախ(1-1 \աջ)d=((a)_(1))=8; \\ & ((a)_(2))=((a)_(1))+\ձախ(2-1 \աջ)d=((a)_(1))+d=8-5= 3; \\ & ((a)_(3))=((a)_(1))+\ձախ(3-1 \աջ)d=((a)_(1))+2d=8-10= -2. \\ \վերջ (հավասարեցնել)\]

Պատասխան՝ (8; 3; −2)

Վե՛րջ: Խնդրում ենք նկատի ունենալ. մեր առաջընթացը նվազում է:

Իհարկե, $n=1$-ը չէր կարող փոխարինվել՝ առաջին տերմինը մեզ արդեն հայտնի է։ Սակայն փոխարինելով միասնությունը՝ մենք համոզվեցինք, որ նույնիսկ առաջին ժամկետում մեր բանաձեւը գործում է։ Մնացած դեպքերում ամեն ինչ հանգում էր բանական թվաբանության։

Առաջադրանք թիվ 2. Գրե՛ք թվաբանական պրոգրեսիայի առաջին երեք անդամները, եթե նրա յոթերորդ անդամը հավասար է -40-ի, իսկ տասնյոթերորդ անդամը հավասար է -50-ի:

Լուծում. Խնդրի պայմանը գրենք ծանոթ տերմիններով.

\[((a)_(7))=-40;\չորս ((ա)_(17))=-50:\]

\[\ձախ\( \սկիզբ(հավասարեցնել) & ((a)_(7))=((a)_(1))+6d \\ & ((a)_(17))=(a) _(1))+16d \\ \վերջ (հավասարեցնել) \աջ:\]

\[\ձախ\( \սկիզբ(հավասարեցնել) & ((a)_(1))+6d=-40 \\ & ((a)_(1))+16d=-50 \\ \վերջ (հավասարեցնել) \ճիշտ\]

Ես դրել եմ համակարգի նշանը, քանի որ այս պահանջները պետք է կատարվեն միաժամանակ: Այժմ նկատենք, որ եթե առաջինը հանենք երկրորդ հավասարումից (մենք իրավունք ունենք դա անելու, քանի որ ունենք համակարգ), կստանանք հետևյալը.

\[\սկիզբ (հավասարեցնել) & ((ա)_(1))+16d-\ձախ (((a)_(1))+6d \աջ)=-50-\ձախ (-40 \աջ); \\ & ((a)_(1))+16d-((a)_(1))-6d=-50+40; \\&10d=-10; \\&d=-1. \\ \վերջ (հավասարեցնել)\]

Ահա թե որքան հեշտ է գտնել առաջընթացի տարբերությունը: Մնում է գտնված թիվը փոխարինել համակարգի ցանկացած հավասարումով: Օրինակ, առաջինում.

\[\սկիզբ (մատրիցան) ((a)_(1))+6d=-40;\quad d=-1 \\ \Ներքև \\ ((a)_(1))-6=-40; \\ ((ա)_(1))=-40+6=-34. \\ \վերջ (մատրիցան)\]

Այժմ, իմանալով առաջին տերմինը և տարբերությունը, մնում է գտնել երկրորդ և երրորդ անդամները.

\[\սկիզբ(հավասարեցնել) & ((a)_(2))=((a)_(1))+d=-34-1=-35; \\ & ((a)_(3))=((a)_(1))+2d=-34-2=-36. \\ \վերջ (հավասարեցնել)\]

Պատրաստ. Խնդիրը լուծված է։

Պատասխան՝ (−34; −35; −36)

Ուշադրություն դարձրեք պրոգրեսիայի հետաքրքիր հատկությանը, որը մենք հայտնաբերեցինք. եթե վերցնենք $n$th և $m$th անդամները և հանենք դրանք միմյանցից, ապա կստանանք առաջընթացի տարբերությունը բազմապատկած $n-m$ թվով.

\[((a)_(n))-((a)_(m))=d\cdot \ձախ(n-m \աջ)\]

Պարզ, բայց շատ օգտակար հատկություն, որը դուք անպայման պետք է իմանաք՝ դրա օգնությամբ դուք կարող եք զգալիորեն արագացնել պրոգրեսիայի բազմաթիվ խնդիրների լուծումը։ Ահա դրա վառ օրինակը.

Առաջադրանք թիվ 3. Թվաբանական առաջընթացի հինգերորդ անդամը 8,4 է, իսկ տասներորդ անդամը 14,4 է։ Գտե՛ք այս առաջընթացի տասնհինգերորդ անդամը:

Լուծում. Քանի որ $((a)_(5))=8.4$, $((a)_(10))=14.4$, և մենք պետք է գտնենք $((a)_(15))$, մենք նշում ենք հետևյալը.

\[\սկիզբ (հավասարեցնել) & ((a)_(15))-((a)_(10))=5d; \\ & ((a)_(10))-((a)_(5))=5դ. \\ \վերջ (հավասարեցնել)\]

Բայց պայմանով $((a)_(10))-((a)_(5))=14.4-8.4=6$, հետևաբար $5d=6$, որից ունենք.

\[\սկիզբ (հավասարեցնել) & ((a)_(15))-14,4=6; \\ & ((ա)_(15))=6+14.4=20.4. \\ \վերջ (հավասարեցնել)\]

Պատասխան՝ 20.4

Վե՛րջ: Մեզ պետք չէր ստեղծել հավասարումների համակարգ և հաշվարկել առաջին անդամն ու տարբերությունը. ամեն ինչ լուծվեց ընդամենը մի քանի տողում:

Հիմա եկեք նայենք մեկ այլ տեսակի խնդրի՝ առաջընթացի բացասական և դրական տերմինների որոնում: Գաղտնիք չէ, որ եթե պրոգրեսիան աճում է, և դրա առաջին տերմինը բացասական է, ապա վաղ թե ուշ դրա մեջ դրական տերմիններ են հայտնվում։ Եվ հակառակը՝ նվազող առաջընթացի պայմանները վաղ թե ուշ կդառնան բացասական։

Միևնույն ժամանակ, միշտ չէ, որ հնարավոր է գտնել այս պահը «գլխով»՝ հաջորդաբար անցնելով տարրերի միջով։ Հաճախ խնդիրներն այնպես են գրված, որ առանց բանաձևերի իմացության, հաշվարկների համար մի քանի թերթ թուղթ կպահանջվի. մենք պարզապես քնում էինք, մինչ գտնում էինք պատասխանը: Ուստի փորձենք այս խնդիրներն ավելի արագ լուծել։

Առաջադրանք թիվ 4. Քանի՞ բացասական անդամ կա թվաբանական առաջընթացում −38,5; −35,8; ...?

Լուծում. Այսպիսով, $((a)_(1))=-38.5$, $((a)_(2))=-35.8$, որտեղից անմիջապես գտնում ենք տարբերությունը.

Նշենք, որ տարբերությունը դրական է, ուստի առաջընթացը մեծանում է: Առաջին տերմինը բացասական է, ուստի իսկապես ինչ-որ պահի մենք կբախվենք դրական թվերի վրա: Հարցը միայն այն է, թե երբ դա տեղի կունենա:

Փորձենք պարզել, թե որքան ժամանակ (այսինքն մինչև $n$ որ բնական թիվ) է մնում տերմինների բացասականությունը.

\[\սկիզբ (հավասարեցնել) & ((a)_(n)) \lt 0\Աջ սլաք ((a)_(1))+\ ձախ (n-1 \աջ)d \lt 0; \\ & -38.5+\ ձախ (n-1 \աջ)\cdot 2.7 \lt 0;\quad \ձախ| \cdot 10 \աջ. \\ & -385+27\cdot \left(n-1 \աջ) \lt 0; \\ & -385+27n-27 \lt 0; \\ & 27n \lt 412; \\ & n \lt 15\frac(7)(27)\Rightarrow ((n)_(\max ))=15: \\ \վերջ (հավասարեցնել)\]

Վերջին տողը որոշակի բացատրություն է պահանջում։ Այսպիսով, մենք գիտենք, որ $n \lt 15\frac(7)(27)$: Մյուս կողմից, մենք բավարարվում ենք թվի միայն ամբողջական արժեքներով (ավելին՝ $n\in \mathbb(N)$), ուստի ամենամեծ թույլատրելի թիվը հենց $n=15$ է, և ոչ մի դեպքում՝ 16։ .

Առաջադրանք թիվ 5. Թվաբանական պրոգրեսիայում $(()_(5))=-150,(()_(6))=-147$: Գտե՛ք այս առաջընթացի առաջին դրական անդամի թիվը:

Սա կլինի ճիշտ նույն խնդիրը, ինչ նախորդը, բայց մենք չգիտենք $((a)_(1))$: Բայց հարևան տերմինները հայտնի են՝ $((a)_(5))$ և $((a)_(6))$, այնպես որ մենք կարող ենք հեշտությամբ գտնել առաջընթացի տարբերությունը.

Բացի այդ, փորձենք արտահայտել հինգերորդ անդամը առաջինի և տարբերության միջոցով՝ օգտագործելով ստանդարտ բանաձևը.

\[\սկիզբ(հավասարեցնել) & ((a)_(n))=((a)_(1))+\left(n-1 \աջ)\cdot d; \\ & ((a)_(5))=((a)_(1))+4d; \\ & -150=((a)_(1))+4\cdot 3; \\ & ((ա)_(1))=-150-12=-162. \\ \վերջ (հավասարեցնել)\]

Այժմ մենք անալոգիայով անցնում ենք նախորդ առաջադրանքին: Եկեք պարզենք, թե մեր հաջորդականության որ կետում կհայտնվեն դրական թվերը.

\[\սկիզբ(հավասարեցնել) & ((a)_(n))=-162+\ձախ(n-1 \աջ)\cdot 3 \gt 0; \\ & -162+3n-3 \gt 0; \\ & 3n \gt 165; \\ & n \gt 55\Աջ սլաք ((n)_(\min ))=56: \\ \վերջ (հավասարեցնել)\]

Այս անհավասարության նվազագույն ամբողջական լուծումը 56 թիվն է։

Խնդրում ենք նկատի ունենալ. վերջին առաջադրանքում ամեն ինչ հանգեցրեց խիստ անհավասարության, ուստի $n=55$ տարբերակը մեզ չի համապատասխանում:

Այժմ, երբ մենք սովորեցինք, թե ինչպես լուծել պարզ խնդիրները, եկեք անցնենք ավելի բարդ խնդիրների: Բայց նախ եկեք ուսումնասիրենք թվաբանական պրոգրեսիաների ևս մեկ շատ օգտակար հատկություն, որը մեզ ապագայում կխնայի շատ ժամանակ և անհավասար բջիջներ :)

Թվաբանական միջին և հավասար նահանջներ

Դիտարկենք $\left((a)_(n)) \right)$ աճող թվաբանական պրոգրեսիայի մի քանի հաջորդական անդամ: Փորձենք դրանք նշել թվային տողի վրա.

Ես հատուկ նշել եմ կամայական $((a)_(n-3)),...,((a)_(n+3))$, և ոչ թե $((a)_(1)) ,\ ((a)_(2)),\ ((a)_(3))$ և այլն: Քանի որ կանոնը, որի մասին ես ձեզ հիմա կասեմ, նույնն է աշխատում ցանկացած «հատվածի» համար:

Իսկ կանոնը շատ պարզ է. Եկեք հիշենք կրկնվող բանաձևը և գրենք այն բոլոր նշված տերմինների համար.

\[\սկիզբ (հավասարեցնել) & ((a)_(n-2))=((a)_(n-3))+d; \\ & ((a)_(n-1))=((a)_(n-2))+d; \\ & ((a)_(n))=((a)_(n-1))+d; \\ & ((a)_(n+1))=((a)_(n))+d; \\ & ((a)_(n+2))=((a)_(n+1))+d; \\ \վերջ (հավասարեցնել)\]

Այնուամենայնիվ, այս հավասարությունները կարող են տարբեր կերպ վերաշարադրվել.

\[\սկիզբ(հավասարեցնել) & ((a)_(n-1))=((a)_(n))-d; \\ & ((a)_(n-2))=((a)_(n))-2d; \\ & ((a)_(n-3))=((a)_(n))-3d; \\ & ((a)_(n+1))=((a)_(n))+d; \\ & ((a)_(n+2))=((a)_(n))+2d; \\ & ((a)_(n+3))=((a)_(n))+3d; \\ \վերջ (հավասարեցնել)\]

Ուրեմն ի՞նչ։ Եվ այն փաստը, որ $((a)_(n-1))$ և $((a)_(n+1))$ տերմինները գտնվում են $((a)_(n)) $-ից նույն հեռավորության վրա: . Եվ այս հեռավորությունը հավասար է $d$-ի։ Նույնը կարելի է ասել $((a)_(n-2))$ և $((a)_(n+2))$ տերմինների մասին - դրանք նույնպես հանված են $((a)_(n)-ից: )$ նույն հեռավորության վրա, որը հավասար է $2d$-ի: Մենք կարող ենք անվերջ շարունակել, բայց իմաստը լավ երևում է նկարից

Ի՞նչ է սա նշանակում մեզ համար: Սա նշանակում է, որ $((a)_(n))$-ը կարելի է գտնել, եթե հայտնի են հարևան թվերը.

\[((a)_(n))=\frac(((a)_(n-1))+((a)_(n+1)))(2)\]

Մենք ստացանք հիանալի պնդում. թվաբանական առաջընթացի յուրաքանչյուր անդամ հավասար է իր հարևան անդամների միջին թվաբանականին: Ավելին. մենք կարող ենք հետ կանգնել մեր $((a)_(n))$-ից ձախ և աջ ոչ թե մեկ քայլով, այլ $k$ քայլով, և բանաձևը դեռ ճիշտ կլինի.

\[((a)_(n))=\frac(((a)_(n-k))+((a)_(n+k)))(2)\]

Նրանք. մենք հեշտությամբ կարող ենք գտնել $((a)_(150))$, եթե գիտենք $((a)_(100))$ և $((a)_(200))$, քանի որ $((a)_ (150))=\frac(((a)_(100))+((a)_(200)))(2)$: Առաջին հայացքից կարող է թվալ, թե այս փաստը մեզ ոչ մի օգտակար բան չի տալիս։ Այնուամենայնիվ, գործնականում շատ խնդիրներ հատուկ մշակված են միջին թվաբանականն օգտագործելու համար: Նայեք.

Առաջադրանք թիվ 6. Գտեք $x$-ի բոլոր արժեքները, որոնց համար $-6((x)^(2))$, $x+1$ և $14+4((x)^(2))$ թվերը հաջորդական են: թվաբանական առաջընթաց (նշված հերթականությամբ):

Լուծում. Քանի որ այս թվերը պրոգրեսիայի անդամներ են, նրանց համար բավարարված է միջին թվաբանական պայմանը. $x+1$ կենտրոնական տարրը կարող է արտահայտվել հարևան տարրերով.

\[\սկիզբ(հավասարեցնել) & x+1=\frac(-6((x)^(2))+14+4((x)^(2)))(2); \\ & x+1=\frac(14-2((x)^(2)))(2); \\ & x+1=7-((x)^(2)); \\ & ((x)^(2))+x-6=0. \\ \վերջ (հավասարեցնել)\]

Դասական է ստացվել քառակուսային հավասարում. Դրա արմատները՝ $x=2$ և $x=-3$ պատասխաններն են։

Պատասխան՝ −3; 2.

Առաջադրանք թիվ 7. Գտեք $$-ի արժեքները, որոնց համար $-1;4-3;()^(2))+1$ թվերը կազմում են թվաբանական առաջընթաց (այդ հերթականությամբ):

Լուծում. Կրկին արտահայտենք միջին անդամը հարևան տերմինների միջին թվաբանականի միջոցով.

\[\սկիզբ(հավասարեցնել) & 4x-3=\frac(x-1+((x)^(2))+1)(2); \\ & 4x-3=\frac(((x)^(2))+x)(2);\quad \ձախ| \cdot 2 \աջ.; \\ & 8x-6=((x)^(2))+x; \\ & ((x)^(2))-7x+6=0. \\ \վերջ (հավասարեցնել)\]

Կրկին քառակուսի հավասարում. Եվ կրկին երկու արմատ կա՝ $x=6$ և $x=1$։

Պատասխան՝ 1; 6.

Եթե ​​խնդրի լուծման գործընթացում դուք ինչ-որ դաժան թվեր եք ներկայացնում, կամ լիովին վստահ չեք գտնված պատասխանների ճիշտության մեջ, ապա կա մի հրաշալի տեխնիկա, որը թույլ է տալիս ստուգել՝ մենք ճիշտ լուծե՞լ ենք խնդիրը:

Ենթադրենք թիվ 6 խնդիրում մենք ստացել ենք −3 և 2 պատասխանները։ Ինչպե՞ս ստուգել, ​​որ այդ պատասխանները ճիշտ են։ Եկեք պարզապես միացնենք դրանք սկզբնական վիճակին և տեսնենք, թե ինչ է տեղի ունենում: Հիշեցնեմ, որ մենք ունենք երեք թիվ ($-6(()^(2))$, $+1$ և $14+4(()^(2))$), որոնք պետք է կազմեն թվաբանական պրոգրեսիա։ Փոխարինենք $x=-3$:

\[\սկիզբ(հավասարեցնել) & x=-3\Աջ սլաք \\ & -6((x)^(2))=-54; \\ & x+1=-2; \\ & 14+4((x)^(2))=50։ \վերջ (հավասարեցնել)\]

Մենք ստացանք −54 թվերը; −2; 50-ը, որոնք տարբերվում են 52-ով, անկասկած, թվաբանական առաջընթաց է: Նույնը տեղի է ունենում $x=2$-ի դեպքում.

\[\սկիզբ(հավասարեցնել) & x=2\Աջ սլաք \\ & -6((x)^(2))=-24; \\ & x+1=3; \\ & 14+4((x)^(2))=30։ \վերջ (հավասարեցնել)\]

Կրկին առաջընթաց, բայց 27 տարբերությամբ: Այսպիսով, խնդիրը ճիշտ լուծվեց։ Ցանկացողները կարող են ինքնուրույն ստուգել երկրորդ խնդիրը, բայց ես անմիջապես կասեմ՝ այնտեղ էլ ամեն ինչ ճիշտ է։

Ընդհանրապես, վերջին խնդիրները լուծելիս հանդիպեցինք մեկ ուրիշի հետաքրքիր փաստ, որը նույնպես պետք է հիշել.

Եթե ​​երեք թվեր այնպիսին են, որ երկրորդը առաջինի և վերջինի միջին թվաբանականն է, ապա այս թվերը կազմում են թվաբանական առաջընթաց:

Հետագայում այս հայտարարության ըմբռնումը թույլ կտա մեզ բառացիորեն «կառուցել» անհրաժեշտ առաջընթացները՝ հիմնվելով խնդրի պայմանների վրա։ Բայց նման «շինարարությամբ» զբաղվելուց առաջ պետք է ուշադրություն դարձնել ևս մեկ փաստի վրա, որն ուղղակիորեն բխում է արդեն քննարկվածից։

Խմբավորում և գումարում տարրեր

Կրկին վերադառնանք թվային առանցքին։ Այստեղ նկատենք պրոգրեսիայի մի քանի անդամներ, որոնց միջև, հավանաբար. արժե շատ այլ անդամներ.

Փորձենք արտահայտել «ձախ պոչը» $((a)_(n))$-ի և $d$-ի միջոցով, իսկ «աջ պոչը»՝ $((a)_(k))$-ի և $d$-ի միջոցով: Դա շատ պարզ է.

\[\սկիզբ(հավասարեցնել) & ((a)_(n+1))=((a)_(n))+d; \\ & ((a)_(n+2))=((a)_(n))+2d; \\ & ((a)_(k-1))=((a)_(k))-d; \\ & ((a)_(k-2))=((a)_(k))-2d. \\ \վերջ (հավասարեցնել)\]

Այժմ նշեք, որ հետևյալ գումարները հավասար են.

\[\սկիզբ(հավասարեցնել) & ((a)_(n))+((a)_(k))=S; \\ & ((a)_(n+1))+((a)_(k-1))=((a)_(n))+d+((a)_(k))-d= Ս; \\ & ((a)_(n+2))+((a)_(k-2))=((a)_(n))+2d+((a)_(k))-2d= Ս. \վերջ (հավասարեցնել)\]

Պարզ ասած, եթե որպես սկիզբ դիտարկենք առաջընթացի երկու տարր, որոնք ընդհանուր առմամբ հավասար են $S$-ի ինչ-որ թվի, այնուհետև սկսենք քայլել այս տարրերից հակառակ ուղղություններով (դեպի միմյանց կամ հակառակը՝ հեռանալ), ապա այն տարրերի գումարները, որոնց վրա մենք կսայթաքենք, նույնպես հավասար կլինեն$S$. Սա կարելի է առավել հստակ ներկայացնել գրաֆիկորեն.

Այս փաստի ըմբռնումը թույլ կտա մեզ հիմնովին լուծել խնդիրները բարձր մակարդակդժվարություններ, քան նրանք, որոնք մենք համարել ենք վերևում: Օրինակ՝ սրանք.

Առաջադրանք թիվ 8. Որոշե՛ք թվաբանական պրոգրեսիայի տարբերությունը, որի առաջին անդամը 66 է, իսկ երկրորդ և տասներկուերորդ անդամների արտադրյալը՝ ամենափոքրը։

Լուծում. Եկեք գրենք այն ամենը, ինչ գիտենք.

\[\սկիզբ (հավասարեցնել) & ((a)_(1))=66; \\&d=? \\ & ((a)_(2))\cdot ((a)_(12))=\min . \վերջ (հավասարեցնել)\]

Այսպիսով, մենք չգիտենք առաջընթացի տարբերությունը $d$: Իրականում, ամբողջ լուծումը կկառուցվի տարբերության շուրջ, քանի որ $((a)_(2))\cdot ((a)_(12))$ արտադրանքը կարող է վերագրվել հետևյալ կերպ.

\[\սկիզբ(հավասարեցնել) & ((a)_(2))=((a)_(1))+d=66+d; \\ & ((a)_(12))=((a)_(1))+11d=66+11d; \\ & ((a)_(2))\cdot ((a)_(12))=\left(66+d \աջ)\cdot \left(66+11d \աջ)= \\ & =11 \cdot \left(d+66 \աջ)\cdot \left(d+6 \աջ): \վերջ (հավասարեցնել)\]

Տանկի մեջ գտնվողների համար ես վերցրեցի 11-ի ընդհանուր բազմապատկիչը երկրորդ փակագծից: Այսպիսով, պահանջվող արտադրյալը քառակուսի ֆունկցիա է $d$ փոփոխականի նկատմամբ։ Հետևաբար, հաշվի առեք $f\left(d \right)=11\left(d+66 \right)\left(d+6 \right)$ ֆունկցիան, որի գրաֆիկը կլինի պարաբոլա՝ ճյուղերով վերև, քանի որ եթե ընդլայնենք փակագծերը, կստանանք.

\[\սկիզբ (հավասարեցնել) & f\ ձախ (d \աջ)=11\ձախ (((d)^(2))+66d+6d+66\cdot 6 \աջ)= \\ & =11(( դ)^(2))+11\cdot 72d+11\cdot 66\cdot 6 \վերջ (հավասարեցնել)\]

Ինչպես տեսնում եք, ամենաբարձր անդամի գործակիցը 11 է, սա է դրական թիվԱյսպիսով, մենք իսկապես գործ ունենք պարաբոլայի հետ՝ ճյուղերով վերև.

ժամանակացույցը քառակուսի ֆունկցիա- պարաբոլա

Խնդրում ենք նկատի ունենալ. նվազագույն արժեքըայս պարաբոլան ընդունում է $((d)_(0))$ իր գագաթին աբսցիսով: Իհարկե, մենք կարող ենք հաշվարկել այս աբսցիսան ըստ ստանդարտ սխեմա(կա $((d)_(0))=(-b)/(2a)\;$ բանաձևը), բայց շատ ավելի խելամիտ կլինի նշել, որ ցանկալի գագաթը գտնվում է համաչափության առանցքի վրա: պարաբոլա, ուստի $((d) _(0))$ կետը հավասար է $f\left(d \right)=0$ հավասարման արմատներից:

\[\սկիզբ (հավասարեցնել) & f\ ձախ (d \աջ)=0; \\ & 11\cdot \left(d+66 \right)\cdot \left(d+6 \right)=0; \\ & ((դ)_(1))=-66;\չորս ((դ)_(2))=-6. \\ \վերջ (հավասարեցնել)\]

Այդ իսկ պատճառով ես առանձնապես չէի շտապում բացել փակագծերը. իրենց սկզբնական տեսքով արմատները շատ ու շատ հեշտ էին գտնել։ Հետևաբար, աբսցիսան հավասար է −66 և −6 թվերի միջին թվաբանականին.

\[((դ)_(0))=\frac(-66-6)(2)=-36\]

Ի՞նչ է մեզ տալիս հայտնաբերված թիվը: Դրանով պահանջվող արտադրանքը ստանում է ամենափոքր արժեքը (ի դեպ, մենք երբեք չենք հաշվարկել $((y)_(\min ))$ - դա մեզանից չի պահանջվում): Միևնույն ժամանակ, այս թիվը սկզբնական առաջընթացի տարբերությունն է, այսինքն. մենք գտանք պատասխանը :)

Պատասխան՝ −36

Առաջադրանք թիվ 9. $-\frac(1)(2)$ և $-\frac(1)(6)$ թվերի միջև տեղադրեք երեք թիվ, որպեսզի այս թվերի հետ միասին կազմեն թվաբանական պրոգրեսիա։

Լուծում. Ըստ էության, մենք պետք է կազմենք հինգ թվերի հաջորդականություն՝ առաջին և վերջին թվերն արդեն հայտնի լինեն։ Բաց թողած թվերը նշենք $x$, $y$ և $z$ փոփոխականներով.

\[\left(((a)_(n)) \right)=\left\( -\frac(1)(2);x;y;z;-\frac(1)(6) \աջ\ )\]

Նկատի ունեցեք, որ $y$ թիվը մեր հաջորդականության «միջինն» է. այն հավասար է $x$ և $z$ թվերից և $-\frac(1)(2)$ և $-\frac թվերից: (1)(6)$. Եվ եթե մենք ներկայումս չենք կարողանում $y$ ստանալ $x$ և $z$ թվերից, ապա իրավիճակն այլ է առաջընթացի ծայրերում։ Հիշենք միջին թվաբանականը.

Այժմ, իմանալով $y$-ը, մենք կգտնենք մնացած թվերը։ Նկատի ունեցեք, որ $x$-ը գտնվում է $-\frac(1)(2)$ և $y=-\frac(1)(3)$ թվերի միջև, որոնք մենք հենց նոր գտանք: Ահա թե ինչու

Օգտագործելով նմանատիպ պատճառաբանություն, մենք գտնում ենք մնացած թիվը.

Պատրաստ. Մենք գտանք բոլոր երեք համարները: Գրենք դրանք պատասխանում այն ​​հաջորդականությամբ, որով դրանք պետք է տեղադրվեն բնօրինակ թվերի միջև։

Պատասխան՝ $-\frac(5)(12);\ -\frac(1)(3);\ -\frac(1)(4)$

Առաջադրանք թիվ 10. 2-ի և 42-ի միջև տեղադրեք մի քանի թվեր, որոնք այս թվերի հետ միասին կազմում են թվաբանական առաջընթաց, եթե գիտեք, որ զետեղված թվերից առաջինի, երկրորդի և վերջինի գումարը 56 է։

Լուծում. Նույնիսկ ավելին դժվար գործ, որը, սակայն, լուծվում է նույն սխեմայով, ինչ նախորդները՝ միջին թվաբանականի միջոցով։ Խնդիրն այն է, որ մենք հստակ չգիտենք, թե քանի թիվ պետք է տեղադրվի: Հետևաբար, որոշակիորեն ենթադրենք, որ ամեն ինչ տեղադրելուց հետո կլինեն ճշգրիտ $n$ թվեր, և դրանցից առաջինը 2 է, իսկ վերջինը 42 է: Այս դեպքում անհրաժեշտ թվաբանական առաջընթացը կարող է ներկայացվել հետևյալ կերպ.

\[\left(((a)_(n)) \աջ)=\ձախ\( 2;((a)_(2));(a)_(3));...;(( ա)_(n-1));42 \աջ\)\]

\[((a)_(2))+((a)_(3))+((a)_(n-1))=56\]

Այնուամենայնիվ, նկատի ունեցեք, որ $((a)_(2))$ և $((a)_(n-1))$ թվերը ստացվում են եզրերում գտնվող 2 և 42 թվերից մեկ քայլ դեպի մեկը մյուսի ուղղությամբ, այսինքն. դեպի հաջորդականության կենտրոն։ Իսկ սա նշանակում է, որ

\[((a)_(2))+((a)_(n-1))=2+42=44\]

Բայց հետո վերևում գրված արտահայտությունը կարելի է վերաշարադրել հետևյալ կերպ.

\[\սկիզբ(հավասարեցնել) & ((a)_(2))+((a)_(3))+((a)_(n-1))=56; \\ & \left(((a)_(2))+((a)_(n-1)) \աջ)+((a)_(3))=56; \\ & 44+((a)_(3))=56; \\ & ((ա)_(3))=56-44=12. \\ \վերջ (հավասարեցնել)\]

Իմանալով $((a)_(3))$ և $((a)_(1))$, մենք հեշտությամբ կարող ենք գտնել առաջընթացի տարբերությունը.

\[\սկիզբ (հավասարեցնել) & ((a)_(3))-((a)_(1))=12-2=10; \\ & ((a)_(3))-((a)_(1))=\ձախ(3-1 \աջ)\cdot d=2d; \\ & 2d=10\Աջ սլաք d=5. \\ \վերջ (հավասարեցնել)\]

Մնում է միայն գտնել մնացած պայմանները.

\[\սկիզբ (հավասարեցնել) & ((a)_(1))=2; \\ & ((ա)_(2))=2+5=7; \\ & ((a)_(3))=12; \\ & ((a)_(4))=2+3\cdot 5=17; \\ & ((a)_(5))=2+4\cdot 5=22; \\ & ((a)_(6))=2+5\cdot 5=27; \\ & ((a)_(7))=2+6\cdot 5=32; \\ & ((a)_(8))=2+7\cdot 5=37; \\ & ((a)_(9))=2+8\cdot 5=42; \\ \վերջ (հավասարեցնել)\]

Այսպիսով, արդեն 9-րդ քայլին մենք կհասնենք հաջորդականության ձախ ծայրին` 42 համարին: Ընդհանուր առմամբ, ընդամենը 7 թիվ պետք է տեղադրվեր. 7; 12; 17; 22; 27; 32; 37.

Պատասխան՝ 7; 12; 17; 22; 27; 32; 37

Բառային խնդիրներ առաջընթացների հետ

Եզրափակելով, ես կցանկանայի դիտարկել մի քանի համեմատաբար պարզ խնդիր: Դե, այնքան պարզ. ուսանողների մեծամասնության համար, ովքեր դպրոցում մաթեմատիկա են սովորում և չեն կարդացել վերևում գրվածը, այս խնդիրները կարող են դժվար թվալ: Այնուամենայնիվ, սրանք խնդիրների տեսակներն են, որոնք ի հայտ են գալիս OGE-ում և մաթեմատիկայի միասնական պետական ​​քննությունում, ուստի խորհուրդ եմ տալիս ծանոթանալ դրանց:

Առաջադրանք թիվ 11. Թիմը հունվարին արտադրել է 62 մաս, իսկ յուրաքանչյուր հաջորդ ամսում նրանք արտադրել են 14-ով ավելի դետալ, քան նախորդ ամսում։ Քանի՞ մաս է արտադրվել թիմը նոյեմբերին:

Լուծում. Ակնհայտ է, որ ըստ ամիսների թվարկված մասերի թիվը կներկայացնի աճող թվաբանական առաջընթաց: Ավելին.

\[\սկիզբ(հավասարեցնել) & ((a)_(1))=62;\քառակուսի d=14; \\ & ((a)_(n))=62+\ձախ(n-1 \աջ)\cdot 14. \\ \վերջ (հավասարեցնել)\]

Նոյեմբերը տարվա 11-րդ ամիսն է, ուստի մենք պետք է գտնենք $((a)_(11))$:

\[((a)_(11))=62+10\cdot 14=202\]

Ուստի նոյեմբերին կարտադրվի 202 դետալ։

Առաջադրանք թիվ 12. Գրքերի սեմինարը հունվարին կապել է 216 գիրք, իսկ յուրաքանչյուր հաջորդ ամսում նախորդի համեմատ 4-ով ավելի գիրք է փակել։ Քանի՞ գիրք է կապել սեմինարը դեկտեմբերին։

Լուծում. Ամեն ինչ նույնն է.

$\սկիզբ (հավասարեցնել) & ((a)_(1))=216;\quad d=4; \\ & ((a)_(n))=216+\ձախ(n-1 \աջ)\cdot 4. \\ \վերջ (հավասարեցնել)$

Դեկտեմբերը տարվա վերջին, 12-րդ ամիսն է, ուստի մենք փնտրում ենք $((a)_(12))$:

\[((a)_(12))=216+11\cdot 4=260\]

Սա է պատասխանը՝ դեկտեմբերին կփակվի 260 գիրք։

Դե, եթե այսքանը կարդացել եք, շտապում եմ շնորհավորել ձեզ՝ հաջողությամբ ավարտել եք թվաբանական առաջընթացների «երիտասարդ մարտիկի կուրսը»։ Դուք կարող եք ապահով կերպով անցնել հաջորդ դասին, որտեղ մենք կուսումնասիրենք առաջընթացի գումարի բանաձևը, ինչպես նաև դրանից բխող կարևոր և շատ օգտակար հետևանքները:

Թվաբանական և երկրաչափական առաջընթացներ

Տեսական տեղեկատվություն

	Թվաբանական առաջընթաց	Երկրաչափական առաջընթաց
Սահմանում	Թվաբանական առաջընթաց a nհաջորդականություն է, որի յուրաքանչյուր անդամ, սկսած երկրորդից, հավասար է նույն թվին ավելացված նախորդ անդամին դ (դ- առաջընթացի տարբերություն)	Երկրաչափական առաջընթաց b nոչ զրոյական թվերի հաջորդականություն է, որի յուրաքանչյուր անդամ, սկսած երկրորդից, հավասար է նախորդ անդամին բազմապատկած նույն թվով. ք (ք- առաջընթացի հայտարար)
Կրկնության բանաձեւ	Ցանկացած բնականի համար n a n + 1 = a n + d	Ցանկացած բնականի համար n b n + 1 = b n ∙ q, b n ≠ 0
Բանաձև n-րդ կիսամյակ	a n = a 1 + d (n – 1)	b n = b 1 ∙ q n - 1 , b n ≠ 0
Բնութագրական հատկություն
Առաջին n անդամների գումարը

Առաջադրանքների օրինակներ մեկնաբանություններով

Առաջադրանք 1

Թվաբանական առաջընթացով ( a n) ա 1 = -6, ա 2

n-րդ անդամի բանաձևի համաձայն.

ա 22 = ա 1+ d (22 - 1) = ա 1+ 21 դ

Ըստ պայմանի.

ա 1= -6, ապա ա 22= -6 + 21 դ .

Անհրաժեշտ է գտնել առաջընթացների տարբերությունը.

դ = ա 2 – ա 1 = -8 – (-6) = -2

ա 22 = -6 + 21 ∙ (-2) = - 48.

Պատասխան. ա 22 = -48.

Առաջադրանք 2

Գտե՛ք երկրաչափական պրոգրեսիայի հինգերորդ անդամը՝ -3; 6;....

1-ին մեթոդ (n-term բանաձևի օգտագործմամբ)

Երկրաչափական առաջընթացի n-րդ անդամի բանաձևի համաձայն.

b 5 = b 1 ∙ q 5 - 1 = b 1 ∙ q 4.

Որովհետև բ 1 = -3,

2-րդ մեթոդ (կրկնվող բանաձևի օգտագործմամբ)

Քանի որ պրոգրեսիայի հայտարարը -2 է (q = -2), ապա.

բ 3 = 6 ∙ (-2) = -12;

բ 4 = -12 ∙ (-2) = 24;

բ 5 = 24 ∙ (-2) = -48.

Պատասխան. բ 5 = -48.

Առաջադրանք 3

Թվաբանական առաջընթացով ( ա ժ) ա 74 = 34; ա 76= 156. Գտե՛ք այս առաջընթացի յոթանասունհինգերորդ անդամը:

Թվաբանական առաջընթացի համար բնորոշ հատկությունն ունի ձևը .

Սրանից հետևում է.

.

Տվյալները փոխարինենք բանաձևով.

Պատասխան՝ 95։

Առաջադրանք 4

Թվաբանական առաջընթացով ( a n ) a n= 3n - 4. Գտե՛ք առաջին տասնյոթ անդամների գումարը:

Թվաբանական պրոգրեսիայի առաջին n անդամների գումարը գտնելու համար օգտագործվում են երկու բանաձև.

.

Որն է այս դեպքումավելի հարմար է օգտագործել.

Ըստ պայմանի, հայտնի է սկզբնական առաջընթացի n-րդ անդամի բանաձևը ( a n) a n= 3n - 4. Դուք կարող եք անմիջապես գտնել և ա 1, Եվ ա 16առանց գտնելու դ. Հետեւաբար, մենք կօգտագործենք առաջին բանաձեւը.

Պատասխան՝ 368։

Առաջադրանք 5

Թվաբանական առաջընթացով ( a n) ա 1 = -6; ա 2= -8. Գտե՛ք առաջընթացի քսաներկուերորդ անդամը:

n-րդ անդամի բանաձևի համաձայն.

ա 22 = ա 1 + դ (22 – 1) = ա 1+ 21 դ.

Պայմանով, եթե ա 1= -6, ապա ա 22= -6 + 21 դ . Անհրաժեշտ է գտնել առաջընթացների տարբերությունը.

դ = ա 2 – ա 1 = -8 – (-6) = -2

ա 22 = -6 + 21 ∙ (-2) = -48.

Պատասխան. ա 22 = -48.

Առաջադրանք 6

Երկրաչափական պրոգրեսիայի մի քանի հաջորդական անդամներ գրված են.

Գտե՛ք x-ով նշված պրոգրեսիայի տերմինը:

Լուծելիս կօգտագործենք n-րդ անդամի բանաձևը b n = b 1 ∙ q n - 1երկրաչափական առաջընթացների համար. Առաջընթացի առաջին տերմինը. q պրոգրեսիայի հայտարարը գտնելու համար անհրաժեշտ է վերցնել պրոգրեսիայի տրված անդամներից որևէ մեկը և բաժանել նախորդի վրա։ Մեր օրինակում մենք կարող ենք վերցնել և բաժանել: Մենք ստանում ենք, որ q = 3: Բանաձևում n-ի փոխարեն փոխարինում ենք 3, քանի որ անհրաժեշտ է գտնել տվյալ երկրաչափական պրոգրեսիայի երրորդ անդամը:

Գտնված արժեքները բանաձևի մեջ փոխարինելով՝ մենք ստանում ենք.

.

Պատասխան.

Առաջադրանք 7

n-րդ անդամի բանաձևով տրված թվաբանական առաջընթացներից ընտրե՛ք այն մեկը, որի համար պայմանը բավարարված է. ա 27 > 9:

Քանի որ տվյալ պայմանը պետք է բավարարվի պրոգրեսիայի 27-րդ անդամի համար, չորս առաջընթացներից յուրաքանչյուրում n-ի փոխարեն փոխարինում ենք 27-ը: 4-րդ առաջընթացում մենք ստանում ենք.

.

Պատասխան՝ 4.

Առաջադրանք 8

Թվաբանական առաջընթացի մեջ ա 1= 3, d = -1,5: Նշեք ամենաբարձր արժեքը n, որի համար անհավասարությունը պահպանվում է a n > -6.

Երբ ուսումնասիրում են հանրահաշիվը միջնակարգ դպրոց(9-րդ դասարան) կարևոր թեմաներից է թվերի հաջորդականությունների ուսումնասիրությունը, որոնք ներառում են առաջընթացներ՝ երկրաչափական և թվաբանական: Այս հոդվածում մենք կանդրադառնանք թվաբանական առաջընթացին և լուծումներով օրինակներին:

Ի՞նչ է թվաբանական առաջընթացը:

Սա հասկանալու համար անհրաժեշտ է սահմանել խնդրո առարկա առաջընթացը, ինչպես նաև տրամադրել հիմնական բանաձևերը, որոնք հետագայում կօգտագործվեն խնդիրների լուծման ժամանակ:

Հայտնի է, որ որոշ հանրահաշվական պրոգրեսիաներում 1-ին անդամը հավասար է 6-ի, իսկ 7-րդ անդամը հավասար է 18-ի։ Անհրաժեշտ է գտնել տարբերությունը և վերականգնել այս հաջորդականությունը 7-րդ անդամին։

Անհայտ տերմինը որոշելու համար օգտագործենք բանաձևը՝ a n = (n - 1) * d + a 1 : Պայմանից հայտնի տվյալները փոխարինենք դրա մեջ, այսինքն՝ a 1 և a 7 թվերը, ունենք՝ 18 = 6 + 6 * d. Այս արտահայտությունից հեշտությամբ կարող եք հաշվարկել տարբերությունը. d = (18 - 6) /6 = 2: Այսպիսով, մենք պատասխանել ենք խնդրի առաջին մասին:

Հերթականությունը 7-րդ անդամին վերականգնելու համար պետք է օգտագործել հանրահաշվական պրոգրեսիայի սահմանումը, այսինքն՝ a 2 = a 1 + d, a 3 = a 2 + d և այլն։ Արդյունքում մենք վերականգնում ենք ամբողջ հաջորդականությունը՝ a 1 = 6, a 2 = 6 + 2=8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 , a 6 = 14 + 2 = 16, a 7 = 18:

Օրինակ թիվ 3. պրոգրեսիա կազմելը

Խնդիրն էլ ավելի բարդացնենք։ Այժմ մենք պետք է պատասխանենք այն հարցին, թե ինչպես գտնել թվաբանական պրոգրեսիա: Կարելի է բերել հետևյալ օրինակը. տրված է երկու թիվ, օրինակ՝ 4 և 5։ Անհրաժեշտ է ստեղծել հանրահաշվական պրոգրեսիա, որպեսզի դրանց միջև դրվեն ևս երեք անդամ։

Նախքան այս խնդրի լուծումը սկսելը, պետք է հասկանալ, թե տվյալ թվերը ինչ տեղ են գրավելու ապագա առաջընթացում։ Քանի որ նրանց միջև կլինեն ևս երեք տերմիններ, ապա 1 = -4 և 5 = 5: Սա հաստատելով, մենք անցնում ենք խնդրին, որը նման է նախորդին: Կրկին, n-րդ անդամի համար մենք օգտագործում ենք բանաձևը, մենք ստանում ենք. a 5 = a 1 + 4 * d: Սկսած՝ d = (a 5 - a 1)/4 = (5 - (-4)) / 4 = 2.25: Այն, ինչ մենք այստեղ ստացանք, տարբերության ամբողջ արժեք չէ, այլ ռացիոնալ թիվ է, ուստի հանրահաշվական առաջընթացի բանաձևերը մնում են նույնը:

Հիմա եկեք ավելացնենք գտնված տարբերությունը 1-ին և վերականգնենք առաջընթացի բացակայող պայմանները: Մենք ստանում ենք՝ a 1 = - 4, a 2 = - 4 + 2,25 = - 1,75, a 3 = -1,75 + 2,25 = 0,5, a 4 = 0,5 + 2,25 = 2,75, a 5 = 2,75 + 2,25 = 5, որը համընկնում է խնդրի պայմաններով։

Օրինակ թիվ 4. առաջընթացի առաջին ժամկետը

Շարունակենք տալ թվաբանական առաջընթացի օրինակներ՝ լուծումներով։ Նախորդ բոլոր խնդիրներում հայտնի էր հանրահաշվական պրոգրեսիայի առաջին թիվը։ Հիմա եկեք դիտարկենք այլ տեսակի խնդիր. թող տրվի երկու թիվ, որտեղ 15 = 50 և 43 = 37: Պետք է գտնել, թե որ թվով է սկսվում այս հաջորդականությունը:

Մինչ այժմ օգտագործված բանաձևերը ենթադրում են 1-ի և դ-ի իմացություն: Խնդրի հայտարարության մեջ այս թվերի մասին ոչինչ հայտնի չէ։ Այնուամենայնիվ, մենք կգրենք արտահայտություններ յուրաքանչյուր տերմինի համար, թե որ տեղեկատվությունն առկա է. a 15 = a 1 + 14 * d և a 43 = a 1 + 42 * d: Մենք ստացանք երկու հավասարումներ, որոնցում կան 2 անհայտ մեծություններ (a 1 և d): Սա նշանակում է, որ խնդիրը կրճատվում է գծային հավասարումների համակարգի լուծման վրա:

Այս համակարգը լուծելու ամենահեշտ ձևը յուրաքանչյուր հավասարման մեջ 1 արտահայտելն է, իսկ հետո ստացված արտահայտությունները համեմատելը: Առաջին հավասարումը. a 1 = a 15 - 14 * d = 50 - 14 * d; երկրորդ հավասարումը. a 1 = a 43 - 42 * d = 37 - 42 * d. Հավասարեցնելով այս արտահայտությունները՝ ստանում ենք՝ 50 - 14 * d = 37 - 42 * d, որտեղից էլ տարբերությունը d = (37 - 50) / (42 - 14) = - 0,464 (տրված է ընդամենը 3 տասնորդական տեղ)։

Իմանալով d-ն, դուք կարող եք օգտագործել վերը նշված 2 արտահայտություններից որևէ մեկը 1-ի համար: Օրինակ, նախ՝ a 1 = 50 - 14 * d = 50 - 14 * (- 0,464) = 56,496:

Ստացված արդյունքի վերաբերյալ կասկածներ ունենալու դեպքում կարող եք ստուգել այն, օրինակ՝ որոշել պրոգրեսիայի 43-րդ տերմինը, որը նշված է պայմանում։ Մենք ստանում ենք՝ a 43 = a 1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008: Փոքր սխալը պայմանավորված է նրանով, որ հաշվարկներում օգտագործվել է կլորացում մինչև հազարերորդական:

Օրինակ թիվ 5՝ գումար

Այժմ նայենք մի քանի օրինակների՝ թվաբանական առաջընթացի գումարի լուծումներով:

Թող տրվի հետևյալ ձևի թվային առաջընթացը՝ 1, 2, 3, 4, ...,: Ինչպե՞ս հաշվարկել այս թվերից 100-ի գումարը:

Համակարգչային տեխնոլոգիաների զարգացման շնորհիվ հնարավոր է լուծել այս խնդիրը, այսինքն՝ հաջորդաբար գումարել բոլոր թվերը, ինչը համակարգիչը կանի հենց որ մարդը սեղմի Enter ստեղնը։ Այնուամենայնիվ, խնդիրը կարող է լուծվել մտովի, եթե ուշադրություն դարձնեք այն փաստին, որ թվերի ներկայացված շարքը հանրահաշվական պրոգրեսիա է, և դրա տարբերությունը հավասար է 1-ի: Կիրառելով գումարի բանաձևը, մենք ստանում ենք S n = n * ( a 1 + a n) / 2 = 100 * (1 + 100) / 2 = 5050:

Հետաքրքիր է նշել, որ այս խնդիրը կոչվում է «գաուսյան», քանի որ ներս վաղ XVIIIդարում հայտնի գերմանացին, դեռ ընդամենը 10 տարեկանում, մի քանի վայրկյանում կարողացավ լուծել այն իր գլխում։ Տղան չգիտեր հանրահաշվական պրոգրեսիայի գումարի բանաձևը, բայց նա նկատեց, որ եթե հաջորդականության ծայրերում թվերը գումարեք զույգերով, ապա միշտ ստանում եք նույն արդյունքը, այսինքն՝ 1 + 100 = 2 + 99։ = 3 + 98 = ..., և քանի որ այդ գումարները կլինեն ուղիղ 50 (100 / 2), ապա ճիշտ պատասխան ստանալու համար բավական է 50-ը բազմապատկել 101-ով:

Օրինակ թիվ 6. n-ից մինչև m տերմինների գումարը

Թվաբանական առաջընթացի գումարի մեկ այլ տիպիկ օրինակ հետևյալն է՝ տրված թվերի շարքը՝ 3, 7, 11, 15, ..., դուք պետք է գտնեք, թե ինչի է հավասար դրա 8-ից 14 անդամների գումարը։ .

Խնդիրը լուծվում է երկու ճանապարհով. Դրանցից առաջինը ներառում է 8-ից 14-ը անհայտ տերմիններ գտնելը, այնուհետև հաջորդաբար գումարելը: Քանի որ տերմինները քիչ են, այս մեթոդը այնքան էլ աշխատատար չէ: Այնուամենայնիվ, առաջարկվում է լուծել այս խնդիրը երկրորդ մեթոդով, որն ավելի ունիվերսալ է։

Գաղափարն է ստանալ բանաձև m և n տերմինների միջև հանրահաշվական առաջընթացի գումարի համար, որտեղ n > m ամբողջ թվեր են: Երկու դեպքում էլ գումարի համար գրում ենք երկու արտահայտություն.

1. S m = m * (a m + a 1) / 2:
2. S n = n * (a n + a 1) / 2:

Քանի որ n > m, ակնհայտ է, որ 2-րդ գումարը ներառում է առաջինը։ Վերջին եզրակացությունը նշանակում է, որ եթե վերցնենք այս գումարների տարբերությունը և դրան գումարենք a m տերմինը (տարբերությունը վերցնելու դեպքում այն ​​հանվում է S n գումարից), ապա կստանանք խնդրի անհրաժեշտ պատասխանը։ Մենք ունենք՝ S mn = S n - S m + a m =n * (a 1 + a n) / 2 - m *(a 1 + a m)/2 + a m = a 1 * (n - m) / 2 + a n * n/2 + a m * (1- m/2): Այս արտահայտության մեջ անհրաժեշտ է փոխարինել a-ի և a-ի բանաձևերը: Այնուհետև մենք ստանում ենք՝ S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2:

Ստացված բանաձևը որոշ չափով դժվար է, սակայն S mn գումարը կախված է միայն n, m, a 1 և d-ից: Մեր դեպքում a 1 = 3, d = 4, n = 14, m = 8: Փոխարինելով այս թվերը, մենք ստանում ենք S mn = 301:

Ինչպես երևում է վերը նշված լուծումներից, բոլոր խնդիրները հիմնված են n-րդ անդամի արտահայտության և առաջին անդամների բազմության գումարի բանաձևի իմացության վրա: Նախքան այս խնդիրներից որևէ մեկի լուծումը սկսելը, խորհուրդ է տրվում ուշադիր կարդալ պայմանը, հստակ հասկանալ, թե ինչ է պետք գտնել, և միայն դրանից հետո շարունակել լուծումը:

Մեկ այլ հուշում է ձգտել պարզության, այսինքն, եթե դուք կարող եք պատասխանել հարցին առանց բարդ մաթեմատիկական հաշվարկներ օգտագործելու, ապա ձեզ հարկավոր է դա անել, քանի որ այս դեպքում սխալվելու հավանականությունն ավելի քիչ է: Օրինակ, թիվ 6 լուծումով թվաբանական առաջընթացի օրինակում կարելի էր կանգ առնել S mn = n * (a 1 + a n) / 2 - m * (a 1 + a m) / 2 + a m բանաձևի վրա և. ընդհանուր խնդիրը բաժանեք առանձին ենթաառաջադրանքների (այս դեպքում նախ գտեք a n և a m տերմինները):

Ստացված արդյունքի վերաբերյալ կասկածներ ունենալու դեպքում խորհուրդ է տրվում ստուգել այն, ինչպես արվել է բերված որոշ օրինակներում։ Մենք պարզեցինք, թե ինչպես կարելի է գտնել թվաբանական առաջընթաց: Եթե ​​դուք դա պարզեք, դա այնքան էլ դժվար չէ:

Թվաբանական առաջընթացի հետ կապված խնդիրներ կային արդեն հին ժամանակներում։ Նրանք հայտնվեցին և լուծում պահանջեցին, քանի որ գործնական կարիք ունեին։

Այսպիսով, պապիրուսներից մեկում Հին Եգիպտոս«, որն ունի մաթեմատիկական բովանդակություն՝ Ռինդ պապիրուսը (մ.թ.ա. 19-րդ դար), պարունակում է հետևյալ առաջադրանքը՝ հացի տասը չափաբաժինը բաժանել տասը հոգու, պայմանով, որ նրանցից յուրաքանչյուրի տարբերությունը չափի մեկ ութերորդն է»։

Իսկ հին հույների մաթեմատիկական աշխատություններում կան էլեգանտ թեորեմներ՝ կապված թվաբանական պրոգրեսիայի հետ։ Այսպիսով, Hypsicles of Alexandria (2-րդ դար, որը հավաքեց շատ հետաքրքիր խնդիրներ և ավելացրեց տասնչորսերորդ գիրքը Էվկլիդեսի տարրերին), ձևակերպեց գաղափարը. մեծ է անդամների 1/2 քառակուսու 1-ին թվերի գումարից»։

Հերթականությունը նշվում է an-ով: Հերթականության համարները կոչվում են նրա անդամներ և սովորաբար նշանակվում են ցուցիչներով տառերով, որոնք ցույց են տալիս այս անդամի սերիական համարը (a1, a2, a3 ... կարդալ՝ «1-ին», «ա 2-րդ», «ա 3-րդ» և այլն):

Հերթականությունը կարող է լինել անվերջ կամ վերջավոր:

Ի՞նչ է թվաբանական առաջընթացը: Դրա տակ նկատի ունենք նախորդ (n) անդամը նույն d թվով գումարելով ստացվածը, որը պրոգրեսիայի տարբերությունն է։

Եթե ​​դ<0, то мы имеем убывающую прогрессию. Если d>0, ապա այս առաջընթացը համարվում է աճող:

Թվաբանական առաջընթացը կոչվում է վերջավոր, եթե հաշվի առնվեն միայն դրա առաջին մի քանի անդամները: Շատ մեծ թվով անդամներով սա արդեն անվերջ առաջընթաց է:

Ցանկացած թվաբանական առաջընթաց սահմանվում է հետևյալ բանաձևով.

an =kn+b, մինչդեռ b և k որոշ թվեր են:

Հակառակ պնդումը բացարձակապես ճիշտ է. եթե հաջորդականությունը տրված է նմանատիպ բանաձևով, ապա դա հենց թվաբանական պրոգրեսիա է, որն ունի հատկություններ.

1. Առաջընթացի յուրաքանչյուր անդամ նախորդ և հաջորդ անդամի միջին թվաբանականն է:
2. Հակադարձ. եթե 2-րդից սկսած յուրաքանչյուր անդամ նախորդ և հաջորդ անդամի միջին թվաբանականն է, այսինքն. եթե պայմանը բավարարված է, ապա այս հաջորդականությունը թվաբանական պրոգրեսիա է: Այս հավասարությունը նույնպես առաջընթացի նշան է, այդ իսկ պատճառով այն սովորաբար կոչվում է պրոգրեսիայի բնորոշ հատկություն։
   Նույն կերպ, այս հատկությունն արտացոլող թեորեմը ճշմարիտ է. հաջորդականությունը թվաբանական առաջընթաց է միայն այն դեպքում, եթե այս հավասարությունը ճշմարիտ է հաջորդականության որևէ անդամի համար՝ սկսած 2-րդից:

Թվաբանական առաջընթացի ցանկացած չորս թվերի բնորոշ հատկությունը կարող է արտահայտվել an + am = ak + al բանաձևով, եթե n + m = k + l (m, n, k պրոգրեսիայի թվեր են):

Թվաբանական առաջընթացում ցանկացած անհրաժեշտ (N-րդ) տերմին կարելի է գտնել հետևյալ բանաձևով.

Օրինակ՝ թվաբանական պրոգրեսիայի առաջին անդամը (a1) տրված է և հավասար է երեքի, իսկ (d) տարբերությունը հավասար է չորսի: Դուք պետք է գտնեք այս առաջընթացի քառասունհինգերորդ անդամը: a45 = 1+4 (45-1) = 177

Բանաձևը an = ak + d(n - k) թույլ է տալիս որոշել թվաբանական առաջընթացի n-րդ անդամը նրա kth անդամներից որևէ մեկի միջոցով, պայմանով, որ այն հայտնի է:

Թվաբանական առաջընթացի (նկատի ունի վերջավոր պրոգրեսիայի 1-ին n անդամները) գումարը հաշվարկվում է հետևյալ կերպ.

Sn = (a1+an) n/2.

Եթե ​​1-ին անդամը նույնպես հայտնի է, ապա հաշվարկման համար հարմար է մեկ այլ բանաձև.

Sn = ((2a1+d(n-1))/2)*n.

Թվաբանական առաջընթացի գումարը, որը պարունակում է n անդամ, հաշվարկվում է հետևյալ կերպ.

Հաշվարկների համար բանաձևերի ընտրությունը կախված է խնդիրների պայմաններից և նախնական տվյալներից:

Ցանկացած թվերի բնական շարքը, օրինակ՝ 1,2,3,...,n,..., թվաբանական առաջընթացի ամենապարզ օրինակն է։

Բացի թվաբանական պրոգրեսիայից, կա նաև երկրաչափական պրոգրեսիա, որն ունի իր առանձնահատկություններն ու առանձնահատկությունները։