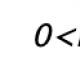Graphiques et propriétés des fonctions trigonométriques sinus et cosinus Graphique de la fonction y = sinx Graphique de la fonction y = sinx Propriétés de la fonction y = sinx Propriétés de la fonction y = sinx Graphique de la fonction y = cosx Graphique de la fonction y = cosx Propriétés de la fonction y = cosx Propriétés de la fonction y = cosx Comparaison des propriétés des fonctions y = sinx et y = cosx Comparaison des propriétés des fonctions y = sinx et y = cosx

Propriétés de la fonction y = sinx 6. Intervalles de signe constant de la fonction y = sinx : sinx> 0 pour x (2k ; + 2k), sinx 0 pour x (2k ; + 2k), sinx 0 pour x (2k ; + 2k), sinx 0 pour x (2k ; + 2k), sinx 0 pour x (2k ; + 2k), sinx title = "(! LANG : Propriétés de la fonction y = sinx 6. Intervalles de signe de la fonction y = sinx : sinx> 0 pour x (2k ; + 2k), sinx

Propriétés de la fonction y = cosx 6. Intervalles de signe constant de la fonction y = cosx : cosx > 0 pour x (- / 2 + k ; / 2 + k), k cosx 0 pour x (- / 2 + k ; / 2 + k), k cosx 0 pour x (- / 2 + k; / 2 + k), k cosx 0 pour x (- / 2 + k; / 2 + k), k cosx 0 pour x (- / 2 + k; / 2 + k), k cosx title = "(! LANG : Propriétés de la fonction y = cosx 6. Intervalles de signe constant de la fonction y = cosx : cosx> 0 pour x (- / 2 + k ; / 2 + k), k cosx

Comparaison des propriétés des fonctions y = sinx et y = cosx Fonction y = sinxy = cosx Domaine D (sinx) = D (cosx) = Ensemble de valeurs E (sinx) = [-1,1] E (cosx ) = [-1,1] Pair et impair impair impair pair Zéros de la fonction x = k, kx = / 2 + k, k Intervalles de signe constant y (x)> 0 x (2k; + 2k) x (- / 2 + k; / 2 + k) ky (x ) 0 x (2k; + 2k) x (- / 2 + k; / 2 + k) ky (x)

"Fonction y = cos x" - Zéros de la fonction, valeurs positives et négatives. Trouvons quelques points pour tracer. Y = cos (x - a). Transformation du graphe de la fonction y = cos x. Fonction y = cos x. Y = cos x + A (propriétés). Propriétés. Réflexion symétrique autour de l'axe des abscisses. Graphique de fonction. Même bizarre.

"Propriétés des fonctions trigonométriques inverses" - Spécifiez la plage de valeurs de la fonction. Résoudre des équations. Trouver le sens de l'expression. Résolution d'équations. Travail de groupe. Cours au choix en mathématiques. Fonctions d'arc. Résolvons le système d'équations. Recherche. Spécifiez la portée de la fonction. Répétition. Le triple satisfait l'équation originale.

"Fonctions de tangente et de cotangente" - Propriétés de la fonction y = tgx. Solutions. Racines de l'équation. Calendrier. Construire un graphique. Propriétés de la fonction. Sens. Fraction. Les principales propriétés de la fonction. Fonction y = tgx. Propriétés de base. y = ctgx. Fonction graphique y = ctgx. Nombres.

"Convertir les graphiques trigonométriques" - Fonction sinus. Conversion de graphiques de fonctions trigonométriques. Caractéristique du graphe d'oscillation harmonique. Graphique de la fonction y = f (x) + m. Fonction cosinus. Graphique de la fonction y = f (| x |). Graphique de la fonction y = | f (x) |. Caractéristique des transformations de graphes de fonctions. Y = f(x). Fonction tangente. Tracés de l'horaire résultant.

"Arcfunctions" - Méthode graphique fonctionnelle pour résoudre des équations. Arctgx. Fonction. Fonctions trigonométriques. Propriétés des fonctions d'arc. Y = arcctgx. Arcctg t = a. Arccosx. Méthode graphique pour résoudre des équations. Plage de valeurs. Égalité. Définitions. Expression. Définition. Arctg t. Arccos t. Beaucoup de nombres réels.

"Algèbre" Fonctions trigonométriques "" - Fonctions trigonométriques d'un argument angulaire. Tableau des valeurs des fonctions trigonométriques de certains angles. Un guide d'algèbre et les débuts de l'analyse. Solution des inégalités trigonométriques. Résolution d'équations trigonométriques. Conversion de sommes de fonctions trigonométriques en produits. Trigonométrie.

L'un des termes importants en trigonométrie est le cosinus. Dans cette présentation, la fonction cosinus sera considérée, son graphe est construit. Toutes les propriétés qu'il possède seront détaillées.

Sur la première diapositive, avant de commencer à considérer la fonction elle-même, l'une des formules de coulée est rappelée. Il a été précédemment démontré en détail avec la preuve.

Cette formule dit que la fonction cosinus peut être remplacée par un sinus avec certains changements dans l'argument. Ainsi, ayant déjà étudié les sinusoïdes, les écoliers pourront construire cette fonction. En conséquence, ils obtiendront un graphique de la fonction cosinus.

Le graphique de fonction peut être vu sur la deuxième diapositive. Vous pouvez noter que la sinusoïde n'a décalé que de pi/2. Ainsi, contrairement à une sinusoïde, le graphe de la fonction cosinus ne passe pas par le point (0 ; 0).

La première étape serait de considérer le domaine de la fonction. C'est un point important et c'est là que commence l'analyse de toute fonction en mathématiques. La portée de cette fonction est l'axe des nombres entier. Cela peut être clairement vu dans le graphique de la fonction.

Contrairement au sinus, la fonction cosinus est paire. C'est-à-dire que si vous changez le signe de l'argument, le signe de la fonction ne changera pas. La parité est déterminée par la propriété sinus.

La fonction augmente à certains intervalles et diminue à certains intervalles. Cela suggère que la fonction cosinus est monotone. Ces intervalles sont indiqués sur la diapositive suivante. Le graphique montre clairement l'augmentation et la diminution de la fonction.

La cinquième propriété est la limitation. La fonction cosinus est bornée à la fois en haut et en bas. La valeur minimale est -1 et la valeur maximale est +1.

Comme il n'y a pas de points de rupture et de pics aigus, la fonction cosinus, comme la fonction sinus, est continue.

La dernière diapositive résume toutes les propriétés qui ont été discutées dans la présentation. Ce sont quelques-unes des principales caractéristiques de la fonction cosinus. Après les avoir mémorisés, vous pouvez facilement faire face à un certain nombre d'équations contenant un cosinus. Il sera plus facile de maîtriser ces propriétés si vous en comprenez parfaitement l'essence.

Pour utiliser l'aperçu des présentations, créez vous-même un compte Google (compte) et connectez-vous : https://accounts.google.com

Légendes des diapositives :

Fonction y = sin x, ses propriétés et son graphique. Objectifs de la leçon : Passer en revue et systématiser les propriétés de la fonction y = sin x. Apprenez à tracer la fonction y = sin x.

y = sin x Domaine de définition - l'ensemble R de tous les nombres réels : D (f) = (- ∞; + ∞) Propriété 1.

y = sin x Puisque sin (-x) = - sin x, alors y = sin x est une fonction impaire, ce qui signifie que son graphique est symétrique par rapport à l'origine. Propriété 2.

y = sin x La fonction y = croît sur le segment et décroît sur le segment [π / 2; ]. Propriété 3.0 / 2

y = sin x La fonction y = sin x est bornée à la fois par le bas et par le haut : - 1 ≤ sin x ≤ 1 Propriété 4.

y = sin x y naim = -1 y naib = 1 Propriété 5. 0 / 2

Construisons un graphique de la fonction y = sin x dans le système de coordonnées rectangulaires Oxy.

y 0 / 2 x

Tout d'abord, construisons une partie du graphique sur un segment. -2 π -3 π / 2 - π - π / 2 0 π / 2 π 3 π / 2 2 π X 1 -1 Y x 0 π / 6 / 3 / 2 2 / 3 5 π / 6 π y 0 1/2 3/2 1 √ 3/2 1/2 0 Tracez maintenant une partie du graphe sur le segment [- π; 0], en tenant compte de la bizarrerie de la fonction y = sin x. Sur le segment [π; 2 π] le graphique de la fonction ressemble à nouveau à ceci : Et sur l'intervalle [-2 π; - π] le graphe de la fonction ressemble à ceci : Ainsi, le graphe entier est une ligne continue, qui s'appelle une sinusoïde. Arc sinus Demi onde sinusoïdale

N ° 168 - par voie orale. -3 π -5 π / 2 -2 π -3 / 2 - π - π / 2 0 / 2 π 3 π / 2 2 π 5 π / 2 3 π Х У 1 -1

Résolvez les exercices 170, 172, 173 (a, b). Devoir : n° 171, 173 (c, d)

Sur le sujet : développements méthodologiques, présentations et notes

Test interactif, qui contient 5 tâches avec le choix d'une bonne réponse sur quatre proposées, en tenant compte du temps passé pour réussir le test ; le test a été créé dans PowerPoint-2007 avec et ...

La section des mathématiques de la trigonométrie comprend l'étude de concepts tels que sinus, cosinus, tangente et cotangente. Séparément, les écoliers devront considérer chaque fonction, étudier la nature du comportement sur le graphique, considérer la fréquence, la portée, la plage de valeurs et d'autres paramètres.

Donc la fonction sinus. La première diapositive montre la vue générale de la fonction. La variable t est utilisée comme argument.

La première étape est, comme pour toute fonction, la portée est considérée, ce qui indique quelles valeurs l'argument peut prendre. Dans le cas du sinus, il s'agit de l'axe des nombres entier. Vous pouvez le voir plus tard sur le graphique de la fonction.

La deuxième propriété, qui est considérée en utilisant l'exemple du sinus, est la parité. La sinusoïde est étrange. C'est parce que la fonction de -x sera égale à la fonction avec un signe moins. Afin de rappeler ce matériel, vous pouvez revenir aux présentations précédentes et visualiser.

Cette propriété est illustrée sur le cercle d'unité qui apparaît sur le côté gauche de la diapositive. Ainsi, la propriété est également prouvée géométriquement.

La troisième propriété qui doit également être considérée est la propriété de la monotonie. Sur certains segments, la fonction augmente, sur certains elle diminue. Cela nous permet d'appeler la sinusoïde une fonction monotone. Puisque les intervalles d'augmentation et de diminution sont infinis, cela est noté par périodicité.

La quatrième propriété est la limitation. La sinusoïde est délimitée en haut et en bas. La valeur minimale, dans ce cas, est 1, la valeur maximale est +1. Ainsi, la fonction sinus est bornée à la fois en haut et en bas.

La définition d'une sinusoïde est donnée, qui doit être remplie. En outre, diverses déformations d'une sinusoïde à différentes valeurs sont prises en compte.

Une fois la définition donnée, l'examen des propriétés de la fonction sinus se poursuit. C'est continu. Cela peut être clairement vu dans le graphique de la fonction. Aucun point de rupture n'existe.

La dernière diapositive montre comment vous pouvez résoudre graphiquement une équation qui contient une fonction sinus. Cette méthode simplifiera la solution et la rendra plus claire.