Раздели на сайта
Избор на редакторите:
- Препоръки и инструкции стъпка по стъпка за кандидата
- Какви документи са необходими за прием в университет Какви документи са необходими за прием в институт
- Функции на лимбичната система
- Възникване и развитие на човешката психика
- Игри за готвене Monster High Игри за момичета Monster High готвене
- Защо да мечтаете за кръв: тълкуване от книги за сънища
- Как да укротите гнева и защо е важно да го направите Какво означава човек да е ядосан
- Manana име от каква националност
- Как да се научим да сдържаме емоциите - съвети от психолог, практически препоръки Способността да контролирате емоциите си
- Кога е Денят на речния флот?
реклама
| Вибрации на механична система са примери за termex. Теоретична механика |
|
Общи теореми за динамиката на система от тела. Теореми за движението на центъра на масата, за изменението на импулса, за изменението на главния момент на импулса, за изменението на кинетичната енергия. Принципи на д'Аламбер и възможни измествания. Общо уравнение на динамиката. Уравнения на Лагранж. Общи теореми за динамиката на твърдото тяло и системите от телаОбщи теореми на динамикатае теоремата за движението на центъра на масата механична система, теоремата за изменението на импулса, теоремата за изменението на главния момент на импулса (кинетичен момент) и теоремата за изменението на кинетичната енергия на механична система. Теорема за движението на центъра на масата на механична системаТеорема за движението на центъра на масата. Тук M е масата на системата: Теорема за промяната на импулса (импулса)Количеството движение (импулс) на систематае равна на произведението на масата на цялата система и скоростта на нейния център на масата или сумата от импулса (сумата от импулси) на отделни точки или части, които съставляват системата: Теорема за промяната на импулса в диференциална форма. Теорема за промяната на импулса в интегрална форма. Законът за запазване на импулса (импулса). Ако сумата от проекциите на външните сили върху която и да е ос е равна на нула, тогава проекцията на импулса на системата върху тази ос ще бъде постоянна. Теорема за промяната на главния момент на импулса (теорема за моментите)Основният момент на количеството на движение на системата спрямо даден център O е стойността, равна на векторната сума на моментите на количествата на движение на всички точки на системата спрямо този център: Фиксирани системиСледващата теорема се отнася за случая, когато механичната система има фиксирана точка или ос, която е фиксирана по отношение на инерциалната отправна система. Например тяло, фиксирано със сферичен лагер. Или система от тела, движещи се около фиксиран център. Може да бъде и неподвижна ос, около която се върти тяло или система от тела. В този случай моментите трябва да се разбират като моменти на импулси и сили спрямо неподвижната ос. Теорема за промяната на главния момент на импулса (теорема за моментите) Законът за запазване на главния момент на импулса (момент на импулса). Ако сумата от моментите на външните сили около някаква фиксирана ос е равна на нула, тогава моментът на импулса на системата около тази ос ще бъде постоянен. Произволни системиСледващата теорема има универсален характер. Приложим е както за неподвижни системи, така и за свободно движещи се. При фиксираните системи е необходимо да се вземат предвид реакциите на връзките във фиксираните точки. Тя се различава от предишната теорема по това, че центърът на масата C на системата трябва да се вземе вместо фиксираната точка O. Теорема за моментите около центъра на масата Закон за запазване на ъгловия момент. инерционен момент на тялотоАко тялото се върти около оста zс ъглова скорост ω z , тогава неговият ъглов момент (кинетичен момент) спрямо оста z се определя по формулата: Инерционният момент на тялото спрямо оста zсе определя по формулата: Теоремата на Щайнер-Хюйгенс. В повече общ случай
: Теорема за промяна на кинетичната енергияНека тяло с маса M извършва постъпателно и въртеливо движение с ъглова скорост ω около някаква ос z. Тогава кинетичната енергия на тялото се определя по формулата: Теорема за изменението на кинетичната енергия на системата в диференциална форма. Теорема за изменението на кинетичната енергия на системата в интегрална форма. Работата, извършена от силата, е равно на скаларното произведение на векторите на силата и безкрайно малкото преместване на точката на нейното приложение: Работата, извършена от момента на силата, е равно на скаларното произведение на векторите на момента и безкрайно малкия ъгъл на завъртане: принцип на д'АламберСъщността на принципа на д'Аламбер е да сведе проблемите на динамиката до проблемите на статиката. За целта се приема (или е известно предварително), че телата на системата имат определени (ъглови) ускорения. След това се въвеждат силите на инерцията и (или) моментите на инерционните сили, които са равни по големина и реципрочни по посока на силите и моментите на силите, които според законите на механиката биха създали дадени ускорения или ъглови ускорения Помислете за пример. Тялото извършва постъпателно движение и върху него действат външни сили. Освен това приемаме, че тези сили създават ускорение на центъра на масата на системата. Според теоремата за движението на центъра на масата центърът на масата на тялото би имал същото ускорение, ако върху тялото действа сила. След това въвеждаме силата на инерцията: За въртеливото движение продължете по подобен начин. Нека тялото се върти около оста z и върху него действат външни моменти на сили M e zk. Приемаме, че тези моменти създават ъглово ускорение ε z . След това въвеждаме момента на инерционните сили M И = - J z ε z . След това задачата на динамиката е: Принципът на възможните движенияПринципът на възможните премествания се използва за решаване на проблеми със статиката. В някои задачи дава по-кратко решение от писането на уравнения за равновесие. Това важи особено за системи с връзки (например системи от тела, свързани с нишки и блокове), състоящи се от много тела Принципът на възможните движения. Възможно преместване на системата- това е малко изместване, при което не се прекъсват връзките, наложени на системата. Перфектни връзки- това са връзки, които не вършат работа при преместване на системата. По-точно сумата на работата, извършена от самите връзки при преместване на системата, е нула. Общо уравнение на динамиката (принцип на Д'Аламбер - Лагранж)Принципът на д'Аламбер-Лагранж е комбинация от принципа на д'Аламбер с принципа на възможните премествания. Тоест, когато решаваме проблема с динамиката, въвеждаме силите на инерцията и свеждаме проблема до проблема със статиката, който решаваме, използвайки принципа на възможните премествания. принцип на д'Аламбер-Лагранж. Уравнения на ЛагранжОбобщени координати q 1 , q 2 , ..., q n е набор от n стойности, които еднозначно определят позицията на системата. Броят на обобщените координати n съвпада с броя на степените на свобода на системата. Обобщени скоростиса производните на обобщените координати по време t. Обобщени сили Q 1 , Q 2 , ..., Q n
. Ако при възможно изместване на системата всички координати се променят, тогава работата, извършена от външни сили по време на такова изместване, има формата: За потенциални силис потенциал Π, Уравнения на Лагранжса уравненията на движение на механична система в обобщени координати: Тук Т е кинетичната енергия. Това е функция на обобщени координати, скорости и вероятно време. Следователно неговата частна производна също е функция на обобщени координати, скорости и време. След това трябва да вземете предвид, че координатите и скоростите са функции на времето. Следователно, за да намерите производната на общото време, трябва да приложите правилото за диференциране на сложна функция: Препратки: Лекция 3 Общи теореми на динамиката Динамика на системата от материални точкие важен раздел на теоретичната механика. Тук основно разглеждаме проблемите на движението на механични системи (системи от материални точки) с краен брой степени на свобода - максималния брой независими параметри, които определят положението на системата. Основната задача на системната динамика е изучаването на законите на движението твърдо тялои механични системи. Най-простият подход за изследване на движението на система, състоящ се от нматериални точки, се свежда до разглеждане на движенията на всяка отделна точка от системата. В този случай трябва да се определят всички сили, действащи върху всяка точка на системата, включително силите на взаимодействие между точките. Определяйки ускорението на всяка точка в съответствие с втория закон на Нютон (1.2), получаваме за всяка точка три скаларни диференциални закона на движение от втори ред, т.е. 3 н диференциален закон на движение за цялата система. За да се намерят уравненията на движение на механична система за дадени сили и начални условия за всяка точка на системата, получените диференциални закони трябва да бъдат интегрирани. Тази задача е трудна дори в случай на две материални точки, които се движат само под действието на сили на взаимодействие съгласно закона за всеобщото привличане (задача на две тела), и изключително трудна в случай на три взаимодействащи точки (задача на три тела ). Следователно е необходимо да се намерят такива методи за решаване на проблеми, които да доведат до разрешими уравнения и да дадат представа за движението на механична система. Общите теореми на динамиката, като следствие от диференциалните закони на движение, позволяват да се избегне сложността, която възниква по време на интегрирането, и да се получат необходимите резултати. 3.1 Общи бележки Точките на механичната система ще бъдат номерирани с индекси аз, й, ки т.н., които преминават през всички стойности 1, 2, 3… н, където н е броят на системните точки. Физически величини, свързани с кточката се обозначават със същия индекс като точката. Например те изразяват съответно радиус вектора и скоростта к-та точка. Във всяка една от точките на системата действат сили с два произхода: първо, сили, чиито източници са извън системата, т.нар. външенсили и се обозначава с ; второ, сили от други точки на тази система, т.нар вътрешнисили и се обозначава с . Вътрешните сили отговарят на третия закон на Нютон. Помислете за най-простите свойства на вътрешните сили, действащи върху цялата механична система във всяко от нейните състояния. Първи имот. Геометричната сума на всички вътрешни сили на системата (основният вектор на вътрешните сили) е равна на нула.
Наистина, ако разгледаме произволни две точки от системата, например и (фиг. 3.1), тогава за тях
Втори имот. Геометричната сума на моментите на всички вътрешни сили спрямо произволна точка в пространството е нула. Разгледайте системата от моменти на силите и по отношение на точката О(фиг. 3.1). от (фиг. 3.1). това е ясно
защото и двете сили имат еднакви рамена и противоположни посоки на векторни моменти. Основната точкавътрешни сили около точка Осе състои от векторната сума на такива изрази и е равна на нула. Следователно,
Нека външни и вътрешни сили, действащи върху механична система, състояща се от нточки (фиг. 3.2). Ако резултантната на външни сили и резултантната на всички вътрешни сили се приложат към всяка точка на системата, тогава за всяка кточка на системата, могат да се съставят диференциални уравнения на движение. Общо такива уравнения ще бъдат н: и в проекции върху фиксирани координатни оси 3 н:
Векторни уравнения (3.3) или еквивалентни скаларни уравнения (3.4) представляват диференциалните закони на движение на материалните точки на цялата система. Ако всички точки се движат успоредно на една равнина или една права линия, тогава броят на уравненията (3.4) в първия случай ще бъде 2 н, във втория н.
Пример 1Два товара с маса и са свързани помежду си с неразтеглив кабел, хвърлен върху блок (фиг. 3.3). Пренебрегвайки силите на триене, както и масата на блока и кабела, определят закона за движение на стоките и напрежението на кабела. Решение. Системата се състои от две материални тела (свързани с неразтеглив кабел), движещи се успоредно на една ос Х.Нека запишем диференциалните закони на движение в проекции върху оста хза всеки. Оставете дясната тежест да се спусне с ускорение, след което лявата тежест ще се издигне с ускорение. Мислено се освобождаваме от връзката (кабела) и я заместваме с реакции и (фиг. 3.3). Приемайки, че телата са свободни, ще съставим диференциалните закони на движение в проекцията върху оста х(което означава, че напреженията на нишката са вътрешни сили, а теглото на товарите са външни): Тъй като и (телата са свързани с неразтеглив кабел), получаваме Решаване на тези уравнения за ускорението и опъна на въжето T, получаваме
Обърнете внимание, че напрежението на кабела при не е равно на гравитацията на съответния товар. 3. 2. Теоремата за движението на центъра на масата Известно е, че твърдо тяло и механична система в равнина могат да се движат доста трудно. До първата теорема за движението на тяло и механична система може да се стигне по следния начин: изпуснете в.-л. обект, състоящ се от много твърди тела, закрепени заедно. Ясно е, че ще лети по парабола. Това беше разкрито при изучаване на движението на точка. Сега обаче обектът не е точка. Той се върти, люлее се в процеса на летене около някакъв ефективен център, който се движи по парабола. Първата теорема за движението на сложни обекти казва, че определен ефективен център е центърът на масата на движещ се обект. Центърът на масата не е задължително да се намира в самото тяло, той може да лежи някъде извън него. Теорема. Центърът на масата на механичната система се движи като материална точка с маса, равна на масата на цялата система, към която се прилагат всички външни сили, действащи върху системата. За да докажем теоремата, пренаписваме диференциалните закони на движение (3.3) в следната форма:
където н е броят на системните точки. Нека съберем уравненията заедно член по член:
Положението на центъра на масата на механичната система спрямо избраната координатна система се определя по формула (2.1): Първата сума, стояща от дясната страна на равенството (а), е равна на главния вектор на външните сили, а последната, по свойството на вътрешните сили, е равна на нула. Тогава равенството (a), като се вземе предвид (b), ще бъде пренаписано
тези. произведението на масата на системата и ускорението на центъра на нейната маса е равно на геометричната сума на всички външни сили, действащи върху системата. От уравнение (3.6) следва, че вътрешните сили не влияят пряко на движението на центъра на масата. Въпреки това, в някои случаи те са причина за появата на външни сили, приложени към системата. По този начин вътрешните сили, които въртят задвижващите колела на автомобила, причиняват действието върху него на външна сила на сцепление, приложена към джантата. Пример 2Механизмът, разположен във вертикална равнина, е монтиран върху хоризонтална гладка равнина и е прикрепен към нея с пръти, здраво закрепени към повърхността. Да сеи Л (фиг. 3.4).
Диск 1 радиус Рнеподвижен. Диск 2 маса ми радиус r закопчава се с манивела, дълж Р+ rв точката От 2. Манивела се върти постоянно ъглова скорост. В началния момент манивелата зае дясното хоризонтално положение. Пренебрегвайки масата на манивелата, определете максималните хоризонтални и вертикални сили, действащи върху прътите, ако общата маса на рамката и колелото 1 е равна на М.Също така вземете предвид поведението на механизма при липса на решетки. Решение. Системата се състои от две маси ( н=2 ): неподвижен диск 1 с рамка и подвижен диск 2. Нека насочим оста припрез центъра на тежестта на неподвижния диск вертикално нагоре, оста х- по хоризонталната равнина. Записваме теоремата за движението на центъра на масата (3.6) в координатна форма Външните сили на тази система са: теглото на рамката и неподвижния диск - мг, тегло на подвижния диск мг, - общата хоризонтална реакция на болтовете, - нормалната обща реакция на самолета. Следователно, След това законите на движение (b) се пренаписват Нека изчислим координатите на центъра на масата на механичната система:
както се вижда от (фиг. 3.4), , ,
Замествайки (c) и (e) в (b), намираме
Хоризонталното налягане, действащо върху прътите, е най-голямо и най-малко, когато cos = 1 съответно, т.е.
включен механизъм за натиск хоризонтална равнинаима най-големи и най-малки стойности, когато грях съответно, т.е.
Всъщност първият проблем на динамиката е решен: съгласно известните уравнения на движение на центъра на масата на системата (e), силите, участващи в движението, се възстановяват. При липса на решетки Ки Л (фиг. 3.4), механизмът може да започне да подскача над хоризонталната равнина. Това ще стане, когато , т.е. когато , следва, че ъгловата скорост на въртене на манивелата, при която механизмът отскача, трябва да удовлетворява равенството
3. 3. Закон за запазване на движението на центъра на масата Ако главният вектор на външните сили, действащи върху системата, е равен на нула, т.е. , след това от(3.6)следва, че ускорението на центъра на масата е нула, следователно скоростта на центъра на масата е постоянна по големина и посока. Ако, по-специално, в началния момент центърът на масата е в покой, то той е в покой през цялото време, докато главният вектор на външните сили стане равен на нула. От тази теорема следват няколко следствия. · Вътрешните сили сами по себе си не могат да променят характера на движението на центъра на масата на системата. · Ако главният вектор на външните сили, действащи върху системата, е равен на нула, тогава центърът на масата е в покой или се движи равномерно и праволинейно. · Ако проекцията на главния вектор на външните сили на системата върху някаква фиксирана ос е равна на нула, тогава проекцията на скоростта на центъра на масата на системата върху тази ос не се променя. · Няколко сили, приложени към твърдо тяло, не могат да променят движението на неговия център на масата (те могат само да накарат тялото да се върти около центъра на масата). Нека разгледаме пример, илюстриращ закона за запазване на движението на центъра на масата.
Пример 3Две тежести с маси и са свързани с неразтеглива нишка, хвърлена върху блок (фиг. 3.5), фиксирани на клин с маса М.Клинът лежи върху гладка хоризонтална равнина. Първоначално системата беше в покой. Намерете изместването на клина по равнината, когато първият товар се спусне на височина Н.Игнорирайте масата на блока и нишката. Решение.Външните сили, действащи върху клина заедно с тежестите, са силите на гравитацията и мг, както и нормалната реакция на гладка хоризонтална повърхност N. Следователно, Тъй като системата е била в покой в началния момент, имаме . Нека изчислим координатата на центъра на масата на системата в и в момента T 1 когато теглото на товара жспуснете се на височина з. За момент:
където , , Х- съответно координатите на центъра на масата на товари с тегло g, g и тегло на клин Мж. Да приемем, че клинът в момента се движи в положителната посока на оста волпо количеството Лако теглото на товара падне на височина Н.След това за момент защото товарите заедно с клина ще се преместят към Лнадясно, тежестта ще се премести на разстояние нагоре по клина. Тъй като , след изчисления получаваме
3.4. Количество на системата за движение 3.4.1. Изчисляване на импулса на система Количеството на движение на материална точка е векторна величина, равна на произведението на масата на точката и вектора на нейната скорост Единица за измерване на количеството движение - Импулсът на механичната система се нарича векторна сума от импулсите на отделните точки на системата, т.е. където н е броят на системните точки. Импулсът на механична система може да бъде изразен чрез масата на системата Ми скоростта на центъра на масата. Наистина ли, тези. импулсът на системата е равен на произведението от масата на цялата система и скоростта на нейния център на масата.Посоката е същата като посоката (фиг. 3.6)
В проекции върху правоъгълни оси имаме където , , - проекции на скоростта на центъра на масата на системата. Тук Ме масата на механичната система; не се променя, докато системата се движи. Особено удобно е тези резултати да се използват при изчисляване на моментите на твърди тела. От формула (3.7) може да се види, че ако една механична система се движи по такъв начин, че нейният център на масата остава неподвижен, тогава импулсът на системата остава равен на нула. 3.4.2. Елементарен и пълен импулс Действието на сила върху материална точка във времето дтможе да се характеризира с елементарен импулс. Общ импулс на сила във времето T, или импулс на сила , се определя по формулата или в проекции върху координатите на оста
Единицата импулс на сила е. 3.4.3. Теорема за промяната на импулса на системата Нека към точките на системата са приложени външни и вътрешни сили. Тогава за всяка точка от системата можем да приложим диференциалните закони на движение (3.3), като имаме предвид, че
Сумирайки всички точки на системата, получаваме По свойството на вътрешните сили и по определение
Умножавайки двете страни на това уравнение по дт, получаваме теоремата за промяната на импулса в диференциална форма:
тези. диференциалът на импулса на механичната система е равен на векторната сума на елементарните импулси на всички външни сили, действащи върху точките на механичната система. Изчисляване на интеграла на двете части на (3.10) за време от 0 до T, получаваме теоремата в крайна или интегрална форма
В проекции върху координатните оси ще имаме Промяна в импулса на механична система във времетоT, е равна на векторната сума на всички импулси на външни сили, действащи върху точките на механичната система за едно и също време. Пример 4Натоварване на маса м се спуска по наклонена равнина от покой под действието на сила Е, пропорционално на времето: , където (фиг. 3.7). Каква е скоростта на тялото след T секунди след началото на движението, ако коефициентът на триене при плъзгане на товара върху наклонената равнина е равен на f.
Решение.Нека изобразим силите, приложени към товара: мг - тежестта на товара, не нормалната реакция на равнината, е силата на триене при плъзгане на товара върху равнината и . Посоката на всички сили е показана в (фиг. 3.7). Нека насочим оста хнадолу по наклонена равнина. Нека напишем теоремата за промяната на импулса (3.11) в проекцията върху оста х:
По условие, защото в началния момент товарът е бил в покой. Сумата от проекциите на импулсите на всички сили върху оста x е
Следователно,
3.4.4. Закони за запазване на импулса Законите за запазване се получават като специални случаи на теоремата за промяна на импулса. Възможни са два специални случая. · Ако векторната сума на всички външни сили, приложени към системата, е равна на нула, т.е. , то следва от теоремата (3.9) , Какво , тези. ако главният вектор на външните сили на системата е равен на нула, тогава импулсът на системата е постоянен по големина и посока. · Ако проекцията на главния вектор на външните сили върху който и да е координатна осе равно на нула, например О, т.е. , тогава проекцията на количеството движение върху тази ос е постоянна. Помислете за пример за прилагане на закона за запазване на импулса.
Пример 5Балистичното махало е тяло с маса, окачено на дълга нишка (фиг. 3.8). Куршум от маса, движещ се със скорост Vи попадайки в неподвижно тяло, се забива в него и тялото се отклонява. Каква беше скоростта на куршума, ако тялото се издигна на височина ч ? Решение.Оставете тялото със заседналия куршум да придобие скорост. След това, използвайки закона за запазване на импулса при взаимодействието на две тела, можем да напишем Скоростта може да се изчисли с помощта на закона за запазване на механичната енергия
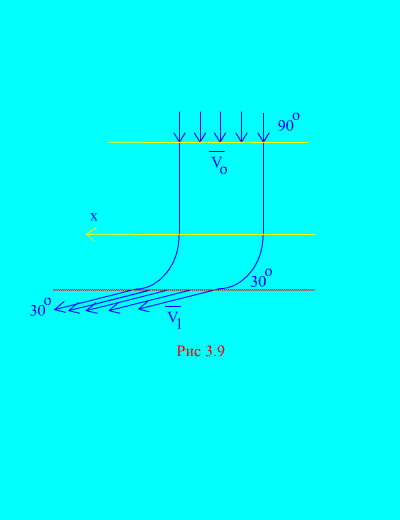
Пример 6. Водата влиза в фиксиран канал (фиг. 3.9)променлив участък със скорост под ъгъл спрямо хоризонта; площ на напречното сечение на канала на входа; скоростта на водата при изхода на канала и сключва ъгъл с хоризонта. Определете хоризонталния компонент на реакцията, която водата упражнява върху стените на канала. Плътност на водата Решение.Ще определим хоризонталния компонент на реакцията, упражнявана от стените на канала върху водата. Тази сила е равна по абсолютна стойност и противоположен по знак на желаната сила. Имаме, съгласно (3.11a),
Изчисляваме масата на обема на течността, влизаща в канала за времето t: Извиква се стойността на rAV 0 втора маса - масата на течността, протичаща през който и да е участък на тръбата за единица време. Едно и също количество вода напуска канала за същото време. В условието са дадени началната и крайната скорост. Нека изчислим дясната страна на равенство (a), което определя сумата от проекциите върху хоризонталната ос на външни сили, приложени към системата (вода). Единствената хоризонтална сила е хоризонталният компонент на резултантната реакция на стените R x. Тази сила е постоянна по време на равномерното движение на водата. Ето защо
Замествайки (b) и (c) в (a), получаваме 3.5. Кинетичен момент на системата 3.5.1. Главен момент на импулса на системата
Нека е радиус вектор на точка с масата на системата спрямо някаква точка A, наречена център (фиг. 3.10). Момент на импулса (кинетичен момент) на точка спрямо центъра Анаречен вектор , определена по формулата
В този случай векторът насочена перпендикулярно на равнината, минаваща през центъра НОи вектор . Момент на импулс (кинетичен момент) на точка около оссе нарича проекция върху тази ос на ъгловия момент на точката спрямо който и да е център, избран на тази ос. Основният момент на импулса (кинетичен момент) на системата спрямо центъра Асе нарича количеството
Основният момент на импулса (кинетичен момент) на системата около остасе нарича проекцията върху тази ос на главния момент на импулса на системата спрямо всеки избран върху дадения централна ос. 3.5.2. Импулс на въртящо се твърдо тяло около оста на въртене Съвместима фиксирана точка Отяло, лежащо върху оста на въртене Оz, с началото на координатната система Охуz, чиито оси ще се въртят с тялото (фиг. 3.11). Нека е радиус-вектор на точката на тялото спрямо началото на координатите, неговите проекции върху осите ще бъдат означени с , , . Векторни проекции ъглова скоросттела на същите оси ще бъдат означени с 0, 0, (). Министерство на образованието и науката Руска федерация Федерална държавна бюджетна образователна институция за висше професионално образование "Кубански държавен технологичен университет" Теоретична механикаЧаст 2 динамикаОдобрено от редакцията и издателството университетски съвет като Краснодар UDC 531.1/3 (075) Теоретична механика. Част 2. Динамика: Учебник / L.I.Draiko; Кубан. състояние техн.ун-т. Краснодар, 2011. 123 с. ISBN 5-230-06865-5 Теоретичният материал е представен в кратка форма, дадени са примери за решаване на проблеми, повечето от които отразяват реални технически проблеми, внимание е обърнато на избора на рационален метод за решение. Предназначен за бакалаври задочно и дистанционно обучение в областта на строителството, транспорта и инженерството. Раздел. 1 Фиг. 68 Библиография. 20 заглавия Научен редактор к.т.н., ст.н.с. В. Ф. Мелников Рецензенти: ръководител на катедрата по теоретична механика и теория на механизмите и машините на Кубанския аграрен университет проф. Ф.М. Канарев; Доцент от катедрата по теоретична механика на Кубанския държавен технологичен университет M.E. Мултих Публикува се с решение на Редакционно-издателския съвет на Кубанския държавен технологичен университет. Преиздаване ISBN 5-230-06865-5 КубГТУ 1998г ПредговорТози учебник е предназначен за задочни студенти по строителни, транспортни и инженерни специалности, но може да се използва при изучаване на раздел "Динамика" от курса по теоретична механика от задочни студенти от други специалности, както и редовни студенти с самостоятелна работа. Ръководството е съставено в съответствие с текущата програма на курса по теоретична механика, обхваща всички въпроси от основната част на курса. Всеки раздел съдържа кратък теоретичен материал, снабден с илюстрации и насоки за използването му при решаване на задачи. Ръководството анализира решението на 30 задачи, които отразяват реалните проблеми на техниката и съответните контролни задачи за независимо решение. За всяка задача е представена изчислителна схема, която ясно илюстрира решението. Дизайнът на решението е съобразен с изискванията за оформление на изпитите на задочниците. Авторът изказва дълбоката си благодарност на преподавателите от катедрата по теоретична механика и теория на механизмите и машините на Кубанския аграрен университет за тяхната голяма работа при рецензирането на учебника, както и на преподавателите от катедрата по теоретична механика на Кубанската държава Технологичен университет за ценните коментари и съвети при подготовката на учебника за издаване. Всички критични коментари и пожелания ще бъдат приемани от автора с благодарност в бъдеще. ВъведениеДинамиката е най-важният раздел на теоретичната механика. Повечето от специфичните задачи, които се срещат в инженерната практика, са свързани с динамиката. Използвайки заключенията на статиката и кинематиката, динамиката установява общите закони на движение на материалните тела под действието на приложени сили. Най-простият материален обект е материална точка. За материална точка може да се приеме материално тяло с произволна форма, чиито размери в разглежданата задача могат да бъдат пренебрегнати. Тяло с крайни размери може да се приеме за материална точка, ако разликата в движението на точките му не е значима за даден проблем. Това се случва, когато размерите на тялото са малки спрямо разстоянията, които изминават точките на тялото. Всяка частица от твърдо тяло може да се счита за материална точка. Силите, приложени към точка или материално тяло, се оценяват в динамика по тяхното динамично въздействие, т.е. по това как променят характеристиките на движението на материалните обекти. Движението на материалните обекти във времето се извършва в пространството спрямо определена отправна система. В класическата механика, въз основа на аксиомите на Нютон, пространството се счита за триизмерно, неговите свойства не зависят от движещите се в него материални обекти. Позицията на точка в такова пространство се определя от три координати. Времето не е свързано с пространството и движението на материалните обекти. Счита се за еднакъв за всички референтни системи. Законите на динамиката описват движението на материални обекти по отношение на абсолютните координатни оси, условно приемани за неподвижни. Началото на абсолютната координатна система е взето в центъра на Слънцето, а осите са насочени към далечни, условно неподвижни звезди. При решаването на много технически проблеми координатните оси, свързани със Земята, могат да се считат за условно неподвижни. Параметрите на механичното движение на материалните обекти в динамиката се установяват чрез математически изводи от основните закони на класическата механика. Първи закон (закон на инерцията): Материалната точка поддържа състояние на покой или равномерно и праволинейно движение, докато действието на някакви сили не я изведе от това състояние. Равномерното и праволинейно движение на точка се нарича движение по инерция. Почивката е частен случай на движение по инерция, когато скоростта на дадена точка е нула. Всяка материална точка има инерция, т.е. тя се стреми да поддържа състояние на покой или равномерно праволинейно движение. Отправната система, по отношение на която се изпълнява законът за инерцията, се нарича инерционна, а движението, наблюдавано по отношение на тази система, се нарича абсолютно. Всяка отправна система, която извършва постъпателно праволинейно и равномерно движение спрямо инерционната система, също ще бъде инерционна система. Вторият закон (основен закон на динамиката): Ускорението на материална точка спрямо инерционната отправна система е пропорционално на силата, приложена към точката, и съвпада със силата в посока: От основния закон на динамиката следва, че със сила Трети закон (закон за действие и реакция): Силите, с които две тела действат едно върху друго, са равни по големина и са насочени по една права линия в противоположни посоки. Прилагат се сили, наречени действие и реакция различни телаи следователно не образуват балансирана система. Четвъртият закон (законът за независимостта на действието на силите): При едновременното действие на няколко сили ускорението на материална точка е равно на геометричната сума от ускоренията, които точката би имала при действието на всяка сила поотделно:
(МЕХАНИЧНИ СИСТЕМИ) - IV вариант 1. Основното уравнение на динамиката на материална точка, както е известно, се изразява с уравнението . Диференциални уравнениядвиженията на произволни точки на несвободна механична система според два начина на разделяне на силите могат да бъдат записани в две форми: (1)
(2)
където е масата на k-тата точка; - радиус-вектор на k-та точка, - дадена (активна) сила, действаща върху k-та точка, или резултат от всички активни сили, действащи върху k-та точка. - резултантната на силите на реакция на връзките, действащи в k-та точка; - равностойна на вътрешни сили, действащи върху k-та точка; - резултантната на външните сили, действащи върху k-тата точка. Уравнения (1) и (2) могат да се използват за решаване както на първия, така и на втория проблем на динамиката. Решението на втория проблем на динамиката на системата обаче става много сложно не само от математическа гледна точка, но и защото срещаме фундаментални трудности. Те се състоят в това, че както за система (1), така и за система (2) броят на уравненията е значителен по-малко от числонеизвестен. Така че, ако използваме (1), тогава известното за втората (обратна) задача на динамиката ще бъде и , а неизвестните ще бъдат и . Векторните уравнения ще бъдат " н“, а неизвестен – „2n”. Ако изхождаме от системата от уравнения (2), тогава известните и част от външните сили . Защо част? Факт е, че броят на външните сили включва и външни реакции на връзки, които са неизвестни. Освен това ще има и неизвестни. Така и системата (1), и системата (2) са ОТВОРЕНИ. Трябва да добавим уравнения, като вземем предвид уравненията на отношенията и може би все още трябва да наложим някои ограничения на самите отношения. Какво да правя? Ако изхождаме от (1), тогава можем да следваме пътя на съставяне на уравненията на Лагранж от първи вид. Но този начин не е рационален, защото по-лесна задача(по-малко степени на свобода), толкова по-трудно е да се реши от гледна точка на математиката. Тогава нека обърнем внимание на системата (2), където - винаги са неизвестни. Първата стъпка в решаването на системата е да се премахнат тези неизвестни. Трябва да се има предвид, че по правило не се интересуваме от вътрешните сили по време на движението на системата, тоест когато системата се движи, не е необходимо да знаем как се движи всяка точка от системата, но е достатъчно, за да знаете как се движи системата като цяло. По този начин, ако различни начиниизключваме неизвестни сили от системата (2), тогава получаваме някои отношения, т.е Основни характеристикиза системата, чието познаване позволява да се прецени как се движи системата като цяло. Тези характеристики се въвеждат с помощта на т.нар общи теоремидинамика. Има четири такива теореми: 1. Теорема за движение на центъра на масата на механичната система; 2. Теорема за промяна в импулса на механична система; 3. Теорема за промяна в ъгловия момент на механична система; 4. Теорема за промяна в кинетичната енергия на механична система. |
Популярен:
Хомогенно и стационарно поле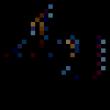
|
Нов
- Сън, падащо дете от високо
- Ако сънувате падащо дете от високо
- „Ходейки защо мечтаете насън?
- Очаквана цена - каква е тя?
- „Не е толкова трудно да завършите проблемни къщи“
- Медицински справочник geotar L треонин инструкции за употреба
- Ползите и значението на хидроаминокиселината треонин за човешкото тяло Инструкции за употреба на треонин
- Плодове от копър: полезни свойства, противопоказания, особености на приложение Резене обикновен химически състав
- Генерализирана атеросклероза: причини, симптоми и лечение
- Контрактури на различни групи стави, причини, симптоми и методи на лечение



 .
. (а)
(а) където Ме масата на системата. Тогава
където Ме масата на системата. Тогава 
 ; (G)
; (G) д)
д)
 .
.
 ,
, .
.
 (3.8a)
(3.8a) .
. (3.9)
(3.9) (3.11)
(3.11)
 (а)
(а)
 ,
, .
.
 . Тогава . В резултат на това намираме
. Тогава . В резултат на това намираме .
.
 .
. . (а)
. (а) . (в)
. (в)
 (3.13)
(3.13) .
. ускорение
ускорение  . Масата на точка характеризира степента на съпротивление на точката при промяна на нейната скорост, т.е. тя е мярка за инерцията на материална точка.
. Масата на точка характеризира степента на съпротивление на точката при промяна на нейната скорост, т.е. тя е мярка за инерцията на материална точка. , където
, където  ,
, ,…,
,…, .
.



