1
/
5
Kepentingan taburan normal dalam banyak bidang sains (contohnya, dalam statistik matematik dan fizik statistik) mengikuti teorem had pusat teori kebarangkalian. Jika hasil pemerhatian ialah hasil tambah banyak rawak, pembolehubah saling bersandar lemah, setiap satunya memberikan sumbangan yang kecil berbanding jumlah keseluruhan, maka apabila bilangan sebutan bertambah, taburan hasil berpusat dan ternormal cenderung kepada normal. Hukum teori kebarangkalian ini mempunyai akibat taburan luas taburan normal, yang merupakan salah satu sebab untuk namanya.
Hartanah
Detik-detik
Jika pembolehubah rawak X 1 (\displaystyle X_(1)) Dan X 2 (\displaystyle X_(2)) adalah bebas dan mempunyai taburan normal dengan jangkaan matematik μ 1 (\displaystyle \mu _(1)) Dan μ 2 (\displaystyle \mu _(2)) dan serakan σ 1 2 (\displaystyle \sigma _(1)^(2)) Dan σ 2 2 (\displaystyle \sigma _(2)^(2)) masing-masing, kemudian X 1 + X 2 (\gaya paparan X_(1)+X_(2)) juga mempunyai taburan normal dengan nilai jangkaan μ 1 + μ 2 (\displaystyle \mu _(1)+\mu _(2)) dan penyebaran σ 1 2 + σ 2 2 . (\displaystyle \sigma _(1)^(2)+\sigma _(2)^(2).) Ini menunjukkan bahawa pembolehubah rawak normal boleh diwakili sebagai hasil tambah bilangan arbitrari pembolehubah rawak normal bebas.
Entropi maksimum
Taburan normal mempunyai entropi pembezaan maksimum antara semua taburan berterusan yang variansnya tidak melebihi nilai tertentu.
Memodelkan Pembolehubah Pseudo-Rawak Biasa
Kaedah pemodelan anggaran paling mudah adalah berdasarkan teorem had pusat. Iaitu, jika kita menambah beberapa kuantiti bebas yang teragih sama dengan varians terhingga, maka jumlah itu akan diagihkan lebih kurang baiklah. Contohnya, jika anda menambah 100 standard bebas sama rata pembolehubah rawak teragih, maka taburan jumlah akan menjadi lebih kurang biasa.
Untuk penjanaan perisian pembolehubah rawak pseudo yang diedarkan secara normal, adalah lebih baik untuk menggunakan transformasi Box - Muller. Ia membolehkan anda menjana satu nilai taburan biasa berdasarkan satu nilai taburan seragam.
Taburan normal dalam sifat dan aplikasi
Taburan normal sering dijumpai di alam semula jadi. Sebagai contoh, pembolehubah rawak berikut dimodelkan dengan baik oleh taburan normal:
- pesongan menembak.
- ralat pengukuran (namun, ralat beberapa alat pengukur mempunyai taburan bukan normal).
- beberapa ciri organisma hidup dalam populasi.
Taburan ini begitu meluas kerana ia merupakan taburan berterusan terbahagi tak terhingga dengan varians terhingga. Oleh itu, sesetengah yang lain mendekatinya dalam had, seperti binomial dan Poisson. Banyak proses fizikal bukan deterministik dimodelkan oleh taburan ini.
Hubungan dengan pengedaran lain
- Taburan normal ialah taburan Pearson jenis XI.
- Nisbah sepasang pembolehubah rawak taburan piawai bebas mempunyai taburan Cauchy. Iaitu, jika pembolehubah rawak X (\displaystyle X) mewakili hubungan X = Y / Z (\displaystyle X=Y/Z)(di mana Y (\gaya paparan Y) Dan Z (\displaystyle Z) adalah pembolehubah rawak normal piawai bebas), maka ia akan mempunyai taburan Cauchy.
- Jika z 1 , … , z k (\displaystyle z_(1),\ldots ,z_(k)) adalah pembolehubah rawak normal piawai bebas bersama, i.e. z i ∼ N (0 , 1) (\displaystyle z_(i)\sim N\kiri(0,1\kanan)), kemudian pembolehubah rawak x = z 1 2 + … + z k 2 (\displaystyle x=z_(1)^(2)+\ldots +z_(k)^(2)) mempunyai taburan khi kuasa dua dengan k darjah kebebasan.
- Jika pembolehubah rawak X (\displaystyle X) tertakluk kepada taburan lognormal, maka logaritma aslinya mempunyai taburan normal. Iaitu, jika X ∼ L o g N (μ , σ 2) (\displaystyle X\sim \mathrm (LogN) \left(\mu ,\sigma ^(2)\kanan)), kemudian Y = ln (X) ∼ N (μ , σ 2) (\displaystyle Y=\ln \kiri(X\kanan)\sim \mathrm (N) \kiri(\mu ,\sigma ^(2)\kanan )). Dan sebaliknya, jika Y ∼ N (μ , σ 2) (\displaystyle Y\sim \mathrm (N) \left(\mu ,\sigma ^(2)\kanan)), kemudian X = exp (Y) ∼ L og N (μ , σ 2) (\displaystyle X=\exp \left(Y\right)\sim \mathrm (LogN) \left(\mu ,\sigma ^(2) \kanan)).
- Nisbah kuasa dua dua pembolehubah rawak normal piawai mempunyai
Undang-undang taburan normal (sering dipanggil undang-undang Gauss) memainkan peranan yang sangat penting dalam teori kebarangkalian dan menduduki kedudukan istimewa antara undang-undang taburan lain. Ini adalah undang-undang pengedaran yang paling biasa dalam amalan. Ciri utama yang membezakan undang-undang biasa daripada undang-undang lain ialah undang-undang yang mengehadkan, yang mana undang-undang pengedaran lain mendekati dalam keadaan biasa yang sangat kerap.
Ia boleh dibuktikan bahawa jumlah bilangan pembolehubah rawak bebas (atau bersandar lemah) yang cukup besar tertakluk kepada undang-undang pengedaran sewenang-wenang (tertakluk kepada sekatan yang sangat longgar tertentu) lebih kurang mematuhi undang-undang biasa, dan ini adalah benar semakin tepat semakin besar bilangan pembolehubah rawak dijumlahkan. Kebanyakan pembolehubah rawak yang ditemui dalam amalan, seperti, sebagai contoh, ralat pengukuran, ralat penangkapan, dsb., boleh diwakili sebagai jumlah bilangan yang sangat besar bagi istilah yang agak kecil - ralat asas, setiap satunya disebabkan oleh tindakan sebab berasingan yang tidak bergantung kepada yang lain . Walau apa pun undang-undang pengedaran yang mungkin tertakluk kepada ralat asas individu, ciri-ciri pengagihan ini dalam jumlah sejumlah besar istilah diratakan, dan jumlahnya ternyata tertakluk kepada undang-undang yang hampir normal. Sekatan utama yang dikenakan ke atas ralat boleh rumus ialah kesemuanya memainkan peranan yang agak kecil dalam jumlah keseluruhan. Sekiranya syarat ini tidak dipenuhi dan, sebagai contoh, salah satu kesilapan rawak ternyata mengatasi semua yang lain dalam pengaruhnya ke atas jumlah, maka undang-undang pengagihan kesilapan yang berlaku ini akan mengenakan pengaruhnya ke atas jumlah dan menentukan dalam ciri utamanya undang-undang pengedarannya.
Teorem yang menetapkan hukum biasa sebagai had bagi hasil tambah sebutan rawak seragam kecil bebas akan dibincangkan dengan lebih terperinci dalam Bab 13.
Hukum taburan normal dicirikan oleh ketumpatan kebarangkalian bentuk:
Keluk taburan mengikut hukum normal mempunyai rupa berbukit simetri (Rajah 6.1.1). Ordinasi maksimum lengkung, sama dengan , sepadan dengan titik ; apabila kita bergerak menjauhi titik, ketumpatan taburan berkurangan, dan pada , lengkung secara asimtotik menghampiri paksi absis.

Mari kita ketahui maksud parameter berangka dan dimasukkan dalam ungkapan hukum biasa (6.1.1); kami akan membuktikan bahawa nilai itu tidak lain hanyalah jangkaan matematik, dan nilainya ialah sisihan piawai bagi nilai . Untuk melakukan ini, kami mengira ciri berangka utama kuantiti - jangkaan dan varians matematik.

Mengaplikasikan perubahan pembolehubah
Adalah mudah untuk mengesahkan bahawa selang pertama daripada dua selang dalam formula (6.1.2) adalah sama dengan sifar; yang kedua ialah integral Euler-Poisson yang terkenal:
 . (6.1.3)
. (6.1.3)
Akibatnya,
mereka. parameter ialah jangkaan matematik bagi nilai . Parameter ini, terutamanya dalam tugas menembak, sering dipanggil pusat penyebaran (disingkatkan sebagai c.r.).
Mari kita mengira serakan kuantiti:
 .
.
Menggunakan semula perubahan pembolehubah
Mengintegrasikan mengikut bahagian, kita dapat:
Sebutan pertama dalam kurungan kerinting adalah sama dengan sifar (sejak apabila berkurangan lebih cepat daripada mana-mana kuasa meningkat), sebutan kedua mengikut formula (6.1.3) adalah sama dengan , dari mana
Oleh itu, parameter dalam formula (6.1.1) hanyalah sisihan piawai bagi nilai .
Mari kita ketahui maksud parameter dan taburan normal. Ia boleh dilihat secara langsung daripada formula (6.1.1) bahawa pusat simetri taburan ialah pusat serakan. Ini jelas daripada fakta bahawa apabila tanda perbezaan diterbalikkan, ungkapan (6.1.1) tidak berubah. Jika anda menukar pusat serakan, lengkung taburan akan beralih sepanjang paksi-x tanpa mengubah bentuknya (Rajah 6.1.2). Pusat serakan mencirikan kedudukan taburan pada paksi-x.

Dimensi pusat serakan adalah sama dengan dimensi pembolehubah rawak .
Parameter tidak mencirikan kedudukan, tetapi bentuk lengkung pengedaran. Ini adalah ciri penyebaran. Ordinasi terbesar keluk taburan adalah berkadar songsang dengan ; apabila meningkat, ordinat maksimum berkurangan. Oleh kerana luas lengkung agihan mesti sentiasa kekal sama dengan perpaduan, apabila lengkung agihan meningkat, ia menjadi lebih rata, meregang sepanjang paksi-x; sebaliknya, dengan penurunan, lengkung pengedaran terbentang ke atas, pada masa yang sama mengecut dari sisi, dan menjadi lebih seperti jarum. Pada rajah. 6.1.3 menunjukkan tiga lengkung normal (I, II, III) pada ; daripada ini, lengkung I sepadan dengan nilai terbesar, dan lengkung III kepada nilai terkecil. Menukar parameter adalah bersamaan dengan menukar skala lengkung pengedaran - meningkatkan skala di sepanjang satu paksi dan penurunan yang sama di sepanjang paksi yang lain.
Contoh pembolehubah rawak yang diedarkan mengikut hukum biasa ialah ketinggian seseorang, jisim ikan yang ditangkap daripada spesies yang sama. Taburan normal bermaksud yang berikut
: terdapat nilai ketinggian manusia, jisim ikan dari spesies yang sama, yang secara intuitif dianggap sebagai "normal" (dan sebenarnya - purata), dan ia lebih biasa dalam sampel yang cukup besar daripada yang yang berbeza atas atau bawah.
Taburan kebarangkalian normal pembolehubah rawak berterusan (kadangkala taburan Gaussian) boleh dipanggil berbentuk loceng kerana fakta bahawa fungsi ketumpatan taburan ini, yang simetri tentang min, adalah sangat serupa dengan potongan loceng ( lengkung merah dalam rajah di atas).
Kebarangkalian untuk memenuhi nilai tertentu dalam sampel adalah sama dengan luas angka di bawah lengkung, dan dalam kes taburan normal, kita melihat bahawa di bawah bahagian atas "loceng" , yang sepadan dengan nilai cenderung kepada purata, kawasan, dan oleh itu kebarangkalian, adalah lebih besar daripada di bawah tepi. Oleh itu, kita mendapat perkara yang sama yang telah diperkatakan: kebarangkalian untuk bertemu dengan seseorang dengan ketinggian "normal", menangkap ikan dengan berat "normal" adalah lebih tinggi daripada nilai yang berbeza naik atau turun. Dalam kebanyakan kes amalan, ralat pengukuran diedarkan mengikut undang-undang yang hampir normal.
Mari kita berhenti semula pada rajah pada permulaan pelajaran, yang menunjukkan fungsi ketumpatan taburan normal. Graf fungsi ini diperoleh dengan mengira beberapa sampel data dalam pakej perisian STATISTIK. Di atasnya, lajur histogram mewakili selang nilai sampel yang taburannya hampir (atau, seperti yang mereka katakan dalam statistik, tidak berbeza dengan ketara daripada) kepada graf fungsi ketumpatan taburan normal itu sendiri, yang merupakan lengkung merah. Graf menunjukkan bahawa lengkung ini sememangnya berbentuk loceng.
Taburan normal adalah bernilai dalam banyak cara kerana hanya mengetahui min pembolehubah rawak berterusan dan sisihan piawai, anda boleh mengira sebarang kebarangkalian yang dikaitkan dengan pembolehubah itu.
Taburan normal mempunyai faedah tambahan sebagai salah satu yang paling mudah untuk digunakan kriteria statistik yang digunakan untuk menguji hipotesis statistik - Ujian-t pelajar- boleh digunakan hanya dalam kes apabila data sampel mematuhi undang-undang taburan normal.
Fungsi ketumpatan taburan normal pembolehubah rawak selanjar boleh didapati menggunakan formula:
 ,
,
di mana x- nilai pembolehubah, - nilai min, - sisihan piawai, e\u003d 2.71828 ... - asas logaritma asli, \u003d 3.1416 ...
Sifat fungsi ketumpatan taburan normal

Perubahan dalam min menggerakkan lengkung loceng ke arah paksi lembu. Jika ia meningkat, lengkung bergerak ke kanan, jika ia menurun, kemudian ke kiri.
Jika sisihan piawai berubah, maka ketinggian bucu lengkung berubah. Apabila sisihan piawai meningkat, bahagian atas lengkung lebih tinggi, apabila ia menurun, ia lebih rendah.
Kebarangkalian bahawa nilai pembolehubah rawak taburan normal akan jatuh dalam selang tertentu
Sudah dalam perenggan ini, kita akan mula menyelesaikan masalah praktikal, yang maknanya ditunjukkan dalam tajuk. Marilah kita menganalisis kemungkinan yang disediakan oleh teori untuk menyelesaikan masalah. Konsep permulaan untuk mengira kebarangkalian pembolehubah rawak taburan normal jatuh ke dalam selang tertentu ialah fungsi kamiran taburan normal.
Fungsi taburan normal kamiran:
 .
.
Walau bagaimanapun, adalah bermasalah untuk mendapatkan jadual bagi setiap kemungkinan gabungan min dan sisihan piawai. Oleh itu, salah satu cara mudah untuk mengira kebarangkalian pembolehubah rawak taburan normal jatuh ke dalam selang tertentu adalah dengan menggunakan jadual kebarangkalian untuk taburan normal piawai.
Taburan normal dipanggil taburan piawai atau ternormal., yang nilai min ialah , dan sisihan piawai ialah .
Fungsi ketumpatan taburan normal piawai:
 .
.
Fungsi kumulatif taburan normal piawai:
 .
.
Rajah di bawah menunjukkan fungsi kamiran taburan normal piawai, yang grafnya diperoleh dengan mengira beberapa sampel data dalam pakej perisian STATISTIK. Graf itu sendiri adalah lengkung merah, dan nilai sampel menghampirinya.

Untuk membesarkan gambar, anda boleh klik padanya dengan butang kiri tetikus.
Penyeragaman pembolehubah rawak bermakna beralih daripada unit asal yang digunakan dalam tugasan kepada unit piawai. Penyeragaman dilakukan mengikut formula
Dalam amalan, semua kemungkinan nilai pembolehubah rawak selalunya tidak diketahui, jadi nilai min dan sisihan piawai tidak dapat ditentukan dengan tepat. Ia digantikan dengan min aritmetik cerapan dan sisihan piawai s. Nilai z menyatakan sisihan nilai pembolehubah rawak daripada min aritmetik semasa mengukur sisihan piawai.
Selang terbuka
Jadual kebarangkalian bagi taburan normal piawai, yang terdapat dalam hampir mana-mana buku tentang statistik, mengandungi kebarangkalian bahawa pembolehubah rawak mempunyai taburan normal piawai. Z mengambil nilai kurang daripada nombor tertentu z. Iaitu, ia akan jatuh ke dalam selang terbuka dari tolak infiniti hingga z. Sebagai contoh, kebarangkalian bahawa nilai Z kurang daripada 1.5 bersamaan dengan 0.93319.
Contoh 1 Syarikat itu mengeluarkan alat ganti yang mempunyai jangka hayat taburan normal dengan min 1000 dan sisihan piawai 200 jam.
Untuk bahagian yang dipilih secara rawak, hitung kebarangkalian hayat perkhidmatannya ialah sekurang-kurangnya 900 jam.
Penyelesaian. Mari kita perkenalkan notasi pertama:
Kebarangkalian yang diingini.
Nilai pembolehubah rawak berada dalam selang terbuka. Tetapi kita boleh mengira kebarangkalian bahawa pembolehubah rawak akan mengambil nilai kurang daripada nilai yang diberikan, dan mengikut keadaan masalah, ia diperlukan untuk mencari nilai yang sama atau lebih besar daripada yang diberikan. Ini adalah bahagian lain ruang di bawah lengkung loceng. Oleh itu, untuk mencari kebarangkalian yang diingini, adalah perlu untuk menolak daripada satu kebarangkalian yang disebutkan bahawa pembolehubah rawak akan mengambil nilai kurang daripada 900 yang ditentukan:
Sekarang pembolehubah rawak perlu diseragamkan.
Kami terus memperkenalkan notasi:
z = (X ≤ 900)
;
x= 900 - nilai yang diberikan bagi pembolehubah rawak;
μ
= 1000 - nilai purata;
σ
= 200 - sisihan piawai.
Berdasarkan data ini, kami memperoleh syarat masalah:
 .
.
Mengikut jadual pembolehubah rawak piawai (sempadan selang) z= -0.5 sepadan dengan kebarangkalian 0.30854. Tolak dari perpaduan dan dapatkan apa yang diperlukan dalam keadaan masalah:
Jadi, kebarangkalian bahawa hayat bahagian akan sekurang-kurangnya 900 jam ialah 69%.
Kebarangkalian ini boleh diperolehi menggunakan fungsi MS Excel NORM.DIST (nilai nilai kamiran ialah 1):
P(X≥900) = 1 - P(X≤900) = 1 - NORM.DIST(900; 1000; 200; 1) = 1 - 0.3085 = 0.6915.
Mengenai pengiraan dalam MS Excel - dalam salah satu perenggan seterusnya dalam pelajaran ini.
Contoh 2 Di bandar tertentu, purata pendapatan keluarga tahunan adalah pembolehubah rawak taburan normal dengan nilai min 300,000 dan sisihan piawai 50,000. Adalah diketahui bahawa pendapatan 40% keluarga adalah kurang daripada nilai A. Cari nilai A.
Penyelesaian. Dalam masalah ini, 40% adalah tidak lebih daripada kebarangkalian bahawa pembolehubah rawak akan mengambil nilai dari selang terbuka yang kurang daripada nilai tertentu, yang ditunjukkan oleh huruf A.
Untuk mencari nilai A, kita mula-mula mengarang fungsi kamiran:

Mengikut tugasan
μ
= 300000 - nilai purata;
σ
= 50000 - sisihan piawai;
x = A ialah nilai yang boleh didapati.
Membentuk kesaksamaan
 .
.
Menurut jadual statistik, kita dapati kebarangkalian 0.40 sepadan dengan nilai sempadan selang z = −0,25
.
Oleh itu, kita membuat kesamarataan

dan cari penyelesaiannya:
A = 287300
.
Jawapan: pendapatan 40% keluarga adalah kurang daripada 287300.
Selang tertutup
Dalam banyak masalah, ia diperlukan untuk mencari kebarangkalian bahawa pembolehubah rawak taburan normal mengambil nilai dalam selang dari z 1 hingga z 2. Iaitu, ia akan jatuh ke dalam selang tertutup. Untuk menyelesaikan masalah sedemikian, adalah perlu untuk mencari dalam jadual kebarangkalian yang sepadan dengan sempadan selang, dan kemudian mencari perbezaan antara kebarangkalian ini. Ini memerlukan penolakan nilai yang lebih kecil daripada yang lebih besar. Contoh untuk menyelesaikan masalah biasa ini adalah seperti berikut, dan dicadangkan untuk menyelesaikannya sendiri, dan kemudian anda boleh melihat penyelesaian dan jawapan yang betul.
Contoh 3 Keuntungan perusahaan untuk tempoh tertentu adalah pembolehubah rawak tertakluk kepada undang-undang pengedaran normal dengan nilai purata 0.5 juta c.u. dan sisihan piawai 0.354. Tentukan, dengan ketepatan dua tempat perpuluhan, kebarangkalian bahawa keuntungan perusahaan adalah dari 0.4 hingga 0.6 c.u.
Contoh 4 Panjang bahagian yang dikilang adalah pembolehubah rawak yang diedarkan mengikut hukum biasa dengan parameter μ
=10 dan σ
=0.071 . Cari, dengan ketepatan dua tempat perpuluhan, kebarangkalian perkahwinan jika dimensi bahagian yang dibenarkan hendaklah 10 ± 0.05.
Petunjuk: dalam masalah ini, selain mencari kebarangkalian pembolehubah rawak jatuh ke dalam selang tertutup (kebarangkalian untuk mendapatkan bahagian yang tidak rosak), satu lagi tindakan diperlukan.

membolehkan anda menentukan kebarangkalian bahawa nilai piawai Z tidak kurang -z dan tiada lagi +z, di mana z- nilai yang dipilih secara sewenang-wenangnya bagi pembolehubah rawak piawai.
Kaedah Anggaran untuk Menyemak Normaliti Taburan
Kaedah anggaran untuk menyemak kenormalan taburan nilai sampel adalah berdasarkan perkara berikut sifat taburan normal: kecondongan β
1
dan pekali kurtosis β
2
sifar.
Pekali asimetri β
1
secara numerik mencirikan simetri taburan empirikal berkenaan dengan min. Jika kecondongan adalah sama dengan sifar, maka min aritmetrik, median dan mod adalah sama: dan keluk ketumpatan taburan adalah simetri tentang min. Jika pekali asimetri kurang daripada sifar (β
1
< 0
), maka min aritmetik adalah kurang daripada median, dan median, seterusnya, adalah kurang daripada mod () dan lengkung dianjak ke kanan (berbanding dengan taburan normal). Jika pekali asimetri lebih besar daripada sifar (β
1
> 0
), maka min aritmetik lebih besar daripada median, dan median pula lebih besar daripada mod () dan lengkung dianjak ke kiri (berbanding dengan taburan normal).
Pekali Kurtosis β
2
mencirikan kepekatan taburan empirikal di sekeliling min aritmetik dalam arah paksi Oy dan tahap kemuncak keluk ketumpatan taburan. Jika pekali kurtosis lebih besar daripada sifar, maka lengkung lebih memanjang (berbanding dengan taburan normal) sepanjang paksi Oy(graf lebih runcing). Jika pekali kurtosis kurang daripada sifar, maka lengkung lebih rata (berbanding dengan taburan normal) sepanjang paksi Oy(graf lebih tumpul).
Pekali kecondongan boleh dikira menggunakan fungsi MS Excel SKRS. Jika anda menyemak satu tatasusunan data, maka anda perlu memasukkan julat data dalam satu kotak "Nombor".

Pekali kurtosis boleh dikira menggunakan kurtosis fungsi MS Excel. Apabila menyemak satu tatasusunan data, ia juga cukup untuk memasukkan julat data dalam satu kotak "Nombor".

Jadi, seperti yang kita sedia maklum, dengan taburan normal, pekali kecondongan dan kurtosis adalah sama dengan sifar. Tetapi bagaimana jika kita mendapat pekali kecondongan sama dengan -0.14, 0.22, 0.43, dan pekali kurtosis sama dengan 0.17, -0.31, 0.55? Persoalannya agak adil, kerana dalam amalan kita hanya berurusan dengan anggaran, nilai selektif asimetri dan kurtosis, yang tertakluk kepada serakan yang tidak dapat dielakkan dan tidak terkawal. Oleh itu, adalah mustahil untuk menghendaki kesamaan ketat bagi pekali ini kepada sifar, ia hanya sepatutnya hampir hampir kepada sifar. Tetapi apakah maksud cukup?
Ia dikehendaki membandingkan nilai empirikal yang diterima dengan nilai yang boleh diterima. Untuk melakukan ini, anda perlu menyemak ketidaksamaan berikut (bandingkan nilai modulo pekali dengan nilai kritikal - sempadan kawasan ujian hipotesis).
Untuk pekali asimetri β
1
.
) memainkan peranan yang sangat penting dalam teori kebarangkalian dan paling kerap digunakan dalam menyelesaikan masalah praktikal. Ciri utamanya ialah ia adalah undang-undang pengehad, yang didekati oleh undang-undang pengedaran lain di bawah keadaan tipikal yang sangat biasa. Sebagai contoh, jumlah bilangan pembolehubah rawak bebas (atau bersandar lemah) yang cukup besar lebih kurang mematuhi hukum biasa, dan ini adalah lebih tepat, lebih banyak pembolehubah rawak dijumlahkan.
Telah terbukti secara eksperimen bahawa ralat pengukuran, sisihan dalam dimensi geometri dan kedudukan elemen struktur bangunan semasa pembuatan dan pemasangannya, kebolehubahan ciri fizikal dan mekanikal bahan dan beban yang bertindak pada struktur bangunan adalah tertakluk kepada undang-undang biasa.
Hampir semua pembolehubah rawak mematuhi taburan Gaussian, sisihan yang daripada nilai purata disebabkan oleh satu set besar faktor rawak, setiap satunya adalah tidak penting secara individu. (teorem had pusat).
taburan normal dipanggil taburan pembolehubah selanjar rawak yang ketumpatan kebarangkaliannya mempunyai bentuk (Rajah 18.1).
nasi. 18.1. Undang-undang pengedaran normal untuk 1< a 2 .
di mana a dan ialah parameter pengedaran.
Ciri-ciri kebarangkalian pembolehubah rawak yang diedarkan mengikut hukum normal ialah:
Jangkaan matematik (18.2)
Penyerakan (18.3)
Sisihan piawai (18.4)
Pekali asimetri A = 0(18.5)
Berlebihan E= 0. (18.6)
Parameter σ termasuk dalam taburan Gaussian adalah sama dengan nisbah punca-min-kuasa dua bagi pembolehubah rawak. Nilai tetapi menentukan kedudukan pusat pengedaran (lihat Rajah 18.1), dan nilai tetapi- lebar pengedaran (Rajah 18.2), i.e. sebaran statistik di sekitar min.
nasi. 18.2. Undang-undang taburan normal untuk σ 1< σ 2 < σ 3
Kebarangkalian jatuh ke dalam selang tertentu (dari x 1 hingga x 2) untuk taburan normal, seperti dalam semua kes, ditentukan oleh kamiran ketumpatan kebarangkalian (18.1), yang tidak dinyatakan dalam sebutan fungsi asas dan ialah diwakili oleh fungsi khas, dipanggil fungsi Laplace (integral kebarangkalian).
Salah satu perwakilan kamiran kebarangkalian:
Nilai Dan dipanggil kuantil.
Ia boleh dilihat bahawa Ф(х) ialah fungsi ganjil, iaitu Ф(-х) = -Ф(х) .
Nilai fungsi ini dikira dan dibentangkan dalam bentuk jadual dalam kesusasteraan teknikal dan pendidikan.
Fungsi taburan hukum normal (Rajah 18.3) boleh dinyatakan dalam sebutan kamiran kebarangkalian:
nasi. 18.2. Fungsi hukum taburan normal.
Kebarangkalian bahawa pembolehubah rawak yang diedarkan mengikut hukum normal jatuh ke dalam selang dari X. kepada x, ditentukan oleh ungkapan:
Perlu diingatkan bahawa
Ф(0) = 0; Ф(∞) = 0.5; Ф(-∞) = -0.5.
Apabila menyelesaikan masalah praktikal yang berkaitan dengan pengagihan, seseorang sering perlu mempertimbangkan kebarangkalian jatuh ke dalam selang yang simetri berkenaan dengan jangkaan matematik, jika panjang selang ini i.e. jika selang itu sendiri mempunyai sempadan dari kepada , kita mempunyai:
Apabila menyelesaikan masalah praktikal, sempadan sisihan pembolehubah rawak dinyatakan melalui piawai, sisihan piawai, didarab dengan faktor tertentu yang menentukan sempadan kawasan sisihan pembolehubah rawak.
Mengambil dan dan juga menggunakan formula (18.10) dan jadual F (x) (Lampiran No. 1), kita perolehi
Formula ini menunjukkan bahawa jika pembolehubah rawak mempunyai taburan normal, maka kebarangkalian sisihan daripada nilai min tidak lebih daripada σ ialah 68.27%, tidak lebih daripada 2σ - 95.45% dan tidak lebih daripada 3σ - 99.73%.
Oleh kerana nilai 0.9973 adalah hampir kepada perpaduan, adalah mustahil untuk taburan normal pembolehubah rawak untuk menyimpang daripada jangkaan matematik lebih daripada 3σ. Peraturan ini, yang hanya sah untuk taburan normal, dipanggil peraturan tiga sigma. Pelanggaran itu berkemungkinan besar P = 1 - 0.9973 = 0.0027. Peraturan ini digunakan apabila menetapkan sempadan sisihan yang dibenarkan bagi toleransi ciri geometri produk dan struktur.
Secara rawak jika, sebagai hasil daripada pengalaman, ia boleh mengambil nilai sebenar dengan kebarangkalian tertentu. Ciri yang paling lengkap dan menyeluruh bagi pembolehubah rawak ialah hukum taburan. Hukum taburan ialah fungsi (jadual, graf, formula) yang membolehkan anda menentukan kebarangkalian pembolehubah rawak X mengambil nilai xi tertentu atau jatuh ke dalam selang tertentu. Jika pembolehubah rawak mempunyai hukum taburan yang diberikan, maka dikatakan ia diedarkan mengikut undang-undang ini atau mematuhi undang-undang taburan ini.
Setiap undang-undang pengedaran ialah fungsi yang menerangkan sepenuhnya pembolehubah rawak dari sudut kebarangkalian. Dalam amalan, taburan kebarangkalian pembolehubah rawak X selalunya perlu dinilai hanya dengan keputusan ujian.
Taburan normal
Taburan normal, juga dipanggil taburan Gaussian, ialah taburan kebarangkalian yang memainkan peranan penting dalam banyak bidang pengetahuan, terutamanya dalam fizik. Kuantiti fizik mematuhi taburan normal apabila ia dipengaruhi oleh sejumlah besar bunyi rawak. Adalah jelas bahawa keadaan ini adalah sangat biasa, jadi kita boleh mengatakan bahawa daripada semua taburan, ia adalah taburan normal yang paling kerap berlaku di alam semula jadi - oleh itu salah satu daripada namanya berasal.
Taburan normal bergantung pada dua parameter - anjakan dan skala, iaitu, dari sudut pandangan matematik, ia bukan satu taburan, tetapi seluruh keluarga mereka. Nilai parameter sepadan dengan nilai min (jangkaan matematik) dan sebaran (sisihan piawai).


Taburan normal piawai ialah taburan normal dengan min 0 dan sisihan piawai 1.


Pekali asimetri

Pekali kecondongan adalah positif jika ekor kanan taburan lebih panjang daripada kiri, dan negatif sebaliknya.
Jika taburan adalah simetri berkenaan dengan jangkaan matematik, maka pekali kecondongannya adalah sama dengan sifar.

Pekali kecondongan sampel digunakan untuk menguji taburan untuk simetri, serta untuk ujian awal kasar untuk kenormalan. Ia membolehkan anda menolak, tetapi tidak membenarkan anda menerima hipotesis normaliti.
Pekali Kurtosis

Pekali kurtosis (koefisien ketajaman) ialah ukuran ketajaman puncak taburan pembolehubah rawak.
"Tolak tiga" pada akhir formula diperkenalkan supaya pekali kurtosis taburan normal adalah sama dengan sifar. Ia positif jika puncak taburan berhampiran nilai jangkaan adalah tajam, dan negatif jika puncak licin.

Detik pembolehubah rawak
Momen pembolehubah rawak ialah ciri berangka bagi taburan pembolehubah rawak yang diberikan.

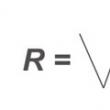



 . (6.1.3)
. (6.1.3) .
.
 ,
, .
. .
.
















