Bir cisimler sisteminin dinamiği üzerine genel teoremler. Kütle merkezinin hareketi, momentum değişimi, ana açısal momentum değişimi, kinetik enerji değişimi ile ilgili teoremler. D'Alembert'in ilkeleri ve olası hareketler. Dinamiğin genel denklemi. Lagrange denklemleri.

Katı bir cismin ve cisimler sisteminin dinamiği üzerine genel teoremler

Dinamiğin genel teoremleri- bu kütle merkezinin hareketiyle ilgili bir teoremdir mekanik sistem, momentum değişimine ilişkin teorem, asal açısal momentumdaki değişime (kinetik momentum) ilişkin teorem ve mekanik bir sistemin kinetik enerjisindeki değişime ilişkin teorem.

Mekanik bir sistemin kütle merkezinin hareketi üzerine teorem

Kütle merkezinin hareketi ile ilgili teorem.
Bir sistemin kütlesi ile kütle merkezinin ivmesinin çarpımı, sisteme etki eden tüm dış kuvvetlerin vektör toplamına eşittir:
.

Burada M sistemin kütlesidir:
;
a C sistemin kütle merkezinin ivmesidir:
;
v C - sistemin kütle merkezinin hızı:
;
r C - sistemin kütle merkezinin yarıçap vektörü (koordinatları):
;
- sistemi oluşturan noktaların koordinatları (sabit merkeze göre) ve kütleleri.

Momentumdaki (momentum) değişime ilişkin teorem

Sistemin hareket (impuls) miktarı tüm sistemin kütlesinin, kütle merkezinin hızına veya sistemi oluşturan bireysel noktaların veya parçaların momentumunun (impulsların toplamına) toplamına eşittir:
.

Momentumun diferansiyel formdaki değişimine ilişkin teorem.
Sistemin hareket miktarının (momentumunun) zamana göre türevi, sisteme etki eden tüm dış kuvvetlerin vektör toplamına eşittir:
.

İntegral formda momentum değişimine ilişkin teorem.
Belirli bir süre boyunca sistemin momentumundaki (momentumundaki) değişim, aynı süre içindeki dış kuvvetlerin darbelerinin toplamına eşittir:
.

Momentumun korunumu kanunu (momentum).
Sisteme etki eden tüm dış kuvvetlerin toplamı sıfır ise sistemin momentum vektörü sabit olacaktır. Yani koordinat eksenlerindeki tüm projeksiyonları sabit değerleri koruyacaktır.

Eğer dış kuvvetlerin herhangi bir eksene izdüşümü toplamı sıfır ise, sistemin hareket miktarının bu eksene izdüşümü sabit olacaktır.

Asal açısal momentumdaki değişime ilişkin teorem (momentler teoremi)

Bir sistemin belirli bir O merkezine göre temel açısal momentumu, sistemin bu merkeze göre tüm noktalarının açısal momentumunun vektör toplamına eşit miktardır:
.
Burada köşeli parantezler çapraz çarpımı göstermektedir.

Ekli sistemler

Aşağıdaki teorem, mekanik bir sistemin eylemsiz bir referans çerçevesine göre sabitlenmiş sabit bir noktaya veya eksene sahip olduğu duruma uygulanır. Örneğin küresel bir yatakla sabitlenmiş bir gövde. Veya sabit bir merkez etrafında hareket eden cisimlerden oluşan bir sistem. Aynı zamanda bir cismin veya cisimler sisteminin etrafında döndüğü sabit bir eksen de olabilir. Bu durumda momentler, itme momentleri ve sabit eksene göre kuvvetler olarak anlaşılmalıdır.

Asal açısal momentumdaki değişime ilişkin teorem (momentler teoremi)
Sistemin ana açısal momentumunun sabit bir O merkezine göre zamana göre türevi, sistemin tüm dış kuvvetlerinin aynı merkeze göre momentlerinin toplamına eşittir.

Asal açısal momentumun korunumu yasası (açısal momentum).
Belirli bir sabit O merkezine göre sisteme uygulanan tüm dış kuvvetlerin momentlerinin toplamı sıfıra eşitse, sistemin bu merkeze göre ana açısal momentumu sabit olacaktır. Yani koordinat eksenlerindeki tüm projeksiyonları sabit değerleri koruyacaktır.

Eğer dış kuvvetlerin sabit bir eksene göre momentlerinin toplamı sıfır ise, sistemin bu eksene göre açısal momentumu sabit olacaktır.

Keyfi sistemler

Aşağıdaki teorem evrensel bir karaktere sahiptir. Hem sabit hem de serbestçe hareket eden sistemler için geçerlidir. Sabit sistemlerde bağlantıların sabit noktalardaki tepkilerinin dikkate alınması gerekir. Sabit bir O noktası yerine sistemin C kütle merkezinin alınması gerektiği açısından önceki teoremden farklıdır.

Kütle merkezi etrafındaki momentler teoremi
Sistemin ana açısal momentumunun C kütle merkezine göre zamana göre türevi, sistemin tüm dış kuvvetlerinin aynı merkeze göre momentlerinin toplamına eşittir.

Açısal momentumun korunumu kanunu.
Sisteme uygulanan tüm dış kuvvetlerin C kütle merkezine göre momentlerinin toplamı sıfıra eşitse, sistemin bu merkeze göre ana momentum momenti sabit olacaktır. Yani koordinat eksenlerindeki tüm projeksiyonları sabit değerleri koruyacaktır.

Vücudun eylemsizlik momenti

Vücut z ekseni etrafında dönüyorsaω z açısal hızıyla, z eksenine göre açısal momentumu (kinetik momenti) aşağıdaki formülle belirlenir:
Lz = Jz ωz ,
burada Jz, cismin z eksenine göre eylemsizlik momentidir.

Cismin z eksenine göre atalet momenti formülle belirlenir:
,
burada h k, m k kütleli bir noktadan z eksenine olan mesafedir.
Kütlesi M ve yarıçapı R olan ince bir halka veya kütlesi kenarı boyunca dağılmış bir silindir için,
J z = MR 2 .
Katı homojen bir halka veya silindir için,
.

Steiner-Huygens teoremi.
Cz cismin kütle merkezinden geçen eksen, Oz ise ona paralel eksen olsun. O zaman cismin bu eksenlere göre eylemsizlik momentleri şu ilişkiyle ilişkilendirilir:
J Oz = J Cz + Ma 2 ,
burada M vücut ağırlığıdır; a eksenler arasındaki mesafedir.

Daha fazlası Genel dava :
,
vücudun atalet tensörü nerede.
Burada cismin kütle merkezinden m k kütleli bir noktaya çizilen bir vektör var.

Kinetik enerjinin değişimine ilişkin teorem

M kütleli bir cismin z ekseni etrafında ω açısal hızıyla öteleme ve dönme hareketi yapmasına izin verin. Daha sonra vücudun kinetik enerjisi aşağıdaki formülle belirlenir:
,
burada v C vücudun kütle merkezinin hareket hızıdır;
J Cz, dönme eksenine paralel olarak cismin kütle merkezinden geçen eksene göre cismin atalet momentidir. Dönme ekseninin yönü zamanla değişebilir. Bu formül kinetik enerjinin anlık değerini verir.

Diferansiyel formdaki bir sistemin kinetik enerjisindeki değişime ilişkin teorem.
Bir hareket sırasında bir sistemin kinetik enerjisinin farkı (artışı), sisteme uygulanan tüm dış ve iç kuvvetlerin bu hareket üzerindeki iş farklarının toplamına eşittir:
.

İntegral formdaki bir sistemin kinetik enerjisindeki değişime ilişkin teorem.
Bir hareket sırasında sistemin kinetik enerjisindeki değişiklik, sisteme uygulanan tüm dış ve iç kuvvetlerin bu hareket üzerindeki çalışmalarının toplamına eşittir:
.

Kuvvetin yaptığı iş, kuvvet vektörlerinin skaler çarpımına ve uygulama noktasının sonsuz küçük yer değiştirmesine eşittir:
,
yani F ve ds vektörlerinin mutlak değerlerinin aralarındaki açının kosinüsüyle çarpımı.

Kuvvet momentinin yaptığı iş, tork vektörlerinin skaler çarpımına ve sonsuz küçük dönme açısına eşittir:
.

d'Alembert ilkesi

D'Alembert ilkesinin özü dinamik problemlerini statik problemlerine indirgemektir. Bunu yapmak için sistem gövdelerinin belirli (açısal) ivmelere sahip olduğu varsayılır (veya önceden bilinir). Daha sonra, mekanik yasalarına göre belirli ivmeler veya açısal ivmeler yaratacak kuvvetlerin kuvvetlerine ve momentlerine büyüklük olarak eşit ve zıt yönde olan atalet kuvvetleri ve/veya atalet kuvvetlerinin momentleri tanıtılır.

Bir örneğe bakalım. Vücut öteleme hareketine maruz kalır ve dış kuvvetler tarafından etkilenir. Ayrıca bu kuvvetlerin sistemin kütle merkezinde bir ivme yarattığını varsayıyoruz. Kütle merkezinin hareketi ile ilgili teoreme göre, bir cisme bir kuvvet etki ettiğinde cismin kütle merkezi aynı ivmeye sahip olacaktır. Daha sonra eylemsizlik kuvvetini tanıtacağız:
.
Bundan sonra dinamik problem:
.
;
.

Dönme hareketi için aynı şekilde ilerleyin. Cismin z ekseni etrafında dönmesine ve M e zk kuvvetinin dış momentlerinin etkisine maruz kalmasına izin verin. Bu momentlerin bir εz açısal ivmesi yarattığını varsayıyoruz. Daha sonra eylemsizlik kuvvetlerinin momentini tanıtıyoruz M И = - J z ε z. Bundan sonra dinamik problem:
.
Statik bir soruna dönüşür:
;
.

Olası hareketlerin ilkesi

Statik problemleri çözmek için olası yer değiştirmeler ilkesi kullanılır. Bazı problemlerde denge denklemlerini oluşturmaktan daha kısa bir çözüm verir. Bu özellikle birçok gövdeden oluşan bağlantıları olan sistemler (örneğin, dişler ve bloklarla birbirine bağlanan gövde sistemleri) için geçerlidir.

Olası hareketlerin ilkesi.
İdeal bağlantılara sahip bir mekanik sistemin dengesi için, sistemin olası herhangi bir hareketi için üzerine etki eden tüm aktif kuvvetlerin temel işlerinin toplamının sıfıra eşit olması gerekli ve yeterlidir.

Olası sistem değişikliği- sisteme dayatılan bağlantıların kopmadığı küçük bir harekettir.

İdeal bağlantılar- bunlar sistem hareket ettiğinde iş yapmayan bağlantılardır. Daha doğrusu, sistemi hareket ettirirken bağlantıların kendilerinin yaptığı iş miktarı sıfırdır.

Dinamiğin genel denklemi (D'Alembert - Lagrange ilkesi)

D'Alembert-Lagrange ilkesi, D'Alembert ilkesinin olası hareketler ilkesiyle birleşimidir. Yani, dinamik bir problemi çözerken, atalet kuvvetlerini devreye sokuyoruz ve problemi, olası yer değiştirmeler ilkesini kullanarak çözdüğümüz statik bir probleme indirgemekteyiz.

D'Alembert-Lagrange ilkesi.
İdeal bağlantılara sahip bir mekanik sistem hareket ettiğinde, zamanın her anında sistemin olası herhangi bir hareketine uygulanan tüm aktif kuvvetlerin ve tüm eylemsizlik kuvvetlerinin temel işlerinin toplamı sıfırdır:
.
Bu denklem denir genel denklem hoparlörler.

Lagrange denklemleri

Genelleştirilmiş q koordinatları 1 , q 2 , ..., q n sistemin konumunu benzersiz bir şekilde belirleyen n adet nicelik kümesidir.

Genelleştirilmiş koordinatların sayısı n, sistemin serbestlik derecesi sayısıyla çakışır.

Genelleştirilmiş hızlar t zamanına göre genelleştirilmiş koordinatların türevleridir.

Genelleştirilmiş kuvvetler Q 1 , Ç 2 , ..., Ç n .
qk koordinatının δqk hareketini alacağı sistemin olası bir hareketini düşünelim. Kalan koordinatlar değişmeden kalır. Böyle bir hareket sırasında dış kuvvetlerin yaptığı iş δA k olsun. Daha sonra
δA k = Q k δq k veya
.

Sistemin olası bir hareketiyle tüm koordinatlar değişirse, bu tür bir hareket sırasında dış kuvvetlerin yaptığı iş şu şekilde olur:
δA = Q 1 δq 1 + Q 2 δq 2 + ... + Q n δq n.
O zaman genelleştirilmiş kuvvetler yer değiştirmeler üzerindeki işin kısmi türevleridir:
.

İçin potansiyel kuvvetler potansiyel Π ile,
.

Lagrange denklemleri mekanik bir sistemin genelleştirilmiş koordinatlardaki hareket denklemleridir:

Burada T kinetik enerjidir. Genelleştirilmiş koordinatların, hızların ve muhtemelen zamanın bir fonksiyonudur. Bu nedenle kısmi türevi aynı zamanda genelleştirilmiş koordinatların, hızların ve zamanın bir fonksiyonudur. Daha sonra koordinatların ve hızların zamanın fonksiyonu olduğunu dikkate almanız gerekir. Bu nedenle zamana göre toplam türevi bulmak için karmaşık bir fonksiyonun türev alma kuralını uygulamanız gerekir:
.

Referanslar:
S.M. Targ, Kısa kurs teorik mekanik, "Yüksekokul", 2010.

Ders 3. Dinamiğin genel teoremleri

Maddi noktalar sisteminin dinamiği teorik mekaniğin önemli bir dalıdır. Burada esas olarak, sonlu sayıda serbestlik derecesine (sistemin konumunu belirleyen maksimum sayıda bağımsız parametreye) sahip mekanik sistemlerin (madde noktaları sistemleri) hareketi ile ilgili problemleri ele alıyoruz. Sistem dinamiğinin asıl görevi hareket yasalarının incelenmesidir. sağlam ve mekanik sistemler.

Bir sistemin hareketini incelemeye yönelik en basit yaklaşım aşağıdakilerden oluşur: N Maddi noktaların belirlenmesi, sistemin her bir noktasının hareketlerinin dikkate alınmasına gelir. Bu durumda noktalar arasındaki etkileşim kuvvetleri de dahil olmak üzere sistemin her noktasına etki eden tüm kuvvetlerin belirlenmesi gerekir.

Newton'un ikinci yasasına (1.2) uygun olarak her noktanın ivmesini belirleyerek, her nokta için ikinci dereceden üç skaler diferansiyel hareket yasasını elde ederiz; 3 N Tüm sistem için diferansiyel hareket yasaları.

Sistemin her noktası için verilen kuvvetlere ve başlangıç ​​koşullarına dayalı olarak mekanik bir sistemin hareket denklemlerini bulmak için, ortaya çıkan diferansiyel yasaların entegre edilmesi gerekir. Bu problem, evrensel çekim yasasına göre (iki cisim problemi) yalnızca etkileşim kuvvetlerinin etkisi altında hareket eden iki maddi nokta durumunda bile zordur ve etkileşen üç nokta durumunda (üç cisim problemi) son derece zordur. ).

Bu nedenle çözülebilir denklemlere yol açacak ve mekanik bir sistemin hareketi hakkında fikir verecek problemlerin çözümüne yönelik yöntemlerin bulunması gerekmektedir. Diferansiyel hareket yasalarının bir sonucu olan genel dinamik teoremleri, entegrasyon sırasında ortaya çıkan karmaşıklıktan kaçınmamıza ve gerekli sonuçları elde etmemize olanak tanır.

3. 1. Genel notlar

Mekanik sistemin noktalarını indekslerle numaralandıracağız Ben, J, k vb. tüm değerlerin içinden geçen 1, 2, 3… N, Nerede N – sistemin nokta sayısı. Fiziksel özellikler ile ilgili k nokta, noktayla aynı indeksle gösterilir. Örneğin, sırasıyla yarıçap vektörünü ve hızı ifade edin k bu nokta.

Sistemin her noktasına iki kaynaklı kuvvetler etki eder: Birincisi, kaynakları sistemin dışında bulunan kuvvetler. harici kuvvetler ve belirlenmiş; ikincisi, belirli bir sistemin diğer noktalarından gelen kuvvetlere denir. dahili kuvvetler ve belirlenmiş. İç kuvvetler Newton'un üçüncü yasasını karşılar. Herhangi bir durumda tüm mekanik sisteme etki eden iç kuvvetlerin en basit özelliklerini ele alalım.

İlk mülk. Sistemin tüm iç kuvvetlerinin geometrik toplamı (iç kuvvetlerin ana vektörü) sıfıra eşittir.

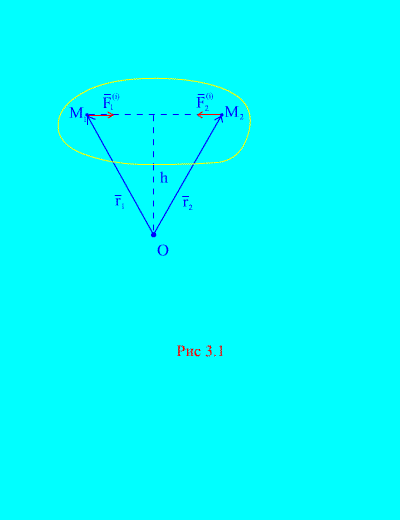
Aslında, sistemin herhangi iki keyfi noktasını ele alırsak, örneğin ve (Şekil 3.1), o zaman onlar için , Çünkü Etki ve tepki kuvvetleri her zaman büyüklük bakımından eşit olup, etkileşen noktaları birbirine bağlayan, zıt yöndeki bir etki çizgisi boyunca etki eder. İç kuvvetlerin ana vektörü, etkileşen noktaların kuvvet çiftlerinden oluşur, bu nedenle

(3.1)

İkinci mülk. Uzaydaki herhangi bir noktaya göre tüm iç kuvvetlerin momentlerinin geometrik toplamı sıfıra eşittir.

Kuvvetlerin momentlerinden ve noktaya göreli bir sistem düşünelim. HAKKINDA(Şekil 3.1). İtibaren (Şekil 3.1). bu açık

,

Çünkü her iki kuvvet de aynı kollara ve vektör momentlerinin zıt yönlerine sahiptir. Ana nokta bir noktaya göre iç kuvvetler HAKKINDA bu tür ifadelerin vektör toplamından oluşur ve sıfıra eşittir. Buradan,

Aşağıdakilerden oluşan bir mekanik sisteme dış ve iç kuvvetler etki etsin. N puan (Şekil 3.2). Dış kuvvetlerin bileşkesi ve tüm iç kuvvetlerin bileşkesi sistemin her noktasına uygulanırsa, o zaman herhangi bir nokta için k Sistemin 3. noktasında diferansiyel hareket denklemleri çizilebilir. Bu tür denklemlerin toplamı olacak N:

ve sabit koordinat eksenleri üzerindeki projeksiyonlarda 3 N:

(3.4)

Vektör denklemleri (3.3) veya eşdeğer skaler denklemler (3.4), tüm sistemin maddi noktalarının diferansiyel hareket yasalarını temsil eder. Tüm noktalar bir düzleme veya bir düz çizgiye paralel hareket ederse, ilk durumda denklemlerin (3.4) sayısı şu şekilde olacaktır: 2 N, saniyede N.

Örnek 1.İki kütle birbirine bir bloğun üzerine atılan uzatılamaz bir kabloyla bağlanır (Şekil 3.3). Sürtünme kuvvetlerinin yanı sıra blok ve kablonun kütlesinin de ihmal edilmesi, yüklerin hareketi ve kablo gerginliği yasasını belirler.

Çözüm. Sistem aynı eksene paralel hareket eden (uzatılamaz bir kabloyla birbirine bağlanan) iki malzeme gövdesinden oluşur. X. Diferansiyel hareket yasalarını eksene izdüşümlerde yazalım X herkes için.

Sağ ağırlığın ivmeyle düşmesine izin verin, sonra sol ağırlık ivmeyle yükselecektir. Kendimizi zihinsel olarak bağlantıdan (kablodan) kurtarır ve onu tepkilerle değiştiririz. (Şekil 3.3). Cisimlerin serbest olduğunu kabul ederek, eksene izdüşümü halinde hareketin diferansiyel yasalarını çizelim. X(bu, iplik gerginliklerinin iç kuvvetler olduğu ve yüklerin ağırlığının dış kuvvetler olduğu anlamına gelir):

Ve (gövdeler uzatılamaz bir kabloyla bağlı olduğundan) elde ederiz

İvme ve kablo gerilimi için bu denklemlerin çözülmesi T, alıyoruz

.

Kablodaki gerilimin karşılık gelen yükün yer çekimi kuvvetine eşit olmadığını unutmayın.

3. 2. Kütle merkezinin hareketine ilişkin teorem

Düzlemdeki katı bir cismin ve mekanik sistemin oldukça karmaşık hareket edebildiği bilinmektedir. Bir cismin ve mekanik bir sistemin hareketiyle ilgili ilk teoreme şu şekilde ulaşılabilir: a k.-l atın. birbirine tutturulmuş birçok katı cisimden oluşan bir nesne. Bir parabolde uçacağı açıktır. Bu, noktanın hareketi incelenirken ortaya çıktı. Ancak artık nesne bir nokta değildir. Bir parabolde hareket eden etkili bir merkezin etrafında uçuşu sırasında döner ve sallanır. Karmaşık nesnelerin hareketiyle ilgili ilk teorem, belirli bir etkili merkezin, hareket eden bir nesnenin kütle merkezi olduğunu söylüyor. Kütle merkezinin mutlaka vücudun içinde olması gerekmez; onun dışında bir yerde bulunabilir.

Teorem. Mekanik bir sistemin kütle merkezi, sisteme etki eden tüm dış kuvvetlerin uygulandığı, tüm sistemin kütlesine eşit kütleye sahip maddi bir nokta olarak hareket eder.

Teoremi kanıtlamak için diferansiyel hareket yasalarını (3.3) aşağıdaki biçimde yeniden yazıyoruz:

(3.5)

Nerede N – sistemin nokta sayısı.

Denklemleri terim terim toplayalım:

(A)

Mekanik sistemin kütle merkezinin seçilen koordinat sistemine göre konumu formül (2.1) ile belirlenir: Nerede M– sistemin kütlesi. Daha sonra Sol Taraf eşitlik (a) yazılacak

Eşitliğin (a) sağ tarafındaki ilk toplam, dış kuvvetlerin ana vektörüne eşittir ve sonuncusu, iç kuvvetlerin özelliği gereği sıfıra eşittir. Daha sonra eşitlik (a), (b) dikkate alınarak yeniden yazılacaktır.

, (3.6)

onlar. sistemin kütlesinin çarpımı ve kütle merkezinin ivmesi, sisteme etki eden tüm dış kuvvetlerin geometrik toplamına eşittir.

Denklem (3.6)'dan iç kuvvetlerin kütle merkezinin hareketini doğrudan etkilemediği sonucu çıkar. Ancak bazı durumlarda sisteme uygulanan dış kuvvetlerin ortaya çıkmasına neden olurlar. Böylece, bir arabanın tahrik tekerleklerini dönmeye iten iç kuvvetler, tekerlek jantına uygulanan bir dış yapışma kuvvetinin jant üzerinde etkili olmasına neden olur.

Örnek 2. Dikey bir düzlemde bulunan mekanizma, yatay ve pürüzsüz bir düzlem üzerine monte edilir ve yüzeye sağlam bir şekilde sabitlenmiş çubuklarla ona bağlanır. İLE Ve L (Şekil 3.4).

Disk 1 yarıçapı R hareketsiz. Disk 2 kütlesi M ve yarıçap R bir kranka bağlı, uzunluk R+ R noktada C2. Krank sabit bir hızla dönüyor

Açısal hız. İlk anda krank sağ tarafı işgal etti yatay pozisyon. Krankın kütlesini ihmal ederek, çerçeve ve tekerlek 1'in toplam kütlesi şuna eşitse, çubuklara etkiyen maksimum yatay ve düşey kuvvetleri belirleyin: M. Ayrıca çubukların yokluğunda mekanizmanın davranışını da göz önünde bulundurun.

Çözüm. Sistem iki kütleden oluşur ( N=2 ): çerçeveli ve hareketli diskli sabit disk 1 2. Ekseni yönlendirin en sabit diskin ağırlık merkezi boyunca dikey olarak yukarı doğru, eksen X– yatay düzlem boyunca.

Kütle merkezinin (3.6) hareketine ilişkin teoremi koordinat biçiminde yazalım.

Bu sistemin dış kuvvetleri şunlardır: çerçevenin ve sabit diskin ağırlığı - Mg, hareketli disk ağırlığı – mg, - cıvataların toplam yatay reaksiyonu, - uçağın normal toplam reaksiyonu. Buradan,

Daha sonra hareket yasaları (b) yeniden yazılacaktır.

Mekanik sistemin kütle merkezinin koordinatlarını hesaplayalım:

; (G)

şuradan görülebileceği gibi (Şekil 3.4), , , (krank açısı), . Bu ifadeleri (d)'de yerine koyarak ikinci türevlerin zamana göre hesaplanması T,'den bunu anlıyoruz

(e)

(c) ve (e)'yi (b)'nin yerine koyarsak, şunu buluruz:

Çubuklara etki eden yatay basınç en büyük ve en az olduğunda çünkü = 1 buna göre, yani

Mekanizma baskısı yatay düzlem en büyük ve en küçük değerlere sahip olduğunda günah buna göre, yani

Aslında dinamiğin ilk problemi çözüldü: Sistemin kütle merkezinin (d) bilinen hareket denklemlerine göre, harekete dahil olan kuvvetler eski durumuna getirildi.

Barların yokluğunda k Ve L (Şekil 3.4) mekanizma yatay düzlemin üzerinde sıçramaya başlayabilir. Bu şu durumlarda gerçekleşecektir: olduğunda, mekanizmanın sıçradığı krankın açısal dönüş hızının eşitliği sağlaması gerektiği sonucu çıkar.

.

3. 3. Kütle merkezinin hareketinin korunumu kanunu

Sisteme etki eden dış kuvvetlerin ana vektörü sıfıra eşitse; , sonra(3.6)kütle merkezinin ivmesinin sıfır olduğu, dolayısıyla kütle merkezinin hızının büyüklük ve yön bakımından sabit olduğu sonucu çıkar. Özellikle ilk anda kütle merkezi hareketsizse, dış kuvvetlerin ana vektörü sıfıra eşitken tüm zaman boyunca hareketsizdir.

Bu teoremden birkaç sonuç çıkar.

· İç kuvvetler tek başına sistemin kütle merkezinin hareketinin doğasını değiştiremez.

· Sisteme etki eden dış kuvvetlerin ana vektörü sıfır ise, kütle merkezi hareketsizdir veya düzgün ve doğrusal olarak hareket eder.

· Sistemin dış kuvvetlerinin ana vektörünün sabit bir eksene izdüşümü sıfıra eşitse, sistemin kütle merkezinin hızının bu eksene izdüşümü değişmez.

· Katı bir cisme uygulanan bir çift kuvvet, kütle merkezinin hareketini değiştiremez (yalnızca cismin kütle merkezi etrafında dönmesine neden olabilir).

Kütle merkezinin hareketinin korunumu yasasını gösteren bir örneği ele alalım.

Örnek 3.İki kütle, bir bloğun içinden atılan uzatılamaz bir iplikle birbirine bağlanır (Şekil 3.5) kütleli bir kama üzerine sabitlenmiş M. Kama düzgün bir yatay düzlem üzerinde durmaktadır. İlk anda sistem hareketsiz durumdaydı. İlk yük belli bir yüksekliğe indirildiğinde kamanın düzlem boyunca yer değiştirmesini bulun N. Bloğun ve ipliğin kütlesini ihmal edin.

Çözüm. Yüklerle birlikte kamaya etki eden dış kuvvetler yerçekimidir ve Mg, ayrıca pürüzsüz bir yatay yüzey N'nin normal reaksiyonunun yanı sıra,

İlk anda sistem hareketsiz olduğundan, .

Sistemin kütle merkezinin o andaki koordinatlarını hesaplayalım. T 1 yük ağırlaştığında G yüksekliğe inecek H.

Şu an için:

,

Nerede , , X– sırasıyla g, g ağırlığındaki yüklerin ve kama ağırlığının kütle merkezinin koordinatları MG.

Kamanın o anda eksenin pozitif yönünde hareket ettiğini varsayalım. Öküz miktara göre L yükün ağırlığı belirli bir yüksekliğe düşerse N. O zaman şimdilik

Çünkü yükler kamayla birlikte hareket edecek L sağa doğru hareket edecek ve yük kama boyunca yukarı doğru hareket edecektir. O zamandan beri, hesaplamalardan sonra şunu elde ederiz:

.

3.4. Sistem hareket miktarı

3.4.1. Sistem momentumunun hesaplanması

Maddi bir noktanın momentumu, noktanın kütlesi ile hız vektörünün çarpımına eşit bir vektör miktarıdır.

Momentum ölçüm birimi -

Mekanik bir sistemin momentumu, sistemin bireysel noktalarının momentumunun vektör toplamıdır;

Nerede N – sistemin nokta sayısı.

Mekanik bir sistemin momentumu sistemin kütlesi cinsinden ifade edilebilir. M ve kütle merkezinin hızı. Gerçekten mi,

onlar. Sistemin momentumu, tüm sistemin kütlesinin ve kütle merkezinin hızının çarpımına eşittir. Yön, yön ile aynıdır (Şekil 3.6)

Dikdörtgen eksenlere yapılan projeksiyonlarda elimizdeki

burada , , sistemin kütle merkezinin hızının izdüşümleridir.

Burada M– mekanik sistemin kütlesi; sistem hareket ettiğinde değişmez.

Bu sonuçların özellikle katı cisimlerin hareket miktarlarının hesaplanmasında kullanılması uygundur.

Formül (3.7)'den, mekanik bir sistemin kütle merkezi sabit kalacak şekilde hareket etmesi durumunda sistemin momentumunun sıfıra eşit kalacağı açıktır.

3.4.2. Temel ve tam kuvvet darbesi

Bir kuvvetin zaman içinde maddi bir noktaya etkisi dt temel bir dürtü ile karakterize edilebilir. Zaman içindeki toplam kuvvet darbesi T, veya formülle belirlenen kuvvet darbesi

veya eksen koordinatları üzerine projeksiyonlarda

(3.8a)

Kuvvet darbesinin birimi.

3.4.3. Bir sistemin momentumundaki değişime ilişkin teorem

Sistemin noktalarına dış ve iç kuvvetler uygulansın. Daha sonra sistemin her noktası için diferansiyel hareket yasalarını (3.3) uygulayabiliriz, bunu aklımızda tutarak :

.

Sistemin tüm noktalarını toplayarak şunu elde ederiz:

İç kuvvetlerin özelliği ve tanımı gereği sahibiz

(3.9)

Bu denklemin her iki tarafının çarpılması dt Momentumdaki değişime ilişkin diferansiyel formda bir teorem elde ederiz:

, (3.10)

onlar. Mekanik bir sistemin diferansiyel momentumu, mekanik sistemin noktalarına etki eden tüm dış kuvvetlerin temel itkilerinin vektör toplamına eşittir.

Her iki tarafın (3.10) 0'dan zamana göre integralinin hesaplanması T, teoremi sonlu veya integral formda elde ederiz

(3.11)

Koordinat eksenleri üzerindeki projeksiyonlarda sahip olacağımız

Mekanik bir sistemin momentumunun zamanla değişmesiT, aynı anda mekanik sistemin noktalarına etki eden dış kuvvetlerin tüm darbelerinin vektör toplamına eşittir.

Örnek 4. Yük ağırlığı M Bir kuvvetin etkisi altında dinlenme halindeyken eğik bir düzlemden aşağıya doğru iner F, zamanla orantılı: , burada (Şekil 3.7). Vücut bundan sonra hangi hızı kazanacak? T Hareketin başlamasından saniyeler sonra, yükün eğimli düzlemdeki kayma sürtünme katsayısı şuna eşitse: F.

Çözüm. Yüke uygulanan kuvvetleri tasvir edelim: mg – yük yerçekimi kuvveti, N düzlemin normal tepkisidir, düzlem üzerindeki yükün kayma sürtünme kuvvetidir ve . Tüm kuvvetlerin yönü şekilde gösterilmiştir. (Şekil 3.7).

Ekseni yönlendirelim X eğik düzlem boyunca aşağıya doğru. Eksene izdüşümdeki momentumdaki (3.11) değişimle ilgili teoremi yazalım. X:

(A)

Şarta göre çünkü zamanın ilk anında yük hareketsizdi. Tüm kuvvetlerin impulslarının x eksenine izdüşümlerinin toplamı şuna eşittir:

Buradan,

,

.

3.4.4. Momentumun korunumu yasaları

Korunum yasaları momentumdaki değişim teoreminin özel durumları olarak elde edilir. İki özel durum mümkündür.

· Sisteme uygulanan tüm dış kuvvetlerin vektör toplamı sıfıra eşitse; , o zaman aşağıdaki teoremden (3.9) , Ne ,

onlar. Sistemin dış kuvvetlerinin ana vektörü sıfır ise, sistemin hareket miktarı büyüklük ve yön bakımından sabittir.

· Dış kuvvetlerin ana vektörünün herhangi bir yere izdüşümü ise koordinat ekseni sıfıra eşit, örneğin Oh, yani. ise momentumun bu eksene izdüşümü sabit bir değerdir.

Momentumun korunumu yasasının uygulanmasına ilişkin bir örneği ele alalım.

Örnek 5. Balistik sarkaç, uzun bir ip üzerinde asılı duran bir kütle gövdesidir. (Şekil 3.8).

Hızla hareket eden bir kütle mermisi V ve sabit bir cisme çarparak sıkışıp kalır ve cisim sapar. Ceset yüksekliğe çıkarsa merminin hızı ne olurdu? H ?

Çözüm. Kurşunun sıkıştığı bedenin hız kazanmasına izin verin. Daha sonra, iki cismin etkileşimi sırasında momentumun korunumu yasasını kullanarak şunu yazabiliriz: .

Hız, mekanik enerjinin korunumu yasası kullanılarak hesaplanabilir . Daha sonra . Sonuç olarak bulduk

.

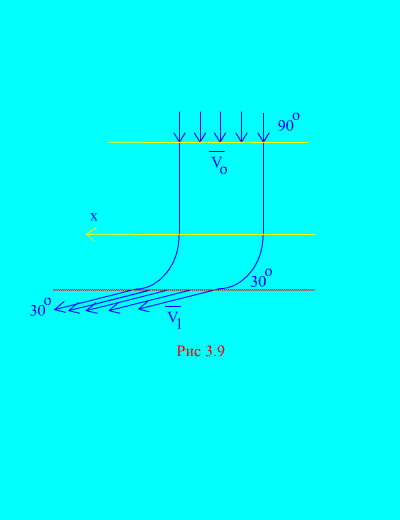
Örnek 6. Su sabit bir kanala giriyor (Şekil 3.9) yataya açılı hıza sahip değişken kesit; kare enine kesit girişteki kanal; Kanaldan çıkışta suyun hızı ufukla açı yapar.

Suyun kanal duvarlarında oluşturduğu reaksiyonun yatay bileşenini belirleyin. Suyun yoğunluğu .

Çözüm. Kanal duvarlarının suya uyguladığı reaksiyonun yatay bileşenini belirleyeceğiz. Bu kuvvet istenilen kuvvete eşit büyüklükte ve zıt işaretlidir. (3.11a)’ya göre elimizde,

. (A)

T süresi boyunca kanala giren sıvı hacminin kütlesini hesaplıyoruz:

rAV 0 değerine denir ikinci kütle - birim zamanda borunun herhangi bir bölümünden akan sıvının kütlesi.

Aynı sürede aynı miktarda su kanaldan çıkar. Başlangıç ​​ve son hızlar durumda verilmiştir.

Sisteme (su) uygulanan dış kuvvetlerin yatay eksene izdüşümlerinin toplamını belirleyen eşitliğin (a) sağ tarafını hesaplayalım. Tek yatay kuvvet, ortaya çıkan duvar reaksiyonunun yatay bileşenidir. Rx. Bu kuvvet sabit su hareketi sırasında sabittir. Bu yüzden

. (V)

(b) ve (c)'yi (a)'da yerine koyarsak, şunu elde ederiz:

3.5. Sistemin kinetik momenti

3.5.1. Sistemin ana momentum anı

Merkez adı verilen bir A noktasına göre sistemin kütlesine sahip bir noktanın yarıçap vektörü olsun. (Şekil 3.10).

Bir noktanın momentumu (kinetik momenti) A merkezine göre vektör denir , formülle belirlenir

. (3.12)

Bu durumda vektör merkezden geçen düzleme dik olarak yönlendirilir A ve vektör .

Bir noktanın eksene göre momentumu (kinetik momenti) bir noktanın momentum momentinin bu eksen üzerinde seçilen herhangi bir merkeze göre bu eksene izdüşümüne denir.

Sistemin A merkezine göre ana momentum momenti (kinetik moment) miktar denir

(3.13)

Sistemin eksene göre ana momentum momenti (kinetik moment) sistemin ana momentum momentinin bu eksen üzerinde seçilen herhangi birine göre bu eksen üzerindeki izdüşümüne denir. merkez ekseni.

3.5.2. Dönen katı bir cismin dönme eksenine göre kinetik momenti

Sabit noktayı hizalayalım HAKKINDA dönme ekseni üzerinde yatan vücut HAKKINDAz, koordinat sisteminin kökeni ile Ohooz eksenleri gövdeyle birlikte dönecek olan (Şekil 3.11). Vücudun bir noktasının koordinatların orijinine göre yarıçap vektörü olsun; eksen üzerindeki izdüşümü , , , ile gösterilecektir. Vektör projeksiyonları açısal hız aynı eksendeki cisimler 0, 0, () ile gösterilir.

Eğitim ve Bilim Bakanlığı Rusya Federasyonu

Federal Devlet Bütçe Yüksek Mesleki Eğitim Kurumu

"Kuban Devlet Teknoloji Üniversitesi"

Teorik mekanik

Bölüm 2 dinamikleri

Yayın ve Yayın Komitesi tarafından onaylandı

üniversite konseyi olarak

öğretim yardımı

Krasnodar

UDC 531.1/3 (075)

Teorik mekanik. Bölüm 2. Dinamik: Ders Kitabı / L.I. Kuban. durum technol.un.t. Krasnodar, 2011. 123 s.

ISBN 5-230-06865-5

Teorik materyal kısa bir biçimde sunulur, çoğu gerçek teknik sorunları yansıtan problem çözme örnekleri verilir ve rasyonel bir çözüm yönteminin seçimine dikkat edilir.

İnşaat, ulaştırma ve makine mühendisliği alanlarında yazışma ve uzaktan eğitim lisans öğrencileri için tasarlanmıştır.

Masa 1 Hasta. 68 Kaynakça 20 başlık

Bilimsel editör Teknik Bilimler Adayı, Doçent. V.F.Melnikov

Hakemler: Teorik Mekanik ve Mekanizmalar ve Makineler Teorisi Bölüm Başkanı, Kuban Tarım Üniversitesi prof. F.M. Kanarev; Doçent, Teorik Mekanik Bölümü, Kuban Devlet Teknoloji Üniversitesi M.E. Multık

Kuban Devlet Teknoloji Üniversitesi Yayın ve Yayın Kurulu kararıyla yayınlandı.

Yeniden yayınlama

ISBN 5-230-06865-5 KubSTU 1998

Önsöz

Bu ders kitabı inşaat, ulaştırma ve makine mühendisliği uzmanlık alanlarındaki yarı zamanlı öğrencilere yöneliktir, ancak diğer uzmanlık alanlarındaki yarı zamanlı öğrencilerin yanı sıra tam zamanlı öğrenciler tarafından teorik mekanik dersinin “Dinamik” bölümünü incelerken kullanılabilir. bağımsız çalışıyor.

Kılavuz, teorik mekanik dersinin mevcut müfredatına uygun olarak derlenmiştir ve dersin ana bölümünün tüm konularını kapsamaktadır. Her bölüm, sorunların çözümünde kullanılmasına yönelik resimler ve metodolojik önerilerle birlikte kısa teorik materyal içermektedir. Kılavuz, gerçek teknik sorunları yansıtan ve test görevlerine karşılık gelen 30 sorunun çözümlerini içerir. bağımsız karar. Her problem için çözümü açıkça gösteren bir hesaplama şeması sunulmaktadır. Çözümün biçimlendirmesi, yarı zamanlı öğrenciler için test kağıtlarının biçimlendirilmesine ilişkin gereksinimleri karşılar.

Yazar, Kuban Tarım Üniversitesi Teorik Mekanik ve Mekanizmalar ve Makineler Teorisi Bölümü öğretmenlerinin yanı sıra Kuban Devlet Teknolojik Fakültesi Teorik Mekanik Bölümü öğretmenlerinin ders kitabını incelemedeki büyük çalışmaları için derin şükranlarını sunar. Ders kitabının yayına hazırlanmasına ilişkin değerli yorumlarınız ve tavsiyeleriniz için Üniversiteye teşekkür ederiz.

Gelecekte tüm eleştirel yorum ve öneriler yazar tarafından şükranla kabul edilecektir.

giriiş

Dinamik, teorik mekaniğin en önemli bölümüdür. Mühendislik uygulamalarında karşılaşılan spesifik problemlerin çoğu dinamikle ilgilidir. Statik ve kinematiğin sonuçlarını kullanan dinamik, uygulanan kuvvetlerin etkisi altında maddi cisimlerin genel hareket yasalarını oluşturur.

En basit maddi nesne maddi bir noktadır. Herhangi bir şekle sahip bir maddi gövde, söz konusu problemde boyutları ihmal edilebilecek maddi bir nokta olarak alınabilir. Belirli bir problem için noktalarının hareketindeki fark önemli değilse, sonlu boyutlu bir cisim maddi bir nokta olarak alınabilir. Bu, vücudun boyutlarının, vücut noktalarının kat ettiği mesafelere kıyasla küçük olması durumunda meydana gelir. Katı bir cismin her parçacığı maddi bir nokta olarak düşünülebilir.

Bir noktaya veya maddi bir gövdeye uygulanan kuvvetler, dinamik etkilerine göre, yani maddi nesnelerin hareketinin özelliklerini nasıl değiştirdiklerine göre dinamik olarak değerlendirilir.

Maddi nesnelerin zaman içindeki hareketi, belirli bir referans çerçevesine göre uzayda gerçekleşir. Newton'un aksiyomlarına dayanan klasik mekanikte uzay üç boyutlu kabul edilir, özellikleri içinde hareket eden maddi nesnelere bağlı değildir. Böyle bir uzayda bir noktanın konumu üç koordinatla belirlenir. Zamanın uzayla ve maddi nesnelerin hareketi ile ilgisi yoktur. Tüm referans sistemleri için aynı kabul edilir.

Dinamik yasaları, maddi nesnelerin hareketini, geleneksel olarak sabit olarak kabul edilen mutlak koordinat eksenlerine göre tanımlar. Mutlak koordinat sisteminin kökeni Güneş'in merkezinde alınır ve eksenler uzak, koşullu olarak sabit yıldızlara yönlendirilir. Birçok teknik problemi çözerken, Dünya'ya bağlı koordinat eksenleri şartlı olarak hareketsiz kabul edilebilir.

Maddi nesnelerin dinamikteki mekanik hareketinin parametreleri, klasik mekaniğin temel yasalarından matematiksel türetmelerle belirlenir.

Birinci yasa (eylemsizlik yasası):

Maddi bir nokta, bazı kuvvetlerin etkisi onu bu durumdan çıkarana kadar dinlenme durumunu veya düzgün ve doğrusal hareket durumunu korur.

Bir noktanın düzgün ve doğrusal hareketine eylemsizlik hareketi denir. Dinlenme, bir noktanın hızının sıfır olduğu atalet yoluyla hareketin özel bir durumudur.

Her maddi noktanın eylemsizliği vardır, yani bir dinlenme durumunu veya düzgün doğrusal hareketi korumaya çalışır. Atalet yasasının geçerli olduğu referans sistemine atalet denir ve bu sisteme göre gözlemlenen harekete mutlak denir. Eylemsiz bir sisteme göre ötelemeli doğrusal ve düzgün hareket gerçekleştiren herhangi bir referans sistemi de eylemsiz bir sistem olacaktır.

İkinci yasa (dinamiğin temel yasası):

Bir maddi noktanın eylemsiz referans çerçevesine göre ivmesi, noktaya uygulanan kuvvetle orantılıdır ve şu yöndeki kuvvetle çakışır:
.

Dinamiğin temel yasasından şunu takip eder: kuvvetle
hızlanma
. Bir noktanın kütlesi, bir noktanın hızındaki değişikliklere karşı direnç derecesini karakterize eder, yani maddi bir noktanın ataletinin bir ölçüsüdür.

Üçüncü Kanun (Etki ve Tepki Kanunu):

İki cismin birbirine etki ettiği kuvvetler eşit büyüklüktedir ve zıt yönlerde bir düz çizgi boyunca yönlendirilir.

Etki ve tepki adı verilen kuvvetler uygulanır. farklı bedenler ve bu nedenle dengeli bir sistem oluşturmazlar.

Dördüncü yasa (kuvvetlerin bağımsızlığı yasası):

Birkaç kuvvetin eşzamanlı etkisi ile, maddi bir noktanın ivmesi, noktanın her bir kuvvetin ayrı ayrı etkisi altında sahip olacağı ivmelerin geometrik toplamına eşittir:

, Nerede
,
,…,
.

(MEKANİK SİSTEMLER) – IV seçeneği

1. Maddi bir noktanın dinamiğinin temel denklemi bilindiği gibi denklem ile ifade edilir. Diferansiyel denklemlerÖzgür olmayan bir mekanik sistemin keyfi noktalarının kuvvetleri bölmenin iki yöntemine göre hareketleri iki biçimde yazılabilir:

(1) , burada k=1, 2, 3, … , n – malzeme sisteminin nokta sayısı.

(2)

k'inci noktanın kütlesi nerede; - k'inci noktanın yarıçap vektörü, - k'inci noktaya etki eden belirli bir (aktif) kuvvet veya k'inci noktaya etki eden tüm aktif kuvvetlerin bileşkesi. - k'inci noktaya etki eden bağ reaksiyon kuvvetlerinin sonucu; - k'inci noktaya etki eden iç kuvvetlerin bileşkesi; - k'inci noktaya etki eden dış kuvvetlerin bileşkesi.

Denklemler (1) ve (2) kullanılarak dinamiğin hem birinci hem de ikinci problemleri çözülmeye çalışılabilir. Ancak bir sistemin ikinci dinamik problemini çözmek, yalnızca matematiksel açıdan değil, aynı zamanda temel zorluklarla karşı karşıya olduğumuz için de çok karmaşık hale gelir. Hem sistem (1) hem de sistem (2) için denklem sayısının önemli olması gerçeğinden oluşurlar. daha az sayı Bilinmeyen.

Yani, eğer (1)'i kullanırsak, o zaman ikinci (ters) problem için bilinen dinamikler ve olacaktır ve bilinmeyenler ve olacaktır. Vektör denklemleri " N”ve bilinmeyenler - “2n”.

Denklem sisteminden (2) devam edersek, dış kuvvetlerin bir kısmı bilinmektedir. Neden ayrılalım? Gerçek şu ki, dış kuvvetlerin sayısı aynı zamanda bilinmeyen bağlantıların dış reaksiyonlarını da içermektedir. Ayrıca .

Böylece hem sistem (1) hem de sistem (2) KAPALI değildir. Bağlantı denklemlerini dikkate alarak denklemler eklemek gerekir ve belki de bağlantıların kendilerine de bazı kısıtlamalar getirmek gerekir. Ne yapalım?

(1)'den başlarsak, birinci türden Lagrange denklemlerini oluşturma yolunu takip edebiliriz. Ancak bu yol rasyonel değil çünkü daha kolay görev(serbestlik derecesi ne kadar azsa) matematiksel açıdan çözmek o kadar zor olur.

O zaman dikkatimizi -'nin her zaman bilinmediği sistem (2)'ye çevirelim. Bir sistemi çözmenin ilk adımı bu bilinmeyenleri ortadan kaldırmaktır. Unutulmamalıdır ki, kural olarak, sistem hareket ederken iç kuvvetlerle ilgilenmiyoruz, yani sistem hareket ettiğinde, sistemin her noktasının nasıl hareket ettiğini bilmek gerekli değildir, ancak yeterlidir. sistemin bir bütün olarak nasıl hareket ettiğini bilmek.

Böylece eğer Farklı yollar bilinmeyen kuvvetleri sistem (2)'den hariç tutarsak, o zaman bazı ilişkiler elde ederiz, yani bazıları görünür Genel özellikleri Bir sistem için, bilgisi sistemin genel olarak nasıl hareket ettiğine karar vermemizi sağlar. Bu özellikler sözde kullanılarak tanıtılır. genel teoremler hoparlörler. Bu tür dört teorem vardır:

1. Teorem mekanik bir sistemin kütle merkezinin hareketi;

2. Teorem Mekanik bir sistemin momentumundaki değişim;

3. Teorem mekanik sistemin kinetik momentindeki değişim;

4. Hakkında Teorem mekanik bir sistemin kinetik enerjisindeki değişim.