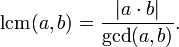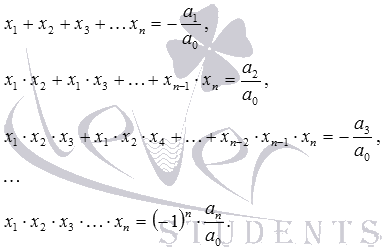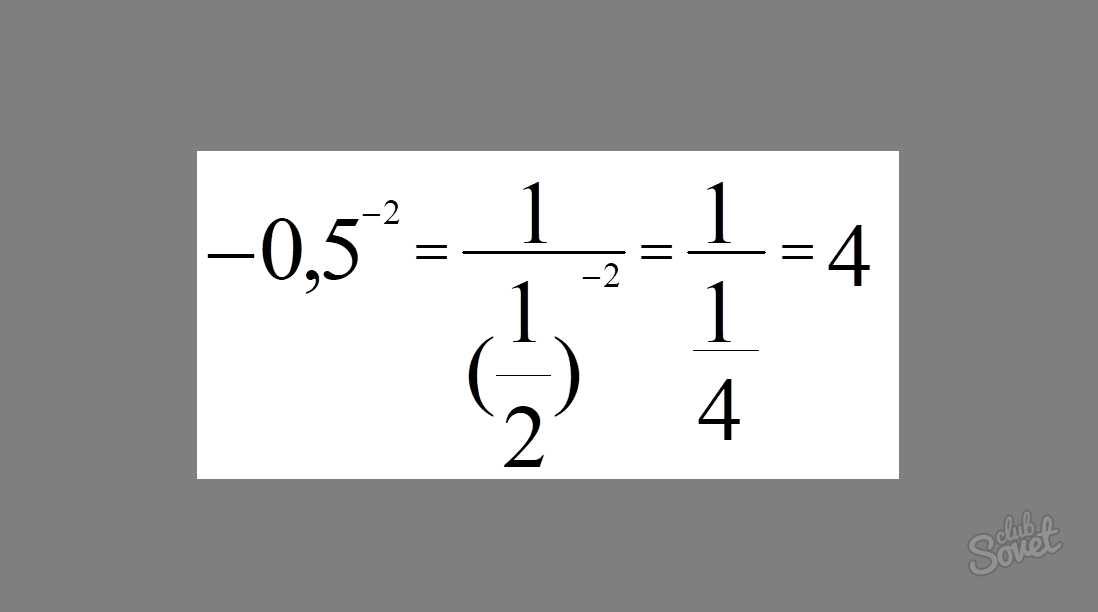Webhely szakaszok
A szerkesztők választása:
hirdetés
| A legkevésbé gyakori többszörös. 2. Hogyan lehet megtalálni a számok legkisebb közös többszörösét? NOC keresése a GCD-n keresztül |
|
De sok természetes számot is teljesen felosztnak más természetes számokra. Például: A 12 szám osztva 1, 2, 3, 4, 6, 12; A 36 szám el van osztva 1, 2, 3, 4, 6, 12, 18, 36-al. Azokat a számokat, amelyekbe a szám teljesen fel van osztva (12-re ez 1, 2, 3, 4, 6 és 12) hívják számválasztó. Természetes szám elválasztó egy egy természetes szám, amely osztja az adott számot egy nyom nélkül. Olyan természetes számot hívnak, amelynél kettőnél több osztó van összetett . Vegye figyelembe, hogy a 12. és a 36. szám közös osztóval rendelkezik. Ezek a számok: 1, 2, 3, 4, 6, 12. Ezeknek a számoknak a legnagyobb osztója 12. A két adott szám közös osztója egy és b az a szám, amellyel mindkét megadott szám osztható maradék nélkül egyés b. Közös többszörös a több számot olyan számnak nevezzük, amelyet ezekkel a számokkal osztunk. Például, a 9-es, a 18-as és a 45-es szám többszörösének 180-szorosa van. De a 90 és a 360 szintén a közös többszörösük. Az összes j-szorzóból mindig a legkisebb van, ebben az esetben 90. Ezt a számot hívják a legkisebbösszesen több (NOC). A NOC mindig egy természetes szám, amelynek nagyobbnak kell lennie, mint a számok közül a legnagyobb, amelyekre meghatározásra kerül. Least Common Multiple (NLC). Tulajdonságok.kommutatív: asszociativitás:
Konkrétan, ha és van példányszám, akkor: Két egész szám legkevesebb közös száma més n az összes többi szorzó osztója més n. Sőt, sok közös szorzó m, n egybeesik a NOC szorzókészletével ( m, n). Az aszimptotikus hatások néhány számelméleti függvényben kifejezhetők. Például, Chebyshev funkció . És még: Ez a Landau függvény meghatározásából és tulajdonságaiból következik g (n). Mi következik a prímek elosztási törvényéből. A legkisebb közös multiplex (LCL) megkeresése.NOC ( a, b) többféle módon kiszámítható: 1. Ha ismert a legnagyobb közös osztó, akkor használhatja a NOC-val fennálló kapcsolatát:
2. Legyen ismert mindkét szám kanonikus tényezője:
ahol p 1, ..., p k - különböző prímszámok, és d 1, ..., d k és e 1, ..., e k - nemnegatív egész számok (azok nullák lehetnek, ha a megfelelő prím nincs a kiterjesztésben). Aztán NOC ( egy,b) kiszámítása a következő képlettel történik: Más szavakkal, az LCL tágulása tartalmazza azokat az elsődleges tényezőket, amelyek a számok legalább egy bomlásában megjelennek a, b, és ennek a tényezőnek a két kitevője közül a legnagyobbat vesszük. példa: A több szám legkisebb közös többszörösének kiszámítása két egymást követő NOC számításra redukálható: A szabály. Több szám NOC-jának megtalálásához a következőkre van szüksége: - bontja a számokat primer tényezőkké; - vigyük át a legnagyobb bomlást a kívánt termék tényezőire (a megadott legnagyobb számú tényezők szorzata), majd adjuk hozzá a többi szám bomlásából származó tényezőket, amelyek nem fordulnak elő az első számban vagy kevesebbszor vannak benne; - az elsődleges tényezők eredményének szorzata az adott szám NOC lesz. Bármely két vagy több természetes számnak megvan a saját NOC. Ha a számok nem sokszorosak, vagy nem rendelkeznek ugyanazokkal a tényezőkkel a kiterjesztésben, akkor LCL egyenlő ezen számok szorzatával.
A 28 (2, 2, 7) egyszerű tényezői, kiegészítve 3-as tényezővel (21. szám), az eredményül kapott termék (84) a legkisebb szám, osztva 21-gyel és 28-val.
A 30 legnagyobb szám egyszerű tényezői, kiegészítve a 25-ös szám 5-es tényezőjével, a kapott 150 termék nagyobb, mint a 30 legnagyobb szám, és maradék nélkül az összes megadott számmal oszlik meg. Ez a lehető legkisebb termék (150, 250, 300 ...), amelyhez az összes megadott szám többszöröse.
A 2,3,11,37 számok primerek, tehát LCL egyenlő az adott szám szorzatával. A szabály. A prím NOC kiszámításához meg kell szorozni ezeket a számokat egymás között. Egy másik lehetőség: Több szám legkisebb közös többszörösének (LCL) a kereséséhez: 1) mindegyik számot a fő tényező szorzataként kell ábrázolni, például: 504 \u003d 2 · 2 · 2 · 3 · 3 · 7, 2) írja le az összes alapvető tényező hatalmát: 504 \u003d 2 · 2 · 2 · 3 · 3 · 7 \u003d 2 3 · 3 2 · 7 1, 3) írja ki ezeknek a számoknak az összes egyszerű osztóját (tényezőjét); 4) válassza ki mindegyikük legnagyobb fokát, amely ezen számok minden kiterjesztésében megtalálható; 5) meg kell szorozni ezeket a fokokat. példa . Keresse meg a NOC-számokat: 168, 180 és 3024. döntés . 168 \u003d 2 · 2 · 2 · 3 · 7 \u003d 2 3 · 3 1 · 7 1, 180 \u003d 2 · 2 · 3 · 3 · 5 \u003d 2 2 · 3 2 · 5 1, 3024 \u003d 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 \u003d 2 4 · 3 3 · 7 1. Kiírjuk az összes egyszerű osztó legnagyobb fokát és szorzzuk meg őket: NOC \u003d 2 4 · 3 3 · 5 1 · 7 1 \u003d 15120. Második szám: b \u003d Bit elválasztó Nincs elválasztó tér "" eredmény: A GCD legnagyobb közös osztója ( egy,b)=6 Legkevésbé gyakori többszörös NOC ( egy,b)=468 Felhívjuk a legnagyobb pozitív egész számot, amellyel az a és b szám osztható maradék nélkül legnagyobb közös tényező (GCD). A jelölés GCD (a, b), (a, b), gcd (a, b) vagy hcf (a, b). Legkevésbé gyakori többszörös Két a és b egész szám (NOC) a legkisebb pozitív egész szám, amely osztható az a és b értékkel maradék nélkül. A jelölés NOC (a, b) vagy lcm (a, b). Az a és b egészeket hívjuk kölcsönösen egyszerűha nincsenek közös tényezőik, csak a +1 és −1. A legnagyobb közös tényezőAdjunk két pozitív számot egy 1 és egy 2 1). Meg kell találni ezeknek a számoknak a közös osztóját, azaz talál egy ilyen számot λ ami osztja a számokat egy 1 és egy 2 ugyanabban az időben. Leírjuk az algoritmust. 1) Ebben a cikkben a szó számát egészként értjük. enged egy 1 ≥ egy 2 és hagyja ahol m 1 , egy 3 egész szám egy 3 <egy 2 (a részleg fennmaradó része egy 1 on egy 2-nek kevesebbnek kell lennie egy 2). Tegyük fel, hogy λ részvény egy 1 és egy Akkor 2 λ részvény m 1 egy És 2 λ részvény egy 1 −m 1 egy 2 =egy 3 (A számok megoszthatósága. A megoszthatóság jele) cikk 2. állítása. Ebből következik, hogy minden közös osztó egy 1 és egy A 2. ábra közös osztó egy És 2 egy 3. Az ellenkezője akkor is igaz, ha λ közös tényező egy És 2 egy Akkor 3 m 1 egy És 2 egy 1 =m 1 egy 2 +egy A 3 szintén fel van osztva λ . Ezért a közös osztó egy És 2 egy A 3. ábrán is van egy közös osztó egy 1 és egy 2. mert egy 3 <egy 2 ≤egy 1, akkor elmondhatjuk, hogy megoldást találtunk a számok közös osztójának megtalálására egy 1 és egy A 2. ábrát a számok közös osztójának megtalálása egyszerűbb problémájára redukálják egy És 2 egy 3 . ha egy 3 ≠ 0, akkor osztható egy 2 be egy 3. majd
ahol m 1 és egy 4 egész szám, ( egy 4 a megosztás fennmaradó része egy 2 be egy 3 (egy 4 <egy 3)). Hasonló érveléssel azt a következtetést vonjuk le, hogy a számok közös osztói egy 3 és egy 4 megegyezik a számok közös osztójával egy És 2 egy 3, valamint a közös elválasztókkal egy 1 és egy 2. mert egy 1 , egy 2 , egy 3 , egy 4, ... számok, amelyek folyamatosan csökkennek, és mivel véges szám van egész szám között egy 2 és 0, majd valamilyen lépésben n, a megosztás fennmaradó része egy n be egy n + 1 nulla lesz ( egy n + 2 \u003d 0).
Minden közös osztó λ szám egy 1 és egy 2 szintén egy osztó egy És 2 egy 3 , egy 3 és egy 4 , .... egy n és egy n + 1. Az ellenkezője is igaz, a számok közös osztói egy n és egy Az n + 1 a szám osztója is egy n - 1 és egy n, ...., egy És 2 egy 3 , egy 1 és egy 2. De a számok közös osztója egy n és egy n + 1 a szám egy n + 1, mert egy n és egy n + 1 osztható el egy n + 1 (emlékezzünk rá egy n + 2 \u003d 0). ezért egy Az n + 1 szintén osztó egy 1 és egy 2 . Vegye figyelembe, hogy a szám egy n a számok osztója közül a legnagyobb egy n és egy n + 1, mivel a legnagyobb osztó egy n + 1 önmagában egy n + 1. ha egy n + 1 egész számok szorzataként ábrázolható, akkor ezek a számok is a számok közös osztói egy 1 és egy 2. szám egy n + 1 hívása legnagyobb közös tényező szám egy 1 és egy 2 . A számok egy 1 és egy 2 lehet pozitív és negatív szám is. Ha a számok egyike nulla, akkor ezeknek a számoknak a legnagyobb közös osztója megegyezik a másik szám abszolút értékével. A nulla számok legnagyobb közös osztója nincs meghatározva. A fenti algoritmust nevezzük euklideszi algoritmushogy megtalálja a két egész szám legnagyobb közös osztóját. Példa a két szám legnagyobb közös osztójának megtalálásáraKeresse meg a 630 és 434 számok legnagyobb közös tényezőjét.
Az 5. lépésben a megosztás fennmaradó értéke 0. Ezért a 630 és 434 számok legnagyobb közös osztója 14. Ne feledje, hogy a 2 és 7 számok a 630 és 434 szám osztói is. Kölcsönösen primerekmeghatározás 1. Legyen a számok legnagyobb közös osztója egy 1 és egy 2 egyenlő egyvel. Akkor ezeket a számokat hívják kölcsönösen prímszámoknincs közös osztó. A tétel 1. ha egy 1 és egy 2 példányszám, és λ valamilyen számot, akkor a számok közös osztóját λa 1 és egy A 2 szintén közönséges osztó λ és egy 2 . Bizonyítás. Vegyük figyelembe az euklideszi algoritmust a számok legnagyobb közös osztójának megtalálására egy 1 és egy 2. ábra (lásd fent).
A tétel feltételeiből következik, hogy a számok legnagyobb közös osztója egy 1 és egy És ezért egy n és egy n + 1 értéke 1. azaz egy n + 1 \u003d 1. Szorozzuk meg ezeket az egyenlőségeket szorzattal λ majd
Hagyja, hogy a közös tényező egy 1 λ és egy 2 enni δ . majd δ egy tényező a egy 1 λ , m 1 egy 2 λ és be egy 1 λ -m 1 egy 2 λ =egy 3 λ (lásd "A számok megoszthatósága", 2. javaslat). további δ egy tényező a egy 2 λ és m 2 egy 3 λ , és ezért a egy 2 λ -m 2 egy 3 λ =egy 4 λ . Indokolás, így meggyőződésünk δ egy tényező a egy n - 1 λ és m n - 1 egy n λ , és ezért a egy n - 1 λ −m n - 1 egy n λ =egy n + 1 λ . mert egy n + 1 \u003d 1, akkor δ egy tényező a λ . Ezért a szám δ egy közös szám elválasztó λ és egy 2 . Az 1. tétel egyes eseteit vesszük figyelembe. eredmény 1. enged egy és c A PRIM viszonylag nagy b. Aztán a termékük ac egy elsődleges viszony a b. Valóban. Az 1. tételből ac és b ugyanazok a közös osztók, mint a c és b. De a számok c és b kölcsönösen egyszerű, azaz legyen egyetlen közös tényezője 1. Akkor ac és b továbbá egyetlen közös tényezőjük van 1. Ezért ac és b kölcsönösen egyszerű. eredmény 2. enged egy és b coprime számokat, és hagyja b részvény ak. majd b osztja és k. Valóban. Az állítás feltételétől ak és b legyen közös osztójuk b. Az 1. tétel alapján b közös osztónak kell lennie b és k. ezért b részvény k. Az 1. következtetés általánosítható. eredmény 3. 1. Hagyja a számokat egy 1 , egy 2 , egy 3 , ..., egy m a szám függvényében b. majd egy 1 egy 2 , egy 1 egy 2 · egy 3 , ..., egy 1 egy 2 egy 3 ··· egy m, ezeknek a számoknak a szorzata a számhoz viszonyítva elsődleges b. 2. Nézzünk két számot
oly módon, hogy az első sorban minden szám elsődleges a második sor minden számához képest. Aztán a termék Meg kell találni azokat a számokat, amelyek oszthatók ezen számok mindegyikével. Ha a szám osztható el egy 1, akkor megkapja a formáját sa 1 ahol s valamilyen szám. ha q a számok legnagyobb közös osztója egy 1 és egy Akkor 2 ahol s 1 valamilyen egész szám. majd van legkisebb közös többszörös egy 1 és egy 2 . egy 1 és egy 2 a coprime, akkor a számok legkevésbé gyakori többszöröse egy 1 és egy 2: Meg kell találnia ezeknek a számoknak a legkisebb közös többszörösét. A fentiekből következik, hogy a számok bármilyen többszöröse egy 1 , egy 2 , egy A 3 számnak többszörösnek kell lennie ε és egy 3, és fordítva. Hagyjuk a legkevésbé gyakori számot ε és egy 3 enni ε 1. Ezután egy szám többszörösét egy 1 , egy 2 , egy 3 , egy A 4 számnak többszörösnek kell lennie ε 1 és egy 4. Hagyjuk a legkevésbé gyakori számot ε 1 és egy 4 enni ε 2. Így kiderült, hogy mind több szám egy 1 , egy 2 , egy 3 ,...,egy m egybeesik egy bizonyos szám szorzóival ε n, amelyet az adott számok legkisebb közös többszöröseinek nevezünk. Abban az esetben, ha a számok egy 1 , egy 2 , egy 3 ,...,egy m másodlagos, akkor a számok legkevésbé gyakori többszöröse egy 1 , egy A 2. ábrán látható, a fentiek szerint (3). Továbbá, azóta egy 3 elsődleges a számok vonatkozásában egy 1 , egy Akkor 2 egy 3 elsődleges a számhoz viszonyítva egy 1 · egy 2 (1. következtetés). Tehát a számok legkevésbé gyakori száma egy 1 ,egy 2 ,egy 3 egy szám egy 1 · egy 2 · egy 3. Hasonló érveléssel érkezünk a következő állításokra. jóváhagyás 1. A kölcsönösen primerek legkevésbé gyakori többszöröse egy 1 , egy 2 , egy 3 ,...,egy m egyenlő a termékükkel egy 1 · egy 2 · egy 3 ··· egy m. jóváhagyás 2. Bármely szám, amely osztható az egyes primerekkel egy 1 , egy 2 , egy 3 ,...,egy m szintén megoszlik termékük szerint egy 1 · egy 2 · egy 3 ··· egy m. Definíció. Felhívjuk a legnagyobb pozitív egész számot, amely osztható az a és b számok fennmaradó száma nélkül legnagyobb közös tényező (GCD) ezeket a számokat. Keresse meg a 24. és a 35. szám legnagyobb közös osztóját. Definíció. A természetes számokat hívják kölcsönösen egyszerűha a legnagyobb közös tényező (GCD) 1. A legnagyobb közös tényező (GCD) megtalálható anélkül, hogy kiírnánk az adott számok összes osztóját. A 48-os és a 36-as tényezőt kapjuk: Megtalálni legnagyobb közös tényező Ha az összes megadott szám el van osztva egyikükkel, akkor ez a szám legnagyobb közös tényező adott számok. Least Common Multiple (NLC)Definíció. Least Common Multiple (NLC) az a és b pozitív egész számok a legkisebb pozitív egész szám, amely az a és b egyaránt többszöröse. A 75. és a 60. szám legkisebb közös többszörösét (LCL) a számok egymást követő többszöröseinek kiírása nélkül lehet megtalálni. Ehhez a 75-et és a 60-at egyszerű tényezőkre bontjuk: 75 \u003d 3 * 5 * 5 és 60 \u003d 2 * 2 * 3 * 5. Megtalálják a legkevésbé gyakori többszöröset három vagy több számhoz. hogy keresse meg a legkevésbé gyakori többszörösét több természetes számra van szükség: Vegye figyelembe, hogy ha ezeknek a számoknak az egyikét elosztjuk az összes többi számmal, akkor ez a szám a számok legkisebb közös száma. Pythagoras (Kr. E. VI. Század) és tanulói a számok oszthatóságának kérdését vizsgálták. Az összes osztó összegével megegyező számot (maga a szám nélkül) a tökéletes számnak hívták. Például a 6 (6 \u003d 1 + 2 + 3), 28 (28 \u003d 1 + 2 + 4 + 7 + 14) szám tökéletes. A következő tökéletes szám a 496, 8128, 33 550 336. A pitagoraiak csak az első három tökéletes számot tudták. A negyedik - 8128 - az 1. században vált ismertté. n. e. Az ötödik - 33 550 336 - a XV. Században található. 1983-ra már 27 tökéletes szám volt ismert. De eddig a tudósok nem tudják, léteznek-e páratlan tökéletes számok, létezik-e a legnagyobb tökéletes szám. A tanulóknak sok feladatot kapnak a matematika. Közülük az ilyen megfogalmazással kapcsolatos problémák nagyon gyakoriak: két jelentése van. Hogyan lehet megtalálni az adott számok legkisebb közös többszörösét? Az ilyen feladatok elvégzésére képesnek kell lennie, mivel a megszerzett készségeket különféle nevezőkkel ellátott frakciókkal való munka során használják fel. A cikkben elemezzük a NOC és az alapfogalmak megtalálását. Mielőtt megválaszolná a NOC megtalálásának kérdését, el kell döntenie a többes kifejezésről. Leggyakrabban ennek a fogalomnak a megfogalmazása a következő: egy A bizonyos értékének szorzóját természetes számnak nevezzük, amelyet oszthatunk az A-val. Maradék nélkül 8, 12, 16, 20 és így tovább, a szükséges határig, 4-es szorzata lesz. Sőt, egy adott érték osztóinak száma korlátozott lehet, és végtelen sok szorzó. Ugyanígy van ugyanaz az érték a természeti értékeknél. Ez egy olyan mutató, amely nyom nélkül oszlik meg rájuk. Miután megvizsgáltuk az egyes mutatók legkisebb értékének fogalmát, továbbmegyünk a továbblépéshez.
Keresse meg a NOC-tA kettő vagy több mutató közül a legkisebb többszöröse a legkisebb természetes szám, amelyet teljes mértékben oszt meg az összes megadott szám. Számos módon lehet megtalálni egy ilyen értéket., vegye figyelembe a következő módszereket:
Most már tudjuk, mi az általános módszer a kettő, három vagy több érték legkisebb értékének meghatározására. Vannak azonban magán módszerek.segít a NOC keresésében, ha az előzőek nem segítenek. Hogyan lehet megtalálni a GCD-t és a NOC-t? Privát módon lehet megtalálniMint minden matematikai szakaszban, vannak olyan speciális esetek, amikor olyan NOC-kat találnak, amelyek segítenek bizonyos helyzetekben:
A különleges esetek kevésbé általánosak, mint a szokásos példák. De nekik köszönhetően megtanulhatja, hogy különféle bonyolultságú frakciókkal dolgozzon. Ez különösen igaz a frakciókra.ahol különböző nevezők vannak.
Néhány példaNézzünk meg néhány példát, amelyeknek köszönhetően megértjük a legkevesebb többszörös megtalálásának elvét:
A példáknak köszönhetően megértheti, hogy a NOC hogyan helyezkedik el, milyen árnyalatok vannak, és mi az ilyen manipulációk értelme.
Sokkal könnyebb megtalálni a NOC-ot, mint az eredetileg tűnhet. Ehhez mind az egyszerű bomlást, mind az egyszerű értékek szorozását használjuk. A matematika ezen szakaszával való munkavégzés elősegíti a matematikai témák további tanulmányozását, különös tekintettel a különböző bonyolultságú frakciókra. Ne felejtse el rendszeresen megoldani a példákat különféle módszerekkel, ez logikai eszközt fejleszti ki, és lehetővé teszi számos kifejezés emlékezetét. Ismerje meg az ilyen mutató megtalálásának módszereit, és jól tudjon működni a matematikai szakaszok többi részével. Jó szórakozást a matematika tanulásában! videóEz a videó segít megérteni és megjegyezni, hogyan lehet megtalálni a legkisebb közös többeset. Folytatjuk a „NOC - a legkisebb közös többszörös, meghatározás, példák” c. Szakaszban a legkevésbé gyakori többszörösről szóló vitát. Ebben a témában megvizsgáljuk a három vagy több szám NOC-jának megtalálásának módját, megvizsgáljuk a negatív szám NOC-jának megtalálásának kérdését. Yandex.RTB R-A-339285-1 A legkisebb közös multiplex (NLC) kiszámítása a GCD-n keresztülMár létrehoztuk a legkevésbé közös multiplex kapcsolatát a legnagyobb közös osztóval. Most megtanuljuk meghatározni a NOC-ot a GCD-n keresztül. Először találjuk ki, hogyan lehet ezt megtenni a pozitív számokhoz. 1. meghatározás A legkisebb közös szorzót a legnagyobb közös tényezővel lehet megtalálni az alábbi képlettel: NOC (a, b) \u003d a · b: GCD (a, b). 1. példa Meg kell találnia a 126 és 70 NOC számot. döntés Vegyük a \u003d 126, b \u003d 70. Kicseréljük a képletben szereplő értékeket a legkevésbé gyakori szorzó kiszámítására az LCL legnagyobb közös osztóján keresztül (a, b) \u003d a · b: GCD (a, b). Keresse meg a 70 és a 126 számú GCD-t. Ehhez szükségünk van az euklideszi algoritmusra: 126 \u003d 70 · 1 + 56, 70 \u003d 56 · 1 + 14, 56 \u003d 14,4, tehát GCD (126 , 70) = 14 . Kiszámítjuk a NOC-ot: NOC (126, 70) \u003d 12670: GCD (126, 70) \u003d 12670: 14 \u003d 630. A válasz: NOC (126, 70) \u003d 630. 2. példa Keresse meg a 68 és 34 számok kopogtatását. döntés A NOD ebben az esetben nem nehéz semlegesíteni, mivel a 68 osztva 34-vel. A legkisebb közös szorzót a következő képlettel számoljuk: NOC (68, 34) \u003d 68,34: GCD (68, 34) \u003d 68,34: 34 \u003d 68. A válasz: NOC (68, 34) \u003d 68. Ebben a példában az a és b pozitív egész számok legkevésbé gyakori többszörösének megtalálására vonatkozó szabályt alkalmaztuk: ha az első szám osztható a másodikval, akkor ezen számok LCM-je megegyezik az első számmal. NOC-k megtalálása a számok faktorozással való faktorozásávalMost nézzük meg azt a módszert, amellyel megtalálhatjuk a NOC-t, amely a számok primer tényezőkre történő felbontására épül. 2. meghatározás A legkevésbé gyakori többszörös megkereséséhez számos egyszerű lépést kell végrehajtanunk:
A legkisebb közös multiplex megtalálásának ez a módszere a NOC (a, b) \u003d a · b: GCD (a, b) egyenlőségén alapszik. Ha megnézzük a képletet, világossá válik: az a és b szám szorzata megegyezik a két szám kibővítésében részt vevő összes tényező szorzatával. Ezenkívül a két szám GCD-je megegyezik az összes olyan primer tényező szorzatával, amelyek egyszerre vannak jelen a két szám faktorizálásában. 3. példa Két számunk van 75 és 210. Az alábbiak szerint számolhatjuk be őket: 75 \u003d 3,5 · 5 és 210 \u003d 2,3 · 5,7. Ha két forrásszám összes tényezőjének eredményét összeállítjuk, akkor a következőt kapjuk: 2,3 · 3 · 5 · 5 · 5 · 7. Ha kizárjuk a közös tényezőket mind a 3-as, mind az 5-ös számokhoz, akkor a következő formában kapjuk meg a terméket: 2,3 · 5 · 5 · 7 \u003d 1050. Ez a munka lesz a 75-es és 210-es számok NOC-ja. 4. példa Keresse meg a számok NOC-ját 441 és 700 faktorozva mindkét számot elsődleges tényezőkké. döntés Keresse meg a feltételben megadott számok összes fő tényezőjét: 441 147 49 7 1 3 3 7 7 700 350 175 35 7 1 2 2 5 5 7 Két számláncot kapunk: 441 \u003d 3 · 3 · 7 · 7 és 700 \u003d 2 · 2 · 5 · 5 · 7. Az összes tényező szorzata, amely részt vett e számok bomlásában, a következőképpen néz ki: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 · 7. Keresse meg a közös tényezőket. Ez a 7-es szám. Kizárjuk az általános munkából: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7. Kiderül, hogy a NOC (441, 700) \u003d 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 \u003d 44 100. A válasz: NOC (441, 700) \u003d 44 100. Adjunk még egy megfogalmazást az LCL megállapítására szolgáló módszerhez, a számokat primer tényezőkké bontva. 3. meghatározás Korábban kizártuk a két tényező közös tényezőit az összes tényezőből. Most másképp tesszük:
5. példa Térjünk vissza a 75 és 210 számhoz, amelyekre a korábbi példák egyikében már keresettük a NOC-t. Főbb tényezőkre bontjuk őket: 75 \u003d 3,5 · 5 és 210 \u003d 2,3 · 5,7. A 3., 5. És 5. Tényező szorzata 5 a 75. szám hozzáadja a hiányzó tényezőket 2 és 7 szám 210. Megkapjuk: 2,3 · 5 · 5 · 7.Ez a 75-es és 210-es szám NOC. 6. példa Ki kell számítani a 84-es és a 648-as NOC-számot. döntés A számokat a feltételtől bontjuk fő tényezőkké: 84 \u003d 2, 2, 3, 3, 7 és 648 \u003d 2 · 2 · 2 · 3 · 3 · 3 · 3. Adja hozzá a 2., 2., 3. és 3. tényező szorzatához 7
84 hiányzó 2., 3., 3. és 3. tényező A válasz: NOC (84, 648) \u003d 4536. Három vagy több szám NOC-jainak megkereséseFüggetlenül attól, hogy hány számmal foglalkozunk, műveleteink algoritmusa mindig azonos lesz: egymás után két szám NOC-ját találjuk meg. Erre az esetre létezik tétel. 1. tétel Tegyük fel, hogy egész számok vannak a 1, 2, ..., k. NOC m k ezeket a számokat m 2 \u003d NOC (a 1, a 2), m 3 \u003d NOC (m 2, a 3), m 3 \u003d NOC (m k - 1, a k) egymást követő számításában találjuk. Most megvizsgáljuk, hogyan lehet a tételt alkalmazni bizonyos problémák megoldására. 7. példa Ki kell számítani a 140, 9, 54 és a négy szám legkisebb közös szorzóját 250 . döntés Bemutatjuk a jelölést: a 1 \u003d 140, a 2 \u003d 9, a 3 \u003d 54, a 4 \u003d 250. Először kiszámoljuk m 2 \u003d NOC (a 1, a 2) \u003d NOC (140, 9). Az Euklideszi algoritmust alkalmazzuk a 140 és 9 számú GCD kiszámításához: 140 \u003d 9 · 15 + 5, 9 \u003d 5 · 1 + 4, 5 \u003d 4 · 1 + 1, 4 \u003d 1 · 4. Kapjuk: GCD (140, 9) \u003d 1, NOC (140, 9) \u003d 140 · 9: GCD (140, 9) \u003d 140 · 9: 1 \u003d 1,260. Ezért m 2 \u003d 1,260. Most ugyanazzal az algoritmussal kiszámoljuk m 3 \u003d NOC (m 2, a 3) \u003d NOC (1,260, 54). A számítások során m 3 \u003d 3780 értéket kapunk. Fenn kell hagyni, hogy kiszámítsuk m 4 \u003d NOC (m 3, a 4) \u003d NOC (3 780, 250). Ugyanezt az algoritmust követjük. Kapunk m 4 \u003d 94 500. A példa feltételei közül a négy szám NOC értéke 94500. A válasz: NOC (140, 9, 54, 250) \u003d 94 500. Mint láthatja, a számítások egyszerűek, ám időigényesek. Időt takaríthat meg a másik irányba. 4. meghatározás A következő műveleti algoritmust kínáljuk Önnek:
8. példa Meg kell találni a 84, 6, 48, 7, 143 öt szám NOC-ját. döntés Mind az öt számot primer tényezőkké bontjuk: 84 \u003d 2 · 2 · 3 · 7, 6 \u003d 2 · 3, 48 \u003d 2 · 2 · 2 · 2 · 3, 7, 143 \u003d 11 · 13. Az elsődleges számok, amelyek a 7-es számok, nem bonthatók primertényezőkké. Ezek a számok egybeesnek a faktorizációval. Most vegyük a 84-es 2-es, 2-es, 3-as és 7-es szorzó szorzatát, és adjuk hozzá a második szám hiányzó tényezõit. A 6-os számot 2-re és 3-ra bontjuk. Ezek a tényezők már az első szám szorzatában vannak. Ezért kihagyjuk őket. Folytatjuk a hiányzó tényezők hozzáadását. Átlépünk a 48-as számra, annak a primer tényezőnek a szorzatából, amelynek 2-et és 2-et veszünk. Ezután adjuk hozzá a negyedik 7-es, illetve az ötödik 11-es és 13-as faktorit. A következőket kapjuk: 2 · 2 · 2 · 2 · 3 · 7 · 11 · 13 \u003d 48 048. Ez az öt forrásszám legkisebb közös szorzója. A válasz: NOC (84, 6, 48, 7, 143) \u003d 48 048. Megtaláljuk a negatív számok legkisebb közös többszörösétAnnak érdekében, hogy megtaláljuk a negatív számok legkisebb közös többszörösét, ezeket a számokat először ellentétes jelű számokkal kell cserélni, majd a fenti algoritmusok segítségével elvégezni a számításokat. 9. példa NOC (54, - 34) \u003d NOC (54, 34) és NOC (- 622, - 46, - 54, - 888) \u003d NOC (622, 46, 54, 888). Ilyen cselekedetek megengedettek, mert ha elfogadjuk ezt egy és - a - ellentétes számok, 10. példa Ki kell számítani a negatív számok NOC-ját − 145 és − 45 . döntés Kicseréljük a számokat − 145 és − 45 az ellenkező számokra 145 és 45 . Most az algoritmus szerint kiszámoljuk a NOC (145, 45) \u003d 145 · 45: GCD (145, 45) \u003d 145 · 45: 5 \u003d 1 305 értékét, miután korábban meghatározzuk a GCD-t az euklideszi algoritmus segítségével. Azt kapjuk, hogy a számok NOC értéke 145 és − 45 jelentése 1 305 . A válasz: NOC (- 145, - 45) \u003d 1 305. Ha hibát észlel a szövegben, válassza ki azt, és nyomja meg a Ctrl + Enter billentyűket |
| Olvasd el: |
|---|
Legnépszerűbb:
A legegyszerűbb trigonometrikus egyenlőtlenségek megoldása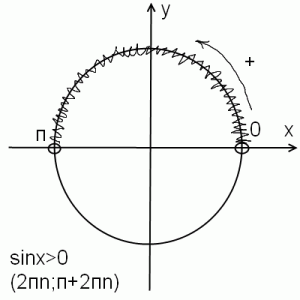
|
új
- Mi törte meg a "merev" bárót?
- A Fehér Mozgalom tagja
- Suvorov és a csapat útja hazájukhoz
- Az F (x) függvényt f (x) függvény antiderivatívájának nevezzük, ha F` (x) \u003d f (x) vagy dF (x) \u003d f (x) dx
- Fokfrekvencia-csökkentő program
- Hasonló kifejezések, redukcióik, példák
- Orosz utazók lazarev
- Nem teljes kvadratikus egyenletek megoldása
- A kvadratikus egyenletek megoldása, a gyökérképlet, példák
- Koordináta sík (6. fokozat) - Tudás hipermarketje




 .
. .
. .
.