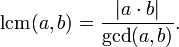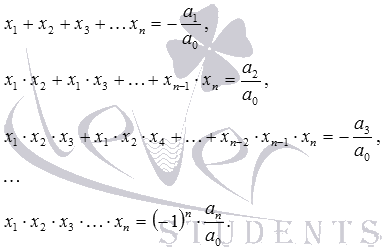Webhely szakaszok
A szerkesztők választása:
hirdetés
| A másodlagos egyenlet gyökereinek összege. Hogyan lehet megtalálni az egyenlet gyökereinek összegét? |
|
A kvadratikus egyenlet gyökerei és együtthatói között, a gyökérképlet mellett, vannak más hasznos kapcsolatok is, amelyeket megadunk viet tétele. Ebben a cikkben nyilatkozatot és bizonyítékot adunk a Hely tétel tételének a másodlagos egyenletre vonatkozóan. Ezután a tételt fordítva vesszük figyelembe a Hely tételhez. Ezt követően elemezzük a legjellemzőbb példák megoldásait. Végül megírjuk azokat a hely-képleteket, amelyek meghatározzák a valódi gyökerek közötti kapcsolatot algebrai egyenlet n fok és annak együtthatói. Oldal navigáció. Hely tétel, állítás, bizonyításA kvadratikus egyenlet gyökeinek képleteiből a forma a · x 2 + b · x + c \u003d 0, ahol D \u003d b 2 –4 · a · c, az x 1 + x 2 \u003d −b / a, x 1 · x 2 \u003d relációk c / a. Ezek az eredmények érvényesek. viet tétele: Tétel. ha x 1 és x 2 az a · x 2 + b · x + c \u003d 0 kvadratikus egyenlet gyökerei, akkor a gyökér összege megegyezik a b együtthatók és az ellentétes jellel vett tényezők arányával, és a gyökér szorzata megegyezik a c és a együtthatók arányával, azaz . Bizonyítás. A hely tételének bizonyítását a következő séma szerint hajtjuk végre: a jól ismert gyökérképletekkel összeállítjuk a másodfokú egyenlet gyökeinek összegét és szorzatát, majd átalakítjuk a kapott kifejezéseket és ellenőrizzük, hogy −b / a és c / a. Kezdjük a gyökerek összegével, töltsük fel. Most elhozzuk a frakciókat egy közös nevezőbe, van. A kapott frakció számlálójában, amely után: Végül, 2 után, megkapjuk. Ez bizonyítja a Hely-tétel első kapcsolatát a másodlagos egyenlet gyökeinek összegével. A másodikra \u200b\u200bmegyünk. A kvadratikus egyenlet gyökeinek szorzata: A frakció szorzásának szabálya szerint az utolsó termék így írható:. Most szorzzuk meg a zárójeleket a számláló zárójelekkel, de gyorsabban tudjuk ezt a terméket összecsukni négyzetkülönbség-formulaSzóval Ezenkívül emlékezetünkre a következő átmenetet hajtjuk végre. És mivel a kvadratikus egyenlet diszkriminátora megegyezik a D \u003d b 2 −4 · a · c képlettel, akkor az utolsó törtben b 2 −4 · a · c helyettesíthetjük D helyett, így kapjuk. A konzolok kinyitása és az ilyen kifejezések csökkentése után egy frakciót kapunk, és annak csökkentése 4 · a-val ad. Ez bizonyítja a Hely-tétel második kapcsolatát a gyökerek termékéhez. Ha elmaradunk a magyarázatoktól, akkor a Hely-tétel bizonyítása lakonikus formába kerül: Csak meg kell jegyezni, hogy a nullával egyenlő diszkrimináns esetében a kvadratikus egyenletnek egy gyökere van. Ha azonban feltételezzük, hogy az egyenletnek ebben az esetben két azonos gyökere van, akkor a Hely-tétel egyenletei is érvényesek. Valójában, D \u003d 0 esetén a kvadratikus egyenlet gyöke akkor van, és mivel D \u003d 0, azaz b 2 −4 · a · c \u003d 0, ahonnan b 2 \u003d 4 · a · c, akkor. A gyakorlatban a Hely-tételt a leggyakrabban az x 2 + p · x + q \u003d 0 formátum kvadratikus egyenletéhez viszonyítva (a legnagyobb együtthatóval egyenlő 1). Időnként az ilyen típusú kvadratikus egyenletekre fogalmazzák meg, amelyek nem korlátozzák az általánosítást, mivel bármely kvadratikus egyenlet helyettesíthető ekvivalens egyenlettel, ha mindkét részét elosztja egy nullán kívüli a számmal. Adjuk a Hely-tétel megfelelő állítását: Tétel. A redukált kvadratikus egyenlet gyökeinek összege x 2 + p · x + q \u003d 0 megegyezik az x-nél mért együtthatóval, az ellenkező jelrel együtt, és a gyökerek szorzata a szabad kifejezés, azaz x 1 + x 2 \u003d −p, x 1 · x 2 \u003d q. A Hely-tétel fordított tételeAz előző bekezdésben megadott Hely tétel második állítása azt jelzi, hogy ha x 1 és x 2 a redukált másodlagos egyenlet gyökerei x 2 + p · x + q \u003d 0, akkor az x 1 + x 2 \u003d −p, x 1 · x összefüggések 2 \u003d q. Másrészt az x 1 + x 2 \u003d −p, x 1 · x 2 \u003d q írásbeli viszonyokból következik, hogy x 1 és x 2 az x 2 + p · x + q \u003d 0 négyzetes egyenlet gyökerei. Más szavakkal, a hely állításával ellentétes állítás igaz. Tétel formájában fogalmazzuk meg és bizonyítjuk. Tétel. Ha az x 1 és x 2 szám olyan, hogy x 1 + x 2 \u003d −p és x 1 · x 2 \u003d q, akkor x 1 és x 2 az x 2 + p · x + q \u003d 0 kvadratikus egyenlet gyökerei. Bizonyítás. Miután a p és q együtthatókat az x 2 + p · x + q \u003d 0-tól x 1-ig és x 2-es egyenletben kicserélték, ekvivalens egyenletké alakul. Kicseréljük az x 1 számot a kapott egyenletre x helyett, egyenlőség van x 1 2 - (x 1 + x 2) x 1 + x 1 x 2 \u003d 0, amely bármelyik x 1 és x 2 esetén a 0 \u003d 0 valódi numerikus egyenlőséget képviseli, mivel x 1 2 - (x 1 + x 2) x 1 + x 1 x 2 \u003d x 1 2 −x 1 2 −x 2 x 1 + x 1 x 2 \u003d 0. Ezért x 1 az egyenlet gyökere x 2 - (x 1 + x 2) x + x 1 x 2 \u003d 0, ami azt jelenti, hogy x 1 az x 2 + p · x + q \u003d 0 egyenlet gyökere, amely ezzel egyenértékű. Ha az egyenletben x 2 - (x 1 + x 2) x + x 1 x 2 \u003d 0 cserélje ki az x 2 számot x-re, akkor megkapjuk az egyenlõt x 2 2 - (x 1 + x 2) x 2 + x 1 x 2 \u003d 0. Ez az igazi egyenlőség x 2 2 - (x 1 + x 2) x 2 + x 1 x 2 \u003d x 2 2 −x 1 · x 2 −x 2 2 + x 1 · x 2 \u003d 0. Ezért x 2 is az egyenlet gyökere x 2 - (x 1 + x 2) x + x 1 x 2 \u003d 0, és így az x 2 + p · x + q \u003d 0 egyenletek. Ez kiegészíti a tétel bizonyítását, fordítva a Hely tételhez. Példák a Hely-tétel alkalmazásáraItt az ideje, hogy beszéljünk a Hely-tétel gyakorlati alkalmazásáról és annak fordított tételéről. Ebben a szakaszban a leggyakoribb példák megoldásait tárgyaljuk. A tételt fordítva alkalmazzuk a Hely-tételre. Kényelmes ellenőrizni, hogy ez a két szám egy adott négyzetes egyenlet gyökerei. Ebben az esetben kiszámítják az összeget és a különbséget, majd ellenőrzik a kapcsolatok érvényességét. Ha mindkét kapcsolat fennáll, akkor a hely tételéhez fordított tétel alapján megállapíthatjuk, hogy ezek a számok az egyenlet gyökerei. Ha a kapcsolatok közül legalább az egyik nem teljesül, akkor ezek a számok nem a négyzetes egyenlet gyökerei. Ez a megközelítés használható a kvadratikus egyenletek megoldására a talált gyökerek igazolására. Egy példa. Az 1) x 1 \u003d −5, x 2 \u003d 3 vagy 2) vagy a 3) számpárok közül melyik a 4 · x 2 ∎ 16 · x + 9 \u003d 0 kvadratikus egyenlet gyökérpárja? Határozat. A megadott négyzetes egyenlet koefficiensei 4 · x 2 –16 · x + 9 \u003d 0 a \u003d 4, b \u003d –16, c \u003d 9. Hely tétel szerint a másodfokú egyenlet gyökeinek összegének -b / a-nak kell lennie, azaz 16/4 \u003d 4-nek, és a gyökér szorzata c / a-nak kell lennie, azaz 9/4-nek. Most kiszámoljuk a három megadott pár számának összegét és szorzatát, és összehasonlítjuk azokat az éppen kapott értékekkel. Az első esetben x 1 + x 2 \u003d −5 + 3 \u003d −2. A kapott érték különbözik a 4-től, ezért további ellenőrzést nem lehet elvégezni, és a téte fordítva a tétel tételéhez azonnal megállapíthatjuk, hogy az első számpár nem egy adott másodlagos egyenlet gyökérpárja. Átmegyünk a második esethez. Tehát az első feltétel teljesül. Ellenőrizzük a második feltételt :, a kapott érték különbözik a 9/4-től. Ezért a második számpár nem egy másodrendű egyenlet gyökérpárja. Az utolsó eset továbbra is fennáll. Itt és. Mindkét feltétel teljesül, tehát ezek az x 1 és x 2 számok a megadott másodlagos egyenlet gyökerei. A válasz: A Place-tételhez fordított tétel a gyakorlatban felhasználható a kvadratikus egyenlet gyökereinek kiválasztására. Általában az adott kvadratikus egyenlet egész gyökerét egész számú együtthatóval vesszük, mivel más esetekben ezt meglehetősen nehéz megtenni. Ugyanakkor használják azt a tényt, hogy ha a két szám összege megegyezik a mínuszjelet tartalmazó kvadratikus egyenlet második együtthatójával, és ezeknek a számoknak a szorzata megegyezik a szabad kifejezéssel, akkor ezek a számok képezik ennek a másodlagos egyenletnek a gyökereit. Példa segítségével foglalkozunk ezzel. Vegyük az x 2 −5 · x + 6 \u003d 0 kvadratikus egyenletet. Ahhoz, hogy az x 1 és x 2 számok ennek az egyenletnek a gyökerei legyenek, két x 1 + x 2 \u003d 5 és x 1 · x 2 \u003d 6 egyenlőségnek teljesülnie kell. Még csak fel kell venni az ilyen számokat. Ebben az esetben ezt meglehetősen egyszerű megtenni: a 2 és a 3 ilyen szám, mivel 2 + 3 \u003d 5 és 2,3 · 6. Így a második és a három a négyzetes egyenlet gyökerei. A Place-tételhez fordított tétel különösen kényelmes a redukált kvadratikus egyenlet második gyökerének megtalálására, ha az egyik gyökér már ismert vagy nyilvánvaló. Ebben az esetben a második gyökér a kapcsolatok bármelyikéből származik. Vegyük például az 512 × 2 –509 × −3 \u003d 0 négyzetes egyenletét. Itt könnyű észrevenni, hogy az egység az egyenlet gyökere, mivel ennek a kvadratikus egyenletnek az együtthatói összege nulla. Tehát x 1 \u003d 1. A második x 2 gyökér például az x 1 · x 2 \u003d c / a relációból található. 1 x 2 \u003d −3 / 512, honnan x 2 \u003d −3 / 512. Tehát meghatároztuk a másodlagos egyenlet mindkét gyökerét: 1 és −3/512. Egyértelmű, hogy a gyökerek kiválasztása csak a legegyszerűbb esetekben ajánlott. Más esetekben a gyökerek megtalálásához a kvadratikus egyenlet gyökérképleteit alkalmazhatja a megkülönböztetőn keresztül. A tétel másik gyakorlati alkalmazása, a Hely-tétel fordítottja, az, hogy kvadratikus egyenleteket állítson össze az adott x 1 és x 2 gyökérre. Ehhez elegendő kiszámítani a gyökerek összegét, amely megadja az x együtthatót a kvadratikus egyenlet ellentétes jelével, és a gyökér szorzatát, amely megadja a szabad kifejezést. Egy példa. Írj egy olyan kvadratikus egyenletet, amelynek gyökerei a −11 és 23 számok. Határozat. Jelölje x 1 \u003d −11 és x 2 \u003d 23. Kiszámoljuk ezen számok összegét és szorzatát: x 1 + x 2 \u003d 12 és x 1 · x 2 \u003d −253. Ezért ezek a számok a redukált kvadratikus egyenlet gyökerei a második együtthatóval –12 és a szabad kifejezéssel –253. Vagyis x 2 −12 · x - 253 \u003d 0 a kívánt egyenlet. A válasz: x 2 −12 x - 253 \u003d 0. Viet tételét gyakran használják a másodfokú egyenlet gyökeinek jeleivel kapcsolatos problémák megoldására. Hogyan kapcsolódik Viet tétele a redukált másodlagos egyenlet gyökeinek jeleire x 2 + p · x + q \u003d 0? Két megfelelő állítást adunk:
Ezek az állítások az x 1 · x 2 \u003d q képletből, valamint a pozitív, negatív számok és a számok különféle jelekkel való megszorozásának szabályaiból következnek. Vegyük szembe az alkalmazásukat. Egy példa. R pozitív. A diszkriminanciaképlet segítségével D \u003d (r + 2) 2 −4 · 1 · (r - 1) \u003d r 2 + 4 · r + 4−4 · r + 4 \u003d r 2 +8, az r 2 +8 kifejezés értéke pozitív bármilyen valós r-re, tehát D\u003e 0 bármely valós r-re. Ezért a kezdeti kvadratikus egyenletnek két gyökere van az r paraméter bármely valós értékéhez. Most megtudja, mikor vannak a gyökerek más jelei. Ha a gyökerek jelei eltérőek, akkor szorzatuk negatív, és a Hely tétel szerint a redukált kvadratikus egyenlet gyökeinek szorzata megegyezik a szabad kifejezéssel. Ezért érdekli azokat az r értékeket, amelyeknél az r - 1 szabad kifejezés negatív. Így ahhoz, hogy megtalálja azokat az r értékeket, amelyek érdekelnek minket, meg kell oldja meg a lineáris egyenlőtlenséget r - 1<0 , откуда находим r<1 . A válasz: r-nél<1 . Vieta képletekA fentiekben a kvadratikus egyenlet Hely-tételéről beszéltünk, és elemeztük az általa megerősített kapcsolatokat. De vannak olyan képletek, amelyek nemcsak a kvadratikus egyenletek valós gyökereit és együtthatóit mutatják össze, hanem a köbös egyenleteket, a négyszeres egyenleteket és általában algebrai egyenletek n fok Felhívják őket vieta képletek. Írjuk Viet képleteit a forma n fokának algebrai egyenletére, és feltételezzük, hogy n valódi gyöke x x, x 2, ..., x n (ezek között lehetnek véletlenszerűek is): A Get képletek lehetővé teszik lineáris faktorizációs polinomi tétel, valamint az egyenlő polinomok meghatározása a hozzájuk tartozó együtthatók egyenlősége révén. Tehát a polinom és annak lineáris tényezőkre történő bomlása egyenlő. Az utolsó munka zárójeleit kinyitva és a megfelelő együtthatókat egyenlővé téve, megkapjuk a Hely képleteket. Különösen, ha n \u003d 2, akkor a kvadratikus egyenlet ismeri a Place formulat. A köbös egyenlethez a Hely képleteknek a formája van Csak azt kell megjegyezni, hogy a Place képletek bal oldalán az úgynevezett elemi elemek vannak szimmetrikus polinomok. Hivatkozásokat.
Az egyenlet gyökereinek összegének meghatározása az egyik szükséges lépés a kvadratikus egyenletek megoldásához (az ax² + bx + c \u003d 0 alak egyenletei, ahol az a, b és c exponensek tetszőleges számok, ráadásul a? 0) a Hely-tétel támogatásával. Használati útmutató1. Írja be a kvadratikus egyenletet ax² + bx + c \u003d 0 formájában. Példa: Kezdeti egyenlet: 12 + x² \u003d 8x Helyesen megírt egyenlet: x² - 8x + 12 \u003d 0 2. Alkalmazza a Hely-tételt, amely szerint az egyenlet gyökere megegyezik az ellentétes jellel vett „b” számmal, és azok szorzata megegyezik a „c” számmal. Példa: A vizsgált egyenletben b \u003d -8, c \u003d 12, illetve: x1 + x2 \u003d 8 × 1 ∗ x2 \u003d 12 3. Tudja meg, hogy a helyes vagy negatív számok-e az egyenletek gyökerei. Ha mind a termék, mind a gyökér összege pozitív szám, akkor az összes gyökér helyes számot ad. Ha a gyökér szorzata helyes, és a gyökér összege negatív szám, akkor mindkét gyökér negatív. Ha a gyökér szorzata negatív, akkor az egyik gyökérnek van „+” jele, a másiknak pedig „-” jele. Ebben az esetben használja a kiegészítő szabályt: „Ha a gyökerek összege pozitív szám, akkor a nagyobb gyökér is pozitív, és ha a gyökerek összege a negatív szám annál nagyobb, ha az abszolút érték gyökér negatív. ”Példa: A vizsgált egyenletben mind az összeg, mind a szorzó helyes szám: 8 és 12, tehát mindkét gyök pozitív szám. 4. Oldja meg a kapott egyenletrendszert a gyökér kiválasztásával. Kényelmesebb lesz a szelekciót tényezőkkel kezdeni, majd annak ellenőrzéséhez kicserélni a tényezőpárokat a második egyenletben, és ellenőrizni, hogy ezeknek a gyökereknek az összege megfelel-e a megoldásnak. 2., 4. és 3. Ellenőrizze a kapott párokat az x1 + x2 \u003d 8 egyenlet támogatásával. Párok 12 + 1 ≠ 86 + 2 \u003d 84 + 3 airs 8 Ennek megfelelõen az egyenlet gyökerei a 6. és a 8. szám. Egy egyenletet f (x, y, ...) \u003d g (x, y, ..) formájú egyenletének hívunk, ahol f és g egy vagy több változó függvényei. Az egyenlet gyökerének felfedezése olyan érvhalmaz felfedezése, amelyben fennáll ez az egyenlőség.
Szüksége lesz
Használati útmutató1. Lehet, hogy van egy formájú egyenlet: x + 2 \u003d x / 5. Először ezt az egyenlőség minden alkotórészét áthelyezzük jobbról balra, miközben az összetevő jelét az ellenkezőre változtatjuk. A nulla ezen egyenlet jobb oldalán marad, vagyis a következőt kapjuk: x + 2-x / 5 \u003d 0. 2. Hasonló feltételeket adunk. A következőket kapjuk: 4x / 5 + 2 \u003d 0. 3. A kapott redukált egyenletből további ismeretlen kifejezést találunk, ebben az esetben x. Az ismeretlen változó eredményeként kapott eredmény lesz a kezdeti egyenlet megoldása. Ebben az esetben a következőt kapjuk: x \u003d -2,5. Kapcsolódó videók Figyelem! Hasznos tanácsok A hely tétele közvetlen kapcsolatot hoz létre a bx2 + cx + d \u003d 0 típusú egyenlet gyökerei (x1 és x2) és exponensei (b és c, d) között. Ennek a tételnek a segítségével a gyökerek jelentését nem szabad meghatározni, összegük - merészen fogalmazva - az elmében kiszámítani. Nincs semmi nehéz, a legfontosabb az, hogy ismerjék néhány szabályt.
Szüksége lesz
Használati útmutató1. Helyezze a vizsgált kvadratikus egyenletet egységes formába, úgy, hogy az összes exponens csökkenő sorrendben megy végbe, azaz először a legmagasabb fok x2, végül a nulla fok x0. Az egyenlet a következőképpen alakul: b * x2 + c * x1 + d * x0 \u003d b * x2 + c * x + d \u003d 0. 2. Ellenőrizze a diszkrimináns negatív jellegét. Ez az ellenőrzés szükséges annak biztosításához, hogy az egyenlet gyökerei legyenek. D (diszkriminancia) formája: D \u003d c2 - 4 * b * d. Számos lehetőség létezik. D - diszkriminatív - helyes, ami azt jelenti, hogy az egyenletnek két gyökere van. D - egyenlő nullával, ebből következik, hogy van egy gyökér, de kettős, azaz x1 \u003d x2. D negatív, az iskolai algebrai kurzusok esetében ez a feltétel azt jelenti, hogy nincsenek gyökerek, a magasabb matematika számára vannak gyökerek, de összetettek. 3. Határozzuk meg az egyenlet gyökereinek összegét. A Place-tétel segítségével ezt könnyű megtenni: b * x2 + c * x + d \u003d 0. Az egyenlet gyökeinek összege közvetlenül arányos a „–c” -vel és fordítottan arányos a „b” kitevővel. Nevezetesen, x1 + x2 \u003d -c / b. Határozzuk meg a gyökér szorzatát az állítás szerint - az egyenlet gyökeinek szorzata közvetlenül arányos a „d” -vel és fordítva arányos a „b” mutatóval: x1 * x2 \u003d d / b. Figyelem! Hasznos tanácsok Ha egy szám helyettesítésével az egyenletben a helyes egyenlőséget kapjuk, akkor ezt a számot gyökérnek nevezzük. A gyökér lehet helyes, negatív és nulla. Az egyenlet minden gyökércsoportja között meg lehet különböztetni a maximumot és a minimumot.
Használati útmutató1. Keresse meg az egyenlet összes gyökerét, közülük válasszon negatívot, ha van. Tegyük fel, hogy megadjuk a 2x? -3x + 1 \u003d 0 kvadratikus egyenletet. Használja a képletet a másodfokú egyenlet gyökereinek meghatározásához: x (1,2) \u003d / 2 \u003d / 2 \u003d / 2, majd x1 \u003d 2, x2 \u003d 1. Könnyű észrevenni, hogy közöttük nincsenek negatívak. 2. A kvadrát egyenlet gyökereit a Place-tétel segítségével is felfedezni lehet. Ezen tétel szerint x1 + x1 \u003d -b, x1? X2 \u003d c, ahol b és c az x? + Bx + c \u003d 0 egyenlet indexei. E tétel alkalmazásával megengedhető, hogy ne számítsuk ki a b? -4ac megkülönböztetőt, ami bizonyos esetekben jelentősen egyszerűsítheti a feladatot. 3. Ha az x pontban szereplő exponens egyenlő a kvadratikus egyenlettel, akkor nem az alap, hanem a rövidített képletet szabad használni a gyökér megkereséséhez. Ha az alapképlet úgy néz ki, mint x (1,2) \u003d [- b ±? (B? -4ac)] / 2a, akkor rövidítve ezt írjuk: x (1,2) \u003d [- b / 2 ±? ( b? / 4-ac)] / a. Ha a kvadratikus egyenletben nincs szabad kifejezés, akkor meglehetősen könnyű x kiszámítani a zárójelből. Időnként a bal oldali részt egy teljes négyzettel egészítik ki: x? + 2x + 1 \u003d (x + 1)?. 4. Vannak olyan típusú egyenletek, amelyek nem egy számot, hanem egy sor megoldást adnak. Mondja el a trigonometrikus egyenleteket. Tehát a 2sin a (2x) + 5sin (2x) -3 \u003d 0 egyenlet eredménye x \u003d? / 4+? K, ahol k egy egész szám. Vagyis ha a k paraméter bármely egész számát helyettesíti, akkor az x argumentum kielégíti az adott egyenletet. 5. Trigonometriai problémák esetén szükség lehet az összes negatív gyökér vagy a legmagasabb negatív gyökerének felismerésére. Az ilyen problémák megoldására logikai érvelést vagy matematikai indukciós módszert használnak. Cserélje ki több egész k értéket az x \u003d? / 4+? K kifejezésben, és figyelje meg, hogyan viselkedik az argumentum. Mellesleg, az előző egyenlet legnagyobb negatív gyöke x \u003d -3? / 4 lesz k \u003d 1-nél. Kapcsolódó videók Figyelem! Hasznos tanácsok A másodfokú egyenlet gyökereinek összege megegyezik a másik együtthatóval az ellenkező jelrel, és a gyökér szorzata megegyezik a szabad kifejezéssel. (Emlékezzünk vissza: a redukált kvadratikus egyenlet az az egyenlet, ahol az első együttható 1). Magyarázat: Legyen a kvadratikus egyenlet ax 2 +bx +c \u003d 0 gyökerei vannak x 1 és x 2. Aztán a Hely tétel szerint: 1. példa: A fenti x 2 - 7x + 10 \u003d 0 egyenletnek a 2. és az 5. gyökere van. A gyökerek összege 7, és a termék 10. És egyenletünkben a második együttható -7, a szabad kifejezés pedig 10. Így a gyökerek összege megegyezik a másik együtthatóval az ellenkező jelrel, és a gyökér szorzata megegyezik a szabad kifejezéssel. Gyakran vannak olyan kvadratikus egyenletek, amelyeket a Place-tétel segítségével könnyen kiszámíthatunk - ráadásul könnyebb kiszámítani őket a segítségével. Ez könnyen ellenőrizhető mind az előző példában, mind a következőben. 2. példa Oldja meg a kvadratikus egyenletet x 2 – 2x – 24 = 0. Határozat. A hely tételét alkalmazzuk és két identitást írunk le: x 1 · x 2 = –24 x 1 + x 2 = 2 Az ilyen tényezőket –24-re választjuk úgy, hogy azok összege megegyezzen 2. Néhány gondolkodás után megkapjuk: 6 és –4. Ellenőrzés: 6 · (- 4) \u003d –24. 6 + (– 4) = 6 – 4 = 2. Mint észrevetted, a gyakorlatban a Hely-tétel lényege, hogy a szabad kifejezést olyan tényezőkre faktorozzuk, amelyek összege megegyezik a másik együtthatóval, az ellenkező jelrel. Ezeknek a tényezőknek a gyökerei lesznek. Ezért a másodfokú egyenletünk gyökerei 6 és –4. A válasz: x 1 = 6, x 2 = –4. 3. példa Megoldjuk a 3x 2 + 2x - 5 \u003d 0 kvadratikus egyenletet. Itt nem a megadott másodlagos egyenlettel foglalkozunk. De ezeket az egyenleteket a Place-tétel segítségével is meg lehet oldani, ha együtthatóik kiegyensúlyozottak - például, ha az első és a harmadik együtthatók összege megegyezik a másikkal, az ellenkező jelzéssel. Határozat. Az egyenlet együtthatói kiegyensúlyozottak: az első és a harmadik kifejezés összege megegyezik a másik jelzéssel, ellentétes jellel: 3 + (–5) = –2. A Hely tétel szerint x 1 + x 2 \u003d –2/3 Két számot kell találnunk, amelyek összege –2/3, és a szorzat –5/3. Ezek a számok lesznek az egyenlet gyökerei. Az első számot azonnal kitalálni lehet: ez 1. Végül is, ha x \u003d 1, akkor az egyenlet a legegyszerűbb összeadás-kivonásból alakul: 3/3 + x 2 \u003d –2/3. Egy egyszerű egyenletet oldunk meg: x 2 \u003d –2 / 3–3 / 3. Válasz: x 1 \u003d 1; x 2 \u003d –5/3 4. példa: Oldja meg a 7. kvadratikus egyenletet x 2 – 6x – 1 = 0. megoldás: Az egyik gyökér azonnal felismerésre kerül - közvetlenül a szemébe rohan: x 1 \u003d 1 (mert egyszerű számtani képletet kapunk: 7 - 6 - 1 \u003d 0). Az egyenlet együtthatói kiegyensúlyozottak: az első és a harmadik összege megegyezik a másikkal, ellentétes jellel: A Hely tétel szerint két identitást állítunk össze (bár ebben az esetben elegendő egy közülük): x 1 · x 2 = –1/7 Kicseréljük x 1 értékét a két kifejezés bármelyikére, és megtaláljuk az x 2 értéket: x 2 = –1/7: 1 = –1/7 A válasz: x 1 = 1; x 2 = –1/7 A csökkentett másodlagos egyenlet megkülönböztetője. A redukált kvadratikus egyenlet megkülönböztető képessége kiszámítható mind az általános, mind az egyszerűsített képlettel: aD \u003d 0, az adott egyenlet gyökerei a következő képlettel számíthatók ki: Ha D< 0, то уравнение не имеет корней. Ha D \u003d 0, akkor az egyenletnek egy gyökere van. Ha D\u003e 0, akkor az egyenletnek két gyökere van. |
| Olvasd el: |
|---|
Legnépszerűbb:
A legegyszerűbb trigonometrikus egyenlőtlenségek megoldása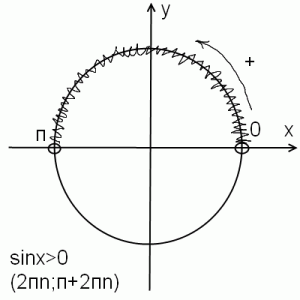
|
új
- Mi törte meg a "merev" bárót?
- A Fehér Mozgalom tagja
- Suvorov és a csapat útja hazájukhoz
- Az F (x) függvényt f (x) függvény antiderivatívájának nevezzük, ha F` (x) \u003d f (x) vagy dF (x) \u003d f (x) dx
- Fokfrekvencia-csökkentő program
- Hasonló kifejezések, redukcióik, példák
- Orosz utazók lazarev
- Nem teljes kvadratikus egyenletek megoldása
- A kvadratikus egyenletek megoldása, a gyökérképlet, példák
- Koordináta sík (6. fokozat) - Tudás hipermarketje