Webhely szakaszok
A szerkesztők választása:
hirdetés
| Algoritmus a függvény gráf érintőjének egyenletének meghatározására. A függvény gráfja érintőjének egyenlete |
|
A magánélete fontos számunkra. Ezért kidolgoztunk egy adatvédelmi irányelvet, amely leírja, hogyan használjuk és tároljuk az Ön adatait. Kérjük, olvassa el adatvédelmi irányelveinket és tudassa velünk, ha bármilyen kérdése van. Személyes adatok gyűjtése és felhasználásaA személyes adatok olyan adatokra vonatkoznak, amelyek felhasználhatók egy adott személy azonosítására vagy kapcsolattartására. Felkérést kaphat arra, hogy adja meg személyes adatait bármikor, amikor kapcsolatba lép velünk. Az alábbiakban néhány példát találunk arra, hogy milyen típusú személyes információkat gyűjthetünk, és hogyan használhatjuk ezeket az információkat. Milyen személyes információkat gyűjtünk:
Hogyan használjuk az Ön személyes adatait:
Közzététel harmadik felek számáraNem adjuk ki az Öntől kapott információkat harmadik felek számára. kivételek:
Személyes adatok védelmeÓvintézkedéseket teszünk - ideértve az adminisztratív, technikai és fizikai - személyes adatait is az adatvesztés, lopás és visszaélés, valamint az illetéktelen hozzáférés, a nyilvánosságra hozatal, a megváltoztatás és a megsemmisítés ellen. A vállalati szintű adatvédelemAnnak érdekében, hogy az Ön személyes adatai biztonságosak legyenek, kommunikáljuk munkatársainkkal a titoktartási és biztonsági szabályokat, és szigorúan ellenőrizzük a titoktartási intézkedések végrehajtását. Ez a matematikai program megtalálja a \\ (f (x) \\) függvény gráfja érintőjének egyenletét egy felhasználó által megadott ponton \\ (a \\). A program nem csak az érintő egyenletet mutatja, hanem a probléma megoldásának folyamatát is. Ez az online számológép hasznos lehet a középiskolások számára a vizsgákra és a vizsgákra való felkészülés során, amikor a vizsga előtti ismeretek tesztelésekor a szülők ellenőrzik a matematika és az algebrai problémák megoldását. Vagy talán túl drága, ha oktatót bérel vagy új tankönyvet vásárol? Vagy csak a lehető leggyorsabban szeretné megcsinálni a matematikai vagy algebrai házi feladatát? Ebben az esetben programokat is használhat részletes megoldással. Így saját képzését és / vagy fiatalabb testvéreidet is kiképzheti, miközben javítani kell a feladatok terén az oktatás szintjét. Ha meg kell találnia egy függvény derivációját, akkor ehhez a feladathoz kell találnunk a deriváltot. Ha nem ismeri a funkciók bevitelének szabályait, javasoljuk, hogy ismerkedjen meg velük. Írja be a \\ (f (x) \\) függvény kifejezését és a \\ (a \\) számot Keresse meg az érintő egyenletet Megállapítást nyert, hogy a probléma megoldásához szükséges néhány szkript nem töltődött be, és lehet, hogy a program nem fog működni. A megoldás megjelenéséhez engedélyeznie kell a JavaScriptet. Itt talál útmutatást a JavaScript engedélyezéséhez a böngészőben. mert Nagyon sok ember akarja megoldani a problémát, kérését sorba rendezték. Ha te hibát észlelt a megoldásban, erről a Visszajelző űrlapon tud írni. Játékok, rejtvények, emulátorok: Egy kicsit az elmélet.A vonalszög együtthatójaEmlékezzünk arra, hogy a \\ (y \u003d kx + b \\) lineáris függvény gráfja egy vonal. A \\ (k \u003d tg \\ alpha \\) számot hívják közvetlen lejtőn, és a \\ (\\ alpha \\) szög a vonal és az Ox tengely közötti szög Ha \\ (k\u003e 0 \\), akkor \\ (0 If \\ (kA függvény gráfja érintőjének egyenlete) Ha az M pont (a; f (a)) az y \u003d f (x) függvény gráfjába tartozik, és ha ezen a ponton lehet húzni olyan érintőt, amely nem merőleges az abszcisszára a függvény gráfjára, akkor a derivátum geometriai jelentése alapján következik, hogy az érintő szögkoeficiense egyenlő f-vel "(a). Ezután kidolgozunk egy algoritmust bármely függvény gráfja érintőjének egyenletének rajzolásához. Legyen az y \u003d f (x) függvény és az M (a; f (a)) pont megadva ennek a függvénynek a grafikonján; tegyük ismertté, hogy létezik f "(a). Összeállítjuk egy adott függvény gráfja érintőjének egyenletét egy adott ponton. Ez az egyenlet, mint bármelyik egyenes vonal egyenlete, amely nem párhuzamos a ordináta tengelyével, y \u003d kx + b formájú, tehát a probléma az együtthatók értékeinek megtalálása. k és b. A k szög együtthatóval minden világos: ismert, hogy k \u003d f "(a). B értékének kiszámításához azt a tényt használjuk, hogy a kívánt vonal áthalad az M ponton (a; f (a)). Ez azt jelenti, hogy ha helyettesítjük az M pont koordinátáit a vonal egyenletébe a helyes egyenletet kapjuk: \\ (f (a) \u003d ka + b \\), azaz \\ (b \u003d f (a) - ka \\). A k és b együtthatók megállapított értékeit a sor egyenletében kell helyettesíteni: Megkaptuk a függvény gráfja érintőjének egyenlete \\ (y \u003d f (x) \\) a \\ (x \u003d a \\) ponton. Algoritmus a \\ (y \u003d f (x) \\) függvény gráfja érintőjének egyenletének meghatározására A magánélete fontos számunkra. Ezért kidolgoztunk egy adatvédelmi irányelvet, amely leírja, hogyan használjuk és tároljuk az Ön adatait. Kérjük, olvassa el adatvédelmi irányelveinket és tudassa velünk, ha bármilyen kérdése van. Személyes adatok gyűjtése és felhasználásaA személyes adatok olyan adatokra vonatkoznak, amelyek felhasználhatók egy adott személy azonosítására vagy kapcsolattartására. Felkérést kaphat arra, hogy adja meg személyes adatait bármikor, amikor kapcsolatba lép velünk. Az alábbiakban néhány példát találunk arra, hogy milyen típusú személyes információkat gyűjthetünk, és hogyan használhatjuk ezeket az információkat. Milyen személyes információkat gyűjtünk:
Hogyan használjuk az Ön személyes adatait:
Közzététel harmadik felek számáraNem adjuk ki az Öntől kapott információkat harmadik felek számára. kivételek:
Személyes adatok védelmeÓvintézkedéseket teszünk - ideértve az adminisztratív, technikai és fizikai - személyes adatait is az adatvesztés, lopás és visszaélés, valamint az illetéktelen hozzáférés, a nyilvánosságra hozatal, a megváltoztatás és a megsemmisítés ellen. A vállalati szintű adatvédelemAnnak érdekében, hogy az Ön személyes adatai biztonságosak legyenek, kommunikáljuk munkatársainkkal a titoktartási és biztonsági szabályokat, és szigorúan ellenőrizzük a titoktartási intézkedések végrehajtását. A cikk részletesen ismerteti a meghatározásokat, a származék geometriai jelentését grafikus ábrázolással. A tangens vonal egyenletét példákkal vesszük figyelembe, a 2. rend görbéihez tartozó tangencia egyenleteit meg kell találni. Yandex.RTB R-A-339285-1 1. meghatározás Az y \u003d k x + b egyenes dőlésszöge az α szög, amelyet az x tengely pozitív irányától az y \u003d k x + b egyenesig pozitív irányban mérnek. Az ábrán az x irányát egy zöld nyíl jelöli és zöld ív formájában, a dőlésszöget pedig egy piros ív jelzi. A kék vonal a vonalra utal. 2. meghatározás Az y \u003d k x + b vonal szög koefficiense k numerikus együttható. A szög együttható megegyezik a vonal lejtésével, vagyis k \u003d t g α.
A szekanta az f (x) függvény 2 pontján áthaladó vonal. Más szavakkal, egy szekvencia egy egyenes, amelyet egy adott függvény gráfjának két pontján húzunk át.
Az ábra azt mutatja, hogy AB egy szekció, és f (x) egy fekete görbe, α egy piros ív, ami azt jelenti, hogy a szekvencia dőlésszöge szögben van. Ha az egyenes szögkoeficiense megegyezik a dőlési szög érintőjével, akkor egyértelmű, hogy az ABC derékszögű háromszög érintője az ellenkező lábnak a szomszédoshoz viszonyított arányában található. 4. meghatározás Megkapjuk a képletet a szektortípus megtalálására: k \u003d tg α \u003d BCAC \u003d f (x B) - fx A x B - x A, ahol az A és B pontok abszcissza értékei x A, x B és f (x A), f (x B) az értékek működik ezeken a pontokon. Nyilvánvaló, hogy a szekanta meredekségét k \u003d f (x B) - f (x A) x B - x A egyenlettel vagy k \u003d f (x A) - f (x B) x A - x B egyenlettel és az egyenlet felhasználásával határozzuk meg. y \u003d f (x B) - f (x A) x B - x A x - x A + f (x A) formátumban kell írni, vagy Egy szekció vizuálisan három részre osztja a gráfot: az A ponttól balra, A-tól B-ig, B-től jobbra. Az alábbi ábra azt mutatja, hogy három szektort egybeesőnek tekintünk, vagyis hasonló egyenlet alapján állítják be.
A meghatározás szerint egyértelmű, hogy a vonal és annak szekvenciája ebben az esetben egybeesnek. A szekanta többször átlépheti az adott függvény grafikonját. Ha az y \u003d 0 alak egyenlete van a szekantával, akkor a sinusoiddal való metszéspontok száma végtelen. 5. meghatározás Az f (x) függvény gráfjának érintője x 0-on; f (x 0) egy egy adott x 0 ponton áthaladó egyenes; f (x 0), olyan szegmenssel, amelynek sok x értéke közel x 0-hoz. 1. példa Vegyük részletesen az alábbi példát. Ezután világossá válik, hogy az y \u003d x + 1 függvény által definiált vonalat y \u003d 2 x érintőjének kell tekinteni az (1; 2) koordináta pontján. Az egyértelműség érdekében figyelembe kell venni az (1; 2) értékhez közeli grafikonokat. Az y \u003d 2 x függvény feketével van jelölve, a kék vonal az érintő, a piros pont az metszéspont.
Nyilvánvaló, hogy y \u003d 2 x beleolvad az y \u003d x + 1 vonalba. Az érintő meghatározásához figyelembe kell venni az A B érintő viselkedését a B pont végtelen megközelítésével az A pontra. Az érthetőség kedvéért az ábrát mutatjuk be.
Az AB szekantum, amelyet a kék vonal jelöl, maga az érintő helyzetére hajlamos, és az α szekció dőlésszöge az α x érintő dőlésszögéhez kezd. 6. meghatározás Az y \u003d f (x) függvény gráfjának érintője az A ponton az A B szekvencia végpontja B-nél, hajlamos A-ra, vagyis B → A. Most a derivált függvény geometriai jelentésének mérlegelésére fordulunk egy ponton. Tegyük át az AB szekvencia figyelembevételét az f (x) függvényben, ahol A és B x 0, f (x 0) és x 0 + ∆ x, f (x 0 + ∆ x) és ∆ x koordinátákkal vannak jelölve az argumentum növekményében. . Most a függvény ∆ y \u003d ∆ f (x) \u003d f (x 0 + ∆ x) - f (∆ x) formában lesz. Az érthetőség kedvéért példát mutatunk be.
Tekintsük a kapott derékszögű háromszöget A B C. A megoldás érintőjének meghatározását használjuk, vagyis ∆ y ∆ x \u003d t g α relációt kapunk. Az érintő meghatározásából következik, hogy lim Δx → 0 Δ y Δ x \u003d t g α x. Az ezen a ponton alkalmazott derivatív szabály szerint azt a tényt kapjuk, hogy az x (0) pontban levő f (x) deriváltot a függvény növekedésének és az argumentum növekedésének viszonyainak határának nevezzük, ahol ∆ x → 0, majd f (x 0) \u003d lim ∆ x → 0 ∆ y ∆ x . Ebből következik, hogy f "(x 0) \u003d lim Δ x → 0 Δ y Δ x \u003d t g α x \u003d k x, ahol k x az érintő jelöli szögkoeficiensen. Vagyis megkapjuk, hogy f '(x) létezhet még az x 0 ponton, valamint a függvény adott gráfjának érintője is az érintkezési ponton, amely egyenlő x 0, f 0 (x 0) -val, ahol az érintő pont szögelõ együtthatójának a pontja megegyezik a származékkal x ponton. 0. Akkor kapjuk, hogy k x \u003d f "(x 0). A derivált függvény geometriai jelentése egy ponton az, hogy megadjuk a gráf érintőjének létezésének fogalmát ugyanazon a ponton. Annak érdekében, hogy bármilyen vonalat egyenletbe lehessen írni a síkon, szögkoeficienst kell alkalmazni azzal a ponttal, amelyen áthalad. Jelölését x 0-nak vesszük a kereszteződésnél. Az y \u003d f (x) függvény gráfja érintőjének egyenlete x 0, f 0 (x 0) formában y \u003d f "(x 0) · x - x 0 + f (x 0) formájú. Ez azt jelenti, hogy az f "(x 0) származék véges értéke meghatározhatja az érintő helyzetét, azaz függőlegesen, feltéve, hogy lim x → x 0 + 0 f" (x) \u003d ∞ és lim x → x 0 - 0 f "(x ) \u003d ∞ vagy egyáltalán nem létezik lim x → x 0 + 0 f "(x) ≠ lim x → x 0 - 0 f" (x) feltétel mellett. Az érintő elhelyezkedése a kx \u003d f "(x 0) szögetényező értékétől függ. Ha az x tengelyre párhuzamos, akkor kk \u003d 0 értéket kapunk, amikor k o - kx \u003d ∞ párhuzamos, és az x \u003d x 0 érintő egyenlet formája növekszik, ahogy: kx\u003e 0, kx-nél csökken< 0 . 2. példa Rajzolja meg az érintő egyenletét az y \u003d e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 függvény gráfjához abban a pontban, ahol a koordináták (1; 3) vannak a dőlési szög meghatározásával. döntés Hipotézis szerint a függvényt minden valós számra meghatározzuk. Azt kapjuk, hogy az (1; 3) feltétel által megadott koordinátákkal rendelkező pont érintőpont, akkor x 0 \u003d - 1, f (x 0) \u003d - 3. Meg kell találni a származékot egy - 1 értékű ponton. Megkapjuk y "\u003d ex + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3" \u003d \u003d ex + 1 "+ x 3 3" - 6 - 3 3 x "- 17 - 3 3" \u003d ex + 1 + x 2 - 6 - 3 3 y "(x 0) \u003d y" (- 1) \u003d e - 1 + 1 + - 1 2 - 6 - 3 3 \u003d 3 3 Az f '(x) értéke a tangencia pontján az érintő meredeksége, amely megegyezik a meredekséggel. Ezután k x \u003d t g α x \u003d y "(x 0) \u003d 3 3 Ebből következik, hogy α x \u003d a r c t g 3 3 \u003d π 6 A válasz:az érintő egyenlet formája lesz y \u003d f "(x 0) · x - x 0 + f (x 0) y \u003d 3 3 (x + 1) - 3 y \u003d 3 3 x - 9 - 3 3 Az érthetőség kedvéért példát mutatunk be egy grafikus ábrán. A fekete szín az eredeti függvény grafikonja, a kék szín az érintő képe, a piros pont az érintési pont. A jobb oldali ábra nagyított képet mutat.
3. példa Megtudhatja, hogy van-e érintő az adott függvény gráfjának döntés Hipotézis szerint úgy gondoljuk, hogy egy adott funkció meghatározásának tartományát az összes valós szám halmazának kell tekinteni. A származék megtalálásához fordulunk y "\u003d 3 · x - 1 5 + 1" \u003d 3 · 1 5 · (x - 1) 1 5 - 1 \u003d 3 5 · 1 (x - 1) 4 5 Ha x 0 \u003d 1, akkor f '(x) nincs meghatározva, de a határokat lim x-ként írják fel: → 1 + 0 3 5 · 1 (x - 1) 4 5 \u003d 3 5 · 1 (+ 0) 4 5 \u003d 3 5 1 + 0 \u003d + ∞ és lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 \u003d 3 5 · 1 (- 0) 4 5 \u003d 3 5 · 1 + 0 \u003d + ∞, ami létezést jelent függőleges érintő (1; 1) -nél. A válasz: az egyenlet formája x \u003d 1, ahol a dőlésszög π 2 lesz. Az érthetőség kedvéért ábrázolja grafikusan.
4. példa Keresse meg az y \u003d 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 függvény gráfpontjait, ahol
döntés Figyelembe kell venni a hatályát. Hipotézis szerint egy függvényt definiálunk az összes valós szám halmazán. Nyitjuk ki a modult és megoldjuk a rendszert x ∈ - ∞ intervallumokkal; 2 és [- 2; + ∞). Megkapjuk y \u003d - 1 15 x 3 + 18 x 2 + 105 x + 176, x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12, x ∈ [- 2; + ∞) Meg kell különböztetni a funkciót. Megvan y "\u003d - 1 15 x 3 + 18 x 2 + 105 x + 176", x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [- 2; + ∞) ⇔ y" \u003d - 1 5 (x 2 + 12 x + 35), x ∈ - ∞; - 2 1 5 x 2 - 4 x + 3, x ∈ [- 2; + ∞) Ha x \u003d - 2, akkor a derivatívum nem létezik, mivel az egyirányú határok ezen a ponton nem azonosak: lim x → - 2 - 0 y "(x) \u003d lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 \u003d - 1 5 (- 2) 2 + 12 (- 2) + 35 \u003d - 3 lim x → - 2 + 0 y "(x) \u003d lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) \u003d 1 5 - 2 2 - 4 - 2 + 3 \u003d 3 Kiszámoljuk a függvény értékét az x \u003d - 2 ponton, ahol ezt kapjuk
Amikor x ∈ - ∞; - 2, akkor - 1 5 (x 2 + 12 x + 35) \u003d 0, és x ∈ (- 2; + ∞) esetén 1 5 (x 2 - 4 x + 3) \u003d 0 értéket kapunk. 1 5 (x 2 + 12 x + 35) \u003d 0 D \u003d 12 2 - 4 · 35 \u003d 144 - 140 \u003d 4 x 1 \u003d - 12 + 4 2 \u003d - 5 ∈ - ∞; - 2 x 2 \u003d - 12 - 4 2 \u003d - 7 ∈ - ∞; - 2 1 5 (x 2 - 4 x + 3) \u003d 0 D \u003d 4 2 - 4 · 3 \u003d 4 x 3 \u003d 4 - 4 2 \u003d 1 - 2; + ∞ x 4 \u003d 4 + 4 2 \u003d 3 - 2; + ∞ Kiszámoljuk a megfelelő függvényértékeket y 1 \u003d y - 5 \u003d 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 \u003d 8 5 y 2 \u003d y (- 7) \u003d 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 \u003d 4 3 y 3 \u003d y (1) \u003d 1 15 1 + 2 3 - 4 5 · 1 2 - 16 5 · 1 - 26 5 + 3 1 + 2 \u003d 8 5 y 4 \u003d y (3) \u003d 1 15 3 + 2 3 - 4 5 · 3 2 - 16 5 · 3 - 26 5 + 3 3 + 2 \u003d 4 3 Tehát - 5; 8 5, - 4; 4, 3; 8 5, 3; 4 3 a keresett pontoknak tekinthető a függvénydiagramban. Vegyük figyelembe a megoldás grafikus ábrázolását.
A fekete vonal a függvénydiagram, a piros pontok az érintési pontok.
Az első egyenletnek nincs gyökere, mivel a diszkrimináns nulla alatt van. Ezt írjuk 1 5 x 2 + 12 x + 35 \u003d 8 5 x 2 + 12 x + 43 \u003d 0 D \u003d 12 2 - 4 · 43 \u003d - 28< 0 A másik egyenletnek tehát két valódi gyökere van 1 5 (x 2 - 4 x + 3) \u003d 8 5 x 2 - 4 x - 5 \u003d 0 D \u003d 4 2 - 4 · (- 5) \u003d 36 x 1 \u003d 4 - 36 2 \u003d - 1 ∈ - 2; + ∞ x 2 \u003d 4 + 36 2 \u003d 5 - 2; + ∞ Folytassuk a függvény értékeinek meghatározását. Megkapjuk y 1 \u003d y (- 1) \u003d 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 \u003d 4 15 y 2 \u003d y (5) \u003d 1 15 5 + 2 3 - 4 5 · 5 2 - 16 5 · 5 - 26 5 + 3 5 + 2 \u003d 8 3 Pontok értékkel - 1; 4 15, 5; 8 3 azok a pontok, ahol az érintõk párhuzamosak az y \u003d 8 5 x + 4 vonallal. A válasz:a fekete vonal a függvény grafikonja, a piros vonal az y \u003d 8 x x 4 gráfja, a kék vonal az - 1 pontok érintõi; 4 15, 5; 8 3.
Lehet, hogy végtelen számú érintő van az adott funkciókhoz. 5. példa Írja meg az összes elérhető érintőfüggvény egyenletét, y \u003d 3 cos 3 2 x - π 4 - 1 3, amelyek merőlegesek az y \u003d - 2 x + 1 2 egyenesre. döntés Az érintő egyenlet összeállításához meg kell találni az érintő pont együtthatóját és koordinátáit, a vonalak merőlegességének feltétele alapján. A meghatározás a következő: Az egyenesekre merőleges szögetényezők szorzata - 1, azaz k x · k ⊥ \u003d - 1-vel van írva. Feltételünk szerint a szög együtthatója merőleges az egyenesre és egyenlő k ⊥ \u003d - 2, akkor k x \u003d - 1 k ⊥ \u003d - 1 - 2 \u003d 1 2. Most meg kell találnia a érintési pontok koordinátáit. Meg kell találnia x-t, amely után az adott függvény értéke. Vegye figyelembe, hogy a származék geometriai jelentése alapján Megkapjuk y "(x 0) \u003d 3 cos 3 2 x 0 - π 4 - 1 3" \u003d 3 · - sin 3 2 x 0 - π 4 · 3 2 x 0 - π 4 "\u003d \u003d - 3 · sin 3 2 x 0 - π 4 · 3 2 \u003d - 9 2 · sin 3 2 x 0 - π 4 ⇒ kx \u003d y "(x 0) ⇔ - 9 2 · sin 3 2 x 0 - π 4 \u003d 1 2 ⇒ sin 3 2 x 0 - π 4 \u003d - 1 9 Ezt a trigonometrikus egyenletet kell használni a érintési pontok koordinátáinak kiszámításához. 3 2 x 0 - π 4 \u003d a r c sin - 1 9 + 2 πk vagy 3 2 x 0 - π 4 \u003d π - a r c sin - 1 9 + 2 πk 3 2 x 0 - π 4 \u003d - a r c sin 1 9 + 2 πk vagy 3 2 x 0 - π 4 \u003d π + a r c sin 1 9 + 2 πk x 0 \u003d 2 3 π 4 - a r c sin 1 9 + 2 πk vagy x 0 \u003d 2 3 5 π 4 + a r c sin 1 9 + 2 πk, k ∈ Z Z az egész szám halmaza. Talált x érintési pontot. Most meg kell keresnie az y értékeket: y 0 \u003d 3 cos 3 2 x 0 - π 4 - 1 3 y 0 \u003d 3 · 1 - sin 2 3 2 x 0 - π 4 - 1 3 vagy y 0 \u003d 3 · - 1 - sin 2 3 2 x 0 - π 4 - 1 3 y 0 \u003d 3 · 1 - - 1 9 2 - 1 3 vagy y 0 \u003d 3 · - 1 - - 1 9 2 - 1 3 y 0 \u003d 4 5 - 1 3 vagy y 0 \u003d - 4 5 + 1 3 Ebből következik, hogy 2 3 π 4 - a r c sin 1 9 + 2 πk; 4 5 - 1 3, 2 3 5 π 4 + a r c sin 1 9 + 2 πk; - 4 5 + 1 3 érintési pont. A válasz: a szükséges egyenleteket így írjuk: y \u003d 1 2 x - 2 3 π 4 - ív sin 1 9 + 2 πk + 4 5 - 1 3, y \u003d 1 2 x - 2 3 5 π 4 + ív sin 1 1 + 2 πk - 4 5 + 1 3 , k ∈ Z Vizuális képhez vegye figyelembe a koordináta vonal funkcióját és érintőjét. Az ábra azt mutatja, hogy a függvény helye [- 10; 10], ahol a fekete vonal a függvény grafikonja, a kék vonalak az érintõk, amelyek merõlegesek az y \u003d - 2 x + 1 2 formájának adott vonalára. A piros pontok érintési pontok.
A másodrendű görbék kanonikus egyenletei nem egyedi függvények. A tangensek egyenleteit közismert sémák szerint állítják össze. Egy kör érintőjeAz x c e n t e r-nél középpontú kör meghatározása; y c e n t e r és R sugárral az x - x c e n t e r 2 + y - y c e n t e r 2 \u003d R2 képletet kell alkalmazni. Ezt az egyenlőséget két funkció összekapcsolásaként lehet megfogalmazni: y \u003d R 2 - x - x c e n t e r 2 + y c e n t e r y \u003d - R 2 - x - x c e n t e r 2 + y c e n t e r Az első funkció felül található, a második pedig alul található, az ábra szerint.
Rajzoljunk egy kör egyenletét az x 0 ponton; y 0, amely a felső vagy az alsó félkörben található, meg kell találni az y \u003d R 2 - x - x c e n t e r 2 + y c e n t e vagy \u003d y \u003d - R 2 - x - x c e n t e r 2 + y c e n t e formájú függvény gráfjának egyenletét a megadott ponton. Mikor az x c e n t e r pontokban; y c e n t e r + R és x c e n t e r; y c e n t e r - R, az érintőket az y \u003d y c e n t e r + R és y \u003d y c e n t e r - R egyenletekkel és az x c e n t e r + R egyenletekkel adhatjuk meg; y c e n t e r és
Érintő az ellipszisigHa az ellipszisnek van egy középpontja az x c e n t e r pontban; y c e n t t r r az a és b féltengelyekkel, akkor az x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 \u003d 1 egyenlettel határozható meg. Egy ellipszis és egy kör két funkció kombinálásával jelölhető meg, nevezetesen: a felső és az alsó fél ellipszis. Akkor megkapjuk y \u003d b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y \u003d - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r
Ha az érintők az ellipszis csúcsain helyezkednek el, akkor x vagy y körül párhuzamosak. Az alábbiakban az érthetőség kedvéért vegye figyelembe az ábrát.
6. példa Írja le az x - 3 2 4 + y - 5 2 25 \u003d 1 ellipszis érintőjének egyenletét x pontokban, ahol x \u003d 2. döntés Meg kell találni azokat az érintkezési pontokat, amelyek megfelelnek az x \u003d 2 értéknek. Kicseréljük a meglévő ellipszis egyenletet és megkapjuk x - 3 2 4 x \u003d 2 + y - 5 2 25 \u003d 1 1 4 + y - 5 2 25 \u003d 1 y - 5 2 \u003d 3 4 · 25 25 y \u003d ± 5 3 2 + 5 Aztán 2; 5 3 2 + 5 és 2; - 5 3 2 + 5 érintési pontok, amelyek a felső és alsó fél ellipszishez tartoznak. Folytatjuk az ellipszis egyenlet megtalálását és megoldását y vonatkozásában. Megkapjuk x - 3 2 4 + y - 5 2 25 \u003d 1 y - 5 2 25 \u003d 1 - x - 3 2 4 (y - 5) 2 \u003d 25 · 1 - x - 3 2 4 y - 5 \u003d ± 5 · 1 - x - 3 2 4 y \u003d 5 ± 5 2 4 - x - 3 2 Nyilvánvaló, hogy a felső fél ellipszis az y \u003d 5 + 5 2 4 - x - 3 2, és az alsó y \u003d 5 - 5 2 4 - x - 3 2 függvény használatával van beállítva. A szokásos algoritmust alkalmazzuk annak érdekében, hogy az érintő egyenletét összeállítsuk egy adott funkció gráfjával. Azt írjuk, hogy az első érintő egyenlete a 2. pontban; 5 3 2 + 5 formája lesz y "\u003d 5 + 5 2 4 - x - 3 2" \u003d 5 2 · 1 2 4 - (x - 3) 2 · 4 - (x - 3) 2 "\u003d \u003d - 5 2 · x - 3 4 - ( x - 3) 2 ⇒ y "(x 0) \u003d y" (2) \u003d - 5 2 · 2 - 3 4 - (2 - 3) 2 \u003d 5 2 3 ⇒ y \u003d y "(x 0) · x - x 0 + y 0 ⇔ y \u003d 5 2 3 (x - 2) + 5 3 2 + 5 Megkapjuk a második érintő egyenletét a pont értékével y "\u003d 5 - 5 2 4 - (x - 3) 2" \u003d - 5 2 · 1 2 4 - (x - 3) 2 · 4 - (x - 3) 2 "\u003d \u003d 5 2 · x - 3 4 - (x - 3) 2 ⇒ y "(x 0) \u003d y" (2) \u003d 5 2 · 2 - 3 4 - (2 - 3) 2 \u003d - 5 2 3 ⇒ y \u003d y "(x 0) · x - x 0 + y 0 ⇔ y \u003d - 5 2 3 (x - 2) - 5 3 2 + 5 Grafikusan az érintőket a következőképpen jelöljük:
Hiperbol érintőHa a hiperbolanak van egy központja az x c e n t e r pontban; y c e n t e r és csúcsok x c e n t e r + α; y c e n t e r és x c e n t e r - α; y c e n t e r, akkor történik az x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 \u003d 1 egyenlőtlenség, ha x c e n t e r csúcsokkal; y c e n t e r + b és x c e n t e r; y c e n t t r - b, akkor azt az x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 \u003d - 1 egyenlőtlenség határozza meg.
A hiperbola a forma két kombinált funkciójaként reprezentálható y \u003d ba * (x - xcenter) 2 - a 2 + ycentery \u003d - ba * (x - xcenter) 2 - a 2 + ycenter vagy y \u003d ba (x - xcenter) 2 + a 2 + ycenter
Az első esetben az érintőink σ-val párhuzamosak, a második esetben σ-val párhuzamosak. Ebből következik, hogy a hiperbol érintőjének egyenletének meghatározásához meg kell határozni, hogy melyik funkcióhoz tartozik az érintő pont. Ennek meghatározásához helyettesíteni kell az egyenleteket és ellenőrizni kell azok identitását. 7. példa Készítsük el a hiperbola érintőjének egyenletét x - 3 2 4 - y + 3 2 9 \u003d 1 a 7. pontban; - 3 3 - 3. döntés A hiperbola megtalálásához 2 függvény felhasználásával meg kell változtatni a megoldás rekordját. Megkapjuk x - 3 2 4 - y + 3 2 9 \u003d 1 ⇒ y + 3 2 9 \u003d x - 3 2 4 - 1 ⇒ y + 3 2 \u003d 9 x - 3 2 4 - 1 ⇒ y + 3 \u003d 3 2 x - 3 2 - 4 és l és y + 3 \u003d - 3 2 · x - 3 2 - 4 ⇒ y \u003d 3 2 · x - 3 2 - 4 - 3 y \u003d - 3 2 · x - 3 2 - 4 - 3 Meg kell határozni, hogy melyik funkcióhoz tartozik az adott pont a 7 koordinátával; - 3 3 - 3. Az első funkció ellenőrzéséhez nyilvánvalóan szükséges y (7) \u003d 3 2 · (7 - 3) 2 - 4 - 3 \u003d 3 3 - 3 3 - 3 3 - 3, akkor a pont nem tartozik a gráfhoz, mivel az egyenlőség nem érvényes. A második függvényhez y (7) \u003d - 3 2 · (7 - 3) 2 - 4 - 3 \u003d - 3 3 - 3 ≠ - 3 3 - 3, azaz a pont az adott gráfhoz tartozik. Innentől meg kell határozni a szög együtthatót. Megkapjuk y "\u003d - 3 2 · (x - 3) 2 - 4 - 3" \u003d - 3 2 · x - 3 (x - 3) 2 - 4 ⇒ kx \u003d y "(x 0) \u003d - 3 2 · x 0 - 3 x 0 - 3 2 - 4 x 0 \u003d 7 \u003d - 3 2 · 7 - 3 7 - 3 2 - 4 \u003d - 3 A válasz: az érintő egyenlet ábrázolható mint y \u003d - 3 · x - 7 - 3 3 - 3 \u003d - 3 · x + 4 3 - 3 Vizuálisan ábrázolva:
Parabolikus érintőAz y \u003d ax 2 + bx + c parabola érintő egyenletének összeállításához x 0, y (x 0) pontban a szokásos algoritmust kell használni, akkor az egyenlet y \u003d y "(x 0) formátumú lesz (x 0) · x - x 0 + y ( x 0.) Egy ilyen érintő a csúcson párhuzamos az ox-tel. Az x \u003d a y 2 + b y + c parabolát két függvény összekapcsolásával kell megadni. Ezért meg kell oldani az y egyenletet. Megkapjuk x \u003d ay 2 + + c ⇔ ay 2 + by + c - x \u003d 0 D \u003d b 2 - 4 a (c - x) y \u003d - b + b 2 - 4 a (c - x) 2 ay \u003d - b - b 2 - 4 a (c - x) 2 a Grafikusan ábrázoljuk, hogyan:
Az x 0, y (x 0) pont függvényhez való tartozásának megismeréséhez óvatosan járjon el a szokásos algoritmus szerint. Egy ilyen érintő az y-vel párhuzamos lesz a parabola vonatkozásában. 8. példa Írja be az érintő egyenletét az x - 2 y 2 - 5 y + 3 gráfra, ha 150 ° érintőszöge van. döntés A megoldást azzal kezdjük, hogy a parabolát két funkcióként ábrázoljuk. Megkapjuk 2 y 2 - 5 y + 3 - x \u003d 0 D \u003d (- 5) 2 - 4 · (- 2) · (3 - x) \u003d 49 - 8 xy \u003d 5 + 49 - 8 x - 4 y \u003d 5 - 49 - 8 x - 4 A szög együttható értéke megegyezik a derivátum értékével ezen függvény x 0-on, és megegyezik a dőlésszög érintőjével. Megkapjuk: k x \u003d y "(x 0) \u003d t g α x \u003d t g 150 ° \u003d - 1 3 Innentől meghatározzuk az x értékét a érintési pontokhoz. Az első függvény így lesz írva y "\u003d 5 + 49 - 8 x - 4" \u003d 1 49 - 8 x ⇒ y "(x 0) \u003d 1 49 - 8 x 0 \u003d - 1 3 ⇔ 49 - 8 x 0 \u003d - 3 Nyilvánvaló, hogy nincsenek valódi gyökerek, mivel negatív értéket kaptak. Megállapítottuk, hogy 150 ° -os szöggel rendelkező érintő nem létezik ilyen funkcióhoz. A második függvény így lesz írva y "\u003d 5 - 49 - 8 x - 4" \u003d - 1 49 - 8 x ⇒ y "(x 0) \u003d - 1 49 - 8 x 0 \u003d - 1 3 ⇔ 49 - 8 x 0 \u003d - 3 x 0 \u003d 23 4 ⇒ y (x 0) \u003d 5 - 49 - 8 · 23 4 - 4 \u003d - 5 + 3 4 Van, hogy a érintési pontok 23 4; - 5 + 3 4. A válasz: az érintő egyenlet formája lesz y \u003d - 1 3x - 23 4 + - 5 + 3 4 Ezt grafikusan ábrázoljuk:
Ha hibát észlel a szövegben, válassza ki azt, és nyomja meg a Ctrl + Enter billentyűket
De mi történik, ha a deriváció x 0-nál nem létezik? Két lehetőség lehetséges:
Érintő egyenletMinden nem függőleges vonalat az y \u003d kx + b alak egyenlete adja meg, ahol k a szögkoeficiens. Az érintő nem kivétel, és az egyenlet valamilyen x 0 ponton való összeállításához elegendő a függvény és a derivátum értékének megismerése ezen a ponton. Tegyük fel az y \u003d f (x) függvényt, amelynek y \u003d f '(x) származéka van a szegmensen. Ezután az x 0 ∈ (a; b) bármely pontján az érintő felhívható ennek a függvénynek a grafikonjára, amelyet az egyenlet ad: y \u003d f '(x 0) · (x - x 0) + f (x 0) Itt f '(x 0) a derivált értéke az x 0 ponton, és f (x 0) maga a függvény értéke.
Az érintő egyenlet y \u003d f '(x 0) · (x - x 0) + f (x 0). Az x 0 \u003d 2 pontot kapjuk nekünk, de az f (x 0) és f '(x 0) értékeket ki kell számolni. Először keresse meg a függvény értékét. Itt minden egyszerű: f (x 0) \u003d f (2) \u003d 2 3 \u003d 8;
Ezúttal nem részletezzük részletesen az egyes műveleteket - csak a legfontosabb lépéseket mutatjuk be. Van: f (x 0) \u003d f (π / 2) \u003d 2sin (π / 2) + 5 \u003d 2 + 5 \u003d 7; Érintő egyenlet: y \u003d 0 · (x - π / 2) + 7 ⇒ y \u003d 7 Az utóbbi esetben a vonal vízszintesnek bizonyult, mert k \u003d 0 szögelõ együtthatója. Nincs semmi baj - csak egy végpontra botlottunk. |
| Olvasd el: |
|---|
Legnépszerűbb:
A legegyszerűbb trigonometrikus egyenlőtlenségek megoldása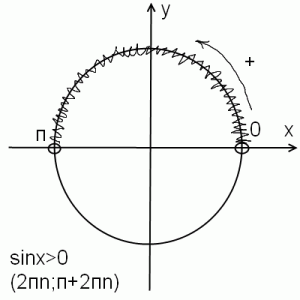
|
új
- Mi törte meg a "merev" bárót?
- A Fehér Mozgalom tagja
- Suvorov és a csapat útja hazájukhoz
- Az F (x) függvényt f (x) függvény antiderivatívájának nevezzük, ha F` (x) \u003d f (x) vagy dF (x) \u003d f (x) dx
- Fokfrekvencia-csökkentő program
- Hasonló kifejezések, redukcióik, példák
- Orosz utazók lazarev
- Nem teljes kvadratikus egyenletek megoldása
- A kvadratikus egyenletek megoldása, a gyökérképlet, példák
- Koordináta sík (6. fokozat) - Tudás hipermarketje