Rubriques du site
Le choix des éditeurs:
- Communication commerciale au téléphone
- Demande de modification de l'horaire de travail - exemple
- Quels sont les paiements dus à l'employé en cas de licenciement
- Ce pour quoi vous pouvez récompenser les employés : quel devrait être le libellé de la raison des primes
- Règles de communication avec les clients par téléphone
- Comment suivre l'étiquette de bureau
- recette de riz basmati cuisine basmati
- Escompte (prime) sur une obligation
- Procédure d'engagement d'heures supplémentaires
- Recette du riz basmati Riz basmati Dois-je rincer ?
Publicité
| Flexion transversale de la tige. Solution de problèmes typiques sur la résistance des matériaux Déterminer le diamètre requis de la section transversale de la poutre |
|
La flexion transversale est obtenue lorsqu'une force agit sur une poutre dans une direction transversale à sa longueur. Considérez deux options pour la flexion transversale: la première, la poutre repose sur deux supports et la charge est située sur la poutre dans les limites entre les supports, et la seconde, la poutre est fermement encastrée dans le mur à une extrémité, et la la charge est située à l'extrémité libre de la poutre. Tout d'abord, nous allons découvrir quel effet le lieu d'application de la force a sur la flexion. Si nous posons la planche sur deux supports et que nous nous déplaçons du support vers le milieu, la déviation de la planche augmentera continuellement à mesure que nous nous approcherons du milieu. De cette expérience, on peut conclure que plus la force est appliquée près du milieu, plus la déviation du faisceau est importante. Nous observerons le même phénomène dans l'expérience avec une poutre encastrée à une extrémité dans le mur, lorsque la charge est déplacée du mur à l'extrémité de la poutre. Dans les bâtiments et les structures, plusieurs forces peuvent agir simultanément sur une poutre et, de plus, elles peuvent se déplacer, comme par exemple des voitures sur un pont. Déterminer l'effet de ces forces sur une poutre n'est pas aussi simple qu'en traction ou en compression. La dépendance s'avère n'être pas simple, et il est difficile pour une personne sans formation technique supérieure de faire face à ce problème. Comme déjà mentionné, la force peut être appliquée n'importe où sur la poutre. Une telle force ayant un point d'application est appelée concentré. Si la force est uniformément répartie sur toute la longueur de la poutre, alors une telle force est appelée uniformément distribué. Par exemple, sur une poutre à un endroit, il y a un sac de sable pesant 100 kg, ce sera une charge concentrée (force), et si la même charge est uniformément répartie sur toute la longueur de la poutre, alors ce sera un charge uniformément répartie. Dans les deux cas, l'amplitude de la force est la même de 100 kg, mais la méthode de distribution est différente. En fonction de cela, la contrainte dans la poutre sera différente, à savoir qu'avec une charge concentrée au milieu de la poutre, la contrainte sera 2 fois plus importante qu'avec une charge uniformément répartie. Nous savons déjà que plus la charge concentrée s'approche du support, moins la déflexion de la poutre sera importante et moins il y aura de contraintes dans le matériau. Par conséquent, si la poutre a une résistance suffisante lorsqu'une charge est située au milieu, elle résistera certainement à cette charge si elle est située n'importe où dans la poutre. De plus, il est très intéressant de savoir quel type de contraintes sont obtenues dans une poutre chargée, et comment elles sont réparties. Faisons l'expérience suivante : prenez une barre et coupez-la dans la partie supérieure, puis chargez-la. Nous verrons que les deux côtés de la coupe se rapprocheront. De cette expérience, nous concluons que dans la partie supérieure de la poutre, sous l'influence de la charge, une compression se produit. Si nous faisons maintenant une coupe dans la partie inférieure de la poutre et que nous la chargeons à nouveau, nous verrons que les bords de la coupe ont divergé et que la coupe dans la partie inférieure est devenue très large. Nous en concluons que dans la partie inférieure de la poutre, sous l'influence de la charge, une tension se produit. Ainsi, par conséquent, dans la partie supérieure de la poutre ou de la poutre sous l'influence de la charge, une compression se produit et dans la partie inférieure - une tension. Mais comme cela se produit dans la même poutre au même moment, il est évident qu'il y a quelque part un endroit où la tension se transforme en compression, et vice versa. En effet, il y a une telle place dans chaque faisceau. Cette ligne, ou plutôt le plan de séparation de la compression de la traction, est appelée l'axe neutre. Dans une poutre en bois rectangulaire, il est situé approximativement au milieu de la hauteur. Puisque nous connaissons maintenant la répartition des forces dans la barre sous la charge, nous comprendrons très bien comment une poutre fortement pliée est parfois redressée. Pour ce faire, il est soutenu et une coupe est pratiquée dans la partie supérieure de la poutre avec un coin enfoncé dans celle-ci avec un levage simultané par le bas. Étant donné que dans une poutre entière sous charge, la force de traction dans la partie inférieure est égale à la force de compression dans la partie supérieure, alors lorsque des coins sont entraînés, la force de compression dans la partie supérieure de la poutre augmentera évidemment, et la poutre plier dans le sens opposé, c'est-à-dire redresser. De plus, il n'est pas difficile de vérifier que lorsque la poutre est pliée, des efforts tranchants apparaissent dans celle-ci. Pour cette expérience, nous prenons deux poutres de même longueur et plaçons une poutre au-dessus de l'autre. À l'état déchargé, leurs extrémités coïncideront, comme le montre la Fig. 4a. Si maintenant nous les chargeons, les faisceaux fléchiront et leurs extrémités seront situées comme indiqué sur la Fig. 4b. On voit que les extrémités des barres ne correspondent pas et que le bord inférieur de l'extrémité de la barre supérieure dépasse de la ligne du bord supérieur de l'extrémité de la barre inférieure. Il est évident qu'un décalage s'est produit le long du plan de contact des barres, à la suite de quoi l'extension des extrémités d'une barre au-dessus de l'autre est apparue. Si la poutre était constituée d'une seule pièce de bois, il est évident que nous ne remarquerions aucun changement aux extrémités de la poutre, mais il ne fait aucun doute que dans cette poutre, il y aurait des forces de cisaillement dans le plan neutre, et si le résistance du bois étaient insuffisantes, alors aux extrémités de la poutre on trouverait une séparation. Riz. 4. Plier une poutre mixte Après cette expérience, la disposition des poutres composites sur les chevilles devient assez claire. Sur la fig. La figure 5 montre une telle poutre, constituée de trois barres, entre lesquelles les goujons sont coupés. Bien entendu, l'extrémité d'une poutre ne peut pas bouger par rapport à l'autre puisque les touches empêchent ce mouvement. Plus le lien entre les clés et les poutres est fort, plus la poutre est rigide. Continuons l'expérience précédente. Si nous traçons des lignes avec un crayon à égale distance à travers les deux faisceaux, comme le montre la Fig. 4a, puis nous chargeons les barres, nous verrons que la ligne médiane sur les deux barres restera inchangée et que tout le reste se déplacera, comme indiqué sur la fig. 4b. Dans ce cas, la divergence des tirets sera d'autant plus grande qu'ils seront éloignés du milieu. De cette expérience, nous concluons que la plus grande force de cisaillement est aux extrémités des poutres. C'est pourquoi dans les poutres sur goujons, les goujons doivent être placés plus souvent vers les extrémités et moins souvent vers le milieu.  Riz. 5. Poutre mixte à clés taillées Riz. 5. Poutre mixte à clés taillées Ainsi, toutes les expériences réalisées nous convainquent que diverses contraintes apparaissent dans une poutre chargée. Apprenons à nouveau de l'expérience. Tout le monde sait que si vous posez une planche à plat et que vous la chargez, elle s'affaissera sensiblement, et si vous posez la même planche sur le bord et la chargez avec la même charge, la déflexion sera à peine perceptible. Cette expérience nous convainc que la quantité de flexion dépend principalement de la hauteur de la poutre et non de sa largeur. Si vous prenez deux poutres carrées et que vous les ralliez avec des goujons et des boulons, de sorte que vous obteniez une poutre de deux carrés de haut, alors une telle poutre peut supporter une charge deux fois plus importante que ces deux poutres posées côte à côte. Avec trois poutres, la charge peut être 4,5 fois plus importante, etc. D'après ces expériences, il est clair pour nous qu'il est beaucoup plus rentable d'augmenter la hauteur du faisceau que sa largeur, mais, bien sûr, dans une certaine limite, car avec un faisceau très haut et fin, il peut se plier sur le côté. Étant donné que les poutres sont taillées ou sciées à partir de grumes, la question se pose de savoir quel rapport doit être entre la hauteur et la largeur de la poutre afin d'obtenir la poutre de la plus grande résistance. La mécanique des structures donne une réponse exacte à cette question, à savoir qu'il devrait y avoir 7 mesures en hauteur et seulement 5 en largeur pour exactement les mêmes mesures.En pratique, cela se fait comme suit. À la fin d'une bûche ronde (Fig. 6), une ligne est tracée à travers le centre et divisée en trois parties égales. Ensuite, à partir de ces points le long du carré, des lignes sont tracées dans des directions opposées au bord de la crosse. Enfin, ces points extrêmes sont reliés aux extrémités de la ligne tracée par le centre de la crosse, et nous obtiendrons un rectangle dans lequel le côté long aura 7 mesures et le côté court aura les mêmes 5. Ces lignes sont utilisés pour scier ou tailler la grume et obtenir la section de poutre rectangulaire la plus durable, qui ne peut être fabriquée qu'à partir d'une grume donnée.  Riz. 6. La poutre la plus solide qui puisse être taillée dans une bûche Riz. 6. La poutre la plus solide qui puisse être taillée dans une bûche Il est intéressant de noter qu'une bûche ronde est moins résistante en termes de flexion que la même bûche avec des dalles légèrement taillées sur le dessus et le dessous. Sur la base de ce qui précède, nous pouvons conclure que la détermination exacte des dimensions des poutres dépend de nombreuses circonstances : du nombre et de l'emplacement des charges, du type de charge, de la méthode de sa répartition (solide ou concentrée), de la forme de la poutre, sa longueur, etc. La prise en compte de toutes ces circonstances est assez compliquée et inaccessible à un menuisier-praticien. Lors de la détermination des dimensions des poutres, il est nécessaire, en plus de la résistance, de tenir compte également de la déflexion des poutres. Parfois, sur le chantier, les charpentiers expriment leur perplexité quant à la raison pour laquelle une poutre aussi épaisse est placée, il serait possible d'en prendre une plus fine. Tout à fait, et une poutre plus fine résistera à la charge qui y sera placée, mais lorsqu'ils marcheront ou danseront par la suite sur le sol sur des poutres fines, un tel sol se pliera comme une balançoire. Pour éviter des fluctuations de plancher très désagréables, les poutres sont posées plus épaisses que ne l'exigent les conditions de résistance. Dans les bâtiments résidentiels, la déflexion des poutres n'est autorisée qu'à 1/250 de la portée. Si, par exemple, la portée est de 9 m, soit 900 cm, la plus grande déviation ne doit pas dépasser 900 : 250, soit 3,6 cm. En conclusion, une règle empirique pour déterminer la hauteur des poutres dans les bâtiments résidentiels doit être mentionnée, à savoir : la hauteur de la poutre doit être d'au moins 1/24 de la longueur de la poutre. Par exemple, si la longueur de la poutre est de 8 m (800 cm), la hauteur doit être de 800 : 24 = 33 cm. Pour des raisons pratiques, en plus de tout ce qui précède, vous devez vous familiariser avec les tableaux ci-joints, qui permettront, sans aucune difficulté, de déterminer facilement et rapidement la taille de faisceau souhaitée pour le cas d'une charge uniformément répartie. Ces tableaux indiquent les charges admissibles sur les poutres rectangulaires et circulaires, pour différentes tailles de poutres et pour différentes portées. Exemple 1. Dans une pièce d'une portée de 8 m, il y a une charge de 2,5 t (2500 kg). Il est nécessaire de sélectionner des poutres pour cette charge.Dans le tableau des poutres rectangulaires, nous considérons une colonne d'une portée de 8 m.Une poutre d'une section de 31 × 22 cm ou deux poutres de 26 × 18,5, ou trois poutres de 24,5 × 17,5 cm peut supporter une charge de 2500 kg etc. Les poutres doivent être réparties avec l'espacement approprié, en tenant compte du fait que les poutres extérieures supportent la moitié de la charge des poutres situées au milieu.Pour une charge concentrée au milieu de la portée, sa valeur doit être la moitié de celle indiquée dans le tableau. Exemple 2 Pour une poutre rectangulaire 7 à 5 à partir d'une bûche de 32 centimètres avec une portée de 6 m, une charge uniformément répartie de 2632 kg peut être autorisée (voir tableau). Si la charge est concentrée au milieu de la poutre, seule la moitié de la charge peut être autorisée, à savoir 2632 : 2 = 1316 kg. Exemple 3 Quelle taille de poutre issue d'un rondin, taillé ou scié en deux bords, peut supporter une charge concentrée au milieu de 1,6 tonne (1600 kg), avec une portée de 8 m ?Dans la tâche, une force concentrée est donnée, nous savons que cette poutre doit supporter deux fois la charge uniformément répartie, soit 1600 × 2 = 3200 kg. Nous recherchons dans le tableau la colonne du chariot pour une portée de 8 m, le chiffre le plus proche de 3200 dans le tableau 3411, ce chiffre correspondant à une bûche d'un diamètre de 34 cm. Si la poutre est fermement encastrée avec une extrémité dans le mur, elle peut supporter la charge concentrée à son extrémité libre, 8 fois moins que la même poutre reposant sur deux supports et portant une charge uniformément répartie. Exemple 4 Quel diamètre de rondin, taillé ou scié sur quatre bords, solidement encastré à une extrémité dans le mur et ayant une extrémité libre de 3 m, peut supporter une charge concentrée de 800 kg attachée à son extrémité libre ? Si cette poutre reposait sur deux supports, il pourrait alors supporter une charge 8 fois plus importante, soit 800 × 8 = 6400 kg. Nous cherchons dans le tableau la colonne à barres de flache pour une portée de 3 m et trouvons les deux chiffres suivants 5644 kg et 6948 kg. Ces chiffres correspondent à des bûches de 30 et 32 cm, vous pouvez prendre une bûche de 31 cm.Si sur une poutre encastrée avec une extrémité dans le mur, la charge est répartie uniformément, une telle poutre peut supporter une charge 4 fois inférieure à la même poutre reposant sur deux supports. Exemple 5 Quelle charge une poutre de section rectangulaire, encastrée à une extrémité dans un mur, avec une extrémité libre de 4 m de long, chargée d'une charge uniformément répartie d'un poids total de 600 kg, peut-elle supporter ? Si cette poutre repose sur deux supports, alors il pourrait supporter une charge 4 fois plus importante, soit 600 × 4 \u003d 2400 kg. Nous recherchons dans le tableau une poutre de 7 à 5 poteaux pour une portée de 4 m.Le chiffre le plus proche est 2746, ce qui correspond à une bûche de 28 cm, soit une poutre de 23 × 16 cm.Lors du calcul des poutres, la question suivante peut se poser : quelle pression les supports (murs ou colonnes) subissent-ils d'une poutre reposant sur eux avec une charge ? Si la charge est répartie uniformément sur toute la poutre ou est concentrée au milieu, les deux supports supportent la même charge. Si la charge est située plus près d'une jambe, alors cette jambe porte plus de charge que l'autre. Pour savoir lequel, vous devez multiplier la valeur de la charge par la distance à l'autre support et diviser par la portée. Exemple 6 Sur une poutre de 4 m de long, il y a une charge de 100 kg, à une distance de 1 m du support gauche et donc à une distance de 3 m du droit. Il est nécessaire de trouver la charge sur le support gauche. Nous multiplions 100 par 3 et divisons le nombre résultant par 4, nous obtenons 75. Par conséquent, le support gauche subit une pression de 75, et le reste de la charge droite, c'est-à-dire , 100-75 \u003d 25 kg.S'il y a plusieurs charges sur la poutre, le calcul doit être effectué pour chaque charge séparément, puis les charges résultantes sur un support doivent être ajoutées. pliez appelée déformation, dans laquelle l'axe de la tige et toutes ses fibres, c'est-à-dire les lignes longitudinales parallèles à l'axe de la tige, sont pliés sous l'action de forces extérieures. Le cas le plus simple de flexion est obtenu lorsque les efforts extérieurs sont situés dans un plan passant par l'axe central de la tige et ne font pas saillie sur cet axe. Un tel cas de flexion est appelé flexion transversale. Distinguer courbe plate et oblique. virage à plat- un tel cas où l'axe plié de la tige est situé dans le même plan dans lequel agissent les forces externes. Coude oblique (complexe)- un tel cas de flexion, lorsque l'axe plié de la tige ne se situe pas dans le plan d'action des forces extérieures. Une barre de flexion est communément appelée faisceau. Avec une flexion transversale à plat des poutres dans une section avec un système de coordonnées y0x, deux forces internes peuvent se produire - une force transversale Q y et un moment de flexion M x; dans ce qui suit, nous introduisons la notation Q Et M S'il n'y a pas d'effort transversal dans la section ou la section de la poutre (Q = 0) et que le moment de flexion n'est pas égal à zéro ou que M est constant, alors une telle courbure est communément appelée nettoyer. Force de cisaillement dans n'importe quelle section de la poutre est numériquement égal à la somme algébrique des projections sur l'axe de toutes les forces (y compris les réactions d'appui) situées d'un côté (n'importe lequel) de la section. Moment de flexion dans la section de poutre est numériquement égal à la somme algébrique des moments de toutes les forces (y compris les réactions d'appui) situées sur un côté (n'importe lequel) de la section dessinée par rapport au centre de gravité de cette section, plus précisément, par rapport à l'axe passant perpendiculairement au plan du dessin par le centre de gravité de la section dessinée. Q-force présente résultant répartis sur la section transversale de l'intérieur les contraintes de cisaillement, mais moment M– somme d'instants autour de l'axe central de la section X interne contraintes normales. Il existe une relation différentielle entre les efforts internes qui sert à la construction et à la vérification des diagrammes Q et M.
Étant donné que certaines des fibres du faisceau sont étirées et que d'autres sont comprimées, et que la transition de la tension à la compression se produit en douceur, sans sauts, dans la partie médiane du faisceau, il y a une couche dont les fibres ne font que se plier, mais ne subissent pas non plus traction ou compression. Une telle couche est appelée couche neutre. La ligne le long de laquelle la couche neutre coupe la section transversale du faisceau est appelée ligne neutre e ou axe neutre sections. Des lignes neutres sont enfilées sur l'axe du faisceau. Les lignes tracées sur la surface latérale de la poutre perpendiculairement à l'axe restent plates lorsqu'elles sont pliées. Ces données expérimentales permettent de fonder les conclusions des formules sur l'hypothèse des sections planes. Selon cette hypothèse, les sections de la poutre sont planes et perpendiculaires à son axe avant pliage, restent planes et deviennent perpendiculaires à l'axe plié de la poutre lorsqu'elle est pliée. La section transversale de la poutre est déformée lors de la flexion. En raison de la déformation transversale, les dimensions de la section transversale dans la zone comprimée de la poutre augmentent et dans la zone de tension, elles sont comprimées. Hypothèses pour dériver des formules. Contraintes normales 1) L'hypothèse des sections plates est vérifiée. 2) Les fibres longitudinales ne s'appuient pas les unes sur les autres et, par conséquent, sous l'action de contraintes normales, des tensions linéaires ou des compressions fonctionnent. 3) Les déformations des fibres ne dépendent pas de leur position le long de la largeur de la section. Par conséquent, les contraintes normales, évoluant sur la hauteur de la section, restent les mêmes sur toute la largeur. 4) La poutre a au moins un plan de symétrie et toutes les forces externes se trouvent dans ce plan. 5) Le matériau de la poutre obéit à la loi de Hooke, et le module d'élasticité en traction et en compression est le même. 6) Les rapports entre les dimensions de la poutre sont tels qu'elle fonctionne dans des conditions de flexion à plat sans déformation ni torsion. Avec une flexion pure d'une poutre sur les plates-formes dans sa section, seule contraintes normales, déterminé par la formule : où y est la coordonnée d'un point arbitraire de la section, mesurée à partir de la ligne neutre - l'axe central principal x. Les contraintes normales de flexion le long de la hauteur de la section sont réparties sur loi linéaire. Sur les fibres extrêmes, les contraintes normales atteignent leur valeur maximale, et au centre de gravité, les sections efficaces sont égales à zéro. La nature des diagrammes de contraintes normales pour les sections symétriques par rapport à la ligne neutre
La nature des diagrammes de contraintes normales pour les sections qui n'ont pas de symétrie autour de la ligne neutre
Les points dangereux sont les plus éloignés de la ligne neutre. Choisissons une section
Pour tout point de la section, appelons-le un point POUR, la condition de résistance de la poutre pour les contraintes normales a la forme :
ce module de section axiale autour de l'axe neutre. Sa dimension est de cm 3, m 3. Le moment résistant caractérise l'influence de la forme et des dimensions de la section sur l'amplitude des contraintes. Condition de résistance pour les contraintes normales :
Si le matériau résiste inégalement à l'étirement et à la compression, alors deux conditions de résistance doivent être utilisées : pour une zone d'étirement avec une contrainte de traction admissible ; pour la zone de compression avec contrainte de compression admissible. Avec la flexion transversale, les poutres sur les plates-formes dans sa section agissent comme Ordinaire, et tangentes Tension. Classification des types de flexion de la tige pliez appelé ce type de déformation, dans lequel des moments de flexion se produisent dans les sections transversales de la tige. Une tige travaillant en flexion s'appelle faisceau. Si les moments de flexion sont les seuls facteurs de force internes dans les sections transversales, alors la tige subit virage propre. Si des moments de flexion se produisent avec des forces transversales, alors un tel pli est appelé transversal. Les poutres, les essieux, les arbres et autres détails structurels fonctionnent en flexion. Introduisons quelques concepts. Le plan passant par l'un des axes centraux principaux de la section et l'axe géométrique de la tige est appelé avion principal. Le plan dans lequel agissent les charges externes, provoquant la flexion de la poutre, est appelé plan de force. La ligne d'intersection du plan de force avec le plan de la section transversale de la tige est appelée ligne électrique. Selon la position relative des plans de puissance et principal du faisceau, on distingue un coude droit ou oblique. Si le plan de force coïncide avec l'un des plans principaux, alors la tige subit virage droit(Fig. 5.1, mais), s'il ne correspond pas - oblique(Fig. 5.1, b). Riz. 5.1. Courbure de tige : mais- droit; b- oblique D'un point de vue géométrique, la flexion de la tige s'accompagne d'une modification de la courbure de l'axe de la tige. L'axe initialement rectiligne de la tige devient curviligne lorsqu'elle est pliée. En flexion directe, l'axe de flexion de la tige se situe dans le plan d'effort, en flexion oblique, dans un plan autre que le plan d'effort. En observant la flexion d'une tige de caoutchouc, on peut remarquer qu'une partie de ses fibres longitudinales est étirée, tandis que l'autre partie est comprimée. Évidemment, entre les fibres étirées et comprimées de la tige, il y a une couche de fibres qui ne subit ni tension ni compression, la soi-disant couche neutre. La ligne d'intersection de la couche neutre de la tige avec le plan de sa section transversale est appelée ligne de section neutre. En règle générale, les charges agissant sur la poutre peuvent être attribuées à l'un des trois types suivants : forces concentrées R, instants concentrés M intensité des charges réparties c(Fig. 5.2). La partie I de la poutre, située entre les appuis, est appelée envergure, partie II de la poutre, située d'un côté de l'appui, - console. Lors de la construction diagrammes des moments fléchissantsM à constructeurs accepté : ordonnées exprimant dans une certaine échelle positif valeurs des moments fléchissants, mises à part étiré fibres, c'est-à-dire - vers le bas, mais négatif - en hausse de l'axe du faisceau. Par conséquent, ils disent que les constructeurs construisent des diagrammes sur des fibres étirées. Mécanique les valeurs positives de la force de cisaillement et du moment de flexion sont tracées en haut. Les mécaniciens construisent des diagrammes sur comprimé fibres. Contraintes principales lors de la flexion. Tensions équivalentes. Dans le cas général de flexion directe dans les sections transversales de la poutre, Ordinaire Et tangentes Ainsi, en cas de flexion, état de contrainte plane. Considérons un schéma où la poutre est chargée avec une force P
La plus grande normale les contraintes surviennent dans extrême, les points les plus éloignés de la ligne neutre, et les contraintes de cisaillement y sont absentes. Donc pour extrême fibres les contraintes principales non nulles sont des contraintes normales en coupe transversale. Au niveau de la ligne neutre dans la section transversale de la poutre apparaissent les plus grandes contraintes de cisaillement, mais les contraintes normales sont nulles. signifie dans les fibres neutre couche les contraintes principales sont déterminées par les valeurs des contraintes de cisaillement. Dans ce modèle de conception, les fibres supérieures de la poutre seront étirées et les fibres inférieures seront comprimées. Pour déterminer les contraintes principales, on utilise l'expression bien connue : Plein analyse de l'état de contrainte présent sur la figure.
Analyse de l'état de contrainte en flexion La plus grande contrainte principale σ 1 est situé sur supérieur fibres extrêmes et est égal à zéro sur les fibres extrêmes inférieures. Contrainte principale σ 3 Il a la plus grande valeur absolue sur les fibres inférieures. Trajectoire de contrainte principale dépend de type de charge Et façon de fixer le faisceau.
Lors de la résolution de problèmes, il suffit séparément Vérifier Ordinaire Et contraintes de cisaillement distinctes. Cependant, parfois le plus stressant s'avérer intermédiaire fibres qui ont à la fois des contraintes normales et de cisaillement. Cela se produit dans les sections où simultanément le moment de flexion et la force transversale atteignent des valeurs élevées- cela peut être dans la terminaison d'une poutre en porte-à-faux, sur le support d'une poutre avec un porte-à-faux, dans des sections sous une force concentrée ou dans des sections avec une largeur fortement variable. Par exemple, dans une section en I, le plus dangereux jonction du mur à l'étagère- il y a contraintes significatives et normales et de cisaillement. Le matériau est dans un état de contrainte plane et nécessite test de tension équivalente. Conditions de résistance des poutres en matériaux ductiles au la troisième(théories des plus grandes contraintes tangentielles) En règle générale, dans les poutres laminées, les contraintes équivalentes ne dépassent pas les contraintes normales dans les fibres les plus externes et aucune vérification particulière n'est requise. Autre chose - poutres métalliques composites, lequel paroi plus mince que celle des profilés laminés à la même hauteur. Les poutres composites soudées en tôles d'acier sont plus couramment utilisées. Calcul de ces poutres pour la résistance: a) sélection de la section - hauteur, épaisseur, largeur et épaisseur des membrures de poutres; b) essai de résistance aux contraintes normales et de cisaillement ; c) vérification de la résistance par contraintes équivalentes. Détermination des contraintes de cisaillement dans une section en I. Considérez la rubrique Je rayonne. S x \u003d 96,9 cm 3; Yx = 2030 cm 4 ; Q=200 kN
Pour déterminer la contrainte de cisaillement, on utilise formule Calculer maximum contrainte de cisaillement : Calculons le moment statique pour étagère supérieure: Calculons maintenant les contraintes de cisaillement: Nous construisons diagramme de contrainte de cisaillement :
Considérez une section d'un profil standard dans le formulaire Je rayonne et définir les contraintes de cisaillement agissant parallèlement à la force transversale :
Calculer moments statiques chiffres simples : Cette valeur peut aussi être calculée Par ailleurs, en utilisant le fait que pour une poutre en I et une section en auge, le moment statique de la moitié de la section est donné en même temps. Pour ce faire, il faut soustraire de la valeur connue du moment statique la valeur du moment statique à la ligne A 1 B 1 : Les contraintes de cisaillement à la jonction de la semelle au mur changent spasmodiquement, car tranchant l'épaisseur de paroi change de t st avant de b. Les tracés des contraintes de cisaillement dans les parois des sections creuses, rectangulaires creuses et autres ont la même forme que dans le cas d'une section en I. La formule inclut le moment statique de la partie ombrée de la section par rapport à l'axe X, et le dénominateur est la largeur de la section (nette) dans la couche où la contrainte de cisaillement est déterminée.
Déterminons les contraintes de cisaillement pour une section circulaire.
Comme les contraintes tangentielles au contour de la section doivent être dirigées tangente au contour, puis aux pointes MAIS Et DANS aux extrémités de toute corde parallèle au diamètre UN B, les contraintes de cisaillement sont dirigées perpendiculaire aux rayons OA Et VO. En conséquence, directions contraintes de cisaillement aux points MAIS, CV converger à un moment donné H sur l'axe Y. Moment statique de la partie coupée : Autrement dit, les contraintes de cisaillement changent en fonction de parabolique loi et sera maximale au niveau de la ligne neutre lorsque y 0 =0
Formule de détermination des contraintes de cisaillement (formule) Considérez une section rectangulaire
A distance à 0 tirer de l'axe central article 1-1 et déterminer les contraintes de cisaillement. Moment statique région partie coupée : Il faut garder à l'esprit que fondamentalement indifférent, prendre le moment statique de la zone ombragé ou repos la Coupe transversale. Les deux moments statiques de signe égal et opposé, afin qu'ils somme, qui représente moment statique de la zone de la section entière par rapport à la ligne neutre, à savoir l'axe central x, sera égal à zéro. Moment d'inertie d'une section rectangulaire :
Puis les contraintes de cisaillement selon la formule
La variable y 0 est incluse dans la formule pendant seconde degrés, c'est-à-dire les contraintes de cisaillement dans une section rectangulaire varient avec la loi d'une parabole carrée. Contrainte de cisaillement atteinte maximum au niveau de la ligne neutre, c'est-à-dire lorsque y 0 =0 :
Condition de résistance pour les contraintes de cisaillement ressemble à:
Cette condition de résistance permet de produire Trois type de calcul (trois types de problèmes en analyse de résistance) : 1. Calcul de vérification ou essai de résistance pour les contraintes de cisaillement : 2. Sélection de la largeur de section (pour section rectangulaire) : 3. Détermination de l'effort transversal admissible (pour une section rectangulaire) :
Pour déterminer tangentes contraintes, considérons une poutre chargée de forces.
La tâche de déterminer les contraintes est toujours statiquement indéterminé et nécessite une implication géométrique Et physiqueéquations. Cependant, on peut prendre hypothèses sur la nature de la distribution des contraintes que la tâche deviendra déterminé statiquement. Deux sections infiniment proches 1-1 et 2-2 sélection élément dz, dessinez-le à grande échelle, puis dessinez une coupe longitudinale 3-3. Dans les sections 1–1 et 2–2, contraintes normales σ 1 , σ 2, qui sont déterminés par les formules bien connues : où M - moment de flexion en coupe dM - incrément moment de flexion sur la longueur dz Force de cisaillement dans les sections 1–1 et 2–2 est dirigée le long de l'axe central principal Y et, évidemment, représente la somme des composantes verticales des contraintes de cisaillement internes réparties sur la section transversale. Dans la résistance des matériaux, il est généralement pris l'hypothèse de leur répartition uniforme sur la largeur de la section. Pour déterminer l'amplitude des contraintes de cisaillement en tout point de la section, situé à une distance à 0à partir de l'axe X neutre, tracez un plan parallèle à la couche neutre (3-3) passant par ce point et retirez l'élément de coupure. Nous déterminerons la tension agissant sur le site ABSD. Projetons toutes les forces sur l'axe Z
La résultante des efforts longitudinaux internes le long du côté droit sera égale à : où A 0 est l'aire de la face de façade, S x 0 est le moment statique de la partie coupée par rapport à l'axe X. De même sur le côté gauche :
Faisons comme si contraintes de cisaillement τ répartis sur la largeur de la section transversale de la poutre b uniformément. Cette hypothèse est d'autant plus probable que la largeur est petite par rapport à la hauteur de la section. Puis résultante des efforts tangentiels dT est égal à la valeur de contrainte multipliée par la surface de la face : Composer maintenant équation d'équilibre Σz=0 : ou d'où
Souvenons-nous dépendances différentielles, selon lequel
Cette formule s'appelle formules. Cette formule a été obtenue en 1855. Ici S x 0 - moment statique d'une partie de la section transversale, situé d'un côté de la couche dans laquelle les contraintes de cisaillement sont déterminées, I x - moment d'inertie toute la section transversale b - largeur de section où la contrainte de cisaillement est déterminée, Q - force transversale dans la section.
- moment maximal (modulo) du diagramme des moments de flexion ; - contrainte normale maximale. Si le calcul est basé sur méthode de l'état limite, puis dans le calcul au lieu de la contrainte admissible est introduite résistance de calcul du matériau R. Types de calculs de résistance à la flexion 1. Vérification calcul ou vérification de la résistance à la contrainte normale 2. Projet calcul ou sélection de rubriques 3. Définition permis charges (définition capacité de levage et ou opérationnel transporteur capacités) Lors de la dérivation d'une formule de calcul des contraintes normales, considérez un tel cas de flexion, lorsque les efforts internes dans les sections de la poutre ne sont réduits qu'à moment de flexion, mais la force transversale est nulle. Ce cas de flexion est appelé flexion pure. Considérons la section médiane d'une poutre en flexion pure.
Étant donné que certaines fibres de la poutre sont étirées et d'autres comprimées, la transition de la tension à la compression se produit en douceur, sans sauts, dans milieu une partie du faisceau est une couche dont les fibres ne font que plier, mais ne subissent ni tension ni compression. Une telle couche est appelée neutre couche. La ligne le long de laquelle la couche neutre coupe la section transversale du faisceau est appelée ligne neutre ou axe neutre sections. Des lignes neutres sont enfilées sur l'axe du faisceau. ligne neutre est la ligne dans laquelle les contraintes normales sont nulles. Les lignes tracées sur la surface latérale de la poutre perpendiculairement à l'axe restent appartement lors de la flexion. Ces données expérimentales permettent de fonder les dérivations des formules hypothèse des sections plates (hypothèse). Selon cette hypothèse, les sections de la poutre sont planes et perpendiculaires à son axe avant pliage, restent planes et deviennent perpendiculaires à l'axe plié de la poutre lorsqu'elle est pliée. Hypothèses pour la dérivation des formules de contraintes normales : 1) L'hypothèse des sections plates est vérifiée. 2) Les fibres longitudinales ne s'appuient pas les unes sur les autres (hypothèse de non-pression) et, par conséquent, chacune des fibres est dans un état de tension ou de compression uniaxiale. 3) Les déformations des fibres ne dépendent pas de leur position le long de la largeur de la section. Par conséquent, les contraintes normales, évoluant sur la hauteur de la section, restent les mêmes sur toute la largeur. 4) La poutre a au moins un plan de symétrie et toutes les forces externes se trouvent dans ce plan. 5) Le matériau de la poutre obéit à la loi de Hooke, et le module d'élasticité en traction et en compression est le même. 6) Les rapports entre les dimensions de la poutre sont tels qu'elle fonctionne dans des conditions de flexion à plat sans déformation ni torsion. Considérons une poutre de section arbitraire, mais ayant un axe de symétrie. Formule (1) exprime statique côté du problème de la flexion d'une barre droite, mais le long de celle-ci selon un moment de flexion connu il est impossible de déterminer les contraintes normales tant que la loi de leur distribution n'est pas établie. Sélectionnez les poutres dans la section centrale et considérez section de longueur dz, sujet à la flexion. Zoomons dessus.
Sections délimitant la section dz, parallèles entre eux avant déformation, et après application de la charge tourner autour de leurs lignes neutres en biais . La longueur du segment des fibres de la couche neutre ne changera pas. et sera égal à : On réduit par et on réduit comme termes, alors on obtient : (2) Cette formule exprime géométrique côté du problème de flexion pure : les déformations des fibres sont directement proportionnelles à leurs distances à la couche neutre. Passons maintenant à stresse, c'est à dire. nous allons le prendre en compte physique côté de la tâche. selon hypothèse de non-pression les fibres sont utilisées en traction-compression axiale : alors, compte tenu de la formule (2)
on a Puis Remplacez l'expression résultante courbure (4) dans une expression (3)
et obtenir formule de calcul des contraintes normales en tout point de la section : Ce. maximum des contraintes surviennent aux points les plus éloignés de la ligne neutre. Attitude Puis tensions maximales : Condition de résistance à la flexion : Pendant la flexion transversale non seulement des contraintes normales, mais aussi des contraintes de cisaillement, car disponible force de cisaillement. Les contraintes de cisaillement compliquer l'image de la déformation, ils conduisent à courbure sections transversales de la poutre, à la suite de quoi l'hypothèse des sections plates est violée. Cependant, des études montrent que les distorsions introduites par les contraintes de cisaillement légèrement affectent les contraintes normales calculées par la formule (5) . Ainsi, lors de la détermination des contraintes normales en cas de flexion transversale la théorie de la flexion pure est tout à fait applicable. Ligne neutre. Question sur la position de la ligne neutre. En flexion, il n'y a pas d'effort longitudinal, on peut donc écrire La condition (absence du moment des efforts internes par rapport à la ligne de champ) donnera En réglant position de la ligne neutre, facile à construire diagramme des contraintes normales par hauteur de section. Son linéaire le caractère est déterminé équation du premier degré.
La nature du diagramme σ pour les sections symétriques par rapport à la ligne neutre, M<0 Lors de la flexion, les tiges sont soumises à un effort transversal ou un moment de flexion. La flexion est dite pure si seul le moment de flexion agit, et transversale si la charge est perpendiculaire à l'axe de la tige. Une poutre (tige) travaillant en flexion est généralement appelée poutre. Les poutres sont les éléments les plus courants des structures et des machines qui prennent les charges d'autres éléments structurels et les transfèrent aux parties qui supportent la poutre (le plus souvent des supports). Dans les structures de construction et les structures de construction de machines, on trouve le plus souvent les cas suivants de poutres de fixation: porte-à-faux - avec une extrémité pincée (avec un joint rigide), double support - avec un support articulé-fixe et un support articulé-mobile et poutres multisupports. Si les réactions de support peuvent être trouvées à partir des seules équations statiques, alors les poutres sont dites statiquement déterminées. Si le nombre de réactions de support inconnues est supérieur au nombre d'équations de la statique, alors ces poutres sont dites statiquement indéterminées. Pour déterminer les réactions dans de telles poutres, il est nécessaire de composer des équations supplémentaires - des équations de déplacement. En flexion transversale à plat, toutes les charges externes sont perpendiculaires à l'axe de la poutre. La détermination des facteurs de force internes agissant dans les sections transversales de la poutre doit commencer par la détermination des réactions d'appui. Après cela, nous utilisons la méthode des sections, coupons mentalement la poutre en deux parties et considérons l'équilibre d'une partie. Nous remplaçons l'interaction des parties de la poutre par des facteurs internes : le moment fléchissant et l'effort transversal. La force transversale dans la section est égale à la somme algébrique des projections de toutes les forces et le moment de flexion est égal à la somme algébrique des moments de toutes les forces situées d'un côté de la section. Les signes des forces et moments agissants doivent être déterminés conformément aux règles acceptées. Il est nécessaire d'apprendre à déterminer correctement la force résultante et le moment de flexion à partir d'une charge uniformément répartie sur la longueur de la poutre. Il convient de garder à l'esprit que lors de la détermination des contraintes survenant lors de la flexion, les hypothèses suivantes sont faites: les sections plates avant la flexion restent plates après la flexion (hypothèse des sections plates); les fibres adjacentes longitudinales ne se pressent pas les unes sur les autres ; la relation entre contraintes et déformations est linéaire. Lors de l'étude de la flexion, il convient de prêter attention à la répartition inégale des contraintes normales dans la section transversale de la poutre. Les contraintes normales varient le long de la hauteur de la section transversale proportionnellement à la distance à l'axe neutre. Vous devriez être en mesure de déterminer les contraintes de flexion, qui dépendent de l'amplitude du moment de flexion effectif M je et module de section en flexion W O(module de section axiale). Condition de résistance à la flexion : σ = М È / W О £ [σ]. Signification W O dépend de la taille, de la forme et de l'emplacement de la section transversale par rapport à l'axe. La présence d'un effort transversal agissant sur une poutre est associée à l'apparition de contraintes de cisaillement dans les sections transversales, et, selon la loi d'appariement des contraintes de cisaillement, dans les sections longitudinales. Les contraintes de cisaillement sont déterminées par la formule de D. I. Zhuravsky. L'effort transversal déplace la section considérée par rapport à la section adjacente. Le moment de flexion, qui consiste en des forces normales élémentaires apparaissant dans la section transversale de la poutre, fait tourner la section par rapport à la section adjacente, ce qui provoque la courbure de l'axe de la poutre, c'est-à-dire sa flexion. Lorsqu'une poutre subit une flexion pure, un moment de flexion d'amplitude constante agit sur toute la longueur de la poutre ou dans sa section distincte dans chaque section, et la force transversale dans n'importe quelle section de cette section est nulle. Dans ce cas, seules les contraintes normales apparaissent dans les sections transversales de la poutre. Afin de mieux comprendre les phénomènes physiques de flexion et la méthodologie de résolution des problèmes de calcul de résistance et de rigidité, il est nécessaire de bien maîtriser les caractéristiques géométriques des sections planes, à savoir : les moments statiques des sections, les moments d'inertie des sections de la forme la plus simple et les sections complexes, détermination du centre de gravité des figures, moments d'inertie principaux des sections et axes d'inertie principaux, moment d'inertie centrifuge, changement des moments d'inertie lorsque les axes tournent, théorèmes sur le transfert des axes. Lors de l'étude de cette section, vous devez apprendre à construire correctement des diagrammes de moments de flexion et d'efforts tranchants, à déterminer les sections dangereuses et les contraintes qui y agissent. En plus de déterminer les contraintes, il faut apprendre à déterminer les déplacements (déviations des poutres) lors de la flexion. Pour cela, l'équation différentielle de l'axe plié de la poutre (ligne élastique), écrite sous forme générale, est utilisée. Pour déterminer les flèches, l'équation de la droite élastique est intégrée. Dans ce cas, il est nécessaire de déterminer correctement les constantes d'intégration À PARTIR DE Et réà partir des conditions d'appui de la poutre (conditions aux limites). Connaître les quantités À PARTIR DE Et ré, vous pouvez déterminer l'angle de rotation et de déviation de n'importe quelle section de la poutre. L'étude de la résistance complexe commence généralement par une courbure oblique. Le phénomène de flexion oblique est particulièrement dangereux pour les sections dont les moments d'inertie principaux sont sensiblement différents ; les poutres avec une telle section fonctionnent bien pour la flexion dans le plan de plus grande rigidité, mais même à de petits angles d'inclinaison du plan des forces externes par rapport au plan de plus grande rigidité, des contraintes et des déformations supplémentaires importantes apparaissent dans les poutres. Pour une poutre de section circulaire, la flexion oblique est impossible, car tous les axes centraux d'une telle section sont les principaux et la couche neutre sera toujours perpendiculaire au plan des forces extérieures. La flexion oblique est également impossible pour une poutre carrée. Lors de la détermination des contraintes en cas de traction ou de compression excentrée, il est nécessaire de connaître la position des axes centraux principaux de la section ; c'est à partir de ces axes que sont mesurées les distances du point d'application de la force et du point de détermination des contraintes. La force de compression excentrique appliquée peut provoquer des contraintes de traction dans la section transversale de la tige. A cet égard, la compression excentrique est particulièrement dangereuse pour les tiges en matériaux fragiles, qui résistent faiblement aux efforts de traction. En conclusion, il convient d'étudier le cas d'une résistance complexe, lorsque le corps subit plusieurs déformations simultanément : par exemple, flexion avec torsion, traction-compression avec flexion, etc. Il faut garder à l'esprit que les moments de flexion agissant dans des plans différents peuvent s'additionner en tant que vecteurs. |
Populaire:
Le volume du cône, son calcul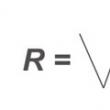
|
Nouvelle
- Pyramide de verres: une pyramide de verres de champagne de vos propres mains Comment faire une pyramide de champagne
- Faire des sachets de thé Comment faire des sachets de thé
- Comment s'habiller avec style pour l'école: recommandations générales Maintenant, voyez ce que cette petite garde-robe peut faire
- Comment s'habiller à la mode pour l'école : un look stylé Maintenant, regardez ce que cette petite armoire peut faire
- Propriétés utiles et nocives de l'ail pendant la grossesse Vous pouvez manger de l'ail pour les femmes enceintes
- Candidose en milieu de gestation Traitement du muguet chez la femme enceinte au deuxième trimestre
- Comment gérer la somnolence pendant la grossesse si vous êtes au travail
- La signification du nom Anna Que signifie le nom Anna pour une fille
- Ce qu'un enfant doit savoir faire à 1 an et demi Ce qu'un bébé doit savoir faire à 1 an
- Comment accoucher après FIV : césarienne ou accouchement naturel Après FIV, une césarienne est obligatoire





 , où i.d. - ce axe neutre
, où i.d. - ce axe neutre
 La contrainte normale est égale au rapport du moment de flexion maximal sur le module de section axiale par rapport à l'axe neutre.
La contrainte normale est égale au rapport du moment de flexion maximal sur le module de section axiale par rapport à l'axe neutre.




















 ,
où A est l'aire de la section entière.
,
où A est l'aire de la section entière.


 Lorsqu'il est chargé, le faisceau se plie de sorte qu'il les fibres inférieures s'allongent et les fibres supérieures se raccourcissent.
Lorsqu'il est chargé, le faisceau se plie de sorte qu'il les fibres inférieures s'allongent et les fibres supérieures se raccourcissent.
 Moment de flexion représente moment résultant des forces normales internes survenant sur des surfaces infiniment petites et peut être exprimé en termes de intégral forme:
Moment de flexion représente moment résultant des forces normales internes survenant sur des surfaces infiniment petites et peut être exprimé en termes de intégral forme: 





