Théorèmes généraux sur la dynamique d'un système de corps. Théorèmes sur le mouvement du centre de masse, sur le changement de moment, sur le changement du moment cinétique principal, sur le changement d'énergie cinétique. Principes de D'Alembert et mouvements possibles. Équation générale de la dynamique. Équations de Lagrange.

Théorèmes généraux sur la dynamique d'un corps rigide et d'un système de corps

Théorèmes généraux de la dynamique- c'est un théorème sur le mouvement du centre de masse système mécanique, le théorème sur le changement de moment cinétique, le théorème sur le changement du moment cinétique principal (moment cinétique) et le théorème sur le changement de l'énergie cinétique d'un système mécanique.

Théorème sur le mouvement du centre de masse d'un système mécanique

Théorème sur le mouvement du centre de masse.
Le produit de la masse d'un système et de l'accélération de son centre de masse est égal à la somme vectorielle de toutes les forces externes agissant sur le système :
.

Ici M est la masse du système :
;
a C est l'accélération du centre de masse du système :
;
v C - vitesse du centre de masse du système :
;
r C - rayon vecteur (coordonnées) du centre de masse du système :
;
- les coordonnées (par rapport au centre fixe) et les masses des points qui composent le système.

Théorème sur le changement de quantité de mouvement (impulsion)

Quantité de mouvement (impulsion) du système est égal au produit de la masse de l'ensemble du système par la vitesse de son centre de masse ou la somme de l'impulsion (somme des impulsions) des points ou parties individuels qui composent le système :
.

Théorème sur le changement de quantité de mouvement sous forme différentielle.
La dérivée temporelle de la quantité de mouvement (impulsion) du système est égale à la somme vectorielle de toutes les forces externes agissant sur le système :
.

Théorème sur le changement de quantité de mouvement sous forme intégrale.
La variation de l'impulsion (impulsion) du système sur une certaine période de temps est égale à la somme des impulsions des forces externes sur la même période de temps :
.

Loi de conservation de la quantité de mouvement (impulsion).
Si la somme de toutes les forces externes agissant sur le système est nulle, alors le vecteur impulsion du système sera constant. Autrement dit, toutes ses projections sur les axes de coordonnées conserveront des valeurs constantes.

Si la somme des projections des forces externes sur n’importe quel axe est nulle, alors la projection de la quantité de mouvement du système sur cet axe sera constante.

Théorème sur la variation du moment cinétique principal (théorème des moments)

Le moment cinétique principal d'un système par rapport à un centre donné O est appelé la quantité égale à la somme vectorielle du moment cinétique de tous les points du système par rapport à ce centre :
.
Ici, les crochets désignent le produit vectoriel.

Systèmes connectés

Le théorème suivant s'applique au cas où un système mécanique a un point ou un axe fixe qui est fixe par rapport à un référentiel inertiel. Par exemple, un corps fixé par une rotule. Ou un système de corps se déplaçant autour d’un centre fixe. Il peut également s'agir d'un axe fixe autour duquel tourne un corps ou un système de corps. Dans ce cas, les moments doivent être compris comme des moments d'impulsion et des forces par rapport à l'axe fixe.

Théorème sur la variation du moment cinétique principal (théorème des moments)
La dérivée temporelle du moment cinétique principal du système par rapport à un centre fixe O est égale à la somme des moments de toutes les forces externes du système par rapport au même centre.

Loi de conservation du moment cinétique principal (moment cinétique).
Si la somme des moments de toutes les forces externes appliquées au système par rapport à un centre fixe donné O est égale à zéro, alors le moment cinétique principal du système par rapport à ce centre sera constant. Autrement dit, toutes ses projections sur les axes de coordonnées conserveront des valeurs constantes.

Si la somme des moments des forces externes par rapport à un axe fixe est nulle, alors le moment cinétique du système par rapport à cet axe sera constant.

Systèmes arbitraires

Le théorème suivant a un caractère universel. Elle s'applique aussi bien aux systèmes fixes que mobiles. Dans le cas de systèmes fixes, il faut tenir compte des réactions des connexions en points fixes. Il diffère du théorème précédent en ce qu’au lieu d’un point fixe O, il faut prendre le centre de masse C du système.

Théorème des moments sur le centre de masse
La dérivée temporelle du moment cinétique principal du système par rapport au centre de masse C est égale à la somme des moments de toutes les forces externes du système par rapport au même centre.

Loi de conservation du moment cinétique.
Si la somme des moments de toutes les forces externes appliquées au système par rapport au centre de masse C est égale à zéro, alors le moment d'impulsion principal du système par rapport à ce centre sera constant. Autrement dit, toutes ses projections sur les axes de coordonnées conserveront des valeurs constantes.

Moment d'inertie du corps

Si le corps tourne autour de l'axe z avec une vitesse angulaire ω z, alors son moment cinétique (moment cinétique) par rapport à l'axe z est déterminé par la formule :
L z = J z ω z ,
où J z est le moment d'inertie du corps par rapport à l'axe z.

Moment d'inertie du corps par rapport à l'axe z déterminé par la formule :
,
où h k est la distance d'un point de masse m k à l'axe z.
Pour un anneau mince de masse M et de rayon R, ou un cylindre dont la masse est répartie le long de son bord,
Jz = MR 2 .
Pour un anneau ou un cylindre solide et homogène,
.

Théorème de Steiner-Huygens.
Soit Cz l'axe passant par le centre de masse du corps, Oz l'axe qui lui est parallèle. Alors les moments d'inertie du corps par rapport à ces axes sont liés par la relation :
J Oz = J Cz + M a 2 ,
où M est le poids corporel ; a est la distance entre les axes.

En plus cas général :
,
où est le tenseur d'inertie du corps.
Voici un vecteur tracé du centre de masse du corps jusqu'à un point de masse m k.

Théorème sur le changement d'énergie cinétique

Supposons qu'un corps de masse M effectue un mouvement de translation et de rotation avec une vitesse angulaire ω autour d'un certain axe z.
,
Ensuite, l'énergie cinétique du corps est déterminée par la formule :
où v C est la vitesse de déplacement du centre de masse du corps ;

J Cz est le moment d'inertie du corps par rapport à l'axe passant par le centre de masse du corps parallèle à l'axe de rotation. La direction de l'axe de rotation peut changer avec le temps. Cette formule donne la valeur instantanée de l'énergie cinétique.
Théorème sur la variation de l'énergie cinétique d'un système sous forme différentielle.
.

Théorème sur la variation de l'énergie cinétique d'un système sous forme intégrale.
La variation de l'énergie cinétique du système lors d'un certain mouvement est égale à la somme du travail effectué sur ce mouvement de toutes les forces externes et internes appliquées au système :
.

Le travail effectué par la force, est égal au produit scalaire des vecteurs force et du déplacement infinitésimal du point de son application :
,
c'est-à-dire le produit des valeurs absolues des vecteurs F et ds par le cosinus de l'angle qui les sépare.

Le travail effectué par le moment de force, est égal au produit scalaire des vecteurs couple et de l'angle de rotation infinitésimal :
.

principe de d'Alembert

L'essence du principe de d'Alembert est de réduire les problèmes de dynamique à des problèmes de statique. Pour ce faire, on suppose (ou on le sait à l'avance) que les corps du système présentent certaines accélérations (angulaires). Ensuite, des forces d'inertie et (ou) des moments de forces d'inertie sont introduits, qui sont égaux en ampleur et de direction opposée aux forces et moments de forces qui, selon les lois de la mécanique, créeraient des accélérations ou des accélérations angulaires données.

Regardons un exemple. Le corps subit un mouvement de translation et est soumis à des forces extérieures. Nous supposons en outre que ces forces créent une accélération du centre de masse du système. Selon le théorème sur le mouvement du centre de masse, le centre de masse d’un corps aurait la même accélération si une force agissait sur le corps. Nous introduisons ensuite la force d'inertie :
.
Après cela, le problème de dynamique :
.
;
.

Pour le mouvement de rotation, procédez de la même manière. Laissez le corps tourner autour de l'axe z et être soumis à des moments de force externes M e zk .
.
Nous supposons que ces moments créent une accélération angulaire ε z.
;
.

Ensuite, nous introduisons le moment des forces d'inertie M И = - J z ε z.

Après cela, le problème de dynamique :

Se transforme en problème de statique :.
Le principe des mouvements possibles

Le principe des déplacements possibles est utilisé pour résoudre des problèmes de statique. Dans certains problèmes, cela donne une solution plus courte que la composition d’équations d’équilibre. Cela est particulièrement vrai pour les systèmes comportant des connexions (par exemple, des systèmes de corps reliés par des fils et des blocs) constitués de plusieurs corps. Le principe des mouvements possibles

Pour l'équilibre d'un système mécanique avec des liaisons idéales, il est nécessaire et suffisant que la somme des travaux élémentaires de toutes les forces actives agissant sur lui pour tout mouvement possible du système soit égale à zéro. Déplacement possible du système

Équation générale de la dynamique (principe de D'Alembert - Lagrange)

Le principe de D'Alembert-Lagrange est une combinaison du principe de D'Alembert avec le principe des mouvements possibles. Autrement dit, lors de la résolution d'un problème dynamique, nous introduisons des forces d'inertie et réduisons le problème à un problème statique, que nous résolvons en utilisant le principe des déplacements possibles.

Principe de D'Alembert-Lagrange.
Lorsqu'un système mécanique avec des connexions idéales se déplace, à chaque instant la somme des travaux élémentaires de toutes les forces actives appliquées et de toutes les forces d'inertie sur tout mouvement possible du système est nulle :
.
Cette équation s'appelle équation générale haut-parleurs.

équations de Lagrange

Coordonnées q généralisées 1 , q 2 , ..., q n est un ensemble de n quantités qui déterminent de manière unique la position du système.

Le nombre de coordonnées généralisées n coïncide avec le nombre de degrés de liberté du système.

Vitesses généralisées sont des dérivées de coordonnées généralisées par rapport au temps t.

Forces généralisées Q 1 , Q 2 , ..., Q n .
Considérons un mouvement possible du système, auquel la coordonnée q k recevra un mouvement δq k.
Les coordonnées restantes restent inchangées. Soit δA k le travail effectué par les forces extérieures lors d'un tel mouvement. Alors
.

δA k = Q k δq k , ou
Si, avec un éventuel mouvement du système, toutes les coordonnées changent, alors le travail effectué par des forces extérieures lors d'un tel mouvement a la forme : δA = Q.
1 δq 1 + Q 2 δq 2 + ... + Q n δq n
.

Alors les forces généralisées sont des dérivées partielles du travail sur les déplacements : Pour forces potentielles
.

avec un potentiel Π,équations de Lagrange

sont les équations du mouvement d'un système mécanique en coordonnées généralisées :
.

Ici T est l'énergie cinétique. C'est une fonction de coordonnées généralisées, de vitesses et, éventuellement, de temps. Par conséquent, sa dérivée partielle est également fonction des coordonnées généralisées, des vitesses et du temps. Ensuite, vous devez tenir compte du fait que les coordonnées et les vitesses sont fonction du temps. Par conséquent, pour trouver la dérivée totale par rapport au temps, vous devez appliquer la règle de différenciation d'une fonction complexe :
Littérature utilisée : S. M. Targ, Cours court

mécanique théorique, "Ecole Supérieure", 2010. Théorèmes généraux de la dynamique

Conférence 3. Dynamique d'un système de points matériels est une branche importante de la mécanique théorique. Ici, nous considérons principalement des problèmes concernant le mouvement de systèmes mécaniques (systèmes de points matériels) avec un nombre fini de degrés de liberté - le nombre maximum de paramètres indépendants qui déterminent la position du système. La tâche principale de la dynamique des systèmes est l'étude des lois du mouvement solide

L'approche la plus simple pour étudier le mouvement d'un système, consistant en N points matériels, revient à considérer les mouvements de chaque point individuel du système. Dans ce cas, toutes les forces agissant sur chaque point du système, y compris les forces d'interaction entre les points, doivent être déterminées.

En déterminant l'accélération de chaque point conformément à la deuxième loi de Newton (1.2), on obtient pour chaque point trois lois différentielles scalaires du mouvement du deuxième ordre, c'est-à-dire 3 N lois différentielles du mouvement pour l’ensemble du système.

Pour trouver les équations du mouvement d'un système mécanique basées sur des forces données et des conditions initiales pour chaque point du système, les lois différentielles résultantes doivent être intégrées. Ce problème est difficile même dans le cas de deux points matériels qui se déplacent uniquement sous l'influence de forces d'interaction selon la loi de l'attraction universelle (problème à deux corps), et extrêmement difficile dans le cas de trois points en interaction (problème à trois corps). ).

Il est donc nécessaire de trouver des méthodes pour résoudre des problèmes qui mèneraient à des équations résolubles et donneraient une idée du mouvement d’un système mécanique. Les théorèmes généraux de la dynamique, conséquence des lois différentielles du mouvement, permettent d'éviter la complexité qui surgit lors de l'intégration et d'obtenir les résultats nécessaires.

3. 1. Remarques générales

Nous numéroterons les points du système mécanique avec des indices je, j, k etc., qui parcourent toutes les valeurs 1, 2, 3… N, Où N – nombre de points du système. Grandeurs physiques lié à k Le point est désigné par le même indice que le point. Par exemple, exprimez respectivement le rayon vecteur et la vitesse k le point.

Chaque point du système est sollicité par des forces de deux origines : d'une part, des forces dont les sources se situent à l'extérieur du système, appelées externe forces et désignées ; deuxièmement, les forces provenant d'autres points d'un système donné, appelées interne forces et désignées. Les forces internes satisfont à la troisième loi de Newton. Considérons les propriétés les plus simples des forces internes agissant sur l'ensemble du système mécanique dans n'importe quel état.

Première propriété. La somme géométrique de toutes les forces internes du système (le vecteur principal des forces internes) est égale à zéro.

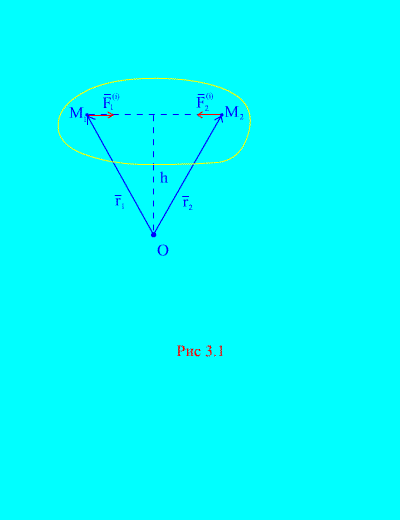
En effet, si l'on considère deux points arbitraires du système, par exemple et (Fig. 3.1), alors pour eux , parce que les forces d'action et de réaction sont toujours de même ampleur, agissant le long d'une ligne d'action dans la direction opposée, qui relie les points d'interaction. Le vecteur principal des forces internes est constitué de paires de forces de points en interaction, donc

(3.1)

Deuxième propriété. La somme géométrique des moments de toutes les forces internes par rapport à un point arbitraire de l'espace est égale à zéro.

Considérons un système de moments de forces et par rapport au point À PROPOS(Fig. 3.1). Depuis (Fig. 3.1). c'est clair que

,

parce que les deux forces ont les mêmes bras et des directions opposées des moments vectoriels. Point principal efforts internes relatifs à un point À PROPOS consiste en la somme vectorielle de ces expressions et est égal à zéro. Ainsi,

Supposons que les forces externes et internes agissant sur un système mécanique constitué de N points (Fig. 3.2). Si la résultante des forces externes et la résultante de toutes les forces internes sont appliquées à chaque point du système, alors pour tout k Au point du système, des équations différentielles du mouvement peuvent être établies. Il y aura un total de telles équations N:

et en projections sur des axes de coordonnées fixes 3 N:

(3.4)

Les équations vectorielles (3.3) ou les équations scalaires équivalentes (3.4) représentent les lois différentielles du mouvement des points matériels de l'ensemble du système. Si tous les points se déplacent parallèlement à un plan ou à une ligne droite, alors le nombre d'équations (3.4) dans le premier cas sera 2 N, dans la seconde N.

Exemple 1. Deux masses sont reliées entre elles par un câble inextensible jeté sur un bloc (Fig. 3.3). En négligeant les forces de frottement, ainsi que la masse du bloc et du câble, déterminez la loi du mouvement des charges et de la tension du câble.

Solution. Le système est constitué de deux corps matériels (reliés par un câble inextensible) se déplaçant parallèlement au même axe X.Écrivons les lois différentielles du mouvement en projections sur l'axe X pour chaque corps.

Laissez le poids droit tomber avec l’accélération, puis le poids gauche augmentera avec l’accélération. Nous nous libérons mentalement de la connexion (câble) et la remplaçons par des réactions et (Fig. 3.3). Considérant les corps libres, dressons les lois différentielles du mouvement en projection sur l'axe X(ce qui signifie que les tensions du fil sont des forces internes et que le poids des charges est externe) :

Puisque et (les corps sont reliés par un câble inextensible), on obtient

Résoudre ces équations d'accélération et de tension de câble T, nous obtenons

.

A noter que la tension dans le câble n'est pas égale à la force de gravité de la charge correspondante.

3. 2. Théorème sur le mouvement du centre de masse

On sait qu'un corps rigide et un système mécanique dans un avion peuvent se déplacer de manière assez complexe. Le premier théorème sur le mouvement d'un corps et d'un système mécanique peut être obtenu de la manière suivante : lancer un k.-l. un objet constitué de nombreux corps solides attachés ensemble. Il est clair qu'il volera en parabole. Cela a été révélé lors de l'étude du mouvement de la pointe. Cependant, désormais, l'objet n'est plus un point. Il tourne et se balance pendant son vol autour d'un centre efficace qui se déplace selon une parabole. Le premier théorème sur le mouvement des objets complexes dit qu'un certain centre effectif est le centre de masse d'un objet en mouvement. Le centre de masse n’est pas nécessairement situé dans le corps lui-même ; il peut se trouver quelque part à l’extérieur de celui-ci.

Théorème. Le centre de masse d'un système mécanique se déplace comme un point matériel avec une masse égale à la masse de l'ensemble du système, auquel sont appliquées toutes les forces externes agissant sur le système.

Pour prouver le théorème, nous réécrivons les lois différentielles du mouvement (3.3) sous la forme suivante :

(3.5)

Où N – nombre de points du système.

Additionnons les équations terme par terme :

(UN)

La position du centre de masse du système mécanique par rapport au système de coordonnées sélectionné est déterminée par la formule (2.1) : Où M– la masse du système. Alors côté gauche l'égalité (a) s'écrira

La première somme du côté droit de l'égalité (a) est égale au vecteur principal des forces externes, et la dernière, par la propriété des forces internes, est égale à zéro. Alors l'égalité (a), compte tenu de (b), sera réécrite

, (3.6)

ceux. le produit de la masse du système et de l'accélération du centre de sa masse est égal à la somme géométrique de toutes les forces externes agissant sur le système.

De l'équation (3.6), il s'ensuit que les forces internes n'affectent pas directement le mouvement du centre de masse. Cependant, dans certains cas, ils sont à l’origine de l’apparition de forces extérieures appliquées au système. Ainsi, les forces internes entraînant en rotation les roues motrices d'une voiture font agir sur celle-ci une force d'adhérence externe appliquée à la jante.

Exemple 2. Le mécanisme, situé dans un plan vertical, est installé sur un plan horizontal lisse et y est fixé par des barres rigidement fixées à la surface. À Et L (Fig. 3.4).

Rayon du disque 1 R. immobile. Masse du disque 2 m et rayon r attaché à une manivelle, longueur R.+ r au point C2. La manivelle tourne à une vitesse constante

vitesse angulaire. Au début, la manivelle occupait la droite position horizontale. En négligeant la masse de la manivelle, déterminer les forces horizontales et verticales maximales agissant sur les barres si la masse totale du cadre et de la roue 1 est égale à M. Considérez également le comportement du mécanisme en l'absence de barres.

Solution. Le système se compose de deux masses ( N=2 ) : disque fixe 1 avec châssis et disque mobile 2. Orienter l'axe à passant par le centre de gravité du disque fixe verticalement vers le haut, axe X– le long du plan horizontal.

Écrivons le théorème sur le mouvement du centre de masse (3.6) sous forme de coordonnées

Les forces extérieures de ce système sont : le poids du châssis et du disque fixe - Mg, poids du disque mobile – mg, - la réaction horizontale totale des boulons, - la réaction totale normale de l'avion. Ainsi,

Alors les lois du mouvement (b) seront réécrites

Calculons les coordonnées du centre de masse du système mécanique :

; (G)

comme on peut le voir de (Fig. 3.4), , , (angle de manivelle), . Substituer ces expressions dans (d) et calculer les dérivées secondes par rapport au temps tà partir de , , on obtient ça

(e)

En remplaçant (c) et (e) dans (b), nous trouvons

La pression horizontale agissant sur les barres est la plus grande et la plus faible lorsque parce que = 1 en conséquence, c'est-à-dire

Pression du mécanisme sur plan horizontal a les valeurs les plus grandes et les plus petites lorsque péché en conséquence, c'est-à-dire

En fait, le premier problème de dynamique a été résolu : selon les équations connues du mouvement du centre de masse du système (d), les forces impliquées dans le mouvement sont restituées.

En l'absence de barreaux K Et L (Fig. 3.4), le mécanisme peut commencer à rebondir au-dessus du plan horizontal. Cela aura lieu lorsque, c'est-à-dire quand , il s'ensuit que la vitesse angulaire de rotation de la manivelle, à laquelle le mécanisme rebondit, doit satisfaire l'égalité

.

3. 3. Loi de conservation du mouvement du centre de masse

Si le vecteur principal des forces externes agissant sur le système est égal à zéro, c'est-à-dire , puis de(3.6)il s'ensuit que l'accélération du centre de masse est nulle, par conséquent, la vitesse du centre de masse est constante en amplitude et en direction. Si, en particulier, au moment initial le centre de masse est au repos, alors il est au repos pendant tout le temps tandis que le vecteur principal des forces extérieures est égal à zéro.

Plusieurs corollaires découlent de ce théorème.

· Les forces internes ne peuvent à elles seules modifier la nature du mouvement du centre de masse du système.

· Si le vecteur principal des forces externes agissant sur le système est nul, alors le centre de masse est au repos ou se déplace uniformément et rectiligne.

· Si la projection du vecteur principal des forces externes du système sur un certain axe fixe est égale à zéro, alors la projection de la vitesse du centre de masse du système sur cet axe ne change pas.

· Une paire de forces appliquées à un corps rigide ne peut pas modifier le mouvement de son centre de masse (elle peut uniquement faire tourner le corps autour du centre de masse).

Considérons un exemple illustrant la loi de conservation du mouvement du centre de masse.

Exemple 3. Deux masses sont reliées par un fil inextensible jeté à travers un bloc (Fig. 3.5), fixé sur une cale avec une masse M. La cale repose sur un plan horizontal lisse. Au début, le système était au repos. Trouver le déplacement de la cale le long du plan lorsque la première charge est abaissée à une hauteur N. Négligez la masse du bloc et du fil.

Solution. Les forces externes agissant sur le coin ainsi que les charges sont la gravité, et Mg, ainsi que la réaction normale d'une surface horizontale lisse N. Par conséquent,

Puisqu’au moment initial le système était au repos, nous avons .

Calculons les coordonnées du centre de masse du système à et à l'instant t 1 quand la charge pèse g descendra à une hauteur H.

Pour le moment:

,

Où , ,X– respectivement, les coordonnées du centre de masse des charges pesant g, g et d'un coin pesant Mg.

Supposons que le coin se déplace à un moment donné dans le sens positif de l'axe Bœuf par le montant L, si le poids de la charge chute à une hauteur N. Alors, pour le moment

parce que les charges avec le coin se déplaceront vers L vers la droite et la charge se déplacera vers le haut le long du coin. Puisque , alors après calculs on obtient

.

3.4. Quantité de mouvement du système

3.4.1. Calcul de la quantité de mouvement du système

L'impulsion d'un point matériel est une quantité vectorielle égale au produit de la masse du point et de son vecteur vitesse.

Unité de mesure de l'élan -

La quantité de mouvement d'un système mécanique est la somme vectorielle de la quantité de mouvement des points individuels du système, c'est-à-dire

Où N – nombre de points du système.

La quantité de mouvement d'un système mécanique peut être exprimée en termes de masse du système M et la vitesse du centre de masse. Vraiment,

ceux. La quantité de mouvement du système est égale au produit de la masse du système entier et de la vitesse de son centre de masse. La direction est la même que la direction (Fig. 3.6)

En projections sur des axes rectangulaires on a

où , , sont des projections de la vitesse du centre de masse du système.

Ici M– la masse du système mécanique ; ne change pas lorsque le système se déplace.

Ces résultats sont particulièrement pratiques à utiliser lors du calcul des quantités de mouvement de corps rigides.

D'après la formule (3.7), il ressort clairement que si un système mécanique se déplace de telle manière que son centre de masse reste stationnaire, alors la quantité de mouvement du système reste égale à zéro.

3.4.2. Impulsion élémentaire et pleine force

L'action d'une force sur un point matériel dans le temps dt peut être caractérisé par une impulsion élémentaire. Impulsion de force totale dans le temps t, ou impulsion de force, déterminée par la formule

ou en projections sur les coordonnées des axes

(3.8a)

L'unité de force d'impulsion est .

3.4.3. Théorème sur le changement de quantité de mouvement d'un système

Laissez les forces externes et internes être appliquées aux points du système. Ensuite pour chaque point du système nous pouvons appliquer les lois différentielles du mouvement (3.3), en gardant à l’esprit que :

.

En sommant tous les points du système, on obtient

Par la propriété des forces internes et par définition nous avons

(3.9)

En multipliant les deux côtés de cette équation par dt, on obtient un théorème sur le changement de quantité de mouvement sous forme différentielle :

, (3.10)

ceux. le moment différentiel d'un système mécanique est égal à la somme vectorielle des impulsions élémentaires de toutes les forces extérieures agissant sur les points du système mécanique.

Calculer l’intégrale des deux côtés (3.10) dans le temps de 0 à t, on obtient le théorème sous forme finie ou intégrale

(3.11)

En projections sur les axes de coordonnées nous aurons

Changement de quantité de mouvement d'un système mécanique au fil du tempst, est égal à la somme vectorielle de toutes les impulsions des forces extérieures agissant sur les points du système mécanique pendant le même temps.

Exemple 4. Poids de la charge m descend un plan incliné depuis son repos sous l'influence d'une force F, proportionnel au temps : , où (Fig. 3.7). Quelle vitesse le corps va-t-il acquérir après t secondes après le début du mouvement, si le coefficient de frottement de glissement de la charge sur le plan incliné est égal à f.

Solution. Décrivons les forces appliquées à la charge : mg – force de gravité de la charge, N est la réaction normale de l'avion, est la force de frottement de glissement de la charge sur l'avion, et . La direction de toutes les forces est indiquée dans (Fig. 3.7).

Dirigons l'axe X le long du plan incliné vers le bas. Écrivons le théorème sur le changement de quantité de mouvement (3.11) en projection sur l'axe X:

(UN)

Selon la condition, parce que au moment initial, la charge était au repos. La somme des projections des impulsions de toutes les forces sur l'axe des x est égale à

Ainsi,

,

.

3.4.4. Lois de conservation de la quantité de mouvement

Les lois de conservation sont obtenues comme cas particuliers du théorème sur le changement de quantité de mouvement. Deux cas particuliers sont possibles.

· Si la somme vectorielle de toutes les forces externes appliquées au système est égale à zéro, c'est-à-dire , alors du théorème il découle (3.9) , Quoi ,

ceux. si le vecteur principal des forces externes du système est nul, alors la quantité de mouvement du système est constante en ampleur et en direction.

· Si la projection du vecteur principal des forces externes sur n'importe quel axe de coordonnéeségal à zéro, par exemple Oh, c'est-à-dire , alors la projection de la quantité de mouvement sur cet axe est une valeur constante.

Considérons un exemple d'application de la loi de conservation de la quantité de mouvement.

Exemple 5. Un pendule balistique est un corps dont la masse est suspendue à un long fil. (Fig. 3.8).

Une balle de masse, se déplaçant avec vitesse V et heurtant un corps immobile, il reste coincé dedans et le corps dévie. Quelle était la vitesse de la balle si le corps atteignait une hauteur h ?

Solution. Laissez le corps avec la balle coincée acquérir de la vitesse. Ensuite, en utilisant la loi de conservation de la quantité de mouvement lors de l’interaction de deux corps, on peut écrire .

La vitesse peut être calculée en utilisant la loi de conservation de l'énergie mécanique . Alors . En conséquence nous trouvons

.

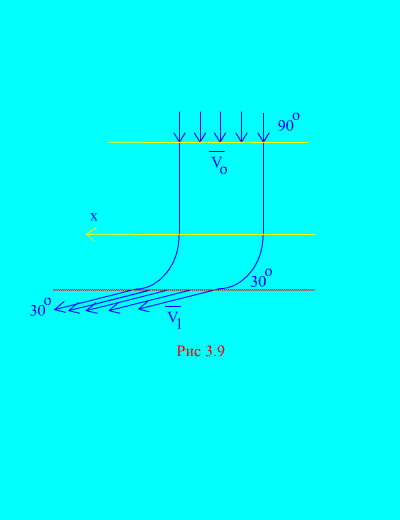
Exemple 6. L'eau pénètre dans un canal stationnaire (Fig. 3.9) section variable avec vitesse inclinée par rapport à l'horizontale ; carré coupe transversale canal à l'entrée; la vitesse de l'eau à la sortie du canal fait un angle avec l'horizon.

Déterminez la composante horizontale de la réaction de l’eau sur les parois du canal. Densité de l'eau .

Solution. Nous déterminerons la composante horizontale de la réaction exercée par les parois des canaux sur l'eau. Cette force est égale en ampleur et de signe opposé à la force souhaitée. On a, d’après (3.11a),

. (UN)

On calcule la masse du volume de liquide entrant dans le canal pendant le temps t :

La quantité rAV 0 est appelée deuxième masse - la masse de liquide circulant à travers n'importe quelle section du tuyau par unité de temps.

La même quantité d’eau quitte le canal au même moment. Les vitesses initiale et finale sont données dans la condition.

Calculons le côté droit de l'égalité (a), qui détermine la somme des projections sur l'axe horizontal des forces externes appliquées au système (eau). La seule force horizontale est la composante horizontale de la réaction du mur qui en résulte réception. Cette force est constante lors d’un mouvement constant de l’eau. C'est pourquoi

. (V)

En remplaçant (b) et (c) dans (a), on obtient

3.5. Moment cinétique du système

3.5.1. Moment principal d'impulsion du système

Soit le rayon vecteur d'un point avec la masse du système par rapport à un point A, appelé centre (Fig. 3.10).

Moment de mouvement (moment cinétique) d'un point par rapport au centre A appelé vecteur , déterminé par la formule

. (3.12)

Dans ce cas, le vecteur dirigé perpendiculairement au plan passant par le centre UN et vecteur .

Moment de mouvement (moment cinétique) d'un point par rapport à l'axe s'appelle la projection sur cet axe du moment d'impulsion d'un point par rapport à tout centre choisi sur cet axe.

Le moment principal d'impulsion (moment cinétique) du système par rapport au centre A s'appelle la quantité

(3.13)

Le moment principal d'impulsion (moment cinétique) du système par rapport à l'axe est appelé la projection sur cet axe du moment d'impulsion principal du système par rapport à tout choisi sur cet axe axe central.

3.5.2. Moment cinétique d'un corps rigide en rotation autour de l'axe de rotation

Alignons le point fixe À PROPOS corps allongé sur l'axe de rotation À PROPOSz, avec l'origine du système de coordonnées Ohooz, dont les axes tourneront avec le corps (Fig. 3.11). Soit le rayon vecteur d'un point du corps par rapport à l'origine des coordonnées ; sa projection sur l'axe sera notée , , . Projections vectorielles vitesse angulaire les corps sur le même axe seront notés 0, 0, ().

Ministère de l'Éducation et des Sciences Fédération de Russie

Établissement d'enseignement budgétaire de l'État fédéral d'enseignement professionnel supérieur

"Université technologique d'État du Kouban"

Mécanique théorique

Dynamique de la partie 2

Approuvé par le comité de rédaction et de publication

conseil universitaire comme

aide pédagogique

Krasnodar

CDU 531.1/3 (075)

Mécanique théorique. Partie 2. Dynamique : Manuel / L.I. Draiko ; Kouban. État technol.un-t. Krasnodar, 2011. 123 p.

ISBN5-230-06865-5

Le matériel théorique est présenté sous une forme brève, des exemples de résolution de problèmes sont donnés, dont la plupart reflètent de véritables problèmes techniques, et une attention particulière est accordée au choix d'une méthode rationnelle de solution.

Conçu pour les bacheliers par correspondance et à distance en construction, transports et génie mécanique.

Tableau 1 malade. 68 Bibliographie 20 titres

Editeur scientifique Candidat en Sciences Techniques, Professeur Associé. V.F. Melnikov

Réviseurs : Chef du Département de mécanique théorique et de théorie des mécanismes et des machines, Université agraire de Kouban prof. F.M. Kanarev ; Professeur agrégé, Département de mécanique théorique, Université technologique d'État de Kouban M.E. Multykh

Publié par décision du Conseil de rédaction et d'édition de l'Université technologique d'État du Kouban.

Rééditer

ISBN 5-230-06865-5KubSTU 1998

Préface

Ce manuel est destiné aux étudiants à temps partiel des spécialités construction, transports et génie mécanique, mais peut être utilisé lors de l'étude de la section « Dynamique » du cours de mécanique théorique par les étudiants à temps partiel d'autres spécialités, ainsi que par les étudiants à temps plein. travaillant de manière indépendante.

Le manuel est rédigé conformément au programme actuel du cours de mécanique théorique et couvre toutes les problématiques de la partie principale du cours. Chaque section contient un bref matériel théorique, accompagné d'illustrations et de recommandations méthodologiques pour son utilisation dans la résolution de problèmes. Le manuel contient des solutions à 30 problèmes qui reflètent des problèmes techniques réels et correspondent à des tâches de test pour décision indépendante. Pour chaque problème, un schéma de calcul est présenté qui illustre clairement la solution. Le formatage de la solution répond aux exigences de formatage des épreuves pour les étudiants à temps partiel.

L'auteur exprime sa profonde gratitude aux enseignants du Département de mécanique théorique et de théorie des mécanismes et des machines de l'Université agraire du Kouban pour leur excellent travail de révision du manuel, ainsi qu'aux enseignants du Département de mécanique théorique de l'Université technologique d'État du Kouban. Université pour ses précieux commentaires et conseils sur la préparation du manuel en vue de sa publication.

Tous les commentaires critiques et suggestions seront acceptés avec gratitude par l'auteur à l'avenir.

Introduction

La dynamique est la section la plus importante de la mécanique théorique. La plupart des problèmes spécifiques rencontrés dans la pratique de l’ingénierie concernent la dynamique. Utilisant les conclusions de la statique et de la cinématique, la dynamique établit les lois générales du mouvement des corps matériels sous l'action de forces appliquées.

L'objet matériel le plus simple est un point matériel. Un corps matériel de n'importe quelle forme peut être considéré comme un point matériel dont les dimensions peuvent être négligées dans le problème considéré. Un corps de dimensions finies peut être considéré comme un point matériel si la différence dans le mouvement de ses points n'est pas significative pour un problème donné. Cela se produit lorsque les dimensions du corps sont petites par rapport aux distances parcourues par les points du corps. Chaque particule d'un corps solide peut être considérée comme un point matériel.

Les forces appliquées à un point ou à un corps matériel sont évaluées dynamiquement par leur impact dynamique, c'est-à-dire par la manière dont elles modifient les caractéristiques du mouvement des objets matériels.

Le mouvement des objets matériels au fil du temps se produit dans l’espace par rapport à un certain cadre de référence. En mécanique classique, basée sur les axiomes de Newton, l'espace est considéré comme tridimensionnel, ses propriétés ne dépendent pas des objets matériels qui s'y déplacent. La position d'un point dans un tel espace est déterminée par trois coordonnées. Le temps n'est pas lié à l'espace et au mouvement des objets matériels. Il est considéré comme identique pour tous les systèmes de référence.

Les lois de la dynamique décrivent le mouvement des objets matériels par rapport à des axes de coordonnées absolues, conventionnellement acceptés comme stationnaires. L'origine du système de coordonnées absolues est considérée comme étant au centre du Soleil et les axes sont dirigés vers des étoiles lointaines et conditionnellement stationnaires. Lors de la résolution de nombreux problèmes techniques, les axes de coordonnées connectés à la Terre peuvent être considérés comme conditionnellement immobiles.

Les paramètres du mouvement mécanique des objets matériels en dynamique sont établis par des dérivations mathématiques des lois fondamentales de la mécanique classique.

Première loi (loi de l'inertie) :

Un point matériel maintient un état de repos ou de mouvement uniforme et linéaire jusqu'à ce que l'action de certaines forces le fasse sortir de cet état.

Le mouvement uniforme et linéaire d’un point est appelé mouvement par inertie. Le repos est un cas particulier de mouvement par inertie, lorsque la vitesse d'un point est nulle.

Chaque point matériel possède une inertie, c’est-à-dire qu’il s’efforce de maintenir un état de repos ou un mouvement linéaire uniforme. Le système de référence par rapport auquel s'applique la loi de l'inertie est appelé inertiel, et le mouvement observé par rapport à ce système est appelé absolu. Tout système de référence qui effectue un mouvement de translation rectiligne et uniforme par rapport à un système inertiel sera également un système inertiel.

Deuxième loi (loi fondamentale de la dynamique) :

L'accélération d'un point matériel par rapport au référentiel inertiel est proportionnelle à la force appliquée sur le point et coïncide avec la force dans la direction :
.

De la loi fondamentale de la dynamique, il résulte qu'avec la force
accélération
. La masse d'un point caractérise le degré de résistance d'un point aux changements de vitesse, c'est-à-dire qu'elle est une mesure de l'inertie d'un point matériel.

Troisième loi (loi d'action et de réaction) :

Les forces avec lesquelles deux corps agissent l'un sur l'autre sont de même ampleur et dirigées le long d'une ligne droite dans des directions opposées.

Les forces appelées action et réaction sont appliquées à différents corps et ne forment donc pas un système équilibré.

Quatrième loi (loi de l'indépendance des forces) :

Avec l'action simultanée de plusieurs forces, l'accélération d'un point matériel est égale à la somme géométrique des accélérations qu'aurait le point sous l'action de chaque force séparément :

, Où
,
,…,
.

(SYSTÈMES MÉCANIQUES) – Option IV

1. Comme on le sait, l'équation de base de la dynamique d'un point matériel est exprimée par l'équation. Équations différentielles les mouvements de points arbitraires d'un système mécanique non libre selon deux méthodes de division des forces peuvent s'écrire sous deux formes :

(1) , où k=1, 2, 3, … , n – le nombre de points du système matériel.

(2)

où est la masse du kième point ; - rayon vecteur du k-ème point, - une force (active) donnée agissant sur le k-ème point ou la résultante de toutes les forces actives agissant sur le k-ème point. - résultante des forces de réaction de liaison agissant sur le kième point ; - résultante des forces internes agissant sur le kème point ; - résultante des forces extérieures agissant sur le kième point.

En utilisant les équations (1) et (2), on peut s'efforcer de résoudre à la fois le premier et le deuxième problèmes de dynamique. Cependant, résoudre le deuxième problème de dynamique d’un système devient très compliqué, non seulement d’un point de vue mathématique, mais aussi parce que l’on est confronté à des difficultés fondamentales. Ils consistent dans le fait que tant pour le système (1) que pour le système (2) le nombre d'équations est significatif moins de nombre inconnu.

Donc, si nous utilisons (1), alors la dynamique connue pour le deuxième problème (inverse) sera et , et les dynamiques inconnues seront et . Les équations vectorielles seront " n», et les inconnus - « 2n ».

Si nous partons du système d'équations (2), alors certaines des forces externes sont connues. Pourquoi se séparer ? Le fait est que le nombre de forces externes comprend également des réactions externes de connexions inconnues. De plus, . sera également inconnu.

Ainsi, le système (1) et le système (2) sont NON FERMÉS. Il est nécessaire d'ajouter des équations en tenant compte des équations des connexions, et peut-être est-il également nécessaire d'imposer certaines restrictions sur les connexions elles-mêmes. Ce qu'il faut faire?

Si nous partons de (1), alors nous pouvons suivre le chemin de la composition des équations de Lagrange du premier type. Mais cette voie n'est pas rationnelle car tâche plus facile(moins de degrés de liberté), plus il est difficile à résoudre d’un point de vue mathématique.

Tournons ensuite notre attention vers le système (2), où - sont toujours inconnus. La première étape pour résoudre un système consiste à éliminer ces inconnues. Il convient de garder à l'esprit qu'en règle générale, nous ne nous intéressons pas aux forces internes lorsque le système se déplace, c'est-à-dire que lorsque le système se déplace, il n'est pas nécessaire de savoir comment chaque point du système se déplace, mais cela suffit pour savoir comment le système évolue dans son ensemble.

Ainsi, si de diverses manières excluons les forces inconnues du système (2), alors nous obtenons des relations, c'est-à-dire que certaines apparaissent caractéristiques générales pour un système dont la connaissance nous permet de juger comment le système se déplace en général. Ces caractéristiques sont introduites à l'aide de ce que l'on appelle théorèmes généraux haut-parleurs. Il existe quatre de ces théorèmes :

1. Théorème sur mouvement du centre de masse d'un système mécanique;

2. Théorème sur changement dans la quantité de mouvement d'un système mécanique;

3. Théorème sur modification du moment cinétique du système mécanique;

4. Théorème sur changement d'énergie cinétique d'un système mécanique.