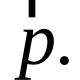Nous avons dit qu'une courbe algébrique du second ordre est déterminée par une équation algébrique du second degré par rapport à X Et à. En général, cette équation s’écrit comme suit :

UN X 2 + V xy+C à 2 +D x+E oui+ F = 0, (6)

et A 2 + B 2 + C 2 ¹ 0 (c'est-à-dire que les nombres A, B, C ne deviennent pas zéro en même temps). Composants A X 2 , V xy, AVEC à 2 sont appelés les termes principaux de l'équation, le nombre

appelé discriminant cette équation. L'équation (6) est appelée équation générale courbe du deuxième ordre.

Pour les courbes considérées précédemment nous avons :

Ellipse: Þ A = , B = 0, C = , D = E = 0, F = –1,

cercle X 2 + à 2 = UN 2 Þ A = C = 1, B = D = E = 0, F = – UN 2, d = 1>0 ;

Hyperbole: Þ A = , B = 0, C = – , D = E = 0, F = –1,

ré = – .< 0.

Parabole: à 2 = 2pxÞ A = B = 0, C = 1, D = –2 r, E = F = 0, d = 0,

X 2 = 2ruÞ A = 1B = C = D = 0, E = –2 r, F = 0, d = 0.

Les courbes données par l'équation (6) sont appelées central courbes si d¹0. Si d> 0, alors la courbe elliptique tapez, si d<0, то кривая hyperbolique taper. Les courbes pour lesquelles d = 0 sont des courbes parabolique taper.

Il a été prouvé que la deuxième ligne d'ordre dans n'importe lequel Le système de coordonnées cartésiennes est donné par une équation algébrique du second ordre. Seulement dans un système, l'équation a une forme complexe (par exemple, (6)), et dans l'autre, elle a une forme plus simple, par exemple (5). Par conséquent, il est pratique de considérer un système de coordonnées dans lequel la courbe étudiée est écrite par l'équation la plus simple (par exemple canonique). La transition d'un système de coordonnées, dans lequel la courbe est donnée par une équation de la forme (6), à un autre, où son équation a une forme plus simple, est appelée transformation de coordonnées.

Considérons les principaux types de transformations de coordonnées.

JE. Porter la transformation axes de coordonnées (avec préservation de la direction). Soit le point M dans le système de coordonnées XOU d'origine ayant des coordonnées ( X, àX¢, à¢). D'après le dessin, on peut voir que les coordonnées du point M dans différents systèmes sont liées par les relations

(7) ou (8).

Les formules (7) et (8) sont appelées formules de transformation de coordonnées.

II. Transformation de rotation coordonner les axes par l'angle a. Si dans le système de coordonnées XOU d'origine, le point M a des coordonnées ( X, à), et dans le nouveau système de coordonnées ХО¢У, il a des coordonnées ( X¢, à¢). Alors la connexion entre ces coordonnées est exprimée par les formules

, (9)

ou

En utilisant la transformation de coordonnées, l'équation (6) peut être réduite à l'un des éléments suivants canoniqueéquations.

1) – des ellipses,

2) – hyperbole,

3) à 2 = 2px, X 2 = 2ru– parabole

4) UN 2 X 2 – b 2 oui 2 = 0 – une paire de lignes qui se croisent (Fig. a)

5) oui 2 – un 2 = 0 – paire de lignes parallèles (Fig. b)

6) x 2 –un 2 = 0 – une paire de lignes parallèles (Fig. c)

7) oui 2 = 0 – lignes droites coïncidentes (axe OX)

8)x 2 = 0 – lignes droites coïncidentes (axe OA)

9) un 2 X 2 + b 2 oui 2 = 0 – point (0, 0)

10) ellipse imaginaire

11)oui 2 + un 2 = 0 – paire de lignes imaginaires

12)x 2 + un 2 = 0 paire de lignes imaginaires.

Chacune de ces équations est une équation linéaire du second ordre. Les droites définies par les équations 4 à 12 sont appelées dégénérer courbes du second ordre.

Considérons des exemples de transformation de l'équation générale d'une courbe sous forme canonique.

1) 9X 2 + 4à 2 – 54X + 8à+ 49 = 0 Þ (9 X 2 – 54X) + (4à 2 + 8à) + 49 = 0 Þ

9(X 2 – 6X+ 9) + 4(à 2 + 2à+ 1) – 81 – 4 + 49 = 0 Þ 9( X –3) 2 + 4(à+ 1) = 36,Þ

.

Mettons X¢ = X – 3, ࢠ= à+ 1, on obtient l'équation canonique de l'ellipse . Égalités X¢ = X – 3, ࢠ= à+ 1 déterminer la transformation du transfert du système de coordonnées vers le point (3, –1). Après avoir construit l’ancien et le nouveau système de coordonnées, il n’est pas difficile de représenter cette ellipse.

2) 3à 2 +4X– 12à+8 = 0. Transformation :

(3à 2 – 12à)+ 4 X+8 = 0

3(à 2 – 4à+4) – 12 + 4 X +8 = 0

3(oui – 2) 2 + 4(X –1) = 0

(à – 2) 2 = – (X – 1) .

Mettons X¢ = X – 1, ࢠ= à– 2, on obtient l’équation de la parabole ࢠ2 = – X¢. Le remplacement choisi correspond au transfert du repère au point O¢(1,2).

Dans cet article, nous considérerons l'équation générale d'une droite sur un plan. Donnons des exemples de construction d'une équation générale d'une droite si deux points de cette droite sont connus ou si un point et le vecteur normal de cette droite sont connus. Présentons des méthodes pour transformer une équation sous forme générale en formes canoniques et paramétriques.

Soit un système de coordonnées rectangulaires cartésiennes arbitraires Oxy. Considérons une équation du premier degré ou linéaire :

Où A, B, C− quelques constantes, et au moins un des éléments UN Et B différent de zéro.

Nous allons montrer qu'une équation linéaire sur un plan définit une droite. Démontrons le théorème suivant.

Théorème 1. Dans un système de coordonnées rectangulaires cartésiennes arbitraires sur un plan, chaque ligne droite peut être spécifiée par une équation linéaire. A l'inverse, chaque équation linéaire (1) dans un système de coordonnées rectangulaires cartésiennes arbitraires sur un plan définit une ligne droite.

Preuve. Il suffit de prouver que la droite L est déterminé par une équation linéaire pour n'importe quel système de coordonnées rectangulaires cartésiennes, puisqu'il sera alors déterminé par une équation linéaire pour tout choix de système de coordonnées rectangulaires cartésiennes.

Soit une ligne droite sur l'avion L. Choisissons un système de coordonnées pour que l'axe Bœuf coïncidait avec une ligne droite L, et l'axe Oy lui était perpendiculaire. Alors l'équation de la droite L prendra la forme suivante :

Tous les points sur une ligne L satisfera l’équation linéaire (2), et tous les points en dehors de cette ligne ne satisferont pas l’équation (2). La première partie du théorème a été prouvée.

Soit un système de coordonnées rectangulaires cartésiennes et soit une équation linéaire (1), où au moins un des éléments UN Et B différent de zéro. Trouvons le lieu géométrique des points dont les coordonnées satisfont à l'équation (1). Puisqu'au moins un des coefficients UN Et B est différent de zéro, alors l'équation (1) a au moins une solution M.(x 0 ,oui 0). (Par exemple, quand UN≠0, point M. 0 (−CALIFORNIE, 0) appartient au lieu géométrique des points donné). En substituant ces coordonnées dans (1) nous obtenons l'identité

Soustrayons l'identité (3) de (1) :

Évidemment, l'équation (4) est équivalente à l'équation (1). Il suffit donc de prouver que (4) définit une certaine droite.

Puisque nous considérons un système de coordonnées rectangulaires cartésiennes, il résulte de l'égalité (4) que le vecteur à composantes ( x−x 0 , oui−oui 0 ) orthogonal au vecteur n avec des coordonnées ( A,B}.

Considérons une ligne droite L, en passant par le point M. 0 (x 0 , oui 0) et perpendiculaire au vecteur n(Fig.1). Laissons le point M.(x,y) appartient à la ligne L. Alors le vecteur de coordonnées x−x 0 , oui−oui 0 perpendiculaire n et l'équation (4) est satisfaite (produit scalaire des vecteurs n et égal à zéro). A l’inverse, si le point M.(x,y) ne se trouve pas sur une ligne L, puis le vecteur de coordonnées x−x 0 , oui−oui 0 n'est pas orthogonal au vecteur n et l'équation (4) n'est pas satisfaite. Le théorème est prouvé.

Preuve. Puisque les lignes (5) et (6) définissent la même ligne, alors les vecteurs normaux n 1 ={UN 1 ,B 1) et n 2 ={UN 2 ,B 2) colinéaire. Puisque les vecteurs n 1 ≠0, n 2 ≠0, alors il existe un tel nombre λ , Quoi n 2 =n 1 λ . De là, nous avons : UN 2 =UN 1 λ , B 2 =B 1 λ . Prouvons que C 2 =C 1 λ . Évidemment, les lignes coïncidentes ont un point commun M. 0 (x 0 , oui 0). Multiplier l'équation (5) par λ et en en soustrayant l’équation (6), nous obtenons :

Puisque les deux premières égalités des expressions (7) sont satisfaites, alors C 1 λ −C 2 =0. Ceux. C 2 =C 1 λ . La remarque est avérée.

Notez que l'équation (4) définit l'équation de la droite passant par le point M. 0 (x 0 , oui 0) et ayant un vecteur normal n={A,B). Par conséquent, si le vecteur normal d'une droite et le point appartenant à cette droite sont connus, alors l'équation générale de la droite peut être construite à l'aide de l'équation (4).

Exemple 1. Une droite passe par un point M.=(4,−1) et a un vecteur normal n=(3, 5). Construire l’équation générale d’une droite.

Solution. Nous avons: x 0 =4, oui 0 =−1, UN=3, B=5. Pour construire l'équation générale d'une droite, on substitue ces valeurs dans l'équation (4) :

Répondre:

Le vecteur est parallèle à la droite L et donc perpendiculaire au vecteur normal de la droite L. Construisons un vecteur ligne normal L, en tenant compte du fait que le produit scalaire des vecteurs n et égal à zéro. On peut écrire par exemple n={1,−3}.

Pour construire l'équation générale d'une droite, nous utilisons la formule (4). Remplaçons les coordonnées du point dans (4) M. 1 (on peut aussi prendre les coordonnées du point M. 2) et vecteur normal n:

Remplacement des coordonnées des points M. 1 et M. 2 dans (9), nous pouvons nous assurer que la droite donnée par l'équation (9) passe par ces points.

Répondre:

Soustraire (10) de (1) :

Nous avons obtenu l'équation canonique de la droite. Vecteur q={−B, UN) est le vecteur directeur de la droite (12).

Voir conversion inverse.

Exemple 3. Une droite sur un plan est représentée par l'équation générale suivante :

Déplaçons le deuxième terme vers la droite et divisons les deux côtés de l'équation par 2,5.

Courbe du deuxième ordre— localisation géométrique des points sur le plan, coordonnées rectangulaires

qui satisfont une équation de la forme :

dans lequel au moins un des coefficients un 11, un 12, un 22 pas égal à zéro.

Invariants des courbes du second ordre.

La forme de la courbe dépend de 4 invariants donnés ci-dessous :

Invariants par rapport à la rotation et au déplacement du système de coordonnées :

Invariant par rapport à la rotation du système de coordonnées ( semi-invariant):

Pour étudier les courbes du second ordre, considérons le produit COMME.

Général équation de courbe du second ordreça ressemble à ça :

Hache 2 +2Bxy+Cy 2 +2Dx+2Ey+F=0

Si A*C > 0 type elliptique. N'importe quel vélo elliptique

l'équation est l'équation soit d'une ellipse ordinaire, soit d'une ellipse dégénérée (point), soit d'une ellipse imaginaire

ellipse (dans ce cas l'équation ne définit pas une seule image géométrique sur le plan) ;

Si A*C< 0 , alors l'équation prend la forme d'équation type hyperbolique. Tout hyperbolique

l'équation exprime soit une hyperbole simple, soit une hyperbole dégénérée (deux lignes sécantes) ;

Si A*C = 0, alors la ligne de second ordre ne sera pas centrale. Les équations de ce type sont appelées

équations type parabolique et exprimer sur le plan soit une simple parabole, soit 2 parallèles

(soit coïncidant) des lignes droites, soit n'exprimant pas une seule image géométrique sur le plan ;

Si A*C ≠ 0, la courbe du second ordre sera

L'équation générale d'une courbe du second ordre sur un plan a la forme :

Hache 2 + 2BXY + Cy 2 + 2Dx + 2Hé + F = 0, (39)

Où UN 2 + B 2 + C 2 0, (UN, B, C, D, E, F) R.. Il définit toutes les sections coniques possibles arbitrairement situées sur le plan.

A partir des coefficients de l'équation (39) on compose deux déterminants :

Appelé discriminant de l'équation(39), et - discriminant des principaux termes de l’équation. A 0, l'équation (39) détermine : > 0 - ellipse ;< 0 - гиперболу; = 0 - параболу. В случае = 0 кривые вырождаются в точку или прямые линии.

De l'équation générale (39), nous pouvons passer à l'équation canonique si nous éliminons les termes linéaires et croisés en passant à un nouveau système de coordonnées qui coïncide avec les axes de symétrie de la figure. Remplaçons dans (39) x sur x + un Et oui sur oui + b, Où un, b quelques constantes. Écrivons les coefficients obtenus pour X Et oui et les assimiler à 0

(Aa + Sib + D)x = 0, (CB + Ba + E)oui = 0. (41)

En conséquence, l’équation (39) prendra la forme :

UN(x) 2 + 2B(x)(oui) + C(oui) 2 + F = 0, (42)

où sont les coefficients UN, B, C n'a pas changé, mais F= / . La solution du système d'équations (41) déterminera les coordonnées du centre de symétrie de la figure :

Si B= 0, alors un = -D/UN, b = -E/C et il est pratique d'éliminer les termes linéaires dans (39) par la méthode de réduction à un carré parfait :

Hache 2 + 2Dx = UN(x 2 + 2xD/UN + (D/UN) 2 - (D/UN) 2) = UN(x + D/UN) 2 - D 2 /UN.

Dans l'équation (42), nous faisons pivoter les coordonnées d'un angle a (38). Écrivons le coefficient résultant pour le terme croisé xoui et réglez-le égal à 0

xy = 0. (44)

La condition (44) détermine l'angle de rotation requis des axes de coordonnées jusqu'à ce qu'ils coïncident avec les axes de symétrie de la figure et prend la forme :

L'équation (42) prend la forme :

UN+X2+ C + Oui 2 + F = 0 (46)

à partir de laquelle il est facile de passer à l'équation canonique de la courbe :

Chances UN + , C+ , sous la condition (45), peut être représenté comme les racines d'une équation quadratique auxiliaire :

t 2 - (UN + C)t + = 0. (48)

De ce fait, la position et la direction des axes de symétrie de la figure, son demi-axe, sont déterminées :

et il peut être construit géométriquement.

Dans le cas = 0 nous avons une parabole. Si son axe de symétrie est parallèle à l'axe Oh, alors l'équation se réduit à :

sinon, regarde :

où les expressions entre parenthèses, égales à 0, définissent les lignes des nouveaux axes de coordonnées : , .

Résoudre les problèmes courants

Exemple 15. Donnez l'équation 2 x 2 + 3oui 2 - 4x + 6oui- 7 = 0 à la forme canonique et construire une courbe.

Solution. B= 0, = -72 0, = 6 > 0 ellipse.

Effectuons une réduction à un carré parfait :

2(x - 1) 2 + 3(oui + 1) 2 - 12 = 0.

Coordonnées du centre de symétrie (1 ; -1), transformation linéaire X = x - 1, Oui = oui+ 1 amène l’équation sous forme canonique.

Exemple 16. Donnez l'équation 2 xy = un 2 à la forme canonique et construisons une courbe.

Solution. B = 1, = un 2 0, = -1 < 0 гипербола .

Le centre du système de coordonnées est au centre de symétrie de la courbe, car il n'y a pas de termes linéaires dans l'équation. Faisons pivoter les axes d'un angle a. D’après la formule (45) on a tan2a = B/(UN - C) = , c'est-à-dire a = 45°. Coefficients de l'équation canonique (46) UN + , C+ sont déterminés par l'équation (48) : t 2 = 1 ou t 1,2 = 1 UN + = 1, C+ = -1, c'est-à-dire
X 2 - Oui 2 = un 2 ou . Donc l'équation 2 xy = UN La figure 2 décrit une hyperbole dont le centre de symétrie est en (0 ; 0). Les axes de symétrie sont situés le long des bissectrices des angles de coordonnées, les axes de coordonnées servent d'asymptotes, les demi-axes de l'hyperbole sont égaux UN.y - 9 =0 ;

9x 2 + oui 2 - 18x + 2oui + 1 = 0;

2x 2 + 4X + oui - 2 = 0;

3x 2 - 6X - oui + 2 = 0;

-x 2 + 4oui 2 - 8x - 9oui + 16 = 0;

4x 2 + 8X - oui - 5 = 0;

9x 2 - oui 2 + 18x + 2oui - 1 = 0;

9x 2 - 4oui 2 + 36x + 16oui - 16 = 0.

Établissons un système de coordonnées rectangulaires sur le plan et considérons l'équation générale du deuxième degré

dans lequel
.

L'ensemble de tous les points du plan dont les coordonnées satisfont à l'équation (8.4.1) est appelé courbé (doubler) deuxième commande.

Pour toute courbe du second ordre il existe un système de coordonnées rectangulaires, dit canonique, dans lequel l'équation de cette courbe a l'une des formes suivantes :

1)
(ellipse);

2)
(ellipse imaginaire);

3)
(une paire de lignes qui se croisent imaginaires) ;

4)
(hyperbole);

5)
(une paire de lignes qui se croisent) ;

6)
(parabole);

7)
(une paire de lignes parallèles);

8)
(une paire de lignes parallèles imaginaires) ;

9)
(une paire de lignes coïncidentes).

Les équations 1) à 9) sont appelées équations canoniques des courbes du second ordre.

Résoudre le problème de la réduction de l'équation d'une courbe du second ordre à une forme canonique implique de trouver l'équation canonique de la courbe et le système de coordonnées canonique. La réduction à la forme canonique permet de calculer les paramètres de la courbe et de déterminer son emplacement par rapport au système de coordonnées d'origine. Transition du système de coordonnées rectangulaires d'origine
à canonique
effectué en faisant pivoter les axes du système de coordonnées d'origine autour du point À PROPOSà un certain angle  et translation parallèle ultérieure du système de coordonnées.

Invariants de courbe du second ordre(8.4.1) sont de telles fonctions des coefficients de son équation dont les valeurs ne changent pas lors du passage d'un système de coordonnées rectangulaires à un autre du même système.

Pour une courbe du second ordre (8.4.1), la somme des coefficients des coordonnées au carré

,

déterminant composé de coefficients de termes dominants

et déterminant du troisième ordre

sont des invariants.

La valeur des invariants s, ,  peut être utilisée pour déterminer le type et composer l'équation canonique de la courbe du second ordre (tableau 8.1).

Tableau 8.1

Classification des courbes du second ordre basées sur des invariants

Regardons de plus près l'ellipse, l'hyperbole et la parabole.

Ellipse(Fig. 8.1) est le lieu géométrique des points du plan pour lequel la somme des distances à deux points fixes
cet avion, appelé foyers d'ellipse, est une valeur constante (supérieure à la distance entre les foyers). Dans ce cas, la coïncidence des foyers de l'ellipse n'est pas exclue. Si les foyers coïncident, alors l’ellipse est un cercle.

La demi-somme des distances d'un point d'une ellipse à ses foyers est notée UN, la moitié des distances entre les foyers – Avec. Si un système de coordonnées rectangulaires sur un plan est choisi pour que les foyers de l'ellipse soient situés sur l'axe À PROPOSx symétriquement par rapport à l'origine, alors dans ce système de coordonnées l'ellipse est donnée par l'équation

, (8.4.2)

appelé équation canonique de l'ellipse, Où
.

Riz. 8.1

Avec le choix spécifié d'un système de coordonnées rectangulaires, l'ellipse est symétrique par rapport aux axes de coordonnées et à l'origine. Les axes de symétrie d'une ellipse sont appelés axes, et le centre de symétrie est centre de l'ellipse. En même temps, les axes de l'ellipse sont souvent appelés chiffres 2 un et 2 b, et les chiffres un Et b – grand Et petit axe respectivement.

Les points d'intersection d'une ellipse avec ses axes sont appelés sommets de l'ellipse. Les sommets de l'ellipse ont des coordonnées ( UN, 0), (–UN, 0), (0, b), (0, –b).

Excentricité de l'ellipse numéro appelé

. (8.4.3)

Depuis 0  c < un, excentricité de l'ellipse 0  < 1, причем у окружности  = 0. Перепишем равенство (8.4.3) в виде

.

Cela montre que l'excentricité caractérise la forme d'une ellipse : plus  est proche de zéro, plus l'ellipse ressemble à un cercle ; à mesure que  augmente, l’ellipse devient plus allongée.

Laisser
– point arbitraire de l'ellipse,
Et
– distance du point M. avant les tours F 1 et F 2 respectivement. Nombres r 1 et r 2 sont appelés rayons focaux d'un point M. ellipse et sont calculés à l'aide des formules

Directrices différent d'un cercle ellipse avec l'équation canonique (8.4.2) deux droites sont appelées

.

Les directrices de l'ellipse sont situées à l'extérieur de l'ellipse (Fig. 8.1).

Rapport du rayon focal pointsM.ellipse à distance  de cette ellipse (le foyer et la directrice sont considérés comme correspondants s'ils sont situés du même côté du centre de l'ellipse).

Hyperbole(Fig. 8.2) est le lieu géométrique des points du plan pour lequel le module de la différence des distances à deux points fixes Et cet avion, appelé astuces d'hyperbole, est une valeur constante (différente de zéro et inférieure à la distance entre les foyers).

Que la distance entre les foyers soit de 2 Avec, et le module spécifié de la différence de distance est égal à 2 UN. Choisissons un système de coordonnées rectangulaires de la même manière que pour l'ellipse. Dans ce système de coordonnées, l'hyperbole est donnée par l'équation

, (8.4.4)

appelé équation canonique de l'hyperbole, Où
.

Riz. 8.2

Avec ce choix d'un repère rectangulaire, les axes de coordonnées sont les axes de symétrie de l'hyperbole, et l'origine est son centre de symétrie. Les axes de symétrie d'une hyperbole sont appelés axes, et le centre de symétrie est centre de l'hyperbole. Rectangle à côtés 2 un et 2 b, situé comme indiqué sur la Fig. 8.2, appelé rectangle de base de l'hyperbole. Numéros 2 un et 2 b sont les axes de l'hyperbole et les nombres un Et b- son arbres d'essieu. Les lignes droites, qui sont la continuation des diagonales du rectangle principal, forment asymptotes d'une hyperbole

.

Points d'intersection de l'hyperbole avec l'axe Bœuf sont appelés sommets d'une hyperbole. Les sommets de l'hyperbole ont des coordonnées ( UN, 0), (–UN, 0).

Excentricité de l'hyperbole numéro appelé

. (8.4.5)

Depuis Avec > un, excentricité de l'hyperbole  > 1. Réécrivons l'égalité (8.4.5) sous la forme

.

Cela montre que l'excentricité caractérise la forme du rectangle principal et, par conséquent, la forme de l'hyperbole elle-même : plus  est petit, plus le rectangle principal s'étend, et après lui l'hyperbole elle-même le long de l'axe Bœuf.

Laisser
– point arbitraire de l'hyperbole,
Et
– distance du point M. avant les tours F 1 et F 2 respectivement. Nombres r 1 et r 2 sont appelés rayons focaux d'un point M. hyperboles et sont calculés à l'aide des formules

Directrices hyperboles avec l'équation canonique (8.4.4) deux droites sont appelées

.

Les directrices de l'hyperbole coupent le rectangle principal et passent entre le centre et le sommet correspondant de l'hyperbole (Fig. 8.2).

À PROPOS rapport du rayon focal pointsM. hyperboles à distance de ce point à celui correspondant au foyer la directrice est égale à l'excentricité de cette hyperbole (le foyer et la directrice sont considérés comme correspondants s'ils sont situés du même côté du centre de l'hyperbole).

Parabole(Fig. 8.3) est le lieu géométrique des points dans le plan pour lequel la distance à un point fixe F (foyer d'une parabole) de ce plan est égale à la distance à une ligne droite fixe ( directrices d'une parabole), également situé dans le plan considéré.

Choisissons le début À PROPOS système de coordonnées rectangulaires au milieu du segment [ FD], qui est une perpendiculaire floue Fà la directrice (on suppose que le foyer n'appartient pas à la directrice), et les axes Bœuf Et Oy Dirigons-le comme indiqué sur la Fig. 8.3. Soit la longueur du segment [ FD] est égal p. Puis dans le système de coordonnées choisi
Et équation canonique de la parabole on dirait

. (8.4.6)

Ampleur p appelé paramètre de parabole.

Une parabole possède un axe de symétrie appelé l'axe de la parabole. Le point d'intersection d'une parabole avec son axe s'appelle le sommet de la parabole. Si une parabole est donnée par son équation canonique (8.4.6), alors l'axe de la parabole est l'axe Bœuf. Évidemment, le sommet de la parabole est l’origine.

Exemple 1. Point UN= (2, –1) appartient à l'ellipse, point F= (1, 0) est son focus, le correspondant F la directrice est donnée par l'équation
. Écrivez une équation pour cette ellipse.

Solution. Nous considérerons que le système de coordonnées est rectangulaire. Puis la distance du point UNà la directrice
conformément à la relation (8.1.8), dans laquelle


, est égal

.

Distance du point UN se concentrer F est égal

,

ce qui permet de déterminer l'excentricité de l'ellipse

.

Laisser M. = (x, oui) est un point arbitraire de l'ellipse. Puis la distance
du point M.à la directrice
selon la formule (8.1.8) est égal à

et la distance du point M. se concentrer F est égal

.

Puisque pour tout point de l’ellipse la relation est une quantité constante égale à l’excentricité de l’ellipse, on a donc

,

Exemple 2. La courbe est donnée par l'équation

dans un système de coordonnées rectangulaires. Trouvez le système de coordonnées canonique et l'équation canonique de cette courbe. Déterminez le type de courbe.

Solution. Forme quadratique
a une matrice

.

Son polynôme caractéristique

a des racines  1 = 4 et  2 = 9. Donc, dans la base orthonormée des vecteurs propres de la matrice UN la forme quadratique considérée a la forme canonique

.

Passons à la construction d'une matrice de transformation orthogonale de variables, amenant la forme quadratique considérée à la forme canonique indiquée. Pour ce faire, nous construirons des systèmes fondamentaux de solutions à des systèmes d'équations homogènes
et les orthonormaliser.

À
ce système ressemble à

Sa solution générale est
. Il y a une variable libre ici. Par conséquent, le système fondamental de solutions consiste en un seul vecteur, par exemple le vecteur
. En le normalisant, nous obtenons le vecteur

.

À
construisons également un vecteur

.

Vecteurs Et sont déjà orthogonaux, puisqu'ils se rapportent à différentes valeurs propres de la matrice symétrique UN. Ils constituent la base canonique orthonormée d'une forme quadratique donnée. La matrice orthogonale requise (matrice de rotation) est construite à partir des colonnes de leurs coordonnées

.

Vérifions si la matrice est trouvée correctement R. selon la formule
, Où
– matrice de forme quadratique dans la base
:

Matrice R. trouvé correctement.

Transformons les variables

et écrivez l'équation de cette courbe dans un nouveau système de coordonnées rectangulaires avec les anciens vecteurs centre et direction
:

Où
.

Nous avons obtenu l'équation canonique de l'ellipse

.

Du fait que la transformation résultante des coordonnées rectangulaires est déterminée par les formules

,

,

système de coordonnées canonique
a un début
et vecteurs de direction
.

Exemple 3.À l'aide de la théorie des invariants, déterminez le type et créez l'équation canonique de la courbe

Solution. Depuis

,

conformément au tableau. 8.1, nous concluons qu’il s’agit d’une hyperbole.

Puisque s = 0, le polynôme caractéristique de la matrice est de forme quadratique

Ses racines
Et
permettons d'écrire l'équation canonique de la courbe

Où AVEC est trouvé à partir de la condition

,

.

L'équation canonique requise de la courbe

.

Dans les tâches de cette section, les coordonnéesx, ouisont supposés rectangulaires.

8.4.1. Pour les ellipses
Et
trouver:

a) les arbres de roue ;

b) astuces ;

c) excentricité ;

d) équations directrices.

8.4.2. Écrivez des équations pour une ellipse, connaissant son objectif
, correspondant à la directrice x= 8 et excentricité . Trouvez le deuxième foyer et la deuxième directrice de l'ellipse.

8.4.3. Écrivez une équation pour une ellipse dont les foyers ont les coordonnées (1, 0) et (0, 1) et dont le grand axe est égal à deux.

8.4.4. Étant donné une hyperbole
. Trouver:

a) arbres de roue un Et b;

b) astuces ;

c) excentricité ;

d) équations d'asymptotes ;

e) équations directrices.

8.4.5. Étant donné une hyperbole
. Trouver:

a) arbres de roue UN Et b;

b) astuces ;

c) excentricité ;

d) équations d'asymptotes ;

e) équations directrices.

8.4.6. Point
appartient à une hyperbole dont le foyer
, et la directrice correspondante est donnée par l'équation
. Écrivez une équation pour cette hyperbole.

8.4.7. Écrire une équation pour une parabole étant donné son foyer
et directrice
.

8.4.8. Étant donné le sommet d'une parabole
et l'équation directrice
. Écrivez une équation pour cette parabole.

8.4.9. Écrivez une équation pour une parabole dont le foyer est à

et la directrice est donnée par l'équation
.

8.4.10. Écrivez une équation du second ordre pour la courbe, connaissant son excentricité
, se concentrer
et la directrice correspondante
.

8.4.11. Déterminez le type de courbe du second ordre, composez son équation canonique et trouvez le système de coordonnées canonique :

G)
;

8.4.12.

est une ellipse. Trouver les longueurs des demi-axes et l'excentricité de cette ellipse, les coordonnées du centre et des foyers, créer des équations pour les axes et les directrices.

8.4.13. Montrer que la courbe du second ordre donnée par l’équation

est une hyperbole. Trouver les longueurs des demi-axes et l'excentricité de cette hyperbole, les coordonnées du centre et des foyers, créer des équations pour les axes, directrices et asymptotes.

8.4.14. Montrer que la courbe du second ordre donnée par l’équation

,

est une parabole. Trouver le paramètre de cette parabole, les coordonnées des sommets et le foyer, écrire les équations de l'axe et de la directrice.

8.4.15. Réduisez chacune des équations suivantes à la forme canonique. Dessinez dans le dessin la courbe du second ordre correspondante par rapport au système de coordonnées rectangulaires d'origine :

8.4.16. À l'aide de la théorie des invariants, déterminez le type et créez l'équation canonique de la courbe.