Après avoir considéré les mouvements de translation et de rotation, nous pouvons établir une analogie entre eux. La cinématique du mouvement de translation utilise un chemin s, vitesse  et accélération UN. Leur rôle dans le mouvement de rotation est joué par l'angle de rotation , la vitesse angulaire  et l'accélération angulaire ε. Dans la dynamique du mouvement de translation, les concepts de force et de masse sont utilisés T et impulsion Dans un mouvement de rotation, le rôle de la force est joué par le moment
forces, le rôle de la masse - moment d'inertie je z et le rôle du moment - moment cinétique Connaissant les formules du mouvement de translation, il est facile d'écrire les formules du mouvement de rotation. Par exemple, avec un mouvement uniforme, la distance parcourue est calculée par la formule : s =  t, et avec un angle de rotation de rotation - selon la formule  =  t. Deuxième loi de Newton
Et
et la loi fondamentale de la dynamique du mouvement de rotation est
Et
Lors d’un mouvement de translation, l’élan du corps est égal à
et pendant le mouvement de rotation, le moment cinétique est
Cette analogie peut être poursuivie plus loin.

Travail de force lors d’un mouvement de translation. Pouvoir

Soit un corps (point matériel) sous l'action d'une force constante , faisant un angle constant avec la direction du mouvement, se déplace de manière rectiligne dans un système de référence et suit la trajectoire je. Ensuite, comme le montre le cours de physique scolaire, le travail UN cette force se trouve par la formule :

UN= Fl.· parce que  = F je je, (1)

Considérons maintenant le cas général du calcul du travail lorsqu'un corps se déplace en translation le long d'une trajectoire courbe sous l'influence d'une force variable. En route je sélectionner une section élémentaire dl, à l'intérieur duquel la force peut être considérée et l'angle  sont des valeurs constantes et la section elle-même est rectiligne. Puis travailler dA dans cette section on trouve en utilisant la formule (1) : dA = F· dl· cos. Emploi UN sur tout le chemin est égal à la somme du travail dA, c'est-à-dire

(2)

Icône je avec intégral signifie que l'intégration s'effectue tout au long du parcours je.

La formule (2) peut prendre une forme différente si nous utilisons le produit scalaire des vecteurs. Alors l'intégrande dA s'écrira sous la forme : dA = F· dl· cos=
Où est le vecteur du déplacement élémentaire, et

(3)

D'après la formule (1), il ressort clairement que le travail est une quantité algébrique. Le signe du travail dépend de l'angle . Si l'angle  est aigu, alors cos  > 0 et le travail est positif, mais si l'angle  est obtus, le travail est négatif.

L'unité de travail SI est le joule (J). Il est introduit à partir de la formule (1), dans laquelle cos  = 1 est supposé 1 J. le travail effectué par une force de 1 N sur une trajectoire de 1 m, à condition que les directions de la force et du déplacement coïncident.

Pour caractériser la vitesse de travail, on introduit la notion de puissance, égale au travail effectué par unité de temps. Si une période élémentaire dt le travail élémentaire est fait dA, alors la puissance R.égal à

(4)

En unités SI, la puissance est mesurée en watts (W). Comme il ressort de (4), 1 W = 1 J / 1 s, c'est-à-dire 1 W- C'est la puissance à laquelle 1 J de travail est effectué en 1 s.

Travail de force lors d'un mouvement de rotation

Considérons un corps rigide qui, sous l'action d'une force variable tourne autour d'un axe z sous un certain angle. Cette force crée un couple M z, faisant tourner le corps. La force est dirigée tangentiellement au cercle le long duquel se déplace le point d'application de la force. Par conséquent, angle = 0. En tenant compte de cela, par analogie avec la formule du travail mécanique (voir (2)), on trouve l'expression par laquelle le travail lors du mouvement de rotation est calculé :

(5)

Le travail sera positif si la direction de la composante tangentielle de la force coïncide avec le sens de rotation, et négatif si elles sont dans le sens opposé.

Plan de la conférence

Moment d'inertie.

Moment de pouvoir. Équation de base pour la dynamique du mouvement de rotation.

Moment d'impulsion. Loi de conservation du moment cinétique.

Travail et énergie cinétique lors du mouvement de rotation.

1. Moment d'inertie.

Lorsqu'on considère le mouvement de rotation, il est nécessaire d'introduire de nouveaux concepts physiques : moment d'inertie, moment de force, moment d'impulsion.

Le moment d'inertie est une mesure de l'inertie d'un corps lors d'un mouvement de rotation du corps.

Moment d'inertie d'un point matériel par rapport à un axe de rotation fixe est égal au produit de sa masse par le carré de la distance à l'axe de rotation considéré (Fig. 1) :

dépend uniquement de la masse du point matériel et de sa position par rapport à l'axe de rotation et ne dépend pas de la présence de rotation elle-même.

Le moment d'inertie est une grandeur scalaire et additive, donc le moment d'inertie d'un corps est égal à la somme des moments d'inertie de tous ses points :

.

Dans le cas d'une distribution de masse continue, cette somme se réduit à l'intégrale :

,

où est la masse d'un petit volume corporel
, - la densité corporelle, - distance de l'élément
à l'axe de rotation.

Le moment d'inertie est un analogue de la masse lors d'un mouvement de rotation. Plus le moment d'inertie du corps est grand, plus il est difficile de modifier la vitesse angulaire du corps en rotation. Le moment d'inertie n'a de sens que pour une position donnée de l'axe de rotation. Cela n’a aucun sens de parler simplement de « moment d’inertie ». Ça dépend:

1) à partir de la position de l'axe de rotation ;

2) de la répartition de la masse corporelle par rapport à l'axe de rotation, c'est-à-dire sur la forme du corps et sa taille.

La preuve expérimentale en est l'expérience avec des cylindres roulants.

En intégrant pour certains corps homogènes, on peut obtenir les formules suivantes (l'axe de rotation passe par le centre de masse du corps).

Moment d'inertie d'un cerceau (on néglige l'épaisseur de paroi) ou d'un cylindre creux :

Moment d'inertie d'un disque ou d'un cylindre solide de rayon R :

.

Moment d'inertie du ballon

Moment d'inertie de la tige

E Si le moment d'inertie autour d'un axe passant par le centre de masse est connu pour un corps, alors le moment d'inertie autour de tout axe parallèle au premier se trouve selon Théorème de Steiner: le moment d'inertie d'un corps par rapport à un axe arbitraire est égal au moment d'inertie J 0 par rapport à un axe parallèle à celui donné et passant par le centre de masse du corps, ajouté au produit de la masse corporelle et le carré de la distance entre les axes.

Où d distance du centre de masse À PROPOSà l'axe de rotation (Fig. 2).

Centre de masse- un point imaginaire dont la position caractérise la répartition de la masse d'un corps donné. Le centre de masse d’un corps se déplace de la même manière qu’un point matériel de même masse se déplacerait sous l’influence de toutes les forces extérieures agissant sur un corps donné.

Le concept de moment d'inertie a été introduit en mécanique par le scientifique national L. Euler au milieu du XVIIIe siècle et a depuis lors été largement utilisé pour résoudre de nombreux problèmes de dynamique des corps rigides. La valeur du moment d'inertie doit être connue en pratique lors du calcul de divers composants et systèmes rotatifs (volants, turbines, rotors de moteurs électriques, gyroscopes). Le moment d'inertie est inclus dans les équations du mouvement d'un corps (navire, avion, projectile, etc.). Elle est déterminée lorsqu'on veut connaître les paramètres du mouvement de rotation d'un avion autour du centre de masse sous l'influence d'une perturbation extérieure (rafale de vent, etc.).

Lorsqu’on observe des mouvements complexes, comme celui du corps humain (marcher, courir, sauter, etc.), il semble difficile, voire impossible, de décrire le mouvement de tous ses points. Cependant, en analysant ces mouvements, on peut remarquer qu'ils sont constitués de mouvements plus simples - des mouvements de translation et de rotation.

Les mécanismes du mouvement de translation sont connus du lecteur, c'est pourquoi la section commence par une considération du mouvement de rotation. Le plus simple est la rotation d’un corps rigide autour d’un axe fixe. Ce cas permet de se familiariser avec les spécificités, la terminologie et les lois du mouvement de rotation.

5.1. CINÉMATIQUE DU MOUVEMENT DE ROTATION D'UN CORPS ABSOLUMENT RIGIDE AUTOUR D'UN AXE FIXE

Un corps absolument rigide est un corps dont la distance entre deux points quelconques est constante.

Les dimensions et la forme d'un corps absolument rigide ne changent pas lorsqu'il se déplace.

Le concept de « corps absolument rigide » est une abstraction physique, puisque tout corps est capable de se déformer. Cependant, dans de nombreux cas, la déformation peut être négligée.

Le cas le plus simple de mouvement de rotation d'un corps absolument rigide est la rotation autour d'un axe fixe. Il s'agit d'un mouvement dans lequel les points du corps se déplacent en cercles dont les centres se trouvent sur une ligne droite, appelée axe de rotation.

On sait que dans certains cas, pour caractériser le mouvement d'un corps, il n'est pas nécessaire d'indiquer le mouvement de tous ses points ; ainsi, par exemple, dans un mouvement de translation, il suffit d'indiquer le mouvement d'un point quelconque du corps.

Lors d'un mouvement de rotation autour d'un axe, les points du corps se déplacent selon des trajectoires différentes, mais pendant le même temps, tous les points et le corps lui-même tournent selon le même angle. Pour les caractéristiques de rotation

dessiner dans un plan perpendiculaire à l'axe un rayon vecteur jusqu'à un certain point je(Fig. 5.1). La dépendance temporelle de l'angle α de rotation du rayon vecteur par rapport à une direction sélectionnée OX est l'équation du mouvement de rotation d'un corps rigide autour d'un axe fixe :

La vitesse de rotation d'un corps est caractérisée par une vitesse angulaire égale à la dérivée première de l'angle de rotation du rayon vecteur par rapport au temps :

La vitesse angulaire est un vecteur dirigé le long de l'axe de rotation et lié au sens de rotation par la règle de la vis droite (Fig. 5.2). Le vecteur vitesse angulaire, contrairement aux vecteurs vitesse et force, est glissant : il n'a pas de point d'application précis, et il peut être situé n'importe où sur l'axe de rotation. Ainsi, spécifier le vecteur ω indique la position de l'axe de rotation, le sens de rotation et l'amplitude de la vitesse angulaire.

Le taux de variation de la vitesse angulaire est caractérisé par une accélération angulaire égale à la dérivée première de la vitesse angulaire par rapport au temps :

ou sous forme vectorielle :

D'après (5.4), il ressort clairement que le vecteur d'accélération angulaire coïncide en direction avec un changement élémentaire et assez faible du vecteur vitesse angulaire dω : avec une rotation accélérée, l'accélération angulaire est dirigée dans le même sens que la vitesse angulaire, avec une rotation lente - dans le sens opposé.

Puisque le déplacement angulaire de tous les points d'un corps absolument rigide est le même, alors, d'après (5.2) et (5.3), tous les points du corps ont en même temps la même vitesse angulaire et la même accélération angulaire. Les caractéristiques linéaires - déplacement, vitesse, accélération - sont différentes selon les points. Indiquons sous forme scalaire la relation, qui peut être dérivée indépendamment, entre les caractéristiques linéaires et angulaires du i-ème point se déplaçant dans un cercle de rayon r je :

Riz. 5.3

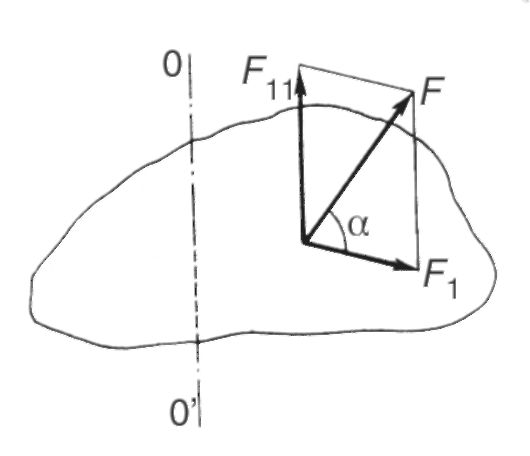
En conclusion, nous présentons les formules de la cinématique du mouvement de rotation d'un corps rigide autour d'un axe fixe obtenues en intégrant les expressions correspondantes :

équation du mouvement de rotation uniforme[cm. (5.2)] :

dépendance de la vitesse angulaire au temps dans un mouvement de rotation uniforme[cm. (5.3)] :

équation du mouvement de rotation uniformément alterné[cm. (5.1) et (5.6)] :

Il est utile de comparer ces formules avec des dépendances similaires pour le mouvement de translation.

5.2. CONCEPTS DE BASE. ÉQUATION POUR LA DYNAMIQUE DU MOUVEMENT DE ROTATION

Moment de force_

Laissez jusqu'à un certain point je force appliquée à un corps rigide F^, situé dans un plan perpendiculaire à l'axe de rotation (Fig. 5.4).

Le moment de force par rapport à l'axe de rotation est le produit vectoriel du rayon vecteur du point i et de la force :

En le développant, vous pouvez écrire :

Où β - angle entre les vecteurs r je Et F i . Depuis l'épaule de la force h je = r je sinβ (voir Fig. 5.4), alors

Si la force agit selon un certain angle α par rapport au plan de rotation (Fig. 5.5), elle peut alors être décomposée en deux composantes. L'un d'eux se situe dans un plan perpendiculaire à l'axe de rotation, et l'autre est parallèle à cet axe et n'affecte pas la rotation du corps (dans le cas réel, il n'agit que sur les roulements). De plus, seules les forces situées dans le plan perpendiculaire à l’axe de rotation seront considérées.

Riz. 5.4

Riz. 5.5

Travailler en mouvement de rotation

Laisser sous l'action de la force F je(voir Fig. 5.4) le corps tourne d'un angle dα suffisamment petit. Trouvons le travail effectué par cette force.

L’expression du travail de force connue au lycée dans ce cas doit s’écrire comme suit :

Donc,

le travail élémentaire de force en mouvement de rotation est égal au produit du moment de force et de l'angle élémentaire de rotation du corps.

Si plusieurs forces agissent sur un corps, alors le travail élémentaire effectué par toutes est déterminé de la même manière que (5.12) :

Où M- le moment total de toutes les forces extérieures agissant sur le corps.

Si, lorsque le corps tourne, la position du rayon vecteur passe de α 1 à α 2, alors le travail des forces externes peut être trouvé en intégrant l'expression (5.13) :

Moment d'inertie

La mesure de l'inertie des corps lors d'un mouvement de translation est la masse. L'inertie des corps lors d'un mouvement de rotation dépend non seulement de la masse, mais aussi de sa répartition dans l'espace par rapport à l'axe. La mesure de l'inertie d'un corps lors d'une rotation est caractérisée par le moment d'inertie du corps par rapport à l'axe de rotation. Signalons d'abord que

Le moment d'inertie d'un point matériel par rapport à l'axe de rotation est une valeur égale au produit de la masse du point par le carré de sa distance à l'axe :

Le moment d'inertie d'un corps par rapport à un axe est la somme des moments d'inertie de tous les points matériels qui composent le corps :

A titre d'exemple, nous dérivons la formule moment d'inertie d'une fine tige homogène longueur je et la masse T par rapport à l'axe perpendiculaire à la tige et passant par son milieu (Fig. 5.6). Choisissons une section de tige suffisamment petite d'une longueur dx et la masse dm,éloigné de l'axe 00" d'une distance X. En raison de la petitesse de cette zone, elle peut être considérée comme un point matériel, son moment d'inertie [voir. (5.15)] est égal à :

La masse d'une section élémentaire est égale au produit de la densité linéaire t/l, multiplié par la longueur de la section élémentaire : dm= (m/l) dx En substituant cette expression dans (5.18), on obtient

Pour trouver le moment d'inertie de la tige entière, on intègre l'expression (5.19) sur la tige entière, soit allant de -1/2 à +1/2 :

Présentons des expressions pour les moments d'inertie de divers corps de masse symétriques T :

cylindre creux homogène(cerceau) avec rayon intérieur r et externe R. par rapport à l'axe OO", coïncidant avec l'axe géométrique du cylindre (Fig. 5.7) :

continu homogène cylindre (r = 0) ou disque [voir (5.21)] :

boule homogène par rapport à un axe passant par son centre :

parallélépipède rectangle par rapport à l'axe OO" passant par son centre perpendiculaire au plan de la base (Fig. 5.8) :

Dans tous les exemples ci-dessus, l’axe de rotation passe par le centre de masse du corps. Lorsque vous résolvez des problèmes pour déterminer le moment d’inertie d’un corps autour d’un axe qui ne passe pas par le centre de masse, vous pouvez utiliser le théorème de Huygens. D'après ce théorème, le moment d'inertie du corps par rapport à un axe OO :

où J 0 est le moment d'inertie autour d'un axe parallèle passant par le centre de masse du corps OO" ; T- le poids corporel ; d- la distance entre deux axes parallèles (Fig. 5.9). L'unité du moment d'inertie est kilogramme mètre carré(kg-m2).

Élan

moment d'impulsion(moment angulaire)un point matériel tournant autour d'un certain axe est appelé valeur égale au produit de l'impulsion du point à sa distance de l'axe de rotation :

Le moment cinétique d'un corps tournant autour d'un certain axe est égal à la somme du moment cinétique des points qui composent le corps :

Puisque la vitesse angulaire de tous les points d'un corps rigide est la même, en retirant ω du signe de la somme [voir. (5.29)], on obtient :

(/ - moment d'inertie du corps par rapport à l'axe), ou sous forme vectorielle :

Ainsi, le moment cinétique est égal au produit du moment d’inertie d’un point et de la vitesse angulaire. Il s'ensuit que les directions des vecteurs moment cinétique et vitesse angulaire coïncident. L'unité du moment cinétique est kilogramme-mètre carré par seconde(kg ? m2 ? s -1).

Il est utile de comparer la formule (5.31) avec une formule similaire pour le moment en mouvement de translation.

Énergie cinétique d'un corps en rotation

Lorsqu'un corps tourne, son énergie cinétique est constituée des énergies cinétiques de points individuels du corps. Pour un solide :

Il est utile de comparer l’expression (5.32) avec une expression similaire pour le mouvement de translation.

En différenciant (5.32), on obtient un changement élémentaire d'énergie cinétique en mouvement de rotation :

Équation de base pour la dynamique du mouvement de rotation

Laissez le corps rigide, sur lequel des forces extérieures ont agi, tourner d'un angle da suffisamment petit. Assumons le travail élémentaire de toutes les forces extérieures lors d'une telle rotation [voir. (5.13)] à un changement élémentaire de l'énergie cinétique [voir. (5.33)] : M dα = Jω dω , d'où :

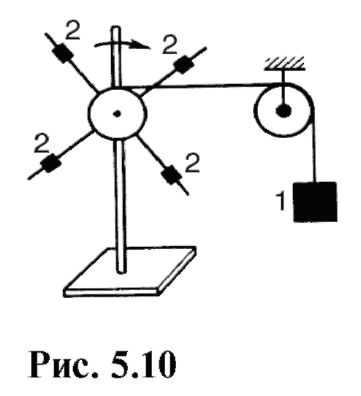
C'est ça basiqueéquation de la dynamique du mouvement de rotation. D'après (5.35), il ressort clairement que le moment d'inertie caractérise les propriétés inertielles d'un corps en mouvement de rotation : sous l'action de forces extérieures, l'accélération angulaire du corps est plus grande, plus le moment d'inertie du corps est petit.

L'équation de base du mouvement de rotation joue le même rôle que la deuxième loi de Newton pour le mouvement de translation. Les grandeurs physiques incluses dans cette équation sont respectivement analogues à la force, à la masse et à l’accélération.

Depuis (5.34) il s’ensuit que :

La dérivée du moment cinétique d'un corps par rapport au temps est égale au moment résultant de toutes les forces extérieures.

La dépendance de l'accélération angulaire sur le moment de force et le moment d'inertie peut être démontrée avec

avec la puissance de l'appareil illustré à la Fig. 5.10. Sous charge 1, suspendue à un fil jeté sur un bloc, la croix tourne rapidement. Déplacer des poids 2 à différentes distances de l'axe de rotation, vous pouvez modifier le moment d'inertie de la traverse. Modification des charges, c'est-à-dire moments de forces, et le moment d'inertie, on peut vérifier que l'accélération angulaire augmente avec une augmentation du moment de force ou une diminution du moment d'inertie.

5.3. LOI DE CONSERVATION DE LA MOMENTUM

Considérons le cas particulier du mouvement de rotation, lorsque le moment total des forces extérieures est nul. Comme le montre (5.37), dL/dt= 0 à M = 0, d'où

Cette disposition est connue sous le nom loi de conservation du moment cinétique : si le moment total de toutes les forces extérieures agissant sur un corps est égal à zéro, alors le moment cinétique de ce corps reste constant.

En omettant la preuve, notons que la loi de conservation du moment cinétique n'est pas valable seulement pour un corps absolument rigide.

Les applications les plus intéressantes de cette loi sont associées à la rotation d'un système de corps autour d'un axe commun. Dans ce cas, il faut prendre en compte le caractère vectoriel du moment cinétique et des vitesses angulaires. Ainsi, pour un système composé de N corps tournant autour d'un axe commun, la loi de conservation du moment cinétique peut s'écrire sous la forme :

Regardons quelques exemples illustrant cette loi.

Un gymnaste effectuant un saut périlleux (Fig. 5.11) dans la phase initiale plie les genoux et les presse contre sa poitrine, réduisant ainsi le moment d'inertie et augmentant la vitesse angulaire de rotation autour d'un axe horizontal passant par le centre de masse. A la fin du saut, le corps se redresse, le moment d'inertie augmente et la vitesse angulaire diminue. Un patineur effectuant une rotation autour d'un axe vertical (Fig. 5.12) au début de la rotation rapproche ses mains du corps, réduisant ainsi le moment d'inertie et augmentant la vitesse angulaire. A la fin de la rotation, le processus inverse se produit : lors du déplacement des bras, le moment d'inertie augmente et la vitesse angulaire diminue, ce qui facilite l'arrêt.

Le même phénomène peut être démontré sur un banc Joukovski, qui est une plate-forme horizontale légère tournant avec un faible frottement autour d'un axe vertical. Lorsque la position des aiguilles change, le moment d'inertie et la vitesse angulaire changent (Fig. 5.13), le moment cinétique reste constant. Pour renforcer l'effet de démonstration, des haltères sont placés entre les mains d'une personne. Sur le banc Joukovski, vous pourrez démontrer le caractère vectoriel de la loi de conservation du moment cinétique.

L'expérimentateur, debout sur un banc fixe, reçoit d'un assistant une roue de vélo tournant autour d'un axe vertical (Fig. 5.14, à gauche). Dans ce cas, le moment cinétique de la personne et du système plate-forme-roue est déterminé uniquement par le moment cinétique de la roue :

ici J h est le moment d'inertie de la personne et de la plateforme ; J K et ω κ - moment d'inertie et vitesse angulaire de la roue. Puisque le moment des forces externes par rapport à l’axe vertical est nul, alors L est préservé (L = const).

Si l'expérimentateur fait tourner l'axe de rotation de la roue de 180° (Fig. 5.14, à droite), alors le moment cinétique de la roue sera dirigé à l'opposé de l'original et égal à J K ω K. Puisque le vecteur moment cinétique de la roue change, et que le moment cinétique du système est conservé, le moment cinétique de la personne et de la plate-forme doit inévitablement changer, il ne sera plus égal à zéro 1 . Le moment cinétique du système dans ce cas

1 Un léger décalage entre l'axe des roues et l'axe de rotation de la plateforme peut être négligé.

À l'aide de la formule (5.42), il est possible d'estimer approximativement le moment d'inertie du corps humain avec la plate-forme, pour lequel il faut mesurer ω κ, ω 4 et trouver J k.

La méthode de mesure des vitesses angulaires de rotation uniforme est connue du lecteur. Connaissant la masse de la roue et en supposant que la masse est principalement répartie le long de la jante, à l'aide de la formule (5.22), nous pouvons déterminer J k.

Pour réduire l'erreur, vous pouvez alourdir la jante d'une roue de vélo en y posant des pneus spéciaux. La personne doit être positionnée symétriquement par rapport à l'axe de rotation.

Une version plus simple de la démonstration envisagée est qu'une personne debout sur un banc Joukovski fait tourner elle-même une roue qu'elle tient sur un axe vertical. Dans ce cas, la personne et la plate-forme commencent à tourner dans des directions opposées (Fig. 5.15).

5.4. LE CONCEPT D'AXES LIBRE DE ROTATION

Un corps tournant autour d’un axe fixe agit généralement sur des roulements ou d’autres dispositifs qui maintiennent constante la position de cet axe. À des vitesses angulaires et des moments d'inertie élevés, ces effets peuvent être importants. Cependant, dans n'importe quel corps, il est possible de sélectionner des axes dont la direction pendant la rotation sera maintenue sans aucun dispositif spécial. Pour comprendre à quelle condition le choix de tels axes doit satisfaire, considérons l'exemple suivant.

En comparant (5.43) avec les coordonnées du centre de masse, on remarque que les forces agissant sur l'axe s'équilibrent si l'axe de rotation passe par le centre de masse.

Un corps de forme arbitraire possède toujours au moins trois axes perpendiculaires entre eux passant par le centre de masse, qui peuvent être des axes de rotation libres. Ces axes sont appelés axes principaux d’inertie. Bien que les trois axes d’inertie principaux soient libres, la rotation la plus stable se fera autour de l’axe ayant le moment d’inertie le plus grand. Le fait est qu'en raison de l'action inévitable de forces extérieures, telles que le frottement, et également du fait qu'il est difficile de régler exactement la rotation autour d'un certain axe, la rotation autour des axes libres restants est instable.

Dans certains cas, lorsqu'un corps tourne autour d'un axe libre avec un petit moment d'inertie, il change lui-même cet axe en l'axe avec le moment le plus élevé.

Ce phénomène est démontré par l'expérience suivante. Une tige cylindrique est suspendue au moteur électrique par un fil, qui peut tourner autour de son axe géométrique (Fig. 5.17, a). Moment d'inertie autour de cet axe J 1 = mR 2 /2.À une vitesse angulaire suffisamment élevée, le bâton changera de position (Fig. 5.17, b). Le moment d'inertie par rapport au nouvel axe est égal à J2 = ml 2/12. Si l 2 >6R 2, alors J 2 > J 1. La rotation autour du nouvel axe sera stable.

Le lecteur peut vérifier indépendamment par expérience que la rotation d'une boîte d'allumettes lancée est stable par rapport à un axe perpendiculaire à la plus grande face, et instable ou moins stable par rapport aux axes perpendiculaires aux autres faces (voir Fig. 5.8).

La rotation des animaux et des humains en vol libre et lors de divers sauts s'effectue autour d'axes libres avec le moment d'inertie le plus élevé ou le plus faible. Puisque la position du centre de masse dépend de la posture du corps, il y aura différents axes libres pour différentes postures.

5.5. LE CONCEPT DE DEGRÉS DE LIBERTÉ

La position d'un point matériel libre dans l'espace est spécifiée par trois coordonnées indépendantes : x, y, z. Si le point n'est pas libre, mais se déplace, par exemple, le long d'une surface, alors les trois coordonnées ne seront pas indépendantes.

Les variables indépendantes caractérisant la position d'un système mécanique sont appelées degrés de liberté.

Un point matériel libre possède trois degrés de liberté, dans l'exemple considéré - deux degrés de liberté. Puisqu’une molécule d’un gaz monoatomique peut être considérée comme un point matériel, une telle molécule libre possède également trois degrés de liberté.

Quelques exemples supplémentaires.

Deux points matériels 1 et 2 sont reliés rigidement l'un à l'autre. La position des deux points est spécifiée par six coordonnées x 1, y 1, z 1, x 2, y 2, z 2, qui sont soumis à une contrainte et une connexion, exprimées mathématiquement sous la forme d'une équation :

Physiquement, cela signifie que la distance entre les points matériels est toujours l. Dans ce cas, le nombre de degrés de liberté est de 5. L'exemple considéré est un modèle de molécule diatomique.

Trois points matériels 1, 2 et 3 sont rigidement reliés les uns aux autres. ami. Neuf coordonnées caractérisent la position d'un tel système : x 1 , oui 1 , z 1, x 2 , oui 2 , z2, x3 oui 3 , z 3 . Cependant, trois connexions entre points déterminent l’indépendance de seulement six coordonnées. Le système possède six degrés de liberté. Puisque la position de trois points qui ne se trouvent pas sur la même ligne droite détermine de manière unique la position d’un corps rigide, celui-ci possède six degrés de liberté.

Les molécules triatomiques et polyatomiques ont le même nombre de degrés de liberté (six), si ces molécules sont considérées comme des formations rigides.

1 Si une valeur imaginaire est obtenue pour la coordonnée dépendante de (5.44), cela signifie que les coordonnées indépendantes sélectionnées ne correspondent à aucun point situé sur une sphère d'un rayon donné.

Dans les molécules polyatomiques réelles, les atomes sont en mouvement vibratoire, le nombre de degrés de liberté de ces molécules est donc supérieur à six.

Le nombre de degrés de liberté détermine non seulement le nombre de variables indépendantes caractérisant la position du système mécanique, mais aussi, ce qui est très important, le nombre de mouvements indépendants du système. Ainsi, trois degrés de liberté d'un point matériel libre signifient que tout mouvement du point peut être décomposé en mouvements indépendants selon trois axes de coordonnées. Puisqu’un point n’a pas de dimensions, cela n’a aucun sens de parler de sa rotation. Ainsi, un point matériel possède trois degrés de liberté de mouvement de translation. Un point matériel sur un plan, une sphère ou une autre surface possède deux degrés de liberté de mouvement de translation. Le mouvement d'un point matériel le long d'une courbe (un exemple conditionnel est le mouvement d'un train sur des rails) correspond à un degré de liberté de mouvement de translation.

Un corps rigide tournant autour d’un axe fixe possède un degré de liberté de mouvement de rotation. La roue du train a deux degrés de liberté : l'un est un mouvement de rotation et l'autre est un mouvement de translation (déplacement de l'axe de la roue le long du rail). Six degrés de liberté d'un corps rigide signifient que tout mouvement de ce corps peut être décomposé en composantes : le mouvement du centre de masse se décompose en trois mouvements de translation le long des axes de coordonnées, et la rotation consiste en trois rotations plus simples autour des axes de coordonnées passant par le centre de masse.

Sur la fig. 5.18-5.20 montrent des articulations charnières correspondant à un, deux et trois degrés de liberté.

Riz. 5.18

Riz. 5.19

Riz. 5h20

5.6. CENTRIFUGEATION

La centrifugation est le processus de séparation (séparation) de systèmes hétérogènes, par exemple de particules des liquides dans lesquels ils se trouvent, en raison de leur rotation.

Considérons la séparation de systèmes inhomogènes dans un champ de gravité. Supposons qu'il existe une suspension aqueuse de particules de densités variables. Au fil du temps, sous l'action de la gravité et de la poussée d'Archimède F.A. la séparation des particules se produit : les particules de densité supérieure à celle de l'eau coulent, les particules de densité inférieure à celle de l'eau flottent. La force résultante agissant, par exemple, sur une particule individuelle plus dense est égale à :

Où ρ 1 - densité de matière particulaire ; ρ - densité de l'eau ; V- le volume des particules.

Si les valeurs de ρ 1 et ρ diffèrent peu les unes des autres, alors la force Fp est petit et la séparation (dépôt) se produit assez lentement. Dans une centrifugeuse (séparateur), cette séparation est effectuée de force en faisant tourner le milieu séparé.

Considérons la physique de ce phénomène.

Laissez le volume de travail de la centrifugeuse (Fig. 5.21 : a - apparence ; b - diagramme du volume de travail) être complètement occupé par un liquide homogène. Sélectionnons mentalement un petit volume V de ce liquide situé à distance r de l'axe de rotation OO". Avec une rotation uniforme de la centrifugeuse, en plus de la force de gravité et de flottabilité, qui s'équilibrent, une force centripète agit sur le volume sélectionné. C'est la force du liquide entourant le volume. C'est naturellement dirigé vers l'axe de rotation et est égal à :

Où ρ est la densité du liquide.

Supposons maintenant que le volume alloué V est une particule séparée dont la densité de substance est ρ 1 (ρ 1 Φ ρ). La force agissant sur la particule à partir du liquide environnant ne changera pas, comme le montre la formule (5.45).

Pour qu’une particule tourne avec le liquide, elle doit être soumise à une force centripète égale à :

Où m1 est la masse de la particule et ρ 1 est la densité correspondante.

Riz. 5.21

Si F> F1, alors la particule se déplace vers l'axe de rotation. Si F< F1, alors l'impact du liquide sur la particule ne suffira pas à la maintenir sur une trajectoire circulaire, et la particule commencera à se déplacer vers la périphérie par inertie. L'effet de séparation est déterminé par la force excessive F, agissant du côté du liquide sur la particule sélectionnée, au-dessus de la valeur de la force centripète F 1, qui détermine le mouvement circulaire :

Cette expression montre que l'effet de la centrifugation est d'autant plus grand que la différence entre les densités des particules séparées et du liquide est grande, et dépend également de manière significative de la vitesse angulaire de rotation 1.

Comparons la séparation par centrifugation avec la séparation par gravité :

1 La gravité et la poussée d'Archimède ne sont pas prises en compte lors de l'élaboration de la formule (5.47), car elles sont dirigées le long de l'axe de rotation et n'ont pas d'effet fondamental sur la centrifugation.

Les ultracentrifugeuses sont capables de séparer des particules inférieures à 100 nm, en suspension ou dissoutes dans un liquide. Ils ont trouvé de nombreuses applications dans la recherche biomédicale pour la séparation des biopolymères, des virus et des particules subcellulaires.

La vitesse de séparation est particulièrement importante dans la recherche biologique et biophysique, car au fil du temps, l'état des objets étudiés peut changer considérablement.

Notions de base.

moment de force par rapport à l'axe de rotation - c'est le produit vectoriel du rayon vecteur et de la force.

(1.14)

Le moment de force est un vecteur , dont la direction est déterminée par la règle de la vrille (vis droite) en fonction de la direction de la force agissant sur le corps. Le moment de force est dirigé le long de l'axe de rotation et n'a pas de point d'application précis.

La valeur numérique de ce vecteur est déterminée par la formule :

M = r F péché (1.15),

où  - l'angle entre le rayon vecteur et la direction de la force.

Si =0 ou  , moment de force M=0, c'est-à-dire une force passant par l'axe de rotation ou coïncidant avec lui ne provoque pas de rotation.

Le couple de module le plus élevé est créé si la force agit selon un angle  =  /2 (M 0) ou  =3  /2 (M 0).

Utiliser le concept d’effet de levier d- il s'agit d'une perpendiculaire abaissée du centre de rotation à la ligne d'action de la force), la formule du moment de force prend la forme :

, Où
(1.16)

Règle des moments de forces(condition d'équilibre d'un corps ayant un axe de rotation fixe) :

Pour qu'un corps ayant un axe de rotation fixe soit en équilibre, il faut que la somme algébrique des moments de forces agissant sur ce corps soit égale à zéro.

 M je =0 (1.17)

L'unité SI pour le moment de force est [Nm]

Lors d'un mouvement de rotation, l'inertie d'un corps dépend non seulement de sa masse, mais aussi de sa répartition dans l'espace par rapport à l'axe de rotation.

L'inertie pendant la rotation est caractérisée par le moment d'inertie du corps par rapport à l'axe de rotation J.

Moment d'inertie le point matériel par rapport à l'axe de rotation est une valeur égale au produit de la masse du point par le carré de sa distance à l'axe de rotation :

J.  =m   r  2 (1.18)

Le moment d'inertie d'un corps par rapport à un axe est la somme des moments d'inertie des points matériels qui composent le corps :

J= m   r  2 (1.19)

Le moment d'inertie d'un corps dépend de sa masse et de sa forme, ainsi que du choix de l'axe de rotation. Pour déterminer le moment d'inertie d'un corps par rapport à un certain axe, le théorème de Steiner-Huygens est utilisé :

J=J 0 +m d 2 (1.20),

Où J. 0 – moment d'inertie autour d'un axe parallèle passant par le centre de masse du corps, d – distance entre deux axes parallèles . Le moment d'inertie en SI se mesure en [kgm 2 ]

Le moment d'inertie lors du mouvement de rotation du corps humain est déterminé expérimentalement et calculé approximativement à l'aide des formules d'un cylindre, d'une tige ronde ou d'une bille.

Le moment d'inertie d'une personne par rapport à l'axe de rotation vertical, qui passe par le centre de masse (le centre de masse du corps humain est situé dans le plan sagittal légèrement en avant de la deuxième vertèbre sacrée), en fonction de la position de la personne, a les valeurs suivantes : au garde-à-vous - 1,2 kg m 2 ; avec la pose « arabesque » – 8 kgm 2 ; en position horizontale – 17 kg  m2.

Travailler en mouvement de rotation se produit lorsqu'un corps tourne sous l'influence de forces extérieures.

Le travail élémentaire de force en mouvement de rotation est égal au produit du moment de force et de l'angle élémentaire de rotation du corps :

dA  =M   d (1.21)

Si plusieurs forces agissent sur un corps, alors le travail élémentaire de la résultante de toutes les forces appliquées est déterminé par la formule :

dA=M d (1.22),

Où M– le moment total de toutes les forces extérieures agissant sur le corps.

Énergie cinétique d'un corps en rotationW À dépend du moment d'inertie du corps et de la vitesse angulaire de sa rotation :

(1.23)

Angle d'impulsion (moment angulaire) – une quantité numériquement égale au produit de l’élan du corps et du rayon de rotation.

L=p r = m V r (1.24).

Après les transformations appropriées, vous pouvez écrire la formule de détermination du moment cinétique sous la forme :

(1.25).

Élan – un vecteur dont la direction est déterminée par la règle de la vis droite. L'unité SI du moment cinétique est kgm 2 /s

Lois fondamentales de la dynamique du mouvement de rotation.

L'équation de base de la dynamique du mouvement de rotation :

L'accélération angulaire d'un corps soumis à un mouvement de rotation est directement proportionnelle au moment total de toutes les forces externes et inversement proportionnelle au moment d'inertie du corps.

(1.26).

Cette équation joue le même rôle dans la description du mouvement de rotation que la deuxième loi de Newton pour le mouvement de translation. D'après l'équation, il ressort clairement que sous l'action de forces extérieures, plus l'accélération angulaire est grande, plus le moment d'inertie du corps est petit.

La deuxième loi de Newton pour la dynamique du mouvement de rotation peut s'écrire sous une autre forme :

(1.27),

ceux. la dérivée première du moment cinétique d'un corps par rapport au temps est égale au moment total de toutes les forces externes agissant sur un corps donné.

Loi de conservation du moment cinétique d'un corps :

Si le moment total de toutes les forces externes agissant sur le corps est égal à zéro, c'est-à-dire

 M  =0 , Alors dL/dt=0 (1.28).

Il en résulte
ou
(1.29).

Cet énoncé constitue l'essence de la loi de conservation du moment cinétique d'un corps, qui est formulée comme suit :

Le moment cinétique d'un corps reste constant si le moment total des forces externes agissant sur un corps en rotation est nul.

Cette loi n'est pas valable seulement pour un corps absolument rigide. Un exemple est un patineur artistique qui effectue une rotation autour d’un axe vertical. En appuyant sur ses mains, le patineur réduit le moment d'inertie et augmente la vitesse angulaire. Pour ralentir la rotation, il écarte au contraire largement les bras ; En conséquence, le moment d'inertie augmente et la vitesse angulaire de rotation diminue.

En conclusion, nous présentons un tableau comparatif des principales grandeurs et lois caractérisant la dynamique des mouvements de translation et de rotation.

Tableau 1.4.

= const,

Par conséquent, de la force externe appliquée au corps, il est nécessaire d’isoler les composants qui ne provoquent pas de rotation. La rotation ne peut être provoquée que par une force (force de rotation) située dans un plan perpendiculaire à l'axe de rotation et dirigée tangentiellement au cercle décrit par le point de son application.

Notez que lorsque le corps tourne, les composants n’effectuent aucun travail, puisque le point d’application de ces forces se déplace perpendiculairement à leurs directions. Le travail est effectué uniquement par la force de rotation ; c'est la projection de la force agissant sur le corps sur la direction de déplacement du point d'application de cette force.

Déterminons la quantité de travail effectué par la force de rotation si son point d'application se déplace le long d'un cercle de rayon par (Fig. 1.19, b). Supposons que l'amplitude de la force reste constante. Alors

Le produit d'une force de rotation et d'un rayon est le moment de la force de rotation, ou le couple agissant sur un corps donné, et est noté (rappelons que le moment d'une force donnée par rapport à n'importe quel axe est le produit de cette force par son bras, c'est-à-dire par la longueur de la perpendiculaire, réalisée à partir de la

axe vers la direction de la force). Ainsi, dans la formule (2.8)

donc le travail effectué par le couple est égal au produit de ce moment et de l'angle de rotation du corps :

Si le couple (la force ou son bras) évolue dans le temps, alors le travail effectué est déterminé comme la somme :

Le couple de la force de rotation est représenté comme un vecteur coïncidant avec l'axe de rotation ; l'orientation positive de ce vecteur est choisie dans la direction dans laquelle se déplacerait la vis droite tournée à ce moment.

Le couple appliqué au corps lui confère une certaine accélération angulaire selon les directions des vecteurs que nous avons choisis, ils sont orientés le long de l'axe de rotation dans le même sens ; La relation entre l'amplitude du couple et l'amplitude de l'accélération angulaire qu'il confère peut être établie de deux manières :

a) on peut utiliser le fait que le travail de la force motrice est égal à la variation de l'énergie cinétique du corps auquel cette force est appliquée : Pour un corps en rotation, d'après les formules (2.9) et (2.4), on avoir

Nous supposons ici que le moment d'inertie du corps ne change pas pendant la rotation. En divisant cette équation par et en la réduisant par on obtient

b) vous pouvez utiliser le fait que le moment de la force de rotation est égal à la somme des moments des forces qui confèrent des accélérations tangentielles aux composants individuels du corps, ces forces sont égales et leurs moments sont ;

Remplaçons les accélérations tangentielles par l'accélération angulaire, qui est la même pour toutes les particules d'un corps en rotation (si le corps n'est pas déformé lors de la rotation) : Alors

La formule (2.12) exprime la loi fondamentale de la dynamique du mouvement de rotation des corps solides (non déformants), pour laquelle

l'accélération angulaire acquise par un corps sous l'influence d'un couple donné est directement proportionnelle à l'amplitude de ce moment et inversement proportionnelle au moment d'inertie du corps par rapport à l'axe de rotation :

Sous forme vectorielle, cette loi s'écrit

Si un corps se déforme pendant la rotation, alors son moment d'inertie par rapport à l'axe de rotation changera. Imaginons mentalement un corps en rotation composé de nombreuses parties élémentaires (ponctuelles) ; alors la déformation de l'ensemble du corps entraînera une modification des distances entre ces parties du corps et l'axe de rotation. Or, une modification de la distance d'une vitesse angulaire de rotation donnée co va s'accompagner d'une modification de la vitesse linéaire de déplacement de cette particule, et donc de son énergie cinétique. Ainsi, à vitesse angulaire constante de rotation du corps, une modification des distances (donc une modification du moment d'inertie du corps) s'accompagnera d'une modification de l'énergie cinétique de rotation de l'ensemble du corps.

A partir de la formule (2.4), si nous supposons des variables, nous pouvons obtenir

Le premier terme montre le changement de l'énergie cinétique d'un corps en rotation, qui s'est produit uniquement en raison d'un changement de la vitesse angulaire de rotation (à un moment d'inertie donné du corps), et le deuxième terme montre le changement de l'énergie cinétique , qui s'est produit uniquement en raison d'une modification du moment d'inertie du corps (à une vitesse angulaire de rotation donnée).

Cependant, lorsque la distance d'un corps ponctuel à l'axe de rotation change, les forces internes reliant ce corps à l'axe de rotation vont faire un travail : négatives si le corps s'éloigne, et positives si le corps se rapproche de l'axe de rotation ; ce travail peut être calculé si l'on suppose que la force reliant la particule à l'axe de rotation est numériquement égale à la force centripète :

Pour le corps entier, constitué de nombreuses particules avec des masses, on obtient

Dans le cas général, lorsqu'un couple externe agit sur un corps, la variation de l'énergie cinétique doit être assimilée à la somme de deux travaux : le couple externe et les forces internes Avec une rotation accélérée, les valeurs auront des signes positifs, - négatifs.

signe (puisque les particules du corps s'éloignent de l'axe de rotation) ; Alors

En substituant ici la valeur de l'expression (2.15) et en la remplaçant par nous obtenons

ou après réduction

Il s'agit d'une forme générale de la loi fondamentale de la mécanique pour les corps tournant autour d'un axe fixe ; elle s'applique également aux corps déformants ; Lorsque la formule (2.16) se transforme en formule (2.14).

A noter que pour les corps déformants, une modification de la vitesse angulaire de rotation est possible même en l'absence de couple externe. En effet, lorsque - de la formule (2.16) on obtient :

Dans ce cas, la vitesse angulaire de rotation ne change qu'en raison d'une modification du moment d'inertie du corps provoquée par les forces internes.