Üldteoreemid kehade süsteemi dünaamika kohta. Teoreemid massikeskme liikumisest, impulsi muutumisest, peamise nurkmomendi muutumisest, kineetilise energia muutumisest. D'Alemberti põhimõtted ja võimalikud liikumised. Dünaamika üldvõrrand. Lagrange'i võrrandid.

Üldteoreemid jäiga keha ja kehade süsteemi dünaamikast

Dünaamika üldteoreemid- see on teoreem massikeskme liikumise kohta mehaaniline süsteem, teoreem impulsi muutumise kohta, teoreem peamise nurkimpulsi (kineetilise impulsi) muutumise kohta ja teoreem mehaanilise süsteemi kineetilise energia muutumise kohta.

Teoreem mehaanilise süsteemi massikeskme liikumise kohta

Massikeskme liikumise teoreem.
Süsteemi massi ja selle massikeskme kiirenduse korrutis võrdub kõigi süsteemile mõjuvate välisjõudude vektorsummaga:
.

Siin on M süsteemi mass:
;
a C on süsteemi massikeskme kiirendus:
;
v C - süsteemi massikeskme kiirus:
;
r C - süsteemi massikeskme raadiuse vektor (koordinaadid):
;
- süsteemi moodustavate punktide koordinaadid (kindla keskpunkti suhtes) ja massid.

Teoreem impulsi (momentum) muutumise kohta

Süsteemi liikumise (impulsi) suurus on võrdne kogu süsteemi massi korrutisega selle massikeskme kiirusega või süsteemi moodustavate üksikute punktide või osade impulsside (impulsside summa) summaga:
.

Teoreem impulsi muutumise kohta diferentsiaalkujul.
Süsteemi liikumishulga (impulsi) aja tuletis on võrdne kõigi süsteemile mõjuvate välisjõudude vektorsummaga:
.

Teoreem impulsi muutumise kohta integraalkujul.
Süsteemi impulsi (impulsi) muutus teatud aja jooksul on võrdne välisjõudude impulsside summaga samal ajavahemikul:
.

Impulsi (momentum) jäävuse seadus.
Kui kõigi süsteemile mõjuvate välisjõudude summa on null, siis on süsteemi impulsivektor konstantne. See tähendab, et kõik selle projektsioonid koordinaattelgedel säilitavad konstantsed väärtused.

Kui välisjõudude projektsioonide summa mis tahes teljele on null, siis on süsteemi liikumishulga projektsioon sellele teljele konstantne.

Teoreem peamise nurkimpulsi muutumise kohta (momentide teoreem)

Süsteemi peamist nurkimpulssi antud keskpunkti O suhtes nimetatakse suuruseks, mis võrdub süsteemi kõigi punktide impulsimomendi vektorsummaga selle keskpunkti suhtes:
.
Siin tähistavad nurksulud ristkorrutist.

Kinnitatud süsteemid

Järgmine teoreem kehtib juhul, kui mehaanilisel süsteemil on fikseeritud punkt või telg, mis on fikseeritud inertsiaalse võrdlusraami suhtes. Näiteks kerakujulise laagriga kinnitatud kere. Või kehade süsteem, mis liiguvad ümber kindla keskpunkti. See võib olla ka fikseeritud telg, mille ümber keha või kehade süsteem pöörleb. Sel juhul tuleb momentide all mõista fikseeritud telje suhtes impulsi ja jõudude momente.

Teoreem peamise nurkimpulsi muutumise kohta (momentide teoreem)
Süsteemi peamise nurkimpulsi ajatuletis mõne fikseeritud keskpunkti O suhtes on võrdne süsteemi kõigi välisjõudude momentide summaga sama keskpunkti suhtes.

Põhimomendi (nurkimpulss) jäävuse seadus.
Kui kõigi süsteemile rakendatud välisjõudude momentide summa antud fikseeritud keskpunkti O suhtes on võrdne nulliga, siis on süsteemi peamine nurkimpulss selle keskpunkti suhtes konstantne. See tähendab, et kõik selle projektsioonid koordinaattelgedel säilitavad konstantsed väärtused.

Kui välisjõudude momentide summa mõne fikseeritud telje suhtes on null, siis on süsteemi nurkimment selle telje suhtes konstantne.

Suvalised süsteemid

Järgmisel teoreemil on universaalne iseloom. See kehtib nii fikseeritud kui ka vabalt liikuvate süsteemide kohta. Fikseeritud süsteemide puhul on vaja arvestada ühenduste reaktsioone fikseeritud punktides. See erineb eelmisest teoreemist selle poolest, et fikseeritud punkti O asemel tuleks võtta süsteemi massikese C.

Momentide teoreem massikeskme kohta
Süsteemi peamise nurkimpulsi ajatuletis massikeskme C suhtes on võrdne süsteemi kõigi välisjõudude momentide summaga sama keskpunkti suhtes.

Nurkmomendi jäävuse seadus.
Kui kõigi süsteemile rakendatud välisjõudude momentide summa massikeskme C suhtes on võrdne nulliga, siis on süsteemi peamine impulsimoment selle keskpunkti suhtes konstantne. See tähendab, et kõik selle projektsioonid koordinaattelgedel säilitavad konstantsed väärtused.

Keha inertsimoment

Kui keha pöörleb ümber z-telje nurkkiirusega ω z, määratakse selle nurkimment (kineetiline moment) z-telje suhtes valemiga:
L z = J z ω z ,
kus J z on keha inertsimoment z-telje suhtes.

Keha inertsmoment z-telje suhtes määratakse valemiga:
,
kus h k on kaugus massipunktist m k z-teljeni.
Õhukese rõnga massiga M ja raadiusega R või silindri puhul, mille mass on jaotatud piki selle serva,
J z = MR 2 .
Tahke homogeense rõnga või silindri jaoks
.

Steiner-Huygensi teoreem.
Olgu keha massikeset läbiv telg Cz ja sellega paralleelne telg Oz. Seejärel seostatakse keha inertsmomendid nende telgede suhtes seosega:
J Oz = J Cz + M a 2 ,
kus M on kehamass; a on telgede vaheline kaugus.

Rohkem üldine juhtum :
,
kus on keha inertsi tensor.
Siin on vektor, mis on tõmmatud keha massikeskmest punktini massiga m k.

Kineetilise energia muutumise teoreem

Laske kehal massiga M sooritada translatsiooni- ja pöörlemisliikumist nurkkiirusega ω ümber mingi telje z.
,
Seejärel määratakse keha kineetiline energia valemiga:
kus v C on keha massikeskme liikumiskiirus;

J Cz on keha inertsimoment telje suhtes, mis läbib keha massikeskmet paralleelselt pöörlemisteljega. Pöörlemistelje suund võib aja jooksul muutuda. See valem annab kineetilise energia hetkeväärtuse.
Teoreem süsteemi kineetilise energia muutumise kohta diferentsiaalkujul.
.

Teoreem süsteemi kineetilise energia muutumise kohta terviklikul kujul.
Süsteemi kineetilise energia muutus mõne liikumise ajal võrdub kõigi süsteemile rakendatavate välis- ja sisejõudude sellel liikumisel tehtud töö summaga:
.

Jõuga tehtud töö, on võrdne jõuvektorite skalaarkorrutisega ja selle rakenduspunkti lõpmatult väikese nihkega:
,
st vektorite F ja ds absoluutväärtuste korrutis nende vahelise nurga koosinusega.

Jõumomendiga tehtud töö, on võrdne pöördemomendi vektorite ja lõpmata väikese pöördenurga skalaarkorrutisega:
.

d'Alemberti põhimõte

D'Alemberti põhimõtte olemus on taandada dünaamikaprobleemid staatika probleemideks. Selleks eeldatakse (või on ette teada), et süsteemi kehadel on teatud (nurk)kiirendused. Järgmisena tuuakse sisse inertsiaaljõud ja (või) inertsijõudude momendid, mis on suuruselt võrdsed ja suunalt vastupidised jõudude ja jõudude momentidega, mis mehaanikaseaduste järgi tekitaksid antud kiirendusi või nurkiirendusi.

Vaatame näidet. Keha läbib translatsioonilise liikumise ja sellele mõjuvad välised jõud. Lisaks eeldame, et need jõud loovad süsteemi massikeskme kiirenduse. Massikeskme liikumise teoreemi kohaselt oleks keha massikeskmeel sama kiirendus, kui kehale mõjuks jõud. Järgmisena tutvustame inertsjõudu:
.
Pärast seda dünaamika probleem:
.
;
.

Pöörleva liikumise korral toimige samal viisil. Laske kehal pöörlema ​​ümber z-telje ja sellele mõjuvad välised jõumomendid M e zk .
.
Eeldame, et need momendid tekitavad nurkkiirenduse ε z.
;
.

Järgmisena tutvustame inertsjõudude M И = - J z ε z momenti.

Pärast seda dünaamika probleem:

Muutub staatikaprobleemiks:.
Võimalike liigutuste põhimõte

Staatikaülesannete lahendamisel kasutatakse võimalike nihkete põhimõtet. Mõnes ülesandes annab see lühema lahenduse kui tasakaaluvõrrandite koostamine. See kehtib eriti paljudest kehadest koosnevate ühendustega süsteemide kohta (näiteks keermete ja plokkidega ühendatud kehade süsteemid) Võimalike liigutuste põhimõte

Ideaalsete ühendustega mehaanilise süsteemi tasakaalu saavutamiseks on vajalik ja piisav, et süsteemi mis tahes võimaliku liikumise korral oleks kõigi sellele mõjuvate aktiivjõudude elementaartööde summa võrdne nulliga. Võimalik süsteemi ümberpaigutamine

Dünaamika üldvõrrand (D'Alembert - Lagrange'i põhimõte)

D'Alembert-Lagrange'i põhimõte on kombinatsioon D'Alembert'i printsiibist võimalike liigutuste põhimõttega. See tähendab, et dünaamilise ülesande lahendamisel võtame kasutusele inertsiaalsed jõud ja taandame ülesande staatiliseks ülesandeks, mille lahendame võimalike nihkete printsiipi kasutades.

D'Alembert-Lagrange'i põhimõte.
Kui ideaalsete ühendustega mehaaniline süsteem liigub, on igal ajahetkel kõigi rakendatud aktiivjõudude ja inertsiaalsete jõudude elementaartööde summa süsteemi mis tahes võimalikule liikumisele null:
.
Seda võrrandit nimetatakse üldvõrrand kõlarid.

Lagrange'i võrrandid

Üldistatud q koordinaadid 1, q 2, ..., q n on n suuruse hulk, mis määravad üheselt süsteemi asukoha.

Üldistatud koordinaatide arv n ühtib süsteemi vabadusastmete arvuga.

Üldised kiirused on üldistatud koordinaatide tuletised aja t suhtes.

Üldised jõud Q 1, Q 2, ..., Q n .
Vaatleme süsteemi võimalikku liikumist, mille juures koordinaat q k saab liikumise δq k.
Ülejäänud koordinaadid jäävad muutumatuks. Olgu δA k töö, mida sellise liikumise ajal teevad välised jõud. Siis
.

δA k = Q k δq k või
Kui süsteemi võimaliku liikumise korral muutuvad kõik koordinaadid, on sellise liikumise ajal välisjõudude poolt tehtav töö vorm: δA = Q.
1 δq 1 + Q 2 δq 2 + ... + Q n δq n
.

Siis on üldistatud jõud nihkete töö osalised tuletised: Sest potentsiaalsed jõud
.

potentsiaaliga Π, Lagrange'i võrrandid

- need on mehaanilise süsteemi liikumisvõrrandid üldistatud koordinaatides:
.

Siin on T kineetiline energia. See on üldistatud koordinaatide, kiiruste ja võib-olla ka aja funktsioon. Seetõttu on selle osatuletis ka üldistatud koordinaatide, kiiruste ja aja funktsioon. Järgmiseks peate arvestama, et koordinaadid ja kiirused on aja funktsioonid. Seetõttu peate aja suhtes kogutuletise leidmiseks rakendama keeruka funktsiooni diferentseerimise reeglit:
Kasutatud kirjandus: S. M. Targ, Lühike kursus

teoreetiline mehaanika, "Kõrgkool", 2010. Dünaamika üldteoreemid

3. loeng. Materiaalsete punktide süsteemi dünaamika on teoreetilise mehaanika oluline haru. Siin käsitletakse peamiselt mehaaniliste süsteemide (materiaalsete punktide süsteemide) liikumisprobleeme, millel on piiratud arv vabadusastmeid - maksimaalne arv sõltumatuid parameetreid, mis määravad süsteemi asukoha. Süsteemidünaamika põhiülesanne on liikumisseaduste uurimine tahke

Lihtsaim lähenemine süsteemi liikumise uurimisele, mis koosneb N materiaalsed punktid, taandub süsteemi iga üksiku punkti liikumise arvestamisele. Sel juhul tuleb määrata kõik süsteemi igale punktile mõjuvad jõud, sealhulgas punktidevahelised vastasmõjujõud.

Määrates iga punkti kiirenduse vastavalt Newtoni teisele seadusele (1.2), saame iga punkti jaoks kolm teist järku skalaarset diferentsiaalliikumise seadust, s.o. 3 N diferentsiaalsed liikumisseadused kogu süsteemi jaoks.

Et leida mehaanilise süsteemi liikumisvõrrandeid etteantud jõudude ja süsteemi iga punkti algtingimuste põhjal, tuleb saadud diferentsiaalseadused integreerida. See probleem on keeruline isegi kahe materiaalse punkti puhul, mis liiguvad ainult vastasmõju jõudude mõjul universaalse külgetõmbeseaduse järgi (kahe keha probleem), ja ülimalt keeruline kolme vastastikku mõjuva punkti puhul (kolme keha probleem) ).

Seetõttu on vaja leida probleemide lahendamise meetodid, mis viiksid lahendatavate võrranditeni ja annaksid ettekujutuse mehaanilise süsteemi liikumisest. Dünaamika üldised teoreemid, mis tulenevad diferentsiaalsetest liikumisseadustest, võimaldavad meil vältida integreerimisel tekkivat keerukust ja saada vajalikke tulemusi.

3. 1. Üldised märkused

Mehaanilise süsteemi punktid nummerdame indeksitega i, j, k jne, mis läbivad kõiki väärtusi 1, 2, 3… N, Kus N – süsteemi punktide arv. Füüsikalised kogused seotud k punktid on tähistatud sama indeksiga kui punkt. Näiteks väljendage vastavalt raadiuse vektorit ja kiirust k punkt.

Süsteemi igale punktile mõjuvad kahe päritoluga jõud: esiteks jõud, mille allikad asuvad väljaspool süsteemi, nn. välised jõud ja määratud ; teiseks jõud antud süsteemi teistest punktidest, nn sisemine jõud ja määratud . Sisejõud vastavad Newtoni kolmandale seadusele. Vaatleme kogu mehaanilisele süsteemile mis tahes olekus mõjuvate sisejõudude lihtsamaid omadusi.

Esimene vara. Süsteemi kõigi sisejõudude geomeetriline summa (sisejõudude põhivektor) on võrdne nulliga.

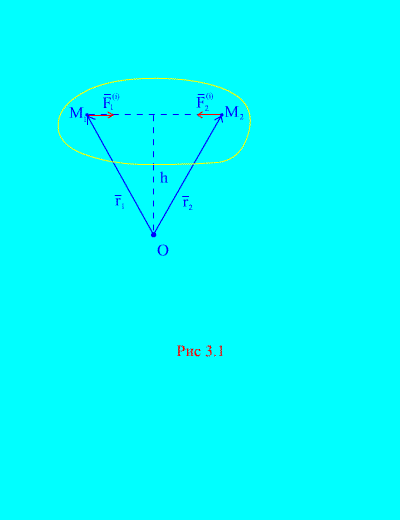
Tõepoolest, kui arvestada süsteemi kaht suvalist punkti, näiteks ja (Joonis 3.1), siis nende jaoks , sest toime- ja reaktsioonijõud on alati suurusjärgus võrdsed, toimides mööda ühte toimejoont vastassuunas, mis ühendab omavahel vastasmõjupunkte. Sisejõudude põhivektor koosneb vastastikku mõjutavate punktide jõudude paaridest, seega

(3.1)

Teine vara. Kõigi sisejõudude momentide geomeetriline summa suvalise ruumipunkti suhtes on võrdne nulliga.

Vaatleme jõudude momentide süsteemi ja punkti suhtes KOHTA(Joonis 3.1). Alates (Joonis 3.1). see on selge

,

sest mõlemal jõul on samad vektorimomentide harud ja vastupidised suunad. Peamine punkt sisemised jõud punkti suhtes KOHTA koosneb selliste avaldiste vektorsummast ja on võrdne nulliga. Seega

Olgu välis- ja sisejõud, mis mõjutavad mehaanilist süsteemi, mis koosneb N punktid (Joonis 3.2). Kui süsteemi igale punktile rakendatakse välisjõudude resultant ja kõigi sisejõudude resultant, siis k süsteemi punktis saab koostada liikumise diferentsiaalvõrrandid. Selliseid võrrandeid tuleb kokku N:

ja projektsioonides fikseeritud koordinaattelgedele 3 N:

(3.4)

Vektorvõrrandid (3.3) või samaväärsed skalaarvõrrandid (3.4) esindavad kogu süsteemi materiaalsete punktide liikumise diferentsiaalseadusi. Kui kõik punktid liiguvad paralleelselt ühe tasapinnaga või ühe sirgega, siis on võrrandite (3.4) arv esimesel juhul 2 N, teises N.

Näide 1. Kaks massi on omavahel ühendatud üle ploki visatud pikendamatu kaabli abil (Joonis 3.3). Hõõrdejõudude, aga ka ploki ja kaabli massi tähelepanuta jätmine määravad koormate liikumise seaduse ja kaabli pinge.

Lahendus. Süsteem koosneb kahest materiaalsest kehast (mis on ühendatud pikendamatu kaabliga), mis liiguvad paralleelselt sama teljega X. Kirjutame üles diferentsiaalliikumise seadused projektsioonides teljele X iga keha jaoks.

Laske õigel raskusel kiirendusega langeda, siis vasak kaal tõuseb kiirendusega. Vabastame end vaimselt ühendusest (kaablist) ja asendame selle reaktsioonidega ja (Joonis 3.3). Arvestades kehasid vabadeks, koostame diferentsiaalliikumise seadused projektsioonis teljele X(see tähendab, et keerme pinged on sisemised jõud ja koormuste kaal on välised):

Kuna ja (kehad on ühendatud venitamatu köiega), saame

Nende võrrandite lahendamine kiirenduse ja kaabli pinge kohta T, saame

.

Pange tähele, et kaabli pinge ei ole võrdne vastava koormuse raskusjõuga.

3. 2. Massikeskme liikumise teoreem

On teada, et jäik keha ja mehaaniline süsteem tasapinnas võivad liikuda üsna keeruliselt. Esimese teoreemi keha ja mehaanilise süsteemi liikumise kohta võib jõuda järgmiselt: viska k.-l. objekt, mis koosneb paljudest omavahel kinnitatud tahketest kehadest. On selge, et ta lendab parabooliga. See selgus punkti liikumist uurides. Kuid nüüd pole objektil punkt. See pöördub ja õõtsub oma lennu ajal ümber mõne efektiivse keskuse, mis liigub paraboolina. Esimene teoreem keerukate objektide liikumise kohta ütleb, et teatud efektiivne kese on liikuva objekti massikese. Massikese ei pruugi asuda kehas endas, see võib asuda kusagil väljaspool seda.

Teoreem. Mehaanilise süsteemi massikese liigub kogu süsteemi massiga võrdse massiga materiaalse punktina, millele rakenduvad kõik süsteemile mõjuvad välisjõud.

Teoreemi tõestamiseks kirjutame diferentsiaalliikumise seadused (3.3) ümber järgmisel kujul:

(3.5)

Kus N – süsteemi punktide arv.

Liidame võrrandid termini kaupa kokku:

(A)

Mehaanilise süsteemi massikeskme asukoht valitud koordinaatsüsteemi suhtes määratakse valemiga (2.1): Kus M– süsteemi mass. Siis vasak pool võrdsus (a) kirjutatakse

Võrdsuse (a) paremal küljel olev esimene summa on võrdne välisjõudude põhivektoriga ja viimane sisejõudude omaduse järgi nulliga. Seejärel kirjutatakse võrdsus (a), võttes arvesse (b), ümber

, (3.6)

need. süsteemi massi ja selle massikeskme kiirenduse korrutis võrdub kõigi süsteemile mõjuvate välisjõudude geomeetrilise summaga.

Võrrandist (3.6) järeldub, et sisejõud massikeskme liikumist otseselt ei mõjuta. Kuid mõnel juhul on need süsteemile rakendatavate välisjõudude ilmnemise põhjuseks. Seega põhjustavad auto veorattaid pöörlema ​​panevad sisemised jõud ratta veljele mõjuva välise haardejõu.

Näide 2. Vertikaalsel tasapinnal asuv mehhanism on paigaldatud horisontaalsele siledale tasapinnale ja kinnitatud selle külge jäigalt pinnale kinnitatud vardadega TO Ja L (Joonis 3.4).

Plaadi 1 raadius R liikumatuks. Ketta 2 mass m ja raadius r vända külge kinnitatud, pikkus R+ r punktis C 2. Vänt pöörleb konstantselt

nurkkiirus. Algmomendil hõivas vänt paremal horisontaalne asend. Jättes tähelepanuta vända massi, määrake varrastele mõjuvad maksimaalsed horisontaalsed ja vertikaalsed jõud, kui raami ja ratta 1 kogumass on võrdne M. Mõelge ka mehhanismi käitumisele lattide puudumisel.

Lahendus. Süsteem koosneb kahest massist ( N=2 ): fikseeritud ketas 1 raami ja liikuva kettaga 2. Suunake telg juures läbi statsionaarse ketta raskuskeskme vertikaalselt ülespoole, telg X– piki horisontaaltasapinda.

Kirjutame massikeskme (3.6) liikumise teoreemi koordinaatide kujul

Selle süsteemi välised jõud on: raami ja fikseeritud ketta kaal - Mg, liikuva ketta kaal - mg, - poltide horisontaalne kogureaktsioon, - tasapinna normaalne kogureaktsioon. Seega

Seejärel kirjutatakse liikumisseadused (b) ümber

Arvutame mehaanilise süsteemi massikeskme koordinaadid:

; (G)

nagu näha on (Joonis 3.4), , , (vända nurk), . Nende avaldiste asendamine (d)-ga ja teise tuletise arvutamine aja suhtes t, , saame selle

(e)

Asendades (c) ja (e) punktiga (b), leiame

Varrastele mõjuv horisontaalne rõhk on suurim ja kõige väiksem siis, kui cos = 1 vastavalt, st.

Mehhanismi surve sisse lülitatud horisontaaltasand on suurimad ja väikseimad väärtused millal patt vastavalt, st.

Tegelikult on esimene dünaamika probleem lahendatud: süsteemi massikeskme (d) teadaolevate liikumisvõrrandite järgi taastatakse liikumises osalevad jõud.

Trellide puudumisel K Ja L (Joonis 3.4), võib mehhanism hakata põrkama horisontaaltasapinnast kõrgemal. See toimub siis, kui s.t. kui , siis järeldub, et vända pöörlemise nurkkiirus, mille juures mehhanism põrkub, peab vastama võrdsusele

.

3. 3. Massikeskme liikumise jäävuse seadus

Kui süsteemile mõjuvate välisjõudude põhivektor on võrdne nulliga, s.o. , siis alates(3.6)sellest järeldub, et massikeskme kiirendus on null, seega on massikeskme kiirus konstantne suuruses ja suunas. Kui just alghetkel on massikese paigal, siis on see puhkeolekus kogu aja, samal ajal kui välisjõudude põhivektor on nulliga.

Sellest teoreemist tulenevad mitmed järeldused.

· Ainuüksi sisemised jõud ei saa muuta süsteemi massikeskme liikumise olemust.

· Kui süsteemile mõjuvate välisjõudude põhivektor on null, siis on massikese paigal või liigub ühtlaselt ja sirgjooneliselt.

· Kui süsteemi välisjõudude peavektori projektsioon mõnele fikseeritud teljele on võrdne nulliga, siis süsteemi massikeskme kiiruse projektsioon sellele teljele ei muutu.

· Jäigale kehale rakendatud jõupaar ei saa muuta selle massikeskme liikumist (võib panna keha pöörlema ​​ainult ümber massikeskme).

Vaatleme näidet, mis illustreerib massikeskme liikumise jäävuse seadust.

Näide 3. Kaks massi on ühendatud läbi ploki visatud venimatu keermega (Joonis 3.5), kinnitatud massiga kiilule M. Kiil toetub siledale horisontaaltasapinnale. Algsel hetkel oli süsteem paigal. Leidke kiilu nihe piki tasapinda, kui esimene koorem on langetatud kõrgusele N. Jäta tähelepanuta ploki ja keerme mass.

Lahendus. Kiilule koos koormustega mõjuvad välised jõud on raskusjõud, ja Mg, samuti sileda horisontaalse pinna N normaalne reaktsioon. Järelikult

Kuna algsel hetkel oli süsteem puhkeolekus, on meil .

Arvutame välja süsteemi massikeskme koordinaadid hetkel ja hetkel t 1 kui koorem kaalub g laskub kõrgusele H.

Hetkel:

,

Kus , , X– vastavalt raskuste g, g ja kiilu massikeskme koordinaadid Mg.

Oletame, et kiil liigub ajahetkel telje positiivses suunas Ox summa järgi L, kui koorma kaal langeb kõrgusele N. Siis hetkeks

sest koormad koos kiiluga liiguvad L paremale ja koorem liigub piki kiilu ülespoole. Alates , siis peale arvutusi saame

.

3.4. Süsteemi liikumise kogus

3.4.1. Süsteemi impulsi arvutamine

Materiaalse punkti impulss on vektorkogus, mis võrdub punkti massi ja selle kiirusvektori korrutisega

Impulsi mõõtühik -

Mehaanilise süsteemi impulss on süsteemi üksikute punktide impulsi vektorsumma, s.o.

Kus N – süsteemi punktide arv.

Mehaanilise süsteemi impulsi saab väljendada süsteemi massina M ja massikeskme kiirust. Tõesti,

need. Süsteemi impulss on võrdne kogu süsteemi massi ja selle massikeskme kiiruse korrutisega. Suund on sama mis suund (Joonis 3.6)

Projektsioonides ristkülikukujulistele telgedele on meil

kus , on süsteemi massikeskme kiiruse projektsioonid.

Siin M– mehaanilise süsteemi mass; ei muutu süsteemi liikumisel.

Neid tulemusi on eriti mugav kasutada jäikade kehade liikumiskoguste arvutamisel.

Valemist (3.7) selgub, et kui mehaaniline süsteem liigub nii, et selle massikese jääb paigale, siis jääb süsteemi impulss võrdseks nulliga.

3.4.2. Elementaarne ja täisjõuline impulss

Jõu mõju materiaalsele punktile ajas dt saab iseloomustada elementaarse impulsiga. Kogu jõuimpulss aja jooksul t, või jõuimpulss, määratud valemiga

või projektsioonides telje koordinaatidele

(3.8a)

Jõuimpulsi ühik on .

3.4.3. Teoreem süsteemi impulsi muutumise kohta

Olgu süsteemi punktidele rakendatud välis- ja sisejõud. Seejärel saame süsteemi iga punkti jaoks rakendada diferentsiaalseid liikumisseadusi (3.3), pidades meeles, et :

.

Summeerides süsteemi kõik punktid, saame

Sisejõudude omaduse järgi ja määratluse järgi meil on

(3.9)

Selle võrrandi mõlema poole korrutamine arvuga dt, saame teoreemi impulsi muutumise kohta diferentsiaalkujul:

, (3.10)

need. mehaanilise süsteemi diferentsiaalimpulss on võrdne kõigi mehaanilise süsteemi punktidele mõjuvate välisjõudude elementaarimpulsside vektorsummaga.

Mõlema poole integraali (3.10) arvutamine aja jooksul vahemikus 0 kuni t, saame teoreemi lõplikul või integraalkujul

(3.11)

Projektsioonides koordinaattelgedele saame

Mehaanilise süsteemi impulsi muutus aja jooksult, on võrdne mehaanilise süsteemi punktidele samal ajal mõjuvate välisjõudude impulsside vektorsummaga.

Näide 4. Koorma kaal m laskub kaldtasapinnal paigalt jõu mõjul alla F, ajaga võrdeline: , kus (Joonis 3.7). Millise kiiruse pärast keha omandab t sekundit pärast liikumise algust, kui koormuse libisemise koefitsient kaldtasandil on võrdne f.

Lahendus. Kujutame koormusele rakendatavaid jõude: mg - koormuse raskusjõud, N on tasapinna normaalne reaktsioon, on tasapinnale mõjuva koormuse libisemishõõrdejõud ja . Kõigi jõudude suund on näidatud (Joonis 3.7).

Suuname telje X piki kaldtasapinda allapoole. Kirjutame teoreemi impulsi muutuse (3.11) kohta projektsioonis teljele X:

(A)

Vastavalt tingimusele, kuna algsel hetkel oli koorem paigal. Kõigi jõudude impulsside projektsioonide summa x-teljel on võrdne

Seega

,

.

3.4.4. Impulsi jäävuse seadused

Jäävusseadused saadakse impulsi muutumise teoreemi erijuhtudena. Võimalikud on kaks erijuhtu.

· Kui kõigi süsteemile rakendatavate välisjõudude vektorsumma on võrdne nulliga, s.o. , siis teoreemist järeldub (3.9) , Mida ,

need. kui süsteemi välisjõudude peavektor on null, siis on süsteemi liikumise hulk suuruselt ja suunalt konstantne.

· Kui välisjõudude peavektori projektsioon mis tahes koordinaatide telg võrdne nulliga, näiteks Oh, st. , siis impulsi projektsioon sellele teljele on konstantne väärtus.

Vaatleme näidet impulsi jäävuse seaduse rakendamisest.

Näide 5. Ballistiline pendel on keha, mille mass on riputatud pikale niidile (Joonis 3.8).

Kiirusega liikuv massikuul V ja tabades paigalseisvat keha, jääb sellesse kinni ja keha kaldub kõrvale. Kui suur oli kuuli kiirus, kui keha tõusis kõrgusele h ?

Lahendus. Laske kinnikiilunud kuuliga kehal kiirust omandada. Seejärel, kasutades impulsi jäävuse seadust kahe keha vastasmõju ajal, saame kirjutada .

Kiirust saab arvutada mehaanilise energia jäävuse seaduse abil . Siis . Selle tulemusena leiame

.

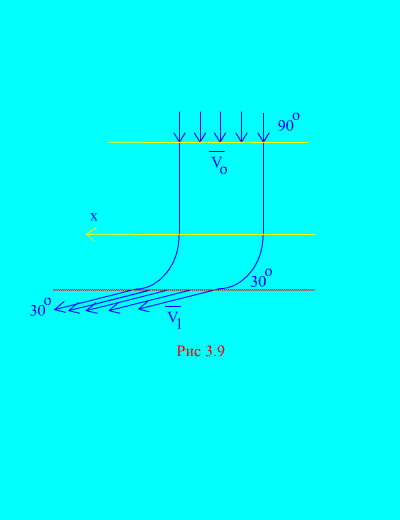
Näide 6. Vesi siseneb statsionaarsesse kanalisse (Joonis 3.9) muutuv ristlõige kiirusega horisontaalsuunas nurga all; ruut ristlõige kanal sissepääsu juures; vee kiirus kanalist väljumisel loob horisondi suhtes nurga.

Määrake reaktsiooni horisontaalne komponent, mida vesi avaldab kanali seintele. Vee tihedus .

Lahendus. Määrame kanali seinte poolt veele avaldatava reaktsiooni horisontaalkomponendi. See jõud on suuruselt võrdne soovitud jõuga ja vastupidine. Meil on vastavalt (3.11a)

. (A)

Arvutame aja t jooksul kanalisse siseneva vedeliku mahu massi:

Suurust rAV 0 nimetatakse teine ​​mass - vedeliku mass, mis voolab läbi toru mis tahes osa ajaühikus.

Kanalist väljub sama aja jooksul sama kogus vett. Alg- ja lõppkiirus on antud tingimuses.

Arvutame välja võrdsuse (a) parema külje, mis määrab süsteemile (vesi) mõjutavate välisjõudude horisontaaltelje projektsioonide summa. Ainus horisontaalne jõud on tekkiva seinareaktsiooni horisontaalkomponent Rx. See jõud on vee ühtlase liikumise ajal konstantne. Sellepärast

. (V)

Asendades (b) ja (c) punktiga (a), saame

3.5. Süsteemi kineetiline moment

3.5.1. Süsteemi peamine impulsimoment

Olgu süsteemi massiga punkti raadiuse vektor mingi punkti A suhtes, mida nimetatakse keskpunktiks (Joonis 3.10).

Punkti impulsimoment (kineetiline moment). keskuse A suhtes nimetatakse vektoriks , määratakse valemiga

. (3.12)

Sel juhul vektor mis on suunatud keskpunkti läbiva tasapinnaga risti A ja vektor .

Punkti impulsimoment (kineetiline moment) telje suhtes nimetatakse punkti impulsimomendi projektsiooniks sellele teljele mis tahes sellel teljel valitud keskpunkti suhtes.

Süsteemi peamine impulsimoment (kineetiline moment) keskpunkti A suhtes nimetatakse koguseks

(3.13)

Süsteemi peamine impulsimoment (kineetiline moment) telje suhtes nimetatakse süsteemi peamise impulsimomendi projektsiooniks sellele teljele mis tahes sellel valitud suhtes kesktelg.

3.5.2. Pöörleva jäiga keha kineetiline moment ümber pöörlemistelje

Joondame fikseeritud punkti KOHTA keha, mis asub pöörlemisteljel KOHTAz, koordinaatsüsteemi alguspunktiga Ohooz, mille teljed hakkavad koos kehaga pöörlema (Joonis 3.11). Laskma olema keha punkti raadiusvektor koordinaatide alguspunkti suhtes, selle projektsioon teljel tähistatakse , , . Vektorprojektsioonid nurkkiirus Samal teljel olevaid kehasid tähistatakse 0, 0, ().

Haridus- ja Teadusministeerium Venemaa Föderatsioon

Föderaalne riigieelarveline kõrgharidusasutus

"Kubani Riiklik Tehnoloogiaülikool"

Teoreetiline mehaanika

2. osa dünaamika

Toimetuse ja kirjastuskomisjoni poolt heaks kiidetud

ülikooli nõukogu as

õppevahend

Krasnodar

UDC 531.1/3 (075)

Teoreetiline mehaanika. 2. osa. Dünaamika: õpik / L.I. Kuban. olek technol.un-t. Krasnodar, 2011. 123 lk.

ISBN 5-230-06865-5

Teoreetiline materjal esitatakse lühidalt, tuuakse näiteid probleemide lahendamisest, millest enamik peegeldab tegelikke tehnilisi küsimusi, ning pööratakse tähelepanu ratsionaalse lahendusmeetodi valikule.

Mõeldud ehitus-, transpordi- ja masinaehituse eriala bakalaureuse- ja kaugõppes õppijatele.

Tabel 1 Ill. 68 Bibliograafia 20 pealkirja

Teadustoimetaja tehnikateaduste kandidaat, dotsent. V.F.Melnikov

Arvustajad: Kubani Põllumajandusülikooli teoreetilise mehaanika ning mehhanismide ja masinate teooria osakonna juhataja prof. F.M. Kanarev; Kubani Riikliku Tehnoloogiaülikooli teoreetilise mehaanika osakonna dotsent M.E. Multykh

Avaldatud Kubani Riikliku Tehnoloogiaülikooli toimetuse ja kirjastusnõukogu otsusega.

Kordusväljaandmine

ISBN 5-230-06865-5 KubSTU 1998

Eessõna

See õpik on mõeldud ehituse, transpordi ja masinaehituse erialade osakoormusega õppuritele, kuid seda saab kasutada teoreetilise mehaanika kursuse osa "Dünaamika" õppimisel nii teiste erialade osakoormusega õppijatel kui ka täiskoormusega õppijatel. iseseisvalt töötades.

Käsiraamat on koostatud vastavalt teoreetilise mehaanika kursuse kehtivale ainekavale ja hõlmab kõiki kursuse põhiosa küsimusi. Iga osa sisaldab lühikest teoreetilist materjali, millele on lisatud illustratsioonid ja metoodilised soovitused selle kasutamiseks probleemide lahendamisel. Käsiraamat sisaldab lahendusi 30 probleemile, mis kajastavad tegelikke tehnilisi probleeme ja vastavad testülesannetele sõltumatu otsus. Iga ülesande jaoks esitatakse arvutusskeem, mis illustreerib selgelt lahendust. Lahenduse vormistus vastab osakoormusega üliõpilaste kontrolltööde vormistamise nõuetele.

Autor avaldab sügavat tänu Kubani Põllumajandusülikooli teoreetilise mehaanika osakonna ning mehhanismide ja masinate teooria õppejõududele suure töö eest õpiku retsenseerimisel, samuti Kubani Riikliku Tehnoloogiaülikooli teoreetilise mehaanika osakonna õppejõududele. Ülikooli väärtuslike kommentaaride ja nõuannete eest õpiku avaldamiseks ettevalmistamisel.

Kõik kriitilised kommentaarid ja ettepanekud võetakse autori poolt edaspidi tänuga vastu.

Sissejuhatus

Dünaamika on teoreetilise mehaanika kõige olulisem osa. Enamik inseneripraktikas esinevatest spetsiifilistest probleemidest on seotud dünaamikaga. Kasutades staatika ja kinemaatika järeldusi, kehtestab dünaamika üldised materiaalsete kehade liikumise seadused rakendatud jõudude toimel.

Lihtsaim materiaalne objekt on materiaalne punkt. Materiaalseks punktiks võib võtta mis tahes kujuga materiaalset keha, mille mõõtmed võib vaadeldavas ülesandes tähelepanuta jätta. Lõplike mõõtmetega keha võib võtta materiaalse punktina, kui selle punktide liikumise erinevus ei ole antud ülesande puhul oluline. See juhtub siis, kui keha mõõtmed on väikesed võrreldes keha punktide läbitavate vahemaadega. Tahke keha iga osakest võib pidada materiaalseks punktiks.

Punktile või materiaalsele kehale rakendatavaid jõude hinnatakse dünaamiliselt nende dünaamilise mõju järgi, st selle järgi, kuidas need muudavad materiaalsete objektide liikumise omadusi.

Materiaalsete objektide liikumine ajas toimub ruumis teatud tugiraamistiku suhtes. Klassikalises mehaanikas, lähtudes Newtoni aksioomidest, peetakse ruumi kolmemõõtmeliseks, selle omadused ei sõltu selles liikuvatest materiaalsetest objektidest. Punkti asukoht sellises ruumis määratakse kolme koordinaadiga. Aeg ei ole seotud ruumi ja materiaalsete objektide liikumisega. Seda peetakse kõigi võrdlussüsteemide jaoks samaks.

Dünaamikaseadused kirjeldavad materiaalsete objektide liikumist absoluutsete koordinaattelgede suhtes, mida tinglikult peetakse statsionaarseteks. Absoluutse koordinaatsüsteemi alguspunktiks peetakse Päikese keskpunkti ja teljed on suunatud kaugetele, tinglikult seisvatele tähtedele. Paljude tehniliste probleemide lahendamisel võib Maaga ühendatud koordinaatteljed lugeda tinglikult liikumatuteks.

Materiaalsete objektide mehaanilise liikumise parameetrid dünaamikas pannakse paika matemaatiliste tuletustega klassikalise mehaanika põhiseadustest.

Esimene seadus (inertsiseadus):

Materiaalne punkt säilitab puhkeoleku või ühtlase ja sirgjoonelise liikumise, kuni mõne jõu mõjul ta sellest olekust välja viib.

Punkti ühtlast ja lineaarset liikumist nimetatakse liikumiseks inertsi teel. Puhkus on inertsi teel liikumise erijuhtum, kui punkti kiirus on null.

Igal materiaalsel punktil on inerts, see tähendab, et see püüab säilitada puhkeolekut või ühtlast lineaarset liikumist. Võrdlussüsteemi, mille suhtes inertsiseadus kehtib, nimetatakse inertsiaalseks ja selle süsteemi suhtes vaadeldavat liikumist nimetatakse absoluutseks. Iga võrdlussüsteem, mis teostab translatsioonilist sirgjoonelist ja ühtlast liikumist inertsiaalsüsteemi suhtes, on samuti inertsiaalsüsteem.

Teine seadus (dünaamika põhiseadus):

Materiaalse punkti kiirendus inertsiaalse tugisüsteemi suhtes on võrdeline punktile rakendatava jõuga ja langeb kokku jõuga, mis on suunatud:
.

Dünaamika põhiseadusest järeldub, et jõuga
kiirendus
. Punkti mass iseloomustab punkti takistuse astet selle kiiruse muutustele, see tähendab, et see on materiaalse punkti inertsi mõõt.

Kolmas seadus (tegevuse ja reaktsiooni seadus):

Jõud, millega kaks keha teineteisele mõjuvad, on võrdse suurusega ja suunatud piki üht sirget vastassuundades.

Rakendatakse jõud, mida nimetatakse tegevuseks ja reaktsiooniks erinevad kehad ja seepärast ei moodusta tasakaalustatud süsteemi.

Neljas seadus (vägede sõltumatuse seadus):

Mitme jõu samaaegsel toimel on materiaalse punkti kiirendus võrdne kiirenduste geomeetrilise summaga, mis sellel punktil oleks iga jõu mõjul eraldi:

, Kus
,
,…,
.

(MEHAANILISED SÜSTEEMID) – IV variant

1. Materiaalse punkti dünaamika põhivõrrand, nagu teada, on väljendatud võrrandiga. Diferentsiaalvõrrandid mittevaba mehaanilise süsteemi suvaliste punktide liikumisi kahe jõudude jagamise meetodi järgi saab kirjutada kahel kujul:

(1) , kus k=1, 2, 3, … , n – materiaalse süsteemi punktide arv.

(2)

kus on k-nda punkti mass; - k-nda punkti raadiuse vektor, - k-ndale punktile mõjuv antud (aktiivne) jõud või kõigi k-ndale punktile mõjuvate aktiivjõudude resultant. - k-ndale punktile mõjuvate sideme reaktsioonijõudude resultant; - k-ndale punktile mõjuvate sisejõudude resultant; - k-ndale punktile mõjuvate välisjõudude resultant.

Kasutades võrrandeid (1) ja (2), võib püüda lahendada nii esimest kui teist dünaamika ülesannet. Süsteemi teise dünaamika probleemi lahendamine muutub aga väga keeruliseks mitte ainult matemaatilisest vaatenurgast, vaid ka seetõttu, et seisame silmitsi fundamentaalsete raskustega. Need seisnevad selles, et nii süsteemi (1) kui ka süsteemi (2) jaoks on võrrandite arv märkimisväärne vähem numbrit teadmata.

Seega, kui kasutada (1), siis on teise (pöörd)ülesande teadaolev dünaamika ja , tundmatute dünaamika on ja . Vektorvõrrandid on " n" ja tundmatud - "2n".

Kui lähtuda võrrandisüsteemist (2), siis on osa välisjõududest teada. Miks lahutada? Fakt on see, et välisjõudude arv hõlmab ka tundmatute ühenduste väliseid reaktsioone. Lisaks jääb tundmatuks.

Seega on nii süsteem (1) kui ka süsteem (2) SULETUD. On vaja lisada võrrandeid, võttes arvesse seoste võrrandeid ja võib-olla on vaja seada ka seostele endile mõned piirangud. Mida teha?

Kui alustame punktist (1), siis saame järgida esimest tüüpi Lagrange'i võrrandite koostamise teed. Kuid see tee ei ole ratsionaalne, sest lihtsam ülesanne(vähem vabadusastmeid), seda keerulisem on seda matemaatilisest vaatenurgast lahendada.

Seejärel pöörame tähelepanu süsteemile (2), kus - on alati tundmatud. Esimene samm süsteemi lahendamisel on nende tundmatute kõrvaldamine. Tuleb meeles pidada, et reeglina ei huvita meid süsteemi liikumisel sisemised jõud ehk kui süsteem liigub, siis pole vaja teada, kuidas süsteemi iga punkt liigub, vaid sellest piisab. teada, kuidas süsteem tervikuna liigub.

Seega, kui erinevatel viisidel jäta süsteemist (2) välja tundmatud jõud, siis saame mingid seosed, st mõned ilmnevad üldised omadused süsteemi jaoks, mille tundmine võimaldab hinnata, kuidas süsteem üldiselt liigub. Neid tunnuseid tutvustatakse kasutades nn üldised teoreemid kõlarid. Selliseid teoreeme on neli:

1. Teoreem umbes mehaanilise süsteemi massikeskme liikumine;

2. Teoreem umbes mehaanilise süsteemi impulsi muutus;

3. Teoreem umbes mehaanilise süsteemi kineetilise momendi muutus;

4. Teoreem umbes mehaanilise süsteemi kineetilise energia muutus.