Ob upoštevanju translacijskih in rotacijskih gibanj lahko vzpostavimo analogijo med njima. Kinematika translacijskega gibanja uporablja pot s, hitrost  in pospeševanje A. Njihovo vlogo pri rotacijskem gibanju igrajo vrtilni kot , kotna hitrost  in kotni pospešek ε. V dinamiki translacijskega gibanja se uporabljata pojma sila in masa T in impulz Pri rotacijskem gibanju vlogo sile igra moment
sile, vloga mase - vztrajnostni moment jaz z in vloga gibalne količine - kotna količina Če poznamo formule za translacijsko gibanje, je enostavno zapisati formule za rotacijsko gibanje. Na primer, pri enakomernem gibanju se prevožena razdalja izračuna po formuli: s =  t, in z rotacijskim kotom vrtenja - po formuli  =  t. Newtonov drugi zakon
in
in osnovni zakon dinamike rotacijskega gibanja je
in
Pri translacijskem gibanju je gibalna količina telesa enaka
med rotacijskim gibanjem pa je kotna količina
To analogijo je mogoče nadaljevati.

Delo sile pri translacijskem gibanju. Moč

Na telo (materialno točko) deluje stalna sila , ki s smerjo gibanja tvori stalni kot , se giblje premočrtno v nekem referenčnem sistemu in prečka pot l. Potem, kot je znano iz šolskega tečaja fizike, delo A to silo najdemo po formuli:

A= Fl· ker  = F l l, (1)

Oglejmo si zdaj splošni primer računanja dela, ko se telo pod vplivom spremenljive sile translacijsko giblje po ukrivljeni poti. Na poti l izberite elementarni del dl, znotraj katerega lahko upoštevamo silo in kot  sta konstantni vrednosti, sam prerez pa je premočrtni. Potem delaj dA v tem razdelku najdemo z uporabo formule (1): dA = F· dl· cos. delo A na celotni poti je enak vsoti dela dA, tj.

(2)

Ikona l z integralom pomeni, da se integracija izvaja vzdolž celotne poti l.

Formulo (2) lahko damo drugačno obliko, če uporabimo skalarni produkt vektorjev. Nato integrand dA bo zapisan v obliki: dA = F· dl· cos=
kje je vektor elementarnega premika in

(3)

Iz formule (1) je razvidno, da je delo algebraična količina. Predznak dela je odvisen od kota . Če je kot  oster, potem je cos  > 0 in je delo pozitivno, če pa je kot  top, je delo negativno.

Enota SI za delo je joule (J). Uveden je iz formule (1), v kateri je predpostavljeno, da je cos  = 1 delo, ki ga opravi sila 1 N na poti 1 m, če smeri sile in premika sovpadata.

Za karakterizacijo hitrosti dela je uveden koncept moči, ki je enak delu, opravljenemu na enoto časa. Če osnovno časovno obdobje dt osnovno delo je opravljeno dA, nato moč R enako

(4)

V enotah SI se moč meri v vatih (W). Kot izhaja iz (4), je 1 W = 1 J / 1 s, tj. 1 W- To je moč, pri kateri je 1 J delo opravljeno v 1 s.

Delo sile med rotacijskim gibanjem

Razmislite o togem telesu, ki pod delovanjem spremenljive sile vrti okoli osi z pod nekim kotom. Ta sila ustvarja navor M z, vrtenje telesa. Sila je usmerjena tangencialno na krožnico, po kateri se premika točka uporabe sile. Zato je kot  = 0. Ob upoštevanju tega po analogiji s formulo za mehansko delo (glej (2)) najdemo izraz, s katerim izračunamo delo med rotacijskim gibanjem:

(5)

Delo bo pozitivno, če smer tangencialne komponente sile sovpada s smerjo vrtenja, in negativno, če sta v nasprotni smeri.

Oris predavanja

Vztrajnostni moment.

Trenutek moči. Osnovna enačba za dinamiko rotacijskega gibanja.

Trenutek impulza. Zakon o ohranitvi kotne količine.

Delo in kinetična energija pri rotacijskem gibanju.

1. Vztrajnostni moment.

Pri obravnavanju rotacijskega gibanja je potrebno uvesti nove fizikalne pojme: vztrajnostni moment, moment sile, moment impulza.

Vztrajnostni moment je merilo vztrajnosti telesa med rotacijskim gibanjem telesa.

Vztrajnostni moment materialne točke glede na fiksno os vrtenja je enak produktu njene mase s kvadratom razdalje do obravnavane osi vrtenja (slika 1):

je odvisna samo od mase materialne točke in njenega položaja glede na vrtilno os in ni odvisna od prisotnosti same rotacije.

Vztrajnostni moment je skalarna in aditivna količina, zato je vztrajnostni moment telesa enak vsoti vztrajnostnih momentov vseh njegovih točk:

.

V primeru zvezne porazdelitve mase se ta vsota zmanjša na integral:

,

kjer je masa majhne prostornine telesa
, - telesna gostota, - oddaljenost od elementa
na os vrtenja.

Vztrajnostni moment je analog mase med rotacijskim gibanjem. Večji kot je vztrajnostni moment telesa, težje je spremeniti kotno hitrost rotirajočega telesa. Vztrajnostni moment je smiseln samo za dano lego vrtilne osi. Nima smisla govoriti zgolj o »vztrajnostnem trenutku«. Odvisno je:

1) od položaja osi vrtenja;

2) iz porazdelitve telesne mase glede na vrtilno os, tj. na obliko telesa in njegovo velikost.

Eksperimentalni dokaz za to je poskus s kotalečimi se valji.

Z integracijo za nekatera homogena telesa lahko dobimo naslednje formule (rotacijska os poteka skozi središče mase telesa).

Vztrajnostni moment obroča (zanemarjamo debelino stene) ali votlega valja:

Vztrajnostni moment diska ali trdnega valja s polmerom R:

.

Vztrajnostni moment žoge

Vztrajnostni moment palice

E Če je za telo znan vztrajnostni moment okoli osi, ki poteka skozi središče mase, se vztrajnostni moment glede na katero koli os, ki je vzporedna s prvo, najde po Steinerjev izrek: vztrajnostni moment telesa glede na poljubno os je enak vztrajnostnemu momentu J 0 glede na os, ki je vzporedna z dano in poteka skozi središče mase telesa, doštetemu zmnožku mase telesa in kvadrat razdalje med osema.

kje d oddaljenost od središča mase O na os vrtenja (slika 2).

Središče mase- namišljena točka, katere položaj označuje porazdelitev mase danega telesa. Središče mase telesa se giblje tako, kot bi se gibala materialna točka enake mase pod vplivom vseh zunanjih sil, ki delujejo na dano telo.

Koncept vztrajnostnega momenta je v mehaniko uvedel domači znanstvenik L. Euler sredi 18. stoletja in se od takrat pogosto uporablja pri reševanju številnih problemov dinamike togega telesa. Vrednost vztrajnostnega momenta je treba poznati v praksi pri izračunih različnih vrtečih sestavnih delov in sistemov (vztrajnikov, turbin, rotorjev elektromotorjev, žiroskopov). Vztrajnostni moment je vključen v enačbe gibanja telesa (ladje, letala, izstrelka itd.). Določimo ga, ko želimo izvedeti parametre rotacijskega gibanja letala okoli središča mase pod vplivom zunanje motnje (sun vetra ipd.).

Ob opazovanju zapletenih gibov, kot je gibanje človeškega telesa (hoja, tek, skoki ipd.), se zdi težko ali celo nemogoče opisati gibanje vseh njegovih točk. Vendar pa je pri analizi takšnih gibanj mogoče opaziti, da so sestavljena iz enostavnejših - translacijskih in rotacijskih gibanj.

Mehanika translacijskega gibanja je bralcu znana, zato se poglavje začne z obravnavo rotacijskega gibanja. Najenostavnejši je vrtenje togega telesa okoli nepremične osi. Ta primer vam omogoča, da se seznanite s posebnostmi, terminologijo in zakonitostmi rotacijskega gibanja.

5.1. KINEMATIKA VRTILNEGA GIBANJA ABSOLUTNO TOGEGA TELESA OKROG NEPREMIČNE OSI

Absolutno togo telo je tisto, pri katerem je razdalja med katerima koli točkama konstantna.

Mere in oblika absolutno togega telesa se pri gibanju ne spremenijo.

Koncept "popolnoma togega telesa" je fizična abstrakcija, saj je vsako telo sposobno deformirati. Vendar pa je v mnogih primerih mogoče deformacijo zanemariti.

Najenostavnejši primer rotacijskega gibanja absolutno togega telesa je vrtenje okoli fiksne osi. To je gibanje, pri katerem se točke telesa gibljejo v krožnicah, katerih središča ležijo na premici, imenovani vrtilna os.

Znano je, da v nekaterih primerih za karakterizacijo gibanja telesa ni treba navesti gibanja vseh njegovih točk; tako je na primer pri translacijskem gibanju dovolj, da označite gibanje katere koli točke telesa.

Med rotacijskim gibanjem okoli osi se točke telesa gibljejo po različnih tirnicah, vendar se v istem času vse točke in telo samo vrtijo pod enakim kotom. Za značilnosti vrtenja

narišite v ravnino, pravokotno na os, radij vektor do določene točke i(slika 5.1). Časovna odvisnost kota rotacije α vektorja radija glede na izbrano smer OX je enačba rotacijskega gibanja togega telesa okoli nepremične osi:

Hitrost vrtenja telesa je označena s kotno hitrostjo, ki je enaka prvemu odvodu kota vrtenja polmernega vektorja glede na čas:

Kotna hitrost je vektor, ki je usmerjen vzdolž osi vrtenja in je povezan s smerjo vrtenja po pravilu desnega vijaka (slika 5.2). Vektor kotne hitrosti je za razliko od vektorjev hitrosti in sile drsen: nima določene točke uporabe in se lahko nahaja kjerkoli na vrtilni osi. Tako določanje vektorja ω označuje položaj vrtilne osi, smer vrtenja in velikost kotne hitrosti.

Hitrost spremembe kotne hitrosti je označena s kotnim pospeškom, ki je enak prvemu odvodu kotne hitrosti glede na čas:

ali v vektorski obliki:

Iz (5.4) je jasno, da vektor kotnega pospeška sovpada v smeri z osnovno, dokaj majhno spremembo vektorja kotne hitrosti dω: s pospešenim vrtenjem je kotni pospešek usmerjen v isto smer kot kotna hitrost, s počasnim vrtenjem - v nasprotni smeri.

Ker je kotni premik vseh točk absolutno togega telesa enak, potem imajo v skladu z (5.2) in (5.3) vse točke telesa istočasno enako kotno hitrost in enak kotni pospešek. Linearne karakteristike - premik, hitrost, pospešek - so različne za različne točke. Označimo v skalarni obliki razmerje, ki ga je mogoče izpeljati neodvisno, med linearno in kotno karakteristiko za i-to točko, ki se giblje v krogu polmera r i:

riž. 5.3

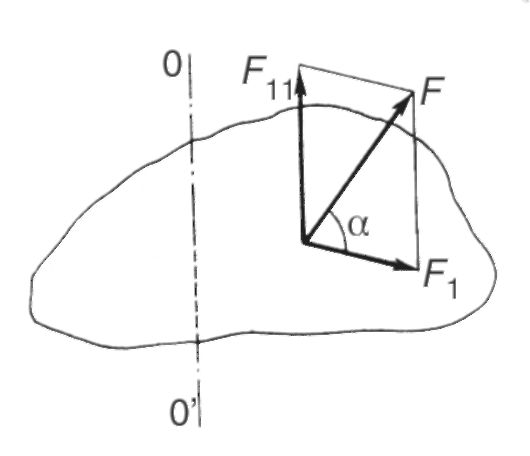
Za zaključek predstavljamo formule za kinematiko rotacijskega gibanja togega telesa okoli nepremične osi, ki jih dobimo z integracijo ustreznih izrazov:

enačba enakomernega rotacijskega gibanja[cm. (5.2)]:

odvisnost kotne hitrosti od časa pri enakomernem rotacijskem gibanju[cm. (5.3)]:

enačba enakomerno izmeničnega rotacijskega gibanja[cm. (5.1) in (5.6)]:

Koristno je primerjati te formule s podobnimi odvisnostmi za translacijsko gibanje.

5.2. OSNOVNI POJMI. ENAČBA ZA DINAMIKO VRTILNEGA GIBANJA

Moment sile_

Naj do neke točke i sila, ki deluje na togo telo F^, ki leži v ravnini, pravokotni na os vrtenja (slika 5.4).

Moment sile glede na vrtilno os je vektorski produkt vektorja polmera točke i in sile:

Če ga razširite, lahko napišete:

kje β - kot med vektorji r i in F i . Od rame sile h i = r i sinβ (glej sliko 5.4), potem

Če sila deluje pod določenim kotom α na ravnino vrtenja (sl. 5.5), jo lahko razdelimo na dve komponenti. Eden od njih leži v ravnini, pravokotni na vrtilno os, drugi pa je vzporeden s to osjo in ne vpliva na vrtenje telesa (v realnem primeru deluje le na ležaje). Nadalje bodo upoštevane le sile, ki ležijo v ravnini, pravokotni na os vrtenja.

riž. 5.4

riž. 5.5

Delajte v rotacijskem gibanju

Naj pod delovanjem sile F i(glej sliko 5.4) se telo zavrti za dovolj majhen kot dα. Poiščimo delo, ki ga opravi ta sila.

Iz srednje šole poznan izraz za delo sile v tem primeru zapišemo takole:

Torej,

elementarno delo sile pri rotacijskem gibanju je enako zmnožku momenta sile in elementarnega rotacijskega kota telesa.

Če na telo deluje več sil, se elementarno delo vseh sil določi podobno kot (5.12):

kje M- skupni moment vseh zunanjih sil, ki delujejo na telo.

Če se pri vrtenju telesa položaj vektorja radija spremeni iz α 1 v α 2, potem lahko delo zunanjih sil ugotovimo z integracijo izraza (5.13):

Vztrajnostni moment

Merilo za vztrajnost teles pri translacijskem gibanju je masa. Vztrajnost teles med rotacijskim gibanjem ni odvisna samo od mase, ampak tudi od njene porazdelitve v prostoru glede na os. Za merilo vztrajnosti telesa med vrtenjem je značilen vztrajnostni moment telesa glede na vrtilno os. Najprej poudarimo to

Vztrajnostni moment materialne točke glede na vrtilno os je vrednost, ki je enaka zmnožku mase točke s kvadratom njene oddaljenosti od osi:

Vztrajnostni moment telesa glede na os je vsota vztrajnostnih momentov vseh materialnih točk, ki sestavljajo telo:

Kot primer izpeljemo formulo vztrajnostni moment tanke homogene palice dolžina l in masa T glede na os, ki je pravokotna na palico in poteka skozi njeno sredino (slika 5.6). Izberimo dovolj majhen odsek palice z dolžino dx in masa dm, oddaljena od osi 00" za razdaljo X. Zaradi majhnosti tega območja ga lahko vzamemo kot materialno točko, njen vztrajnostni moment [glej. (5.15)] je enako:

Masa elementarnega odseka je enaka produktu linearne gostote t/l, pomnoženo z dolžino osnovnega odseka: dm= (m/l) dx Če ta izraz nadomestimo v (5.18), dobimo

Da bi našli vztrajnostni moment celotne palice, integriramo izraz (5.19) po celotni palici, tj. v območju od -1/2 do +1/2:

Predstavimo izraze za vztrajnostne momente različnih simetričnih masnih teles T:

votel homogeni valj(obroč) z notranjim radijem r in zunanje R glede na os OO", ki sovpada z geometrijsko osjo valja (sl. 5.7):

neprekinjeno homogeno valj (r = 0) ali disk [glej (5.21)]:

homogena žoga glede na os, ki poteka skozi njegovo središče:

pravokotni paralelopiped glede na os OO", ki poteka skozi središče pravokotno na ravnino osnove (slika 5.8):

V vseh zgornjih primerih poteka vrtilna os skozi središče mase telesa. Pri reševanju nalog za določitev vztrajnostnega momenta telesa okoli osi, ki ne poteka skozi središče mase, lahko uporabite Huygensov izrek. V skladu s tem izrekom je vztrajnostni moment telesa glede na neko os OO":

kjer je J 0 vztrajnostni moment okoli vzporedne osi, ki poteka skozi središče mase telesa OO"; T- telesna teža; d- razdalja med dvema vzporednima osema (slika 5.9). Enota za vztrajnostni moment je kilogram meter na kvadrat(kg-m2).

Zagon

trenutek impulza(kotni moment)materialna točka, ki se vrti okoli določene osi, se imenuje vrednost, ki je enaka zmnožku momenta točke na njeni razdalji od osi vrtenja:

Kotni moment telesa, ki se vrti okoli določene osi, je enak vsoti kotnih momentov točk, ki tvorijo telo:

Ker je kotna hitrost vseh točk togega telesa enaka, vzamemo ω iz predznaka vsote [glej. (5.29)], dobimo:

(/ - vztrajnostni moment telesa glede na os) ali v vektorski obliki:

Kotna količina je torej enaka produktu vztrajnostnega momenta točke in kotne hitrosti. Iz tega sledi, da smeri vektorjev kotne količine in kotne hitrosti sovpadata. Enota za kotno količino je kilogram-meter na kvadrat na sekundo(kg? m2? s -1).

Koristno je primerjati formulo (5.31) s podobno formulo za gibalno količino pri translacijskem gibanju.

Kinetična energija rotacijskega telesa

Ko se telo vrti, je njegova kinetična energija sestavljena iz kinetičnih energij posameznih točk telesa. Za trdno:

Koristno je primerjati izraz (5.32) s podobnim izrazom za translacijsko gibanje.

Z razlikovanjem (5.32) dobimo osnovno spremembo kinetične energije pri rotacijskem gibanju:

Osnovna enačba za dinamiko rotacijskega gibanja

Naj se togo telo, na katerega delujejo zunanje sile, zavrti za dovolj majhen kot da. Izenačimo osnovno delo vseh zunanjih sil med takim vrtenjem [glej. (5.13)] na osnovno spremembo kinetične energije [glej. (5.33)]: M dα = Jω dω , od koder je:

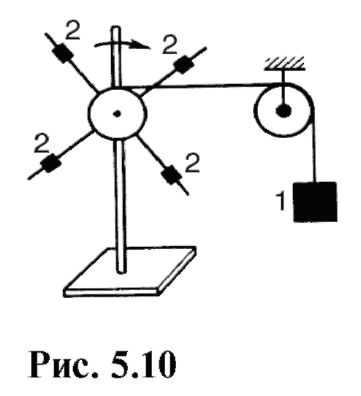
To je to osnovnienačba dinamike rotacijskega gibanja. Iz (5.35) je jasno, da vztrajnostni moment označuje vztrajnostne lastnosti telesa pri rotacijskem gibanju: pod delovanjem zunanjih sil je kotni pospešek telesa večji, manjši je vztrajnostni moment telesa.

Osnovna enačba za rotacijsko gibanje igra enako vlogo kot drugi Newtonov zakon za translacijsko gibanje. Fizikalne količine, vključene v to enačbo, so analogne sili, masi in pospešku.

Od (5.34) sledi:

Odvod vrtilne količine telesa glede na čas je enak rezultantnemu momentu vseh zunanjih sil.

Odvisnost kotnega pospeška od momenta sile in vztrajnostnega momenta lahko dokažemo z

z močjo naprave, prikazano na sl. 5.10. Pod obremenitvijo 1, obešen na nit, vrženo čez blok, se križ hitro vrti. Premikanje uteži 2 na različnih razdaljah od osi vrtenja lahko spremenite vztrajnostni moment prečke. Spreminjanje obremenitev, tj. momentov sil in vztrajnostnega momenta, lahko preverimo, da se kotni pospešek povečuje s povečanjem momenta sile ali zmanjšanjem vztrajnostnega momenta.

5.3. ZAKON OHRANJENJA MOMENTA

Oglejmo si poseben primer rotacijskega gibanja, ko je skupni moment zunanjih sil enak nič. Kot je razvidno iz (5.37), dL/dt= 0 pri M = 0, od kje

Ta določba je znana kot zakon o ohranitvi gibalne količine: če je skupni moment vseh zunanjih sil, ki delujejo na telo, enak nič, potem ostane gibalna količina tega telesa konstantna.

Če izpustimo dokaz, ugotavljamo, da zakon o ohranitvi kotne količine ne velja le za absolutno togo telo.

Najbolj zanimive uporabe tega zakona so povezane z vrtenjem sistema teles okoli skupne osi. V tem primeru je treba upoštevati vektorsko naravo vrtilne količine in kotnih hitrosti. Torej, za sistem, sestavljen iz n telesa, ki se vrtijo okoli skupne osi, lahko zakon o ohranitvi kotne količine zapišemo v obliki:

Oglejmo si nekaj primerov, ki ponazarjajo ta zakon.

Telovadec, ki izvaja salto (slika 5.11), v začetni fazi upogne kolena in jih pritisne na prsi, s čimer zmanjša vztrajnostni moment in poveča kotno hitrost vrtenja okoli vodoravne osi, ki poteka skozi središče mase. Na koncu skoka se telo zravna, vztrajnostni moment se poveča, kotna hitrost pa zmanjša. Drsalec, ki izvaja rotacijo okoli navpične osi (slika 5.12), na začetku rotacije približa roke k telesu, s čimer zmanjša vztrajnostni moment in poveča kotno hitrost. Na koncu vrtenja pride do nasprotnega procesa: pri premikanju rok se vztrajnostni moment poveča in kotna hitrost zmanjša, kar olajša zaustavitev.

Isti pojav je mogoče prikazati na klopi Žukovskega, ki je lahka vodoravna ploščad, ki se z nizkim trenjem vrti okoli navpične osi. Ko se položaj rok spremeni, se vztrajnostni moment in kotna hitrost spremenita (slika 5.13), kotni moment ostane konstanten. Da bi povečali demonstracijski učinek, so v rokah osebe dumbbells. Na klopi Žukovskega lahko dokažete vektorsko naravo zakona o ohranitvi kotne količine.

Eksperimentator, ki stoji na nepremični klopi, dobi od pomočnika kolo kolesa, ki se vrti okoli navpične osi (slika 5.14, levo). V tem primeru je kotni moment osebe in sistema platforma-kolo določen samo s kotnim momentom kolesa:

tukaj je J h vztrajnostni moment osebe in ploščadi; J K in ω κ - vztrajnostni moment in kotna hitrost kolesa. Ker je moment zunanjih sil glede na navpično os enak nič, potem L je ohranjen (L = const).

Če eksperimentator zavrti os vrtenja kolesa za 180 ° (slika 5.14, desno), bo kotna količina kolesa usmerjena nasprotno od prvotnega in enaka J K ω K. Ker se vektor kotne količine kolesa spremeni in se kotna količina sistema ohrani, se mora kotna količina osebe in ploščadi neizogibno spremeniti; ne bo več enaka nič 1 . Kotna količina sistema v tem primeru

1 Rahlo neusklajenost med osjo kolesa in osjo vrtenja ploščadi je mogoče zanemariti.

Z uporabo formule (5.42) je mogoče približno oceniti vztrajnostni moment človeškega telesa skupaj s ploščadjo, za katero je treba izmeriti ω κ, ω 4 in najti J k.

Metoda za merjenje kotnih hitrosti enakomernega vrtenja je bralcu znana. Ob poznavanju mase kolesa in ob predpostavki, da je masa v glavnem porazdeljena po platišču, lahko z uporabo formule (5.22) določimo J k.

Da bi zmanjšali napako, lahko obtežite platišče kolesa, tako da nanj položite posebne pnevmatike. Oseba mora biti nameščena simetrično glede na os vrtenja.

Enostavnejša različica obravnavane demonstracije je, da oseba, ki stoji na klopi Žukovskega, sama vrti kolo, ki ga drži na navpični osi. V tem primeru se oseba in ploščad začneta vrteti v nasprotnih smereh (slika 5.15).

5.4. KONCEPT PROSTIH OSI ROTACIJE

Telo, ki se vrti okoli fiksne osi, običajno deluje na ležaje ali druge naprave, ki ohranjajo položaj te osi konstanten. Pri visokih kotnih hitrostih in vztrajnostnih momentih so ti učinki lahko pomembni. Vendar pa je v vsakem telesu mogoče izbrati osi, katerih smer med vrtenjem se bo ohranila brez posebnih naprav. Da bi razumeli, kateri pogoj mora izpolnjevati izbira takšnih osi, upoštevajte naslednji primer.

Če primerjamo (5.43) s koordinatami masnega središča, opazimo, da so sile, ki delujejo na os, uravnotežene, če vrtilna os poteka skozi masno središče.

Telo poljubne oblike ima skozi masno središče vedno vsaj tri med seboj pravokotne osi, ki so lahko proste osi vrtenja. Te osi se imenujejo glavne vztrajnostne osi. Čeprav so vse tri glavne vztrajnostne osi proste, bo najbolj stabilno vrtenje okoli osi z največjim vztrajnostnim momentom. Dejstvo je, da je zaradi neizogibnega delovanja zunanjih sil, kot je trenje, in tudi zaradi dejstva, da je težko nastaviti vrtenje točno okoli določene osi, vrtenje okoli preostalih prostih osi nestabilno.

V nekaterih primerih, ko se telo vrti okoli proste osi z majhnim vztrajnostnim momentom, samo spremeni to os v os z največjim momentom.

Ta pojav dokazuje naslednji poskus. Cilindrična palica je obešena na elektromotor z nitjo, ki se lahko vrti okoli svoje geometrijske osi (slika 5.17, a). Vztrajnostni moment okoli te osi J 1 = mR 2 /2. Pri dovolj veliki kotni hitrosti bo palica spremenila svoj položaj (slika 5.17, b). Vztrajnostni moment glede na novo os je enak J 2 = ml 2/12. Če je l 2 >6R 2, potem je J 2 > J 1. Vrtenje okoli nove osi bo stabilno.

Bralec lahko iz izkušenj neodvisno preveri, da je rotacija vržene škatlice vžigalic stabilna glede na os, ki poteka pravokotno na večjo ploskev, in nestabilna ali manj stabilna glede na osi, ki potekajo pravokotno na druge ploskve (glej sliko 5.8).

Vrtenje živali in ljudi v prostem letu in med različnimi skoki poteka okoli prostih osi z najvišjim ali najnižjim vztrajnostnim momentom. Ker je položaj središča mase odvisen od drže telesa, bodo za različne drže različne proste osi.

5.5. POJEM STOPNJ SVOBODE

Položaj proste materialne točke v prostoru določajo tri neodvisne koordinate: x, y, z. Če točka ni prosta, ampak se premika na primer po neki površini, potem vse tri koordinate ne bodo neodvisne.

Neodvisne spremenljivke, ki označujejo položaj mehanskega sistema, se imenujejo prostostne stopnje.

Prosta materialna točka ima tri prostostne stopnje, v obravnavanem primeru - dve prostostni stopnji. Ker lahko molekulo enoatomskega plina obravnavamo kot materialno točko, ima torej tudi taka prosta molekula tri prostostne stopnje.

Še nekaj primerov.

Dve materialni točki 1 in 2 sta med seboj togo povezani. Položaj obeh točk je določen s šestimi koordinatami x 1, y 1, z 1, x 2, y 2, z 2, za katere velja ena omejitev in ena povezava, matematično izražena v obliki enačbe:

Fizično to pomeni, da je razdalja med materialnimi točkami vedno l. V tem primeru je število prostostnih stopinj 5. Obravnavani primer je model dvoatomne molekule.

Tri materialne točke 1, 2 in 3 so med seboj togo povezane. prijatelj. Devet koordinat označuje položaj takega sistema: x 1, y 1, z 1, x 2, y 2, z2, x 3 y 3 , z 3 . Vendar pa tri povezave med točkami določajo neodvisnost le šestih koordinat. Sistem ima šest prostostnih stopenj. Ker lega treh točk, ki ne ležijo na isti premici, enolično določa lego togega telesa, ima togo telo šest prostostnih stopenj.

Triatomske in poliatomske molekule imajo enako število prostostnih stopinj (šest), če te molekule obravnavamo kot toge tvorbe.

1 Če dobimo imaginarno vrednost za odvisno koordinato iz (5.44), to pomeni, da izbrane neodvisne koordinate ne ustrezajo nobeni točki, ki se nahaja na krogli danega radija.

V pravih poliatomskih molekulah so atomi v vibracijskem gibanju, zato je število prostostnih stopinj takih molekul več kot šest.

Število stopenj svobode ne določa le števila neodvisnih spremenljivk, ki označujejo položaj mehanskega sistema, ampak tudi, kar je zelo pomembno, število neodvisnih gibov sistema. Tako tri prostostne stopnje proste materialne točke pomenijo, da je mogoče vsako gibanje točke razstaviti na neodvisna gibanja po treh koordinatnih oseh. Ker točka nima dimenzij, nima smisla govoriti o njeni rotaciji. Torej ima materialna točka tri stopnje svobode translacijskega gibanja. Materialna točka na ravnini, krogli ali drugi površini ima dve stopnji svobode translatornega gibanja. Gibanje materialne točke vzdolž krivulje (pogojni primer je gibanje vlaka po tirnicah) ustreza eni stopnji svobode translacijskega gibanja.

Togo telo, ki se vrti okoli nepremične osi, ima eno stopnjo svobode rotacijskega gibanja. Kolo vlaka ima dve prostostni stopnji: ena je rotacijsko gibanje, druga pa translacijska (premikanje osi kolesa vzdolž tirnice). Šest prostostnih stopenj togega telesa pomeni, da je vsako gibanje tega telesa mogoče razstaviti na komponente: gibanje središča mase se razgradi na tri translacijske premike vzdolž koordinatnih osi, vrtenje pa je sestavljeno iz treh preprostejših vrtljajev okoli koordinatnih osi. ki poteka skozi središče mase.

Na sl. 5.18-5.20 prikazujejo tečajne spoje, ki ustrezajo eni, dvema in trem stopnjam svobode.

riž. 5.18

riž. 5.19

riž. 5.20

5.6. CENTRIFUGIRANJE

Centrifugiranje je proces separacije (ločevanja) heterogenih sistemov, na primer delcev iz tekočin, v katerih se nahajajo, zaradi njihovega vrtenja.

Razmislimo o ločevanju nehomogenih sistemov v gravitacijskem polju. Predpostavimo, da obstaja vodna suspenzija delcev različnih gostot. Sčasoma zaradi delovanja gravitacije in vzgonske sile F A pride do ločevanja delcev: delci z večjo gostoto od vode potonejo, delci z manjšo gostoto od vode plavajo. Rezultantna sila, ki deluje na primer na gostejši posamezni delec, je enaka:

kje ρ 1 - gostota delcev; ρ - gostota vode; V- prostornina delcev.

Če se vrednosti ρ 1 in ρ med seboj malo razlikujejo, potem sila Fp je majhna in separacija (odlaganje) poteka precej počasi. V centrifugi (separatorju) takšno ločevanje izvajamo prisilno z vrtenjem izločenega medija.

Razmislimo o fiziki tega pojava.

Naj bo delovna prostornina centrifuge (slika 5.21: a - videz; b - diagram delovne prostornine) popolnoma zasedena z neko homogeno tekočino. Miselno izberimo majhen volumen V te tekočine, ki se nahaja na daljavo r od osi vrtenja OO". Pri enakomernem vrtenju centrifuge poleg gravitacijske in vzgonske sile, ki se medsebojno uravnovesita, deluje na izbrano prostornino še centripetalna sila. To je sila tekočine, ki obdaja prostornino. naravno usmerjena proti osi vrtenja in je enaka:

kje ρ je gostota tekočine.

Predpostavimo zdaj, da je dodeljena prostornina V je ločeni delec, katerega gostota snovi je ρ 1 (ρ 1 Φ ρ). Sila, ki deluje na delec iz okoliške tekočine, se ne bo spremenila, kot je razvidno iz formule (5.45).

Da bi se delec vrtel skupaj s tekočino, mora nanj delovati centripetalna sila, ki je enaka:

kje m 1 je masa delca, ρ 1 pa pripadajoča gostota.

riž. 5.21

če F> F 1, takrat se delec premakne proti osi vrtenja. če F< F 1, takrat udarec tekočine na delec ne bo zadosten, da bi ga obdržal na krožni tirnici, in delec se bo po vztrajnosti začel premikati na obrobje. Učinek ločevanja je določen s presežno silo F, ki deluje s strani tekočine na izbrani delec, nad vrednostjo centripetalne sile F 1, ki določa krožno gibanje:

Iz tega izraza je razvidno, da je učinek centrifugiranja tem večji, čim večja je razlika v gostotah ločenih delcev in tekočine, bistveno pa je odvisen tudi od kotne hitrosti vrtenja 1.

Primerjajmo ločevanje s centrifugiranjem z ločevanjem z gravitacijo:

1 Gravitacija in sila vzgona pri izpeljavi formule (5.47) nista upoštevani, ker sta usmerjeni vzdolž osi vrtenja in nimata temeljnega vpliva na centrifugiranje.

Ultracentrifuge lahko ločujejo delce, manjše od 100 nm, suspendirane ali raztopljene v tekočini. Našli so široko uporabo v biomedicinskih raziskavah za ločevanje biopolimerov, virusov in subceličnih delcev.

Hitrost ločevanja je še posebej pomembna pri bioloških in biofizikalnih raziskavah, saj se lahko sčasoma stanje preučevanih predmetov bistveno spremeni.

Osnovni pojmi.

moment sile glede na vrtilno os - to je vektorski produkt vektorja radija in sile.

(1.14)

Moment sile je vektor , katere smer je določena s pravilom gimlet (desni vijak) v odvisnosti od smeri sile, ki deluje na telo. Moment sile je usmerjen vzdolž osi vrtenja in nima določene točke uporabe.

Številčna vrednost tega vektorja je določena s formulo:

M=r F greh (1.15),

kjer  - kot med vektorjem radija in smerjo sile.

če =0 oz  , moment sile M=0, tj. sila, ki poteka skozi vrtilno os ali sovpada z njo, ne povzroči vrtenja.

Največji modul navora nastane, če sila deluje pod kotom  =  /2 (M 0) oz  =3  /2 (M 0).

Uporaba koncepta finančnega vzvoda d- to je pravokotnik, spuščen iz središča vrtenja na linijo delovanja sile), formula za moment sile ima obliko:

, Kje
(1.16)

Pravilo momentov sil(pogoj ravnovesja telesa s fiksno vrtilno osjo):

Da je telo s fiksno vrtilno osjo v ravnotežju, mora biti algebraična vsota momentov sil, ki delujejo na to telo, enaka nič.

 M i =0 (1.17)

Enota SI za moment sile je [Nm]

Pri rotacijskem gibanju je vztrajnost telesa odvisna ne le od njegove mase, temveč tudi od njegove porazdelitve v prostoru glede na vrtilno os.

Za vztrajnost med vrtenjem je značilen vztrajnostni moment telesa glede na os vrtenja. J.

Vztrajnostni moment materialna točka glede na vrtilno os je vrednost, ki je enaka zmnožku mase točke s kvadratom njene oddaljenosti od vrtilne osi:

J  =m   r  2 (1.18)

Vztrajnostni moment telesa glede na os je vsota vztrajnostnih momentov materialnih točk, ki sestavljajo telo:

J= m   r  2 (1.19)

Vztrajnostni moment telesa je odvisen od njegove mase in oblike ter od izbire vrtilne osi. Za določitev vztrajnostnega momenta telesa glede na določeno os se uporablja Steiner-Huygensov izrek:

J=J 0 +m d 2 (1.20),

kje J 0 – vztrajnostni moment okoli vzporedne osi, ki poteka skozi središče mase telesa, d – razdalja med dvema vzporednima osema . Vztrajnostni moment v SI se meri v [kgm 2 ]

Vztrajnostni moment med rotacijskim gibanjem človeškega telesa se določi eksperimentalno in približno izračuna po formulah za valj, okroglo palico ali kroglo.

Vztrajnostni moment osebe glede na navpično os vrtenja, ki poteka skozi središče mase (središče mase človeškega telesa se nahaja v sagitalni ravnini nekoliko pred drugim sakralnim vretencem), odvisno od položaj osebe, ima naslednje vrednosti: pri miru - 1,2 kg m 2; z "arabesko" pozo - 8 kgm 2; v vodoravnem položaju - 17 kg  m 2.

Delajte v rotacijskem gibanju nastane, ko se telo vrti pod vplivom zunanjih sil.

Elementarno delo sile pri rotacijskem gibanju je enako zmnožku momenta sile in elementarnega rotacijskega kota telesa:

dA  =M   d (1.21)

Če na telo deluje več sil, potem je osnovno delo rezultante vseh uporabljenih sil določeno s formulo:

dA=M d (1.22),

kje M– skupni moment vseh zunanjih sil, ki delujejo na telo.

Kinetična energija rotacijskega telesaW Za odvisno od vztrajnostnega momenta telesa in kotne hitrosti njegovega vrtenja:

(1.23)

Kot impulza (kotni moment) – količina, ki je številčno enaka zmnožku gibalne količine telesa in polmera vrtenja.

L=p r=m V r (1.24).

Po ustreznih transformacijah lahko formulo za določitev vrtilne količine zapišete v obliki:

(1.25).

Zagon – vektor, katerega smer je določena s pravilom desnega vijaka. Enota SI za kotno količino je kgm 2 /s

Osnovni zakoni dinamike rotacijskega gibanja.

Osnovna enačba za dinamiko rotacijskega gibanja:

Kotni pospešek telesa, ki se vrti, je neposredno sorazmeren s skupnim momentom vseh zunanjih sil in obratno sorazmeren z vztrajnostnim momentom telesa.

(1.26).

Ta enačba igra enako vlogo pri opisovanju rotacijskega gibanja kot drugi Newtonov zakon za translacijsko gibanje. Iz enačbe je razvidno, da je pod delovanjem zunanjih sil večji kotni pospešek, manjši je vztrajnostni moment telesa.

Drugi Newtonov zakon za dinamiko rotacijskega gibanja lahko zapišemo v drugi obliki:

(1.27),

tiste. prvi odvod vrtilne količine telesa glede na čas je enak skupnemu momentu vseh zunanjih sil, ki delujejo na dano telo.

Zakon ohranitve vrtilne količine telesa:

Če je skupni moment vseh zunanjih sil, ki delujejo na telo, enak nič, tj.

 M  =0 , Potem dL/dt=0 (1.28).

Iz tega izhaja
oz
(1.29).

Ta izjava predstavlja bistvo zakona o ohranitvi kotne količine telesa, ki je formuliran na naslednji način:

Kotna količina telesa ostane konstantna, če je skupni moment zunanjih sil, ki delujejo na rotirajoče telo, enak nič.

Ta zakon ne velja le za absolutno togo telo. Primer je umetnostni drsalec, ki izvaja rotacijo okoli navpične osi. S pritiskom na roke drsalec zmanjša vztrajnostni moment in poveča kotno hitrost. Da bi upočasnil vrtenje, nasprotno široko razširi roke; Posledično se poveča vztrajnostni moment in zmanjša kotna hitrost vrtenja.

Na koncu predstavljamo primerjalno tabelo glavnih količin in zakonov, ki označujejo dinamiko translacijskih in rotacijskih gibanj.

Tabela 1.4.

=const,

Zato je treba od zunanje sile, ki deluje na telo, izolirati komponente, ki ne povzročajo vrtenja. Vrtenje lahko povzroči le sila (rotacijska sila), ki leži v ravnini, pravokotni na os vrtenja in usmerjena tangencialno na krog, ki ga opisuje točka njenega delovanja.

Upoštevajte, da ko se telo vrti, komponente ne opravljajo nobenega dela, saj se točka uporabe teh sil premika pravokotno na njihove smeri. Delo opravlja samo rotacijska sila, to je projekcija sile, ki deluje na telo, na smer gibanja točke delovanja te sile.

Določimo količino dela, ki ga opravi vrtilna sila, če se njena točka uporabe premakne vzdolž kroga s polmerom (slika 1.19, b). Predpostavimo, da velikost sile ostane konstantna. Potem

Produkt rotacijske sile in polmera je moment rotacijske sile ali navora, ki deluje na dano telo, in je označen z (spomnimo se, da je moment dane sile glede na katero koli os produkt te sile z njenega kraka, to je po dolžini navpičnice, izvedene iz navedenega

os glede na smer sile). Tako je v formuli (2.8)

zato je delo, ki ga opravi navor, enako zmnožku tega trenutka in kota vrtenja telesa:

Če se navor (sila ali njen krak) s časom spreminja, se opravljeno delo določi kot vsota:

Navor vrtilne sile je predstavljen kot vektor, ki sovpada z osjo vrtenja; pozitivna orientacija tega vektorja je izbrana v smeri, v kateri bi se premaknil desni vijak, ki se vrti v tem trenutku.

Navor, ki deluje na telo, mu daje nekaj kotnega pospeška v skladu s smermi vektorjev, ki smo jih izbrali; ti so usmerjeni vzdolž osi vrtenja v isto smer. Razmerje med velikostjo navora in velikostjo kotnega pospeška, ki ga povzroča, je mogoče ugotoviti na dva načina:

a) lahko uporabite dejstvo, da je delo gonilne sile enako spremembi kinetične energije telesa, na katerega ta sila deluje: Za vrteče se telo po formulah (2.9) in (2.4) imajo

Pri tem predpostavimo, da se vztrajnostni moment telesa med vrtenjem ne spreminja. Če to enačbo delimo z in zmanjšamo z, dobimo

b) lahko uporabite dejstvo, da je moment rotacijske sile enak vsoti momentov sil, ki dajejo posameznim delom telesa tangencialne pospeške; te sile so enake in njihovi momenti so

Tangencialne pospeške nadomestimo s kotnimi pospeški, ki so enaki za vse delce rotirajočega telesa (če se telo med vrtenjem ne deformira): Tedaj

Formula (2.12) izraža osnovni zakon dinamike rotacijskega gibanja trdnih (nedeformirajočih) teles, za katerega

kotni pospešek, ki ga telo pridobi pod vplivom danega navora, je neposredno sorazmeren z velikostjo tega momenta in obratno sorazmeren z vztrajnostnim momentom telesa glede na vrtilno os:

V vektorski obliki je ta zakon zapisan kot

Če se telo med vrtenjem deformira, se bo njegov vztrajnostni moment glede na vrtilno os spremenil. V mislih si predstavljajmo rotirajoče telo, sestavljeno iz številnih elementarnih (točkovnih) delov; potem bo deformacija celotnega telesa pomenila spremembo razdalje od teh delov telesa do osi vrtenja. Vendar pa bo spremembo razdalje dane kotne hitrosti vrtenja co spremljala sprememba linearne hitrosti gibanja tega delca in s tem njegove kinetične energije. Tako bo pri konstantni kotni hitrosti vrtenja telesa spremembo razdalj (torej spremembo vztrajnostnega momenta telesa) spremljala sprememba kinetične energije vrtenja celotnega telesa.

Iz formule (2.4), če predpostavimo spremenljivke, lahko dobimo

Prvi člen prikazuje spremembo kinetične energije rotirajočega telesa, ki je nastala samo zaradi spremembe kotne hitrosti vrtenja (v danem vztrajnostnem momentu telesa), drugi člen pa spremembo kinetične energije , ki je nastal le zaradi spremembe vztrajnostnega momenta telesa (pri določeni kotni hitrosti vrtenja).

Ko pa se spremeni razdalja od konicastega telesa do vrtilne osi, bodo notranje sile, ki povezujejo to telo z vrtilno osjo, opravljale delo: negativno, če se telo oddaljuje, in pozitivno, če se telo približuje vrtilni osi; to delo lahko izračunamo, če predpostavimo, da je sila, ki povezuje delec z vrtilno osjo, številčno enaka centripetalni sili:

Za celotno telo, sestavljeno iz številnih delcev z masami, dobimo

V splošnem primeru, ko na telo deluje zunanji navor, je treba spremembo kinetične energije izenačiti z vsoto dveh del: zunanjega navora in notranjih sil. Pri pospešenem vrtenju bodo vrednosti imele pozitivne predznake - negativne

znak (ker se delci telesa odmaknejo od osi vrtenja); Potem

Če tukaj nadomestimo vrednost iz izraza (2.15) in jo nadomestimo z, dobimo

ali po zmanjšanju

To je splošna oblika temeljnega zakona mehanike za telesa, ki se vrtijo okoli nepremične osi; uporabna je tudi za telesa, ki se deformirajo. Ko se formula (2.16) pretvori v formulo (2.14).

Upoštevajte, da je pri deformacijskih telesih možna sprememba kotne hitrosti vrtenja tudi brez zunanjega navora. Dejansko, ko - iz formule (2.16) dobimo:

V tem primeru se kotna hitrost vrtenja spreminja le zaradi spremembe vztrajnostnega momenta telesa, ki ga povzročajo notranje sile.