Splošni izreki o dinamiki sistema teles. Izreki o gibanju središča mase, o spremembi gibalne količine, o spremembi glavnega kota, o spremembi kinetične energije. D'Alembertova načela in možna gibanja. Splošna enačba dinamike. Lagrangeove enačbe.

Splošni izreki o dinamiki togega telesa in sistema teles

Splošni izreki dinamike- to je izrek o gibanju središča mase mehanski sistem, izrek o spremembi gibalne količine, izrek o spremembi glavne kotne količine (kinetične količine) in izrek o spremembi kinetične energije mehanskega sistema.

Izrek o gibanju težišča mehanskega sistema

Izrek o gibanju središča mase.
Produkt mase sistema in pospeška njegovega masnega središča je enak vektorski vsoti vseh zunanjih sil, ki delujejo na sistem:
.

Tukaj je M masa sistema:
;
a C je pospešek središča mase sistema:
;
v C - hitrost središča mase sistema:
;
r C - polmer vektorja (koordinate) središča mase sistema:
;
- koordinate (glede na fiksno središče) in mase točk, ki sestavljajo sistem.

Izrek o spremembi gibalne količine (gibalne količine)

Količina gibanja (impulza) sistema je enak zmnožku mase celotnega sistema s hitrostjo njegovega masnega središča ali vsoti gibalne količine (vsote impulzov) posameznih točk ali delov, ki sestavljajo sistem:
.

Izrek o spremembi gibalne količine v diferencialni obliki.
Časovni odvod količine gibanja (impulz) sistema je enak vektorski vsoti vseh zunanjih sil, ki delujejo na sistem:
.

Izrek o spremembi gibalne količine v integralni obliki.
Sprememba gibalne količine (gibalne količine) sistema v določenem časovnem obdobju je enaka vsoti impulzov zunanjih sil v istem časovnem obdobju:
.

Zakon ohranitve gibalne količine (moment).
Če je vsota vseh zunanjih sil, ki delujejo na sistem, enaka nič, bo vektor gibalne količine sistema konstanten. To pomeni, da bodo vse njegove projekcije na koordinatne osi ohranile konstantne vrednosti.

Če je vsota projekcij zunanjih sil na katero koli os enaka nič, potem bo projekcija količine gibanja sistema na to os konstantna.

Izrek o spremembi glavnega kotnega momenta (izrek momentov)

Glavni kotni moment sistema glede na dano središče O je količina, ki je enaka vektorski vsoti kotnih momentov vseh točk sistema glede na to središče:
.
Oglati oklepaji tukaj označujejo navzkrižni produkt.

Pritrjeni sistemi

Naslednji izrek velja za primer, ko ima mehanski sistem fiksno točko ali os, ki je fiksna glede na inercialni referenčni okvir. Na primer telo, pritrjeno s sferičnim ležajem. Ali sistem teles, ki se gibljejo okoli fiksnega središča. Lahko je tudi nepremična os, okoli katere se vrti telo ali sistem teles. V tem primeru je treba trenutke razumeti kot momente impulzov in sil glede na fiksno os.

Izrek o spremembi glavnega kotnega momenta (izrek momentov)
Časovni odvod glavne kotne količine sistema glede na neko fiksno središče O je enak vsoti momentov vseh zunanjih sil sistema glede na isto središče.

Zakon o ohranitvi glavnega kotnega momenta (gibalne količine).
Če je vsota momentov vseh zunanjih sil, ki delujejo na sistem glede na določeno fiksno središče O, enaka nič, bo glavni kotni moment sistema glede na to središče konstanten. To pomeni, da bodo vse njegove projekcije na koordinatne osi ohranile konstantne vrednosti.

Če je vsota momentov zunanjih sil glede na neko fiksno os enaka nič, bo kotna količina sistema glede na to os konstantna.

Poljubni sistemi

Naslednji izrek ima univerzalen značaj. Velja tako za fiksne kot za prosto gibljive sisteme. Pri fiksnih sistemih je potrebno upoštevati reakcije povezav na fiksnih točkah. Od prejšnjega izreka se razlikuje po tem, da je treba namesto fiksne točke O vzeti središče mase C sistema.

Izrek momentov o masnem središču
Časovni odvod glavne kotne količine sistema glede na središče mase C je enak vsoti momentov vseh zunanjih sil sistema glede na isto središče.

Zakon o ohranitvi kotne količine.
Če je vsota momentov vseh zunanjih sil, ki delujejo na sistem glede na središče mase C, enaka nič, potem bo glavni moment količine sistema glede na to središče konstanten. To pomeni, da bodo vse njegove projekcije na koordinatne osi ohranile konstantne vrednosti.

Vztrajnostni moment telesa

Če se telo vrti okoli osi z s kotno hitrostjo ω z, potem je njegov kotni moment (kinetični moment) glede na os z določen s formulo:
L z = J z ω z ,
kjer je J z vztrajnostni moment telesa glede na os z.

Vztrajnostni moment telesa glede na os z določeno s formulo:
,
kjer je h k razdalja od točke z maso m k do osi z.
Za tanek obroč z maso M in polmerom R ali valj, katerega masa je razporejena vzdolž njegovega roba,
J z = M R 2 .
Za trden homogen obroč ali valj,
.

Steiner-Huygensov izrek.
Naj bo Cz os, ki poteka skozi središče mase telesa, Oz os, ki je z njim vzporedna. Potem so vztrajnostni momenti telesa glede na te osi povezani z razmerjem:
J Oz = J Cz + M a 2 ,
kjer je M telesna masa; a je razdalja med osema.

V več splošni primer :
,
kjer je vztrajnostni tenzor telesa.
Tukaj je vektor, narisan iz središča mase telesa v točko z maso m k.

Izrek o spremembi kinetične energije

Naj se telo z maso M translacijsko in rotacijsko giblje s kotno hitrostjo ω okoli neke osi z. Potem je kinetična energija telesa določena s formulo:
,
kjer je v C hitrost gibanja središča mase telesa;
J Cz je vztrajnostni moment telesa glede na os, ki poteka skozi središče mase telesa vzporedno z osjo vrtenja. Smer vrtilne osi se lahko sčasoma spremeni. Ta formula daje trenutno vrednost kinetične energije.

Izrek o spremembi kinetične energije sistema v diferencialni obliki.
Diferencial (prirast) kinetične energije sistema med nekim gibanjem je enak vsoti diferencialov dela pri tem gibanju vseh zunanjih in notranjih sil, ki delujejo na sistem:
.

Izrek o spremembi kinetične energije sistema v integralni obliki.
Sprememba kinetične energije sistema med nekim gibanjem je enaka vsoti dela vseh zunanjih in notranjih sil, ki delujejo na sistem pri tem gibanju:
.

Delo, ki ga opravi sila, je enak skalarnemu zmnožku vektorjev sile in infinitezimalnega premika točke njegove uporabe:
,
to je produkt absolutnih vrednosti vektorjev F in ds s kosinusom kota med njima.

Delo, ki ga opravi moment sile, je enak skalarnemu produktu vektorjev navora in infinitezimalnega kota vrtenja:
.

d'Alembertovo načelo

Bistvo d'Alembertovega načela je reducirati probleme dinamike na probleme statike. Za to se predpostavi (ali je vnaprej znano), da imajo telesa sistema določene (kotne) pospeške. Nato se uvedejo vztrajnostne sile in (ali) vztrajnostni momenti, ki so po velikosti enaki in nasprotni po smeri silam in momentom sil, ki bi po zakonih mehanike ustvarili dane pospeške ali kotne pospeške.

Poglejmo si primer. Telo je podvrženo translacijskemu gibanju in nanj delujejo zunanje sile. Nadalje predpostavljamo, da te sile ustvarjajo pospešek središča mase sistema. Po izreku o gibanju težišča mase bi imelo središče mase telesa enak pospešek, če bi na telo delovala sila. Nato uvedemo vztrajnostno silo:
.
Po tem, problem dinamike:
.
;
.

Za rotacijsko gibanje postopamo na enak način. Naj se telo vrti okoli osi z in nanj delujejo zunanji momenti sile M e zk. Predpostavimo, da ti momenti ustvarjajo kotni pospešek ε z. Nato uvedemo moment vztrajnostnih sil M И = - J z ε z. Po tem, problem dinamike:
.
Spremeni se v problem statike:
;
.

Načelo možnih premikov

Za reševanje problemov statike se uporablja princip možnih pomikov. Pri nekaterih problemih daje krajšo rešitev kot sestavljanje ravnotežnih enačb. To še posebej velja za sisteme s povezavami (na primer sisteme teles, povezanih z nitmi in bloki), sestavljene iz številnih teles

Načelo možnih premikov.
Za ravnotežje mehanskega sistema z idealnimi povezavami je nujno in zadostno, da je vsota elementarnih del vseh aktivnih sil, ki delujejo nanj za morebitno gibanje sistema, enaka nič.

Možna prestavitev sistema- to je majhno gibanje, pri katerem se povezave, ki so vsiljene sistemu, ne prekinejo.

Idealne povezave- to so povezave, ki ob premikanju sistema ne opravljajo dela. Natančneje, količina dela, ki ga opravijo same povezave pri premikanju sistema, je enaka nič.

Splošna enačba dinamike (D'Alembertovo - Lagrangeovo načelo)

D'Alembertov-Lagrangeov princip je kombinacija D'Alembertovega principa z načelom možnih gibov. Se pravi, da pri reševanju dinamičnega problema uvedemo vztrajnostne sile in problem reduciramo na statični problem, ki ga rešujemo po principu možnih pomikov.

D'Alembert-Lagrangeovo načelo.
Ko se mehanski sistem z idealnimi povezavami premika, je v vsakem trenutku vsota elementarnih del vseh uporabljenih aktivnih sil in vseh vztrajnostnih sil na morebitno gibanje sistema enaka nič:
.
Ta enačba se imenuje splošna enačba zvočniki.

Lagrangeove enačbe

Posplošene koordinate q 1 , q 2 , ..., q n je niz n količin, ki enolično določajo položaj sistema.

Število posplošenih koordinat n sovpada s številom prostostnih stopenj sistema.

Splošne hitrosti so odpeljanke posplošenih koordinat glede na čas t.

Posplošene sile Q 1, Q 2, ..., Q n .
Razmislimo o možnem gibanju sistema, pri katerem bo koordinata q k deležna gibanja δq k. Preostale koordinate ostanejo nespremenjene. Naj bo δA k delo zunanjih sil med takim gibanjem. Potem
δA k = Q k δq k , oz
.

Če se ob morebitnem gibanju sistema spremenijo vse koordinate, potem ima delo zunanjih sil med takšnim gibanjem obliko:
δA = Q 1 δq 1 + Q 2 δq 2 + ... + Q n δq n.
Potem so posplošene sile delni odvodi dela na premike:
.

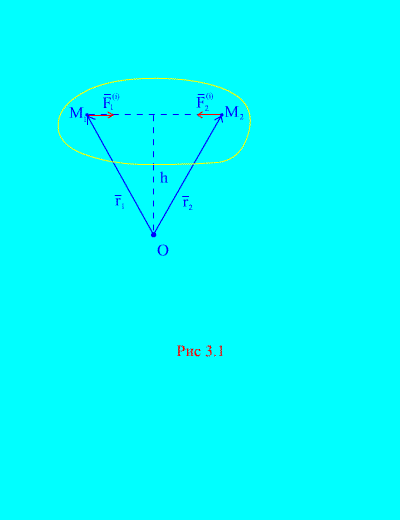
Za potencialne sile s potencialom Π,
.

Lagrangeove enačbe so enačbe gibanja mehanskega sistema v posplošenih koordinatah:

Tukaj je T kinetična energija. Je funkcija posplošenih koordinat, hitrosti in po možnosti časa. Zato je tudi njen delni odvod funkcija posplošenih koordinat, hitrosti in časa. Nato morate upoštevati, da so koordinate in hitrosti funkciji časa. Zato morate za iskanje celotnega odvoda glede na čas uporabiti pravilo diferenciacije kompleksne funkcije:
.

Reference:
S. M. Targ, Kratek tečaj teoretična mehanika, "Višja šola", 2010.

Predavanje 3. Splošni izreki dinamike

Dinamika sistema materialnih točk je pomembna veja teoretične mehanike. Tu obravnavamo predvsem probleme gibanja mehanskih sistemov (sistemov materialnih točk) s končnim številom prostostnih stopenj – največjim številom neodvisnih parametrov, ki določajo položaj sistema. Glavna naloga sistemske dinamike je preučevanje zakonov gibanja trdna in mehanski sistemi.

Najenostavnejši pristop k preučevanju gibanja sistema, sestavljen iz n materialnih točk, se spušča v upoštevanje gibanja vsake posamezne točke sistema. V tem primeru je treba določiti vse sile, ki delujejo na vsako točko sistema, vključno s silami interakcije med točkami.

Če določimo pospešek vsake točke v skladu z drugim Newtonovim zakonom (1.2), dobimo za vsako točko tri skalarne diferencialne zakone gibanja drugega reda, tj. 3 n diferencialnih zakonov gibanja za celoten sistem.

Za iskanje enačb gibanja mehanskega sistema na podlagi danih sil in začetnih pogojev za vsako točko sistema je treba integrirati nastale diferencialne zakone. Ta problem je težaven že v primeru dveh materialnih točk, ki se gibljeta samo pod vplivom interakcijskih sil po zakonu univerzalne privlačnosti (problem dveh teles), izredno težak pa v primeru treh medsebojno delujočih točk (problem treh teles). ).

Zato je treba najti metode za reševanje problemov, ki bi vodile do rešljivih enačb in dale predstavo o gibanju mehanskega sistema. Splošni izreki dinamike, ki so posledica diferencialnih zakonov gibanja, nam omogočajo, da se izognemo kompleksnosti, ki nastane pri integraciji, in pridobimo potrebne rezultate.

3. 1. Splošne opombe

Točke mehanskega sistema bomo oštevilčili z indeksi jaz, j, k itd., ki tečejo skozi vse vrednosti 1, 2, 3… n, Kje n – število točk sistema. Fizikalne količine navezujoč se k točke so označene z istim indeksom kot točka. Na primer, izrazite vektor radij oziroma hitrost k th točka.

Na vsako točko sistema delujejo sile dveh izvorov: prvič, sile, katerih viri ležijo zunaj sistema, imenovane zunanji sile in imenovani ; drugič, sile iz drugih točk danega sistema, imenovane notranji sile in imenovani . Notranje sile zadoščajo tretjemu Newtonovemu zakonu. Oglejmo si najpreprostejše lastnosti notranjih sil, ki delujejo na celoten mehanski sistem v katerem koli stanju.

Prva lastnina. Geometrična vsota vseh notranjih sil sistema (glavni vektor notranjih sil) je enaka nič.

Dejansko, če upoštevamo kateri koli dve poljubni točki sistema, na primer in (slika 3.1), potem za njih , Ker akcijske in reakcijske sile so vedno enake po velikosti, delujejo vzdolž ene linije delovanja v nasprotni smeri, ki povezuje medsebojno delujoče točke. Glavni vektor notranjih sil je sestavljen iz parov sil medsebojno delujočih točk, torej

(3.1)

Druga lastnost. Geometrična vsota momentov vseh notranjih sil glede na poljubno točko v prostoru je enaka nič.

Razmislimo o sistemu momentov sil in glede na točko O(slika 3.1). Od (slika 3.1). to je jasno

,

Ker obe sili imata enake krake in nasprotne smeri vektorskih momentov. Glavna točka notranje sile glede na točko O je sestavljena iz vektorske vsote takih izrazov in je enaka nič. torej

Naj zunanje in notranje sile delujejo na mehanski sistem, sestavljen iz n točke (slika 3.2). Če rezultanta zunanjih sil in rezultanta vseh notranjih sil delujeta na vsako točko sistema, potem za katero koli k točki sistema je mogoče sestaviti diferencialne enačbe gibanja. Takih enačb bo skupno n:

in v projekcijah na fiksne koordinatne osi 3 n:

(3.4)

Vektorske enačbe (3.3) ali enakovredne skalarne enačbe (3.4) predstavljajo diferencialne zakone gibanja materialnih točk celotnega sistema. Če se vse točke premikajo vzporedno z eno ravnino ali eno premico, bo število enačb (3.4) v prvem primeru 2 n, v drugem n.

Primer 1. Dve masi sta med seboj povezani z neraztegljivim kablom, vrženim čez blok (slika 3.3). Zanemarjanje tornih sil, pa tudi mase bloka in kabla določajo zakon gibanja bremen in napetosti kabla.

rešitev. Sistem je sestavljen iz dveh materialnih teles (povezanih z neraztegljivim kablom), ki se premikata vzporedno z isto osjo. X. Zapišimo diferencialne zakone gibanja v projekcijah na os X za vsako telo.

Pustite, da desna utež pada s pospeškom, nato pa se bo leva utež dvignila s pospeškom. Miselno se osvobodimo povezave (kabla) in jo nadomestimo z reakcijami in (slika 3.3). Glede na to, da so telesa prosta, narišimo diferencialne zakone gibanja v projekciji na os X(kar pomeni, da so napetosti niti notranje sile, teža bremen pa zunanje):

Ker in (telesa sta povezana z neraztegljivim kablom), dobimo

Reševanje teh enačb za pospešek in napetost kabla T, dobimo

.

Upoštevajte, da napetost v kablu ni enaka gravitacijski sili ustrezne obremenitve.

3. 2. Izrek o gibanju masnega središča

Znano je, da se lahko togo telo in mehanski sistem v ravnini gibljeta precej zapleteno. Do prvega izreka o gibanju telesa in mehanskega sistema pridemo takole: vrzi k.-l. predmet, sestavljen iz številnih trdnih teles, pritrjenih skupaj. Jasno je, da bo letel v paraboli. To se je pokazalo pri proučevanju gibanja točke. Vendar zdaj predmet ni točka. Med letom se obrača in niha okoli nekega efektivnega središča, ki se giblje po paraboli. Prvi izrek o gibanju kompleksnih objektov pravi, da je določeno efektivno središče središče mase premikajočega se predmeta. Središče mase ni nujno v samem telesu; lahko leži nekje zunaj njega.

Izrek. Masno središče mehanskega sistema se giblje kot materialna točka z maso, ki je enaka masi celotnega sistema, na katero delujejo vse zunanje sile, ki delujejo na sistem.

Za dokaz izreka prepišemo diferencialne zakone gibanja (3.3) v naslednji obliki:

(3.5)

Kje n – število točk sistema.

Seštejmo enačbe po členih:

(A)

Položaj središča mase mehanskega sistema glede na izbrani koordinatni sistem je določen s formulo (2.1): Kje M– masa sistema. Potem leva stran enakost (a) bo zapisana

Prva vsota na desni strani enakosti (a) je enaka glavnemu vektorju zunanjih sil, zadnja pa je po lastnosti notranjih sil enaka nič. Nato bo enakost (a) ob upoštevanju (b) prepisana

, (3.6)

tiste. produkt mase sistema in pospeška središča njegove mase je enak geometrijski vsoti vseh zunanjih sil, ki delujejo na sistem.

Iz enačbe (3.6) sledi, da notranje sile ne vplivajo neposredno na gibanje središča mase. Vendar pa so v nekaterih primerih vzrok za pojav zunanjih sil, ki delujejo na sistem. Tako notranje sile, ki poganjajo pogonska kolesa avtomobila v vrtenje, povzročijo, da na platišče deluje zunanja adhezijska sila.

Primer 2. Mehanizem, ki se nahaja v navpični ravnini, je nameščen na vodoravni gladki ravnini in pritrjen nanjo s palicami, togo pritrjenimi na površino TO in L (slika 3.4).

Radij diska 1 R nepremično. Disk 2 masa m in polmer r pritrjen na ročico, dolžina R+ r na točki C 2. Gonilka se vrti konstantno

kotna hitrost. V začetnem trenutku je ročica zasedla desno vodoravni položaj. Ob zanemaritvi mase gonilke določite največje vodoravne in navpične sile, ki delujejo na palice, če je skupna masa okvirja in kolesa 1 enaka M. Upoštevajte tudi obnašanje mehanizma v odsotnosti palic.

rešitev. Sistem je sestavljen iz dveh mas ( n=2 ): fiksni disk 1 z okvirjem in premični disk 2. Usmerite os pri skozi težišče mirujočega diska navpično navzgor, os X– vzdolž vodoravne ravnine.

Zapišimo izrek o gibanju masnega središča (3.6) v koordinatni obliki

Zunanje sile tega sistema so: teža okvirja in fiksnega diska - Mg, teža premikajočega se diska – mg, - skupna vodoravna reakcija vijakov, - normalna skupna reakcija ravnine. torej

Nato bodo zakoni gibanja (b) prepisani

Izračunajmo koordinate središča mase mehanskega sistema:

; (G)

kot je razvidno iz (slika 3.4), , , (kot ročične gredi), . Zamenjava teh izrazov v (d) in izračun drugih odvodov glede na čas t od , , to dobimo

(e)

Če nadomestimo (c) in (e) v (b), ugotovimo

Vodoravni pritisk, ki deluje na palice, je največji in najmanjši, ko cos = 1 temu primerno, tj.

Pritisk na mehanizem vodoravna ravnina ima največje in najmanjše vrednosti, ko greh temu primerno, tj.

Pravzaprav je bil prvi problem dinamike rešen: po znanih enačbah gibanja središča mase sistema (d) se obnovijo sile, ki sodelujejo pri gibanju.

V odsotnosti palic K in L (slika 3.4), lahko mehanizem začne poskakovati nad vodoravno ravnino. To se bo zgodilo, ko bo, tj. ko sledi, da mora kotna hitrost vrtenja gonilke, pri kateri mehanizem odskoči, izpolnjevati enakost

.

3. 3. Zakon o ohranitvi gibanja središča mase

Če je glavni vektor zunanjih sil, ki delujejo na sistem, enak nič, tj. , nato od(3.6)iz tega sledi, da je pospešek središča mase enak nič, zato je hitrost središča mase konstantna po velikosti in smeri. Če zlasti v začetnem trenutku težišče miruje, potem miruje ves čas, medtem ko je glavni vektor zunanjih sil enak nič.

Iz tega izreka sledi več posledic.

· Notranje sile same ne morejo spremeniti narave gibanja središča mase sistema.

· Če je glavni vektor zunanjih sil, ki delujejo na sistem, enak nič, potem središče mase miruje oziroma se giblje enakomerno in premočrtno.

· Če je projekcija glavnega vektorja zunanjih sil sistema na neko fiksno os enaka nič, se projekcija hitrosti središča mase sistema na to os ne spremeni.

· Par sil, ki delujejo na togo telo, ne more spremeniti gibanja njegovega masnega središča (lahko le povzroči, da se telo vrti okoli masnega središča).

Oglejmo si primer, ki ponazarja zakon o ohranitvi gibanja središča mase.

Primer 3. Dve masi sta povezani z neraztegljivo nitjo, vrženo skozi blok (slika 3.5), pritrjen na zagozdo z maso M. Klin leži na gladki vodoravni ravnini. V začetnem trenutku je sistem miroval. Poiščite premik klina vzdolž ravnine, ko se prvo breme spusti na višino n. Zanemarimo maso bloka in niti.

rešitev. Zunanje sile, ki delujejo na klin skupaj z obremenitvami, so gravitacija in Mg, kot tudi normalna reakcija gladke vodoravne površine N. Posledično je

Ker je v začetnem trenutku sistem miroval, imamo .

Izračunajmo koordinate središča mase sistema v in v trenutku t 1 ko breme tehta g se bo spustil v višino H.

Trenutno:

,

Kje , , X– koordinate središča mase bremen s težo g, g in težo klina Mg.

Predpostavimo, da se klin v trenutku premika v pozitivni smeri osi Ox po količini L, če teža bremena pade na višino n. Potem, za trenutek

Ker se bodo obremenitve skupaj s klinom premaknile na L v desno, breme pa se bo po klinu pomikalo navzgor. Ker , potem po izračunih dobimo

.

3.4. Količina gibanja sistema

3.4.1. Izračun gibalne količine sistema

Gibalna količina materialne točke je vektorska količina, ki je enaka produktu mase točke in njenega vektorja hitrosti.

Merska enota gibalne količine -

Gibalna količina mehanskega sistema je vektorska vsota gibalnih količin posameznih točk sistema, tj.

Kje n – število točk sistema.

Gibalno količino mehanskega sistema lahko izrazimo z maso sistema M in hitrost središča mase. res,

tiste. Gibalna količina sistema je enaka produktu mase celotnega sistema in hitrosti njegovega masnega središča. Smer je enaka smeri (slika 3.6)

V projekcijah na pravokotne osi imamo

kjer so , , projekcije hitrosti središča mase sistema.

Tukaj M– masa mehanskega sistema; se ne spremeni, ko se sistem premika.

Ti rezultati so še posebej priročni za uporabo pri izračunu količin gibanja togih teles.

Iz formule (3.7) je razvidno, da če se mehanski sistem giblje tako, da njegovo središče mase ostane nepremično, ostane gibalna količina sistema enaka nič.

3.4.2. Elementarni impulz s polno močjo

Delovanje sile na materialno točko skozi čas dt lahko označimo z elementarnim impulzom. Skupni impulz sile skozi čas t, ali impulz sile, določen s formulo

ali v projekcijah na koordinate osi

(3.8a)

Enota impulza sile je .

3.4.3. Izrek o spremembi gibalne količine sistema

Naj na točke sistema delujejo zunanje in notranje sile. Potem lahko za vsako točko sistema uporabimo diferencialne zakone gibanja (3.3), pri čemer upoštevamo, da :

.

Če seštejemo vse točke sistema, dobimo

Po lastnosti notranjih sil in po definiciji imamo

(3.9)

Če pomnožimo obe strani te enačbe s dt, dobimo izrek o spremembi gibalne količine v diferencialni obliki:

, (3.10)

tiste. diferenčna gibalna količina mehanskega sistema je enaka vektorski vsoti elementarnih impulzov vseh zunanjih sil, ki delujejo na točke mehanskega sistema.

Izračun integrala obeh strani (3.10) v času od 0 do t, dobimo izrek v končni ali integralni obliki

(3.11)

V projekcijah na koordinatne osi bomo imeli

Sprememba gibalne količine mehanskega sistema skozi čast, je enaka vektorski vsoti vseh impulzov zunanjih sil, ki v istem času delujejo na točke mehanskega sistema.

Primer 4. Teža tovora m se spusti po nagnjeni ravnini iz mirovanja pod vplivom sile F, sorazmerno s časom: , kjer (slika 3.7). Kakšno hitrost bo telo pridobilo po t sekund po začetku gibanja, če je koeficient drsnega trenja bremena na nagnjeni ravnini enak f.

rešitev. Predstavimo sile, ki delujejo na breme: mg – gravitacijska sila bremena, n je normalna reakcija ravnine, je sila drsnega trenja bremena na ravnini in . Smer vseh sil je prikazana v (slika 3.7).

Usmerimo os X po nagnjeni ravnini navzdol. Zapišimo izrek o spremembi gibalne količine (3.11) v projekciji na os X:

(A)

Glede na stanje, saj v začetnem trenutku je obremenitev mirovala. Vsota projekcij impulzov vseh sil na os x je enaka

torej

,

.

3.4.4. Zakoni ohranitve gibalne količine

Ohranitvene zakone dobimo kot posebne primere izreka o spremembi gibalne količine. Možna sta dva posebna primera.

· Če je vektorska vsota vseh zunanjih sil, ki delujejo na sistem, enaka nič, tj. , potem iz izreka sledi (3.9) , Kaj ,

tiste. če je glavni vektor zunanjih sil sistema enak nič, potem je količina gibanja sistema konstantna po velikosti in smeri.

· Če projekcija glavnega vektorja zunanjih sil na katerokoli koordinatna os enako nič, na primer Oh, tj. , potem je projekcija gibalne količine na to os konstantna vrednost.

Oglejmo si primer uporabe zakona o ohranitvi gibalne količine.

Primer 5. Balistično nihalo je telo z maso, obešeno na dolgi niti (slika 3.8).

Krogla velike mase, ki se premika s hitrostjo V in pri udarcu v mirujoče telo se zatakne vanj in telo odstopi. Kolikšna je bila hitrost krogle, če se je telo dvignilo v višino h ?

rešitev. Naj telo z zataknjeno kroglo pridobi hitrost. Nato lahko z uporabo zakona o ohranitvi gibalne količine med interakcijo dveh teles zapišemo .

Hitrost je mogoče izračunati z uporabo zakona o ohranjanju mehanske energije . Potem. Kot rezultat ugotovimo

.

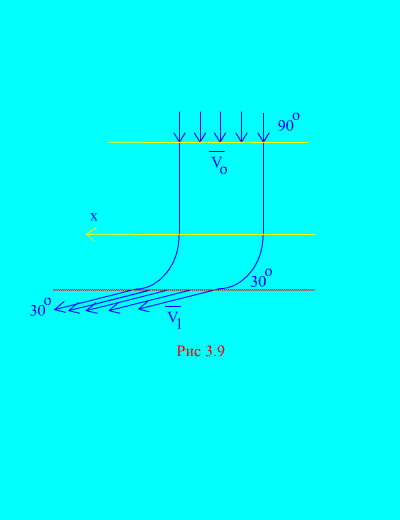
Primer 6. Voda vstopi v stacionarni kanal (slika 3.9) spremenljiv prečni prerez s hitrostjo pod kotom na horizontalo; kvadrat prečni prerez kanal na vhodu; hitrost vode pri izstopu iz kanala tvori kot z obzorjem.

Določite vodoravno komponento reakcije, ki jo ima voda na stenah kanala. Gostota vode .

rešitev. Določili bomo horizontalno komponento reakcije sten kanala na vodo. Ta sila je enaka po velikosti in nasprotnega predznaka želeni sili. Po (3.11a) imamo

. (A)

Izračunamo maso prostornine tekočine, ki vstopi v kanal v času t:

Pokliče se vrednost rAV 0 druga masa - masa tekočine, ki teče skozi kateri koli del cevi na časovno enoto.

V istem času iz kanala odteče enaka količina vode. Začetna in končna hitrost sta podani v pogoju.

Izračunajmo desno stran enačbe (a), ki določa vsoto projekcij na vodoravno os zunanjih sil, ki delujejo na sistem (vodo). Edina vodoravna sila je vodoravna komponenta nastale reakcije stene R x. Ta sila je med enakomernim gibanjem vode konstantna. Zato

. (V)

Če nadomestimo (b) in (c) v (a), dobimo

3.5. Kinetični moment sistema

3.5.1. Glavni gibalni moment sistema

Naj bo radij vektor točke z maso sistema glede na neko točko A, imenovano središče (slika 3.10).

Gibalna količina gibalne količine (kinetični moment) točke glede na sredino A imenujemo vektor , določeno s formulo

. (3.12)

V tem primeru vektor usmerjena pravokotno na ravnino, ki poteka skozi središče A in vektor .

Gibalna količina gibalne količine (kinetični moment) točke glede na os imenujemo projekcija gibalne količine točke glede na katero koli središče, izbrano na tej osi, na to os.

Glavni moment količine (kinetični moment) sistema glede na središče A se imenuje količina

(3.13)

Glavni moment količine (kinetični moment) sistema glede na os se imenuje projekcija na to os glavnega gibalnega momenta sistema glede na katero koli izbrano na tej osi središčna os.

3.5.2. Kinetični moment rotacijskega togega telesa okoli osi vrtenja

Poravnajmo fiksno točko O telo, ki leži na vrtilni osi Oz, z izhodiščem koordinatnega sistema Ohooz, katerih osi se bodo vrtele s telesom (Slika 3.11). Pustimo polmer vektorja točke telesa glede na izhodišče koordinat, njegovo projekcijo na os pa označimo z , , . Vektorske projekcije kotna hitrost telesa na isti osi označimo z 0, 0, ().

Ministrstvo za izobraževanje in znanost Ruska federacija

Zvezna državna proračunska izobraževalna ustanova za visoko strokovno izobraževanje

"Kubanska državna tehnološka univerza"

Teoretična mehanika

2. del dinamika

Odobrila uredniški in založniški odbor

svet univerze kot

učna pomoč

Krasnodar

UDK 531.1/3 (075)

Teoretična mehanika. 2. del. Dinamika: učbenik / L.I. Draiko; Kuban. država technol.un.t. Krasnodar, 2011. 123 str.

ISBN 5-230-06865-5

Teoretično gradivo je predstavljeno v kratki obliki, podani so primeri reševanja problemov, ki večinoma odražajo realna tehnična vprašanja, pozornost pa je namenjena izbiri racionalnega načina reševanja.

Zasnovan za diplomante dopisnega študija in študija na daljavo v gradbeništvu, prometu in strojništvu.

Tabela 1 ilustr. 68 Bibliografija 20 naslovov

Znanstveni urednik, kandidat za tehnične vede, izredni profesor. V.F.Melnikov

Recenzenti: predstojnik katedre za teoretično mehaniko in teorijo mehanizmov in strojev Kubanske agrarne univerze prof. F.M. Kanarev; Izredni profesor, Oddelek za teoretično mehaniko, Kubanska državna tehnološka univerza M.E. Multih

Objavljeno s sklepom uredniškega in založniškega sveta Kubanske državne tehnološke univerze.

Ponovna izdaja

ISBN 5-230-06865-5 KubSTU 1998

Predgovor

Ta učbenik je namenjen izrednim študentom gradbenih, transportnih in strojnih specialnosti, vendar ga lahko uporabljajo pri študiju oddelka "Dinamika" predmeta teoretične mehanike izredni študenti drugih specialnosti, pa tudi redni študenti samostojno delo.

Priročnik je sestavljen v skladu z veljavnim učnim načrtom predmeta teoretična mehanika in zajema vsa vprašanja glavnega dela predmeta. Vsak razdelek vsebuje kratko teoretično gradivo, ki ga spremljajo ilustracije in metodološka priporočila za njegovo uporabo pri reševanju problemov. Priročnik vsebuje rešitve 30 nalog, ki odražajo resnične tehnične težave in ustrezajo testnim nalogam za neodvisna odločitev. Za vsako težavo je predstavljen računski diagram, ki nazorno prikazuje rešitev. Oblikovanje rešitve ustreza zahtevam za oblikovanje izpitnih nalog za izredne študente.

Avtor se globoko zahvaljuje učiteljem Oddelka za teoretično mehaniko in teorijo mehanizmov in strojev Kubanske agrarne univerze za njihovo veliko delo pri pregledu učbenika, pa tudi učiteljem Oddelka za teoretično mehaniko Kubanske državne tehnološke univerze Univerzi za dragocene pripombe in nasvete pri pripravi učbenika za objavo.

Vse kritične pripombe in predloge bo avtor v prihodnje s hvaležnostjo sprejel.

Uvod

Dinamika je najpomembnejši del teoretične mehanike. Večina specifičnih problemov, s katerimi se srečujemo v inženirski praksi, se nanaša na dinamiko. Z uporabo zaključkov statike in kinematike dinamika določa splošne zakone gibanja materialnih teles pod delovanjem uporabljenih sil.

Najenostavnejši materialni objekt je materialna točka. Materialno telo poljubne oblike lahko vzamemo za materialno točko, katere dimenzije lahko v obravnavanem problemu zanemarimo. Telo končnih dimenzij lahko vzamemo za materialno točko, če razlika v gibanju njegovih točk za dani problem ni pomembna. To se zgodi, ko so dimenzije telesa majhne v primerjavi z razdaljami, ki jih pokrivajo točke telesa. Vsak delec trdnega telesa lahko štejemo za materialno točko.

Sile, ki delujejo na točko ali materialno telo, se dinamično ocenjujejo po njihovem dinamičnem vplivu, to je po tem, kako spreminjajo značilnosti gibanja materialnih predmetov.

Gibanje materialnih predmetov skozi čas poteka v prostoru glede na določen referenčni okvir. V klasični mehaniki, ki temelji na Newtonovih aksiomih, se prostor šteje za tridimenzionalen, njegove lastnosti niso odvisne od materialnih predmetov, ki se gibljejo v njem. Položaj točke v takem prostoru določajo tri koordinate. Čas ni povezan s prostorom in gibanjem materialnih predmetov. Velja za enako za vse referenčne sisteme.

Zakoni dinamike opisujejo gibanje materialnih predmetov glede na absolutne koordinatne osi, ki so običajno sprejete kot stacionarne. Izhodišče absolutnega koordinatnega sistema je v središču Sonca, osi pa so usmerjene v oddaljene, pogojno mirujoče zvezde. Pri reševanju številnih tehničnih problemov se lahko koordinatne osi, povezane z Zemljo, štejejo za pogojno nepremične.

Parametri mehanskega gibanja materialnih objektov v dinamiki so določeni z matematičnimi izpeljavami iz osnovnih zakonov klasične mehanike.

Prvi zakon (zakon vztrajnosti):

Materialna točka ohranja stanje mirovanja oziroma enakomernega in premotečnega gibanja, dokler je delovanje nekaterih sil ne popelje iz tega stanja.

Enakomerno in linearno gibanje točke imenujemo gibanje po vztrajnosti. Mirovanje je poseben primer gibanja po vztrajnosti, ko je hitrost točke enaka nič.

Vsaka snovna točka ima vztrajnost, to pomeni, da si prizadeva ohraniti stanje mirovanja ali enakomernega linearnega gibanja. Referenčni sistem, glede na katerega velja vztrajnostni zakon, se imenuje inercialni, gibanje, ki ga opazujemo glede na ta sistem, pa absolutno. Vsak referenčni sistem, ki izvaja translacijsko premočrtno in enakomerno gibanje glede na inercialni sistem, bo prav tako inercialni sistem.

Drugi zakon (osnovni zakon dinamike):

Pospešek materialne točke glede na vztrajnostni referenčni sistem je sorazmeren s silo, ki deluje na točko, in sovpada s silo v smeri:
.

Iz osnovnega zakona dinamike sledi, da s silo
pospešek
. Masa točke označuje stopnjo odpornosti točke na spremembe njene hitrosti, to je merilo vztrajnosti materialne točke.

Tretji zakon (zakon akcije in reakcije):

Sili, s katerimi dve telesi delujeta druga na drugo, sta enaki po velikosti in usmerjeni vzdolž ene premice v nasprotni smeri.

Uporabljajo se sile, imenovane akcija in reakcija različna telesa in zato ne tvorijo uravnoteženega sistema.

Četrti zakon (zakon neodvisnosti sil):

Ob sočasnem delovanju več sil je pospešek materialne točke enak geometrijski vsoti pospeškov, ki bi jih točka imela pod delovanjem vsake sile posebej:

, Kje
,
,…,
.

(MEHANSKI SISTEMI) – IV možnost

1. Osnovna enačba dinamike materialne točke je, kot je znano, izražena z enačbo. Diferencialne enačbe premike poljubnih točk neprostega mehanskega sistema po dveh metodah delitve sil lahko zapišemo v dveh oblikah:

(1) , kjer je k=1, 2, 3, … , n – število točk materialnega sistema.

(2)

kjer je masa k-te točke; - radij vektor k-te točke, - dana (aktivna) sila, ki deluje na k-to točko ali rezultanta vseh aktivnih sil, ki delujejo na k-to točko. - rezultanta reakcijskih sil vezi, ki delujejo na k-to točko; - rezultanta notranjih sil, ki delujejo na k-to točko; - rezultanta zunanjih sil, ki delujejo na k-to točko.

Z uporabo enačb (1) in (2) si lahko prizadevamo rešiti tako prvi kot drugi problem dinamike. Reševanje drugega problema dinamike za sistem pa postane zelo zapleteno, ne le z matematičnega vidika, ampak tudi zato, ker se soočamo s temeljnimi težavami. Sestavljeni so iz dejstva, da je tako za sistem (1) kot za sistem (2) število enačb pomembno manjše število neznano.

Torej, če uporabimo (1), bo znana dinamika za drugi (inverzni) problem in , neznana pa in . Vektorske enačbe bodo " n«, in neznani - »2n«.

Če izhajamo iz sistema enačb (2), potem so nekatere zunanje sile znane. Zakaj del? Dejstvo je, da med zunanje sile sodijo tudi zunanje reakcije povezav, ki so neznane. Poleg tega bo tudi neznano.

Tako sta tako sistem (1) kot sistem (2) NEZAPRTA. Dodati je treba enačbe, pri čemer je treba upoštevati enačbe povezav, morda pa je treba postaviti tudi nekatere omejitve na same povezave. Kaj storiti?

Če izhajamo iz (1), potem lahko sledimo poti sestavljanja Lagrangeovih enačb prve vrste. A ta pot ni racionalna, ker lažja naloga(manj svobodnih stopenj), težje ga je rešiti z matematičnega vidika.

Potem bodimo pozorni na sistem (2), kjer - so vedno neznane. Prvi korak pri reševanju sistema je izločitev teh neznank. Pri tem se je treba zavedati, da nas pri gibanju sistema praviloma ne zanimajo notranje sile, torej pri gibanju sistema ni treba vedeti, kako se giblje posamezna točka sistema, ampak je dovolj vedeti, kako se sistem giblje kot celota.

Torej, če različne poti izključimo neznane sile iz sistema (2), potem dobimo nekaj relacij, tj Splošne značilnosti za sistem, katerega poznavanje nam omogoča presojo, kako se sistem na splošno giblje. Te značilnosti uvedemo s pomočjo t.i splošni izreki zvočniki. Obstajajo štirje takšni izreki:

1. Izrek o premikanje težišča mehanskega sistema;

2. Izrek o sprememba gibalne količine mehanskega sistema;

3. Izrek o sprememba kinetičnega momenta mehanskega sistema;

4. Izrek o sprememba kinetične energije mehanskega sistema.