След като разгледахме транслационните и ротационните движения, можем да установим аналогия между тях. Кинематиката на постъпателното движение използва път s, скорост  и ускорение А. Тяхната роля при въртеливото движение се играе от ъгъла на завъртане , ъгловата скорост  и ъгловото ускорение ε. В динамиката на постъпателното движение се използват понятията сила и маса Ти импулс При въртеливото движение ролята на сила се играе от момента
сили, ролята на масата - инерционен момент аз z и ролята на импулса - ъглов момент Познавайки формулите за транслационно движение, е лесно да запишете формулите за ротационно движение. Например при равномерно движение изминатото разстояние се изчислява по формулата: s =  t, а с ротационен ъгъл на завъртане - по формулата  =  t. Втори закон на Нютон
И
а основният закон на динамиката на въртеливото движение е
И
При постъпателно движение импулсът на тялото е равен на
а при въртеливо движение ъгловият момент е
Тази аналогия може да бъде продължена по-нататък.

Работа на силата при транслационно движение. Мощност

Нека тяло (материална точка) е под действието на постоянна сила , сключвайки постоянен ъгъл с посоката на движение, се движи праволинейно в някаква отправна система и изминава пътя л. Тогава, както е известно от училищния курс по физика, работата Атази сила се намира по формулата:

А= Ет· защото  = Е л л, (1)

Нека сега разгледаме общия случай на изчисляване на работата, когато тялото се движи постъпателно по крива траектория под въздействието на променлива сила. На път лизберете елементарен раздел дл, в рамките на които може да се разглежда силата и ъгъл  са постоянни величини, а самото сечение е праволинейно. Тогава работете dAв този раздел намираме с помощта на формула (1): dA = Е· дл· cos. работа Апо целия път е равна на сбора на работата dA, т.е.

(2)

Икона лс интеграл означава, че интегрирането се извършва по целия път л.

Формула (2) може да получи различна форма, ако използваме скаларното произведение на векторите. След това интегралната функция dAще се запише във формата: dA = Е· дл· cos=
Къде е векторът на елементарното преместване, и

(3)

От формула (1) става ясно, че работата е алгебрична величина. Знакът на произведението зависи от ъгъла . Ако ъгълът  е остър, тогава cos  > 0 и работата е положителна, но ако ъгълът  е тъп, работата е отрицателна.

Единицата за работа в SI е джаул (J). Въвежда се от формула (1), в която се приема cos  = 1 работата, извършена от сила от 1 N върху път от 1 m, при условие че посоките на силата и изместването съвпадат.

За характеризиране на скоростта на работа се въвежда понятието мощност, равна на извършената работа за единица време. Ако елементарен период от време дтсвършена е елементарна работа dA, след това силата Рравно на

(4)

В единици SI мощността се измерва във ватове (W). Както следва от (4), 1 W = 1 J / 1 s, т.е. 1 W- Това е мощността, при която 1 J работа се извършва за 1 s.

Работа на силата при въртеливо движение

Помислете за твърдо тяло, което под действието на променлива сила се върти около ос zпод някакъв ъгъл. Тази сила създава въртящ момент М z, въртене на тялото. Силата е насочена тангенциално към окръжността, по която се движи точката на приложение на силата. Следователно ъгъл  = 0. Като вземем това предвид, по аналогия с формулата за механична работа (виж (2)), намираме израза, чрез който се изчислява работата при въртеливо движение:

(5)

Работата ще бъде положителна, ако посоката на тангенциалната компонента на силата съвпада с посоката на въртене, и отрицателна, ако са в противоположна посока.

Конспект на лекцията

Инерционен момент.

Момент на сила. Основно уравнение за динамиката на въртеливото движение.

Момент на импулс. Закон за запазване на ъгловия момент.

Работа и кинетична енергия при въртеливо движение.

1. Инерционен момент.

При разглеждането на въртеливото движение е необходимо да се въведат нови физически понятия: момент на инерция, момент на сила, момент на импулс.

Инерционният момент е мярка за инерцията на тялото по време на въртеливо движение на тялото.

Инерционен моментна материална точка спрямо фиксирана ос на въртене е равна на произведението на нейната маса от квадрата на разстоянието до разглежданата ос на въртене (фиг. 1):

зависи само от масата на материалната точка и нейното положение спрямо оста на въртене и не зависи от наличието на самото въртене.

Инерционният момент е скаларна и адитивна величина, следователно инерционният момент на тялото е равен на сумата от инерционните моменти на всички негови точки:

.

В случай на непрекъснато разпределение на масата тази сума се свежда до интеграла:

,

където е масата на малък обем на тялото
, - телесна плътност, - разстояние от елемента
към оста на въртене.

Инерционният момент е аналог на масата при въртеливо движение. Колкото по-голям е инерционният момент на тялото, толкова по-трудно е да се промени ъгловата скорост на въртящото се тяло. Инерционният момент има смисъл само за дадено положение на оста на въртене. Няма смисъл да говорим просто за „инерционния момент“. Зависи:

1) от позицията на оста на въртене;

2) от разпределението на телесната маса спрямо оста на въртене, т.е. върху формата на тялото и неговия размер.

Експериментално доказателство за това е експериментът с търкалящи се цилиндри.

Чрез интегриране за някои еднородни тела можем да получим следните формули (оста на въртене минава през центъра на масата на тялото).

Инерционен момент на обръч (пренебрегваме дебелината на стената) или кух цилиндър:

Инерционен момент на диск или твърд цилиндър с радиус R:

.

Инерционен момент на топката

Инерционен момент на пръта

д Ако за дадено тяло е известен инерционният момент около ос, минаваща през центъра на масата, тогава инерционният момент спрямо всяка ос, успоредна на първата, се намира съгласно Теорема на Щайнер: инерционният момент на тяло спрямо произволна ос е равен на инерционния момент J 0 спрямо ос, успоредна на дадената и минаваща през центъра на масата на тялото, добавен към произведението на масата на тялото и квадрат на разстоянието между осите.

Къде dразстояние от центъра на масата ЗАкъм оста на въртене (фиг. 2).

Център на масата- въображаема точка, чието положение характеризира разпределението на масата на дадено тяло. Центърът на масата на едно тяло се движи по същия начин, както би се движила материална точка със същата маса под въздействието на всички външни сили, действащи върху дадено тяло.

Концепцията за инерционния момент е въведена в механиката от местния учен Л. Ойлер в средата на 18 век и оттогава се използва широко при решаването на много проблеми на динамиката на твърдото тяло. Стойността на инерционния момент трябва да се знае на практика при изчисляване на различни въртящи се компоненти и системи (маховици, турбини, ротори на електродвигатели, жироскопи). Инерционният момент се включва в уравненията за движение на тяло (кораб, самолет, снаряд и др.). Определя се, когато се искат да се знаят параметрите на въртеливото движение на самолет около центъра на масата под въздействието на външно смущение (порив на вятър и др.).

При наблюдение на сложни движения, като например движението на човешкото тяло (ходене, бягане, скачане и т.н.), изглежда трудно или дори невъзможно да се опише движението на всички негови точки. Въпреки това, анализирайки такива движения, може да се забележи, че те се състоят от по-прости - транслационни и ротационни движения.

Механиката на постъпателното движение е известна на читателя, така че разделът започва с разглеждане на ротационното движение. Най-простият е въртенето на твърдо тяло около фиксирана ос. Този случай ви позволява да се запознаете със спецификата, терминологията и законите на въртеливото движение.

5.1. КИНЕМАТИКА НА РОТАЦИОННО ДВИЖЕНИЕ НА АБСОЛЮТНО ТВЪРДО ТЯЛО ОКОЛО ФИКСИРАНА ОС

Абсолютно твърдо тяло е това, чието разстояние между две точки е постоянно.

Размерите и формата на абсолютно твърдо тяло не се променят, когато се движи.

Концепцията за „абсолютно твърдо тяло“ е физическа абстракция, тъй като всяко тяло е способно на деформация. Въпреки това, в много случаи деформацията може да бъде пренебрегната.

Най-простият случай на въртеливо движение на абсолютно твърдо тяло е въртенето около фиксирана ос. Това е движение, при което точки от тялото се движат в кръгове, чиито центрове лежат на права линия, наречена ос на въртене.

Известно е, че в някои случаи, за да се характеризира движението на тялото, не е необходимо да се посочи движението на всички негови точки; така, например, при транслационно движение е достатъчно да се посочи движението на която и да е точка от тялото.

При въртеливо движение около ос точките на тялото се движат по различни траектории, но през същото време всички точки и самото тяло се въртят под един и същи ъгъл. За ротационни характеристики

начертайте в равнина, перпендикулярна на оста, радиус вектор към определена точка аз(фиг. 5.1). Времевата зависимост на ъгъла α на въртене на радиус вектора спрямо избрана посока OX е уравнението на въртеливото движение на твърдо тяло около фиксирана ос:

Скоростта на въртене на тялото се характеризира с ъглова скорост, равна на първата производна на ъгъла на въртене на радиус-вектора по отношение на времето:

Ъгловата скорост е вектор, който е насочен по оста на въртене и е свързан с посоката на въртене по правилото на десния винт (фиг. 5.2). Векторът на ъгловата скорост, за разлика от векторите на скоростта и силата, е плъзгащ се: той няма определена точка на приложение и може да бъде разположен навсякъде по оста на въртене. По този начин, определянето на вектора ω показва позицията на оста на въртене, посоката на въртене и големината на ъгловата скорост.

Скоростта на промяна на ъгловата скорост се характеризира с ъглово ускорение, равно на първата производна на ъгловата скорост по отношение на времето:

или във векторна форма:

От (5.4) е ясно, че векторът на ъгловото ускорение съвпада по посока с елементарна, сравнително малка промяна на вектора на ъгловата скорост dω: при ускорено въртене ъгловото ускорение е насочено в същата посока като ъгловата скорост, при бавно въртене - в обратна посока.

Тъй като ъгловото изместване на всички точки на абсолютно твърдо тяло е еднакво, тогава, съгласно (5.2) и (5.3), в същото време всички точки на тялото имат една и съща ъглова скорост и същото ъглово ускорение. Линейните характеристики - преместване, скорост, ускорение - са различни за различните точки. Нека посочим в скаларна форма връзката, която може да бъде получена независимо, между линейните и ъгловите характеристики за i-тата точка, движеща се в окръжност с радиус r аз:

ориз. 5.3

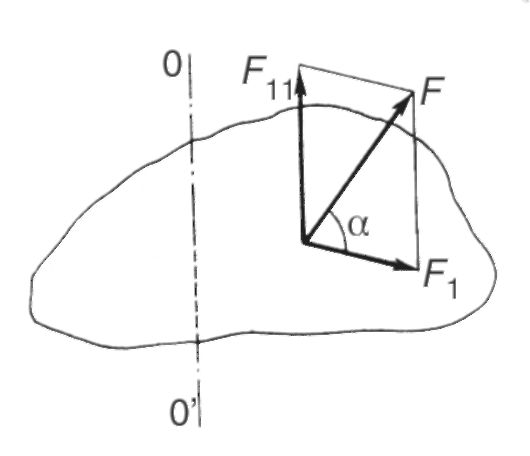
В заключение представяме формулите за кинематиката на въртеливото движение на твърдо тяло около неподвижна ос, получени чрез интегриране на съответните изрази:

уравнение за равномерно въртеливо движение[см. (5.2)]:

зависимост на ъгловата скорост от времето при равномерно въртеливо движение[см. (5.3)]:

уравнение на равномерно редуващо се въртеливо движение[см. (5.1) и (5.6)]:

Полезно е да се сравнят тези формули с подобни зависимости за транслационно движение.

5.2. ОСНОВНИ ПОНЯТИЯ. УРАВНЕНИЕ ЗА ДИНАМИКАТА НА РОТАЦИОННОТО ДВИЖЕНИЕ

Момент на сила_

Нека до някакъв момент азсила, приложена към твърдо тяло F^,лежаща в равнина, перпендикулярна на оста на въртене (фиг. 5.4).

Моментът на сила спрямо оста на въртене е векторното произведение на радиус вектора на точка i и силата:

Разширявайки го, можете да напишете:

Къде β - ъгъл между векторите r iИ F i .Тъй като рамото на силата h i = r i sinβ (виж фиг. 5.4), тогава

Ако силата действа под определен ъгъл α спрямо равнината на въртене (фиг. 5.5), тогава тя може да се разложи на две компоненти. Единият от тях лежи в равнина, перпендикулярна на оста на въртене, а другият е успореден на тази ос и не влияе на въртенето на тялото (в реалния случай действа само върху лагерите). Освен това ще се вземат предвид само сили, лежащи в равнината, перпендикулярна на оста на въртене.

ориз. 5.4

ориз. 5.5

Работете във въртеливо движение

Нека под действие на сила F i(виж фиг. 5.4) тялото се завърта на достатъчно малък ъгъл dα. Нека намерим работата, извършена от тази сила.

Изразът за работата на силата, познат от гимназията, в този случай трябва да се напише по следния начин:

така че

елементарната работа на силата при въртеливо движение е равна на произведението на момента на силата и елементарния ъгъл на завъртане на тялото.

Ако върху едно тяло действат няколко сили, тогава елементарната работа, извършена от всички тях, се определя подобно на (5.12):

Къде М- общият момент на всички външни сили, действащи върху тялото.

Ако, когато тялото се върти, позицията на радиус вектора се променя от α 1 на α 2, тогава работата на външните сили може да се намери чрез интегриране на израз (5.13):

Инерционен момент

Мярката за инерция на телата по време на транслационно движение е масата. Инерцията на телата при въртеливо движение зависи не само от масата, но и от нейното разпределение в пространството спрямо оста. Мярката за инерция на тялото по време на въртене се характеризира с инерционния момент на тялото спрямо оста на въртене. Нека първо да посочим това

Инерционният момент на материална точка спрямо оста на въртене е стойност, равна на произведението на масата на точката на квадрата на нейното разстояние от оста:

Инерционният момент на тялото спрямо ос е сумата от инерционните моменти на всички материални точки, които изграждат тялото:

Като пример извеждаме формулата инерционен момент на тънък хомогенен прътдължина ли маса Тспрямо оста, перпендикулярна на пръта и минаваща през средата му (фиг. 5.6). Нека изберем достатъчно малък участък от пръта с дължина dxи маса дм,разстояние от оста 00" на разстояние X.Поради малката площ на тази област, тя може да се приеме за материална точка, нейният инерционен момент [вж. (5.15)] е равно на:

Масата на елементарно сечение е равна на произведението на линейната плътност t/l,умножено по дължината на елементарния участък: дм= (m/l) dx Замествайки този израз в (5.18), получаваме

За да намерим инерционния момент на целия прът, интегрираме израза (5.19) върху целия прът, т.е. вариращи от -1/2 до +1/2:

Нека представим изрази за инерционните моменти на различни симетрични тела с маса Т:

кух хомогенен цилиндър(обръч) с вътрешен радиус rи външни Рспрямо оста OO", съвпадаща с геометричната ос на цилиндъра (фиг. 5.7):

непрекъснат хомогенен цилиндър (r = 0) или диск [вж (5.21)]:

хомогенна топка спрямо ос, минаваща през центъра му:

правоъгълен паралелепипед спрямо оста OO", минаваща през нейния център перпендикулярно на равнината на основата (фиг. 5.8):

Във всички горепосочени примери оста на въртене минава през центъра на масата на тялото. Когато решавате задачи за определяне на инерционния момент на тяло около ос, която не минава през центъра на масата, можете да използвате теоремата на Хюйгенс. Според тази теорема инерционният момент на тялото спрямо някаква ос OO":

където J 0 е инерционният момент около успоредна ос, минаваща през центъра на масата на тялото OO"; Т- телесно тегло; d- разстоянието между две успоредни оси (фиг. 5.9). Единицата за инерционен момент е килограм метър на квадрат(kg-m2).

Инерция

момент на импулс(ъглов момент)материална точка, въртяща се около определена ос, се нарича стойност, равна на произведението на импулса на точката на нейното разстояние от оста на въртене:

Ъгловият импулс на тяло, въртящо се около определена ос, е равен на сумата от ъгловите импулси на точките, които изграждат тялото:

Тъй като ъгловата скорост на всички точки на твърдо тяло е една и съща, изваждането на ω от знака на сумата [виж. (5.29)], получаваме:

(/ - инерционен момент на тялото спрямо оста), или във векторна форма:

И така, ъгловият момент е равен на произведението на инерционния момент на точка и ъгловата скорост. От това следва, че посоките на векторите на ъгловия момент и ъгловата скорост съвпадат. Единицата за ъглов момент е килограм-метър на квадрат за секунда(kg? m2? s -1).

Полезно е да се сравни формула (5.31) с подобна формула за импулс при транслационно движение.

Кинетична енергия на въртящо се тяло

Когато едно тяло се върти, неговата кинетична енергия се състои от кинетичните енергии на отделните точки на тялото. За твърдо:

Полезно е да се сравни израз (5.32) с подобен израз за постъпателно движение.

Диференцирайки (5.32), получаваме елементарна промяна в кинетичната енергия при въртеливо движение:

Основно уравнение за динамиката на въртеливото движение

Нека твърдото тяло, върху което са действали външни сили, се завърти на достатъчно малък ъгъл da. Нека приравним елементарната работа на всички външни сили по време на такова въртене [виж. (5.13)] до елементарна промяна в кинетичната енергия [вж. (5.33)]: М dα = Джω dω , от където:

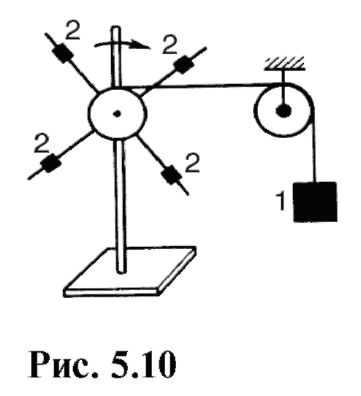
Това е основенуравнение на динамиката на въртеливото движение.От (5.35) става ясно, че инерционният момент характеризира инерционните свойства на тялото при въртеливо движение: под действието на външни сили ъгловото ускорение на тялото е по-голямо, толкова по-малък е инерционният момент на тялото.

Основното уравнение за въртеливото движение играе същата роля като втория закон на Нютон за транслационното движение. Физическите величини, включени в това уравнение, са аналогични съответно на сила, маса и ускорение.

от (5.34) следва, че:

Производната на ъгловия момент на тялото спрямо времето е равна на резултантния момент на всички външни сили.

Зависимостта на ъгловото ускорение от момента на силата и момента на инерцията може да се демонстрира с

с мощността на устройството, показано на фиг. 5.10. Под натоварване 1, окачен на нишка, хвърлена върху блок, кръстът се върти бързо. Преместване на тежести 2 на различни разстояния от оста на въртене можете да промените инерционния момент на напречната част. Сменящи се товари, т.е. моменти на силите и инерционния момент, може да се провери, че ъгловото ускорение нараства с увеличаване на момента на силата или намаляване на момента на инерцията.

5.3. ЗАКОН ЗА ЗАПАЗВАНЕ НА ИМПУЛСА

Нека разгледаме специалния случай на въртеливо движение, когато общият момент на външните сили е нула. Както може да се види от (5.37), dL/dt= 0 при М = 0, от къде

Тази разпоредба е известна като закон за запазване на ъгловия момент: ако общият момент на всички външни сили, действащи върху тялото, е равен на нула, тогава ъгловият момент на това тяло остава постоянен.

Пропускайки доказателството, отбелязваме, че законът за запазване на ъгловия момент е валиден не само за абсолютно твърдо тяло.

Най-интересните приложения на този закон са свързани с въртенето на система от тела около обща ос. В този случай е необходимо да се вземе предвид векторната природа на ъгловия момент и ъгловите скорости. И така, за система, състояща се от Нтела, въртящи се около обща ос, законът за запазване на ъгловия импулс може да се запише във формата:

Нека да разгледаме някои примери, илюстриращи този закон.

Гимнастичка, изпълняваща салто (фиг. 5.11), в началната фаза огъва коленете си и ги притиска към гърдите си, като по този начин намалява инерционния момент и увеличава ъгловата скорост на въртене около хоризонтална ос, минаваща през центъра на масата. В края на скока тялото се изправя, инерционният момент се увеличава, а ъгловата скорост намалява. Скейтър, извършващ въртене около вертикална ос (фиг. 5.12), в началото на въртенето приближава ръцете си към тялото, като по този начин намалява инерционния момент и увеличава ъгловата скорост. В края на въртенето се случва обратният процес: при движение на ръцете инерционният момент се увеличава и ъгловата скорост намалява, което улеснява спирането.

Същият феномен може да бъде демонстриран на пейка Жуковски, която е лека хоризонтална платформа, въртяща се с ниско триене около вертикална ос. Когато позицията на ръцете се промени, инерционният момент и ъгловата скорост се променят (фиг. 5.13), ъгловият момент остава постоянен. За да се подобри демонстрационният ефект, в ръцете на човек има дъмбели. На пейката на Жуковски можете да демонстрирате векторния характер на закона за запазване на ъгловия момент.

Експериментаторът, стоящ на неподвижна пейка, получава от асистент велосипедно колело, въртящо се около вертикална ос (фиг. 5.14, вляво). В този случай ъгловият импулс на системата човек и платформа-колело се определя само от ъгловия импулс на колелото:

тук J h е инерционният момент на човека и платформата; J K и ω κ - инерционен момент и ъглова скорост на колелото. Тъй като моментът на външните сили спрямо вертикалната ос е нула, тогава Лсе запазва (L = const).

Ако експериментаторът завърти оста на въртене на колелото на 180 ° (фиг. 5.14, вдясно), тогава ъгловият импулс на колелото ще бъде насочен обратно на оригинала и равен на J K ω K. Тъй като векторът на импулса на колелото се променя и ъгловият импулс на системата се запазва, ъгловият импулс на човека и платформата неизбежно трябва да се промени; той вече няма да бъде равен на нула 1 . Ъгловият импулс на системата в този случай

1 Леко несъответствие между оста на колелото и оста на въртене на платформата може да бъде пренебрегнато.

Използвайки формула (5.42), е възможно приблизително да се оцени инерционният момент на човешкото тяло заедно с платформата, за което е необходимо да се измери ω κ, ω 4 и да се намери J k.

Методът за измерване на ъглови скорости на равномерно въртене е известен на читателя. Познавайки масата на колелото и приемайки, че масата е разпределена главно по джантата, използвайки формула (5.22), можем да определим J k.

За да намалите грешката, можете да направите ръба на колелото на велосипеда по-тежък, като поставите специални гуми върху него. Човекът трябва да бъде разположен симетрично спрямо оста на въртене.

По-проста версия на разглежданата демонстрация е, че човек, който стои на пейката на Жуковски, сам върти колело, което държи на вертикална ос. В този случай човекът и платформата започват да се въртят в противоположни посоки (фиг. 5.15).

5.4. КОНЦЕПЦИЯТА ЗА СВОБОДНИ ОСИ НА ВЪРТЕНЕ

Тяло, въртящо се около фиксирана ос, обикновено действа върху лагери или други устройства, които поддържат позицията на тази ос постоянна. При високи ъглови скорости и моменти на инерция тези ефекти могат да бъдат значителни. Във всяко тяло обаче е възможно да изберете оси, чиято посока по време на въртене ще се поддържа без специални устройства. За да разберете на какво условие трябва да отговаря изборът на такива оси, разгледайте следния пример.

Сравнявайки (5.43) с координатите на центъра на масата, забелязваме, че силите, действащи върху оста, се уравновесяват, ако оста на въртене минава през центъра на масата.

Тяло с произволна форма винаги има най-малко три взаимно перпендикулярни оси, минаващи през центъра на масата, които могат да бъдат свободни оси на въртене. Тези оси се наричат ​​главни инерционни оси. Въпреки че и трите основни инерционни оси са свободни, най-стабилното въртене ще бъде около оста с най-голям инерционен момент. Факт е, че в резултат на неизбежното действие на външни сили, като триене, а също и поради факта, че е трудно да се зададе точно въртене около определена ос, въртенето около останалите свободни оси е нестабилно.

В някои случаи, когато тялото се върти около свободна ос с малък инерционен момент, самото то променя тази ос на оста с най-висок момент.

Това явление се доказва от следния експеримент. Цилиндричен прът е окачен от електрическия двигател с резба, която може да се върти около геометричната си ос (фиг. 5.17, а). Инерционният момент около тази ос J 1 = mR 2 /2.При достатъчно висока ъглова скорост пръчката ще промени позицията си (фиг. 5.17, b). Инерционният момент спрямо новата ос е равен на J 2 = ml 2/12. Ако l 2 >6R 2, тогава J 2 > J 1. Въртенето около новата ос ще бъде стабилно.

Читателят може самостоятелно да провери от опит, че въртенето на хвърлена кибритена кутия е стабилно по отношение на ос, която е перпендикулярна на по-голямата страна, и е нестабилна или по-малко стабилна по отношение на оси, които се движат перпендикулярно на други лица (виж Фиг. 5.8).

Въртенето на животни и хора в свободен полет и по време на различни скокове се извършва около свободни оси с най-висок или най-нисък момент на инерция. Тъй като позицията на центъра на масата зависи от позата на тялото, ще има различни свободни оси за различните пози.

5.5. КОНЦЕПЦИЯТА ЗА СТЕПЕНИТЕ НА СВОБОДА

Позицията на свободна материална точка в пространството се определя от три независими координати: x, y, z. Ако точката не е свободна, а се движи, например, по някаква повърхност, тогава не всичките три координати ще бъдат независими.

Независими променливи, характеризиращи положението на механична система, се наричат ​​степени на свобода.

Свободната материална точка има три степени на свобода, в разглеждания пример - две степени на свобода. Тъй като една молекула на моноатомен газ може да се разглежда като материална точка, следователно, такава свободна молекула също има три степени на свобода.

Още няколко примера.

Две материални точки 1 и 2 са твърдо свързани помежду си. Позицията на двете точки се определя от шест координати x 1, y 1, z 1, x 2, y 2, z 2,които са обект на едно ограничение и една връзка, математически изразени под формата на уравнение:

Физически това означава, че разстоянието между материалните точки е винаги л.В този случай броят на степените на свобода е 5. Разглежданият пример е модел на двуатомна молекула.

Три материални точки 1, 2 и 3 са твърдо свързани помежду си. приятел. Девет координати характеризират позицията на такава система: x 1, y 1, z 1, x 2, y 2, z2, х 3 y 3 , z 3 . Три връзки между точки обаче определят независимостта само на шест координати. Системата има шест степени на свобода. Тъй като позицията на три точки, които не лежат на една и съща права линия, еднозначно определя позицията на твърдото тяло, твърдото тяло има шест степени на свобода.

Триатомните и многоатомните молекули имат еднакъв брой степени на свобода (шест), ако тези молекули се разглеждат като твърди образувания.

1 Ако се получи имагинерна стойност за зависимата координата от (5.44), това означава, че избраните независими координати не съответстват на никакви точки, разположени върху сфера с даден радиус.

В реалните многоатомни молекули атомите са във вибрационно движение, така че броят на степените на свобода на такива молекули е повече от шест.

Броят на степените на свобода определя не само броя на независимите променливи, характеризиращи положението на механичната система, но и, което е много важно, броя на независимите движения на системата. По този начин трите степени на свобода на свободна материална точка означават, че всяко движение на точката може да се разложи на независими движения по три координатни оси. Тъй като точката няма размери, няма смисъл да говорим за нейното въртене. И така, материалната точка има три степени на свобода на постъпателно движение. Материална точка върху равнина, сфера или друга повърхност има две степени на свобода на транслационно движение. Движението на материална точка по крива (условен пример е движението на влак по релси) съответства на една степен на свобода на транслационно движение.

Твърдо тяло, въртящо се около фиксирана ос, има една степен на свобода на въртеливо движение. Колелото на влака има две степени на свобода: едната е въртеливо движение, а другата е постъпателно (преместване на оста на колелото по релсата). Шест степени на свобода на твърдо тяло означават, че всяко движение на това тяло може да бъде разложено на компоненти: движението на центъра на масата се разлага на три транслационни движения по координатните оси, а въртенето се състои от три по-прости завъртания около координатните оси преминаващ през центъра на масата.

На фиг. 5.18-5.20 показват шарнирни съединения, съответстващи на една, две и три степени на свобода.

ориз. 5.18

ориз. 5.19

ориз. 5.20

5.6. ЦЕНТРОФУГИРАНЕ

Центрофугирането е процесът на отделяне (отделяне) на хетерогенни системи, например частици от течностите, в които се намират, поради тяхното въртене.

Нека разгледаме разделянето на нехомогенни системи в гравитационно поле. Да приемем, че има водна суспензия от частици с различна плътност. С течение на времето, поради действието на гравитацията и плаващата сила Ф Анастъпва отделяне на частиците: частици с плътност по-голяма от тази на водата потъват, частици с плътност по-малка от тази на водата плават. Резултантната сила, действаща например върху по-плътна отделна частица, е равна на:

Къде ρ 1 - плътност на частиците; ρ - плътност на водата; V- обем на частиците.

Ако стойностите на ρ 1 и ρ се различават малко една от друга, тогава силата Fpе малък и отделянето (отлагането) става доста бавно. В центрофуга (сепаратор) такова разделяне се извършва принудително чрез въртене на отделената среда.

Нека разгледаме физиката на това явление.

Нека работният обем на центрофугата (фиг. 5.21: a - външен вид; b - диаграма на работния обем) е напълно зает от някаква хомогенна течност. Нека психически изберем малък обем Vот тази течност, разположена на разстояние rот оста на въртене OO". При равномерно въртене на центрофугата, в допълнение към силата на гравитацията и плаваемостта, които се балансират взаимно, върху избрания обем действа центростремителна сила. Това е силата от течността, заобикаляща обема. Тя е естествено насочен към оста на въртене и е равен на:

Къде ρ е плътността на течността.

Нека сега приемем, че разпределеният обем Vе отделена частица, чиято плътност на веществото е ρ 1 (ρ 1 Φ ρ). Силата, действаща върху частицата от околната течност, няма да се промени, както се вижда от формула (5.45).

За да може една частица да се върти заедно с течността, върху нея трябва да действа центростремителна сила, равна на:

Къде m 1е масата на частицата, а ρ 1 е съответната плътност.

ориз. 5.21

Ако Е> F 1,тогава частицата се движи към оста на въртене. Ако Е< F 1,тогава въздействието върху частицата от течността няма да е достатъчно, за да я задържи на кръгова траектория, и частицата ще започне да се движи към периферията по инерция. Ефектът на разделяне се определя от излишната сила Е,действаща от страната на течността върху избраната частица, над стойността на центростремителната сила F 1, която определя кръговото движение:

Този израз показва, че ефектът от центрофугирането е толкова по-голям, колкото по-голяма е разликата в плътностите на отделените частици и течност, а също така значително зависи от ъгловата скорост на въртене 1.

Нека сравним разделянето чрез центрофугиране с разделянето чрез гравитация:

1 Гравитацията и плаващата сила не се вземат предвид при извеждането на формула (5.47), тъй като те са насочени по протежение на оста на въртене и нямат фундаментален ефект върху центрофугирането.

Ултрацентрофугите са способни да отделят частици, по-малки от 100 nm, суспендирани или разтворени в течност. Те са намерили широко приложение в биомедицинските изследвания за разделяне на биополимери, вируси и субклетъчни частици.

Скоростта на разделяне е особено важна при биологичните и биофизичните изследвания, тъй като с течение на времето състоянието на изследваните обекти може да се промени значително.

Основни понятия.

момент на силаспрямо оста на въртене - това е векторното произведение на радиус вектора и силата.

(1.14)

Силовият момент е вектор , чиято посока се определя от правилото на гимлета (десен винт) в зависимост от посоката на силата, действаща върху тялото. Силовият момент е насочен по оста на въртене и няма определена точка на приложение.

Числената стойност на този вектор се определя по формулата:

M=r Е грях (1.15),

където  - ъгълът между радиус вектора и посоката на силата.

Ако =0 или  , момент на сила М=0, т.е. сила, преминаваща през оста на въртене или съвпадаща с нея, не предизвиква въртене.

Най-големият модул на въртящ момент се създава, ако силата действа под ъгъл  =  /2 (М 0) или  =3  /2 (М 0).

Използване на концепцията за ливъридж d- това е перпендикуляр, спуснат от центъра на въртене към линията на действие на силата), формулата за момента на силата приема формата:

, Къде
(1.16)

Правило за моментите на силите(условие на равновесие на тяло с фиксирана ос на въртене):

За да бъде тяло с фиксирана ос на въртене в равновесие, е необходимо алгебричната сума на моментите на силите, действащи върху това тяло, да бъде равна на нула.

 М аз =0 (1.17)

Единицата SI за момент на сила е [Nm]

При въртеливо движение инерцията на тялото зависи не само от неговата маса, но и от разпределението му в пространството спрямо оста на въртене.

Инерцията по време на въртене се характеризира с инерционния момент на тялото спрямо оста на въртене Дж.

Инерционен моментматериална точка спрямо оста на въртене е стойност, равна на произведението на масата на точката на квадрата на нейното разстояние от оста на въртене:

Дж  =m   r  2 (1.18)

Инерционният момент на тялото спрямо ос е сумата от инерционните моменти на материалните точки, които изграждат тялото:

J= м   r  2 (1.19)

Инерционният момент на тялото зависи от неговата маса и форма, както и от избора на оста на въртене. За да се определи инерционният момент на тялото спрямо определена ос, се използва теоремата на Щайнер-Хюйгенс:

J=J 0 +м d 2 (1.20),

Къде Дж 0 – инерционен момент спрямо успоредна ос, минаваща през центъра на масата на тялото, d – разстояние между две успоредни оси . Инерционният момент в SI се измерва в [kgm 2 ]

Инерционният момент по време на въртеливото движение на човешкото тяло се определя експериментално и се изчислява приблизително по формулите за цилиндър, кръгъл прът или топка.

Инерционният момент на човек спрямо вертикалната ос на въртене, която минава през центъра на масата (центърът на масата на човешкото тяло е разположен в сагиталната равнина малко пред втория сакрален прешлен), в зависимост от положение на човека, има следните стойности: при изправено положение - 1,2 kg m 2; с поза “арабеск” – 8 kgm 2; в хоризонтално положение – 17 кг  м 2.

Работете във въртеливо движениевъзниква, когато тялото се върти под въздействието на външни сили.

Елементарната работа на силата при въртеливо движение е равна на произведението на момента на силата и елементарния ъгъл на завъртане на тялото:

dA  =М   d (1.21)

Ако върху едно тяло действат няколко сили, тогава елементарната работа на резултата от всички приложени сили се определя по формулата:

dA=M d (1.22),

Къде М– сумарният момент на всички външни сили, действащи върху тялото.

Кинетична енергия на въртящо се тялоУ дозависи от инерционния момент на тялото и ъгловата скорост на неговото въртене:

(1.23)

Ъгъл на импулса (ъглов момент) – количество, числено равно на произведението на импулса на тялото и радиуса на въртене.

L=p r=m V r (1.24).

След подходящи трансформации можете да напишете формулата за определяне на ъглов импулс във формата:

(1.25).

Инерция – вектор, чиято посока се определя от правилото на десния винт. Единицата SI за ъглов момент еkgm 2 /s

Основни закони на динамиката на въртеливото движение.

Основното уравнение за динамиката на въртеливото движение:

Ъгловото ускорение на тялото, което се върти, е право пропорционално на общия момент на всички външни сили и обратно пропорционално на инерционния момент на тялото.

(1.26).

Това уравнение играе същата роля при описването на ротационното движение, както вторият закон на Нютон за транслационното движение. От уравнението става ясно, че под действието на външни сили, колкото по-голямо е ъгловото ускорение, толкова по-малък е инерционният момент на тялото.

Вторият закон на Нютон за динамиката на въртеливото движение може да бъде записан в друга форма:

(1.27),

тези. първата производна на ъгловия момент на тялото по отношение на времето е равна на общия момент на всички външни сили, действащи върху дадено тяло.

Закон за запазване на ъгловия момент на тялото:

Ако общият момент на всички външни сили, действащи върху тялото, е равен на нула, т.е.

 М  =0 , Тогава dL/dt=0 (1.28).

От това следва
или
(1.29).

Това твърдение съставлява същността на закона за запазване на ъгловия момент на тялото, който се формулира по следния начин:

Ъгловият момент на тялото остава постоянен, ако общият момент на външните сили, действащи върху въртящо се тяло, е нула.

Този закон е валиден не само за абсолютно твърдо тяло. Пример е фигурист, който извършва въртене около вертикална ос. Чрез натискане на ръцете си скейтърът намалява инерционния момент и увеличава ъгловата скорост. За да забави въртенето, той, напротив, разперва широко ръцете си; В резултат на това инерционният момент се увеличава и ъгловата скорост на въртене намалява.

В заключение представяме сравнителна таблица на основните количества и закони, характеризиращи динамиката на транслационните и ротационните движения.

Таблица 1.4.

=конст,

Следователно от външната сила, приложена към тялото, е необходимо да се изолират компонентите, които не причиняват въртене. Въртенето може да бъде причинено само от сила (сила на въртене), разположена в равнина, перпендикулярна на оста на въртене и насочена тангенциално към окръжността, описана от точката на нейното приложение.

Имайте предвид, че когато тялото се върти, компонентите не извършват никаква работа, тъй като точката на прилагане на тези сили се движи перпендикулярно на техните посоки. Работата се извършва само от силата на въртене, тя е проекцията на силата, действаща върху тялото върху посоката на движение на точката на приложение на тази сила.

Нека определим количеството работа, извършена от въртящата се сила, ако нейната точка на приложение се движи по окръжност с радиус (фиг. 1.19, b). Да приемем, че величината на силата остава постоянна. Тогава

Произведението на сила на въртене и радиус е моментът на силата на въртене или въртящият момент, действащ върху дадено тяло, и се означава с (припомнете си, че моментът на дадена сила спрямо всяка ос е произведението на тази сила от рамото му, т.е. по дължината на перпендикуляра, проведен от посочения

ос спрямо посоката на силата). Така във формула (2.8)

следователно работата, извършена от въртящия момент, е равна на произведението на този момент и ъгъла на въртене на тялото:

Ако въртящият момент (силата или нейното рамо) се променя с времето, тогава извършената работа се определя като сумата:

Въртящият момент на въртящата сила се представя като вектор, съвпадащ с оста на въртене; положителната ориентация на този вектор се избира в посоката, в която ще се движи десният винт, завъртян до този момент.

Въртящият момент, приложен към тялото, му придава известно ъглово ускорение в съответствие с посоките на векторите, които сме избрали; те са ориентирани по оста на въртене в същата посока. Връзката между големината на въртящия момент и величината на придаденото от него ъглово ускорение може да се установи по два начина:

а) можете да използвате факта, че работата на движещата сила е равна на промяната в кинетичната енергия на тялото, към което се прилага тази сила: За въртящо се тяло, съгласно формули (2.9) и (2.4), ние имат

Тук приемаме, че инерционният момент на тялото не се променя по време на въртене. Като разделим това уравнение на и намалим с, получаваме

б) можете да използвате факта, че моментът на въртящата се сила е равен на сумата от моментите на силите, които придават тангенциални ускорения на отделните компоненти на тялото; тези сили са равни и техните моменти са

Нека заменим тангенциалните ускорения с ъглово ускорение, което е еднакво за всички частици на въртящо се тяло (ако тялото не се деформира по време на въртене): Тогава

Формула (2.12) изразява основния закон на динамиката на въртеливото движение на твърди (недеформиращи) тела, за които

ъгловото ускорение, придобито от тялото под въздействието на даден въртящ момент, е право пропорционално на големината на този момент и обратно пропорционално на момента на инерцията на тялото спрямо оста на въртене:

Във векторна форма този закон се записва като

Ако тялото се деформира по време на въртене, неговият инерционен момент спрямо оста на въртене ще се промени. Нека мислено си представим въртящо се тяло, състоящо се от много елементарни (точкови) части; тогава деформацията на цялото тяло ще означава промяна в разстоянията от тези части на тялото до оста на въртене. Въпреки това, промяната в разстоянието на дадена ъглова скорост на въртене co ще бъде придружена от промяна в линейната скорост на движение на тази частица и следователно нейната кинетична енергия. Така, при постоянна ъглова скорост на въртене на тялото, промяната в разстоянията (следователно промяната в инерционния момент на тялото) ще бъде придружена от промяна в кинетичната енергия на въртене на цялото тяло.

От формула (2.4), ако приемем променливи, можем да получим

Първият член показва промяната в кинетичната енергия на въртящо се тяло, възникнала само поради промяна в ъгловата скорост на въртене (в даден момент на инерция на тялото), а вторият член показва промяната в кинетичната енергия , което е възникнало само поради промяна в инерционния момент на тялото (при дадена ъглова скорост на въртене).

Въпреки това, когато разстоянието от точково тяло до оста на въртене се промени, вътрешните сили, свързващи това тяло с оста на въртене, ще вършат работа: отрицателна, ако тялото се отдалечи, и положителна, ако тялото се приближи до оста на въртене; тази работа може да бъде изчислена, ако приемем, че силата, свързваща частицата с оста на въртене, е числено равна на центростремителната сила:

За цялото тяло, състоящо се от много частици с маси, получаваме

В общия случай, когато върху тялото действа външен въртящ момент, промяната в кинетичната енергия трябва да се приравни към сумата от две работи: външен въртящ момент и вътрешни сили. При ускорено въртене стойностите ще имат положителни знаци, - отрицателни

знак (тъй като частиците на тялото се отдалечават от оста на въртене); Тогава

Замествайки тук стойността от израз (2.15) и замествайки с получаваме

или след намаление

Това е обща форма на основния закон на механиката за тела, въртящи се около фиксирана ос; той е приложим и за деформиращи се тела. Когато формула (2.16) се трансформира във формула (2.14).

Имайте предвид, че за деформиращите се тела е възможна промяна в ъгловата скорост на въртене дори при липса на външен въртящ момент. Наистина, когато - от формула (2.16) получаваме:

В този случай ъгловата скорост на въртене се променя само поради промяна в инерционния момент на тялото, причинена от вътрешни сили.