Mga seksyon ng site
Pinili ng Editor:
- Kilusang partisan noong Digmaang Patriotiko noong 1812
- Itinalaga ni Stalin ang commander-in-chief ng hukbong Sobyet
- Ang sinaunang soberanya. III. Ang soberanya at ang kanyang hukuman. Diocletian: Quae fuerunt vitia, mores sunt - Kung ano ang mga bisyo noon ay pumasok na sa mores
- Order reporma sa Russia
- Digmaang gerilya: kahalagahang pangkasaysayan
- Kaarawan ng Soviet Guard
- Sa makasaysayang sitwasyon bago ang labanan ng Borodino
- Sikretong opisina ng Shishkovsky
- Ang kahulugan ng pangalang Yasmina sa kasaysayan
- Bakit nangangarap ang isang Excavator sa isang panaginip, isang pangarap na libro upang makita ang isang Excavator ano ang ibig sabihin nito?
Advertising
| Mga pangunahing pormula ng teoretikal na mekanika ng dinamika. Ang dynamics ng tel. Mga pangunahing teorema at konsepto |
|
MINISTRY NG AGRIKULTURA AT PAGKAIN NG REPUBLIKA NG BELARUS Institusyong pang-edukasyon "BELARUSIAN STATE AGRARIAN TECHNICAL UNIVERSITY" Kagawaran teoretikal na mekanika at ang teorya ng mga mekanismo at makina THEORETICAL MECHANICS methodological complex para sa mga mag-aaral ng isang pangkat ng mga specialty 74 06 Agroengineering Sa 2 bahagi Part 1 UDC 531.3 (07) BBK 22.213ya7 T 33 Compiled by: kandidato ng pisikal at matematikal na agham, associate professor S. Biza, kandidato mga teknikal na agham, associate professor L. Rakova, senior lecturer A. Tarasevich Mga Reviewer: Kagawaran ng Theoretical Mechanics ng Educational Institution "Belarusian National Technical University" (Head Department of Theoretical Mechanics BNTU Doctor of Physical and Mathematical Sciences, Propesor A. V. Chigarev); nangungunang mananaliksik ng laboratoryo "Proteksyon ng vibration ng mga mekanikal na sistema" Institusyon ng Siyentipiko ng Estado "United Institute of Mechanical Engineering NAS ng Belarus ", Kandidato ng Teknikal na Agham, Associate Professor A. M. Goman Teoretikal na mekanika. Seksyon "Dynamics": pang-edukasyon Paraan ng T33. kumplikado. Sa 2 oras, Bahagi 1 / comp .: Yu. S. Biza, N. L. Rakova, I. A. Tarasevich. - Minsk: BGATU, 2013 .-- 120 p. ISBN 978-985-519-616-8. Ang educational-methodical complex ay naglalaman ng mga materyales para sa pag-aaral ng seksyong "Dynamics", bahagi 1, na bahagi ng disiplina na "Theoretical Mechanics". May kasamang kurso ng mga lektura, mga pangunahing materyales para sa pagpapatupad praktikal na pagsasanay, mga takdang-aralin at mga halimbawa ng mga takdang-aralin para sa independiyenteng trabaho at kontrol mga aktibidad sa pagkatuto full-time at part-time na mga mag-aaral. UDC 531.3 (07) BBK 22.213ya7
PANIMULA Ang teoretikal na mekanika ay ang agham ng mga pangkalahatang batas ng mekanikal na paggalaw, balanse at pakikipag-ugnayan ng mga materyal na katawan. Ito ay isa sa mga pangunahing pangkalahatang siyentipikong pisikal at matematikal na disiplina. Ito ang teoretikal na batayan ng modernong teknolohiya. Ang pag-aaral ng teoretikal na mekanika, kasama ang iba pang mga pisikal at matematikal na disiplina, ay nag-aambag sa pagpapalawak ng mga pang-agham na abot-tanaw, bumubuo ng kakayahan para sa kongkreto at abstract na pag-iisip at nag-aambag sa isang pagtaas sa pangkalahatang teknikal na kultura ng hinaharap na espesyalista. Ang teoretikal na mekanika, bilang siyentipikong batayan ng lahat ng mga teknikal na disiplina, ay nag-aambag sa pag-unlad ng mga kasanayan makatwirang desisyon mga gawaing pang-inhinyero na may kaugnayan sa pagpapatakbo, pagkukumpuni at disenyo ng makinarya at kagamitan sa pagsasaka at pagbawi ng lupa. Sa likas na katangian ng mga problemang isinasaalang-alang, ang mekanika ay nahahati sa statics, kinematics at dynamics. Ang dinamika ay isang sangay ng teoretikal na mekanika na nag-aaral sa paggalaw ng mga materyal na katawan sa ilalim ng pagkilos ng mga puwersang inilapat. V pang-edukasyon na pamamaraan complex (CMD) ay nagtatanghal ng mga materyales para sa pag-aaral ng seksyong "Dynamics", na kinabibilangan ng kurso ng mga lektura, mga pangunahing materyales para sa pagsasagawa Praktikal na trabaho, mga takdang-aralin at mga halimbawa ng pagpapatupad para sa pansariling gawain at pagsubaybay sa mga aktibidad na pang-edukasyon ng mga full-time at part-time na mga mag-aaral. V bilang resulta ng pag-aaral sa seksyong "Dynamics", dapat matuto ang mag-aaral teoretikal na batayan dinamika at makabisado ang mga pangunahing pamamaraan ng paglutas ng mga problema sa dinamika: Alamin ang mga pamamaraan para sa paglutas ng mga problema ng dinamika, pangkalahatang teorema dinamika, mga prinsipyo ng mekanika; Upang matukoy ang mga batas ng paggalaw ng isang katawan depende sa mga puwersang kumikilos dito; ilapat ang mga batas at teorema ng mekanika upang malutas ang mga problema; matukoy ang mga static at dynamic na reaksyon ng mga hadlang na naglilimita sa paggalaw ng mga katawan. Ang kurikulum ng disiplinang "Theoretical Mechanics" ay nagbibigay ng kabuuang bilang ng mga oras sa silid-aralan - 136, kasama ang 36 na oras para sa pag-aaral ng seksyong "Dynamics". 1. SCIENTIFIC AND THEORETICAL CONTENT NG EDUCATIONAL AND METHODOLOGICAL COMPLEX 1.1. Talasalitaan Statics - isang seksyon ng mechanics, na nagtatakda ng pangkalahatang doktrina ng pwersa, pinag-aaralan ang pagbabawas kumplikadong mga sistema pwersa sa pinakasimpleng anyo at mga kondisyon ng ekwilibriyo ay itinatag iba't ibang sistema pwersa. Ang Kinematics ay isang sangay ng theoretical mechanics kung saan pinag-aaralan ang paggalaw ng mga materyal na bagay anuman ang mga dahilan na nagdudulot ng paggalaw na ito, iyon ay, anuman ang mga puwersang kumikilos sa mga bagay na ito. Ang dinamika ay isang sangay ng teoretikal na mekanika na nag-aaral sa paggalaw ng mga materyal na katawan (mga punto) sa ilalim ng pagkilos ng mga puwersang inilapat. Materyal na punto- isang materyal na katawan, ang pagkakaiba sa paggalaw ng mga punto na kung saan ay hindi gaanong mahalaga. Ang body mass ay isang scalar positive quantity na nakadepende sa dami ng substance na nakapaloob sa isang partikular na katawan at tinutukoy ang sukat nito ng inertia sa panahon ng translational motion. Sistema ng sanggunian - isang sistema ng coordinate na nauugnay sa isang katawan, na may kaugnayan kung saan pinag-aaralan ang paggalaw ng ibang katawan. Inertial system- isang sistema kung saan natutupad ang una at pangalawang batas ng dinamika. Ang momentum ng puwersa ay isang sukat ng vector ng pagkilos ng puwersa sa paglipas ng panahon. Ang dami ng paggalaw ng isang materyal na punto Ang sukat ba ng vector ng paggalaw nito, ay katumbas ng produkto ng masa ng punto sa pamamagitan ng vector ng bilis nito. Kinetic energy- scalar mekanikal na paggalaw. Pangunahing gawain ng lakas Ay isang walang katapusang maliit na halaga ng scalar na katumbas ng scalar product ng force vector ng vector ng walang katapusang maliit na displacement ng point of application ng force. Kinetic energy Ay isang scalar na sukat ng mekanikal na paggalaw. Ang kinetic energy ng isang materyal na punto ay isang scalar isang negatibong halaga na katumbas ng kalahati ng produkto ng masa ng punto sa pamamagitan ng parisukat ng bilis nito. Kinetic energy ng isang mekanikal na sistema - arithme- ang kabuuan ng kinetic energies ng lahat ng materyal na punto ng sistemang ito. Ang puwersa ay isang sukatan ng mekanikal na pakikipag-ugnayan ng mga katawan, na nagpapakilala sa intensity at direksyon nito. 1.2. Mga paksa ng mga lektura at ang kanilang nilalaman Seksyon 1. Panimula sa dinamika. Pangunahing konsepto klasikal na mekanika Paksa 1. Dynamics ng isang materyal na punto Ang mga batas ng dinamika ng isang materyal na punto (ang mga batas ng Galileo - Newton). Differential equation ng paggalaw ng isang materyal na punto. Dalawang pangunahing problema ng dinamika para sa isang materyal na punto. Solusyon ng pangalawang problema ng dinamika; integration constants at ang kanilang pagpapasiya mula sa mga paunang kondisyon. Panitikan :, pp. 180-196, pp. 12-26. Paksa 2. Dynamics ng relatibong paggalaw ng materyal Ang kamag-anak na paggalaw ng isang materyal na punto. Differential equation ng relatibong paggalaw ng isang punto; portable at Coriolis forces of inertia. Ang prinsipyo ng relativity sa klasikal na mekanika. Isang kaso ng medyo kalmado. Panitikan: pp. 180-196, pp. 127-155. Paksa 3. Geometry ng masa. Sentro ng grabidad ng mekanikal na sistema Timbang ng system. Ang sentro ng masa ng system at ang mga coordinate nito. Panitikan: pp. 86-93, pp. 264-265 Paksa 4. Mga sandali ng pagkawalang-galaw ng isang matibay na katawan Mga sandali ng pagkawalang-galaw ng isang matibay na katawan tungkol sa isang axis at isang poste. Radius ng gyration. Theorem on moments of inertia about parallel axes. Axial moments ng inertia ng ilang katawan. Centrifugal moments of inertia bilang isang katangian ng body asymmetry. Panitikan: pp. 265-271, pp. 155-173. Seksyon 2. Pangkalahatang theorems ng dinamika ng isang materyal na punto at mekanikal na sistema Paksa 5. Ang teorama sa paggalaw ng sentro ng masa ng sistema Ang theorem sa paggalaw ng sentro ng masa ng system. Mga kahihinatnan mula sa theorem sa paggalaw ng sentro ng masa ng system. Panitikan: pp. 274-277, pp. 175-192. Paksa 6. Ang dami ng paggalaw ng isang materyal na punto at mekanikal na sistema Ang dami ng paggalaw ng isang materyal na punto at isang mekanikal na sistema. Elementarya na salpok at salpok ng puwersa para sa isang may hangganang tagal ng panahon. Isang teorama sa pagbabago sa momentum ng isang punto at isang sistema sa mga kaugalian at integral na anyo. Ang batas ng konserbasyon ng momentum. Panitikan: pp. 280-284, pp. 192-207. Paksa 7. Sandali ng dami ng paggalaw ng isang materyal na punto at mekanikal na sistema na may paggalang sa sentro at axis Ang angular momentum ng isang punto na nauugnay sa sentro at axis. Ang theorem sa pagbabago sa angular momentum ng isang punto. Ang kinetic moment ng isang mekanikal na sistema na may kaugnayan sa sentro at axis. Ang kinetic moment ng isang umiikot na matibay na katawan tungkol sa axis ng pag-ikot. Theorem tungkol sa pagbabago sa angular momentum ng system. Ang batas ng konserbasyon ng kinetic moment. Panitikan: pp. 292-298, pp. 207-258. Paksa 8. Trabaho at kapangyarihan ng mga puwersa Ang elementarya na gawain ng puwersa, ang analytical expression nito. Ang gawain ng puwersa sa huling landas. Ang gawain ng grabidad, nababanat na puwersa. Pagkakapantay-pantay sa zero ng kabuuan ng gawain ng mga panloob na pwersa na kumikilos sa isang solid. Ang gawain ng mga puwersa na inilapat sa isang matibay na katawan na umiikot sa paligid ng isang nakapirming axis. kapangyarihan. Kahusayan. Panitikan: pp. 208-213, pp. 280-290. Paksa 9. Kinetic energy ng isang materyal na punto at mekanikal na sistema Kinetic energy ng isang materyal na punto at isang mekanikal na sistema. Pagkalkula ng kinetic energy ng isang matibay na katawan sa iba't ibang mga kaso ng paggalaw nito. Ang teorama ni Koenig. Isang theorem sa pagbabago sa kinetic energy ng isang punto sa differential at integral forms. Isang theorem sa pagbabago sa kinetic energy ng isang mekanikal na sistema sa mga differential at integral form. Panitikan: pp. 301-310, pp. 290-344. Paksa 10. Potensyal na larangan ng puwersa at potensyal Ang konsepto ng isang force field. Potensyal na patlang ng puwersa at paggana ng puwersa. Sapilitang trabaho sa panghuling paglilipat ng isang punto sa isang potensyal na field ng puwersa. Potensyal na enerhiya. Panitikan: pp. 317-320, pp. 344-347. Paksa 11. Dynamics ng isang matibay na katawan Differential equation ng translational motion ng isang matibay na katawan. Differential equation para sa rotational motion ng isang matibay na katawan sa paligid ng isang fixed axis. Pisikal na pendulum. Differential equation para sa paggalaw ng eroplano ng isang matibay na katawan. Panitikan: pp. 323-334, pp. 157-173. Seksyon 1. Panimula sa dinamika. Pangunahing konsepto klasikal na mekanika Ang dinamika ay isang sangay ng teoretikal na mekanika na nag-aaral sa paggalaw ng mga materyal na katawan (mga punto) sa ilalim ng pagkilos ng mga puwersang inilapat. Katawan ng materyal- isang katawan na may masa. Materyal na punto- isang materyal na katawan, ang pagkakaiba sa paggalaw ng mga punto na kung saan ay hindi gaanong mahalaga. Maaari itong maging parehong katawan, ang mga sukat kung saan sa panahon ng paggalaw nito ay maaaring mapabayaan, at isang katawan ng may hangganan na sukat, kung ito ay gumagalaw sa pagsasalin. Ang mga particle ay tinatawag ding mga materyal na punto, kung saan ang isang matibay na katawan ay nasira sa pag-iisip kapag tinutukoy ang ilan sa mga dynamic na katangian nito. Mga halimbawa ng materyal na punto (Larawan 1): a - ang paggalaw ng Earth sa paligid ng Araw. Earth - materyal na punto; b - translational motion ng isang matibay na katawan. Solid na katawan - ina- punto, dahil V B = V A; isang B = isang A; c - pag-ikot ng katawan sa paligid ng axis. Ang isang butil ng isang katawan ay isang materyal na punto. Ang pagkawalang-galaw ay ang pag-aari ng mga materyal na katawan upang baguhin ang bilis ng kanilang paggalaw nang mas mabilis o mas mabagal sa ilalim ng pagkilos ng mga puwersang inilapat. Ang body mass ay isang scalar positive quantity na nakadepende sa dami ng matter na nakapaloob sa isang partikular na katawan at tinutukoy ang sukat ng inertia nito sa panahon ng translational motion. Sa klasikal na mekanika, ang masa ay isang pare-parehong dami. Ang puwersa ay isang quantitative measure ng mekanikal na interaksyon sa pagitan ng mga katawan o sa pagitan ng isang katawan (punto) at isang field (electric, magnetic, atbp.). Ang puwersa ay isang dami ng vector na nailalarawan sa pamamagitan ng halaga, punto ng aplikasyon at direksyon (linya ng pagkilos) (Larawan 2: A - punto ng aplikasyon; AB - linya ng pagkilos ng puwersa). kanin. 2 Sa dynamics, kasama ang mga pare-parehong pwersa, mayroon ding mga variable na pwersa na maaaring depende sa oras t, bilis, distancer o sa kabuuan ng mga dami na ito, i.e. F = const; F = F (t); F = F (ϑ); F = F (r); F = F (t, r, ϑ).
de-kuryenteng tren; c - F = F (r) - ang puwersa ng pagtanggi mula sa sentro O o pagkahumaling dito.
Sistema ng sanggunian - isang sistema ng coordinate na nauugnay sa isang katawan, na may kaugnayan kung saan pinag-aaralan ang paggalaw ng ibang katawan. Ang inertial system ay isang sistema kung saan natutupad ang una at pangalawang batas ng dinamika. Ito ay isang fixed coordinate system o isang sistema na gumagalaw nang pare-pareho at sa isang tuwid na linya. Ang paggalaw sa mekanika ay isang pagbabago sa posisyon ng isang katawan sa espasyo at oras na may kaugnayan sa ibang mga katawan. Ang espasyo sa classical na mechanics ay three-dimensional, napapailalim sa Euclidean geometry. Ang oras ay isang scalar na dami na dumadaloy sa parehong paraan sa anumang reference system. Ang sistema ng mga yunit ay isang koleksyon ng mga yunit ng pagsukat ng mga pisikal na dami. Upang sukatin ang lahat ng mekanikal na dami, tatlong pangunahing mga yunit ay sapat: mga yunit ng haba, oras, masa o puwersa.
Ang lahat ng iba pang mga yunit ng pagsukat ng mga mekanikal na dami ay nagmula sa mga ito. Dalawang uri ng mga sistema ng mga yunit ang ginagamit: ang internasyonal na sistema ng mga yunit ng SI (o mas maliit - CGS) at ang teknikal na sistema ng mga yunit - ICGSS. Paksa1. Dynamics ng isang materyal na punto 1.1. Ang mga batas ng dinamika ng isang materyal na punto (ang mga batas ng Galileo - Newton) Unang batas (batas ng pagkawalang-galaw). Ang isang materyal na punto na nakahiwalay sa mga panlabas na impluwensya ay nagpapanatili ng estado ng pahinga nito o gumagalaw nang pantay at patuwid hanggang sa pilitin ito ng mga puwersang inilapat na baguhin ang estadong ito. Ang paggalaw na ginawa ng isang punto sa kawalan ng pwersa o sa ilalim ng pagkilos ng isang balanseng sistema ng pwersa ay tinatawag na inertial motion. Halimbawa, ang paggalaw ng isang katawan sa isang makinis (frictional force ay zero) ang pahalang na ibabaw (Larawan 4: G - timbang ng katawan; N - normal na reaksyon ng eroplano). Dahil G = - N, pagkatapos G + N = 0. Kapag ϑ 0 ≠ 0, ang katawan ay gumagalaw sa parehong bilis; para sa 0 = 0 ang katawan ay nakapahinga (ϑ 0 ang paunang bilis). Ang pangalawang batas (ang pangunahing batas ng dinamika).
Ang produkto ng masa ng isang punto sa pamamagitan ng acceleration na natatanggap nito sa ilalim ng pagkilos ng isang ibinigay na puwersa ay katumbas ng magnitude sa puwersang ito, at ang direksyon nito ay tumutugma sa direksyon ng acceleration. a b Sa matematika, ang batas na ito ay ipinahayag ng pagkakapantay-pantay ng vector
Sa F = 0, a 0 = 0 = ϑ 0 = const - ang punto ay gumagalaw nang pantay at patuwid, o sa 0 = 0 - ay nakapahinga (ang batas ng pagkawalang-galaw). Pangalawa ginagawang posible ng batas na magtatag ng ugnayan sa pagitan ng mass m ng isang katawan na matatagpuan malapit sa ibabaw ng mundo at ang bigat nito G.G = mg, kung saan g - acceleration of gravity. Ang ikatlong batas (ang batas ng pagkakapantay-pantay ng aksyon at reaksyon). Dalawang materyal na punto ang kumikilos sa isa't isa na may mga puwersa na katumbas ng magnitude at nakadirekta sa isang tuwid na linya na nagdudugtong ang mga puntong ito ay nasa magkasalungat na direksyon. Dahil ang mga puwersa F 1 = - F 2 ay inilapat sa iba't ibang mga punto, ang sistema ng mga puwersa (F 1, F 2) ay hindi balanse, ibig sabihin (F 1, F 2) ≈ 0 (Larawan 6).
ang masa ng mga nakikipag-ugnayan na mga punto ay inversely proportional sa kanilang mga acceleration. Ang ikaapat na batas (ang batas ng kalayaan ng pagkilos ng mga puwersa). Ang acceleration na nakuha ng isang punto kapag kumikilos dito nang sabay-sabay ngunit ang ilang pwersa ay katumbas ng geometrical na kabuuan ng mga acceleration na iyon na matatanggap ng isang punto kapag ang bawat puwersa ay kumilos dito nang hiwalay. Paliwanag (fig. 7). kulay-balat isang 1 isang kF n Ang resultang R pwersa (F 1, ... F k, ... F n). Dahil ma = R, F 1 = ma 1, ..., F k = ma k, ..., F n = ma n, kung gayon a = a 1 + ... + a k + ... + a n = ∑ a k, ibig sabihin, ang ikaapat na batas ay katumbas ng k = 1 ang panuntunan ng pagdaragdag ng mga puwersa.
1.2. Differential equation ng paggalaw ng isang materyal na punto Hayaang kumilos ang ilang pwersa nang sabay-sabay sa isang materyal na punto, kung saan mayroong parehong pare-pareho at variable. Isinulat namin ang pangalawang batas ng dinamika sa anyo
point, pagkatapos (1.2) ay naglalaman ng mga derivatives ng r at kumakatawan sa differential equation ng paggalaw ng isang materyal na punto sa vector form o ang pangunahing equation ng dynamics ng isang materyal na punto. Mga projection ng pagkakapantay-pantay ng vector (1.2): - sa gilid-Cartesian coordinate (Fig. 8, a)
Natural na axis (Larawan 8, b)
mab = m0 = ∑ Fk b k = 1 M t oM oa
Ang mga equation (1.3) at (1.4) ay ang mga differential equation ng paggalaw ng isang materyal na punto, ayon sa pagkakabanggit, sa Cartesian coordinate axes at natural axes, ibig sabihin, natural differential equation na karaniwang ginagamit sa curvilinear motion ng isang punto kung ang trajectory ng ang punto at ang radius ng curvature nito ay kilala. 1.3. Dalawang pangunahing problema ng dinamika para sa isang materyal na punto at ang kanilang solusyon Ang unang (direktang) gawain. Alam ang batas ng paggalaw at ang masa ng punto, tukuyin ang puwersa na kumikilos sa punto. Upang malutas ang problemang ito, kailangan mong malaman ang acceleration ng punto. Sa mga problema ng ganitong uri, maaari itong direktang tukuyin, o ang batas ng paggalaw ng isang punto ay maaaring tukuyin, ayon sa kung saan maaari itong matukoy. 1. Kaya, kung ang paggalaw ng isang punto ay tinukoy sa mga coordinate ng Cartesian x = f 1 (t), y = f 2 (t) at z = f 3 (t), pagkatapos ay ang mga projection ng acceleration
Ang teorama sa paggalaw ng sentro ng masa. Differential equation ng paggalaw ng isang mekanikal na sistema. Isang teorama sa paggalaw ng sentro ng masa ng isang mekanikal na sistema. Ang batas ng konserbasyon ng paggalaw ng sentro ng masa. Ang theorem sa pagbabago sa dami ng paggalaw. Ang dami ng paggalaw ng isang materyal na punto. Elementarya na salpok ng kapangyarihan. Salpok ng puwersa para sa isang may hangganang tagal ng panahon at ang projection nito sa mga coordinate axes. Isang teorama sa pagbabago sa dami ng paggalaw ng isang materyal na punto sa kaugalian at may hangganan na mga anyo. Ang dami ng paggalaw ng mekanikal na sistema; pagpapahayag nito sa pamamagitan ng masa ng sistema at ang bilis ng sentro ng masa nito. Isang teorama sa pagbabago sa momentum ng isang mekanikal na sistema sa mga anyo ng kaugalian at may hangganan. Ang batas ng konserbasyon ng momentum ng mekanikal (Ang konsepto ng isang katawan at isang punto ng variable na masa. Meshchersky's equation. Tsiolkovsky's formula.) Ang theorem sa pagbabago sa angular momentum. Ang angular momentum ng isang materyal na punto na nauugnay sa gitna at nauugnay sa axis. Theorem tungkol sa pagbabago sa angular momentum ng isang materyal na punto. sentral na kapangyarihan. Pag-iingat ng angular na momentum ng isang materyal na punto sa kaso ng isang sentral na puwersa. (Ang konsepto ng bilis ng sektor. Ang batas ng mga lugar.) Ang pangunahing sandali ng mga dami ng paggalaw o ang angular na momentum ng isang mekanikal na sistema tungkol sa gitna at tungkol sa axis. Ang kinetic moment ng isang umiikot na matibay na katawan tungkol sa axis ng pag-ikot. Theorem tungkol sa pagbabago sa angular momentum ng isang mekanikal na sistema. Ang batas ng konserbasyon ng angular momentum ng isang mekanikal na sistema. (Ang theorem sa pagbabago sa angular momentum ng isang mekanikal na sistema sa relatibong paggalaw na may paggalang sa sentro ng masa.) Ang theorem sa pagbabago sa kinetic energy. Kinetic energy ng isang materyal na punto. Pang-elementarya na gawaing kapangyarihan; analitikal na pagpapahayag ng gawaing elementarya. Ang gawain ng puwersa sa huling pag-aalis ng punto ng aplikasyon nito. Ang gawain ng puwersa ng grabidad, ang puwersa ng pagkalastiko at ang puwersa ng grabidad. Isang teorama sa pagbabago sa kinetic energy ng isang materyal na punto sa kaugalian at may hangganan na mga anyo. Kinetic energy ng isang mekanikal na sistema. Mga formula para sa pagkalkula ng kinetic energy ng isang matibay na katawan sa translational motion, sa pag-ikot sa paligid ng isang nakapirming axis at sa pangkalahatang kaso paggalaw (sa partikular, na may plane-parallel na paggalaw). Isang teorama sa pagbabago sa kinetic energy ng isang mekanikal na sistema sa mga differential at finite forms. Pagkakapantay-pantay sa zero ng kabuuan ng gawain ng mga panloob na pwersa sa isang solid. Trabaho at kapangyarihan ng mga puwersa na inilapat sa isang matibay na katawan na umiikot sa paligid ng isang nakapirming axis. Ang konsepto ng isang force field. Potensyal na patlang ng puwersa at paggana ng puwersa. Pagpapahayag ng mga projection ng puwersa sa pamamagitan ng function ng puwersa. Mga ibabaw ng pantay na potensyal. Sapilitang trabaho sa panghuling paglilipat ng isang punto sa isang potensyal na field ng puwersa. Potensyal na enerhiya. Mga halimbawa ng potensyal na force field: homogeneous gravity field at gravitational field. Ang batas ng konserbasyon ng mekanikal na enerhiya. Matibay na dinamika ng katawan. Differential equation ng translational motion ng isang matibay na katawan. Differential equation ng pag-ikot ng isang matibay na katawan tungkol sa isang nakapirming axis. Pisikal na pendulum. Differential equation para sa paggalaw ng eroplano ng isang matibay na katawan. Ang prinsipyo ng d'Alembert. Prinsipyo ng D'Alembert para sa isang materyal na punto; puwersa ng pagkawalang-galaw. Ang prinsipyo ng d'Alembert para sa isang mekanikal na sistema. Dinadala ang mga puwersa ng pagkawalang-galaw ng mga punto ng isang matibay na katawan sa gitna; pangunahing vector at pangunahing punto pwersa ng pagkawalang-galaw. (Pagpapasiya ng mga dynamic na reaksyon ng mga bearings kapag ang isang matibay na katawan ay umiikot sa paligid ng isang nakapirming axis. Ang kaso kapag ang axis ng pag-ikot ay ang pangunahing gitnang axis ng inertia ng katawan.) Ang prinsipyo ng mga posibleng displacement at ang pangkalahatang equation ng dynamics. Ang mga hadlang na ipinataw sa isang mekanikal na sistema. Mga posibleng (o virtual) na paggalaw ng isang materyal na punto at isang mekanikal na sistema. Ang bilang ng mga antas ng kalayaan ng system. Mga perpektong koneksyon. Ang prinsipyo ng mga posibleng displacements. Pangkalahatang equation ng dynamics. Mga equation ng paggalaw ng system sa pangkalahatan na mga coordinate (Lagrange equation). Pangkalahatang mga coordinate ng system; pangkalahatang bilis. Pagpapahayag ng elementarya na gawain sa pangkalahatan na mga coordinate. Pangkalahatang pwersa at ang kanilang pagkalkula; ang kaso ng mga pwersang may potensyal. Mga kondisyon ng balanse ng system sa mga pangkalahatang coordinate. Differential equation ng motion ng system sa generalised coordinate o Lagrange equation ng pangalawang uri. Lagrange equation sa kaso ng mga potensyal na pwersa; Lagrange function (kinetic potential). Ang konsepto ng katatagan ng ekwilibriyo. Maliit na libreng vibrations ng isang mekanikal na sistema na may isang antas ng kalayaan tungkol sa isang matatag na posisyon ng balanse ng system at ang kanilang mga katangian. Mga elemento ng teorya ng epekto. Kababalaghan ng epekto. Puwersa ng epekto at salpok ng epekto. Puwersa ng epekto sa isang materyal na punto. Ang theorem sa pagbabago sa momentum ng isang mekanikal na sistema sa epekto. Direktang sentral na epekto ng katawan sa isang nakatigil na ibabaw; nababanat at hindi nababanat na mga epekto. Salik sa pagbawi ng epekto at ang pang-eksperimentong pagpapasiya nito. Direktang gitnang suntok ng dalawang katawan. Ang teorama ni Carnot. BIBLIOGRAPIYA Basic Butenin N.V., Lunts Ya- L., Merkin D.R. Kurso ng teoretikal na mekanika. T. 1, 2. M., 1985 at mga nakaraang edisyon. Dobronravov V.V., Nikitin N.N. Kurso ng teoretikal na mekanika. M., 1983. Starzhinsky V.M. Teoretikal na mekanika. M., 1980. Targ S.M.Maikling kurso teoretikal na mekanika. M., 1986 at mga nakaraang edisyon. Yablonsky A.A., Nikiforova V.M. Kurso ng teoretikal na mekanika. Bahagi 1. M., 1984 at mga nakaraang edisyon. A. A. Yablonsky Kurso ng teoretikal na mekanika. Bahagi 2. M., 1984 at mga nakaraang edisyon. I. V. Meshchersky Koleksyon ng mga problema sa theoretical mechanics. M., 1986 at mga nakaraang edisyon. Koleksyon ng mga problema sa theoretical mechanics / Ed. K. S. Kolesnikova. M., 1983. Dagdag Bat M.I., Dzhanelidze G.Yu., Kelzon A.S. Teoretikal na mekanika sa mga halimbawa at problema. Bahagi 1, 2. M., 1984 at mga nakaraang edisyon. Koleksyon ng mga problema sa theoretical mechanics / 5razhnichen / co N.A., Kan V.L., Mintsberg B.L. et al. M., 1987. Novozhilov I.V., Zatsepin M.F. Mga tipikal na kalkulasyon sa theoretical mechanics batay sa isang computer. M., 1986, Koleksyon ng mga gawain para sa mga term paper sa theoretical mechanics / Ed. A. A. Yablonsky. M., 1985 at mga nakaraang edisyon (naglalaman ng mga halimbawa ng paglutas ng problema). Lektura 3. Pangkalahatang theorems ng dynamics Dynamics ng isang sistema ng mga materyal na puntos ay isang mahalagang seksyon ng theoretical mechanics. Pangunahing tinatalakay nito ang mga problema ng paggalaw ng mga mekanikal na sistema (mga sistema ng mga materyal na punto) na may isang tiyak na bilang ng mga antas ng kalayaan - ang maximum na bilang ng mga independiyenteng mga parameter na tumutukoy sa posisyon ng system. Ang pangunahing gawain ng dinamika ng isang sistema ay pag-aralan ang mga batas ng paggalaw ng isang matibay na katawan at mga mekanikal na sistema. Ang pinakasimpleng diskarte sa pag-aaral ng galaw ng isang sistema, na binubuo ng N materyal na mga punto, na bawasan sa pagsasaalang-alang sa mga paggalaw ng bawat indibidwal na punto ng system. Sa kasong ito, dapat matukoy ang lahat ng pwersang kumikilos sa bawat punto ng system, kabilang ang mga puwersa ng pakikipag-ugnayan sa pagitan ng mga punto. Ang pagtukoy sa acceleration ng bawat punto alinsunod sa pangalawang batas ni Newton (1.2), nakukuha namin para sa bawat punto ang tatlong scalar second-order differential laws of motion, i.e. 3 N differential laws of motion para sa buong sistema. Upang mahanap ang mga equation ng paggalaw ng isang mekanikal na sistema para sa mga ibinigay na pwersa at mga paunang kondisyon para sa bawat punto ng system, ang mga resultang kaugalian ng mga batas ay dapat na isama. Ang problemang ito ay mahirap kahit na sa kaso ng dalawang materyal na punto na gumagalaw lamang sa ilalim ng pagkilos ng mga puwersa ng pakikipag-ugnayan ayon sa batas ng unibersal na pagkahumaling (ang problema ng dalawang katawan), at lubhang mahirap sa kaso ng tatlong nakikipag-ugnayan na mga punto (ang problema ng tatlong katawan). Samakatuwid, kinakailangan upang makahanap ng mga pamamaraan para sa paglutas ng mga problema na hahantong sa nalulusaw na mga equation at magbigay ng ideya ng paggalaw ng isang mekanikal na sistema. Pangkalahatang theorems ng dinamika, bilang isang kinahinatnan ng mga kaugalian ng mga batas ng paggalaw, ay nagbibigay-daan sa pag-iwas sa pagiging kumplikado na nagmumula sa pagsasama at pagkuha ng mga kinakailangang resulta. 3. 1. Pangkalahatang pangungusap Ang mga punto ng mekanikal na sistema ay mabibilang sa mga indeks i, j, k at iba pa na tumatakbo sa lahat ng mga halaga 1, 2, 3… N, saan N Ay ang bilang ng mga puntos sa system. Mga pisikal na dami na nauugnay sa k-th point ay ipinahiwatig ng parehong index bilang ang punto. Halimbawa, ipahayag ang radius vector at bilis, ayon sa pagkakabanggit k ika punto. Para sa bawat punto ng system, kumikilos ang mga puwersa ng dobleng pinanggalingan: una, ang mga puwersa na ang mga pinagmumulan ay nasa labas ng system, na tinatawag na panlabas pwersa at itinalaga; pangalawa, ang mga puwersa mula sa ibang mga punto ng sistemang ito, na tinatawag panloob pwersa at itinalaga. Ang mga panloob na puwersa ay nasiyahan sa ikatlong batas ni Newton. Isaalang-alang natin ang pinakasimpleng katangian ng mga panloob na pwersa na kumikilos sa buong sistema ng makina sa alinman sa mga estado nito. Unang ari-arian. Ang geometric na kabuuan ng lahat ng panloob na puwersa ng system (ang pangunahing vector ng mga panloob na puwersa) ay katumbas ng zero.
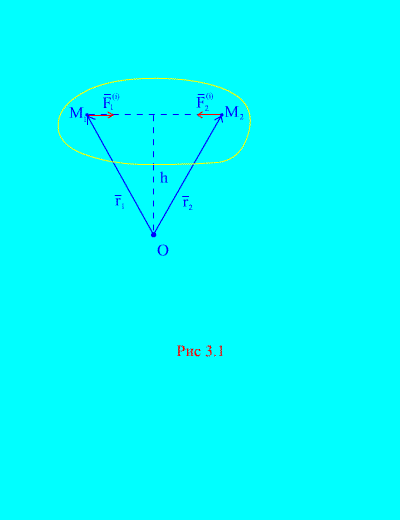
Sa katunayan, kung isasaalang-alang namin ang anumang dalawang di-makatwirang punto ng system, halimbawa, at (fig. 3.1), saka para sa kanila
Pangalawang ari-arian. Ang geometric na kabuuan ng mga sandali ng lahat ng panloob na pwersa na nauugnay sa isang arbitrary na punto sa espasyo ay zero. Isaalang-alang ang sistema ng mga sandali ng mga puwersa at nauugnay sa punto O(fig. 3.1)... Mula sa (fig. 3.1)... malinaw na yan
mula noon ang parehong mga puwersa ay may parehong mga balikat at magkasalungat na direksyon ng mga sandali ng vector. Ang pangunahing sandali ng panloob na pwersa tungkol sa isang punto O ay binubuo ng vector sum ng naturang mga expression at katumbas ng zero. Kaya naman,
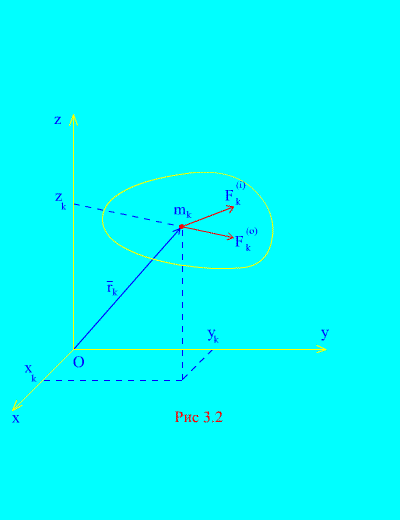
Hayaan ang mga panlabas at panloob na pwersa na kumikilos sa isang mekanikal na sistema na binubuo ng N puntos (fig. 3.2)... Kung ang resulta ng panlabas na puwersa at resulta ng lahat ng panloob na puwersa ay inilapat sa bawat punto ng system, kung gayon para sa alinmang k-th point ng system, maaari kang bumuo ng mga differential equation ng paggalaw. Magkakaroon ng kabuuan ng mga naturang equation N: at sa mga projection sa mga nakapirming axes ng mga coordinate 3 N:
Ang mga vector equation (3.3) o katumbas na scalar equation (3.4) ay kumakatawan sa mga differential laws ng paggalaw ng mga materyal na punto ng buong system. Kung ang lahat ng mga punto ay gumagalaw parallel sa isang eroplano o isang tuwid na linya, ang bilang ng mga equation (3.4) sa unang kaso ay magiging 2 N, sa pangalawa N.
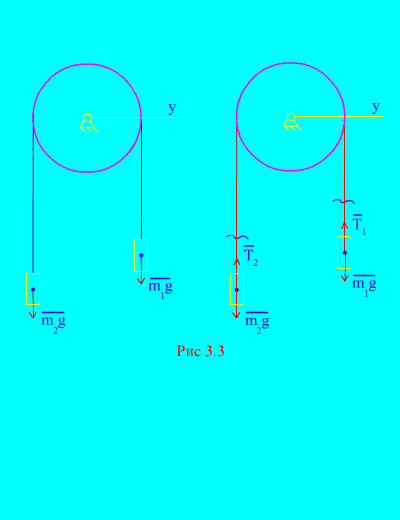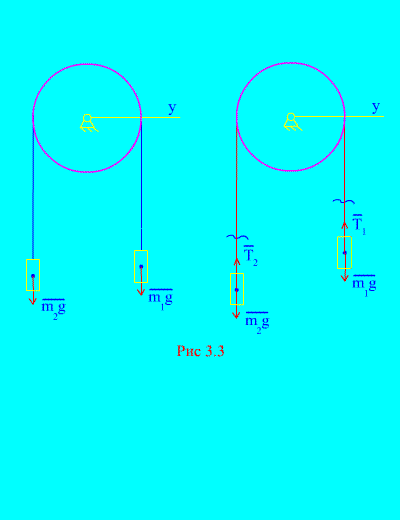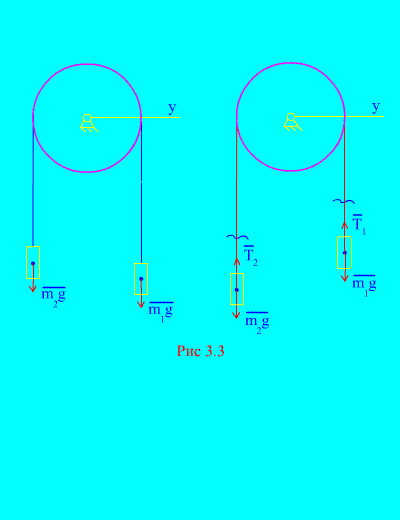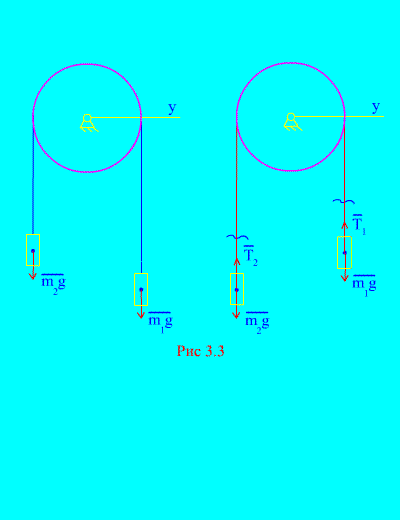
Halimbawa 1. Dalawang pabigat na tumitimbang at magkakaugnay sa pamamagitan ng isang hindi mapalawak na kable na itinapon sa ibabaw ng bloke (fig. 3.3)... Ang pagpapabaya sa mga puwersa ng alitan, pati na rin ang masa ng bloke at cable, matukoy ang batas ng paggalaw ng mga naglo-load at pag-igting ng cable. Solusyon... Binubuo ang system ng dalawang materyal na katawan (nakakonekta sa pamamagitan ng isang hindi mapapahaba na cable) na gumagalaw parallel sa isang axis NS. Isulat natin ang pagkakaiba ng mga batas ng paggalaw sa mga projection sa axis NS para sa lahat. Hayaang bumaba ang tamang timbang sa pagbilis, pagkatapos ay tataas ang kaliwang timbang sa pagbilis. Pinalaya natin ang ating sarili mula sa koneksyon (cable) at pinapalitan ito ng mga reaksyon at (fig. 3.3)... Ipagpalagay na ang mga katawan ay malaya, binubuo namin ang mga kaugalian ng mga batas ng paggalaw sa projection papunta sa axis NS(ibig sabihin, ang mga tensyon ng thread ay panloob na puwersa, at ang bigat ng mga timbang ay panlabas): Dahil at (ang mga katawan ay konektado sa pamamagitan ng isang hindi mapapahaba na cable), nakuha namin Paglutas ng mga equation na ito para sa acceleration at tension ng cable T, nakukuha namin
Tandaan na ang tensyon ng cable ay hindi katumbas ng gravity ng kaukulang load. 3. 2. Theorem sa paggalaw ng sentro ng masa Ito ay kilala na ang isang matibay na katawan at isang mekanikal na sistema sa isang eroplano ay maaaring kumilos nang medyo kumplikado. Ang unang teorama sa paggalaw ng isang katawan at isang mekanikal na sistema ay maaaring maabot tulad ng sumusunod: itapon ang K.-L. isang bagay na binubuo ng maraming matibay na katawan na pinagdikit. Malinaw na lilipad ito sa isang parabola. Inihayag ito nang pag-aralan ang paggalaw ng punto. Gayunpaman, ngayon ang bagay ay hindi isang punto. Ito ay lumiliko, umiindayog habang lumilipad sa paligid ng ilang epektibong sentro, na gumagalaw sa isang parabola. Ang unang teorama sa paggalaw ng mga kumplikadong bagay ay nagsasabi na ang isang tiyak na epektibong sentro ay ang sentro ng masa ng isang gumagalaw na bagay. Ang sentro ng masa ay hindi kinakailangang matatagpuan sa katawan mismo; maaari rin itong nakahiga sa isang lugar sa labas nito. Teorama. Ang sentro ng masa ng isang mekanikal na sistema ay gumagalaw tulad ng isang materyal na punto na may mass na katumbas ng masa ng buong sistema, kung saan ang lahat ng mga panlabas na puwersa na kumikilos sa sistema ay inilalapat. Upang patunayan ang teorama, muling isinulat namin ang pagkakaiba ng mga batas ng paggalaw (3.3) sa sumusunod na anyo:
saan N Ay ang bilang ng mga puntos sa system. Idagdag natin ang mga equation sa mga tuntunin ng bawat isa:
Ang posisyon ng sentro ng masa ng mekanikal na sistema na nauugnay sa napiling sistema ng coordinate ay tinutukoy ng formula (2.1): Ang unang kabuuan sa kanang bahagi ng pagkakapantay-pantay (a) ay katumbas ng pangunahing vector ng mga panlabas na puwersa, at ang huli, sa pamamagitan ng pag-aari ng mga panloob na pwersa, ay katumbas ng zero. Pagkatapos ang pagkakapantay-pantay (a), na isinasaalang-alang ang (b), ay muling isusulat
mga. ang produkto ng masa ng system sa pamamagitan ng pagpabilis ng sentro ng masa nito ay katumbas ng geometric na kabuuan ng lahat ng panlabas na pwersa na kumikilos sa system. Mula sa equation (3.6) sumusunod na ang mga panloob na pwersa ay hindi direktang nakakaapekto sa paggalaw ng sentro ng masa. Gayunpaman, sa ilang mga kaso, sila ang dahilan para sa paglitaw ng mga panlabas na puwersa na inilapat sa system. Kaya, ang mga panloob na puwersa na nagtutulak sa mga gulong sa pagmamaneho ng isang kotse sa pag-ikot ay nagiging sanhi ng isang panlabas na puwersa ng pagdirikit na inilapat sa rim ng gulong upang kumilos dito. Halimbawa 2. Ang mekanismo, na matatagpuan sa isang patayong eroplano, ay naka-install sa isang pahalang na makinis na eroplano at nakakabit dito ng mga bar na mahigpit na naayos sa ibabaw. SA at L (fig. 3.4).
Disc 1 radius R hindi gumagalaw. Disk 2 mass m at radius r fastened sa isang pihitan, haba R+ r sa punto C 2... Ang pihitan ay umiikot sa pare-pareho angular velocity... Sa unang sandali, ang pihitan ay sinakop ang kanan pahalang na posisyon... Hindi pinapansin ang masa ng crank, tukuyin ang pinakamalaking pahalang at patayong pwersa na kumikilos sa mga bar, kung ang kabuuang masa ng kama at gulong 1 ay katumbas ng M. Isaalang-alang din ang pag-uugali ng mekanismo sa kawalan ng mga bar. Solusyon... Ang sistema ay binubuo ng dalawang masa ( N=2 ): isang nakatigil na disk 1 na may kama at isang movable disk 2. Idirekta natin ang axis sa sa pamamagitan ng sentro ng grabidad ng nakatigil na disk patayo pataas, ang axis NS- kasama ang pahalang na eroplano. Isulat natin ang theorem sa motion ng center of mass (3.6) sa coordinate form Ang mga panlabas na puwersa ng sistemang ito ay: ang bigat ng kama at ang nakatigil na disk - Mg, bigat ng gumagalaw na disk - mg, ay ang kabuuang pahalang na reaksyon ng mga bolts; ay ang normal na kabuuang reaksyon ng eroplano. Kaya naman, Pagkatapos ay muling isusulat ang mga batas ng paggalaw (b). Kalkulahin natin ang mga coordinate ng sentro ng masa ng mekanikal na sistema:
tulad ng nakikita mula sa (fig. 3.4), , ,
Ang pagpapalit ng (c) at (e) sa (b), makikita natin
Ang pahalang na presyon na kumikilos sa mga bar ay may pinakamataas at pinakamababang halaga kung kailan cos = 1 ayon sa pagkakabanggit, i.e.
Naka-on ang presyon ng mekanismo pahalang eroplano may pinakamalaki at pinakamaliit na halaga kapag kasalanan ayon sa pagkakabanggit, i.e.
Sa katunayan, ang unang problema ng dinamika ay nalutas na: ayon sa mga kilalang equation ng paggalaw ng sentro ng masa ng sistema (e), ang mga puwersang kasangkot sa paggalaw ay naibalik. Sa kawalan ng mga bar K at L (fig. 3.4), ang mekanismo ay maaaring magsimulang tumalbog sa pahalang na eroplano. Ito ang mangyayari kapag, i.e. kapag, ito ay sumusunod na ang angular velocity ng pag-ikot ng crank, kung saan ang mekanismo ay tumalbog, ay dapat masiyahan ang pagkakapantay-pantay
3. 3. Batas ng konserbasyon ng paggalaw ng sentro ng masa Kung ang pangunahing vector ng mga panlabas na puwersa na kumikilos sa system ay zero, i.e. pagkatapos ay mula sa(3.6)sumusunod na ang acceleration ng center of mass ay zero, samakatuwid, ang velocity ng center of mass ay pare-pareho sa magnitude at direksyon. Kung, sa partikular, sa paunang sandali ang sentro ng masa ay nagpapahinga, kung gayon ito ay nasa pahinga sa buong oras hanggang sa ang pangunahing vector ng mga panlabas na puwersa ay katumbas ng zero. Maraming mga kahihinatnan ang sumusunod mula sa teorama na ito. · Ang mga panloob na pwersa lamang ay hindi maaaring baguhin ang likas na katangian ng paggalaw ng sentro ng masa ng sistema. · Kung ang pangunahing vector ng mga panlabas na puwersa na kumikilos sa sistema ay zero, kung gayon ang sentro ng masa ay nasa pahinga o gumagalaw nang pantay at patuwid. · Kung ang projection ng pangunahing vector ng mga panlabas na puwersa ng system sa ilang nakapirming axis ay katumbas ng zero, kung gayon ang projection ng bilis ng sentro ng masa ng system sa axis na ito ay hindi nagbabago. · Ang isang pares ng mga puwersa na inilapat sa isang matibay na katawan ay hindi maaaring baguhin ang paggalaw ng sentro ng masa nito (maaari lamang itong maging sanhi ng pag-ikot ng katawan sa paligid ng sentro ng masa). Isaalang-alang natin ang isang halimbawa na naglalarawan ng batas ng konserbasyon ng paggalaw ng sentro ng masa.
Halimbawa 3. Ang dalawang pabigat ay masa at pinagdugtong ng isang hindi mapalawak na sinulid na inihagis sa ibabaw ng bloke (fig. 3.5) naka-mount sa isang wedge na may masa M. Ang wedge ay nakasalalay sa isang makinis na pahalang na eroplano. Sa unang sandali, ang sistema ay nagpapahinga. Hanapin ang displacement ng wedge sa kahabaan ng eroplano kapag ang unang load ay ibinaba sa isang taas N. Huwag pansinin ang masa ng bloke at sinulid. Solusyon. Ang mga panlabas na puwersa na kumikilos sa wedge kasama ang mga timbang ay ang mga puwersa ng grabidad, at Mg, pati na rin ang normal na reaksyon ng isang makinis na pahalang na ibabaw N. Samakatuwid, Dahil sa unang sandali ang sistema ay nagpapahinga, mayroon kami. Kalkulahin natin ang coordinate ng sentro ng masa ng sistema sa at sa sandaling ito t 1 kapag tumitimbang ang load g bumaba sa isang taas H. Sa sandaling ito:
saan , , NS- ayon sa pagkakabanggit, ang mga coordinate ng sentro ng masa ng mga load na tumitimbang ng g, g at wedge weight Mg. Ipagpalagay na ang wedge sa sandali ng oras ay gumagalaw sa positibong direksyon ng axis baka sa dami L kung ang timbang ay bumaba sa isang taas N. Pagkatapos, pansamantala mula noon ang mga load kasama ang wedge ay lilipat sa L sa kanan, at ang pagkarga ay lilipat paitaas kasama ang wedge. Dahil, pagkatapos ng mga kalkulasyon na nakukuha namin
3.4. Dami ng Paggalaw ng System 3.4.1. Kinakalkula ang dami ng paggalaw ng system Ang dami ng paggalaw ng isang materyal na punto ay isang dami ng vector na katumbas ng produkto ng masa ng isang punto sa pamamagitan ng vector ng bilis nito Unit ng paggalaw - Ang dami ng paggalaw ng isang mekanikal na sistema ay tinatawag na vector sum ng dami ng paggalaw ng mga indibidwal na punto ng system, i.e. saan N Ay ang bilang ng mga puntos sa system. Ang dami ng paggalaw ng isang mekanikal na sistema ay maaaring ipahayag sa mga tuntunin ng masa ng sistema M at ang bilis ng sentro ng masa. Talaga, mga. ang momentum ng sistema ay katumbas ng produkto ng masa ng buong sistema sa bilis ng sentro ng masa nito. Ang direksyon ay pareho sa direksyon (fig. 3.6)
Sa mga projection sa mga hugis-parihaba na palakol, mayroon kami kung saan,, ay ang mga projection ng bilis ng sentro ng masa ng system. Dito M- ang masa ng mekanikal na sistema; hindi nagbabago kapag gumagalaw ang system. Ang mga resultang ito ay lalong kapaki-pakinabang kapag kinakalkula ang mga dami ng paggalaw ng mga matibay na katawan. Makikita mula sa formula (3.7) na kung ang isang mekanikal na sistema ay gumagalaw upang ang sentro ng masa nito ay nananatiling nakatigil, kung gayon ang momentum ng sistema ay nananatiling zero. 3.4.2. Elementarya at buong salpok ng puwersa Ang pagkilos ng isang puwersa sa isang materyal na punto sa paglipas ng panahon dt maaaring mailalarawan sa pamamagitan ng isang elementarya na salpok. Buong salpok ng kapangyarihan sa paglipas ng panahon t, o ang salpok ng puwersa, ay tinutukoy ng formula o sa mga projection sa mga coordinate ng axis
Ang yunit ng puwersa ng salpok ay. 3.4.3. Ang theorem sa pagbabago sa dami ng paggalaw ng system Hayaang mailapat ang mga panlabas at panloob na puwersa sa mga punto ng system. Pagkatapos, para sa bawat punto ng sistema ay maaaring ilapat ng isa ang mga kaugalian ng mga batas ng paggalaw (3.3), na isinasaisip na
Summing sa lahat ng mga punto ng system, nakukuha namin Sa pamamagitan ng pag-aari ng mga panloob na pwersa at sa pamamagitan ng kahulugan
Pagpaparami ng magkabilang panig ng equation na ito sa pamamagitan ng dt, nakakakuha tayo ng theorem sa pagbabago ng momentum sa differential form:
mga. ang pagkakaiba ng momentum ng isang mekanikal na sistema ay katumbas ng kabuuan ng vector ng mga elementarya na impulses ng lahat ng mga panlabas na puwersa na kumikilos sa mga punto ng mekanikal na sistema. Kinakalkula ang integral ng magkabilang panig ng (3.10) sa paglipas ng panahon mula 0 hanggang t, makuha natin ang teorama sa may hangganan o integral na anyo
Sa mga projection papunta sa coordinate axes, magkakaroon tayo Pagbabago sa dami ng paggalaw ng isang mekanikal na sistema sa paglipas ng panahont, ay katumbas ng vector sum ng lahat ng impulses ng mga panlabas na puwersa na kumikilos sa mga punto ng mekanikal na sistema sa parehong oras. Halimbawa 4. Mass weight m bumababa sa isang hilig na eroplano mula sa pahinga sa ilalim ng pagkilos ng puwersa F, proporsyonal sa oras: saan (fig. 3.7)... Anong bilis ang mararating ng katawan t segundo pagkatapos ng pagsisimula ng paggalaw, kung ang koepisyent ng sliding friction ng load sa inclined plane ay f.
Solusyon. Ilarawan natin ang mga puwersang inilapat sa pagkarga: mg - ang puwersa ng gravity ng load, N Ay ang normal na reaksyon ng eroplano, ay ang sliding friction force ng load sa eroplano, at. Ang direksyon ng lahat ng pwersa ay inilalarawan sa (fig. 3.7). Idirekta natin ang axis NS kasama ang inclined plane pababa. Isulat natin ang theorem sa pagbabago sa momentum (3.11) sa projection sa axis NS:
Sa kondisyon, mula noon sa unang sandali ng oras, ang pagkarga ay nakapahinga. Ang kabuuan ng mga projection ng mga impulses ng lahat ng pwersa sa x-axis ay
Kaya naman,
3.4.4. Ang mga batas ng konserbasyon ng momentum Ang mga batas sa konserbasyon ay nakuha bilang mga espesyal na kaso ng theorem tungkol sa pagbabago ng momentum. Dalawang espesyal na kaso ang posible. · Kung ang kabuuan ng vector ng lahat ng panlabas na puwersa na inilapat sa sistema ay zero, i.e. , kung gayon ang teorama ay nagpapahiwatig (3.9) , Ano , mga. kung ang pangunahing vector ng mga panlabas na puwersa ng system ay katumbas ng zero, kung gayon ang momentum ng system ay pare-pareho sa magnitude at direksyon. · Kung ang projection ng pangunahing vector ng mga panlabas na pwersa sa anumang coordinate axis ay katumbas ng zero, halimbawa, Oh, i.e. , pagkatapos ay pare-pareho ang projection ng momentum sa axis na ito. Isaalang-alang natin ang isang halimbawa ng aplikasyon ng batas ng konserbasyon ng momentum.
Halimbawa 5. Ang ballistic pendulum ay isang katawan ng masa na sinuspinde ng mahabang sinulid (fig. 3.8). Bullet na may mass na gumagalaw sa bilis V at nahuhulog sa isang hindi gumagalaw na katawan, natigil dito, at ang katawan ay napalihis. Ano ang bilis ng bala kung tumaas ang katawan sa taas h ? Solusyon. Hayaang makakuha ng bilis ang katawan na may nakaipit na bala. Pagkatapos, gamit ang batas ng konserbasyon ng momentum sa pakikipag-ugnayan ng dalawang katawan, maaari tayong sumulat Ang bilis ay maaaring kalkulahin gamit ang batas ng konserbasyon ng mekanikal na enerhiya
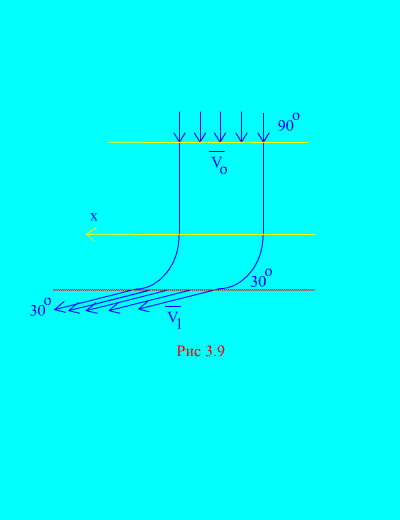
Halimbawa 6... Ang tubig ay pumapasok sa isang nakapirming channel (fig. 3.9) variable na seksyon na may bilis sa isang anggulo sa abot-tanaw; cross-sectional area ng channel sa pasukan; ang bilis ng tubig sa labasan mula sa channel at gumagawa ng isang anggulo sa abot-tanaw. Tukuyin ang pahalang na bahagi ng reaksyon na mayroon ang tubig sa mga dingding ng channel. Densidad ng tubig Solusyon. Matutukoy namin ang pahalang na bahagi ng reaksyon ng mga pader ng channel sa tubig. Ang puwersang ito ay katumbas ng magnitude at kabaligtaran ng tanda sa kinakailangang puwersa. Mayroon kaming, ayon sa (3.11a),
Kinakalkula namin ang masa ng dami ng likido na pumapasok sa channel sa oras na t: Ang halaga rАV 0 ay tinatawag pangalawang masa - ang masa ng likido na dumadaloy sa anumang seksyon ng tubo bawat yunit ng oras. Ang parehong dami ng tubig ay umaalis sa kanal sa parehong oras. Ang paunang at panghuling bilis ay ibinibigay sa kondisyon. Kalkulahin natin ang kanang bahagi ng pagkakapantay-pantay (a) na tumutukoy sa kabuuan ng mga projection sa pahalang na axis ng mga panlabas na puwersa na inilapat sa system (tubig). Ang tanging pahalang na puwersa ay ang pahalang na bahagi ng resultang reaksyon ng pader R x... Ang puwersang ito ay pare-pareho sa isang tuluy-tuloy na daloy ng tubig. kaya lang
Ang pagpapalit ng (b) at (c) sa (a), makuha namin 3.5. Kinetic moment ng system 3.5.1. Ang pangunahing sandali ng momentum ng system
Hayaan ang radius vector ng isang punto na may mass ng system na may kaugnayan sa ilang punto A, na tinatawag na sentro (fig. 3.10). Ang angular momentum (kinetic moment) ng punto kaugnay sa sentro A ay tinatawag na vector , tinutukoy ng formula
Bukod dito, ang vector nakadirekta patayo sa eroplanong dumadaan sa gitna A at vector . Ang angular momentum (angular momentum) ng isang punto na nauugnay sa axis ay tinatawag na projection sa axis na ito ng angular momentum ng isang punto na may kaugnayan sa anumang sentro na pinili sa isang ibinigay na axis. Ang pangunahing sandali ng momentum (kinetic moment) ng system na may kaugnayan sa sentro A tinatawag na halaga
Ang pangunahing sandali ng momentum (kinetic moment) ng system tungkol sa axis ay tinatawag na projection papunta sa axis na ito ng pangunahing sandali ng momentum ng system na nauugnay sa anumang napili sa isang naibigay gitnang axis. 3.5.2. Kinetic moment ng isang umiikot na matibay na katawan tungkol sa axis ng pag-ikot Mga katugmang nakapirming punto O katawan na nakahiga sa axis ng pag-ikot Oz, na may pinagmulan ng coordinate system Oohz, ang mga palakol nito ay iikot kasama ng katawan (fig. 3.11)... Hayaan ang radius vector ng isang punto ng katawan na may kaugnayan sa pinagmulan, at tukuyin ang projection nito sa axis sa pamamagitan ng,,. Ang mga projection ng vector ng angular velocity ng katawan sa parehong axes ay ilalarawan ng 0, 0, (). Pangkalahatang theorems ng dinamika ng isang sistema ng mga katawan. Theorems tungkol sa paggalaw ng sentro ng masa, tungkol sa pagbabago ng momentum, tungkol sa pagbabago ng pangunahing sandali ng momentum, tungkol sa pagbabago ng kinetic energy. Mga prinsipyo at posibleng paglilipat ni D'Alembert. Pangkalahatang equation ng dynamics. Lagrange equation. Pangkalahatang theorems ng dynamics ng isang matibay na katawan at isang sistema ng mga katawanPangkalahatang theorems ng dynamics- ito ay isang theorem sa paggalaw ng sentro ng masa ng isang mekanikal na sistema, isang teorem sa isang pagbabago sa dami ng paggalaw, isang teorem sa isang pagbabago sa pangunahing sandali ng momentum (angular momentum) at isang teorem sa isang pagbabago sa kinetic energy ng isang mekanikal na sistema. Ang teorama sa paggalaw ng sentro ng masa ng isang mekanikal na sistemaAng teorama sa paggalaw ng sentro ng masa. Narito ang M ay ang masa ng system: Ang teorama sa pagbabago sa dami ng paggalaw (momentum)Ang dami ng paggalaw (impulse) ng system ay katumbas ng produkto ng masa ng buong sistema sa pamamagitan ng bilis ng sentro ng masa nito o ang kabuuan ng momentum (kabuuan ng mga impulses) ng mga indibidwal na punto o bahagi na bumubuo sa sistema: Ang theorem sa pagbabago sa momentum sa differential form. Ang theorem sa pagbabago ng momentum sa integral form. Ang batas ng konserbasyon ng momentum (momentum). Kung ang kabuuan ng mga projection ng mga panlabas na puwersa sa anumang axis ay katumbas ng zero, kung gayon ang projection ng momentum ng system sa axis na ito ay magiging pare-pareho. Ang theorem sa pagbabago ng pangunahing sandali ng momentum (ang theorem ng mga sandali)Ang pangunahing sandali ng momentum ng system na may paggalang sa isang naibigay na sentro O ay tinatawag na isang halaga na katumbas ng vector sum ng mga sandali ng mga dami ng paggalaw ng lahat ng mga punto ng system na may kaugnayan sa sentro na ito: Mga nakapirming sistemaAng sumusunod na theorem ay tumutukoy sa kaso kapag ang mekanikal na sistema ay may nakapirming punto o axis, na naayos na may kaugnayan sa inertial frame ng sanggunian. Halimbawa, ang isang katawan na naayos na may isang spherical na tindig. O isang sistema ng mga katawan na gumagalaw sa isang nakapirming sentro. Maaari rin itong isang nakapirming axis sa paligid kung saan umiikot ang isang katawan o isang sistema ng mga katawan. Sa kasong ito, ang mga sandali ay dapat na maunawaan bilang ang mga sandali ng salpok at pwersa na nauugnay sa nakapirming axis. Ang theorem sa pagbabago ng pangunahing sandali ng momentum (ang theorem ng mga sandali) Ang batas ng konserbasyon ng pangunahing angular momentum (angular momentum). Kung ang kabuuan ng mga sandali ng mga panlabas na puwersa na may paggalang sa ilang nakapirming axis ay katumbas ng zero, kung gayon ang sandali ng momentum ng system na may paggalang sa axis na ito ay magiging pare-pareho. Mga sistemang arbitraryoAng susunod na teorama ay unibersal. Naaangkop ito sa parehong mga nakapirming system at malayang gumagalaw. Sa kaso ng mga naka-angkla na sistema, kinakailangang isaalang-alang ang mga reaksyon ng mga bono sa mga naka-angkla na punto. Ito ay naiiba sa naunang teorama sa halip na ang nakapirming puntong O, ang isa ay dapat kunin ang sentro ng mass C ng sistema. Center of Mass Moment Theorem Ang batas ng konserbasyon ng angular momentum. Body moment of inertiaKung umiikot ang katawan sa paligid ng z-axis na may angular velocity ω z, pagkatapos ang angular momentum nito (angular momentum) na may kaugnayan sa z axis ay tinutukoy ng formula: Moment of inertia ng isang katawan tungkol sa z-axis tinutukoy ng formula: Steiner-Huygens theorem. Mas pangkalahatan: Ang theorem sa pagbabago sa kinetic energyHayaang ang isang katawan ng mass M ay magsagawa ng translational at rotational motion na may angular velocity ω sa paligid ng ilang axis z. Pagkatapos ang kinetic energy ng katawan ay tinutukoy ng formula: Isang theorem sa pagbabago sa kinetic energy ng isang system sa differential form. Ang theorem sa pagbabago sa kinetic energy ng system sa integral form. Ang gawain na ginagawa ng kapangyarihan, ay katumbas ng scalar product ng force vectors at ang infinitesimal na displacement ng punto ng aplikasyon nito: Ang gawain na ginagawa ng sandali ng mga puwersa, ay katumbas ng scalar product ng mga vectors ng moment at ang infinitesimal na anggulo ng pag-ikot: Prinsipyo ng D'AlembertAng kakanyahan ng prinsipyo ng d'Alembert ay upang bawasan ang mga problema ng dynamics sa mga problema ng statics. Para dito, ipinapalagay (o ito ay kilala nang maaga) na ang mga katawan ng system ay may ilang (angular) accelerations. Susunod, ang mga inertial na pwersa at (o) mga sandali ng mga puwersa ng pagkawalang-galaw ay ipinakilala, na katumbas ng magnitude at kabaligtaran ng direksyon sa mga puwersa at mga sandali ng mga puwersa, na, ayon sa mga batas ng mekanika, ay lilikha ng mga tinukoy na acceleration o angular accelerations. Tingnan natin ang isang halimbawa. Sa daan, ang katawan ay gumagawa ng pasulong na paggalaw at ang mga panlabas na puwersa ay kumikilos dito. Dagdag pa, ipinapalagay namin na ang mga puwersang ito ay lumilikha ng acceleration ng sentro ng masa ng system. Ayon sa theorem sa paggalaw ng sentro ng masa, ang sentro ng masa ng isang katawan ay magkakaroon ng parehong acceleration kung ang isang puwersa ay kumilos sa katawan. Susunod, ipinakilala namin ang puwersa ng pagkawalang-galaw: Para sa rotary motion, magpatuloy sa parehong paraan. Hayaang umikot ang katawan sa paligid ng z-axis at ang mga panlabas na sandali ng mga pwersang M e zk ay kumilos dito. Ipinapalagay namin na ang mga sandaling ito ay lumilikha ng isang angular acceleration ε z. Susunod, ipinakilala namin ang sandali ng mga puwersa ng inertia M И = - J z ε z. Pagkatapos nito, ang problema sa dinamika: Ang prinsipyo ng mga posibleng displacementsAng prinsipyo ng posibleng mga displacement ay ginagamit upang malutas ang mga static na problema. Sa ilang mga problema, nagbibigay ito ng mas maikling solusyon kaysa sa equation ng equilibrium. Ito ay totoo lalo na para sa mga system na may mga hadlang (halimbawa, mga sistema ng mga katawan na konektado ng mga thread at mga bloke), na binubuo ng maraming mga katawan Ang prinsipyo ng mga posibleng displacements. Posibleng paggalaw ng system- ito ay isang maliit na displacement, na hindi masira ang mga koneksyon na ipinataw sa system. Mga perpektong koneksyon- ito ay mga koneksyon na hindi gumaganap ng trabaho kapag ang sistema ay inilipat. Mas tiyak, ang dami ng trabahong ginawa ng mga link mismo kapag gumagalaw ang system ay katumbas ng zero. Pangkalahatang equation ng dynamics (d'Alembert - Lagrange na prinsipyo)Ang prinsipyo ng d'Alembert-Lagrange ay isang kumbinasyon ng prinsipyo ng d'Alembert na may prinsipyo ng posibleng mga displacement. Iyon ay, kapag nilulutas ang problema ng dynamics, ipinakilala namin ang mga puwersa ng pagkawalang-galaw at binabawasan ang problema sa problema ng statics, na nilulutas namin gamit ang prinsipyo ng posibleng mga displacement. D'Alembert - Prinsipyo ng Lagrange. Mga Equation ng LagrangePangkalahatang mga coordinate q 1, q 2, ..., q n ay isang koleksyon ng mga n value na natatanging tumutukoy sa posisyon ng system. Ang bilang ng mga pangkalahatang coordinate n ay tumutugma sa bilang ng mga antas ng kalayaan ng system. Mga pangkalahatang bilis ay mga derivatives ng mga pangkalahatang coordinate na may paggalang sa oras t. Pangkalahatang pwersa Q 1, Q 2, ..., Q n
. Kung, sa isang posibleng paggalaw ng system, nagbabago ang lahat ng mga coordinate, kung gayon ang gawaing isinagawa ng mga panlabas na puwersa sa panahon ng naturang paggalaw ay may anyo: Para sa mga potensyal na pwersa may potensyal na Π, Mga Equation ng Lagrange ay ang mga equation ng paggalaw ng isang mekanikal na sistema sa pangkalahatang mga coordinate: Narito ang T ay kinetic energy. Ito ay isang function ng mga pangkalahatang coordinate, bilis, at posibleng oras. Samakatuwid, ang partial derivative nito ay isang function din ng generalized coordinates, velocities at time. Dagdag pa, kailangan mong isaalang-alang na ang mga coordinate at bilis ay mga function ng oras. Samakatuwid, upang mahanap ang kabuuang derivative ng oras, kinakailangan na ilapat ang panuntunan para sa pagkakaiba-iba ng isang kumplikadong function: Mga sanggunian: Sa isang malaking bilang ng mga materyal na punto na bahagi ng isang mekanikal na sistema, o kung kabilang dito ang ganap na matibay na mga katawan () na nagsasagawa ng di-translational na paggalaw, ang paggamit ng isang sistema ng mga differential equation ng paggalaw sa paglutas ng pangunahing problema ng dynamics ng ang isang mekanikal na sistema ay lumalabas na halos hindi praktikal. Gayunpaman, kapag nilulutas ang maraming mga problema sa engineering, hindi na kailangang matukoy nang hiwalay ang paggalaw ng bawat punto ng mekanikal na sistema. Minsan sapat na upang makagawa ng mga konklusyon tungkol sa pinakamahalagang aspeto ng pinag-aralan na proseso ng paggalaw nang hindi ganap na nilulutas ang sistema ng mga equation ng paggalaw. Ang mga konklusyong ito mula sa mga differential equation ng paggalaw ng isang mekanikal na sistema ay bumubuo sa nilalaman ng mga pangkalahatang theorems ng dinamika. Pangkalahatang theorems, una, release mula sa pangangailangan sa bawat indibidwal na kaso upang isakatuparan ang mga mathematical transformations na karaniwan para sa iba't ibang mga problema at ang mga ito ay ginanap nang isang beses at para sa lahat kapag kumukuha ng theorems mula sa differential equation ng paggalaw. Pangalawa, ang mga pangkalahatang teorema ay nagbibigay ng koneksyon sa pagitan ng mga pangkalahatang pinagsama-samang katangian ng paggalaw ng isang mekanikal na sistema, na may malinaw na pisikal na kahulugan. Ang mga ito Pangkalahatang katangian, tulad ng momentum, angular momentum, kinetic energy ng isang mekanikal na sistema ay tinatawag mga sukat ng paggalaw ng mekanikal na sistema. Ang unang sukat ng paggalaw ay ang dami ng paggalaw ng isang mekanikal na sistema
Ang dami ng paggalaw ng isang materyal na punto ay ang sukat ng vector ng paggalaw nito, katumbas ng produkto ng masa ng punto sa pamamagitan ng bilis nito:
Ang dami ng paggalaw ng isang mekanikal na sistema ay ang sukat ng vector ng paggalaw nito, katumbas ng kabuuan ng mga dami ng paggalaw ng mga punto nito:
Binabago namin ang kanang bahagi ng formula (23.1): saan Kaya naman, ang momentum ng isang mekanikal na sistema ay katumbas ng momentum ng sentro ng masa nito, kung ang buong masa ng sistema ay puro dito:
Salpok ng puwersaAng produkto ng isang puwersa sa pamamagitan ng isang elementarya na yugto ng panahon ng pagkilos nito Simbuyo ng kapangyarihan
Ang theorem sa pagbabago sa momentum ng isang mekanikal na sistemaHayaan para sa bawat punto Isaalang-alang ang mga pangunahing equation ng dynamics ng isang mekanikal na sistema Pagdaragdag ng term-by-term equation (13.2) para sa n puntos ng system, nakukuha namin
Ang unang kabuuan sa kanan ay katumbas ng pangunahing vector Kaya, nakukuha namin ang:
o sa mga projection sa coordinate axes
Ang mga pagkakapantay-pantay (13.4) at (13.5) ay nagpapahayag ng teorama sa pagbabago sa momentum ng isang mekanikal na sistema: Ang derivative ng oras ng momentum ng mekanikal na sistema ay katumbas ng pangunahing vector ng lahat ng panlabas na puwersa ng mekanikal na sistema. Ang teorama na ito ay maaari ding ipakita sa integral na anyo sa pamamagitan ng pagsasama ng magkabilang panig ng pagkakapantay-pantay (13.4) sa paglipas ng panahon sa saklaw mula sa t 0 hanggang t:
saan oras t-t 0 . Ang pagkakapantay-pantay (13.6) ay kumakatawan sa theorem sa integral form: Ang pagtaas sa momentum ng isang mekanikal na sistema sa isang takdang panahon ay katumbas ng salpok ng mga panlabas na puwersa sa panahong ito. Ang teorama ay tinatawag din ang impulse theorem. Sa mga projection sa coordinate axes, ang theorem ay nakasulat sa form: Mga kahihinatnan (mga batas ng konserbasyon ng momentum) 1). Kung ang pangunahing vector ng mga panlabas na puwersa para sa isinasaalang-alang na tagal ng panahon ay katumbas ng zero, kung gayon ang momentum ng mekanikal na sistema ay pare-pareho, i.e. kung 2). Kung ang projection ng pangunahing vector ng mga panlabas na puwersa sa anumang axis sa ibabaw ng itinuturing na agwat ng oras ay katumbas ng zero, kung gayon ang projection ng momentum ng mekanikal na sistema sa axis na ito ay pare-pareho, mga. kung |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sikat:
Bago
- Sorpresa para sa isang mahal sa buhay sa kanyang kaarawan - mga ideya ng pinakamahusay na sorpresa para sa isang lalaki
- Wastong nutrisyon para sa mga batang may kabag - ano ang posible at ano ang hindi?
- Ang kasarian ng bata sa pamamagitan ng tibok ng puso - posible bang malaman?
- Pagtukoy sa kasarian ng bata sa pamamagitan ng tibok ng puso
- Paano gumawa ng diyeta para sa isang bata na may gastritis: pangkalahatang rekomendasyon
- LAHAT tungkol sa osteochondrosis: ano ito, sanhi, sintomas, uri, paggamot
- Ano ang tamang paraan ng pag-uugali sa isang lalaki upang siya ay umibig?
- Bogatyrs ng lupain ng Russia - listahan, kasaysayan at mga kagiliw-giliw na katotohanan
- Organisasyon ng mga aktibidad sa negosyo
- "Hindi kilalang" mga bayani ng Russia




 .
. (a)
(a) saan M Ay ang masa ng sistema. Pagkatapos ay isusulat ang kaliwang bahagi ng pagkakapantay-pantay (a).
saan M Ay ang masa ng sistema. Pagkatapos ay isusulat ang kaliwang bahagi ng pagkakapantay-pantay (a).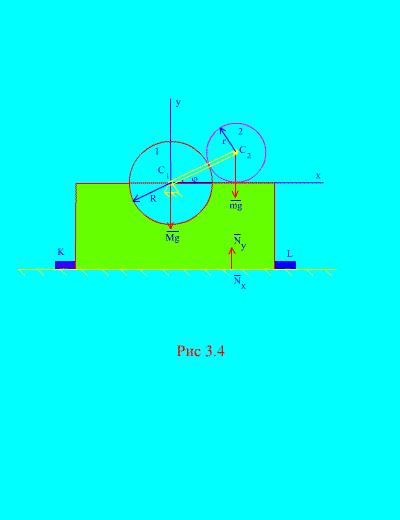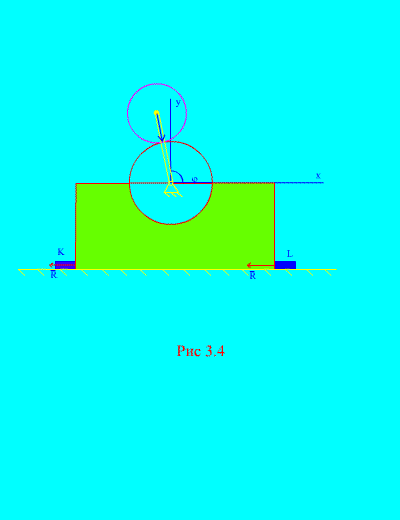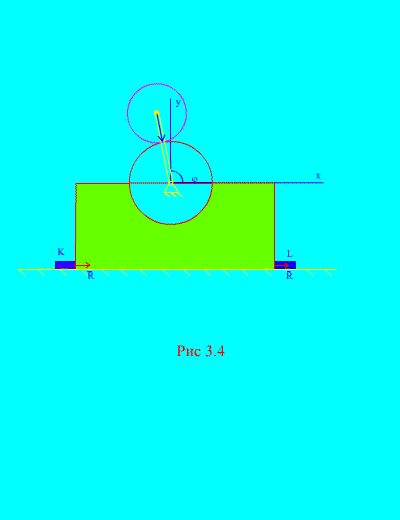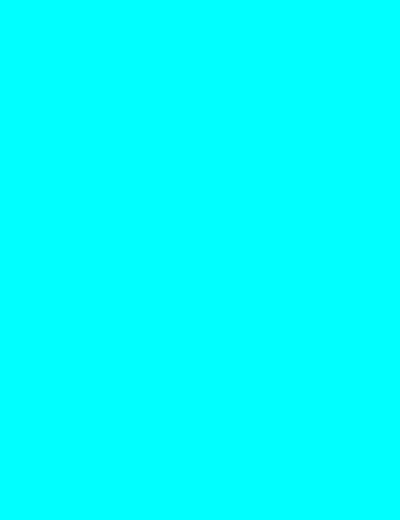
 ; (G)
; (G) (e)
(e)
 .
.
 ,
, .
.
 (3.8a)
(3.8a) .
. (3.9)
(3.9) (3.11)
(3.11)
 (a)
(a)
 ,
, .
.
 ... Tapos . Bilang resulta, nahanap namin
... Tapos . Bilang resulta, nahanap namin .
.
 .
. ... (a)
... (a) ... (v)
... (v)
 (3.13)
(3.13)


 materyal na puntos
materyal na puntos  .Ang posisyon ng bawat punto ng masa
.Ang posisyon ng bawat punto ng masa  ay tinukoy sa inertial reference frame
ay tinukoy sa inertial reference frame  radius vector
radius vector  (fig.13.1) .
Hayaan
(fig.13.1) .
Hayaan  - bilis ng punto
- bilis ng punto  .
. .
. , (13.1)
, (13.1) - ang masa ng buong sistema,
- ang masa ng buong sistema,  ay ang bilis ng sentro ng masa.
ay ang bilis ng sentro ng masa. .
. ay tinatawag na elementary impulse of force.
ay tinatawag na elementary impulse of force. sa loob ng isang yugto ng panahon ay tinatawag na integral ng elementarya na salpok ng puwersa
sa loob ng isang yugto ng panahon ay tinatawag na integral ng elementarya na salpok ng puwersa .
. ang mekanikal na sistema ay ginagampanan ng resulta ng mga panlabas na puwersa
ang mekanikal na sistema ay ginagampanan ng resulta ng mga panlabas na puwersa  at ang resulta ng mga panloob na pwersa
at ang resulta ng mga panloob na pwersa  .
. (13.3)
(13.3) panlabas na puwersa ng sistema. Ang pangalawang kabuuan ay katumbas ng zero sa pamamagitan ng pag-aari ng mga panloob na puwersa ng system. Isipin mo
panlabas na puwersa ng sistema. Ang pangalawang kabuuan ay katumbas ng zero sa pamamagitan ng pag-aari ng mga panloob na puwersa ng system. Isipin mo  , (13.4)
, (13.4) (13.5)
(13.5) , (13.6)
, (13.6) , at ang integral sa kanang bahagi ay ang salpok ng mga panlabas na pwersa sa likod
, at ang integral sa kanang bahagi ay ang salpok ng mga panlabas na pwersa sa likod ,
, .
. pagkatapos
pagkatapos  .
.




