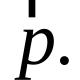Toute expression fractionnaire (article 48) peut être écrite sous la forme , où P et Q sont des expressions rationnelles et Q contient nécessairement des variables. Une telle fraction est appelée fraction rationnelle.

Exemples de fractions rationnelles :

La propriété principale d'une fraction s'exprime par une identité qui est juste dans les conditions ici - une expression rationnelle globale. Cela signifie que le numérateur et le dénominateur d'une fraction rationnelle peuvent être multipliés ou divisés par le même nombre non nul, monôme ou polynôme.

Par exemple, la propriété d’une fraction peut être utilisée pour modifier les signes des membres d’une fraction. Si le numérateur et le dénominateur d'une fraction sont multipliés par -1, nous obtenons Ainsi, la valeur de la fraction ne changera pas si les signes du numérateur et du dénominateur sont modifiés simultanément. Si vous changez le signe uniquement du numérateur ou uniquement du dénominateur, alors la fraction changera de signe :

Par exemple,

60. Réduire les fractions rationnelles.

Réduire une fraction signifie diviser le numérateur et le dénominateur de la fraction par un facteur commun. La possibilité d’une telle réduction est due à la propriété fondamentale de la fraction.

Afin de réduire une fraction rationnelle, vous devez factoriser le numérateur et le dénominateur. S'il s'avère que le numérateur et le dénominateur ont des facteurs communs, la fraction peut être réduite. S’il n’y a pas de facteurs communs, la conversion d’une fraction par réduction est impossible.

Exemple. Réduire une fraction

Solution. Nous avons

La réduction d'une fraction s'effectue sous la condition .

61. Réduire les fractions rationnelles à un dénominateur commun.

Le dénominateur commun de plusieurs fractions rationnelles est l'ensemble de l'expression rationnelle, qui est divisée par le dénominateur de chaque fraction (voir paragraphe 54).

Par exemple, le dénominateur commun des fractions est un polynôme puisqu'il est divisible à la fois par et par et polynôme et polynôme et polynôme, etc. Habituellement, ils prennent un dénominateur commun tel que tout autre dénominateur commun est divisible par Echosen. Ce dénominateur le plus simple est parfois appelé le plus petit dénominateur commun.

Dans l’exemple discuté ci-dessus, le dénominateur commun est Nous avons

La réduction de ces fractions à un dénominateur commun est obtenue en multipliant le numérateur et le dénominateur de la première fraction par 2. et le numérateur et le dénominateur de la deuxième fraction par Les polynômes sont appelés facteurs supplémentaires pour la première et la deuxième fraction, respectivement. Le facteur supplémentaire pour une fraction donnée est égal au quotient de la division du dénominateur commun par le dénominateur de la fraction donnée.

Pour réduire plusieurs fractions rationnelles à un dénominateur commun, il vous faut :

1) factoriser le dénominateur de chaque fraction ;

2) créer un dénominateur commun en incluant comme facteurs tous les facteurs obtenus à l'étape 1) des développements ; si un certain facteur est présent dans plusieurs développements, alors il est pris avec un exposant égal au plus grand de ceux disponibles ;

3) trouver des facteurs supplémentaires pour chacune des fractions (pour cela, le dénominateur commun est divisé par le dénominateur de la fraction) ;

4) en multipliant le numérateur et le dénominateur de chaque fraction par un facteur supplémentaire, ramener la fraction à un dénominateur commun.

Exemple. Réduire une fraction à un dénominateur commun

Solution. Factorisons les dénominateurs :

Les facteurs suivants doivent être inclus dans le dénominateur commun : et le plus petit commun multiple des nombres 12, 18, 24, soit Cela signifie que le dénominateur commun a la forme

Facteurs supplémentaires : pour la première fraction pour la seconde pour la troisième On obtient donc :

62. Addition et soustraction de fractions rationnelles.

La somme de deux (et en général de tout nombre fini) fractions rationnelles de mêmes dénominateurs est identiquement égale à une fraction de même dénominateur et de numérateur égal à la somme des numérateurs des fractions additionnées :

La situation est similaire dans le cas de la soustraction de fractions ayant les mêmes dénominateurs :

Exemple 1 : simplifier une expression

Solution.

Pour additionner ou soustraire des fractions rationnelles avec des dénominateurs différents, vous devez d'abord réduire les fractions à un dénominateur commun, puis effectuer des opérations sur les fractions résultantes avec les mêmes dénominateurs.

Exemple 2 : simplifier une expression

Solution. Nous avons

63. Multiplication et division de fractions rationnelles.

Le produit de deux fractions rationnelles (et en général de tout nombre fini) est identiquement égal à une fraction dont le numérateur est égal au produit des numérateurs, et le dénominateur est égal au produit des dénominateurs des fractions multipliées :

Le quotient de division de deux fractions rationnelles est identiquement égal à une fraction dont le numérateur est égal au produit du numérateur de la première fraction et du dénominateur de la deuxième fraction, et le dénominateur est le produit du dénominateur de la première fraction et du numérateur de la deuxième fraction :

Les règles formulées de multiplication et de division s'appliquent également au cas de multiplication ou de division par un polynôme : il suffit d'écrire ce polynôme sous la forme d'une fraction de dénominateur 1.

Étant donné la possibilité de réduire une fraction rationnelle obtenue en multipliant ou en divisant des fractions rationnelles, ils s'efforcent généralement de factoriser les numérateurs et les dénominateurs des fractions originales avant d'effectuer ces opérations.

Exemple 1 : Effectuer une multiplication

Solution. Nous avons

En utilisant la règle de multiplication des fractions, on obtient :

Exemple 2 : Effectuer une division

Solution. Nous avons

En utilisant la règle de division, on obtient :

64. Élever une fraction rationnelle à une puissance entière.

Pour élever une fraction rationnelle à une puissance naturelle, il faut élever séparément le numérateur et le dénominateur de la fraction à cette puissance ; la première expression est le numérateur et la deuxième expression est le dénominateur du résultat :

Exemple 1 : Convertir en une fraction de puissance 3.

SolutionSolution.

Lors de l'élévation d'une fraction à une puissance entière négative, on utilise une identité valable pour toutes les valeurs des variables pour lesquelles .

Exemple 2 : Convertir une expression en fraction

65. Transformation des expressions rationnelles.

Transformer toute expression rationnelle revient à additionner, soustraire, multiplier et diviser des fractions rationnelles, ainsi qu'à élever une fraction à une puissance naturelle. Toute expression rationnelle peut être convertie en une fraction dont le numérateur et le dénominateur sont des expressions rationnelles entières ; C'est généralement le but des transformations identiques d'expressions rationnelles.

Exemple. Simplifier une expression

66. Les transformations les plus simples des racines arithmétiques (radicaux).

Lors de la conversion des korias arithmétiques, leurs propriétés sont utilisées (voir paragraphe 35).

Examinons plusieurs exemples d'utilisation des propriétés des racines arithmétiques pour les transformations de radicaux les plus simples. Dans ce cas, nous considérerons que toutes les variables ne prennent que des valeurs non négatives.

Exemple 1. Extraire la racine d'un produit

Solution. En appliquant la 1° propriété, on obtient :

Exemple 2. Supprimez le multiplicateur sous le signe racine

Solution.

Cette transformation est appelée suppression du facteur sous le signe racine. Le but de la transformation est de simplifier l'expression radicale.

Exemple 3 : Simplifier.

Solution. Par la propriété de 3° nous avons. Habituellement, ils essaient de simplifier l'expression radicale, pour laquelle ils retirent les facteurs du signe du corium. Nous avons

Exemple 4 : Simplifier

Solution. Transformons l'expression en introduisant un facteur sous le signe de la racine : Par propriété 4° on a

Exemple 5 : Simplifier

Solution. Par la propriété de 5°, on a le droit de diviser l'exposant de la racine et l'exposant de l'expression radicale par le même nombre naturel. Si dans l'exemple considéré on divise les indicateurs indiqués par 3, on obtient .

Exemple 6. Simplifiez les expressions :

Solution, a) Par la propriété 1° on trouve que pour multiplier des racines de même degré, il suffit de multiplier les expressions radicales et d'extraire la racine de même degré du résultat obtenu. Moyens,

b) Tout d'abord, il faut réduire les radicaux à un seul indicateur. D'après la propriété de 5°, on peut multiplier l'exposant de la racine et l'exposant de l'expression radicale par le même nombre naturel. Par conséquent, nous avons maintenant le résultat obtenu en divisant les exposants de la racine et le degré de l'expression radicale par 3, nous obtenons.

Cette leçon couvrira des informations de base sur les expressions rationnelles et leurs transformations, ainsi que des exemples de transformations d'expressions rationnelles. Ce sujet résume les sujets que nous avons étudiés jusqu'à présent. Les transformations d'expressions rationnelles impliquent l'addition, la soustraction, la multiplication, la division, l'exponentiation de fractions algébriques, la réduction, la factorisation, etc. Dans le cadre de la leçon, nous examinerons ce qu'est une expression rationnelle et analyserons également des exemples de leur transformation.

Sujet:Fractions algébriques. Opérations arithmétiques sur les fractions algébriques

Leçon:Informations de base sur les expressions rationnelles et leurs transformations

Définition

Expression rationnelle est une expression composée de nombres, de variables, d'opérations arithmétiques et d'opérations d'exponentiation.

Regardons un exemple d'expression rationnelle :

Cas particuliers d'expressions rationnelles :

1er degré : ;

2. monôme : ;

3. fraction : .

Conversion d'une expression rationnelle est une simplification d’une expression rationnelle. L'ordre des actions lors de la transformation d'expressions rationnelles : il y a d'abord les opérations entre parenthèses, puis les opérations de multiplication (division), puis les opérations d'addition (soustraction).

Examinons plusieurs exemples de transformation d'expressions rationnelles.

Exemple 1

Solution:

Résolvons cet exemple étape par étape. L'action entre parenthèses est exécutée en premier.

Répondre:

Exemple 2

Solution:

Répondre:

Exemple 3

Solution:

Répondre: .

Note: Peut-être qu’en voyant cet exemple, une idée vous est venue : réduire la fraction avant de la réduire à un dénominateur commun. En effet, c'est tout à fait correct : il convient d'abord de simplifier au maximum l'expression, puis de la transformer. Essayons de résoudre ce même exemple de la deuxième manière.

Comme vous pouvez le constater, la réponse s'est avérée absolument similaire, mais la solution s'est avérée un peu plus simple.

Dans cette leçon, nous avons examiné expressions rationnelles et leurs transformations, ainsi que plusieurs exemples précis de ces transformations.

Références

1. Bashmakov M.I. Algèbre 8e année. - M. : Éducation, 2004.

2. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. et autres. Algèbre 8. - 5e éd. - M. : Éducation, 2010.

Conversion d'expressions rationnelles

Dans cette leçon, nous travaillerons avec des expressions rationnelles. À l'aide d'exemples spécifiques, nous examinerons des méthodes pour résoudre des problèmes impliquant des transformations d'expressions rationnelles et prouver les identités qui leur sont associées.

Une expression rationnelle est une expression algébrique composée de nombres, de variables alphabétiques, d'opérations arithmétiques, élevant à une puissance naturelle, et de symboles pour la séquence de ces opérations (parenthèses). Avec l'expression « expression rationnelle » en algèbre, les termes « entier » ou « fraction » sont parfois utilisés.

Par exemple, les expressions

sont à la fois rationnels et entiers.

Expressions

sont à la fois rationnels et fractionnaires, car le dénominateur contient une expression avec une variable.

Il ne faut pas oublier qu'une fraction n'a plus de sens si le dénominateur tend vers zéro.

L'objectif principal de la leçon sera d'acquérir de l'expérience dans la résolution de problèmes de simplification d'expressions rationnelles.

La simplification des expressions rationnelles est l'utilisation de transformations d'identité afin de simplifier l'écriture d'une expression (la rendre plus courte et plus pratique pour un travail ultérieur).

Pour transformer des expressions rationnelles, nous avons besoin de règles d'addition (soustraction), de multiplication, de division et d'exponentiation des fractions algébriques ; toutes ces actions sont effectuées selon les mêmes règles que les actions avec des fractions ordinaires :

Et aussi des formules de multiplication abrégées :

Lors de la résolution d'exemples de transformation d'expressions rationnelles, l'ordre d'actions suivant doit être suivi : d'abord, les actions entre parenthèses sont effectuées, puis le produit/division (ou exponentiation), et enfin les actions d'addition/soustraction.

Regardons donc l'exemple 1 :

il faut simplifier l'expression

Tout d’abord, nous effectuons les actions entre parenthèses.

Nous ramenons les fractions algébriques à un dénominateur commun et additionnons (soustrayons) les fractions avec les mêmes dénominateurs selon les règles écrites ci-dessus.

En utilisant la formule abrégée (à savoir le carré de la différence), l'expression résultante prend la forme :

Deuxièmement, selon les règles de multiplication des fractions algébriques, on multiplie les numérateurs et les dénominateurs séparément :

Et puis on réduit l'expression résultante :

Grâce aux transformations effectuées, on obtient une expression simple

Considérons un exemple 2 plus complexe de transformation d'expressions rationnelles : il faut prouver l'identité :

Prouver une identité, c'est établir que, pour toutes les valeurs admissibles des variables, ses côtés gauche et droit sont égaux.

Preuve:

Pour prouver cette identité, il faut transformer l’expression du côté gauche. Pour ce faire, vous devez suivre l'ordre des actions décrit ci-dessus : tout d'abord, les actions entre parenthèses sont effectuées, puis la multiplication, puis l'addition.

Donc action 1 :

effectuer l'addition/soustraction d'une expression entre parenthèses.

Pour ce faire, factorisez les expressions dans les dénominateurs des fractions et ramenez ces fractions à un dénominateur commun.

Donc au dénominateur de la première fraction on met 3 entre parenthèses, au dénominateur de la seconde on met le signe moins et, en utilisant la formule de multiplication abrégée, on le factorise en deux facteurs, et au dénominateur de la troisième fraction nous mettons x entre parenthèses.

Le dénominateur commun de ces trois fractions est l'expression

Action 2 :

multiplier une fraction

Pour ce faire, vous devez d’abord factoriser le numérateur de la première fraction et élever cette fraction à la puissance 2.

Et lorsque vous multipliez des fractions, effectuez la réduction correspondante.

Action 3 :

Nous additionnons la première fraction de l'expression originale et la fraction résultante

Pour ce faire, factorisez d'abord le numérateur et le dénominateur de la première fraction et réduisez :

Il ne reste plus qu'à additionner les fractions algébriques résultantes avec des dénominateurs différents :

Ainsi, grâce à 3 actions et à la simplification du côté gauche de l'identité, nous avons obtenu une expression de son côté droit, et avons donc prouvé cette identité. Rappelons cependant que l'identité n'est valable que pour les valeurs admissibles de la variable x. Dans cet exemple, il s'agit de toutes les valeurs de x, à l'exception de celles qui rendent nuls les dénominateurs des fractions. Cela signifie que toutes les valeurs de x sont acceptables, à l'exception de celles pour lesquelles au moins une des égalités est satisfaite :

Les valeurs suivantes seront invalides :

Ainsi, à l’aide d’exemples spécifiques, nous avons cherché à résoudre des problèmes impliquant des transformations d’expressions rationnelles et à prouver les identités qui leur sont associées.

Liste de la littérature utilisée :

1. Mordkovitch A.G. "Algèbre" 8e année. À 14 heures, partie 1. Manuel pour les établissements d'enseignement / A.G. Mordkovitch. – 9e éd., révisée. – M. : Mnémosyne, 2007. – 215 p. : ill.
2. Mordkovitch A.G. "Algèbre" 8e année. À 14 heures, partie 2. Cahier de problèmes pour les établissements d'enseignement / A.G. Mordkovitch, T.N. Mishustina, E.E. Tulchinskaya.. – 8e éd., – M. : Mnemosyne, 2006 – 239 p.
3. Algèbre. 8e année. Tests pour les étudiants des établissements d'enseignement de L.A. Alexandrov, éd. A.G. Mordkovich 2e éd., effacé. - M. : Mnémosyne 2009. - 40 p.
4. Algèbre. 8e année. Travail indépendant pour les étudiants des établissements d'enseignement : au manuel d'A.G. Mordkovitch, L.A. Alexandrov, éd. A.G. Mordkovitch. 9e éd., effacée. - M. : Mnémosyne 2013. - 112 p.

>>Mathématiques : Conversion d'expressions rationnelles

Conversion d'expressions rationnelles

Ce paragraphe résume tout ce dont nous avons parlé, à partir de la 7e année, sur le langage mathématique, le symbolisme mathématique, les nombres, les variables, les puissances, les polynômes et fractions algébriques. Mais d’abord, faisons une petite excursion dans le passé.

Rappelez-vous comment les choses se passaient avec l'étude des nombres et des expressions numériques dans les classes inférieures.

Et, disons, une seule étiquette peut être attachée à une fraction : un nombre rationnel.

La situation est similaire avec les expressions algébriques : la première étape de leur étude concerne les nombres, les variables, les degrés (« chiffres ») ; la deuxième étape de leur étude est celle des monômes (« nombres naturels ») ; la troisième étape de leur étude est celle des polynômes (« entiers ») ; la quatrième étape de leur étude - les fractions algébriques
(« nombres rationnels »). De plus, chaque étape suivante, pour ainsi dire, absorbe la précédente : par exemple, les nombres, les variables, les puissances sont des cas particuliers de monômes ; monômes - cas particuliers de polynômes ; les polynômes sont des cas particuliers de fractions algébriques. D'ailleurs, les termes suivants sont parfois utilisés en algèbre : polynôme - entier expression, une fraction algébrique est une expression fractionnaire (cela ne fait que renforcer l'analogie).

Continuons l'analogie ci-dessus. Vous savez que toute expression numérique, après avoir effectué toutes les opérations arithmétiques qu'elle contient, prend une valeur numérique spécifique - un nombre rationnel (bien sûr, cela peut s'avérer être un nombre naturel, un entier ou une fraction - ce n'est pas le cas). ça n'a pas d'importance). De même, toute expression algébrique composée de nombres et de variables utilisant des opérations arithmétiques et remontant au naturel degré, après avoir effectué les transformations prend la forme d'une fraction algébrique et encore, notamment, le résultat peut être non pas une fraction, mais un polynôme ou même un monôme). Pour de telles expressions en algèbre, le terme expression rationnelle est utilisé.

Exemple. Prouver l'identité

Solution.
Prouver une identité signifie établir que pour toutes les valeurs admissibles des variables, ses côtés gauche et droit sont des expressions identiquement égales. En algèbre, les identités se prouvent de différentes manières :

1) effectuer des transformations sur le côté gauche et finalement obtenir le côté droit ;

2) effectuer des transformations sur le côté droit et finalement obtenir le côté gauche ;

3) transformer les côtés droit et gauche séparément et obtenir la même expression dans le premier et le deuxième cas ;

4) combler la différence entre les côtés gauche et droit et, grâce à ses transformations, obtenir zéro.

La méthode à choisir dépend du type spécifique identités qu'il vous est demandé de prouver. Dans cet exemple, il est conseillé de choisir la première méthode.

Pour convertir des expressions rationnelles, la même procédure est adoptée que pour convertir des expressions numériques. Cela signifie qu'ils effectuent d'abord les actions entre parenthèses, puis les actions de la deuxième étape (multiplication, division, exponentiation), puis les actions de la première étape (addition, soustraction).

Réalisons des transformations basées sur les règles algorithmes qui ont été développées dans les paragraphes précédents.

Comme vous pouvez le constater, nous avons pu transformer le côté gauche de l'identité en cours de vérification en la forme du côté droit. Cela signifie que l'identité est prouvée. Rappelons cependant que l'identité n'est valable que pour les valeurs admissibles des variables. Dans cet exemple, il s'agit de toutes les valeurs de a et b, à l'exception de celles qui rendent nuls les dénominateurs des fractions. Cela signifie que toutes les paires de nombres (a; b) sont valides, à l'exception de celles pour lesquelles au moins une des égalités est satisfaite :

2a - b = 0, 2a + b = 0, b = 0.

Mordkovitch A.G., Algèbre. 8e année : Manuel. pour l'enseignement général institutions. - 3e éd., révisée. - M. : Mnémosyne, 2001. - 223 p. : ill.

Une liste complète des sujets par année, un plan de calendrier selon le programme scolaire en mathématiques en ligne, du matériel vidéo sur les mathématiques pour la 8e année à télécharger

Cette leçon couvrira des informations de base sur les expressions rationnelles et leurs transformations, ainsi que des exemples de transformations d'expressions rationnelles. Ce sujet résume les sujets que nous avons étudiés jusqu'à présent. Les transformations d'expressions rationnelles impliquent l'addition, la soustraction, la multiplication, la division, l'exponentiation de fractions algébriques, la réduction, la factorisation, etc. Dans le cadre de la leçon, nous examinerons ce qu'est une expression rationnelle et analyserons également des exemples de leur transformation.

Sujet:Fractions algébriques. Opérations arithmétiques sur les fractions algébriques

Leçon:Informations de base sur les expressions rationnelles et leurs transformations

Définition

Expression rationnelle est une expression composée de nombres, de variables, d'opérations arithmétiques et d'opérations d'exponentiation.

Regardons un exemple d'expression rationnelle :

Cas particuliers d'expressions rationnelles :

1er degré : ;

2. monôme : ;

3. fraction : .

Conversion d'une expression rationnelle est une simplification d’une expression rationnelle. L'ordre des actions lors de la transformation d'expressions rationnelles : il y a d'abord les opérations entre parenthèses, puis les opérations de multiplication (division), puis les opérations d'addition (soustraction).

Examinons plusieurs exemples de transformation d'expressions rationnelles.

Exemple 1

Solution:

Résolvons cet exemple étape par étape. L'action entre parenthèses est exécutée en premier.

Répondre:

Exemple 2

Solution:

Répondre:

Exemple 3

Solution:

Répondre: .

Note: Peut-être qu’en voyant cet exemple, une idée vous est venue : réduire la fraction avant de la réduire à un dénominateur commun. En effet, c'est tout à fait correct : il convient d'abord de simplifier au maximum l'expression, puis de la transformer. Essayons de résoudre ce même exemple de la deuxième manière.

Comme vous pouvez le constater, la réponse s'est avérée absolument similaire, mais la solution s'est avérée un peu plus simple.

Dans cette leçon, nous avons examiné expressions rationnelles et leurs transformations, ainsi que plusieurs exemples précis de ces transformations.

Références

1. Bashmakov M.I. Algèbre 8e année. - M. : Éducation, 2004.

2. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. et autres. Algèbre 8. - 5e éd. - M. : Éducation, 2010.