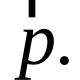Tavaline diferentsiaalvõrrand on võrrand, mis seob sõltumatu muutuja, selle muutuja tundmatu funktsiooni ja selle erinevat järku tuletisi (või diferentsiaale).

Diferentsiaalvõrrandi järjekord nimetatakse selles sisalduva kõrgeima tuletise järguks.

Lisaks tavalistele uuritakse ka osadiferentsiaalvõrrandeid. Need on võrrandid, mis seostavad sõltumatuid muutujaid, nende muutujate tundmatut funktsiooni ja selle osalisi tuletisi samade muutujate suhtes. Kuid me kaalume ainult tavalised diferentsiaalvõrrandid ja seetõttu jätame lühiduse huvides sõna "tavaline".

Näited diferentsiaalvõrrandid:

(1) ;

(3) ;

(4) ;

Võrrand (1) on neljandat järku, võrrand (2) on kolmandat järku, võrrandid (3) ja (4) on teist järku, võrrand (5) on esimest järku.

Diferentsiaalvõrrand n järjekord ei pea tingimata sisaldama selgesõnalist funktsiooni, kõiki selle tuletisi esimesest kuni n-th järk ja sõltumatu muutuja. See ei tohi sisaldada teatud järjestuste selgesõnalisi tuletisi, funktsiooni ega sõltumatut muutujat.

Näiteks võrrandis (1) puuduvad selgelt kolmandat ja teist järku tuletised, samuti funktsioon; võrrandis (2) - teist järku tuletis ja funktsioon; võrrandis (4) - sõltumatu muutuja; võrrandis (5) - funktsioonid. Ainult võrrand (3) sisaldab selgesõnaliselt kõiki tuletisi, funktsiooni ja sõltumatut muutujat.

Diferentsiaalvõrrandi lahendamine kutsutakse iga funktsioon y = f(x), kui võrrandisse asendada, muutub see identiteediks.

Diferentsiaalvõrrandi lahenduse leidmise protsessi nimetatakse selle protsessiks integratsiooni.

Näide 1. Leia diferentsiaalvõrrandi lahendus.

Lahendus. Kirjutame selle võrrandi kujul . Lahendus on leida funktsioon selle tuletisest. Algfunktsioon, nagu on teada integraalarvutusest, on antiderivaat, s.o.

See on see selle diferentsiaalvõrrandi lahendus . Muutumine selles C, saame erinevaid lahendusi. Saime teada, et esimest järku diferentsiaalvõrrandil on lõpmatu arv lahendusi.

Diferentsiaalvõrrandi üldlahend n järjekord on selle lahendus, mis on sõnaselgelt väljendatud tundmatu funktsiooni suhtes ja sisaldab n sõltumatud suvalised konstandid, st.

Näite 1 diferentsiaalvõrrandi lahendus on üldine.

Diferentsiaalvõrrandi osalahend nimetatakse lahendust, kus suvalistele konstantidele antakse konkreetsed arvväärtused.

Näide 2. Leia diferentsiaalvõrrandi üldlahendus ja konkreetne lahendus .

Lahendus. Integreerime võrrandi mõlemad pooled mitu korda, mis on võrdne diferentsiaalvõrrandi järjekorraga.

,

.

Selle tulemusena saime üldise lahenduse -

antud kolmandat järku diferentsiaalvõrrandist.

Nüüd leiame konkreetse lahenduse kindlaksmääratud tingimustel. Selleks asendage suvaliste koefitsientide asemel nende väärtused ja hankige

.

Kui lisaks diferentsiaalvõrrandile on algtingimus antud kujul , siis sellist ülesannet nn. Cauchy probleem . Asendage väärtused ja võrrandi üldlahendisse ning leidke suvalise konstandi väärtus C, ja seejärel leitud väärtuse võrrandi konkreetne lahendus C. See on lahendus Cauchy probleemile.

Näide 3. Lahendage näite 1 diferentsiaalvõrrandi Cauchy ülesanne objektiga .

Lahendus. Asendame algtingimuse väärtused üldlahendusega y = 3, x= 1. Saame

Kirjutame selle esimest järku diferentsiaalvõrrandi Cauchy probleemi lahenduse:

Diferentsiaalvõrrandite, ka kõige lihtsamate, lahendamine nõuab häid integreerimis- ja tuletamisoskusi, sealhulgas keerulisi funktsioone. Seda võib näha järgmises näites.

Näide 4. Leia diferentsiaalvõrrandi üldlahendus.

Lahendus. Võrrand on kirjutatud sellisel kujul, et saate kohe integreerida mõlemad pooled.

.

Rakendame integreerimise meetodit muutuja muutmise teel (asendamine). Las siis olla.

Kohustuslik võtta dx ja nüüd - tähelepanu - teeme seda vastavalt kompleksfunktsiooni eristamise reeglitele, kuna x ja seal on keeruline funktsioon ("õun" - ekstrakt ruutjuur või mis on sama asi - "pooleks" tõstmine ja "hakkliha" on juure all olev väljend):

Leiame integraali:

Tulles tagasi muutuja juurde x, saame:

.

See on selle esimese astme diferentsiaalvõrrandi üldine lahendus.

Diferentsiaalvõrrandite lahendamisel pole vaja mitte ainult kõrgema matemaatika eelmiste osade oskusi, vaid ka alg-, st koolimatemaatika oskusi. Nagu juba mainitud, ei pruugi mis tahes järku diferentsiaalvõrrandis olla sõltumatut muutujat, see tähendab muutujat x. Seda probleemi aitavad lahendada koolist saadud teadmised proportsioonide kohta, mis pole (olenevalt aga kes) koolist unustatud. See on järgmine näide.

Diferentsiaalvõrrandid (DE). Need kaks sõna tekitavad tavainimesel tavaliselt hirmu. Diferentsiaalvõrrandid näivad olevat paljude õpilaste jaoks üle jõu käivad ja raskesti omandatavad. Uuuuuu... diferentsiaalvõrrandid, kuidas ma seda kõike üle elan?!

See arvamus ja suhtumine on põhimõtteliselt vale, sest tegelikult DIFERENTSIVÕRRADID – SEE ON LIHTNE JA ISEGI LÕBUS. Mida peate teadma ja oskama, et õppida diferentsiaalvõrrandeid lahendama? Difuuside edukaks õppimiseks peate olema osav integreerimises ja eristamises. Mida paremini teemasid õpitakse Ühe muutuja funktsiooni tuletis Ja Määramatu integraal, seda lihtsam on diferentsiaalvõrranditest aru saada. Ütlen veel, kui sul on enam-vähem korralik lõimumisoskus, siis on teema peaaegu omandatud! Mida rohkem integraale erinevat tüüpi sa tead, kuidas otsustada – seda parem. Miks? Sest peate palju integreerima. Ja eristada. Samuti väga soovitadaõppige leidma kaudselt määratud funktsiooni tuletis.

95% juhtudest sisse testid Esimest järku diferentsiaalvõrrandeid on 3 tüüpi: eraldatavate muutujatega võrrandid, mida selles õppetükis vaatleme; homogeensed võrrandid Ja lineaarsed mittehomogeensed võrrandid. Neil, kes hakkavad difuusoreid õppima, soovitan lugeda õppetükke selles järjekorras. On veelgi haruldasemaid diferentsiaalvõrrandite tüüpe: võrrandid summaarsetes diferentsiaalides, Bernoulli võrrandid ja mõned teised. Kahest viimasest tüübist kõige olulisemad on summaarsete diferentsiaalide võrrandid, kuna lisaks sellele diferentsiaalvõrrandile arvestan uus materjal– erasektori integratsioon.

Kõigepealt meenutame tavalisi võrrandeid. Need sisaldavad muutujaid ja numbreid. Lihtsaim näide: . Mida tähendab tavalise võrrandi lahendamine? See tähendab leidmist numbrite komplekt, mis vastavad sellele võrrandile. Lihtne on märgata, et laste võrrandil on üks juur: . Lõbu pärast kontrollime leitud juurt ja asendame selle võrrandiga:

– saadakse õige võrdsus, mis tähendab, et lahendus leiti õigesti.

Hajutid on disainitud umbes samamoodi!

Diferentsiaalvõrrand esimene tellimus, sisaldab:
1) sõltumatu muutuja;
2) sõltuv muutuja (funktsioon);
3) funktsiooni esimene tuletis: .

Mõnel juhul võib esimest järku võrrandis puududa "x" ja/või "y" - oluline juhtimisruumi minema oli esimene tuletis ja ei olnud kõrgema järgu tuletised – jne.

Mida see tähendab? Diferentsiaalvõrrandi lahendamine tähendab leidmist palju funktsioone, mis vastavad sellele võrrandile. Seda funktsioonide komplekti nimetatakse diferentsiaalvõrrandi üldlahendus.

Näide 1

Lahendage diferentsiaalvõrrand

Täis laskemoon. Kust alustada mis tahes esimest järku diferentsiaalvõrrandi lahendamist?

Kõigepealt tuleb tuletis veidi teistsugusel kujul ümber kirjutada. Tuletagem meelde tuletise tülikat tähistust: . See tuletise tähistus tundus paljudele teist ilmselt naeruväärne ja ebavajalik, kuid just nii kehtib difuusorites!

Niisiis kirjutame esimeses etapis tuletise ümber vajalikul kujul:

Teises etapis Alati vaatame, kas see on võimalik eraldi muutujad? Mida tähendab muutujate eraldamine? Jämedalt öeldes, vasakul küljel me peame lahkuma ainult "kreeklased", A paremal küljel korraldada ainult "X". Muutujate jagamine toimub “kooli” manipulatsioonide abil: sulgudest välja jätmine, terminite ülekandmine osast osasse märgivahetusega, tegurite ülekandmine osast osasse proportsioonireegli järgi jne.

Diferentsiaalid ja on täielikud kordistajad ja aktiivsed vaenutegevuses osalejad. Vaatlusaluses näites on muutujad kergesti eraldatavad, visates tegurid vastavalt proportsioonireeglile:

Muutujad on eraldatud. Vasakul pool on ainult "Y", paremal - ainult "X".

Järgmine etapp on diferentsiaalvõrrandi integreerimine. See on lihtne, paneme integraalid mõlemale poole:

Muidugi peame võtma integraalid. IN antud juhul need on tabelina:

Nagu mäletame, määratakse igale antiderivaadile konstant. Siin on kaks integraali, kuid konstandi kirjutamisest piisab üks kord. See on peaaegu alati määratud paremale küljele.

Rangelt võttes loetakse diferentsiaalvõrrand pärast integraalide võtmist lahendatuks. Ainus asi on see, et meie "y" ei väljendata "x" kaudu, see tähendab, et lahendus on esitatud implitsiitses vormi. Diferentsiaalvõrrandi lahendust kaudsel kujul nimetatakse diferentsiaalvõrrandi üldintegraal. See tähendab, et see on üldine integraal.

Nüüd peame püüdma leida üldist lahendust, st proovima funktsiooni eksplitsiitselt esitada.

Pidage meeles esimest tehnikat, see on väga levinud ja seda kasutatakse sageli praktilistes ülesannetes. Kui pärast integreerimist ilmub paremale poole logaritm, on peaaegu alati soovitatav konstant kirjutada ka logaritmi alla.

see tähendab, asemel kirjed kirjutatakse tavaliselt .

Siin on see sama täiskonstant nagu . Miks see vajalik on? Ja selleks, et "mängu" väljendamine oleks lihtsam. Kasutame logaritmide kooli omadust: . Sel juhul:

Nüüd saab logaritme ja mooduleid kasutada puhas südametunnistus eemaldage mõlemast osast:

Funktsioon on selgelt esitatud. See on üldine lahendus.

Palju funktsioone on diferentsiaalvõrrandi üldlahendus.

Konstanti andmine erinevaid tähendusi, võite saada lõpmatult palju privaatsed lahendused diferentsiaalvõrrand. Ükskõik milline funktsioon , jne. rahuldab diferentsiaalvõrrandi.

Mõnikord nimetatakse üldist lahendust funktsioonide perekond. IN selles näitesüldine lahendus on lineaarsete funktsioonide perekond või täpsemalt otsese proportsionaalsuse perekond.

Paljusid diferentsiaalvõrrandeid on üsna lihtne testida. Seda tehakse väga lihtsalt, võtame leitud lahenduse ja leiame tuletise:

Asendame oma lahenduse ja leitud tuletise algsesse võrrandisse:

– saadakse õige võrdsus, mis tähendab, et lahendus leiti õigesti. Teisisõnu, üldlahend rahuldab võrrandit.

Pärast esimese näite põhjalikku läbivaatamist on asjakohane vastata mitmele naiivsele küsimusele diferentsiaalvõrrandite kohta.

1)Selles näites saime muutujad eraldada: . Kas seda saab alati teha? Ei, mitte alati. Ja veelgi sagedamini ei saa muutujaid eraldada. Näiteks sisse homogeensed esimest järku võrrandid, peate selle esmalt välja vahetama. Teist tüüpi võrrandites, näiteks lineaarses ebahomogeenses esimest järku võrrandis, vaja kasutada erinevaid tehnikaid ja meetodid üldise lahenduse leidmiseks. Eraldatavate muutujatega võrrandid, mida käsitleme esimeses õppetükis, on kõige lihtsamad diferentsiaalvõrrandid.

2) Kas diferentsiaalvõrrandit on alati võimalik integreerida? Ei, mitte alati. Väga lihtne on välja mõelda “väljamõeldud” võrrand, mida ei saa integreerida, lisaks on integraale, mida ei saa võtta. Kuid selliseid DE-sid saab ligikaudu lahendada spetsiaalsete meetodite abil. D'Alemberti ja Cauchy garantii. ...uh, lurkmore.ru Lugesin just praegu palju.

3) Selles näites saime lahenduse üldintegraali kujul . Kas üldintegraalist on alati võimalik leida üldist lahendust, st väljendada "y" eksplitsiitselt? Ei, mitte alati. Näiteks:. No kuidas saab siin "kreeka keelt" väljendada?! Sellistel juhtudel tuleks vastus kirjutada üldise integraalina. Lisaks on mõnikord võimalik leida üldine lahendus, kuid see on nii kohmakalt ja kohmakalt kirjutatud, et parem on jätta vastus üldise integraali kujul

Me ei kiirusta. Veel üks lihtne kaugjuhtimispult ja veel üks tüüpiline lahendus.

Näide 2

Leidke diferentsiaalvõrrandile konkreetne lahendus, mis rahuldab algtingimust

Vastavalt seisundile peate leidma privaatne lahendus DE vastab esialgsele tingimusele. Seda küsimuse sõnastust nimetatakse ka Cauchy probleem.

Kõigepealt leiame üldise lahenduse. Võrrandis pole muutujat “x”, kuid see ei tohiks segadusse ajada, peaasi, et sellel oleks esimene tuletis.

Kirjutame tuletise ümber õigel kujul:

Ilmselgelt saab muutujaid eraldada, poisid vasakule, tüdrukud paremale:

Integreerime võrrandi:

Üldine integraal saadakse. Siia olen joonistanud tärniga konstandi, tõsiasi on see, et varsti muutub see teiseks konstandiks.

Nüüd proovime muuta üldise integraali üldlahenduseks (väljendage "y" selgesõnaliselt). Meenutagem vanu häid asju kooliajast: . Sel juhul:

Indikaatori konstant näeb kuidagi ebakosher välja, nii et see on tavaliselt maa peale toodud. Üksikasjalikult see juhtub nii. Kasutades kraadide omadust, kirjutame funktsiooni ümber järgmiselt:

Kui on konstant, siis on ka mingi konstant, mida tähistame tähega:

Pidage meeles konstandi “allakandmist”, see on teine ​​tehnika, mida sageli kasutatakse diferentsiaalvõrrandite lahendamisel.

Seega on üldine lahendus: . See on kena eksponentsiaalsete funktsioonide perekond.

Viimases etapis peate leidma konkreetse lahenduse, mis vastab antud algtingimusele. See on ka lihtne.

Mis on ülesanne? Vaja korjata selline konstandi väärtus, et määratud algtingimus oleks täidetud.

Seda saab vormindada erineval viisil, kuid see on ilmselt kõige selgem viis. Üldlahenduses asendame "X" asemel nulliga ja "Y" asemel kahega:



see tähendab,

Standardse disaini versioon:

Asendame konstandi leitud väärtuse üldlahendiga:
– see on konkreetne lahendus, mida me vajame.

Kontrollime. Privaatse lahenduse kontrollimine hõlmab kahte etappi.

Kõigepealt peate kontrollima, kas leitud lahendus vastab tõesti algtingimusele? "X" asemel asendame nulliga ja vaatame, mis juhtub:
- jah, tõepoolest, kahene saadi, mis tähendab, et esialgne tingimus on täidetud.

Teine etapp on juba tuttav. Võtame saadud konkreetse lahenduse ja leiame tuletise:

Asendame algsesse võrrandisse:

– saavutatakse õige võrdsus.

Järeldus: konkreetne lahendus leiti õigesti.

Liigume edasi sisukamate näidete juurde.

Näide 3

Lahendage diferentsiaalvõrrand

Lahendus: Kirjutame tuletise ümber meile vajalikul kujul:

Hindame, kas muutujaid on võimalik eraldada? Saab. Teisaldame teise liikme märgivahetusega paremale:

Ja me kanname kordajad üle vastavalt proportsioonireeglile:

Muutujad on eraldatud, integreerime mõlemad osad:

Pean teid hoiatama, et kohtupäev on lähenemas. Kui sa pole hästi õppinud määramata integraalid, on lahendanud vähe näiteid, siis pole enam kuhugi minna – peate need nüüd selgeks tegema.

Vasaku külje integraali on lihtne leida Integratsioon trigonomeetrilised funktsioonid eelmisel aastal:

Paremal pool on meil logaritm, minu esimese tehnilise soovituse kohaselt tuleks sel juhul logaritmi alla kirjutada ka konstant.

Nüüd proovime üldist integraali lihtsustada. Kuna meil on ainult logaritmid, siis on täiesti võimalik (ja vajalik) neist lahti saada. "Pakime" logaritme nii palju kui võimalik. Pakendamine toimub kolme omaduse abil:

Palun kirjuta need kolm valemit oma sisse töövihik, hajutite lahendamisel kasutatakse neid väga sageli.

Kirjeldan lahendust üksikasjalikult:

Pakkimine on lõpetatud, eemaldage logaritmid:

Kas on võimalik väljendada "mängu"? Saab. Mõlemad osad on vaja ruudukujuliseks muuta. Kuid te ei pea seda tegema.

Kolmandaks tehniline nõustamine: Kui üldlahenduse saamiseks on vaja tõsta võimu või juurduda, siis enamikul juhtudel peaksite nendest tegevustest hoiduma ja jätma vastuse üldise integraali kujul. Fakt on see, et üldine lahendus näeb välja pretensioonikas ja kohutav - suurte juurte, siltidega.

Seetõttu kirjutame vastuse üldise integraali kujul. Heas korras Arvatakse, et see esindab üldist integraali kujul , st paremale küljele jätke võimaluse korral ainult konstant. Seda pole vaja teha, kuid alati on kasulik professorile meeldida ;-)

Vastus:üldine integraal:

Märkus.Mis tahes võrrandi üldintegraali saab kirjutada rohkem kui ühel viisil. Seega, kui teie tulemus ei kattu varem teadaoleva vastusega, ei tähenda see, et lahendasite võrrandi valesti.

Üldintegraali on ka üsna lihtne kontrollida, peaasi, et leiaks kaudselt määratletud funktsiooni tuletised. Eristagem vastust:

Korrutame mõlemad terminid arvuga:

Ja jagage:

Algne diferentsiaalvõrrand on saadud täpselt, mis tähendab, et üldintegraal on leitud õigesti.

Näide 4

Leidke diferentsiaalvõrrandile konkreetne lahendus, mis rahuldab algtingimust. Tehke kontroll.

See on näide sõltumatu otsus. Lubage mul teile meelde tuletada, et Cauchy probleem koosneb kahest etapist:
1) Üldise lahenduse leidmine.
2) Konkreetse lahenduse leidmine.

Kontrollimine toimub samuti kahes etapis (vt ka näide 2), peate:
1) Veenduge, et leitud lahendus vastab tõesti esialgsele tingimusele.
2) Kontrollige, kas konkreetne lahendus üldiselt rahuldab diferentsiaalvõrrandit.

Täislahendus ja vastus tunni lõpus.

Näide 5

Leidke diferentsiaalvõrrandile konkreetne lahendus , mis rahuldab esialgset tingimust. Tehke kontroll.

Lahendus: Esiteks leiame üldlahenduse. See võrrand sisaldab juba valmis diferentsiaale ja see tähendab, et lahendus on lihtsustatud. Eraldame muutujad:

Integreerime võrrandi:

Vasakpoolne integraal on tabelikujuline, parempoolne integraal on võetud meetod funktsiooni diferentsiaalmärgi alla liitmiseks:

Üldine integraal on saadud, kas üldlahendust on võimalik edukalt väljendada? Saab. Me riputame logaritmid:

(Loodan, et kõik saavad transformatsioonist aru, selliseid asju peaks juba teadma)

Seega on üldine lahendus järgmine:

Leiame konkreetse lahenduse, mis vastab antud algtingimusele. Üldlahenduses asendame “X” asemel nulli ja “Y” asemel kahe logaritmi:

Tuntum disain:

Asendame konstandi leitud väärtuse üldlahendiga.

Vastus: privaatne lahendus:

Kontrollige: kõigepealt kontrollime, kas esialgne tingimus on täidetud:
- kõik sumiseb.

Nüüd kontrollime, kas leitud konkreetne lahendus diferentsiaalvõrrandit üldse rahuldab. Tuletise leidmine:

Vaatame algset võrrandit: – see esitatakse diferentsiaalidena. Kontrollimiseks on kaks võimalust. Diferentsiaali leitud tuletisest on võimalik väljendada:

Asendame leitud konkreetse lahenduse ja saadud diferentsiaali algse võrrandiga :

Kasutame põhilogaritmilist identiteeti:

Saavutatakse õige võrdsus, mis tähendab, et konkreetne lahendus leiti õigesti.

Teine kontrollimeetod on peegeldatud ja tuttavam: võrrandist Avaldame tuletist, selleks jagame kõik tükid järgmisega:

Ja teisendatud DE-sse asendame saadud osalahendi ja leitud tuletise. Lihtsustuste tulemusena tuleks saavutada ka õige võrdsus.

Näide 6

Lahendage diferentsiaalvõrrand. Esitage vastus üldise integraali kujul.

See on näide, mida saate ise lahendada, lõpetage lahendus ja vastake tunni lõpus.

Millised raskused seisavad ees eraldatavate muutujatega diferentsiaalvõrrandite lahendamisel?

1) Alati pole (eriti teekannu puhul) ilmne, et muutujaid saab eraldada. Mõelgem tingimuslik näide: . Siin tuleb sulgudest välja võtta tegurid: ja eraldada juured: . On selge, mida edasi teha.

2) Integratsiooni endaga seotud raskused. Integraalid ei ole sageli kõige lihtsamad ja kui leidmise oskustes on vigu määramatu integraal, siis on see paljude difuusoritega keeruline. Lisaks on kogumike ja koolituskäsiraamatute koostajate seas populaarne loogika “kuna diferentsiaalvõrrand on lihtne, siis olgu integraalid keerulisemad”.

3) Teisendused konstandiga. Nagu kõik on märganud, saate diferentsiaalvõrrandis konstandiga teha peaaegu kõike. Ja sellised transformatsioonid pole algajale alati arusaadavad. Vaatame veel ühte tingimuslikku näidet: . Soovitatav on kõik terminid korrutada 2-ga: . Saadud konstant on ka mingi konstant, mida saab tähistada järgmiselt: . Jah, ja kuna paremal küljel on logaritm, siis on soovitatav konstant ümber kirjutada teise konstandi kujul: .

Probleem on selles, et nad sageli ei vaeva end indeksite pärast ja kasutavad sama tähte. Selle tulemusena on lahenduskirje järgmine vorm:

Mis kurat see on? On ka vigu. Formaalselt jah. Aga mitteametlikult - viga pole, saadakse aru, et konstandi teisendamisel saadakse ikkagi mingi muu konstant.

Või oletame seda näidet, et võrrandi lahendamise käigus saadakse üldintegraal. See vastus näeb kole välja, seetõttu on soovitatav muuta kõigi tegurite märke: . Vormiliselt on salvestuse järgi jälle viga, oleks tulnud kirja panna. Aga mitteametlikult saadakse aru, et tegemist on ikkagi mingi muu konstandiga (pealegi võib ta omandada mis tahes väärtuse), nii et konstandi märgi muutmisel pole mõtet ja võib kasutada sama tähte.

Püüan vältida hoolimatut lähenemist ja ikkagi panen erinevad indeksid nende teisendamisel.

Näide 7

Lahendage diferentsiaalvõrrand. Tehke kontroll.

Lahendus: See võrrand võimaldab muutujaid eraldada. Eraldame muutujad:

Integreerime:

Siin ei ole vaja konstanti defineerida logaritmina, sest sellest ei tule midagi kasulikku.

Vastus:üldine integraal:

Kontrollige: eristage vastust (kaudne funktsioon):

Murdudest vabaneme, korrutades mõlemad terminid arvuga:

Saadud on algne diferentsiaalvõrrand, mis tähendab, et üldintegraal on leitud õigesti.

Näide 8

Leidke DE konkreetne lahendus.
,

See on näide, mille saate ise lahendada. Ainus kommentaar on see, et siin saate üldise integraali ja õigemini öeldes peate leidma mitte konkreetse lahenduse, vaid osaline integraal. Täislahendus ja vastus tunni lõpus.

Nagu juba märgitud, ei teki eraldatavate muutujatega difuusides sageli mitte kõige lihtsamad integraalid. Ja siin on veel paar sellist näidet, mida saate ise lahendada. Soovitan kõigil lahendada näited nr 9-10, olenemata ettevalmistustasemest, see võimaldab värskendada oma oskusi integraalide leidmisel või täita teadmistes lünki.

Näide 9

Lahendage diferentsiaalvõrrand

Näide 10

Lahendage diferentsiaalvõrrand

Pidage meeles, et üldise integraali kirjutamiseks on rohkem kui üks viis ja teie vastused võivad erineda. välimus minu vastused. Lühilahendus ja vastused tunni lõpus.

Head edutamist!

Näide 4:Lahendus: Leiame üldise lahenduse. Eraldame muutujad:


Integreerime:



Üldine integraal on saadud, proovime seda lihtsustada. Pakime logaritmid kokku ja vabaneme neist:

I. Tavalised diferentsiaalvõrrandid

1.1. Põhimõisted ja määratlused

Diferentsiaalvõrrand on võrrand, mis seob sõltumatu muutuja x, vajalik funktsioon y ja selle tuletised või diferentsiaalid.

Sümboolselt kirjutatakse diferentsiaalvõrrand järgmiselt:

F(x,y,y")=0, F(x,y,y")=0, F(x,y,y",y",.., y (n))=0

Diferentsiaalvõrrandit nimetatakse tavaliseks, kui vajalik funktsioon sõltub ühest sõltumatust muutujast.

Diferentsiaalvõrrandi lahendamine nimetatakse funktsiooniks, mis muudab selle võrrandi identiteediks.

Diferentsiaalvõrrandi järjekord on selles võrrandis sisalduva kõrgeima tuletise järjekord

Näited.

1. Vaatleme esimest järku diferentsiaalvõrrandit

Selle võrrandi lahenduseks on funktsioon y = 5 ln x. Tõepoolest, asendamine y" võrrandisse, saame identiteedi.

Ja see tähendab, et funktsioon y = 5 ln x– on selle diferentsiaalvõrrandi lahendus.

2. Vaatleme teist järku diferentsiaalvõrrandit y" - 5a" + 6y = 0. Funktsioon on selle võrrandi lahendus.

Tõesti,.

Asendades need avaldised võrrandisse, saame: , – identiteedi.

Ja see tähendab, et funktsioon on selle diferentsiaalvõrrandi lahendus.

Diferentsiaalvõrrandite integreerimine on diferentsiaalvõrrandite lahenduste leidmise protsess.

Diferentsiaalvõrrandi üldlahend nimetatakse vormi funktsiooniks , mis sisaldab sama palju sõltumatuid suvalisi konstante kui võrrandi järjekord.

Diferentsiaalvõrrandi osalahend on lahendus, mis saadakse suvaliste konstantide erinevate arvväärtuste üldlahendusest. Suvaliste konstantide väärtused leitakse argumendi ja funktsiooni teatud algväärtuste juures.

Diferentsiaalvõrrandi konkreetse lahenduse graafikut nimetatakse integraalkõver.

Näited

1. Leidke konkreetne lahendus esimest järku diferentsiaalvõrrandile

xdx + ydy = 0, Kui y= 4 kl x = 3.

Lahendus. Integreerides võrrandi mõlemad pooled, saame

Kommenteeri. Integreerimise tulemusena saadud suvalist konstanti C saab esitada mis tahes kujul, mis sobib edasiste teisenduste jaoks. Sel juhul on ringi kanoonilist võrrandit arvesse võttes mugav suvalist konstanti C esitada kujul .

- diferentsiaalvõrrandi üldlahendus.

Võrrandi konkreetne lahendus, mis vastab algtingimustele y = 4 kl x = 3 leitakse üldisest, asendades üldlahendiga algtingimused: 3 2 + 4 2 = C 2 ; C=5.

Asendades üldlahendisse C=5, saame x 2 + y 2 = 5 2 .

See on eriline lahendus diferentsiaalvõrrandile, mis on saadud üldlahendusest antud algtingimustes.

2. Leia diferentsiaalvõrrandi üldlahend

Selle võrrandi lahenduseks on mis tahes funktsioon kujul , kus C on suvaline konstant. Tõepoolest, asendades võrranditesse , saame: , .

Järelikult on sellel diferentsiaalvõrrandil lõpmatu arv lahendusi, kuna konstandi C erinevate väärtuste korral määrab võrdsus võrrandi erinevad lahendid.

Näiteks saate otsese asendamise abil kontrollida, kas funktsioonid toimivad on võrrandi lahendid.

Probleem, mille puhul peate leidma võrrandile konkreetse lahenduse y" = f(x,y) esialgset tingimust rahuldama y(x 0) = y 0, nimetatakse Cauchy probleemiks.

Võrrandi lahendamine y" = f(x,y), mis vastab esialgsele tingimusele, y(x 0) = y 0, nimetatakse Cauchy probleemi lahenduseks.

Cauchy probleemi lahendusel on lihtne geomeetriline tähendus. Tõepoolest, nende määratluste kohaselt lahendage Cauchy probleem y" = f(x,y) arvestades seda y(x 0) = y 0, tähendab võrrandi integraalkõvera leidmist y" = f(x,y) mis läbib see punkt M 0 (x 0,y 0).

II. Esimest järku diferentsiaalvõrrandid

2.1. Põhimõisted

Esimest järku diferentsiaalvõrrand on vormi võrrand F(x,y,y") = 0.

Esimest järku diferentsiaalvõrrand sisaldab esimest tuletist ja ei sisalda kõrgemat järku tuletisi.

Võrrand y" = f(x,y) nimetatakse esimest järku võrrandiks, mis on lahendatud tuletise suhtes.

Esimest järku diferentsiaalvõrrandi üldlahend on funktsioon vormist , mis sisaldab ühte suvalist konstanti.

Näide. Mõelge esimest järku diferentsiaalvõrrandile.

Selle võrrandi lahendus on funktsioon.

Tõepoolest, asendades selle võrrandi selle väärtusega, saame

see tähendab 3x = 3x

Seetõttu on funktsioon mis tahes konstandi C võrrandi üldine lahendus.

Leidke sellele võrrandile konkreetne lahendus, mis rahuldab algtingimust y(1)=1 Algtingimuste asendamine x = 1, y = 1 võrrandi üldlahendisse, saame kust C=0.

Seega saame konkreetse lahenduse üldisest, asendades selle võrrandi saadud väärtuse C=0- privaatne lahendus.

2.2. Eraldatavate muutujatega diferentsiaalvõrrandid

Eraldatavate muutujatega diferentsiaalvõrrand on järgmise kujuga võrrand: y"=f(x)g(y) või diferentsiaalide kaudu, kus f(x) Ja g(y)– määratud funktsioonid.

Nende jaoks y, mille jaoks võrrand y"=f(x)g(y) on võrdne võrrandiga, milles muutuja y on olemas ainult vasakul küljel ja muutuja x on ainult paremal. Nad ütlevad: "Eq. y"=f(x)g(y Eraldame muutujad."

Vormi võrrand nimetatakse eraldatud muutuja võrrandiks.

Võrrandi mõlema poole integreerimine Autor x, saame G(y) = F(x) + C on võrrandi üldlahend, kus G(y) Ja F(x)– mõned antiderivaadid vastavalt funktsioonide ja f(x), C suvaline konstant.

Algoritm eraldatavate muutujatega esimest järku diferentsiaalvõrrandi lahendamiseks

Näide 1

Lahenda võrrand y" = xy

Lahendus. Funktsiooni tuletis y" asendada see

eraldame muutujad

Integreerime võrdsuse mõlemad pooled:

Näide 2

2yy" = 1-3x2, Kui y 0 = 3 juures x 0 = 1

See on eraldatud muutuja võrrand. Kujutleme seda diferentsiaalides. Selleks kirjutame selle võrrandi ümber kujul Siit

Integreerides viimase võrdsuse mõlemad pooled, leiame

Algväärtuste asendamine x 0 = 1, y 0 = 3 me leiame KOOS 9=1-1+C, st. C = 9.

Seetõttu on vajalik osaline integraal või

Näide 3

Kirjutage võrrand punkti läbiva kõvera jaoks M(2;-3) ja millel on nurkkoefitsiendiga puutuja

Lahendus. Vastavalt seisundile

See on eraldatavate muutujatega võrrand. Jagades muutujad, saame:

Integreerides võrrandi mõlemad pooled, saame:

Kasutades algtingimusi, x = 2 Ja y = -3 me leiame C:

Seetõttu on nõutaval võrrandil vorm

2.3. Esimest järku lineaarsed diferentsiaalvõrrandid

Esimest järku lineaarne diferentsiaalvõrrand on vormi võrrand y" = f(x)y + g(x)

Kus f(x) Ja g(x)- mõned täpsustatud funktsioonid.

Kui g(x)=0 siis nimetatakse lineaarset diferentsiaalvõrrandit homogeenseks ja selle kuju on: y" = f(x)y

Kui siis võrrand y" = f(x)y + g(x) nimetatakse heterogeenseks.

Lineaarse homogeense diferentsiaalvõrrandi üldlahendus y" = f(x)y on antud valemiga: kus KOOS– suvaline konstant.

Eelkõige siis, kui C = 0, siis on lahendus y = 0 Kui lineaarne homogeenne võrrand näeb välja nagu y" = ky Kus k on mingi konstant, siis on selle üldlahend kujul: .

Lineaarse mittehomogeense diferentsiaalvõrrandi üldlahendus y" = f(x)y + g(x) on antud valemiga ,

need. on võrdne vastava lineaarse homogeense võrrandi üldlahendi ja selle võrrandi konkreetse lahendi summaga.

Vormi lineaarse mittehomogeense võrrandi jaoks y" = kx + b,

Kus k Ja b- mõned arvud ja konkreetne lahendus on konstantne funktsioon. Seetõttu on üldlahendusel vorm .

Näide. Lahenda võrrand y" + 2a +3 = 0

Lahendus. Esitame võrrandit kujul y" = -2y - 3 Kus k = -2, b = -3Üldine lahendus on antud valemiga.

Seetõttu kus C on suvaline konstant.

2.4. Esimest järku lineaarsete diferentsiaalvõrrandite lahendamine Bernoulli meetodil

Üldlahenduse leidmine esimest järku lineaarsele diferentsiaalvõrrandile y" = f(x)y + g(x) taandub kahe eraldatud muutujatega diferentsiaalvõrrandi lahendamiseks asendamise abil y=uv, Kus u Ja v- tundmatud funktsioonid x. Seda lahendusmeetodit nimetatakse Bernoulli meetodiks.

Algoritm esimest järku lineaarse diferentsiaalvõrrandi lahendamiseks

y" = f(x)y + g(x)

1. Sisestage asendus y=uv.

2. Eristage seda võrdsust y" = u"v + uv"

3. Asendus y Ja y" sellesse võrrandisse: u"v + uv" =f(x)uv + g(x) või u"v + uv" + f(x)uv = g(x).

4. Rühmitage võrrandi liikmed nii, et u võtke see sulgudest välja:

5. Leia funktsioon sulust, võrdsustades selle nulliga

See on eraldatav võrrand:

Jagame muutujad ja saame:

Kus . .

6. Asendage saadud väärtus v võrrandisse (alates 4. sammust):

ja leidke funktsioon See on eraldatavate muutujatega võrrand:

7. Kirjutage üldlahendus kujul: , st. .

Näide 1

Leidke võrrandile konkreetne lahendus y" = -2y +3 = 0 Kui y=1 juures x = 0

Lahendus. Lahendame selle asendamise abil y=uv,.y" = u"v + uv"

Asendamine y Ja y" sellesse võrrandisse saame

Rühmitades võrrandi vasakule küljele teise ja kolmanda liikme, võtame välja ühisteguri u sulgudest välja

Võrdsustame sulgudes oleva avaldise nulliga ja pärast saadud võrrandi lahendamist leiame funktsiooni v = v(x)

Saame eraldatud muutujatega võrrandi. Integreerime selle võrrandi mõlemad pooled: Leia funktsioon v:

Asendame saadud väärtuse v võrrandisse saame:

See on eraldatud muutuja võrrand. Integreerime võrrandi mõlemad pooled: Leiame funktsiooni u = u(x,c) Leiame üldise lahenduse: Leiame võrrandile konkreetse lahenduse, mis vastab algtingimustele y = 1 juures x = 0:

III. Kõrgemat järku diferentsiaalvõrrandid

3.1. Põhimõisted ja määratlused

Teist järku diferentsiaalvõrrand on võrrand, mis sisaldab mitte kõrgemat kui teist järku tuletisi. Üldjuhul kirjutatakse teist järku diferentsiaalvõrrand järgmiselt: F(x,y,y,y") = 0

Teist järku diferentsiaalvõrrandi üldlahend on funktsioon vormist , mis sisaldab kahte suvalist konstanti C 1 Ja C 2.

Teist järku diferentsiaalvõrrandi erilahendus on suvaliste konstantide teatud väärtuste üldlahendusest saadud lahendus C 1 Ja C 2.

3.2. Teist järku lineaarsed homogeensed diferentsiaalvõrrandid koos konstantsed koefitsiendid.

Teist järku lineaarne homogeenne diferentsiaalvõrrand konstantsete koefitsientidega nimetatakse vormi võrrandiks y" + py" +qy = 0, Kus lk Ja q- konstantsed väärtused.

Algoritm homogeensete konstantsete koefitsientidega teist järku diferentsiaalvõrrandite lahendamiseks

1. Kirjutage diferentsiaalvõrrand kujul: y" + py" +qy = 0.

2. Loo selle karakteristlik võrrand, tähistades y" läbi r 2, y" läbi r, y 1-s: r 2 + pr + q = 0

Artikli sisu

DIFERENTSIVÕRDED. Paljud füüsikalised seadused, millele teatud nähtused alluvad, on kirjutatud matemaatilise võrrandi kujul, mis väljendab teatud seost mingite suuruste vahel. Sageli me räägime ajas muutuvate suuruste seostest, näiteks mootori kasutegur, mõõdetuna vahemaaga, mille auto suudab ühe liitri kütusega läbida, sõltub auto kiirusest. Vastav võrrand sisaldab ühte või mitut funktsiooni ja nende tuletisi ning seda nimetatakse diferentsiaalvõrrandiks. (Kauguse muutumise kiiruse ajas määrab kiirus; seetõttu on kiirus vahemaa tuletis; samamoodi on kiirendus kiiruse tuletis, kuna kiirendus määrab kiiruse muutumise kiiruse ajas.) Suurepärane väärtus, mis diferentsiaalvõrranditel on matemaatika ja eriti selle rakenduste jaoks, on seletatav asjaoluga, et paljude füüsikaliste ja tehniliste probleemide uurimine taandub selliste võrrandite lahendamisele. Diferentsiaalvõrrandid mängivad olulist rolli ka teistes teadustes, näiteks bioloogias, majanduses ja elektrotehnikas; tegelikult tekivad need kõikjal, kus on vajadus nähtuste kvantitatiivse (numbrilise) kirjelduse järele (kuna meid ümbritsev maailm muutub aja jooksul ja tingimused muutuvad ühest kohast teise).

Näited.

Järgmised näited annavad parema ülevaate sellest, kuidas erinevaid probleeme diferentsiaalvõrrandite keeles formuleeritakse.

1) Mõnede radioaktiivsete ainete lagunemise seadus on see, et lagunemiskiirus on võrdeline selle aine saadaoleva kogusega. Kui x– aine kogus teatud ajahetkel t, siis saab selle seaduse kirjutada järgmiselt:

Kus dx/dt on lagunemiskiirus ja k– mingi antud ainet iseloomustav positiivne konstant. (Paremal küljel olev miinusmärk näitab seda x aja jooksul väheneb; plussmärk, mis on alati viidatud, kui märki pole selgesõnaliselt öeldud, tähendaks seda x suureneb aja jooksul.)

2) Anumas on algselt 10 kg soola lahustatuna 100 m 3 vees. Kui puhas vesi valab anumasse kiirusega 1 m 3 minutis ja seguneb lahusega ühtlaselt ning saadud lahus voolab sama kiirusega anumast välja, siis kui palju soola on anumas igal järgneval ajahetkel? Kui x– soola kogus (kg) mahutis korraga t, siis igal ajal t 1 m 3 lahust mahutis sisaldab x/100 kg soola; seetõttu väheneb soola kogus kiirusega x/100 kg/min või

3) Kehal olgu massid m vedru otsast riputatud, toimib taastav jõud võrdeliselt vedru pingega. Lase x– keha tasakaaluasendist kõrvalekaldumise suurus. Seejärel vastavalt Newtoni teisele seadusele, mis ütleb, et kiirendus (teine ​​tuletis x aja järgi, määratud d 2 x/dt 2) võrdeline jõuga:

Paremal küljel on miinusmärk, kuna taastav jõud vähendab vedru venitust.

4) Keha jahtumise seadus ütleb, et soojushulk kehas väheneb võrdeliselt kehatemperatuuri erinevusega ja keskkond. Kui 90°C temperatuurini kuumutatud kohvitass on ruumis, kus temperatuur on 20°C, siis

Kus T– kohvi temperatuur õigel ajal t.

5) Blefuscu osariigi välisminister väidab, et Lilliputi vastu võetud relvaprogramm sunnib tema riiki suurendama sõjalisi kulutusi nii palju kui võimalik. Lilliputi välisminister teeb sarnaseid avaldusi. Tekkinud olukorda (selle kõige lihtsamas tõlgenduses) saab täpselt kirjeldada kahe diferentsiaalvõrrandiga. Lase x Ja y- Lilliputi ja Blefuscu relvastuse kulud. Eeldades, et Lilliput suurendab oma kulutusi relvastusele proportsionaalselt Blefuscu relvastusele tehtavate kulutuste kasvumääraga ja vastupidi, saame:

kus liikmed on kirves Ja - poolt kirjeldada iga riigi sõjalisi kulutusi, k Ja l on positiivsed konstandid. (Selle probleemi sõnastas esmakordselt sel viisil 1939. aastal L. Richardson.)

Peale ülesande kirjutamist diferentsiaalvõrrandite keeles tuleks proovida neid lahendada, s.t. leidke suurused, mille muutumismäärad on võrrandites sisalduvad. Mõnikord leitakse lahendused selgesõnaliste valemite kujul, kuid sagedamini saab neid esitada vaid ligikaudsel kujul või saab nende kohta kvalitatiivset teavet. Sageli võib olla keeruline kindlaks teha, kas lahendus on üldse olemas, rääkimata selle leidmisest. Diferentsiaalvõrranditeooria olulise osa moodustavad nn “eksistentsi teoreemid”, milles tõestatakse lahenduse olemasolu üht või teist tüüpi diferentsiaalvõrrandi jaoks.

Füüsikalise probleemi algne matemaatiline sõnastus sisaldab tavaliselt lihtsustavaid eeldusi; nende mõistlikkuse kriteeriumiks võib olla matemaatilise lahenduse kooskõla aste olemasolevate vaatlustega.

Diferentsiaalvõrrandite lahendused.

Näiteks diferentsiaalvõrrand dy/dx = x/y, ei rahulda mitte arv, vaid funktsioon, antud juhul nii, et selle graafikul on mis tahes punktis, näiteks punktis koordinaatidega (2,3), puutuja kalle, võrdub koordinaatide suhtega (meie näites 2/3). Seda on ehitamisel lihtne kontrollida suur hulk punktid ja igast kõrvale jätta lühike vastava kaldega lõik. Lahenduseks on funktsioon, mille graafik puudutab iga punkti vastava lõiguga. Kui punkte ja lõike on piisavalt, siis saame ligikaudselt visandada lahenduskõverate kulgemise (joonis 1 on näidatud kolm sellist kõverat). Iga punkti läbib täpselt üks lahenduskõver y Nr 0. Iga üksikut lahendit nimetatakse diferentsiaalvõrrandi osalahendiks; kui on võimalik leida valem, mis sisaldab kõiki konkreetseid lahendusi (välja arvatud mõned erilahendused), siis öeldakse, et on saadud üldlahend. Konkreetne lahendus esindab ühte funktsiooni, samas kui üldine lahendus esindab tervet nende perekonda. Diferentsiaalvõrrandi lahendamine tähendab kas selle konkreetse või üldise lahenduse leidmist. Vaadeldavas näites on üldlahendusel vorm y 2 – x 2 = c, Kus c– mis tahes number; punkti (1,1) läbival konkreetsel lahendusel on vorm y = x ja selgub millal c= 0; punkti (2,1) läbival konkreetsel lahendusel on vorm y 2 – x 2 = 3. Tingimust, mis nõuab lahenduskõvera läbimist näiteks punktist (2,1), nimetatakse algtingimuseks (kuna see määrab lahenduskõvera alguspunkti).

Võib näidata, et näites (1) on üldlahendusel vorm x = ce –kt, Kus c– konstant, mida saab määrata näiteks aine koguse näidates juures t= 0. Võrrand näitest (2) – erijuhtum võrrand näitest (1), vastav k= 1/100. Esialgne seisund x= 10 kl t= 0 annab konkreetse lahenduse x = 10e –t/100 . Näite (4) võrrandil on üldlahend T = 70 + ce –kt ja privaatne lahendus 70 + 130 – kt; väärtuse määramiseks k, on vaja täiendavaid andmeid.

Diferentsiaalvõrrand dy/dx = x/y nimetatakse esimest järku võrrandiks, kuna see sisaldab esimest tuletist (diferentsiaalvõrrandi järku peetakse tavaliselt selles sisalduva kõrgeima tuletise järguks). Enamiku (kuigi mitte kõigi) esimest tüüpi diferentsiaalvõrrandite puhul, mis praktikas tekivad, läbib iga punkti ainult üks lahenduskõver.

Esimest järku diferentsiaalvõrrandeid on mitut olulist tüüpi, mida saab lahendada ainult elementaarfunktsioone sisaldavate valemite kujul - astmed, eksponendid, logaritmid, siinused ja koosinused jne. Sellised võrrandid hõlmavad järgmist.

Eraldatavate muutujatega võrrandid.

Vormi võrrandid dy/dx = f(x)/g(y) saab lahendada, kirjutades selle diferentsiaalidesse g(y)dy = f(x)dx ja mõlema osa integreerimine. Halvimal juhul saab lahenduse esitada tuntud funktsioonide integraalidena. Näiteks võrrandi puhul dy/dx = x/y meil on f(x) = x, g(y) = y. Kirjutades selle vormi ydy = xdx ja integreerides saame y 2 = x 2 + c. Eraldatavate muutujatega võrrandid hõlmavad võrrandeid näidetest (1), (2), (4) (neid saab lahendada ülalkirjeldatud viisil).

Võrrandid summaarsetes diferentsiaalides.

Kui diferentsiaalvõrrandil on vorm dy/dx = M(x,y)/N(x,y), Kus M Ja N on kaks antud funktsiooni, siis saab seda esitada kui M(x,y)dx – N(x,y)dy= 0. Kui vasak pool on mõne funktsiooni diferentsiaal F(x,y), siis saab diferentsiaalvõrrandi kirjutada kujul dF(x,y) = 0, mis on võrdne võrrandiga F(x,y) = konst. Seega on võrrandi lahenduskõverad funktsiooni "konstantsete tasemete jooned" ehk võrrandeid rahuldavate punktide asukoht. F(x,y) = c. Võrrand ydy = xdx(joon. 1) - eraldatavate muutujatega ja sama - summaarsetes diferentsiaalides: viimases veendumiseks kirjutame selle kujul ydy – xdx= 0, st. d(y 2 – x 2) = 0. Funktsioon F(x,y) on sel juhul võrdne (1/2)( y 2 – x 2); Mõned selle konstantse taseme jooned on näidatud joonisel fig. 1.

Lineaarvõrrandid.

Lineaarvõrrandid on "esimese astme" võrrandid - tundmatu funktsioon ja selle tuletised esinevad sellistes võrrandites ainult esimesel astmel. Seega on esimest järku lineaarsel diferentsiaalvõrrandil vorm dy/dx + lk(x) = q(x), Kus lk(x) Ja q(x) – funktsioonid, mis sõltuvad ainult x. Selle lahenduse saab alati kirjutada tuntud funktsioonide integraalide abil. Paljud muud tüüpi esimest järku diferentsiaalvõrrandid lahendatakse spetsiaalsete tehnikate abil.

Kõrgemat järku võrrandid.

Paljud diferentsiaalvõrrandid, millega füüsikud kokku puutuvad, on teist järku võrrandid (st teist tuletisi sisaldavad võrrandid, näiteks lihtsa harmoonilise liikumise võrrand näitest (3). md 2 x/dt 2 = –kx. Üldiselt võime eeldada, et teist järku võrrandil on osalahendused, mis vastavad kahele tingimusele; Näiteks võib nõuda, et lahenduskõver läbiks antud punkti antud suunas. Juhtudel, kui diferentsiaalvõrrand sisaldab mõnda parameetrit (arvu, mille väärtus sõltub asjaoludest), on nõutavat tüüpi lahendused olemas ainult siis, kui teatud väärtused see parameeter. Näiteks kaaluge võrrandit md 2 x/dt 2 = –kx ja me nõuame seda y(0) = y(1) = 0. Funktsioon yє 0 on ilmselgelt lahendus, kuid kui see on täisarv lk, st. k = m 2 n 2 lk 2, kus n on täisarv, kuid tegelikult on ainult sel juhul muid lahendusi, nimelt: y= patt npx. Parameetrite väärtusi, mille jaoks võrrandil on erilahendused, nimetatakse iseloomulikeks või omaväärtusteks; neil on paljude ülesannete täitmisel oluline roll.

Lihtsa harmoonilise liikumise võrrand on näide olulisest võrrandiklassist, nimelt konstantsete koefitsientidega lineaarsetest diferentsiaalvõrranditest. Rohkem üldine näide(ka teist järku) – võrrand

Kus a Ja b- antud konstandid, f(x) on antud funktsioon. Selliseid võrrandeid saab lahendada erinevatel viisidel, kasutades näiteks integraali Laplace'i teisendust. Sama võib öelda konstantsete koefitsientidega kõrgema järgu lineaarsete võrrandite kohta. Neil on ka oluline roll lineaarvõrrandid muutuva koefitsiendiga.

Mittelineaarsed diferentsiaalvõrrandid.

Võrrandeid, mis sisaldavad tundmatuid funktsioone ja nende tuletisi astmetest, mis on suuremad kui esimene või mõnel keerulisemal viisil, nimetatakse mittelineaarseteks. IN viimastel aastatel nad tõmbavad üha rohkem tähelepanu. Fakt on see, et füüsikalised võrrandid on tavaliselt lineaarsed ainult esimese lähendusega; Edasised ja täpsemad uuringud nõuavad reeglina mittelineaarsete võrrandite kasutamist. Lisaks on paljud probleemid olemuselt mittelineaarsed. Kuna mittelineaarsete võrrandite lahendused on sageli väga keerulised ja lihtsate valemite abil raskesti esitatavad, on oluline osa kaasaegne teooria on pühendatud nende käitumise kvalitatiivsele analüüsile, s.t. meetodite väljatöötamine, mis võimaldavad ilma võrrandit lahendamata öelda midagi olulist lahenduste olemuse kohta tervikuna: näiteks, et need kõik on piiratud või perioodilised või sõltuvad teatud viisil koefitsiendid.

Diferentsiaalvõrrandite ligikaudsed lahendused on leitavad numbriliselt, kuid see nõuab palju aega. Kiirete arvutite tulekuga vähenes see aeg oluliselt, mis avas uued võimalused paljude probleemide arvuliseks lahendamiseks, mis varem olid sellise lahenduse jaoks raskesti lahendatavad.

Olemasoluteoreemid.

Eksisteerimise teoreem on teoreem, mis väidab, et teatud tingimustel on antud diferentsiaalvõrrandil lahendus. On diferentsiaalvõrrandeid, millel pole lahendusi või on neid oodatust rohkem. Olemisteoreemi eesmärk on veenda meid, et antud võrrandil on tegelikult lahendus, ja kõige sagedamini kinnitada, et sellel on täpselt üks nõutavat tüüpi lahend. Näiteks võrrand, mida oleme juba kohanud dy/dx = –2y millel on täpselt üks lahendus, mis läbib iga tasandi punkti ( x,y) ja kuna oleme ühe sellise lahenduse juba leidnud, oleme seega selle võrrandi täielikult lahendanud. Teisest küljest võrrand ( dy/dx) 2 = 1 – y 2-l on palju lahendusi. Nende hulgas on sirged y = 1, y= –1 ja kõverad y= sin( x + c). Lahendus võib koosneda nende sirgjoonte ja kõverate mitmest segmendist, mis lähevad kokkupuutepunktides üksteise sisse (joonis 2).

Osadiferentsiaalvõrrandid.

Tavaline diferentsiaalvõrrand on väide ühe muutuja tundmatu funktsiooni tuletise kohta. Osaline diferentsiaalvõrrand sisaldab kahe või enama muutuja funktsiooni ja selle funktsiooni tuletisi vähemalt kahe erineva muutuja suhtes.

Füüsikas on selliste võrrandite näideteks Laplace'i võrrand

X, y) ringi sees, kui väärtused u määratud piiritleva ringi igas punktis. Kuna füüsikas on rohkem kui ühe muutujaga seotud probleemid pigem reegel kui erand, on lihtne ette kujutada, kui ulatuslik on osadiferentsiaalvõrrandite teooria teema.

Antud Interneti-kalkulaator võimaldab lahendada diferentsiaalvõrrandeid võrgus. Piisab, kui sisestate oma võrrandi vastavale väljale, tähistades apostroofiga funktsiooni tuletist, ja klõpsate nupul "lahenda võrrand". diferentsiaalvõrrandi lahendamine täiesti tasuta. Samuti saate Cauchy probleemi määratleda nii, et see hõlmab kogu komplekti võimalikud lahendused vali etteantud algtingimustele vastav jagatis. Cauchy probleem sisestatakse eraldi väljale.

Diferentsiaalvõrrand

Vaikimisi funktsioon võrrandis y on muutuja funktsioon x. Kui aga kirjutate võrrandisse näiteks y(t), tunneb kalkulaator selle automaatselt ära y muutujast on funktsioon t. Kalkulaatori abil saate lahendada diferentsiaalvõrrandeid mis tahes keerukuse ja tüübiga: homogeensed ja ebahomogeensed, lineaarsed või mittelineaarsed, esimest või teist ja kõrgemat järku, eraldatavate või mitteeraldatavate muutujatega võrrandid jne. Lahenduse erinevus. võrrand on antud analüütilisel kujul, on üksikasjalik kirjeldus. Diferentsiaalvõrrandid on füüsikas ja matemaatikas väga levinud. Ilma nende arvutamiseta on paljude ülesannete lahendamine võimatu (eriti matemaatilises füüsikas).

Diferentsiaalvõrrandite lahendamise üks etappe on funktsioonide integreerimine. Diferentsiaalvõrrandite lahendamiseks on olemas standardmeetodid. Võrrandid on vaja taandada eraldatavate muutujatega y ja x vormiks ning eraldatud funktsioonid eraldi integreerida. Selleks tuleb mõnikord teha teatud asendus.