Vietņu sadaļas
Redaktoru izvēle:
- Divslīpu jumta darīšana ar pašiem - izveidojiet pareizo rāmi ar pareizu aprēķinu
- Koka grīdas nokasīšana: soli pa solim dariet pats, kā pārstrādāt grīdu no dēļiem
- Jumta latojuma uzstādīšana uz spārēm
- Grīdas izolācijas kūka koka mājā
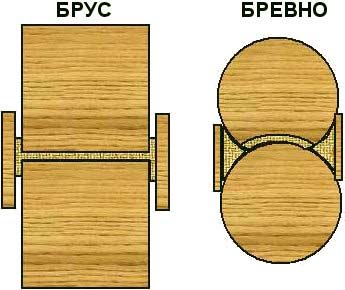
- Zāģmateriālu izlaides procenta noteikšana, zāģējot koksni, jo īpaši apaļo kokmateriālu.
- Kokmateriālu aprēķins vienā kubā
- Lamināts uz betona grīdas: pareizas uzstādīšanas iezīmes Finiera klāšana uz betona zem lamināta
- Kā piestiprināt bloku māju pie sienas, kā to izdarīt pareizi?
- Cik daudz kokmateriālu ir kubā: aprēķina metodes un aprēķinu piemēri
- Kāda ir atšķirība starp parketu un laminātu, kas ir labāks
Reklāma
| Aritmētiskā progresija, kā atrast e., Kā atrast aritmētiskās progresijas atšķirību |
|
Uzmanību! Aritmētiskā progresija ir skaitļu virkne, kurā katrs skaitlis ir lielāks (vai mazāks) nekā iepriekšējais ar tādu pašu summu. Šī tēma bieži šķiet sarežģīta un nesaprotama. Burtu indeksi, progresijas n-tais termiņš, progresijas atšķirība - tas viss kaut kā mulsina, jā ... Mēs sapratīsim aritmētiskās progresijas nozīmi, un viss uzreiz tiks pielāgots.) Aritmētiskās progresijas jēdziens.Aritmētiskā progresija ir ļoti vienkāršs un skaidrs jēdziens. Šaubies? Ne velti.) Skaties pats. Es uzrakstīšu nepabeigtu numuru sēriju: 1, 2, 3, 4, 5, ... Vai jūs varat pagarināt šo rindu? Kādi numuri brauks tālāk, par pieciem? Katrs ... uh-uh ..., īsi sakot, visi sapratīs, ka skaitļi 6, 7, 8, 9 utt. Sarežģīsim uzdevumu. Es dodu nepabeigtu numuru sēriju: 2, 5, 8, 11, 14, ... Jūs varat noķert modeli, pagarināt sēriju un piezvanīt septītais rindas numurs? Ja jūs saprotat, ka tas ir skaitlis 20, es jūs apsveicu! Jūs ne tikai jutāties galvenie aritmētiskās progresijas punkti, bet arī veiksmīgi izmantoja tos biznesā! Ja neesat to izdomājis, mēs lasām tālāk. Un tagad galvenos punktus no sensācijām pārveidosim matemātikā.) Pirmais galvenais punkts. Aritmētiskā progresija attiecas uz skaitļu rindām. Sākumā tas ir mulsinoši. Mēs esam pieraduši risināt vienādojumus, veidot grafikus un visu to ... Un tad pagariniet rindu, atrodiet rindas numuru ... Par neko nav jāuztraucas. Tikai progresēšana ir pirmā iepazīšanās ar jaunu matemātikas sadaļu. Sadaļu sauc par “Rindas”, un tā darbojas ar skaitļu un izteiksmju rindām. Pierod.) Otrais būtiskais punkts. Aritmētiskā progresijā jebkurš skaitlis atšķiras no iepriekšējā par tādu pašu summu. Pirmajā piemērā šī atšķirība ir viena. Lai kādu numuru jūs ņemtu, tas ir par vienu vairāk nekā iepriekšējais. Otrajā - trīs. Jebkurš skaitlis ir trīs reizes lielāks nekā iepriekšējais. Faktiski tieši šis brīdis dod mums iespēju noķert modeli un aprēķināt nākamos skaitļus. Trešais svarīgākais punkts. Šis brīdis nav pārsteidzošs, jā ... Bet ļoti, ļoti svarīgs. Šeit tas ir: katrs progresijas skaitlis stāv savā vietā. Ir pirmais numurs, ir septītais, ir četrdesmit piektais utt. Ja tie tik un tā tiek sajaukti, modelis pazudīs. Arī aritmētiskā progresija izzudīs. Atliek tikai skaitļu virkne. Tāda ir visa jēga. Protams, jaunajā tēmā parādās jauni termini un simboli. Jums tie jāzina. Pretējā gadījumā jūs nesapratīsit uzdevumu. Piemēram, jums jāizlemj kaut kas līdzīgs: Pierakstiet pirmos sešus aritmētiskās progresijas nosacījumus (a n), ja a 2 \u003d 5, d \u003d -2,5. Iedvesmo?) Burti, daži indeksi ... Un, starp citu, uzdevums nav nekur vienkāršāks. Jums vienkārši jāsaprot terminu un apzīmējumu nozīme. Tagad mēs apgūsim šo biznesu un atgriezīsimies pie uzdevuma. Noteikumi un apzīmējumi.Aritmētiskā progresija ir skaitļu virkne, kurā katrs skaitlis atšķiras no iepriekšējā par tādu pašu summu. Šis daudzums tiek saukts . Mēs sīkāk aplūkosim šo koncepciju. Aritmētiskās progresijas atšķirība.Starpības aritmētiskā progresija ir vērtība, pēc kuras tiek sasniegts jebkāds progresijas skaits vairāk iepriekšējā. Viens svarīgs jautājums. Lūdzu, pievērsiet uzmanību vārdam vairāk. Matemātiski tas nozīmē, ka tiek iegūts katrs progresijas skaitlis pievienojot aritmētiskās progresijas starpība ar iepriekšējo skaitli. Lai aprēķinātu, teiksim, otrais rindu numuri, tas ir nepieciešams pirmais numuru pievienot tieši šī aritmētiskās progresijas atšķirība. Aprēķinam piektais - atšķirība ir nepieciešama pievienot uz ceturtais labi utt. Starpības aritmētiskā progresija varbūt pozitīvs tad katrs sērijas numurs ir reāls vairāk nekā iepriekšējā. Šī progresija tiek saukta pieaug. Piemēram: 8; 13; 18; 23; 28; ..... Šeit tiek iegūts katrs numurs pievienojot pozitīvs skaitlis, +5 pret iepriekšējo. Var būt atšķirība negatīvs tad katras rindas numurs izrādīsies mazāk nekā iepriekšējā. Šo progresu sauc (neticēsit!) mazināsies. Piemēram: 8; 3; -2; -7; -12; ..... Šeit tiek iegūts arī katrs numurs pievienojot uz iepriekšējo, bet jau negatīvo skaitli -5. Starp citu, strādājot ar progresēšanu, ir ļoti noderīgi nekavējoties noteikt tā raksturu - vai tas palielinās, vai samazinās. Tas ļoti palīdz orientēties lēmumā, precīzi noteikt kļūdas un novērst tās, pirms nav par vēlu. Starpības aritmētiskā progresija parasti apzīmē ar burtu d. Kā atrast d ? Ļoti vienkārši. Ir nepieciešams noņemt no jebkura rindu skaita iepriekšējā numuru. Atņem. Starp citu, atņemšanas rezultātu sauc par "starpību".) Definējiet, piemēram, d aritmētiskās progresijas palielināšanai: 2, 5, 8, 11, 14, ... Mēs ņemam jebkuru sērijas numuru, kuru vēlamies, piemēram, 11. Mēs no tā atņemam iepriekšējais numurs t.i. 8: Tā ir pareizā atbilde. Šai aritmētiskajai progresijai starpība ir trīs. Jūs varat to ņemt jebkāds progresēšanas skaits, jo noteiktai progresijai d -vienmēr tas pats. Vismaz kaut kur rindas sākumā, vismaz pa vidu, vismaz jebkur. Jūs nevarat ņemt tikai pašu pirmo numuru. Tikai tāpēc, ka pats pirmais numurs neviena iepriekšējā.) Starp citu, to zinot d \u003d 3Šīs progresijas septīto numuru atrast ir ļoti vienkārši. Piektajam skaitlim pievienojiet 3 - mēs iegūstam sesto, tas būs 17. Pievienojiet trīs sestajam skaitlim, mēs iegūsim septīto numuru - divdesmit. Definēt d aritmētiskās progresijas samazināšanai: 8; 3; -2; -7; -12; ..... Es atgādinu, ka neatkarīgi no pazīmēm, lai noteiktu d vajadzība no jebkura numura ņem iepriekšējo. Izvēlieties jebkuru progresiju skaitu, piemēram, -7. Iepriekšējais ir skaitlis -2. Tad: d \u003d -7 - (-2) \u003d -7 + 2 \u003d -5 Aritmētiskās progresijas starpība var būt jebkura: vesels skaitlis, dalīta, iracionāla, jebkura. Citi termini un apzīmējumi.Katrs rindas numurs tiek izsaukts aritmētiskās progresijas loceklis. Katrs progresijas dalībnieks ir viņa numurs. Cipari iet stingri kārtībā, bez trikiem. Pirmais, otrais, trešais, ceturtais utt. Piemēram, 2., 5., 8., 11., 14., ... progresā divi ir pirmais loceklis, pieci ir otrais, vienpadsmit ir ceturtais, labi, jūs saprotat ...) Lūdzu, skaidri saprotiet - skaitļi paši var būt absolūti kādi veseli, daļēji, negatīvi, kas ir briesmīgi, bet numerācija - stingri kārtībā! Kā vispār uzrakstīt progresiju? Jautājumu nav! Katru rindas numuru raksta kā burtu. Parasti burtu izmanto, lai norādītu aritmētisko progresiju. a. Locekļa numuru norāda indekss labajā apakšējā stūrī. Locekļus raksta ar komatu (vai semikolu), piemēram: a 1, 2, 3, 4, 5, ... a 1ir pirmais numurs a 3 - trešais utt. Nekas viltīgs. Jūs varat uzrakstīt šo sēriju īsi šādi: (a n). Ir progresijas ierobežots un bezgalīgs. Galīgais progresēšanai ir ierobežots locekļu skaits. Pieci, trīsdesmit astoņi, cik vien vēlaties. Bet - baigais skaitlis. Bezgalīgs progresēšana - tajā ir bezgalīgs dalībnieku skaits, kā jūs varētu uzminēt.) Jūs varat uzrakstīt galīgo progresu, izmantojot virkni, piemēram, šo, visi dalībnieki, un punktu beigās: a, 2, 3, 4, 5. Vai arī tā, ja dalībnieku ir daudz: a, 1, 2, ..., 14, 15. Īsā ierakstā būs papildus jānorāda dalībnieku skaits. Piemēram (divdesmit biedriem), piemēram: (a n), n \u003d 20 Bezgalīgu progresiju var atpazīt ar elipsi rindas beigās, kā parādīts šīs stundas piemēros. Tagad jūs varat atrisināt uzdevumus. Uzdevumi ir vienkārši, lai izprastu aritmētiskās progresijas nozīmi. Aritmētiskās progresijas uzdevumu piemēri.Mēs detalizēti analizēsim iepriekš doto uzdevumu: 1. Pierakstiet pirmos sešus aritmētiskās progresijas locekļus (a n), ja a 2 \u003d 5, d \u003d -2,5. Mēs tulkojam uzdevumu saprotamā valodā. Tiek dota bezgalīga aritmētiskā progresija. Ir zināms šīs progresijas otrais numurs: a 2 \u003d 5. Progresijas atšķirība ir zināma: d \u003d -2,5. Jums jāatrod šīs progresijas pirmais, trešais, ceturtais, piektais un sestais loceklis. Skaidrības labad es uzrakstīšu sēriju atbilstoši problēmas apstākļiem. Pirmie seši dalībnieki, ja otrais loceklis ir pieci: 1, 5, 3, 4, 5, 6, ... a 3 = a 2 + d Aizstājējs izteiksmē a 2 \u003d 5 un d \u003d -2,5. Neaizmirstiet par mīnusu! a 3=5+(-2,5)=5 - 2,5 = 2,5 Trešais termiņš ir mazāks par otro. Viss ir loģiski. Ja skaitlis ir lielāks par iepriekšējo negatīvs vērtību, tad pats skaitlis būs mazāks nekā iepriekšējais. Progresija samazinās. Labi, apsveriet.) Mēs uzskatām mūsu sērijas ceturto dalībnieku: a 4 = a 3 + d a 4=2,5+(-2,5)=2,5 - 2,5 = 0 a 5 = a 4 + d a 5=0+(-2,5)= - 2,5 a 6 = a 5 + d a 6=-2,5+(-2,5)=-2,5 - 2,5 = -5 Tātad tiek aprēķināts trešais līdz sestais loceklis. Izrādījās šāda sērija: a 1, 5, 2,5, 0, -2,5, -5, ... Atliek atrast pirmo dalībnieku a 1 pa slaveno otro. Tas ir solis otrā virzienā, pa kreisi.) Tāpēc aritmētiskās progresijas atšķirība d nav jāpievieno a 2un atņemt: a 1 = a 2 - d a 1=5-(-2,5)=5 + 2,5=7,5 Tas arī viss. Darba atbilde: 7,5, 5, 2,5, 0, -2,5, -5, ... Pa ceļam es atzīmēju, ka mēs šo uzdevumu atrisinājām atkārtots veids. Šis biedējošais vārds nozīmē tikai progresijas dalībnieka meklēšanu pēc iepriekšējā (blakus esošā) numura. Par citiem veidiem, kā strādāt ar progresēšanu, tiks runāts vēlāk. No šī vienkāršā uzdevuma var izdarīt vienu svarīgu secinājumu. Atcerieties: Ja mēs zinām vismaz vienu locekli un aritmētiskās progresijas atšķirību, mēs varam atrast jebkuru šīs progresijas dalībnieku. Vai tu atceries? Šis vienkāršais secinājums ļauj mums atrisināt lielāko daļu skolas kursa problēmu par šo tēmu. Visi uzdevumi balstās uz trim galvenajiem parametriem: aritmētiskais progresijas loceklis, progresijas starpība, progresijas locekļa numurs. Tas arī viss. Protams, visa iepriekšējā algebra netiek atcelta.) Progresēšanai tiek pievienota nevienlīdzība, vienādojumi un citas lietas. Bet par pašu progresēšanu - Viss griežas ap trim parametriem. Piemēram, apsveriet dažus populārus uzdevumus par šo tēmu. 2. Pierakstiet galīgo aritmētisko progresiju kā virkni, ja n \u003d 5, d \u003d 0,4 un a 1 \u003d 3,6. Šeit viss ir vienkārši. Viss jau ir dots. Nepieciešams atcerēties, kā tiek uzskatīti aritmētiskās progresijas locekļi, saskaitīt un pierakstīt. Darba uzdevumā ieteicams nepalaist garām vārdus: "galīgais" un " n \u003d 5". Lai nerēķinātos ar pilnīgu zilo krāsu.) Šajā progresijā ir tikai 5 (pieci) locekļi: a 2 \u003d a 1 + d \u003d 3,6 + 0,4 \u003d 4 a 3 \u003d a 2 + d \u003d 4 + 0,4 \u003d 4,4 a 4 = a 3 + d \u003d 4,4 + 0,4 \u003d 4,8 a 5 = a 4 + d \u003d 4,8 + 0,4 \u003d 5,2 Atliek pierakstīt atbildi: 3,6; 4; 4,4; 4,8; 5,2. Vēl viens uzdevums: 3. Nosakiet, vai skaitlis 7 ir aritmētiskās progresijas loceklis (a n), ja a 1 \u003d 4,1; d \u003d 1,2. Hmm ... Kas zina? Kā kaut ko noteikt? Kā-kā ... Jā, pierakstiet progresiju sērijas formā un pārbaudiet, vai septiņi tur ir vai nav! Mēs uzskatām: a 2 \u003d a 1 + d \u003d 4,1 + 1,2 \u003d 5,3 a 3 \u003d a 2 + d \u003d 5,3 + 1,2 \u003d 6,5 a 4 = a 3 + d \u003d 6,5 + 1,2 \u003d 7,7 4,1; 5,3; 6,5; 7,7; ... Tagad ir skaidri redzams, ka mēs esam tikai septiņi izslīdēja cauri no 6,5 līdz 7,7! Septiņi neietilpa mūsu skaitļu sērijās, un tāpēc septiņi nebūs šīs progresēšanas dalībnieces. Atbilde ir nē. Un šeit ir problēma, kuras pamatā ir reālā GIA versija: 4. Tiek izrakstīti vairāki secīgi aritmētiskās progresijas locekļi: ...; 15; x; 9; 6; ...
Šeit ir ierakstīta sērija bez beigām un sākuma. Nav dalībnieku skaita, atšķirības d. Par neko nav jāuztraucas. Lai atrisinātu uzdevumu, pietiek ar izpratni par aritmētiskās progresijas nozīmi. Mēs skatāmies un saprotam, ka tas ir iespējams uzzini no šīs rindas? Kādi ir trīs galvenie parametri? Biedru skaits? Šeit nav neviena numura. Bet ir trīs cipari un - uzmanība! - vārds "secīgs" stāvoklī. Tas nozīmē, ka skaitļi ir kārtībā, bez atstarpēm. Vai šajā rindā ir divi? kaimiņu slaveni numuri? Jā, ir! Tie ir 9 un 6. Tāpēc mēs varam aprēķināt aritmētiskās progresijas starpību! Mēs atņemam no sešiem iepriekšējā skaitlis, t.i. deviņi: Palika vienkārši sīkumi. Kāds ir iepriekšējais skaitlis x? Piecpadsmit. Tātad X var viegli atrast, vienkārši pievienojot. Lai pievienotu 15, pievienojiet aritmētiskās progresijas starpību: Tas arī viss. Atbilde ir: x \u003d 12 Šīs problēmas mēs risinām paši. Piezīme: šie uzdevumi nav paredzēti formulām. Tīri saprotot aritmētiskās progresijas nozīmi.) Vienkārši uzrakstiet sēriju ar cipariem un burtiem, apskatiet un padomājiet. 5. Atrodiet aritmētiskās progresijas pirmo pozitīvo vērtību, ja a \u003d 5; d \u003d 1,1. 6. Ir zināms, ka skaitlis 5.5 ir aritmētiskās progresijas (a n) loceklis, kur a 1 \u003d 1,6; d \u003d 1,3. Nosakiet šī locekļa numuru n. 7. Ir zināms, ka aritmētiskajā progresijā a 2 \u003d 4; a 5 \u003d 15,1. Atrodiet 3. 8. Tiek izrakstīti vairāki secīgi aritmētiskās progresijas locekļi: ...; 15,6; x; 3.4; ... Atrodiet progresēšanas termiņu, kas norādīts ar burtu x. 9. Vilciens sāka virzīties no stacijas, vienmērīgi palielinot ātrumu par 30 metriem minūtē. Kāds būs vilciena ātrums piecās minūtēs? Sniedziet atbildi km / h. 10. Ir zināms, ka aritmētiskajā progresijā a 2 \u003d 5; a 6 \u003d -5. Atrodiet 1. Atbildes (strīdā): 7,7; 7,5; 9,5; 9; 0,3; 4. Vai tas izdevās? Lieliski! Nākamajās nodarbībās jūs varat apgūt aritmētisko progresēšanu augstākā līmenī. Vai viss neizdevās? Tam nav nozīmes. Īpašajā 555. sadaļā visi šie uzdevumi tiek izjaukti.) Un, protams, ir aprakstīts vienkāršs praktisks paņēmiens, kas skaidri, skaidri, skaidri izceļ šādu uzdevumu risinājumu. Starp citu, mīklā par vilcienu ir divas problēmas, uz kurām cilvēki bieži paklupa. Viens ir tikai progresīvs, un otrs ir kopīgs visām matemātikas un arī fizikas problēmām. Tas ir dimensiju tulkojums no viena uz otru. Rakstā parādīts, kā šīs problēmas atrisināt. Šajā nodarbībā mēs pārbaudījām aritmētiskās progresijas elementāro nozīmi un tās galvenos parametrus. Tas ir pietiekami, lai atrisinātu gandrīz visas problēmas par šo tēmu. Pievienot d uz cipariem, uzrakstiet numuru, viss tiks izlemts. Kā uz šīs stundas piemēriem, risinājums “uz pirkstiem” ir labi piemērots ļoti īsiem rindu gabaliem. Ja sērija ir autentiskāka, aprēķini ir sarežģīti. Piemēram, ja jautājuma 9. problēmā aizstājiet piecas minūtes ieslēgts trīsdesmit piecas minūtes uzdevums kļūs ievērojami dusmīgāks.) Ir arī uzdevumi, kas pēc būtības ir vienkārši, bet aprēķinos nav konsekventi: Dota aritmētiskā progresija (a n). Atrodiet 121, ja a 1 \u003d 3 un d \u003d 1/6. Un ko, mēs pievienosim daudzas reizes virs 1/6 ?! Vai jūs to varat nogalināt !? Jūs varat.) Ja nezināt vienkāršo formulu, pēc kuras šādus uzdevumus var atrisināt minūtē. Šī formula būs nākamajā nodarbībā. Un šī problēma tur tiek atrisināta. Pēc minūtes.) Ja jums patīk šī vietne ...Starp citu, man jums ir vēl pāris interesantas vietnes.) Jūs varat praktizēt piemēru risināšanu un uzzināt savu līmeni. Pārbaude ar tūlītēju verifikāciju. Mācības - ar interesi!) Jūs varat iepazīties ar funkcijām un atvasinājumiem.  Jā, jā: aritmētiskā progresija jums nav rotaļlieta :) Jā, jā: aritmētiskā progresija jums nav rotaļlieta :) Nu, draugi, ja jūs lasāt šo tekstu, iekšējā robeža liecina, ka jūs joprojām nezināt, kas ir aritmētiskā progresija, bet jūs tiešām (nē, piemēram: Oooooo!) Vēlaties zināt. Tāpēc es ne mocīšu jūs ar gariem ievadiem un nekavējoties ķēros pie biznesa. Pirmkārt, pāris piemēri. Apsveriet vairākas numuru kopas:
Kas visiem šiem kopiem ir kopīgs? No pirmā acu uzmetiena nekas. Bet patiesībā ir kaut kas. Proti: katrs nākamais elements atšķiras no iepriekšējā ar vienu un to pašu skaitli. Spriediet paši. Pirmais komplekts ir vienkārši cipari pēc kārtas, katrs nākamais ir vairāk nekā iepriekšējais. Otrajā gadījumā starpība starp blakus esošajiem skaitļiem jau ir pieci, bet šī atšķirība joprojām ir nemainīga. Trešajā gadījumā saknes parasti ir. Tomēr $ 2 \\ sqrt (2) \u003d \\ sqrt (2) + \\ sqrt (2) $ un $ 3 \\ sqrt (2) \u003d 2 \\ sqrt (2) + \\ sqrt (2) $, t.i. un šajā gadījumā katrs nākamais elements vienkārši palielinās par $ \\ sqrt (2) $ (un nebaidieties, ka šis skaitlis ir neracionāls). Tātad: visas šādas secības sauc par aritmētisko progresiju. Mēs sniedzam stingru definīciju:
Un uzreiz pāris svarīgi punkti. Pirmkārt, tiek ņemta vērā tikai progresēšana pasūtīts ciparu secība: viņiem ir atļauts stingri lasīt rakstīšanas secībā - un nekas cits. Jūs nevarat pārkārtot un apmainīt numurus. Otrkārt, pati secība var būt ierobežota vai bezgalīga. Piemēram, kopa (1; 2; 3) acīmredzami ir ierobežota aritmētiskā progresija. Bet, ja jūs kaut ko uzrakstāt garā (1; 2; 3; 4; ...) - tas jau ir bezgalīgs progresējums. Elipsis pēc četriem it kā liek domāt, ka turpinās diezgan daudz skaitļu. Piemēram, bezgala daudz. :) Es arī vēlētos atzīmēt, ka progresija pieaug un samazinās. Mēs jau esam redzējuši pieaugošos - to pašu komplektu (1; 2; 3; 4; ...). Šeit ir daži progresējošas attīstības samazināšanas piemēri:
Labi, labi: pēdējais piemērs var šķist pārāk sarežģīts. Bet pārējie, es domāju, jums ir skaidri saprotami. Tāpēc mēs ieviešam jaunas definīcijas:
Atlicis tikai viens jautājums: kā atšķirt pieaugošo progresu no samazināšanās? Par laimi, viss ir atkarīgs no tā, kāda ir skaitļa $ d $ zīme, t.i. progresijas atšķirības:
Mēģināsim aprēķināt starpību $ d $ trim iepriekš norādītajām samazinošajām progresijām. Lai to izdarītu, vienkārši ņemiet divus blakus esošos elementus (piemēram, pirmo un otro) un atņemiet no skaitļa labajā pusē, skaitļa kreisajā pusē. Tas izskatīsies šādi:
Kā redzat, visos trīs gadījumos atšķirība patiešām izrādījās negatīva. Un tagad, kad mēs esam vairāk vai mazāk sakārtojuši definīcijas, ir pienācis laiks izdomāt, kā tiek aprakstītas progresijas un kādas ir to īpašības. Progresijas un atkārtošanās formulas dalībniekiTā kā mūsu secību elementus nevar mainīt, tos var numurēt: \\ [\\ pa kreisi (((a) _ (n)) \\ pa labi) \u003d \\ pa kreisi \\ (((a) _ (1)), \\ ((a) _ (2)), ((a) _ (3) )), ... \\ pa labi \\) \\] Šīs kopas atsevišķos elementus sauc par progresijas locekļiem. Viņiem tos norāda ar numura palīdzību: pirmais loceklis, otrais loceklis utt. Turklāt, kā mēs jau zinām, blakus esošie progresijas locekļi ir saistīti ar formulu: \\ [(((a) _ (n)) - ((a) _ (n-1)) \u003d d \\ Rightarrow ((a) _ (n)) \u003d ((a) _ (n-1)) + d \\] Īsāk sakot, lai atrastu progresijas termiņu $ n $, jums jāzina $ n-1 $ ceturtais termiņš un starpība $ d $. Šādu formulu sauc par atkārtotu, jo ar tās palīdzību jūs varat atrast jebkuru numuru, tikai zinot iepriekšējo (un faktiski - visus iepriekšējos). Tas ir ļoti neērti, tāpēc ir sarežģītāka formula, kas samazina visus aprēķinus līdz pirmajam termiņam un starpību: \\ [(((a) _ (n)) \u003d ((a) _ (1)) + \\ pa kreisi (n-1 \\ pa labi) d \\] Protams, jūs jau esat izpildījis šo formulu. Viņiem patīk to sniegt visu veidu uzziņu grāmatās un rezolūcijās. Jebkurā saprātīgā matemātikas mācību grāmatā viņa iet viena no pirmajām. Neskatoties uz to, es iesaku nelielu praksi.
Tas ir viss! Lūdzu, ņemiet vērā: mūsu progresija samazinās. Protams, $ n \u003d 1 $ nevarēja aizstāt - pirmais termins mums jau ir zināms. Tomēr, aizstājot vienību, mēs pārliecinājāmies, ka pat pirmo termiņu mūsu formula darbojas. Citos gadījumos tas nonāca līdz banālai aritmētikai.
Pievērsiet uzmanību atklātai progresijas ziņkārīgajai īpašībai: ja mēs ņemam $ n $ th un $ m $ th nosacījumus un tos atņemam viens no otra, mēs iegūstam starpību starp progresijas reizinājumu ar skaitli $ n-m $: \\ [(((a) _ (n)) - ((a) _ (m)) \u003d d \\ cdot \\ pa kreisi (n-m \\ pa labi) \\] Vienkāršs, bet ļoti noderīgs īpašums, kas jums noteikti jāzina - ar tā palīdzību jūs varat ievērojami paātrināt daudzu problēmu progresēšanu. Šeit ir spilgts piemērs:
Tas ir viss! Mums nevajadzēja izveidot vienādojumu sistēmas un saskaitīt pirmo termiņu un starpību - viss tika izlemts burtiski pāris rindās. Tagad apskatīsim cita veida uzdevumu - meklēt negatīvos un pozitīvos progresēšanas dalībniekus. Nav noslēpums, ka, ja progresēšana palielinās, kamēr pirmais termins ir negatīvs, tad agrāk vai vēlāk tajā parādīsies pozitīvi vārdi. Un otrādi: mazinošās progresēšanas dalībnieki agrāk vai vēlāk kļūs negatīvi. Turklāt ne vienmēr ir iespējams šo brīdi sagraut “uz pieres”, secīgi šķirojot pa elementiem. Bieži vien uzdevumi ir strukturēti tā, ka bez zināšanām par formulām aprēķiniem būtu vajadzīgas vairākas lapas - mēs vienkārši aizmigtu, līdz atradīsim atbildi. Tāpēc mēs centīsimies šīs problēmas atrisināt ātrāk.
Pēdējā rindiņa ir jāprecizē. Tātad, mēs zinām, ka $ n \\ lt 15 \\ frac (7) (27) $. No otras puses, mēs esam apmierināti tikai ar skaitļa veselām vērtībām (turklāt: $ n \\ in \\ mathbb (N) $), tāpēc lielākais atļautais skaitlis ir precīzi $ n \u003d 15 $ un nekādā gadījumā 16.
Lūdzu, ņemiet vērā: pēdējā uzdevumā viss saruka uz stingru nevienlīdzību, tāpēc opcija $ n \u003d 55 $ mums nebūs piemērota. Tagad, kad esam iemācījušies atrisināt vienkāršas problēmas, pāriesim pie sarežģītākām. Bet vispirms izpētīsim vēl vienu ļoti noderīgu aritmētisko progresiju īpašību, kas nākotnē mums ietaupīs daudz laika un nevienlīdzīgas šūnas. :) Aritmētiskais vidējais un vienādi ievilkumiApsveriet vairākus secīgus nosacījumus, kā palielināt aritmētisko progresiju $ \\ left (((a) _ (n)) \\ right) $. Mēģināsim tos iezīmēt ciparu rindā: Ciparu līnijas aritmētiskās progresijas locekļiEs īpaši atzīmēju $ ((a) _ (n-3)), ..., ((a) _ (n + 3)) $, nevis dažus $ ((a) _ (1)) patvaļīgus dalībniekus. , \\ ((a) _ (2)), \\ ((a) _ (3)) $ utt. Tā kā noteikums, par kuru es tagad runāšu, darbojas vienādi attiecībā uz visiem “segmentiem”. Un noteikums ir ļoti vienkāršs. Atgādināsim atkārtošanās formulu un uzrakstīsim to visiem atzīmētajiem dalībniekiem: \\ [\\ sākt (izlīdzināt) & ((a) _ (n-2)) \u003d ((a) _ (n-3)) + d; \\\\ & ((a) _ (n-1)) \u003d ((a) _ (n-2)) + d; \\\\ & ((a) _ (n)) \u003d ((a) _ (n-1)) + d; \\\\ & ((a) _ (n + 1)) \u003d ((a) _ (n)) + d; \\\\ & ((a) _ (n + 2)) \u003d ((a) _ (n + 1)) + d; \\\\ \\ beigas (izlīdzināt) \\] Tomēr šīs vienlīdzības var pārrakstīt atšķirīgi: \\ [\\ sākt (izlīdzināt) & ((a) _ (n-1)) \u003d ((a) _ (n)) - d; \\\\ & ((a) _ (n-2)) \u003d ((a) _ (n)) - 2d; \\\\ & ((a) _ (n-3)) \u003d ((a) _ (n)) - 3d; \\\\ & ((a) _ (n + 1)) \u003d ((a) _ (n)) + d; \\\\ & ((a) _ (n + 2)) \u003d ((a) _ (n)) + 2d; \\\\ & ((a) _ (n + 3)) \u003d ((a) _ (n)) + 3d; \\\\ \\ beigas (izlīdzināt) \\] Ko tad? Un tas, ka termini $ ((a) _ (n-1)) $ un $ ((a) _ (n + 1)) $ atrodas vienādā attālumā no $ ((a) _ (n)) USD. Un šis attālums ir $ d $. To pašu var teikt par terminiem $ ((a) _ (n-2)) $ un $ ((a) _ (n + 2)) $ - tie tiek noņemti arī no $ ((a) _ (n)) $ tāds pats attālums, kas vienāds ar USD 2d $. Jūs varat turpināt līdz bezgalībai, bet attēls labi ilustrē nozīmi  Progresijas locekļi atrodas vienādā attālumā no centra Progresijas locekļi atrodas vienādā attālumā no centra Ko tas nozīmē mums? Tas nozīmē, ka jūs varat atrast $ ((a) _ (n)) $, ja ir zināmi blakus esošie skaitļi: \\ [(((a) _ (n)) \u003d \\ frac (((a) _ (n-1)) + ((a) _ (n + 1))) (2) \\] Mēs esam secinājuši lielisku paziņojumu: katrs aritmētiskās progresijas loceklis ir vienāds ar kaimiņu locekļu vidējo aritmētisko! Turklāt: mēs varam atkāpties no mūsu $ ((a) _ (n)) $ pa kreisi un pa labi nevis ar vienu soli, bet gan ar $ k $ soļiem - un joprojām formula būs taisnība: \\ [(((a) _ (n)) \u003d \\ frac (((a) _ (n-k)) + ((a) _ (n + k))) (2) \\] T. i. mēs viegli atrodam dažus USD (a) _ (150)) $, ja zinām $ ((a) _ (100)) $ un $ ((a) _ (200)) $, jo $ (( a) _ (150)) \u003d \\ frac (((a) _ (100)) + ((a) _ (200))) (2) $. No pirmā acu uzmetiena var šķist, ka šis fakts nedod mums neko noderīgu. Tomēr praksē daudzi uzdevumi ir īpaši “asināti”, lai izmantotu aritmētisko vidējo. Apskatiet:
Ja problēmas risināšanas procesā jūs saņemat dažus brutālus skaitļus vai arī neesat pilnīgi pārliecināts par atrasto atbilžu pareizību, tad ir kāds brīnišķīgs triks, kas ļauj jums pārbaudīt, vai problēmu esam atrisinājuši pareizi? Pieņemsim, ka uzdevumā Nr. 6 mēs saņēmām atbildes −3 un 2. Kā es varu pārliecināties, ka šīs atbildes ir pareizas? Aizstāsim tos tikai sākotnējā stāvoklī un redzēsim, kas notiks. Atgādināšu, ka mums ir trīs skaitļi ($ -6 (() ^ (2)) $, $ + 1 $ un $ 14 + 4 (() ^ (2)) $), kuriem vajadzētu būt aritmētiskai progresijai. Aizstājējs $ x \u003d -3 $: \\ [\\ sākt (izlīdzināt) & x \u003d -3 \\ labā bulta \\\\ & -6 ((x) ^ (2)) \u003d - 54; \\\\ & x + 1 \u003d -2; \\\\ & 14 + 4 ((x) ^ (2)) \u003d 50. \\ beigas (izlīdzināt) \\] Ieguvuši ciparus −54; −2; 50, kas atšķiras par 52, bez šaubām, ir aritmētiskā progresija. Tas pats notiek ar $ x \u003d 2 $: \\ [\\ sākt (izlīdzināt) & x \u003d 2 \\ labo pusi \\\\ & -6 ((x) ^ (2)) \u003d - 24; \\\\ & x + 1 \u003d 3; \\\\ & 14 + 4 ((x) ^ (2)) \u003d 30. \\ beigas (izlīdzināt) \\] Atkal progresija, bet ar starpību 27. Tādējādi problēma tiek atrisināta pareizi. Tie, kas vēlas, var pats pārbaudīt otro uzdevumu, bet man uzreiz jāsaka: viss ir arī tur. Kopumā, risinot pēdējos uzdevumus, mēs saskārāmies ar vēl vienu interesantu faktu, kas arī jāatceras:
Nākotnē šī apgalvojuma izpratne ļaus mums burtiski “konstruēt” nepieciešamos progresus, balstoties uz problēmas stāvokli. Bet pirms mēs veicam šāda veida “būvniecību”, mums vajadzētu pievērst uzmanību citam faktam, kas tieši izriet no jau apsvērtā. Elementu grupēšana un summaAtkal atgriezīsimies pie skaitliskās ass. Mēs atzīmējam vairākus progresēšanas dalībniekus, starp kuriem, iespējams,. ir daudz citu dalībnieku: Skaitļu rindā ir atzīmēti 6 elementiMēģināsim izteikt “kreiso asti” kā $ ((a) _ (n)) $ un $ d $, bet “labo asti” - USD ((a) _ (k)) $ un $ d $ izteiksmē. Tas ir ļoti vienkārši: \\ [\\ sākt (izlīdzināt) & ((a) _ (n + 1)) \u003d ((a) _ (n)) + d; \\\\ & ((a) _ (n + 2)) \u003d ((a) _ (n)) + 2d; \\\\ & ((a) _ (k-1)) \u003d ((a) _ (k)) - d; \\\\ & ((a) _ (k-2)) \u003d ((a) _ (k)) - 2d. \\\\ \\ beigas (izlīdzināt) \\] Tagad ņemiet vērā, ka šādas summas ir vienādas: \\ [\\ sākt (izlīdzināt) & ((a) _ (n)) + ((a) _ (k)) \u003d S; \\\\ & ((a) _ (n + 1)) + ((a) _ (k-1)) \u003d ((a) _ (n)) + d + ((a) _ (k)) - d \u003d S; \\\\ & ((a) _ (n + 2)) + ((a) _ (k-2)) \u003d ((a) _ (n)) + 2d + ((a) _ (k)) - 2d \u003d S. \\ beigas (izlīdzināt) \\] Vienkārši sakot, ja par sākumu ņemsim divus progresijas elementus, kas kopumā ir vienādi ar kaut kādu skaitli $ S $, un tad mēs sākam soli no šiem elementiem pretējos virzienos (pret otru vai pretēji dzēšanai), tad to elementu summa, uz kuriem mēs paklupsim, arī būs vienāda $ S $. To grafiski vislabāk var attēlot:  Vienāda atkāpe dod vienādas summas Vienāda atkāpe dod vienādas summas Izpratne par šo faktu ļaus mums atrisināt principiāli augstāka sarežģītības līmeņa problēmas, nekā mēs apskatījām iepriekš. Piemēram, piemēram:
Teksta uzdevumi ar progresēšanuNoslēgumā es vēlētos apsvērt pāris samērā vienkāršus uzdevumus. Nu, kā vienkārši: lielākajai daļai studentu, kuri skolā mācās matemātiku un nav lasījuši iepriekš rakstīto, šie uzdevumi var šķist kā žests. Neskatoties uz to, tieši šādas problēmas ietilpst eksāmenā un eksāmenā matemātikā, tāpēc iesaku ar tiem iepazīties.
Ja jūs lasāt līdz šai vietai, es steidzos jūs apsveikt: jūs aritmētiskā progresijā esat veiksmīgi pabeidzis “jauno cīnītāju kursu”. Varat droši pāriet uz nākamo nodarbību, kur mēs izpētīsim progresijas summas formulu, kā arī svarīgas un ļoti noderīgas tās sekas. Aritmētiskā un ģeometriskā progresija Teorētiskā informācija
Teorētiskā informācija
Paraugu uzdevumi ar komentāriem 1. uzdevums Aritmētiskā progresijā ( a n) a 1 = -6, a 2 Pēc n-tā locekļa formulas: a 22 = a 1 + d (22 - 1) \u003d a 1 + 21 d Pēc nosacījuma: a 1 \u003d -6, tad a 22 \u003d -6 + 21 d. Ir jāatrod progresiju atšķirība: d \u003d a 2 - a 1 = -8 – (-6) = -2 a 22 = -6 + 21 ∙ (-2) = - 48. Atbilde ir: a 22 = -48. 2. uzdevums Atrodiet ģeometriskās progresijas piekto terminu: -3; 6; .... 1. metode (izmantojot n-termina formulu) Pēc ģeometriskās progresijas n-tā termiņa formulas: b 5 \u003d b 1 ∙ q 5 - 1 = b 1 ∙ q 4. Kopš b 1 = -3, 2. metode (izmantojot atkārtošanās formulu) Tā kā progresijas saucējs ir -2 (q \u003d -2), tad: b 3 = 6 ∙ (-2) = -12; b 4 = -12 ∙ (-2) = 24; b 5 = 24 ∙ (-2) = -48. Atbilde ir: b 5 = -48. 3. uzdevums Aritmētiskā progresijā ( a n) 74 = 34; a 76 \u003d 156. Atrodiet šīs progresijas septiņdesmit piekto locekli. Aritmētiskajai progresēšanai raksturīgajam īpašumam ir šāda forma No tā izriet: Aizstāt datus formulā: Atbilde: 95. 4. uzdevums Aritmētiskā progresijā ( a n) a n \u003d 3n - 4. Atrodiet septiņpadsmit pirmo dalībnieku summu. Lai uzzinātu aritmētiskās progresijas n-pirmo locekļu summu, tiek izmantotas divas formulas: Kurš šajā gadījumā ir ērtāks? Pēc nosacījuma ir zināma sākotnējās progresēšanas n-tā termiņa formula ( a n) a n \u003d 3n - 4. Jūs varat atrast tūlīt un a 1un a 16 nebūdams d. Tāpēc mēs izmantojam pirmo formulu. Atbilde: 368. 5. uzdevums Aritmētiskā progresijā ( a n) a 1 = -6; a 2 \u003d -8. Atrodiet progresijas divdesmit otro locekli. Pēc n-tā locekļa formulas: a 22 \u003d a 1 + d (22 – 1) = a 1 + 21d. Pēc nosacījuma, ja a 1 \u003d -6, tad a 22 \u003d -6 + 21d. Ir jāatrod progresiju atšķirība: d \u003d a 2 - a 1 = -8 – (-6) = -2 a 22 = -6 + 21 ∙ (-2) = -48. Atbilde ir: a 22 = -48. 6. uzdevums Reģistrē vairākus secīgus ģeometriskās progresijas nosacījumus: Atrodiet progresēšanas termiņu, kas norādīts ar burtu x. Risinot, mēs izmantojam n-tā termina formulu b n \u003d b 1 ∙ q n - 1 ģeometriskām progresijām. Pirmais progresijas dalībnieks. Lai atrastu progresijas saucēju q, jums jāņem jebkurš no šiem progresijas dalībniekiem un jāsadala ar iepriekšējo. Mūsu piemērā mēs varam ņemt un dalīt. Mēs iegūstam, ka q \u003d 3. n vietā formulā aizstājam 3, jo jāatrod dotās ģeometriskās progresijas trešais termins. Aizstājot atrastās vērtības formulā, iegūstam: Atbilde:. 7. uzdevums No aritmētiskās progresijas, ko nosaka n-tā termina formula, izvēlieties to, kuram nosacījums a 27 > 9: Tā kā dotajam nosacījumam jābūt izpildītam progresijas 27. dalībniekam, katrā no četrām progresijām n aizvietojiet 27, nevis n. Ceturtajā progresijā mēs iegūstam: Atbilde: 4. 8. uzdevums Aritmētiskā progresijā a 1 \u003d 3, d \u003d -1,5. Norādiet lielāko n vērtību, kurai pieder nevienlīdzība a n > -6. Studējot algebru vispārizglītojošajā skolā (9. klase), viena no svarīgām tēmām ir skaitlisko secību izpēte, kas ietver progresijas - ģeometrisko un aritmētisko. Šajā rakstā mēs apskatīsim aritmētisko progresiju un piemērus ar risinājumiem. Kas ir aritmētiskā progresija?Lai to saprastu, ir jāsniedz aplūkojamās progresijas definīcija, kā arī jāsniedz pamata formulas, kuras turpmāk izmantos problēmu risināšanā. Ir zināms, ka dažās algebriskās progresijās 1. termiņš ir 6, bet 7. termiņš ir 18. Ir jāatrod atšķirība un jāatjauno šī secība 7 locekļiem. Mēs izmantojam formulu, lai noteiktu nezināmu terminu: a n \u003d (n - 1) * d + a 1. Mēs tajā aizstājam zināmos nosacījuma datus, tas ir, skaitļus a 1 un 7, mums ir: 18 \u003d 6 + 6 * d. Izmantojot šo izteiksmi, var viegli aprēķināt starpību: d \u003d (18 - 6) / 6 \u003d 2. Tādējādi tika atbildēta uz problēmas pirmo daļu. Lai atjaunotu secību līdz 7 terminiem, jāizmanto algebriskās progresijas definīcija, tas ir, a 2 \u003d a 1 + d, a 3 \u003d a 2 + d utt. Rezultātā mēs atjaunojam visu secību: a 1 \u003d 6, a 2 \u003d 6 + 2 \u003d 8, a 3 \u003d 8 + 2 \u003d 10, a 4 \u003d 10 + 2 \u003d 12, a 5 \u003d 12 + 2 \u003d 14, a 6 \u003d 14 + 2 \u003d 16, a 7 \u003d 18. 3. piemērs: virzība uz priekšu
Mēs vēl vairāk sarežģījam problēmas stāvokli. Tagad ir nepieciešams atbildēt uz jautājumu, kā atrast aritmētisko progresiju. Jūs varat sniegt šādu piemēru: doti divi cipari, piemēram, 4 un 5. Nepieciešams sastādīt algebrisko progresiju, lai starp tiem būtu izvietoti vēl trīs termini. Pirms sākat risināt šo problēmu, jums ir jāsaprot, kurai vietai nākotnē tiks doti skaitļi. Tā kā starp tiem būs vēl trīs termini, tad 1 \u003d -4 un 5 \u003d 5. To konstatējot, mēs pāriesim pie problēmas, kas ir līdzīga iepriekšējai. Atkal n-tajā termiņā mēs izmantojam formulu, iegūstot: a 5 \u003d a 1 + 4 * d. Kur: d \u003d (a 5 - a 1) / 4 \u003d (5 - (-4)) / 4 \u003d 2,25. Viņi nesaņēma starpības veselo vērtību, bet tas ir racionāls skaitlis, tāpēc algebriskās progresijas formulas paliek tās pašas. Tagad mēs pievienojam atrasto atšķirību 1 un atjaunojam trūkstošos progresēšanas nosacījumus. Mēs iegūstam: a 1 \u003d - 4, a 2 \u003d - 4 + 2,25 \u003d - 1,75, a 3 \u003d -1,75 + 2,25 \u003d 0,5, a 4 \u003d 0,5 + 2,25 \u003d 2,75, a 5 \u003d 2,75 + 2,25 \u003d 5, kas sakrita ar problēmas stāvokli. 4. piemērs: pirmais progresijas dalībnieks
Mēs turpinām sniegt aritmētiskās progresijas piemērus ar risinājumu. Visās iepriekšējās problēmās bija zināms pirmais algebriskās progresijas numurs. Tagad apsveriet cita veida uzdevumu: dodiet divus skaitļus, kur 15 \u003d 50 un 43 \u003d 37. Ir jāatrod, ar kuru numuru šī secība sākas. Līdz šim izmantotajām formulām ir vajadzīgas zināšanas par 1 un d. Šo skaitļu problēmas apstākļos nekas nav zināms. Neskatoties uz to, katram dalībniekam mēs izrakstām izteicienus, par kuriem ir pieejama informācija: a 15 \u003d a 1 + 14 * d un 43 \u003d a 1 + 42 * d. Mēs ieguvām divus vienādojumus, kuros bija 2 nezināmi lielumi (a 1 un d). Tas nozīmē, ka problēma tiek samazināta līdz lineāru vienādojumu sistēmas risināšanai. Norādīto sistēmu ir visvieglāk atrisināt, katrā vienādojumā izsakot 1 un pēc tam salīdzinot iegūtās izteiksmes. Pirmais vienādojums: a 1 \u003d a 15 - 14 * d \u003d 50 - 14 * d; otrais vienādojums: a 1 \u003d a 43 - 42 * d \u003d 37 - 42 * d. Vienādojot šos izteicienus, iegūstam: 50 - 14 * d \u003d 37 - 42 * d, no kurienes starpība d \u003d (37 - 50) / (42 - 14) \u003d - 0,464 (aiz komata tiek norādītas tikai 3 zīmes aiz komata). Zinot d, jūs varat izmantot jebkuru no iepriekšminētajiem 2 izteiksmēm 1. Piemēram, pirmais: a 1 \u003d 50 - 14 * d \u003d 50 - 14 * (- 0,464) \u003d 56,496. Ja rodas šaubas par rezultātu, varat to pārbaudīt, piemēram, noteikt 43 progresēšanas termiņu, kas ir norādīts nosacījumā. Mēs iegūstam: a 43 \u003d a 1 + 42 * d \u003d 56,496 + 42 * (- 0,464) \u003d 37,008. Neliela kļūda ir saistīta ar faktu, ka aprēķinos izmantoja noapaļošanu līdz tūkstošdaļām. Piemērs Nr. 5: summaTagad apsveriet dažus piemērus ar risinājumiem aritmētiskās progresijas apjomā. Ļaujiet iegūt šādas formas skaitlisku progresiju: \u200b\u200b1, 2, 3, 4, ...,. Kā aprēķināt 100 no šiem skaitļiem? Pateicoties datortehnoloģijas attīstībai, šo problēmu var atrisināt, tas ir, secīgi saskaitīt visus numurus, ko dators darīs, tiklīdz cilvēks nospiedīs taustiņu Enter. Tomēr problēmu var atrisināt prātā, ja pievēršat uzmanību, ka uzrādītā skaitļu virkne ir algebriska progresija un tās starpība ir 1. Izmantojot summas formulu, iegūstam: S n \u003d n * (a 1 + an) / 2 \u003d 100 * (1) + 100) / 2 \u003d 5050. Interesanti atzīmēt, ka šo problēmu sauc par "Gaussian", jo XVIII gadsimta sākumā slavenais vācietis, būdams tikai 10 gadus vecs, dažās sekundēs spēja to savā prātā atrisināt. Zēns nezināja algebriskās progresijas summas formulu, taču viņš pamanīja, ka, ja skaitļus secības malās pievienojat pa pāriem, vienmēr tiek iegūts viens rezultāts, tas ir, 1 + 100 \u003d 2 + 99 \u003d 3 + 98 \u003d ..., un kopš no šīm summām būs precīzi 50 (100/2), tad, lai iegūtu pareizo atbildi, vienkārši reiziniet 50 ar 101.
Piemērs Nr. 6: dalībnieku summa no n līdz mVēl viens tipisks aritmētiskās progresijas summas piemērs ir šāds: tiek dota skaitļu virkne: 3, 7, 11, 15, ..., jums jāatrod, ar ko tās locekļu summa no 8 līdz 14 būs vienāda. Problēma tiek atrisināta divos veidos. Pirmais no tiem ietver nezināmu locekļu atrašanu no 8 līdz 14 un pēc tam viņu secīgu summēšanu. Tā kā ir maz terminu, šī metode nav laikietilpīga. Neskatoties uz to, tiek ierosināts šo problēmu atrisināt ar otro universālāko metodi. Ideja ir iegūt formulu algebriskās progresijas summai starp terminiem m un n, kur n\u003e m ir veseli skaitļi. Abos gadījumos mēs izrakstām divas izteiksmes summai:
Kopš n\u003e m ir acīmredzams, ka 2 summā ietilpst pirmais. Pēdējais secinājums nozīmē, ka, ja ņemam starpību starp šīm summām un pievienojam tai terminu a m (starpības ņemšanas gadījumā to atņem no summas S n), mēs iegūstam vajadzīgo atbildi uz problēmu. Mums ir: S mn \u003d S n - S m + am \u003d n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am \u003d a 1 * (n - m) / 2 + an * n / 2 + am * (1 m / 2). Šajā izteiksmē ir jāaizstāj formulas ar n un m. Tad mēs iegūstam: S mn \u003d a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) \u003d a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2. Iegūtā formula ir nedaudz apgrūtinoša, tomēr summa S mn ir atkarīga tikai no n, m, a 1 un d. Mūsu gadījumā a 1 \u003d 3, d \u003d 4, n \u003d 14, m \u003d 8. Aizstājot šos skaitļus, iegūstam: S mn \u003d 301.
Kā redzams no iepriekšminētajiem risinājumiem, visu uzdevumu pamatā ir zināšanas par n-tā termiņa izteiksmi un pirmo terminu kopas formulas zināšanām. Pirms sākat risināt kādu no šīm problēmām, ieteicams rūpīgi izlasīt nosacījumu, skaidri saprast, kas jums jāatrod, un tikai tad turpināt risinājumu. Vēl viens padoms ir tiekties pēc vienkāršības, tas ir, ja jūs varat atbildēt uz jautājumu, nepielietojot sarežģītus matemātiskus aprēķinus, tad jums tas jādara tieši tā, jo šajā gadījumā kļūdas pieļaušanas varbūtība ir mazāka. Piemēram, aritmētiskās progresijas piemērā ar risinājumu Nr. 6 varētu apstāties pie formulas S mn \u003d n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am, un vispārējo problēmu sadalīt atsevišķos apakšuzdevumos. (šajā gadījumā vispirms atrodiet vārdus an un am). Ja rodas šaubas par rezultātu, ieteicams to pārbaudīt, kā tas tika darīts dažos no sniegtajiem piemēriem. Uzzināts, kā atrast aritmētisko progresiju. Ja paskatās, tas nav tik grūti. Aritmētiskās progresēšanas problēmas pastāvēja jau senatnē. Viņi parādījās un pieprasīja risinājumu, jo viņiem bija praktiska vajadzība. Tātad vienā no Senās Ēģiptes papiriem, kam ir matemātiskais saturs, - Rinda papiruss (XIX gs. Pirms mūsu ēras) - ir šāds uzdevums: sadaliet desmit maizes mērus desmit cilvēkiem ar nosacījumu, ka atšķirība starp katru no tiem ir viena astotā daļa no pasākuma. ” Un seno grieķu matemātiskajos darbos ir elegantas teorēmas, kas saistītas ar aritmētisko progresēšanu. Tātad Aleksandrijas ģipšakmens (II gadsimts, kas apkopoja daudzus interesantus uzdevumus un pievienoja četrpadsmito grāmatu Eiklida "sākumiem", formulēja ideju: "Aritmētiskā progresijā, kurā ir pāra locekļu skaits, otrās puses dalībnieku summa ir lielāka nekā pirmās puses dalībnieku summa kvadrātā 1 / 2 dalībnieku skaits. " Tiek apzīmēta secība a. Sērijas numurus sauc par tās locekļiem, un tos parasti apzīmē ar burtiem ar indeksiem, kas norāda šī locekļa kārtas numuru (a1, a2, a3 ... tas skan: “1.”, “2.”, “3.” un tā tālāk ) Secība var būt bezgalīga vai ierobežota. Bet kas ir aritmētiskā progresija? Tas tiek saprasts kā iegūts, pievienojot iepriekšējo terminu (n) ar tādu pašu skaitli d, kas ir progresijas starpība. Ja d<0, то мы имеем убывающую прогрессию. Если d>0, tad tiek uzskatīts, ka šāda progresija pieaug. Aritmētisko progresiju sauc par ierobežotu, ja tiek ņemti vērā tikai daži no tās pirmajiem locekļiem. Ar ļoti lielu dalībnieku skaitu tas jau ir bezgalīgs progress. Jebkuru aritmētisko progresiju aprēķina pēc šādas formulas: an \u003d kn + b, savukārt b un k ir daži skaitļi. Apgalvojums ir pilnīgi patiess, un tas ir tieši pretējs: ja secību piešķir ar līdzīgu formulu, tad tā ir tieši aritmētiskā progresija, kurai ir šādas īpašības:
Raksturīgo īpašību jebkuram četram aritmētiskās progresijas skaitlim var izteikt ar formulu an + am \u003d ak + al, ja n + m \u003d k + l (m, n, k ir progresijas skaitļi). Aritmētiskā progresijā jebkuru vajadzīgo (N) terminu var atrast, izmantojot šādu formulu: Piemēram: pirmais aritmētiskās progresijas termiņš (a1) ir trīs un vienāds ar trīs, un starpība (d) ir vienāda ar četriem. Jums jāatrod četrdesmit piektais šīs progresijas dalībnieks. a45 \u003d 1 + 4 (45-1) \u003d 177 Formula an \u003d ak + d (n - k) ļauj mums noteikt aritmētiskās progresijas n-to termiņu, izmantojot jebkuru no tā k-tajiem noteikumiem, ar nosacījumu, ka tas ir zināms. Aritmētiskās progresijas locekļu summu (kas nozīmē pirmos n galīgās progresijas dalībniekus) aprēķina šādi: Sn \u003d (a1 + an) n / 2. Ja 1. termins ir arī zināms, tad ir ērti aprēķināt citu formulu: Sn \u003d ((2a1 + d (n-1)) / 2) * n. Aritmētiskās progresijas summu, kurā ir n locekļi, aprēķina šādi: Aprēķinu formulu izvēle ir atkarīga no uzdevumu apstākļiem un avota datiem. Jebkura skaitļa dabiskā virkne, piemēram, 1,2,3, ..., n, ..., ir vienkāršākais aritmētiskās progresijas piemērs. Papildus aritmētiskajai progresijai ir arī ģeometriskā progresija, kurai ir savas īpašības un raksturlielumi. |
| Lasīt: |
|---|
Jauns
- DIY kāpnes uz bēniņiem: izveidojiet kāpnes uz bēniņiem ar foto instrukcijām
- Koka karkasa garāža - droša pašizveidota konstrukcija
- DIY grīdas ieklāšana - soli pa solim instrukcijas ar fotoattēlu
- Koka un akmens mājas spāru sistēmas īpatnības
- Dariet to viegli pie galda
- Pašdarināts galds no dēļiem
- Māju celtniecība no profilētiem kokmateriāliem
- Kādu galdu no savām rokām var izgatavot no nevajadzīgiem dēļiem?
- Krēsla izgatavošana no koka
- Kā izlīdzināt grīdu zem flīzes Kā izlīdzināt grīdu zem flīzes

 kvadrātiskās funkcijas grafiks - parabola
kvadrātiskās funkcijas grafiks - parabola