Sections du site
Choix des éditeurs:
- Chevrons à faire soi-même sur un toit à deux versants - faire le bon cadre avec le bon calcul
- Gratter un plancher en bois: un bricolage pas à pas Comment recycler un plancher à partir de planches
- Installation du lattage de toiture sur les chevrons
- Gâteau d'isolation au sol dans une maison en bois
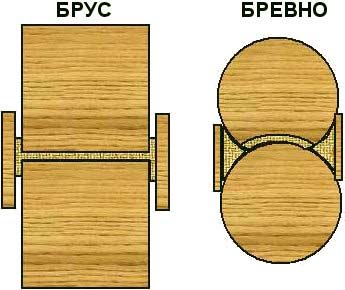
- Détermination du pourcentage de la production de bois lors du sciage de bois, en particulier de bois ronds.
- Calcul du bois dans un cube
- Stratifié sur sol en béton: caractéristiques d'une bonne installation Pose de contreplaqué sur béton sous le stratifié
- Comment fixer le blockhaus au mur, comment le faire correctement?
- Quantité de bois dans un cube: méthodes de calcul et exemples de calcul
- Quelle est la différence entre le parquet et le stratifié, ce qui est meilleur
La publicité
| La base du logarithme à être. Propriétés des logarithmes et exemples de leurs solutions. Guide exhaustif (2019) |
|
Manuel d'instruction Enregistrez l'expression logarithmique donnée. Si l'expression utilise le logarithme de 10, alors son entrée est raccourcie et ressemble à ceci: lg b est le logarithme décimal. Si le logarithme a le nombre e comme base, alors écrivez l'expression: ln b est le logarithme naturel. Il est entendu que le résultat de any est le degré auquel le nombre de base doit être élevé pour obtenir le nombre b. Lorsque vous trouvez la somme de deux fonctions, il vous suffit de les différencier tour à tour et d'ajouter les résultats: (u + v) "\u003d u" + v "; Lors de la recherche de la dérivée du produit de deux fonctions, il est nécessaire de multiplier la dérivée de la première fonction par la seconde et d'ajouter la dérivée de la deuxième fonction multipliée par la première fonction: (u * v) "\u003d u" * v + v "* u; Pour trouver la dérivée du quotient de deux fonctions, il faut, à partir du produit de la dérivée divisible multiplié par la fonction diviseur, soustraire le produit du dérivé diviseur multiplié par la fonction divisible, et diviser tout cela par la fonction diviseur au carré. (u / v) "\u003d (u" * v-v "* u) / v ^ 2; Si une fonction complexe est donnée, alors il faut multiplier la dérivée de la fonction interne et la dérivée de l'externe. Soit y \u003d u (v (x)), puis y "(x) \u003d y" (u) * v "(x). En utilisant ce qui précède, vous pouvez différencier presque toutes les fonctions. Alors, regardons quelques exemples: y \u003d x ^ 4, y "\u003d 4 * x ^ (4-1) \u003d 4 * x ^ 3; y \u003d 2 * x ^ 3 * (e ^ xx ^ 2 + 6), y "\u003d 2 * (3 * x ^ 2 * (e ^ xx ^ 2 + 6) + x ^ 3 * (e ^ x-2 * x)); 2) Calculez la valeur de la fonction au point donné y "(1) \u003d 8 * e ^ 0 \u003d 8 Vidéos connexes Conseils utiles Apprenez le tableau des dérivés élémentaires. Cela vous fera gagner beaucoup de temps. Sources:
Alors, quelle est la différence entre une équation irrationnelle et une équation rationnelle? Si la variable inconnue est sous le signe de la racine carrée, alors l'équation est considérée comme irrationnelle.
Manuel d'instruction La principale méthode pour résoudre ces équations est la construction des deux parties équations au carré. Cependant. c'est naturel, la première chose à faire est de se débarrasser du signe. Techniquement, cette méthode n'est pas compliquée, mais elle peut parfois entraîner des problèmes. Par exemple, l'équation v (2x-5) \u003d v (4x-7). En quadrillant les deux côtés, vous obtenez 2x-5 \u003d 4x-7. Il n'est pas difficile de résoudre une telle équation; x \u003d 1. Mais le numéro 1 ne sera pas donné équations. Pourquoi Remplacez-en un dans l'équation au lieu de la valeur de x. Et les côtés droit et gauche contiendront des expressions qui n'ont pas de sens, c'est-à-dire. Cette valeur n'est pas valide pour la racine carrée. Par conséquent, 1 est une racine étrangère, et donc cette équation n'a pas de racine. Ainsi, l'équation irrationnelle est résolue en utilisant la méthode de la quadrature de ses deux parties. Et après avoir résolu l'équation, il est nécessaire de couper les racines étrangères. Pour ce faire, remplacez les racines trouvées dans l'équation d'origine. Considérez un de plus. La résolution des identités est assez simple. Pour cela, il faut faire des transformations identiques jusqu'à ce que l'objectif soit atteint. Ainsi, en utilisant les opérations arithmétiques les plus simples, le problème sera résolu.
Vous aurez besoin
Manuel d'instruction La plus simple de ces transformations est la multiplication abrégée algébrique (comme le carré de la somme (différence), la différence de carrés, la somme (différence), le cube de la somme (différence)). De plus, il existe de nombreuses formules trigonométriques, qui sont essentiellement les mêmes identités. En effet, le carré de la somme de deux termes est égal au carré du premier plus le double produit du premier et du second et plus le carré du second, c'est-à-dire (a + b) ^ 2 \u003d (a + b) (a + b) \u003d a ^ 2 + ab + ba + b ^ 2 \u003d a ^ 2 + 2ab + b ^ 2. Simplifiez les deux Principes généraux de décisionRépétez le manuel sur l'analyse mathématique ou les mathématiques supérieures, qui est une certaine intégrale. Comme on le sait, la solution d'une certaine intégrale est une fonction dont la dérivée donnera un intégrande. Cette fonction s'appelle l'antidérive. Selon ce principe, les intégrales principales sont construites.Déterminez par le type d'intégrale et quelles intégrales de table conviennent dans ce cas. Il n'est pas toujours possible de le déterminer immédiatement. Souvent, la vue tabulaire ne devient perceptible qu'après plusieurs transformations pour simplifier l'intégrande. Méthode de remplacement variableSi l'intégrande est une fonction trigonométrique avec un polynôme dans son argument, essayez d'utiliser la méthode de remplacement de variable. Pour ce faire, remplacez le polynôme dans l'argument de l'intégrande par une nouvelle variable. En utilisant le rapport entre les nouvelles et les anciennes variables, déterminez les nouvelles limites d'intégration. En différenciant cette expression, trouvez le nouveau différentiel dans. Ainsi, vous obtiendrez une nouvelle forme de l'intégrale précédente, proche ou même correspondant à une tabulaire.Solution d'intégrales du second typeSi l'intégrale est une intégrale du deuxième type, la forme vectorielle de l'intégrande, alors vous devrez utiliser les règles pour la transition de ces intégrales à celles scalaires. L'une de ces règles est le rapport Ostrogradsky-Gauss. Cette loi nous permet de passer du flux rotorique d'une certaine fonction vectorielle à l'intégrale triple sur la divergence d'un champ vectoriel donné.Substitution des limites d'intégrationAprès avoir trouvé l'antidérivatif, il faut substituer les limites de l'intégration. Tout d'abord, remplacez la valeur limite supérieure dans l'expression par l'antidérivative. Vous obtiendrez un certain nombre. Ensuite, soustrayez du nombre résultant un autre nombre obtenu à partir de la limite inférieure de l'antidérivatif. Si l'une des limites de l'intégration est l'infini, alors en la substituant à la fonction primitive, il faut aller à la limite et trouver ce que cherche l'expression.Si l'intégrale est bidimensionnelle ou tridimensionnelle, vous devrez tracer géométriquement les limites de l'intégration afin de comprendre comment calculer l'intégrale. En effet, dans le cas, par exemple, d'une intégrale tridimensionnelle, les limites d'intégration peuvent être des plans entiers qui limitent le volume intégrable. Pas mal du tout, non? Alors que les mathématiciens choisissent des mots pour vous donner une définition longue et confuse, examinons de plus près cette définition simple et claire. Le nombre e signifie croissanceLe nombre e signifie une croissance continue. Comme nous l'avons vu dans l'exemple précédent, e x nous permet de lier le pourcentage et le temps: 3 ans avec une augmentation de 100% équivalent à 1 an avec 300%, sous la condition d '«intérêt composé». Vous pouvez remplacer n'importe quel pourcentage et valeurs de temps (50% pendant 4 ans), mais il est préférable de définir le pourcentage à 100% pour plus de commodité (il s'avère que 100% pendant 2 ans). En raison du passage à 100%, nous pouvons nous concentrer exclusivement sur la composante temps: e x \u003d e pour cent * temps \u003d e 1.0 * temps \u003d e temps De toute évidence, e x signifie:
e x est un facteur d'échelle montrant à quel niveau nous allons croître dans x segments de temps. Le logarithme naturel signifie le tempsLe logarithme naturel est l'inverse de e, un terme si bizarre pour le contraire. En parlant de bizarreries; en latin, on l'appelle logarithmus naturali, d'où l'abréviation ln. Et que signifie cette inversion ou opposé?
Par exemple:
Toujours en train de lire? Le logarithme naturel montre le temps qu'il faut pour atteindre le niveau souhaité. Ce score logarithmique non standardVous avez traversé des logarithmes - ce sont des créatures étranges. Comment ont-ils réussi à transformer la multiplication en addition? Et la division en soustraction? Voyons voir. À quoi ln (1) est-il égal? Intuitivement, la question est la suivante: combien de temps dois-je attendre pour obtenir 1 fois plus que ce que j'ai? Zéro Zéro Pas du tout. Vous l'avez déjà une fois. Il ne faut pas de temps pour passer du niveau 1 de la route au niveau 1.
Et la valeur fractionnaire? Après combien aurons-nous la moitié de la quantité disponible? Nous savons qu'avec une croissance continue à cent pour cent, ln (2) signifie le temps nécessaire pour doubler. Si nous temps inverse (c'est-à-dire attendre un temps négatif), nous obtenons alors la moitié de ce que nous avons.
Logique, non? Si nous remontons (reculons) de 0,693 seconde, nous trouverons la moitié du montant disponible. En général, vous pouvez inverser la fraction et prendre une valeur négative: ln (1/3) \u003d -ln (3) \u003d -1,09. Cela signifie que si nous revenons au passé de 1,09 fois, nous ne trouverons qu'un tiers du nombre actuel. D'accord, qu'en est-il du logarithme d'un nombre négatif? Combien de temps faut-il pour "faire croître" une colonie de bactéries de 1 à -3? C'est impossible! Vous ne pouvez pas obtenir un nombre négatif de bactéries, non? Vous pouvez obtenir le maximum (euh ... minimum) zéro, mais vous ne pouvez pas obtenir le nombre négatif de ces petites créatures. Un nombre négatif de bactéries n'a tout simplement aucun sens.
«Indéfini» signifie qu'il n'y a pas d'intervalle de temps qui devrait attendre pour obtenir une valeur négative. La multiplication logarithmique est juste un criCombien de temps faut-il pour croître quatre fois? Bien sûr, vous pouvez simplement prendre ln (4). Mais c'est trop simple, on ira dans l'autre sens. Vous pouvez imaginer une croissance quadruple comme un doublement (nécessitant ln (2) unités de temps), puis doublant à nouveau (nécessitant encore ln (2) unités de temps):
Intéressant. Tout indicateur de croissance, disons 20, peut être considéré comme un doublement immédiatement après une augmentation de 10 fois. Ou croissance 4 fois, puis 5 fois. Ou tripler puis une augmentation de 6,666 fois. Vous voyez le motif?
Le logarithme de A fois B est log (A) + log (B). Cette attitude prend tout de suite un sens si vous opérez en termes de croissance. Si vous êtes intéressé par une croissance de 30 fois, vous pouvez attendre ln (30) en une seule séance, ou vous pouvez attendre ln (3) pour tripler, puis ln (10) pour tripler. Le résultat final est le même, donc bien sûr le temps doit rester constant (et reste). Et la division? En particulier, ln (5/3) signifie: combien de temps faut-il pour croître 5 fois, puis obtenir 1/3 de cela? Grande, la croissance 5x est ln (5). 1/3 fois la croissance prendra -ln (3) unités de temps. Donc
Cela signifie: laissez-le croître 5 fois, puis "remontez dans le temps" au point où il ne restera plus qu'un tiers de ce montant, de manière à obtenir une croissance de 5/3. En général, il s'avère
J'espère que l'étrange arithmétique des logarithmes commence à avoir un sens: la multiplication des indicateurs de croissance devient l'addition d'unités de temps de croissance, et la division se transforme en soustraction d'unités de temps. Pas besoin de se souvenir des règles, essayez de les comprendre. Utilisation du logarithme naturel de la croissance arbitraire"Bien sûr", dites-vous, "tout va bien si la croissance est de 100%, mais qu'en est-il des 5% que j'obtiens?" Pas de problème Le «temps» que nous calculons en utilisant ln () est en fait une combinaison de taux d'intérêt et de temps, le même X de l'équation e x. Nous avons simplement décidé de définir le pourcentage à 100% pour plus de simplicité, mais nous sommes libres d'utiliser n'importe quel nombre. Supposons que nous voulons atteindre une croissance de 30 fois: prenez ln (30) et obtenez 3,4 Cela signifie:
De toute évidence, cette équation signifie «un rendement de 100% sur 3,4 ans donne une croissance de 30 fois». Nous pouvons écrire cette équation sous la forme suivante:
Nous pouvons changer les valeurs de «taux» et de «temps», si seul le taux * temps reste 3.4. Par exemple, si nous voulons une croissance de 30 fois - combien devra-t-on attendre à un taux d'intérêt de 5%?
Je raisonne comme ceci: "ln (30) \u003d 3,4, ce qui signifie qu'avec une croissance de 100%, cela prendra 3,4 ans. Si je double le taux de croissance, le temps nécessaire sera divisé par deux."
Super, non? Le logarithme naturel peut être utilisé avec n'importe quelle valeur du taux d'intérêt et du temps, car leur produit reste constant. Vous pouvez déplacer les valeurs des variables comme vous le souhaitez. Grand exemple: règle de soixante-douzeLa règle des soixante-douze est une technique mathématique qui vous permet d'estimer combien de temps il faudra pour que votre argent double. Maintenant, nous allons le sortir (oui!), Et en plus, nous allons essayer de comprendre son essence. Combien de temps faut-il pour doubler votre argent à un taux de 100% croissant chaque année? Oups. Nous avons utilisé le logarithme naturel pour le cas d'une croissance continue, et maintenant vous parlez d'accumulation annuelle? Cette formule deviendra-t-elle inadaptée à un tel cas? Oui, ce sera le cas, mais pour des taux d'intérêt réels comme 5%, 6% ou même 15%, la différence entre le calcul des intérêts annuels et la croissance continue sera faible. Donc, une estimation approximative fonctionne, mm, approximative, donc nous ferons comme si nous avions une charge complètement continue. Maintenant, la question est simple: à quelle vitesse pouvez-vous doubler avec une croissance de 100%? ln (2) \u003d 0,693. Il faut 0,693 unités de temps (des années dans notre cas) pour doubler notre quantité avec une croissance continue de 100%. Alors, que se passe-t-il si le taux d'intérêt n'est pas de 100%, mais disons de 5% ou 10%? Facile! Puisque l'enchère * heure \u003d 0,693, nous doublerons le montant:
Il s'avère que si la croissance est de 10%, il faudra 0,693 / 0,10 \u003d 6,93 ans pour doubler. Pour simplifier les calculs, multiplions les deux parties par 100, puis nous pouvons dire "10", pas "0,10":
Maintenant, le tour est doublé à un taux de 5%, 69,3 / 5 \u003d 13,86 ans. Cependant, 69,3 n'est pas le dividende le plus pratique. Choisissons un nombre proche, 72, qui est commodément divisé par 2, 3, 4, 6, 8 et d'autres nombres.
qui est la règle de soixante-douze. Tout est cousu à l'intérieur. Si vous avez besoin de trouver le temps de tripler, vous pouvez utiliser ln (3) ~ 109,8 et obtenir
Ce qui est une autre règle utile. La règle 72 s'applique à la croissance des taux d'intérêt, à la croissance de la population, aux cultures bactériennes et à tout ce qui croît de façon exponentielle. Et ensuite?J'espère que le logarithme naturel a maintenant un sens pour vous - il montre le temps nécessaire à la croissance de n'importe quel nombre avec une croissance exponentielle. Je pense qu'il est appelé naturel parce que e est une mesure universelle de la croissance, donc ln peut être considéré comme un moyen universel de déterminer le temps nécessaire à la croissance. Chaque fois que vous voyez ln (x), rappelez-vous «le temps qu'il faut pour croître X fois». Dans le prochain article, je décrirai e et ln en groupe, afin que l'arôme frais des mathématiques remplisse l'air. Addition: le logarithme naturel de eQuiz rapide: combien coûtera ln (e)?
Pensez clairement. 9 septembre 2013Expressions logarithmiques, exemples de solutions. Dans cet article, nous examinerons les problèmes associés à la résolution des logarithmes. Les tâches posent la question de trouver le sens de l'expression. Il convient de noter que le concept du logarithme est utilisé dans de nombreuses tâches et pour comprendre sa signification est extrêmement important. Quant à l'examen d'État unifié, le logarithme est utilisé pour résoudre des équations, dans des problèmes appliqués, ainsi que dans des tâches liées à l'étude des fonctions. Voici quelques exemples pour comprendre la signification même du logarithme:
Identité logarithmique de base:
Propriétés des logarithmes dont vous devez toujours vous souvenir:
* Le logarithme du produit est égal à la somme des logarithmes des facteurs. * * *
* Le logarithme du quotient (fraction) est égal à la différence des logarithmes des facteurs. * * *
* Le logarithme du degré est égal au produit de l'exposant et au logarithme de sa fondation. * * *
* Transition vers une nouvelle fondation * * * Plus de propriétés:
* * * Le calcul des logarithmes est étroitement lié à l'utilisation des propriétés des exposants. Nous en énumérons quelques-uns: L'essence de cette propriété est que lorsque le numérateur est transféré au dénominateur et vice versa, le signe de l'exposant change à l'opposé. Par exemple:
La conséquence de cette propriété: * * *
Quand on élève un pouvoir à un pouvoir, la fondation reste la même et les indicateurs se multiplient. * * * Comme vous l'avez vu, le concept même d'un logarithme est simple. L'essentiel est que de bonnes pratiques soient nécessaires, ce qui confère une certaine compétence. Bien entendu, la connaissance des formules est requise. Si l'habileté dans la transformation des logarithmes élémentaires n'est pas formée, alors lors de la résolution de tâches simples, vous pouvez facilement faire une erreur. Pratiquez, résolvez d'abord les exemples les plus simples du cours de mathématiques, puis passez à des exemples plus complexes. À l'avenir, je vais certainement montrer comment les logarithmes «laids» sont résolus, il n'y en aura pas sur l'UTILISATION, mais ils sont intéressants, ne les manquez pas! C’est tout! Succès à vous! Cordialement, Alexander Krutitskikh P.S: Je vous serais reconnaissant de bien vouloir parler du site sur les réseaux sociaux. Donc, devant nous sont des pouvoirs de deux. Si vous prenez un nombre de la ligne du bas, vous pouvez facilement trouver le degré auquel vous devez augmenter un diable pour obtenir ce nombre. Par exemple, pour obtenir 16, vous devez élever deux au quatrième degré. Et pour obtenir 64, vous devez élever de deux au sixième degré. Cela peut être vu sur le tableau. Et maintenant - en fait, la définition du logarithme:
Désignation: log a x \u003d b, où a est la base, x est l'argument, b est en fait ce qu'est le logarithme. Par exemple, 2 3 \u003d 8 ⇒ log 2 8 \u003d 3 (le logarithme de base 2 de 8 est trois car 2 3 \u003d 8). Avec le même succès, log 2 64 \u003d 6, puisque 2 6 \u003d 64. L'opération de recherche du logarithme d'un nombre sur une base donnée est appelée logarithme. Ainsi, nous complétons notre table avec une nouvelle ligne:
Malheureusement, tous les logarithmes ne sont pas considérés comme si faciles. Par exemple, essayez de trouver le journal 2 5. Le nombre 5 n'est pas dans le tableau, mais la logique suggère que le logarithme se situera quelque part sur le segment. Parce que 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число. De tels nombres sont appelés irrationnels: les chiffres décimaux peuvent être écrits indéfiniment et ne se répètent jamais. Si le logarithme s'avère irrationnel, il vaut mieux le laisser ainsi: log 2 5, log 3 8, log 5 100. Il est important de comprendre que le logarithme est une expression à deux variables (base et argument). Beaucoup ont d'abord confondu où se trouve le fondement et où se trouve l'argument. Pour éviter les malentendus gênants, regardez simplement l'image: Devant nous, rien de plus que la définition d'un logarithme. Rappelez-vous: logarithme est un degré, dans lequel le fondement doit être élevé pour obtenir un argument. C'est la base qui est élevée au pouvoir - dans l'image, elle est surlignée en rouge. Il s'avère que la base est toujours en dessous! Je raconte cette merveilleuse règle à mes élèves dans la première leçon - et il n'y a pas de confusion. Nous avons compris la définition - il reste à apprendre à compter les logarithmes, c'est-à-dire se débarrasser du signe du journal. Pour commencer, nous notons que deux faits importants découlent de la définition:
Ces restrictions sont appelées plage valide (DLD). Il s'avère que l'ODZ du logarithme ressemble à ceci: log a x \u003d b ⇒ x\u003e 0, a\u003e 0, a ≠ 1. Notez qu'il n'y a aucune restriction sur le nombre b (la valeur du logarithme). Par exemple, le logarithme peut très bien être négatif: log 2 0,5 \u003d −1, car 0,5 \u003d 2 -1. Cependant, nous ne considérons maintenant que les expressions numériques, où il n'est pas nécessaire de connaître l'équation différentielle linéaire logistique. Toutes les restrictions sont déjà prises en compte par les rédacteurs des tâches. Mais lorsque les équations et les inégalités logarithmiques disparaîtront, les exigences de l'ODZ deviendront obligatoires. Après tout, la base et l'argument peuvent être des constructions assez non faibles, qui ne correspondent pas nécessairement aux restrictions ci-dessus. Considérons maintenant le schéma général de calcul des logarithmes. Il se compose de trois étapes:
C'est tout! Si le logarithme s'avère irrationnel, cela sera déjà vu dans la première étape. L'exigence que la base soit plusieurs est très pertinente: cela réduit le risque d'erreur et simplifie considérablement les calculs. De même pour les fractions décimales: si vous les traduisez immédiatement en fractions régulières, il y aura plusieurs fois moins d'erreurs. Voyons comment ce schéma fonctionne avec des exemples spécifiques:
Nous composons et résolvons l'équation:
Une petite note pour le dernier exemple. Comment s'assurer qu'un nombre n'est pas le degré exact d'un autre nombre? Très simple - il suffit de le factoriser en facteurs simples. S'il y a au moins deux facteurs différents dans l'expansion, le nombre n'est pas une puissance exacte.
8 \u003d 2 · 2 · 2 \u003d 2 3 - le degré exact, car il n'y a qu'un seul facteur; Nous notons également que les nombres premiers sont toujours des degrés exacts d’eux-mêmes. Logarithme décimalCertains logarithmes sont si courants qu’ils ont un nom et une désignation spéciaux.
Par exemple, lg 10 \u003d 1; lg 100 \u003d 2; lg 1000 \u003d 3 - etc. A partir de maintenant, quand une phrase comme "Find lg 0.01" est trouvée dans un manuel, sachez qu'il ne s'agit pas d'une faute de frappe. C'est le logarithme décimal. Cependant, si vous n'êtes pas familier avec cette notation, vous pouvez toujours la récrire: Tout ce qui est vrai pour les logarithmes ordinaires l'est également pour le nombre décimal. Logarithme naturelIl existe un autre logarithme qui a sa propre notation. En un sens, c'est encore plus important que le nombre décimal. C'est un logarithme naturel.
Beaucoup demanderont: quel est le nombre e? C'est un nombre irrationnel, son sens exact ne peut pas être trouvé et écrit. Je n'en donnerai que les premiers chiffres: Nous n'entrerons pas dans les détails de ce nombre et de la raison pour laquelle il est nécessaire. Rappelez-vous simplement que e est la base du logarithme naturel: Ainsi, ln e \u003d 1; ln e 2 \u003d 2; l e 16 \u003d 16 - etc. D'autre part, ln 2 est un nombre irrationnel. En général, le logarithme naturel de tout nombre rationnel est irrationnel. Sauf, bien sûr, les unités: ln 1 \u003d 0. Pour les logarithmes naturels, toutes les règles qui sont vraies pour les logarithmes ordinaires sont vraies. Le logarithme du nombre b (b\u003e 0) à la base a (a\u003e 0, a 1) Est un exposant pour lequel le nombre a doit être élevé pour obtenir b. Le logarithme en base 10 de b peut s’écrire comme suit: lg (b)et le logarithme de base de e (le logarithme naturel) est ln (b). Souvent utilisé dans la résolution de problèmes avec les logarithmes: Logarithme PropriétésIl y a quatre principaux propriétés du logarithme. Soit a\u003e 0, a ≠ 1, x\u003e 0 et y\u003e 0. Propriété 1. Logarithme du produitLogarithme du produit égal à la somme des logarithmes: journal a (x ⋅ y) \u003d journal a x + journal a y Propriété 2. Logarithme du quotientLogarithme de privé égal à la différence des logarithmes: journal a (x / y) \u003d journal a x - journal a y Propriété 3. Logarithme de degréLogarithme de degré égal au produit du degré par le logarithme: Si la base du logarithme est en degré, une autre formule s'applique: Propriété 4. Logarithme de la racineCette propriété peut être obtenue à partir de la propriété du logarithme du degré, puisque la racine du nième degré est égale au degré 1 / n: La formule pour passer d'un logarithme d'une base à un logarithme d'une autreCette formule est également souvent utilisée pour résoudre différentes tâches sur les logarithmes: Cas particulier: Comparaison des logarithmes (inégalités)Supposons que nous ayons 2 fonctions f (x) et g (x) sous des logarithmes ayant les mêmes bases et entre elles un signe d'inégalité: Pour les comparer, vous devez d’abord regarder la base des logarithmes d’un:
Comment résoudre des problèmes avec les logarithmes: exemplesLogarithme Jobs inclus dans l'examen de mathématiques pour la 11e année aux tâches 5 et 7, vous pouvez trouver des tâches avec des solutions sur notre site Web dans les sections correspondantes. En outre, les tâches avec des logarithmes se trouvent dans la banque de tâches en mathématiques. Vous pouvez trouver tous les exemples en effectuant une recherche sur le site. Quel est le logarithmeLes logarithmes ont toujours été considérés comme un sujet complexe dans les cours de mathématiques à l'école. Il existe de nombreuses définitions différentes du logarithme, mais la plupart des manuels utilisent, pour une raison quelconque, la plus complexe et la plus infructueuse d'entre elles. Nous déterminerons le logarithme simplement et clairement. Pour ce faire, compilez un tableau: Donc, devant nous sont des puissances de deux. Logarithmes - propriétés, formules, comment résoudreSi vous prenez un nombre dans la ligne du bas, vous pouvez facilement trouver le degré auquel vous devez relancer un dieux pour obtenir ce nombre. Par exemple, pour obtenir 16 ans, vous devez en élever deux au quatrième degré. Et pour obtenir 64 ans, vous devez en élever deux au sixième degré. Ceci peut être vu de la table. Et maintenant - en fait, la définition du logarithme:
Désignation: log a x \u003d b, où a est la base, x l'argument, b est ce que le logarithme est. Par exemple, 2 3 \u003d 8 ⇒log 2 8 \u003d 3 (le logarithme en base 2 de 8 est trois, puisque 2 3 \u003d 8). Avec le même succès, log 2 64 \u003d 6, puisque 2 6 \u003d 64. On appelle l'opération de trouver le logarithme d'un nombre sur une base donnée. Nous complétons donc notre table avec une nouvelle ligne:
Malheureusement, tous les logarithmes ne sont pas considérés comme faciles. Par exemple, essayez de trouver le journal 2 5. Le nombre 5 ne figure pas dans le tableau, mais la logique suggère que le logarithme se trouve quelque part sur le segment. Parce que 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число. Ces nombres sont appelés irrationnels: les chiffres décimaux peuvent être écrits indéfiniment et ne se répètent jamais. Si le logarithme s'avère irrationnel, il est préférable de le laisser ainsi: log 2 5, log 3 8, log 5 100. Il est important de comprendre que le logarithme est une expression à deux variables (base et argument). Beaucoup ont d'abord confondu où se trouve le fondement et où se trouve l'argument. Pour éviter les malentendus gênants, regardez simplement l'image: Devant nous, rien de plus que la définition d'un logarithme. Rappelez-vous: logarithme est un degré, dans lequel le fondement doit être élevé pour obtenir un argument. C'est la base qui est élevée au pouvoir - dans l'image, elle est surlignée en rouge. Il s'avère que la base est toujours en dessous! Je raconte cette merveilleuse règle à mes élèves dans la première leçon - et il n'y a pas de confusion. Comment compter les logarithmesNous avons compris la définition - il reste à apprendre à compter les logarithmes, c'est-à-dire se débarrasser du signe du journal. Pour commencer, nous notons que deux faits importants découlent de la définition:
Ces restrictions sont appelées plage valide (DLD). Il s'avère que l'ODZ du logarithme se présente comme suit: log a x \u003d b ⇒x\u003e 0, a\u003e 0, a 1. Notez qu'il n'y a aucune restriction sur le nombre b (la valeur du logarithme). Par exemple, le logarithme peut être négatif: log 2 0.5 \u003d −1, car 0,5 \u003d 2 -1. Cependant, nous ne considérons maintenant que les expressions numériques, où il n'est pas nécessaire de connaître l'équation différentielle linéaire logistique. Toutes les restrictions sont déjà prises en compte par les rédacteurs des tâches. Mais lorsque les équations et les inégalités logarithmiques disparaîtront, les exigences de l'ODZ deviendront obligatoires. Après tout, la base et l'argument peuvent être des constructions assez non faibles, qui ne correspondent pas nécessairement aux restrictions ci-dessus. Considérons maintenant le schéma général de calcul des logarithmes. Il se compose de trois étapes:
C'est tout! Si le logarithme s'avère irrationnel, cela sera déjà vu dans la première étape. L'exigence que la base soit plusieurs est très pertinente: cela réduit le risque d'erreur et simplifie considérablement les calculs. De même pour les fractions décimales: si vous les traduisez immédiatement en fractions régulières, il y aura plusieurs fois moins d'erreurs. Voyons comment ce schéma fonctionne avec des exemples spécifiques:
Nous composons et résolvons l'équation:
Une petite note pour le dernier exemple. Comment s'assurer qu'un nombre n'est pas le degré exact d'un autre nombre? Très simple - il suffit de le factoriser en facteurs simples. S'il y a au moins deux facteurs différents dans l'expansion, le nombre n'est pas une puissance exacte.
8 \u003d 2 · 2 · 2 \u003d 2 3 - le degré exact, car il n'y a qu'un seul facteur; Nous notons également que les nombres premiers sont toujours des degrés exacts d’eux-mêmes. Logarithme décimalCertains logarithmes sont si courants qu’ils ont un nom et une désignation spéciaux.
Par exemple, lg 10 \u003d 1; lg 100 \u003d 2; lg 1000 \u003d 3 - etc. A partir de maintenant, quand une phrase comme "Find lg 0.01" est trouvée dans un manuel, sachez qu'il ne s'agit pas d'une faute de frappe. C'est le logarithme décimal. Cependant, si vous n'êtes pas familier avec cette notation, vous pouvez toujours la récrire: Tout ce qui est vrai pour les logarithmes ordinaires l'est également pour le nombre décimal. Logarithme naturelIl existe un autre logarithme qui a sa propre notation. En un sens, c'est encore plus important que le nombre décimal. C'est un logarithme naturel.
Beaucoup demanderont: quel est le nombre e? C'est un nombre irrationnel, son sens exact ne peut pas être trouvé et écrit. Je n'en donnerai que les premiers chiffres: Nous n'entrerons pas dans les détails de ce nombre et de la raison pour laquelle il est nécessaire. Rappelez-vous simplement que e est la base du logarithme naturel: Ainsi, ln e \u003d 1; ln e 2 \u003d 2; l e 16 \u003d 16 - etc. D'autre part, ln 2 est un nombre irrationnel. En général, le logarithme naturel de tout nombre rationnel est irrationnel. Sauf, bien sûr, les unités: ln 1 \u003d 0. Pour les logarithmes naturels, toutes les règles qui sont vraies pour les logarithmes ordinaires sont vraies. Voir aussi: Logarithme Propriétés du logarithme (degré du logarithme).Comment représenter un nombre sous forme de logarithme? Nous utilisons la définition du logarithme. Le logarithme est un indicateur du degré auquel la base doit être surélevée pour obtenir le nombre sous le signe du logarithme. Ainsi, pour représenter un certain nombre c en tant que logarithme sur la base de a, il faut placer une puissance sous le signe du logarithme avec la même base que la base du logarithme et écrire le nombre c dans l'exposant: Sous la forme d'un logarithme, vous pouvez imaginer absolument n'importe quel nombre - positif, négatif, entier, fractionnaire, rationnel, irrationnel:
Afin de ne pas confondre a et c dans des conditions de contrôle ou d’examen stressantes, vous pouvez utiliser cette règle pour vous rappeler: ce qui est en bas descend, ce qui est en haut monte. Par exemple, vous devez représenter le nombre 2 sous forme de logarithme en base 3. Nous avons deux nombres - 2 et 3. Ces nombres sont la base et l'exposant, que nous écrivons sous le signe du logarithme. Il reste à déterminer lequel de ces nombres doit être inscrit à la base du degré et lequel à la place de l'indicateur. La base 3 de l'entrée du logarithme est en bas, ce qui signifie que lorsque nous représentons les deux sous la forme d'un logarithme à la base 3, 3, nous écrivons également à la base. 2 se situe au-dessus du triple. Et dans l'enregistrement des diplômes, nous écrivons le dieux au-dessus du triple, c'est-à-dire dans l'exposant: Logarithmes Niveau d'entrée.LogarithmesLogarithme nombre positif b sur la base de unoù a\u003e 0, a ≠ 1est appelé l'exposant auquel le nombre doit être élevé unpour obtenir b. Logarithme Définition peut se résumer comme suit: Cette égalité est valable pour b\u003e 0, a\u003e 0, a ≠ 1. On l'appelle habituellement identité logarithmique. Logarithme Propriétés: Logarithme du produit: Logarithme du quotient de division: Remplacement de la base du logarithme:
Logarithme de degré: Logarithme Racine:
Logarithme de puissance:
Logarithmes décimaux et naturels.Logarithme décimal les numéros appellent le logarithme en base 10 de ce numéro et écrivent & nbsp lg b Autres notes sur l'algèbre et la géométrie Propriétés de base des logarithmesPropriétés de base des logarithmesLes logarithmes, comme tous les nombres, peuvent être ajoutés, soustraits et convertis de toutes les manières. Mais comme les logarithmes ne sont pas des nombres tout à fait ordinaires, il existe des règles appelées propriétés de base. Vous devez connaître ces règles - aucun problème logarithmique sérieux ne peut être résolu sans elles. En outre, ils sont très peu nombreux - tout peut être appris en une journée. Alors commençons. Addition et soustraction de logarithmeConsidérez deux logarithmes de même base: enregistrez un x et enregistrez un y. Ensuite, ils peuvent être ajoutés et soustraits, de plus:
Ainsi, la somme des logarithmes est égale au logarithme du produit et la différence correspond au logarithme du quotient. S'il vous plaît noter: le point clé ici est motifs égaux. Si les motifs sont différents, ces règles ne fonctionnent pas! Ces formules aideront à calculer l'expression logarithmique même lorsque ses parties individuelles ne sont pas comptées (voir la leçon "Qu'est-ce que le logarithme"). Regardez les exemples et voyez:
Puisque les bases des logarithmes sont les mêmes, nous utilisons la formule de somme:
Les bases sont les mêmes, nous utilisons la formule de différence:
Encore une fois, les bases sont les mêmes, nous avons donc: Comme vous pouvez le constater, les expressions d'origine sont constituées de «mauvais» logarithmes non comptabilisés séparément. Mais après les transformations, des nombres tout à fait normaux sont obtenus. Sur ce fait, de nombreux tests sont construits. Oui, le contrôle - de telles expressions très sérieuses (parfois - presque inchangées) sont proposées à l'examen. Suppression de l'exposant du logarithmeMaintenant, compliquons un peu la tâche. Que se passe-t-il s'il y a un degré dans la base ou l'argument du logarithme? Ensuite, un indicateur de ce degré peut être extrait du logarithme selon les règles suivantes: Il est facile de voir que la dernière règle suit leurs deux premières. Mais il vaut mieux ne pas l’oublier: dans certains cas, cela réduira considérablement la quantité de calculs. Bien sûr, toutes ces règles ont un sens lorsque vous observez le logarithme DLD: a\u003e 0, a ≠ 1, x\u003e 0. Et aussi: apprendre à appliquer toutes les formules non seulement de gauche à droite, mais aussi l’inverse, c.-à-d. vous pouvez entrer les nombres devant le logarithme dans le logarithme lui-même. Comment résoudre les logarithmesC'est ce qui est le plus souvent requis.
Supprimons le degré dans l'argument par la première formule:
Notez que le dénominateur est le logarithme, dont la base et l'argument sont des degrés exacts: 16 \u003d 2 4; 49 \u003d 7 2. Nous avons: Je pense que le dernier exemple doit être clarifié. Où les logarithmes ont-ils disparu? Jusqu'au tout dernier moment, nous travaillons uniquement avec le dénominateur. Ils y ont présenté la base et l'argumentation du logarithme sous forme de diplômes et ont réalisé des indicateurs - ils ont reçu une fraction de «trois étages». Regardons maintenant la fraction principale. Le numérateur et le dénominateur ont le même numéro: log 2 7. Puisque log 2 7 0, nous pouvons réduire la fraction - 2/4 resteront dans le dénominateur. Selon les règles de l'arithmétique, les quatre peuvent être transférés au numérateur, ce qui a été fait. Le résultat fut la réponse: 2. Transition vers une nouvelle fondationEn parlant des règles d’addition et de soustraction des logarithmes, j’ai particulièrement insisté sur le fait qu’ils ne fonctionnent que sur les mêmes bases. Mais que se passe-t-il si les motifs sont différents? Et si ce ne sont pas des puissances exactes du même nombre? Des formules pour la transition vers une nouvelle fondation viennent à la rescousse. Nous les formulons sous la forme d'un théorème:
De la deuxième formule, il est possible d’échanger la base et l’argument du logarithme, mais en même temps l’expression entière est «retournée», c.-à-d. le logarithme est au dénominateur. Ces formules sont rarement trouvées en termes numériques ordinaires. Il est possible d'évaluer leur utilité uniquement lors de la résolution d'équations et d'inégalités logarithmiques. Cependant, certaines tâches ne peuvent être résolues que par le passage à une nouvelle fondation. Considérez quelques-uns de ceux-ci:
Notez que les arguments des deux logarithmes contiennent des degrés exacts. Nous sortons les indicateurs: log 5 16 \u003d log 5 2 4 \u003d 4 log 5 2; log 2 25 \u003d log 2 5 2 \u003d 2 log 2 5; Et maintenant, "retournez" le deuxième logarithme: Puisque le produit ne change pas par rapport à la permutation des facteurs, nous avons tranquillement multiplié les quatre et les deux, puis déterminé les logarithmes.
La base et l'argument du premier logarithme sont des degrés exacts. Nous écrivons ceci et nous débarrassons des indicateurs: Nous allons maintenant nous débarrasser du logarithme décimal pour passer à une nouvelle base: Identité logarithmique de baseDans le processus de résolution, il est souvent nécessaire de représenter le nombre sous forme de logarithme pour une base donnée. Dans ce cas, les formules nous aideront: Dans le premier cas, le nombre n devient un indicateur du degré dans l'argument. Le nombre n peut être absolument n'importe quoi, parce que c'est juste la valeur du logarithme. La deuxième formule est en réalité une définition reformulée. Cela s'appelle: En fait, que se passe-t-il si le nombre b est élevé à un point tel que le nombre b de ce degré donne le nombre a? C'est vrai: c'est le nombre même a. Lisez attentivement ce paragraphe à nouveau - beaucoup sur "accrocher". À l'instar des formules de transition vers une nouvelle fondation, l'identité logarithmique de base est parfois la seule solution possible.
Notez que log 25 64 \u003d log 5 8 - vient de sortir le carré de la base et l’argument du logarithme. Étant donné les règles de multiplication des degrés avec la même base, on obtient: Si quelqu'un n'était pas au courant, c'était un véritable défi de l'examen Unité logarithmique et zéro logarithmiqueEn conclusion, je donnerai deux identités que l’on peut difficilement appeler des propriétés - c’est plutôt des conséquences de la définition du logarithme. On les retrouve constamment dans les tâches et, étonnamment, créent des problèmes même pour les étudiants «avancés».
C'est toutes les propriétés. Assurez-vous de les appliquer dans la pratique! Téléchargez la feuille de triche au début de la leçon, imprimez-la et résolvez les problèmes. |
Populaire:
Nouveau
- Escalier de bricolage au grenier: faites un escalier au grenier avec des instructions de photo
- Garage à ossature bois - Construction sécurisée à faire soi-même
- Pose de sols en bricolage - instructions pas à pas avec photo
- Caractéristiques du système de chevrons d'une maison en bois et en pierre
- Faites-le vous-même facilement
- Table faite maison en planches
- Construction de maisons en bois profilé
- Quelle table puis-je créer avec des mains inutiles?
- Faire une chaise en bois
- Comment niveler un sol sous une dalle Comment niveler un sol sous une dalle